Угол между скрещивающимися прямыми и расстояние между ними. Расстояние от точки до плоскости и от прямой до параллельной ей плоскости
Скрещивающиеся прямые не параллельны и не пересекаются. Они лежат в параллельных плоскостях, и поместить их в одну плоскость невозможно.
Часто в задачах требуется найти угол между скрещивающимися прямыми. Как это сделать?
Угол между прямыми, лежащими в одной плоскости, найти нетрудно. Можно измерить его транспортиром. Можно найти из какого-нибудь треугольника по теореме синусов или косинусов.
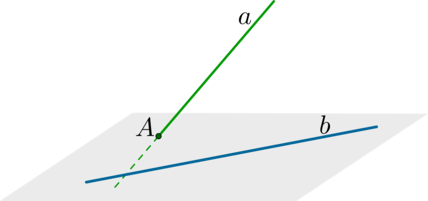
Пусть скрещивающиеся прямые a и b лежат в параллельных плоскостях α и β . Проведем в плоскости β прямую с, параллельную прямой а. Угол между прямыми а и b равен углу между прямыми b и с.
Можно сказать, что угол между скрещивающимися прямыми — это угол между параллельными им прямыми, лежащими в одной плоскости.
Расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра.
Другими словами, расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, в которых они лежат.
Дадим еще два полезных определения.
Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из точки на плоскость.
Расстояние от прямой до параллельной ей плоскости — длина перпендикуляра, опущенного на плоскость из любой точки этой прямой.
Заметим, что расстояние от точки до плоскости или угол между скрещивающимися прямыми иногда проще найти с помощью координатно-векторного метода.
Читаем дальше: Теорема о трех перпендикулярах.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Угол между скрещивающимися прямыми и расстояние между ними. Расстояние от точки до плоскости и от прямой до параллельной ей плоскости» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
07.05.2023
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Нахождение угла между прямыми
(blacktriangleright) Угол между прямыми – это такой угол (alpha), что (0leqslant alphaleqslant 90^circ).
(blacktriangleright) В пространстве существует 4 типа взаимного расположения прямых: совпадают, пересекаются, параллельны, скрещиваются.
(blacktriangleright) Скрещивающиеся прямые – это прямые, через которые нельзя провести одну плоскость.
Признак скрещивающихся прямых: если первая прямая пересекает плоскость, в которой лежит вторая прямая, в точке, не лежащей на второй прямой, то такие прямые скрещиваются.
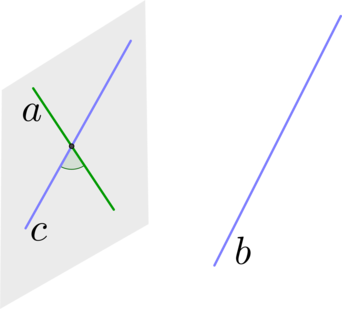
(blacktriangleright) Порядок нахождения угла между скрещивающимися прямыми:
Шаг 1: через одну из двух прямых (a) провести плоскость, параллельную второй прямой (b) (напомним признак: прямая параллельна плоскости, если она параллельна какой-нибудь прямой из этой плоскости);
Шаг 2: в этой плоскости найти прямую (c), параллельную прямой (b);
Шаг 3: тогда угол между прямыми (a) и (b) будет равен углу между прямыми (a) и (c).
Задание
1
#934
Уровень задания: Равен ЕГЭ
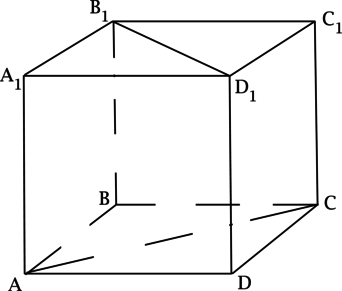
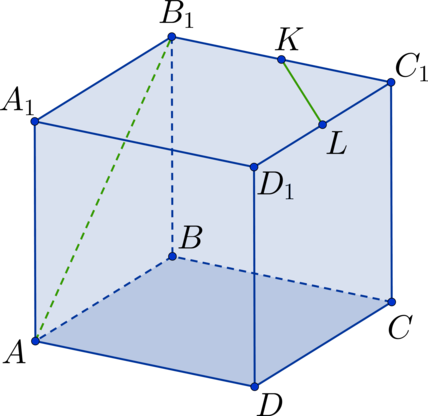
(ABCDA_1B_1C_1D_1) – куб. Найдите угол между прямыми, содержащими отрезки (AC) и (B_1D_1). Ответ дайте в градусах.
Прямая (BD) параллельна прямой (B_1D_1), тогда угол между (AC) и (B_1D_1) равен углу между (AC) и (BD), но (AC) и (BD) – диагонали квадрата, тогда они пересекаются под прямым углом, следовательно ответ (90^{circ}).
Ответ: 90
Задание
2
#2847
Уровень задания: Равен ЕГЭ
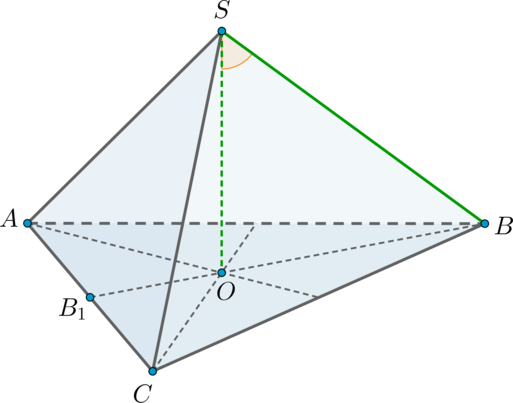
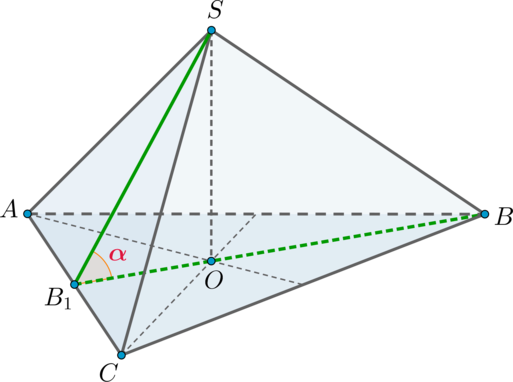
Дана правильная треугольная пирамида (SABC) с вершиной (S). Найдите угол между высотой пирамиды и ребром (SB), если высота пирамиды равна (2sqrt3), а сторона основания пирамиды равна (6). Ответ дайте в градусах.
Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, высота (SO) падает в точку пересечения медиан основания.
Пусть (BB_1) – медиана, а значит, и высота. По теореме Пифагора [BB_1=sqrt{BC^2-B_1C^2}=3sqrt3 quadRightarrowquad BO=dfrac23BB_1=2sqrt3,] так как медианы точкой пересечения делятся в отношении (2:1), считая от вершины.
Следовательно, прямоугольный (triangle SOB) является равнобедренным ((SO=BO=2sqrt3)), значит, острые углы равны по (45^circ).
Ответ: 45
Задание
3
#933
Уровень задания: Равен ЕГЭ
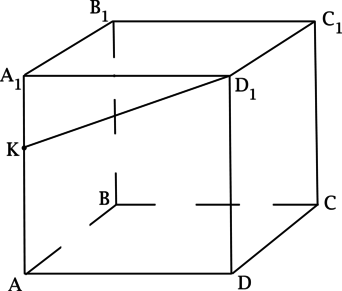
(ABCDA_1B_1C_1D_1) – куб. Точка (K) лежит на ребре (AA_1). Найдите угол между прямыми, содержащими отрезки (D_1K) и (AB). Ответ дайте в градусах.
Так как (ABCDA_1B_1C_1D_1) – куб, то (AB) перпендикулярен плоскости ((ADD_1)), тогда (AB) перпендикулярен любой прямой, лежащей в плоскости ((ADD_1)), следовательно, угол между прямыми, содержащими отрезки (D_1K) и (AB) равен (90^{circ}).
Ответ: 90
Задание
4
#2845
Уровень задания: Равен ЕГЭ
Дан правильный тетраэдр (SABC). Найдите квадрат тангенса угла между высотой грани (SAC), опущенной из вершины (S), и высотой грани (ABC), опущенной из вершины (B).
Пусть (SB_1) – высота грани (SAC). Так как тетраэдр правильный, то все его грани – равные правильные треугольники, то есть (SB_1) также является и медианой, значит, (AB_1=B_1C). Также у правильного тетраэдра высота из каждой вершины падает в точку пересечения медиан (биссектрис, высот) противоположной грани. Следовательно, если (SO) – высота, то (O) – точка пересечения медиан треугольника (ABC), а значит и высот, так как (triangle ABC) правильный. Следовательно, (BB_1) — медиана и высота.
Таким образом, необходимо найти (mathrm{tg}^2angle (SB_1,
BB_1)).
Пусть (a) – ребро тетраэдра. Тогда (BC=a, B_1C=0,5a), следовательно, по теореме Пифагора [BB_1=sqrt{BC^2-B_1C^2}=dfrac{sqrt3}2a] Так как (O) – точка пересечения медиан, а медианы точкой пересечения делятся в отношении (2:1), считая от вершины, то (OB_1=frac13BB_1=frac{sqrt3}6a).
Так как (triangle ABC=triangle SAC), то (SB_1=BB_1). Следовательно, из прямоугольного (triangle SB_1O): [cos
alpha=dfrac{OB_1}{SB_1}=dfrac13 quadRightarrowquad sin alpha
=sqrt{1-cos^2alpha}=dfrac{2sqrt2}3 quadRightarrowquad
mathrm{tg}^2alpha=(2sqrt2)^2=8.]
Ответ: 8
Задание
5
#1846
Уровень задания: Равен ЕГЭ
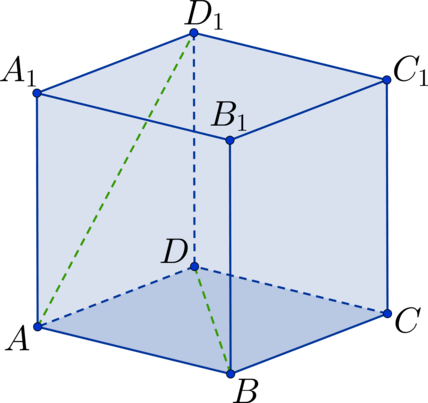
Дан куб (ABCDA_1B_1C_1D_1). Найдите угол между прямыми (AD_1) и (BD). Ответ дайте в градусах.
Заметим, что (BC_1 || AD_1), тогда рассмотрим треугольник (triangle BDC_1), в котором необходимо определить (angle DBC_1). Он состоит из диагоналей соответствующих квадратов. Так как квадраты между собой равны, то равны и диагонали (Rightarrow) (triangle BDC_1) – равносторонний треугольник (Rightarrow) (angle DBC_1 = 60^circ).
Ответ: 60
Задание
6
#1847
Уровень задания: Равен ЕГЭ
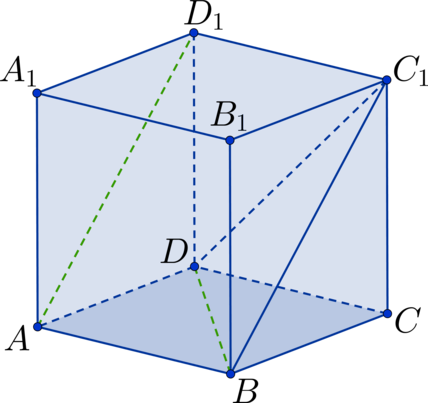
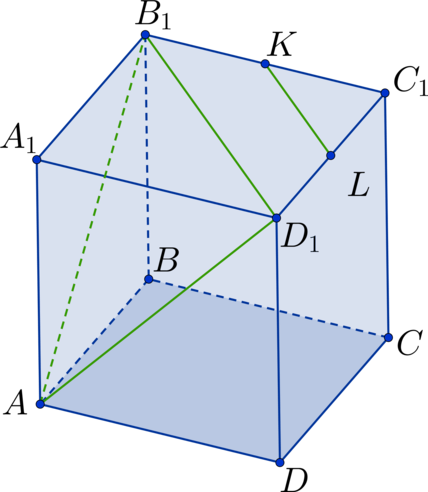
Дан куб (ABCDA_1B_1C_1D_1). Точка (K) – середина стороны (B_1C_1), а точка (L) – середина стороны (C_1D_1). Найдите угол между прямыми (AB_1) и (KL). Ответ дайте в градусах.
Проведем диагональ (B_1D_1) в квадрате (A_1B_1C_1D_1). Тогда (KL) – средняя линия в (triangle B_1C_1D_1) (Rightarrow) (KL || B_1D_1) (Rightarrow) (angle AB_1D_1) – искомый угол. Рассмотрим (triangle AB_1D_1). Он состоит из диагоналей соответствующих квадратов (Rightarrow) треугольник является равносторонним (Rightarrow) (angle AB_1D_1 = 60^circ).
Ответ: 60
Задание
7
#2846
Уровень задания: Сложнее ЕГЭ
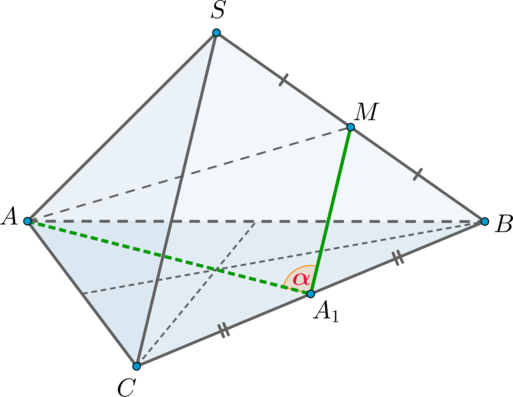
Дана правильная треугольная пирамида (SABC) с вершиной (S). Найдите косинус угла между высотой основания (AA_1) и ребром (SC), если сторона основания равна (sqrt3), а боковое ребро равно (2).
Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, (AA_1) также является и медианой.
Заметим, что прямые (AA_1) и (SC) скрещиваются. Проведем (A_1Mparallel SC), следовательно, (angle (AA_1, SC)=angle (AA_1,
A_1M)).
Так как (A_1Mparallel SC) и (A_1) – середина (BC), то (M) – середина (SB). Следовательно, (A_1M) – средняя линия и [A_1M=frac12SC=1.] По теореме Пифагора из (triangle ABA_1): [AA_1=sqrt{AB^2-A_1B^2}=dfrac32.] Медиану (AM) из (triangle SAB) можно найти по формуле медианы: [AM^2=dfrac{2AS^2+2AB^2-SB^2}4=dfrac52.] Следовательно, по теореме косинусов из (triangle AA_1M): [cos alpha=dfrac{AA_1^2+A_1M^2-AM^2}{2AA_1cdot A_1M}=dfrac14=0,25.]
Ответ: 0,25
Каждому школьнику, который готовится к ЕГЭ по математике, будет полезно повторить тему «Нахождение угла между прямыми». Как показывает статистика, при сдаче аттестационного испытания задачи по данному разделу стереометрии вызывают трудности у большого количества учащихся. При этом задания, требующие найти угол между прямыми, встречаются в ЕГЭ как базового, так и профильного уровня. Это значит, что уметь их решать должны все.
Основные моменты
В пространстве существует 4 типа взаимного расположения прямых. Они могут совпадать, пересекаться, быть параллельными или скрещивающимися. Угол между ними может быть острым или прямым.
Для нахождения угла между прямыми в ЕГЭ или, например, в решении задач по теореме о трех перпендикулярах, школьники Москвы и других городов могут использовать несколько способов решения задач по данному разделу стереометрии. Выполнить задание можно путем классических построений. Для этого стоит выучить основные аксиомы и теоремы стереометрии. Школьнику нужно уметь логически выстраивать рассуждение и создавать чертежи, для того чтобы привести задание к планиметрической задаче.
Также можно использовать векторно-координатный метод, применяя простые формулы, правила и алгоритмы. Главное в этом случае — правильно выполнить все вычисления. Отточить свои навыки решения задач по стереометрии и другим разделам школьного курса вам поможет образовательный проект «Школково».

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Содержание
- Определение угла между скрещивающимися прямыми
- Как найти угол между скрещивающимися прямыми
- Примеры задач на вычисления угла между прямыми на плоскости
- Пример решения задачи
- Угол между прямыми в пространстве
- Определение угла между прямыми
- Условие параллельности прямых
Определение угла между скрещивающимися прямыми
Пересечение двух линий на плоскости указывает на то, что у них есть общая точка. Он также является центром их пересечения и делит их на лучи.
Балки образуют четыре неразвитых угла. Зная размер одного из них, можно рассчитать стоимость остальных. Можно с уверенностью сказать, что если один из них прямоугольный, то остальные три эквивалентны, а линии будут перпендикулярными.
Рис. 1 Графическое изображение пересечения прямых
Как найти угол между скрещивающимися прямыми
Чтобы определить угол между двумя пересекающимися линиями, можно воспользоваться специальным онлайн-калькулятором или применить традиционный математический алгоритм расчетов.
Предположим, что две бесконечные прямые заданы общими уравнениями:
A1 + B1 + C1 = 0
A2 + B2 + C2 = 0
Искомое значение следует обозначить как φ. Числовое значение угла измеряется в градусах от 0 до 90 °, то есть угол будет острым или прямоугольным. Необходимо ввести еще одно понятие: угол между векторами нормалей этих прямых:
Если он меньше или равен 90 °, сам желаемый угол будет соответствовать его измерению в градусах. Если оно больше 90 °, для расчета φ необходимо применить известную формулу:
= 1800.
Для обоих вариантов утверждение, что cos φ = lcos ψl, является достоверным. После проведения необходимых расчетов можно рассчитать желаемое значение:
Если по условию задачи существует некий прямоугольный треугольник с известными сторонами, расположенный на двух прямых, то для вычисления угла между этими прямыми необходимо знать синус, тангенс и косинус искомого угла.
Чтобы найти значение синуса угла, образованного пересечением двух прямых, вычислите модуль косинуса этого угла, образованного направляющими векторами этих прямых.
Примеры задач на вычисления угла между прямыми на плоскости
- Пример 1. Найдите угол между прямыми y = 2x — 1 и y = -3x + 1.
Решение: мы используем формулу для вычисления угла между линиями, заданными уравнениями с наклоном:
tg γ = k1 — k21 + k1 k2 = 2 — (-3) 1 + 2 (-3) = 5-5 = 1
Ответ: γ = 45°
- Пример 2. Найдите угол между прямыми y = 2x — 1 и x = 2t + 1y = t.
Решение: мы используем формулу для вычисления угла между линиями, векторы направления которого известны.
Для первой строки вектор направления {1; 2}, для второй линии вектор направления {2; 1}
cos = | 1 2 + 2 1 | 12 + 22 22 + 12 = 45 5 = 0,8
Ответ: φ ≈ 36,87°
- Пример 3 Найдите угол между прямыми 2x + 3y = 0 и x — 23 = y4.
Решение: чтобы решить эту проблему, вы можете найти векторы направления и вычислить угол, используя векторы направления, или преобразовать уравнения в уравнения уклона и вычислить угол, используя уклоны.
Преобразуем существующие уравнения в уравнения с наклоном.
2x + 3y = 0 => y = -23x (k1 = -23)
х — 23 = у4 => у = 43 х — 83 (k2 = 43)
tg γ = k1 — k21 + k1 k2 = -23 — 431 + (-23) 43 = -631 — 89 = 18
Ответ: γ ≈ 86,82°
Пример решения задачи
На школьных уроках геометрии для решения в классе часто предлагают следующий тип задач, чтобы найти угол между двумя линиями.
Ниже приведен алгоритм решения задачи, в которой бесконечные прямые на плоскости задаются уравнениями общего вида, в которых присутствует наклон.
Обозначим прямые как (L1) и (L2). Каждый из них задается уравнением следующего вида:
A1x + B1y + C1 = 0;
A2x + B2y + C2 = 0;
Зная, что нормальные векторы каждого из них имеют вид:
Суть задачи сводится к вычислению угла, образованного векторами нормалей.
Мы используем определение точечного произведения векторов:
и согласованное выражение их длин, а также их скалярное произведение:
В практических задачах математики часто требуется найти не сам угол между пересекающимися линиями, а уравнять их все при условии, что линии пересекаются друг с другом.
Итак, если прямые задаются уравнениями общего вида с коэффициентами, то
Последнее равенство часто называют уравнением биссектрис углов, образованных в результате пересечения прямых. Понятие «биссектриса» в геометрии — это своего рода геометрическое место точек, находящихся на одинаковом расстоянии от сторон угла.
Если прямые задаются уравнениями, включающими наклон, который определяется тангенсом угла, довольно просто найти значение углов, образующихся при их пересечении:
Рис. 2 Углы, образованные пересечением двух прямых на плоскости
tan α = k1;
tan = k2;
где k1 и k2 — одинаковые наклоны.
Поэтому для расчета стоимости следует применять формулы:
= α — β
tan γ = tan (α — β)
Решение очевидно:
Угол между прямыми в пространстве
Определение угла между прямыми
Прямые L1 и L2 в пространстве задаются каноническими уравнениями
 , , |
(2.1) |
а также
 , , |
(2.2) |
где q1 = (m1, p1, l1) — вектор направления прямой L1, а q2 = (m2, p2, l2) — вектор направления прямой L2.
Проблема определения угла между прямыми L1 и L2 сводится к задаче определения угла между направляющими векторами q1 и q2 .
Из определения скалярного произведения:
 , , |
(2.3) |
где | q1 | и | q2 | модулей векторов направлений q1 и q2 соответственно — угол между векторами q1 и q2.
Из выражения (2.3) получаем:
Следовательно, из формулы (2.4) можно найти угол между прямыми L1 и L2. Если найденный угол больше 90 °, можно найти минимальный угол между прямыми L1 и L2: φ1 = 180-φ.
Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.
- Пример 1. Определить угол между прямыми линиями
 . . |
(2.5) |
а также
 |
(2,6) |
Решение. Прямая (2.5) имеет вектор направления q1 = (m1, p1, l1) = (1, 1, 3), а прямая (2.6) — q2 = (m2, p2, l2) = (- 3, 1, 2). Для определения угла между линиями (2.5) и (2.6) подставим значения m1, p1, l1, m2, p2, l2 в (2.4):
 . . |
Мы упрощаем и решаем:
 . . |
Найдите угол φ
 |
Отвечать.
Угол между линиями равен:
 |
Условие параллельности прямых
Условие параллельности линий эквивалентно условию коллинеарности направляющих векторов q1 и q2, т.е соответствующие координаты этих векторов пропорциональны, не говоря уже о
| m1 = αm2, p1 = αp2, l1 = αl2 | (2,7) |
где α — число. Тогда соответствующие координаты векторов q1 и q2 пропорциональны, а значит, прямые L1 и L2 параллельны.
Условие параллельности линий можно представить следующим образом:
 |
(2,8) |
Обратите внимание, что любая пропорция
его следует понимать как равенство ad = bc.
- Пример 2. Определите, параллельны ли линии

а также

Решение. Прямая (2.9) имеет вектор направления q1 = (m1, p1, l1) = (3, 2, 4), а прямая (2.10) — q2 = (m2, p2, l2) = (6, 4, 8). Следовательно



Равенство (2.8) (или (2.7)) выполняется, поэтому прямые (2.9) и (2.10) параллельны.
Отвечать. Прямые (2.9) и (2.10) параллельны.
- Пример 3. Определите, параллельны ли линии

а также

Решение. Прямая (2.9) имеет вектор направления q1 = (m1, p1, l1) = (1, 2, 0), а прямая (2.10) — q2 = (m2, p2, l2) = (2, 4, 0). Подставляя значения m1, p1, l1, m2, p2, l2 в (2.8), получаем

Выражение (2.13) следует понимать следующим образом:
Как видно из (2.14), условия (2.13) выполнены. Следовательно, прямые (2.11) и (2.12) параллельны.
Отвечать. Прямые (2.11) и (2.12) параллельны.