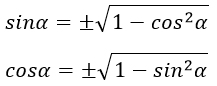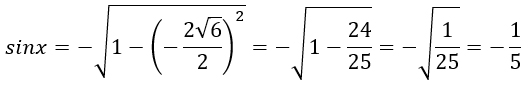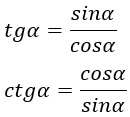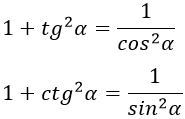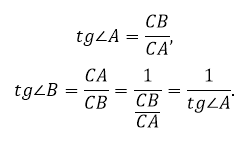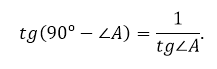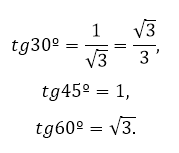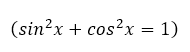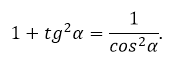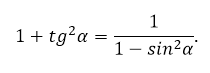Как найти тангенс по основному тригонометрическому тождеству

Основное тригонометрическое тождество

12 ноября 2011

Это последний и самый главный урок, необходимый для решения задач B11. Мы уже знаем, как переводить углы из радианной меры в градусную (см. урок «Радианная и градусная мера угла»), а также умеем определять знак тригонометрической функции, ориентируясь по координатным четвертям (см. урок «Знаки тригонометрических функций»).

Дело осталось за малым: вычислить значение самой функции — то самое число, которое записывается в ответ. Здесь на помощь приходит основное тригонометрическое тождество.

Основное тригонометрическое тождество. Для любого угла α верно утверждение:

sin² α + cos² α = 1.

Эта формула связывает синус и косинус одного угла. Теперь, зная синус, мы легко найдем косинус — и наоборот. Достаточно извлечь квадратный корень:

Обратите внимание на знак «±» перед корнями. Дело в том, что из основного тригонометрического тождества непонятно, каким был исходный синус и косинус: положительным или отрицательным. Ведь возведение в квадрат — четная функция, которая «сжигает» все минусы (если они были).

Именно поэтому во всех задачах B11, которые встречаются в ЕГЭ по математике, обязательно есть дополнительные условия, которые помогают избавиться от неопределенности со знаками. Обычно это указание на координатную четверть, по которой можно определить знак.

Внимательный читатель наверняка спросит: «А как быть с тангенсом и котангенсом?» Напрямую вычислить эти функции из приведенных выше формул нельзя. Однако существуют важные следствия из основного тригонометрического тождества, которые уже содержат тангенсы и котангенсы. А именно:

Важное следствие: для любого угла α можно переписать основное тригонометрическое тождество следующим образом:

Эти уравнения легко выводятся из основного тождества — достаточно разделить обе стороны на cos² α (для получения тангенса) или на sin² α (для котангенса).

Рассмотрим все это на конкретных примерах. Ниже приведены настоящие задачи B11, которые взяты из пробных вариантов ЕГЭ по математике 2012.

Задача. Найдите sin α, если известно следующее:

Нам известен косинус, но неизвестен синус. Основное тригонометрическое тождество (в «чистом» виде) связывает как раз эти функции, поэтому будем работать с ним. Имеем:

sin² α + cos² α = 1 ⇒ sin² α + 99/100 = 1 ⇒ sin² α = 1/100 ⇒ sin α = ±1/10 = ±0,1.

Для решения задачи осталось найти знак синуса. Поскольку угол α ∈ (π/2; π), то в градусной мере это записывается так: α ∈ (90°; 180°).

Следовательно, угол α лежит во II координатной четверти — все синусы там положительны. Поэтому sin α = 0,1.

Задача. Найдите cos α, если известно следующее:

Итак, нам известен синус, а надо найти косинус. Обе эти функции есть в основном тригонометрическом тождестве. Подставляем:

sin² α + cos² α = 1 ⇒ 3/4 + cos² α = 1 ⇒ cos² α = 1/4 ⇒ cos α = ±1/2 = ±0,5.

Осталось разобраться со знаком перед дробью. Что выбрать: плюс или минус? По условию, угол α принадлежит промежутку (π 3π/2). Переведем углы из радианной меры в градусную — получим: α ∈ (180°; 270°).

Очевидно, это III координатная четверть, где все косинусы отрицательны. Поэтому cos α = −0,5.

Задача. Найдите tg α, если известно следующее:

Тангенс и косинус связаны уравнением, следующим из основного тригонометрического тождества:

Получаем: tg α = ±3. Знак тангенса определяем по углу α. Известно, что α ∈ (3π/2; 2π). Переведем углы из радианной меры в градусную — получим α ∈ (270°; 360°).

Очевидно, это IV координатная четверть, где все тангенсы отрицательны. Поэтому tg α = −3.

Задача. Найдите cos α, если известно следующее:

Снова известен синус и неизвестен косинус. Запишем основное тригонометрическое тождество:

sin² α + cos² α = 1 ⇒ 0,64 + cos² α = 1 ⇒ cos² α = 0,36 ⇒ cos α = ±0,6.

Знак определяем по углу. Имеем: α ∈ (3π/2; 2π). Переведем углы из градусной меры в радианную: α ∈ (270°; 360°) — это IV координатная четверть, косинусы там положительны. Следовательно, cos α = 0,6.

Задача. Найдите sin α, если известно следующее:

Запишем формулу, которая следует из основного тригонометрического тождества и напрямую связывает синус и котангенс:

Отсюда получаем, что sin² α = 1/25, т.е. sin α = ±1/5 = ±0,2. Известно, что угол α ∈ (0; π/2). В градусной мере это записывается так: α ∈ (0°; 90°) — I координатная четверть.

Итак, угол находится в I координатной четверти — все тригонометрические функции там положительны, поэтому sin α = 0,2.

Смотрите также:

1. Как формулы приведения работают в задаче B11
2. Тест к уроку «Знаки тригонометрических функций» (1 вариант)
3. Тест к параграфу «Что такое логарифм» (легкий)
4. Решение задач B12: №440—447
5. Задачи про температуру и энергию звезд
6. Задача B4 про шерсть и свитер

Основное тригонометрическое тождество

Классическое основное тригонометрическое тождество.

Перед тем, как переходить к различным тригонометрическим ужасам, в школе разбирают основное тригонометрическое тождество, благодаря которому, можно находить синус угла, зная его косинус, и наоборот.

Само тождество выглядит весьма мило:

Из этой формулы выразим синус и косинус:

Стоит обратить особое внимание на знаки «±». Почему их важно не забыть?

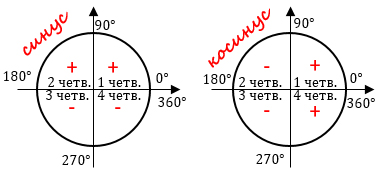
Посмотри на картинку ниже.

Если угол находится в первой четверти, то знаки его синуса и косинуса положительны.

Если угол находится во второй четверти, то знак его синуса положительный, а знак косинуса отрицательный.

Если угол находится в третьей четверти, то знаки его синуса и косинуса отрицательны.

Если угол находится в четвертой четверти, то знак его синуса отрицательный, а знак косинуса положительный.

Давай попробуем решить парочку примеров.

Задание 1.

Найдите sinx, если cosx = и 180° < x < 270°.

Угол х находится в третьей четверти, значит синус этого угла будет отрицательный и при выражении синуса из основного тригонометрического тождества мы должны перед корнем поставить знак минус.

Переводим дробь в десятичную.

Ответ: -0,2.

Задание 2.

Найдите cosx, если sinx = 0.6 и 90° < x < 180°.

Определяем знак косинуса. Угол х находится во второй четверти, значит значение косинуса будет отрицательным (см. окружности выше).

Тогда

Ответ: -0,8.

Другие полезные тождества.

Еще нельзя не упомянуть другие тригонометрические тождества, которые в своей сущности также являются основными.

1. Базовые формулы.

2. Связь между тангенсом и котангенсом.

3. Следствия из основного тригонометрического тождества.

Эти формулы получаются путем деления обеих частей равенства на косинус (первая формула) и на синус (вторая формула). 

Рекомендую к изучению: статья о синусе, косинусе, тангенсе и котангенсе.

Успехов в учебе!

Для удобства сразу же приведем таблицу с всеми тригонометрическими тождествами. Всегда удобно открыть формулы в одном месте, выбрать нужную и решить пример. После таблицы мы по отдельности рассмотрим каждую тригонометрическую формулу: обсудим ее вывод и порешаем примеры.

1. Основное тригонометрическое тождество:
   $$sin(alpha)^2+cos(alpha)^2=1;$$
2. Определение тангенса и котангенса через синус и косинус:
   $$tg(alpha)=frac{sin(alpha)}{cos(alpha)};$$
   $$ctg(alpha)=frac{cos(alpha)}{sin(alpha)};$$
3. Cвязь тангенса и котангенса:
   $$tg(alpha)=frac{1}{ctg(alpha)};$$
   $$tg(alpha)*ctg(alpha)=1;$$
4. Тангенс через косинус. Котангенс через синус:
   $$tg(alpha)^2+1=frac{1}{cos(alpha)^2};$$
   $$ctg(alpha)^2+1=frac{1}{sin(alpha)^2};$$
5. Синус суммы и разности:
   $$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
   $$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
6. Косинус суммы и разности:
   $$cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);$$
   $$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
7. Тангенс суммы и разности:
   $$tg(alpha+beta)=frac{tg(alpha)+tg(beta)}{1-tg(alpha)*tg(beta)};$$
   $$tg(alpha-beta)=frac{tg(alpha)-tg(beta)}{1+tg(alpha)*tg(beta)};$$
8. Котангенс суммы и разности:
   $$сtg(alpha+beta)=frac{-1+сtg(alpha)*ctg(beta)}{ctg(alpha)+ctg(beta)};$$
   $$сtg(alpha-beta)=frac{-1-сtg(alpha)*ctg(beta)}{ctg(alpha)-ctg(beta)};$$
9. Двойной угол:
   $$cos(2*alpha)=cos(alpha)^2-sin(alpha)^2=1-2*sin(alpha)^2=2*cos(alpha)^2-1;$$
   $$sin(2*alpha)=2*sin(alpha)*cos(alpha);$$
   $$tg(2*alpha)=frac{2*tg(alpha)}{1-tg(alpha)^2};$$
   $$ctg(2*alpha)=frac{ctg(alpha)^2-1}{2*ctg(alpha)};$$
10. Тройной угол:
    $$cos(3*alpha)=cos(alpha)^3-3*sin(alpha)^2*cos(alpha)=-3*cos(alpha)+4*cos(alpha)^3;$$
    $$sin(3*alpha)=3*sin(alpha)*cos(alpha)^2-sin(alpha)^3=3*sin(alpha)-4*sin(alpha)^3;$$
    $$tg(3*alpha)=frac{3*tg(alpha)-tg(alpha)^3}{1-3*tg(alpha)^2};$$
    $$ctg(3*alpha)=frac{ctg(alpha)^3-3*ctg(alpha)}{3*ctg(alpha)^2-1};$$
11. Формулы половинного угла:
    $$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
    $$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
    $$tg(frac{alpha}{2})^2=frac{1-cos(alpha)}{1+cos(alpha)};$$
    $$ctg(frac{alpha}{2})^2=frac{1+cos(alpha)}{1-cos(alpha)};$$
12. Понижение степени:
    $$sin(alpha)^2=frac{1-cos(2*alpha)}{2};$$
    $$cos(alpha)^2=frac{1+cos(2*alpha)}{2};$$
    $$sin(alpha)^3=frac{3*sin(alpha)-sin(3*alpha)}{4};$$
    $$cos(alpha)^3=frac{3*cos(alpha)+cos(3*alpha)}{4};$$
    $$sin(alpha)^4=frac{3-4*cos(2*alpha)+cos(4*alpha)}{8};$$
    $$cos(alpha)^4=frac{3+4*cos(2*alpha)+cos(4*alpha)}{8};$$
13. Преобразование суммы и разности тригонометрических функций:
    $$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
    $$sin(alpha)-sin(beta)=2*sinleft(frac{alpha-beta}{2}right)*cosleft(frac{alpha+beta}{2}right);$$
    $$cos(alpha)+cos(beta)=2*cosleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
    $$cos(alpha)-cos(beta)=-2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{alpha-beta}{2}right);$$
    $$cos(alpha)-cos(beta)=2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{beta-alpha}{2}right);$$
    $$tg(alpha)+tg(beta)=frac{sin(alpha+beta)}{cos(alpha)*cos(beta)};$$
    $$tg(alpha)-tg(beta)=frac{sin(alpha-beta)}{cos(alpha)*cos(beta)};$$
    $$ctg(alpha)+ctg(beta)=frac{sin(alpha+beta)}{sin(alpha)*sin(beta)};$$
    $$ctg(alpha)-ctg(beta)=frac{sin(beta-alpha)}{sin(alpha)*sin(beta)};$$
14. Преобразование произведения тригонометрических функций:
    $$sin(alpha)*sin(beta)=frac{1}{2}*left(cos(alpha-beta)-cos(alpha+beta)right);$$
    $$cos(alpha)*cos(beta)=frac{1}{2}*left(cos(alpha-beta)+cos(alpha+beta)right);$$
    $$sin(alpha)*cos(beta)=frac{1}{2}*left(sin(alpha-beta)+sin(alpha+beta)right);$$
15. Формулы подстановки тангенса:
    $$sin(alpha)=frac{2*tg(frac{alpha}{2})}{1+tg(frac{alpha}{2})^2};$$
    $$cos(alpha)=frac{1-tg(frac{alpha}{2})^2}{1+tg(frac{alpha}{2})^2};$$
    $$tg(alpha)=frac{2*tg(frac{alpha}{2})}{1-tg(frac{alpha}{2})^2};$$
    $$ctg(alpha)=frac{1-tg(frac{alpha}{2})^2}{2*tg(frac{alpha}{2})};$$
16. Формулы приведения можно найти в отдельной статье

Зачем нужны тригонометрические формулы?

Как видите, тригонометрических формул очень много. Тут еще и не все приведены. Но на ваше счастье, учить всю эту таблицу не нужно. Достаточно знать только основные: №1-6, 9. Остальные на ЕГЭ по профильной математике встречаются крайне редко, а если и попадутся, то, скорее всего, будут даны в справочных материалах.

Но для участия в олимпиадах или, если вы хотите поступать в сильный математический ВУЗ через вступительные экзамены, то вам может понадобиться вся таблица. По крайней мере, у вас точно должно быть представление о существовании таких формул, чтобы их вывести в случае необходимости. Да, большинство из них легко выводятся.

Тригонометрические формулы нужны, чтобы связать все тригонометрические функции между собой. Если вы знаете одну из функций, например, синус, то, используя эти формулы, можно легко найти оставшиеся три тригонометрические функции (косинус, тангенс и котангенс). Кроме этого тождества позволяют упростить выражение под тригонометрической функцией: например, выразить синус от двойного угла через комбинацию тригонометрических функций от одинарного угла, что бывает очень полезно при решении тригонометрических уравнений и неравенств.

Обсудим и порешаем примеры на все формулы из таблицы.

Основное тригонометрическое тождество

$$mathbf{sin(alpha)^2+cos(alpha)^2=1;}$$

Эту формулу можно считать главной и самой часто используемой в тригонометрии. Она выводится при помощи определения синуса и косинуса через прямоугольный треугольник и теоремы Пифагора. Не буду еще раз описывать вывод, с ним можно познакомиться в самой первой главе по тригонометрии.

При помощи основного тригонометрического тождества очень удобно искать значение синуса, если известен косинус и наоборот. Разберем пример:

Пример 1
Найдите (3sqrt{2}*sin(alpha)=?), если (cos(alpha)=frac{1}{3}) и (alphain(0;frac{pi}{2})). (ЕГЭ)

Чтобы найти значение выражения (3sqrt{2}*sin(alpha)) необходимо сначала найти значение синуса.

Формула, которая связывает и синус, и косинус — это основное тригонометрическое тождество:
$$sin(alpha)^2+cos(alpha)^2=1;$$
Просто подставим в нее известное значение косинуса
$$sin(alpha)^2+left(frac{1}{3}right)^2=1;$$
$$sin(alpha)^2+frac{1}{9}=1;$$
$$sin(alpha)^2=1-frac{1}{9};$$
$$sin(alpha)^2=frac{8}{9};$$
$$sin(alpha)=pmsqrt{frac{8}{9}}=pmfrac{2sqrt{2}}{3};$$
Обратите внимание на знак (pm), отрицательное значение синуса нас тоже устраивает, так как при подстановке и возведении в квадрат знак минус исчезает.

В задании указано, что это пример из ЕГЭ первой части, значит должен быть только один ответ. Какое же значение синуса нам выбрать: положительное или отрицательное?

В этом нам поможет дополнительное условие на (alphain(0;frac{pi}{2})), что соответсвует первой четверти на тригонометрической окружности. Раз (alpha) лежит в первой четверти, то синус должен быть положительный. Выбираем положительное значение синуса:
$$sin(alpha)=frac{2sqrt{2}}{3};$$
И подставим найденное значение в искомое выражение:
$$3sqrt{2}*sin(alpha)=3sqrt{2}*frac{2sqrt{2}}{3}=4.$$

Ответ: (4.)

Аналогично по основному тригонометрическому тождеству можно находить значение косинуса, если известен синус.

Основные тригонометрическое тождество это ключ к решению более половины всех тригонометрических уравнений.

Основные связи тригонометрических функций

А как найти тангенс или котангенс, если нам, например, известен косинус? Посмотрите на формулы №2, для того, чтобы найти тангенс, нужно знать и косинус, и синус:

$$mathbf{tg(alpha)=frac{sin(alpha)}{cos(alpha)};}$$
$$mathbf{ctg(alpha)=frac{cos(alpha)}{sin(alpha)};}$$

Но зная косинус, мы легко можем найти синус по основному тригонометрическому тождеству, а потом уже найти тангенс.

Пример 2
Найдите (tg(alpha)) и (ctg(alpha)), если (cos(alpha)=frac{sqrt{10}}{10}) и (alpha in (frac{3pi}{2};2pi)).

Сначала находим значение синуса:
$$sin(alpha)^2+cos(alpha)^2=1;$$
$$sin(alpha)^2+left(frac{sqrt{10}}{10}right)^2=1;$$
$$sin(alpha)^2+frac{1}{10}=1;$$
$$sin(alpha)^2=1-frac{1}{10};$$
$$sin(alpha)^2=frac{9}{10};$$
$$sin(alpha)=pmsqrt{frac{9}{10}}=pmfrac{3}{sqrt{10}};$$
Так как по условию задачи (alpha in (frac{3pi}{2};2pi)), что соответсвует четвертой четверти на тригонометрической окружности, то (sin(alpha)<0). Выбираем отрицательное значение:
$$sin(alpha)=-frac{3}{sqrt{10}};$$
Теперь нам известны значения и косинуса, и синуса, можем найти тангенс:
$$tg(alpha)=frac{sin(alpha)}{cos(alpha)}=frac{-frac{3}{sqrt{10}}}{frac{sqrt{10}}{10}}=-frac{3}{sqrt{10}}*frac{10}{sqrt{10}}=-3;$$
Котангенс можно найти аналогично по формуле:
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)};$$
Но поступим проще и воспользуемся тригонометрической формулой, связывающей тангенс с котангенсом:
$$mathbf{сtg(alpha)=frac{1}{tg(alpha)};}$$
$$сtg(alpha)=frac{1}{-3}=-frac{1}{3};$$

Ответ: (tg(alpha)=-3;) (ctg(alpha)=-frac{1}{3}.)

Как видите, чтобы найти тангенс или котангенс через косинус или синус, необходимо воспользоваться сразу двумя тригонометрическими формулами. Это не очень удобно, поэтому очень полезны тригонометрические формулы, связывающие тангенс с косинусом или котангенс с синусом напрямую:
$$mathbf{tg(alpha)^2+1=frac{1}{cos(alpha)^2};}$$
$$mathbf{ctg(alpha)^2+1=frac{1}{sin(alpha)^2};}$$

Вывод связи тангенса с косинусом и котангенса с синусом

Полезно знать, как они выводятся. Вывод, на самом деле, элементарный, с использованием основного тригонометрического тождества и определения тангенса через синус и косинус:
$$tg(alpha)^2+1=frac{1}{cos(alpha)^2};$$
$$left(frac{sin(alpha)}{cos(alpha)}right)^2+1=frac{1}{cos(alpha)^2};$$
Приводим левую часть к общему знаменателю:
$$frac{sin(alpha)^2}{cos(alpha)^2}+frac{cos(alpha)^2}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
$$frac{sin(alpha)^2+cos(alpha)^2}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
В числителе у нас получилось основное тригонометрическое тождество:
$$frac{1}{cos(alpha)^2}=frac{1}{cos(alpha)^2};$$
Получилось верное равенство — формула доказана. Аналогично доказывается формула для котангенса и синуса. (В качестве упражнения докажите ее сами).

Если решать пример №2 по этим формулам, то решение заметно сокращается:
$$tg(alpha)^2+1=frac{1}{left(frac{sqrt{10}}{10}right)^2};$$
$$tg(alpha)^2+1=10;$$
$$tg(alpha)^2=9;$$
$$tg(alpha)=pm3;$$
Так как (alpha in (frac{3pi}{2};2pi)), то тангенс будет отрицательным:
$$tg(alpha)=-3;$$

Формулы суммы и разности тригонометрических функций

1. Синус суммы и разности:
   $$mathbf{sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);}$$
   $$mathbf{sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);}$$
2. Косинус суммы и разности:
   $$mathbf{cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);}$$
   $$mathbf{cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);}$$
3. Тангенс суммы и разности:
   $$mathbf{tg(alpha+beta)=frac{tg(alpha)+tg(beta)}{1-tg(alpha)*tg(beta)};}$$
   $$mathbf{tg(alpha-beta)=frac{tg(alpha)-tg(beta)}{1+tg(alpha)*tg(beta)};}$$
4. Котангенс суммы и разности:
   $$mathbf{сtg(alpha+beta)=frac{-1+сtg(alpha)*ctg(beta)}{ctg(alpha)+ctg(beta)};}$$
   $$mathbf{сtg(alpha-beta)=frac{-1-сtg(alpha)*ctg(beta)}{ctg(alpha)-ctg(beta)};}$$

Формулы суммы разности тригонометрических функций попадаются в ЕГЭ по профильной математике в №12. В прошлые года эти формулы давались в справочные материалах и учить их было не обязательно. Тем не менее, я бы рекомендовал выучить хотя бы формулы суммы и разности для синуса и косинуса.

Это не очень удобно, но иногда формулы суммы разности используют для вывода формул приведения:

Пример 3
Упростить выражение (sin(frac{pi}{2}+alpha)).

Воспользуемся формулой синуса суммы:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(frac{pi}{2}+alpha)=sin(frac{pi}{2})*cos(alpha)+sin(alpha)*cos(frac{pi}{2})=$$
$$=1*cos(alpha)+sin(alpha)*0=cos(alpha);$$

Формулы суммы разности так же полезны, когда нужно посчитать значение тригонометрических функций некоторых нестандартных углов:

Пример 4
Найдите значение (sin(15^o)=?)

(15^o) нестандартный угол, вы его не найдете в тригонометрической таблице углов. Представим (15^o) в виде разности стандартных углов (15^o=45^o-30^o). И воспользуемся формулой синуса разности:
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
$$sin(15^o)=sin(45^o-30^o)=sin(45^o)*cos(30^o)-sin(30^o)*cos(45^o)=$$
$$=frac{sqrt{2}}{2}*frac{sqrt{3}}{2}-frac{1}{2}*frac{sqrt{2}}{2}=$$
$$=frac{sqrt{6}}{4}-frac{sqrt{2}}{4}=frac{sqrt{6}-sqrt{2}}{4};$$
Вот мы наши синус (15^o). Получилось такое иррациональное некрасивое выражение, так и оставляем.

Ответ: (sin(15^o)=frac{sqrt{6}-sqrt{2}}{4}.)

Пример 5
Найдите значение (cos(75^o)=?)

(75^o) можно представить в виде суммы стандартных углов (75^o=30^o+45^o). Здесь воспользуемся формулой косинуса суммы:
$$cos(alpha+beta)=cos(30^o)*cos(45^o)-sin(30^0)*sin(45^0)=$$
$$=frac{sqrt{3}}{2}*frac{sqrt{2}}{2}-frac{1}{2}*frac{sqrt{2}}{2}=$$
$$=frac{sqrt{6}}{4}-frac{sqrt{2}}{4}=frac{sqrt{6}-sqrt{2}}{4};$$
У нас получился опять отвратительный ответ, но внимательный читатель заметит, что ответ такой же, как в предыдущем примере, это значит, что (cos(75^o)=sin(15^o)). Такой же вывод можно было бы сделать исходя из формул приведения и знания тригонометрической окружности.

Ответ: (cos(75^o)=frac{sqrt{6}-sqrt{2}}{4}.)

Мы не будем выводить эти формулы — это не самое приятное занятие. Их проще выучить, а вывод вам вряд ли когда-либо пригодится. Но сами формулы суммы и разности служат основой для доказательства других тригонометрических формул.

Формулы двойного угла

$$cos(2*alpha)=cos(alpha)^2-sin(alpha)^2=1-2*sin(alpha)^2=2*cos(alpha)^2-1;$$
$$sin(2*alpha)=2*sin(alpha)*cos(alpha);$$
$$tg(2*alpha)=frac{2*tg(alpha)}{1-tg(alpha)^2};$$
$$ctg(2*alpha)=frac{ctg(alpha)^2-1}{2*ctg(alpha)};$$

Формулы двойного угла для синуса, косинуса, тангенса и котангенса дают возможность выразить двойной угол (2alpha) через (alpha). Формулы для синуса и косинуса очень часто встречаются на ЕГЭ. Их обязательно нужно знать. Все они легко выводятся из формул синуса и косинуса суммы (формулы №5 и №6) :

$$cos(2alpha)=cos(alpha+alpha)=cos(alpha)*cos(alpha)-sin(alpha)*sin(alpha)=cos(alpha)^2-sin(alpha)^2;$$
Воспользовавшись основным тригонометрическим тождеством можно преобразовать эту формулу:
$$cos(2alpha)=cos(alpha)^2-sin(alpha)^2=1-sin(alpha)^2-sin(alpha)^2=1-2sin(alpha)^2;$$
$$cos(2alpha)=cos(alpha)^2-sin(alpha)^2=cos(alpha)^2-(1-cos(alpha)^2)=2cos(alpha)^2-1;$$

Синус двойного угла выводится аналогичным образом только с использованием формулы синуса суммы:
$$sin(2alpha)=sin(alpha)*cos(alpha)+sin(alpha)*cos(alpha)=2sin(alpha)cos(alpha);$$

Для вывода формул двойного угла для тангенса нам понадобится представить тангенс в виде отношения синуса к косинуса по определению и только что выведенные формулы синуса и косинуса двойного угла:
$$tg(2alpha)=frac{sin(2alpha)}{cos(2alpha)}=frac{2sin(alpha)cos(alpha)}{cos(alpha)^2-sin(alpha)^2}=frac{frac{2sin(alpha)cos(alpha)}{cos(alpha)^2}}{frac{cos(alpha)^2-sin(alpha)^2}{cos(alpha)^2}}=frac{frac{2sin(alpha)}{cos(alpha)}}{1-frac{sin(alpha)^2}{cos(alpha)^2}}=frac{2tg(alpha)}{1-tg(alpha)^2};$$
Котангенс двойного угла выводится абсолютно также:
$$сtg(2alpha)=frac{cos(2alpha)}{sin(2alpha)}=frac{cos(alpha)^2-sin(alpha)^2}{2sin(alpha)cos(alpha)}=frac{frac{cos(alpha)^2-sin(alpha)^2}{sin(alpha)^2}}{frac{2sin(alpha)cos(alpha)}{sin(alpha)^2}}=frac{frac{cos(alpha)^2}{sin(alpha)^2}-1}{frac{2cos(alpha)}{sin(alpha)}}=frac{ctg(alpha)^2-1}{2ctg(alpha)};$$

В первой части на ЕГЭ попадаются номера на преобразование тригонометрических выражений, где часто содержится двойной угол:

Пример 6
Найти значение (24cos(2alpha)=?), если (sin(alpha)=-0,2.)

Воспользуемся формулой косинуса двойного угла:
$$cos(2alpha)=1-2sin(alpha)^2;$$
$$24cos(2alpha)=24(1-2sin(alpha)^2)=24-48sin(alpha)^2=24-48*(-0,2)^2=24-48*0,04=22,08.$$

Пример 7
Найти значение (frac{10sin(6alpha)}{3cos(3alpha)}=?), если (sin(3alpha)=0,6.)

Используем синус двойного угла, для этого представим (6alpha=2*(3alpha)):
$$sin(6alpha)=sin(2*(3alpha))=2sin(3alpha)cos(3alpha);$$
$$frac{10sin(6alpha)}{3cos(3alpha)}=frac{10*2sin(3alpha)cos(3alpha)}{3cos(3alpha)}=frac{20sin(3alpha)}{3}=frac{20*0,6}{3}=frac{12}{3}=4.$$

Пример 8
Найти значение выражения (frac{12sin(11^o)cos(11^o)}{sin(22^o)}=?)

Замечаем, что (22^o=2*11^o) и воспользуемся синусом двойного угла:
$$frac{12sin(11^o)cos(11^o)}{sin(22^o)}=frac{12sin(11^o)cos(11^o)}{2sin(11^o)cos(11^o)}=frac{12}{2}=6.$$

Формулы тройного угла

Формулы тройного угла обычно попадаются на математических олимпиадах или вступительных экзаменах в математические ВУЗы. Учить их необязательно, но знать о существовании полезно, тем более, что они достаточно легко выводятся.
$$cos(3*alpha)=cos(alpha)^3-3*sin(alpha)^2*cos(alpha)=-3*cos(alpha)+4*cos(alpha)^3;$$
$$sin(3*alpha)=3*sin(alpha)*cos(alpha)^2-sin(alpha)^3=3*sin(alpha)-4*sin(alpha)^3;$$
$$tg(3*alpha)=frac{3*tg(alpha)-tg(alpha)^3}{1-3*tg(alpha)^2};$$
$$ctg(3*alpha)=frac{ctg(alpha)^3-3*ctg(alpha)}{3*ctg(alpha)^2-1};$$

Выведем эти формулы, использую формулы сложения. Начнем с косинуса тройного угла:
$$cos(3*alpha)=cos(2alpha+alpha)=cos(2alpha)*cos(alpha)-sin(2alpha)*sin(alpha)=$$
$$=(cos(alpha)^2-sin(alpha)^2)*cos(alpha)-2sin(alpha)*cos(alpha)*sin(alpha)=$$
$$=cos(alpha)^3-sin(alpha)^2*cos(alpha)-2sin(alpha)^2*cos(alpha)=$$
$$=cos(alpha)^3-3sin(alpha)^2*cos(alpha);$$

Если расписать (sin(alpha)^2=1-cos(alpha)^2), то получим еще один вариант формулы тройного угла:
$$cos(3*alpha)=cos(alpha)^3-3sin(alpha)^2*cos(alpha)=cos(alpha)^3-3(1-cos(alpha)^2)*cos(alpha)=$$
$$=4cos(alpha)^3-3cos(alpha);$$

Аналогично выводится формула синуса тройного угла:
$$sin(3alpha)=sin(2alpha+alpha)=sin(2alpha)*cos(alpha)+sin(alpha)*cos(2alpha)=$$
$$=2sin(alpha)*cos(alpha)*cos(alpha)+sin(alpha)*(cos(alpha)^2-sin(alpha)^2)=$$
$$=2sin(alpha)*cos(alpha)^2+sin(alpha)*cos(alpha)^2-sin(alpha)^3=3sin(alpha)*cos(alpha)^2-sin(alpha)^3;$$
Распишем по основному тригонометрическому тождеству (cos(alpha)^2=1-sin(alpha)^2) и подставим:
$$sin(3alpha)=3sin(alpha)*cos(alpha)^2-sin(alpha)^3=$$
$$=3sin(alpha)*(1-sin(alpha)^2)-sin(alpha)^3=3sin(alpha)-4sin(alpha)^3;$$

Для тангенса и котангенса формулы тройного угла здесь выводить не будем, так как они достаточно редки. Но в качестве упражнения можете сами выполнить вывод, представив тангенс или котангенс по определению: через отношение синуса тройного угла к косинусу тройного угла или наоборот соотвественно.

Формулы тройного угла обычно используются при преобразовании сложных тригонометрических выражений. Например, на вступительных экзаменах в МФТИ любят давать тригонометрические уравнения на тройной угол и больше.

Формулы половинного угла (двойного аргумента)

$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$tg(frac{alpha}{2})^2=frac{1-cos(alpha)}{1+cos(alpha)};$$
$$ctg(frac{alpha}{2})^2=frac{1+cos(alpha)}{1-cos(alpha)};$$

Формулы половинного угла это по сути формулы обратные формулам двойного угла. Достаточно запомнить их элементарный вывод, тогда учить совсем необязательно. Здесь важный момент, что любой угол (alpha) всегда можно представить в виде удвоенного угла (frac{alpha}{2}):
$$alpha=2*frac{alpha}{2};$$

Выведем формулу синуса половинного угла, для этого нам понадобится формула косинуса двойного угла:
$$cos(alpha)=1-2*sin(frac{alpha}{2})^2;$$
Выразим отсюда (sin(frac{alpha}{2})):
$$sin(frac{alpha}{2})^2=frac{1-cos(alpha)}{2};$$
Иногда эту формулу записывают без квадрата:
$$sin(frac{alpha}{2})=pmsqrt{frac{1-cos(alpha)}{2}};$$
Плюс минус возникает при избавлении от квадрата.
Вывод косинуса половинного угла тоже получается из формулы косинуса двойного угла:
$$cos(alpha)=2*cos(frac{alpha}{2})^2-1;$$
$$cos(frac{alpha}{2})^2=frac{cos(alpha)+1}{2};$$
$$cos(frac{alpha}{2})=pmsqrt{frac{cos(alpha)+1}{2}};$$

Доказательство формул половинного угла для тангенса и котангенса следует из выше доказанных формул:
$$tg(frac{alpha}{2})=frac{sin(frac{alpha}{2})}{cos(frac{alpha}{2})}=frac{pmsqrt{frac{1-cos(alpha)}{2}}}{pmsqrt{frac{cos(alpha)+1}{2}}}=sqrt{frac{frac{1-cos(alpha)}{2}}{frac{cos(alpha)+1}{2}}}=frac{1-cos(alpha)}{1+cos(alpha)};$$
Точно так же для котангенса:
$$сtg(frac{alpha}{2})=frac{cos(frac{alpha}{2})}{sin(frac{alpha}{2})}=frac{pmsqrt{frac{cos(alpha)+1}{2}}}{pmsqrt{frac{1-cos(alpha)}{2}}}=sqrt{frac{frac{cos(alpha)+1}{2}}{frac{1-cos(alpha)}{2}}}=frac{1+cos(alpha)}{1-cos(alpha)};$$

Пример 9
При помощи формул половинного угла можно, например, посчитать (cos(15^o)):

$$cos(frac{alpha}{2})^2=frac{1+cos(alpha)}{2};$$
$$cos(15^o)^2=frac{1+cos(30^o)}{2}=frac{1+frac{sqrt{3}}{2}}{2}=frac{2+sqrt{3}}{4};$$
$$cos(15^o)=sqrt{frac{2+sqrt{3}}{4}}.$$

Кстати, формулы половинного угла справедливы не только в явном виде, когда аргумент правой части формулы (alpha), а левой (frac{alpha}{2}). Но и в неявном, достаточно, чтобы аргумент правой части был больше аргумента левой в два раза:
$$sin(5alpha)=pmsqrt{frac{1-cos(10alpha)}{2}};$$

Формулы понижения степени

$$sin(alpha)^2=frac{1-cos(2*alpha)}{2};$$
$$cos(alpha)^2=frac{1+cos(2*alpha)}{2};$$
$$sin(alpha)^3=frac{3*sin(alpha)-sin(3*alpha)}{4};$$
$$cos(alpha)^3=frac{3*cos(alpha)+cos(3*alpha)}{4};$$
$$sin(alpha)^4=frac{3-4*cos(2*alpha)+cos(4*alpha)}{8};$$
$$cos(alpha)^4=frac{3+4*cos(2*alpha)+cos(4*alpha)}{8};$$

Формулы понижения второй степени на самом деле дублируют формулы половинного угла.

Формулы понижения третей степени перестановкой слагаемых дублируют формулы тройного угла.

Преобразование суммы и разности тригонометрических функций:

$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(alpha)-sin(beta)=2*sinleft(frac{alpha-beta}{2}right)*cosleft(frac{alpha+beta}{2}right);$$
$$cos(alpha)+cos(beta)=2*cosleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=-2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{alpha-beta}{2}right);$$
$$cos(alpha)-cos(beta)=2*sinleft(frac{alpha+beta}{2}right)*sinleft(frac{beta-alpha}{2}right);$$
$$tg(alpha)+tg(beta)=frac{sin(alpha+beta)}{cos(alpha)*cos(beta)};$$
$$tg(alpha)-tg(beta)=frac{sin(alpha-beta)}{cos(alpha)*cos(beta)};$$
$$ctg(alpha)+ctg(beta)=frac{sin(alpha+beta)}{sin(alpha)*sin(beta)};$$
$$ctg(alpha)-ctg(beta)=frac{sin(beta-alpha)}{sin(alpha)*sin(beta)};$$

Формулы для суммы и разности тригонометрических функций полезны, если необходимо превратить сумму двух функций в произведение. Они в основном используются в уравнениях и преобразованиях сложных выражений, когда необходимо слагаемые разложить на множители.

Для вывода формул суммы и разности синусов и косинусов нам понадобится пара трюков и формулы синуса и косинуса суммы и разности (тут можно запутаться, в названиях формул, будьте внимательны). Вывод получается не самый очевидный.

Обратите внимание, что любой угол (alpha) можно представить в таком странном виде:
$$alpha=frac{alpha}{2}+frac{alpha}{2}+frac{beta}{2}-frac{beta}{2}=frac{alpha+beta}{2}+frac{alpha-beta}{2};$$
Аналогично угол (beta):
$$beta=frac{alpha+beta}{2}-frac{alpha-beta}{2};$$
Эти странности нам понадобятся при выводе формул, просто обратите на них внимание.
А теперь перейдем непосредственно к выводу формулы суммы синусов двух углов. Для начала распишем угла (alpha) и (beta) по формулам выше:
$$sin(alpha)+sin(beta)=sin(frac{alpha+beta}{2}+frac{alpha-beta}{2})+sin(frac{alpha+beta}{2}-frac{alpha-beta}{2}); qquad (*)$$
Теперь воспользуемся формулами синуса суммы и синуса разности:

$$sin(gamma+sigma)=sin(gamma)*cos(sigma)+sin(sigma)*cos(gamma);$$
$$sin(gamma-sigma)=sin(gamma)*cos(sigma)-sin(sigma)*cos(gamma);$$

Только у нас под синусами будут стоять не (gamma) и (sigma), а целые выражения.
Пусть:
$$gamma=frac{alpha+beta}{2};$$
$$sigma=frac{alpha-beta}{2};$$
Применим формулы синуса суммы и разности в (*):
$$sin(alpha)+sin(beta)=sin(frac{alpha+beta}{2}+frac{alpha-beta}{2})+sin(frac{alpha+beta}{2}-frac{alpha-beta}{2})=$$
$$=left(sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2})+sin(frac{alpha-beta}{2})*cos(frac{alpha+beta}{2})right)+$$
$$+left(sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2})-sin(frac{alpha-beta}{2})*cos(frac{alpha+beta}{2})right)=$$
$$=2*sin(frac{alpha+beta}{2})*cos(frac{alpha-beta}{2}); $$
В самом конце мы просто раскрыли большие скобки и привели подобные слагаемые.

Аналогично выводятся все остальные формулы.

Пример 10
Вычислить (sin(165)+sin(75)=?)

(165^o) и (75^o) это не табличные углы. Значения синусов этих углов мы не знаем. Для решения этого примера воспользуемся формулой суммы синусов:
$$sin(alpha)+sin(beta)=2*sinleft(frac{alpha+beta}{2}right)*cosleft(frac{alpha-beta}{2}right);$$
$$sin(165^o)+sin(75^o)=2*sinleft(frac{165^o+75^o}{2}right)*cosleft(frac{165^o-75^o}{2}right)=$$
$$=2*sin(120^o)*cos(45^o)=2*frac{sqrt{3}}{2}*frac{sqrt{2}}{2}=frac{sqrt{6}}{2}.$$

Преобразование произведения тригонометрических функций

$$sin(alpha)*sin(beta)=frac{1}{2}*left(cos(alpha-beta)-cos(alpha+beta)right);$$
$$cos(alpha)*cos(beta)=frac{1}{2}*left(cos(alpha-beta)+cos(alpha+beta)right);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*left(sin(alpha-beta)+sin(alpha+beta)right);$$

В некотором смысле формулы произведения синуса, косинуса, тангенса и котангенса являются обратными к тригонометрическим формулам суммы и разности тригонометрических функций. При помощи этих формул возможно перейти от произведения к сумме или разности.

Для вывода нам опять понадобятся формулы косинуса суммы и разности:
$$cos(alpha+beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha);$$
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$

Сложим эти две формулы. Для этого складываем их левые части и приравниваем сумме правых частей:

$$cos(alpha+beta)+cos(alpha-beta)=cos(alpha)*cos(beta)-sin(beta)*sin(alpha)+cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Приводим подобные слагаемые:
$$cos(alpha+beta)+cos(alpha-beta)=2*cos(alpha)*cos(beta);$$
Отсюда получаем:
$$cos(alpha)*cos(beta)=frac{1}{2}*(cos(alpha+beta)+cos(alpha-beta));$$
Формула произведения косинусов доказана.

Произведение синусов доказывается похожим образом. Для этого домножим формулу косинуса суммы слева и справа на ((-1)):
$$-cos(alpha+beta)=-cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Косинус разности оставим без изменений:
$$cos(alpha-beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
Сложим опять эти две формулы:
$$cos(alpha-beta)-cos(alpha+beta)=cos(alpha)*cos(beta)+sin(beta)*sin(alpha)-cos(alpha)*cos(beta)+sin(beta)*sin(alpha);$$
$$cos(alpha-beta)-cos(alpha+beta)=2*sin(beta)*sin(alpha);$$
$$sin(beta)*sin(alpha)=frac{1}{2}*(cos(alpha-beta)-cos(alpha+beta));$$
Произведение синусов тоже доказано.

Для того, чтобы вывести формулу произведения синуса и косинуса, нам понадобятся формулы синуса суммы и разности:
$$sin(alpha+beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha);$$
$$sin(alpha-beta)=sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
Сложим их:
$$sin(alpha+beta)+sin(alpha-beta)=sin(alpha)*cos(beta)+sin(beta)*cos(alpha)+sin(alpha)*cos(beta)-sin(beta)*cos(alpha);$$
$$sin(alpha+beta)+sin(alpha-beta)=2*sin(alpha)*cos(beta);$$
$$sin(alpha)*cos(beta)=frac{1}{2}*(sin(alpha+beta)+sin(alpha-beta));$$

Пример 11
Вычислить (sin(75^o)*cos(15^o)=?)

Воспользуемся формулой произведения синуса и косинуса:
$$sin(alpha)*cos(beta)=frac{1}{2}*(sin(alpha+beta)+sin(alpha-beta));$$
$$sin(75^o)*cos(15^o)=frac{1}{2}*(sin(75^o+15^o)+sin(75^o-15^o))=$$
$$=frac{1}{2}*(sin(90^o)+sin(60^o))=frac{1}{2}*(1+frac{sqrt{3}}{2})=frac{2+sqrt{3}}{4}.$$

План урока:

Основное тригонометрическое тождество

Тригонометрические функции суммы и разности

Формулы двойного угла

Формулы понижения степени

Формулы приведения

Сумма тригонометрических функций

Произведение тригонометрических функций

Основное тригонометрическое тождество

Несложно догадаться, что синус и косинус угла – это величины, связанные друг с другом. Отложим на единичной окружности произвольный угол α и опустим из точки А перпендикуляр на ось Ох, в некоторую точку В:

Изучим треугольник АОВ. Он прямоугольный, а потому для него можно записать теорему Пифагора:

АВ² + ОВ² = ОА²

Мы рассматриваем единичную окружность, а потому ОА = 1, ОВ = соsα, AB = sinα. Подставив эти величины в равенство, получим тождество:

sin²α + соs²α = 1

Его называют основным тригонометрическим тождеством, ведь именно оно связывает значение двух прямых тригонометрических ф-ций – синуса и косинуса.

Задание. В прямоугольном треугольнике есть угол α. Известно, что sin α = 0,8. Чему равен соsα?

Решение. Подставим в основное тригон-кое тождество значение sinα = 0,8 и получим уравнение:

sin²α + соs²α = 1

0,8² + соs²α = 1

0,64 + соs²α = 1

соs²α = 1 – 0,64

соs²α = 0,36

соsα = – 0,6 или соsα = 0,6

Нашли два возможных значения косинуса. Но по условию α – это острый угол, ведь в прямоугольном треугольнике угол не может быть больше 90°. То есть угол α относится к первой четверти, а потому его косинус положителен. Значит, соsα = 0,6.

Ответ: 0,6.

Рассмотренный пример показал, что одному заданному значению синуса соответствует сразу два противоположных друг другу значения косинуса. Верно и обратное. Действительно, отложим по оси Ох некоторую величину соsα и проведем вертикальную линию, чтобы найти соответствующие ему значения синуса. Она пересечет единичную окружность в двух точках с противоположными ординатами:

По этой причине при решении задач на использование основного тригон-кого тождества обычно указывают, к какой четверти относится угол α.

Задание. Вычислите sinα, если соsα = 0,28 и α принадлежит IV четверти.

Решение.

sin²α + соs²α = 1

0,28² + sin²α = 1

0,0784 + sin²α = 1

sin²α = 1 – 0,0784

sin²α = 0,9216

sin α = –0,96 или sin α = 0,96

Так как α принадлежит IV четверти, то sinα должен быть отрицательным, поэтому sinα = – 0,96.Напомним, что в IV четверти значение косинуса положительно, ведь соответствующая ей дуга единичной окружности располагается правее оси Оу, то есть абсциссы точек, принадлежащих ей, положительны.

Ответ: – 0,96.

Задание. Найдите tgα, если sinα = 5/13 и π/2 < α < π.

Решение. Здесь задача уже в два действия! Сначала определим соsα:

sin²α + соs²α = 1

соs²α = 1 – sin²α = 1 – (5/13)² = 169/169 – 25/169 = 144/169

соsα = – 12/13 или соsα = 12/13

Условие π/2 < α < π указывает на то, что угол относится ко II четверти, в которой косинус отрицателен, поэтому соsα = – 12/13.

Далее находим тангенс, просто деля синус на косинус:

tgα = sinα:соsα = (5/13):(12/13) = (5/13)•(13/12) = 5/12

Ответ: 5/12

Рассмотренный пример показал нам, что, зная синус, можно рассчитать не только косинус, но и тангенс. А возможно ли совершить обратное действие, найти по тангенсу синус или косинус? Да, но для этого нужно получить новую тригонометрическую формулу.

Запишем тождество

sin²α + соs²α = 1

Далее поделим его на величину соs²α:

Крайнее левое слагаемое – это величина tg²α, а следующая дробь равна единице, так как у неё совпадают числитель и знаменатель:

В итоге нам удалось получить ф-лу, которая связывает значение тангенса и косинуса угла. Есть такая формула и для котангенса. Для ее получения необходимо поделить основное тригон-кое тождество на sin²α:

Задание. Известно, что tgα = 0,75. Найдите соsα и sinα, если угол α принадлежит III четверти.

Решение.

Просто подставляем в ф-лу известное значение тангенса и решаем получившееся уравнение. Для простоты вычислении заменим десятичную дробь 0,75 на обычную 3/4:

Так как угол относится к III четверти, где косинус отрицателен, то

соsα = – 0,8

Синус угла найдем, используя основное тригон-кое тождество:

sin²α + соs²α = 1

sin²α = 1 – соs²α = 1 – (– 0,8)² = 1 – 0,64 = 0,36

sinα = – 0,6 или sinα = 0,6

С учетом того, что в III четверти синус становится отрицательным, следует выбрать вариант sinα = – 0,6

Ответ: sinα = – 0,6; соsα = – 0,8.

Иногда ф-лы используют не для вычисления значений тригон-ких выражений, а для упрощения выражений. Из тождества sin²α + соs²α = 1 несложно получить из выражения

sin²α = 1 – соs²α

и

соs²α = 1 – sin²α

которые помогают в работе с длинными ф-лами.

Задание. Упростите выражение

4sin²α + 9соs²α – 6

таким образом, чтобы в нем не содержалось синуса.

Решение. Произведем замену sin²α = 1 – соs²α:

4sin²α+ 9соs²α – 6 = 4(1 – соs²α)+ 9соs²α – 6 =

= 4 – 4 соs²α + 9соs²α – 6 = 5соs²α – 2

Видим, что получилось значительно более простое выражение.

Ответ: 5соs²α – 2.

Задание. Избавьтесь от синуса в выражении

sin⁴α – соs⁴α

Решение. Воспользуемся ф-лой разности квадратов:

sin⁴α – соs⁴α = (sin²α – соs²α)(sin²α + соs²α) = (sin²α – соs²α)•1 =

= 1 – соs²α– соs²α = 1 – 2 соs²α

Ответ:1 – 2 соs²α.

Задание. Упростите дробь

Решение.

Ответ: ctg⁶α.

Тригонометрические функции суммы и разности

Легко проводить вычисления, когда все тригонометрические действия выполняются над одним углом α. Однако иногда в задачах добавляется ещё один угол, который обычно обозначают как β. Существуют ф-лы, с помощью которых можно вычислять тригон-кие ф-ции от суммы и разности углов α и β.

Вывод этих ф-л достаточно сложен, поэтому сначала мы просто без доказательства приведем две из них, позволяющие вычислять синус суммы и косинус суммы:

Достаточно запомнить их, а далее следующие формулы можно выводить из них. Так, если вместо β подставить угол (–β), то получим формулы для разности. При этом мы используем тот факт, что синус – нечетная ф-ция, то естьsin (– β) = – sinβ, а косинус – четная ф-ция, то есть соs (– β) = соsβ:

Теперь поступим также с ф-лой для косинуса разности:

Итак, нам удалось получить ф-лы для нахождения синуса и косинуса суммы и разности углов.

С помощью этих формул возможно вычислить значение тригон-ких ф-ций для некоторых нестандартных углов. (Стандартными считаются углы в 0°, 30°, 45°, 60° и 90°, ведь для них значение тригон-ких ф-ций можно узнать из таблички.)

Задание. Вычислите соs 150°.

Решение. В табличке стандартных углов есть углы, равные 90° и 60°. Их сумма как раз равна 150°. Поэтому запишем:

Задание. Вычислите синус, косинус и тангенс для угла 15°.

Решение. Угол в 15° можно представить как разность 45° – 30°. Тогда синус будет вычисляться так:

Далее вычислим косинус:

Можно выполнить проверку. Полученные значения должны удовлетворять основному тригон-кому тождеству. И действительно:

Проверка пройдена: сумма квадратов синуса и косинуса оказалась равной единице. Теперь посчитаем tg 15°, используя определение тангенса:

Задание. Вычислите значение тригонометрического выражения

sinπ/7 соsπ/42 + sinπ/42 соsπ/7

Решение: Значение тригон-ких ф-ций для углов π/7 и π/42 мы не знаем, однако это не помешает вычислениям. Можно заметить, что исходное выражение представляет собой синус суммы π/7 и π/42:

sinπ/7 соsπ/42 + sinπ/42 соsπ/7 = sin (π/7 + π/42) = sinπ/6 = 1/2

Ответ: 1/2.

Задание. Упростите выражение

Решение.

Вынесем за скобки множитель 2:

Теперь произведем замену:

C учетом этого можно переписать выражение и использовать ф-лу суммы косинусов:

Ответ: 2соs (π/6 + α).

Формулы двойного угла

Что будет, если формулу синуса суммы подставить не два различных угла α и β, а два одинаковых угла α и α? Получится ф-ла для синуса двойного угла:

Аналогично можно составить ф-лу и для косинуса двойного угла:

Итак, справедливы следующие ф-лы:

Задание. Вычислите sin 120° и соs 120°.

Решение.

Задание. Упростите выражение

соs²t– соs 2t

Решение.

соs²t – соs 2t = соs²t – (соs² t – sin²t) = соs²t – соs² t + sin²t = sin²t

Ответ: sin²t.

Задание. Докажите, что функция

является периодической и имеет период, равный π.

Решение. Используем ф-лу квадрата суммы:

Таким образом, исходную ф-цию можно переписать в виде

у = 1 + sin 2x

По определению, ф-ция является периодической с периодом Т, если выполняется условие у(х + Т) = у(х). Поэтому подставим в нашу ф-цию величину х + π:

Получили, что у(х + π) = y(x), то есть ф-ция имеет период, равный π.

Задание. Выведите формулы синуса и косинуса тройного угла.

Решение. Для их получения следует использовать ф-лу синуса суммы углов, в которую подставляют вместо β величину 2α:

Аналогично можно получить и ф-лу для косинуса тройного угла:

Формулы понижения степени

Если нам необходимо узнать косинус угла, который вдвое больше табличного, мы используем ф-лу:

соs 2α = соs²α – sin²α

А что делать, если нам надо вычислить косинус угла, который вдвое меньше известного? Попробуем преобразовать ф-лу косинуса двойного угла:

В результате нам удалось получить тождество, позволяющее по косинусу удвоенного угла найти косинус самого угла! Однако значительно чаще в тригонометрии это равенство записывают в обратном порядке:

и называют ф-лой понижения степени. Действительно, в левой части стоит косинус в квадрате, а справа – косинус без квадрата, но вычисляется он от угла 2α, а не α.

Попробуем получить аналогичную ф-лу и для синуса. Для этого используем основное тригон-кое тождество:

С помощью этих ф-л можно вычислять тригон-кие ф-ции для некоторых малых углов. Так, ранее мы с использованием ф-лу разности синусов определили, что

При этом мы представляли угол 15° как разность 45° – 30°. Но как посчитать соs 7,5°? Этот угол невозможно представить как разницу или сумму известных нам табличных углов (0°, 30°; 45°; 60° и 90°). Однако поможет ф-ла понижения степени. Действительно, ведь 2•7,5° = 15°. Тогда можно записать:

Мы нашли соs² 7,5°. Чтобы узнать соs 7,5°, необходимо извлечь квадратный корень:

Так как угол 7,5° принадлежит I четверти, то его косинус должен быть положительным, поэтому можно записать:

Видно, что получается довольно громоздкое выражение. Используя ф-лу понижения степени, можно найти косинус и угла, который ещё вдвое меньше, то есть равен 3,75°, но в результате получится ещё более громоздкое выражение.

Задание. Вычислите sinπ/8.

Решение. Угол π/4 является табличным (его градусная мера составляет 45°). Поэтому можно записать:

Эти примеры показывают, что тригон-кие ф-ции многих нестандартных углов можно выразить, используя квадратные корни. Возникает вопрос – а любую ли тригонометрическую ф-цию можно выразить таким способом? Оказывается, что нет. Например, sin 10° невозможно найти ни в одной, даже самой подробной тригонометрической таблице. Мы не будем это доказывать, но эту величину невозможно представить в виде выражения, используя арифметические операции и корни. Однако существуют приближенные методы, позволяющие с любой наперед заданной точностью вычислять значение тригонометрических ф-ций.

Формулы приведения

Возможно, вы уже заметили, что синусы и косинусы принимают одинаковые значения в углах, чья сумма равна 90°. Например, sin30° = соs60° = 1/2, и при этом 30° + 60° = 90°. Также мы знаем, что sin 45° = соs 45° (45° + 45° = 90°) и sin60° = соs30° (60° + 30°). В чем причина такой закономерности и справедлива ли она для нестандартных углов?

Используя ф-лу синуса разности, мы можем записать, что

Полученная ф-ла sin (90° – α) = соsα называется формулой приведения. При ее выводе мы использовали тот факт, что sin 90° = 1, а соs 90° = 0, поэтому формула получилась очень простой. Однако синусы и косинусы других углов, кратных 90° (или кратных π/2, если измерять углы в радианах), также равны 0, 1 или – 1, поэтому для них тоже можно получить подобные простые ф-лы, например:

Похожих ф-л можно написать несколько десятков! Все их запоминать не надо, так как существует особое мнемоническое правило, позволяющее записать необходимую ф-лу.

Пусть есть некоторое тригон-кое выражение вида

f(k ± α)

где f – тригонометрическая ф-ция (sin; соs; tg; ctg)

k– угол, кратный π/2 (π/2, π, 3π/2, 2π)

Мы хотим заменить ее другой ф-цией, только от угла α. На первом шаге мы смотрим на слагаемое k. Если оно кратно π (– π, π, 2π), то ф-ция f остается неизменной. Если же слагаемое k – это число π/2 или 3π/2, то ф-цию f надо поменять на так называемую кофункцию (синус меняем на косинус, тангенс на котангенс и наоборот).

Далее надо определить знак, стоящий перед новой ф-цией. Для этого мы предполагаем, что α – это острый угол, то есть он принадлежит I четверти. Далее с учетом этого предположения смотрим, в какую четверть попадает угол k ± α, и какое значение принимает там исходная тригонометрическая ф-ция. Если она отрицательна, то перед новой тригонометрической ф-цией надо поставить минус. В противном случае ничего ставить не надо.

Лучше всего изучить это алгоритм на примерах.

Задание. Упростите выражение соs (π/2 + α).

Решение. Первый шаг – смотрим на слагаемое под знаком косинуса. Это число π/2. Оно НЕ кратно π, а потому мы должны поменять косинус на синус:

sinα

Второй шаг – надо определить, надо ли ставить минус перед синусом. Если α – это острый угол, то угол (π/2 + α) попадет во II четверть:

Во второй четверти косинус отрицателен, а потому перед синусом следует поставить минус:

соs (π/2 + α) = – sinα

Ответ: – sinα.

Важное примечание. В этом примере для составления формулы приведения мы «предположили», что угол α является острым. В результате нам удалось получить формулу соs (π/2 + α) = – sinα. Однако отметим, что полученная нами формула выполняется для абсолютно любых значений угла α, а не только для 0° < α < 90°. Предположение об остроте угла – это лишь часть мнемонического правила для составления формул приведения, позволяющая быстро определить, надо ли в ней перед тригонометрической функцией ставить знак минус или не надо.

Это мнемоническое правило работает абсолютно точно, однако надо понимать, что всё-таки для строгого вывода формул приведения следует использовать формулу косинуса суммы

соs (π/2 + α) = cosπ/2 cos α – sin π/2 sin α = 0•cos α – 1•sin α = – sin α

Получили тот же результат, что и с помощью формулы приведения. При этом нам не потребовалось предположение об остроте угла α, то есть формула верна для любых α. Но практика показывает, что люди просто не могут запомнить формулу косинусов суммы. Поэтому для «упрощения жизни» школьникам рассказывают об относительно простом мнемоническом правиле.

Задание. Составьте ф-лу приведения для выражения tg (α – π).

Решение. Сначала смотрим на слагаемое под знаком тангенса. Это число (– π), кратное π. Поэтому сама ф-ция не меняется на кофункцию:

tgα

Примем, что угол α принадлежит I четверти, тогда угол α – π будет ему противоположен и окажется в III четверти:

Тангенс в III четверти положителен. Значит, минуса перед тангенсом ставить не надо:

tg (α– π) = tgα

Задание. Вычислите sin 7π/6.

Решение. Представим угол 7π/6 как сумму: 7π/6 = π + π/6. Получается, нам надо вычислить величину sin (π + π/6). Составим ф-лу приведения для выражения π + α Так как в скобках стоит слагаемое π, то ф-ция sin остается, а не меняется на косинус:

sinα

Угол (π + α) относится к III четверти, где синус отрицателен. Следовательно, надо добавить знак минус:

sin (π + α) = – sinα

Остается подставить вместо α величину π/6:

sin (π + π/6) = – sinπ/6 = – 1/2

Ответ: – 1/2.

Задание. Чему равен ctg7π/4?

Решение. Угол 7π/4 можно представить как 3π/2 + π/4. Найдем ф-лу приведения для ctg (3π/2 + α). Из-за слагаемого 3π/2, не кратного π, ф-ция должна измениться с котангенса на тангенс:

ctg (3π/2 + α) = tgα

Угол 3π/2 + α попадает в IV четверть, где котангенс отрицателен. Поэтому необходимо добавить знак минуса перед ф-цией:

ctg (3π/2 + α) = –tgα

Ф-ла приведения получена. Осталось подставить в неё значение α = π/4:

ctg (7π/4) = ctg (3π/2 + π/4) = – tgπ/4 = – 1

Ответ: – 1.

Откуда же возникло название «формула приведения»? Дело в том, что с их помощью вычисление тригонометрических ф-ций от углов из диапазона 0 ≤ π ≤ 2π можно привести к вычислению ф-ций от углов из I четверти, то есть из диапазона 0 ≤ α ≤ π/2. Это означает, что нет смысла заучивать большие таблицы, в которых указаны синусы и косинусы углов, больших 90°. Достаточно знать ф-ции от стандартных углов: 0, π/6; π/4, π/3 и π/2.

Если всё же использование ф-л приведения вызывает сложности, то вместо них всегда можно использовать обычные ф-лы косинуса и синуса суммы, которые дадут такой же результат.

В прошлом уроке, строя графики косинуса, мы заметили, что он представляет собой синусоиду, смещенную на π/2 единиц:

Теперь становится ясна причина этого смещения. Дело в ф-ле приведения

соsx = sin (x + π/2)

Она показывает, что точки графика косинуса могут быть получены параллельным переносом точек синусоиды на π/2 единиц влево.

Сумма тригонометрических функций

Мы видим, что тригон-ких формул довольно много. Надо ли все их учить? Этого делать не надо. Достаточно иметь под рукой справочник при решении задач, связанных с преобразованием тригонометрических выражений, в котором все эти ф-лы можно посмотреть. В крайнем случае можно всегда самостоятельно вывести все ф-лы, используя только основное тригон-кое тождество и ф-лы синуса и косинуса суммы. Они, кстати, выдаются в качестве раздаточного материала учащимся при сдаче ЕГЭ. Ещё важно помнить определение тангенса, которое в раздаточном материале не записано.

Пусть есть два произвольных угла s и t. Найдем синусы их разности и суммы:

Сложим эти два уравнения:

Теперь произведем замену. Будем считать, что

x = s + t

у = s – t

Это значит, чтох + у = 2s, или

s = (x + y)/2

С другой стороны

х – у = s + t– (s– t) = 2t

то есть

t = (x – у)/2

Подставляем всё это в ф-лу (1):

Получили формулу, с помощью которой можно найти сумму любых двух синусов! Теперь попытаемся составить аналогичную ф-лу и для их разности синусов. При этом мы учтем нечетность синуса (это значит, что sin (– у) = – sinу):

Задание. Упростите выражения

Решение.

Теперь попробуем составить ф-лы для сложения и вычитания косинусов. Для этого запишем ф-лы для произвольных величин s и t:

Сложив уравнения, мы получим тождество

Далее произведем замены, которые выполняли и ранее:

x = s + t

у = s – t

s = (x + y)/2

t = (x – у)/2

Подставляя всё это в (3), получим:

Получили ф-лу, с помощью которой можно складывать косинусы. Чтобы их можно было вычитать, вычтем из (1) уравнение (2):

Снова произведем замены переменных s и t:

Получили ф-лу и для разности косинусов.

Задание. Упростить тригонометрические выражения

Решение.

в) Здесь мы сталкиваемся с более сложным случаем, так как из косинуса надо вычесть синус. У нас нет готовой ф-лы для такого действия. Однако вспомним, что с помощью формул приведения легко заменить синус на косинус:

sinx = соs (π/2 – х)

Тогда исходное выражение уже можно будет преобразовать:

Произведение тригонометрических функций

В предыдущем разделе, когда мы выводили ф-лы для вычисления суммы синусов и косинусов, мы сначала получали уравнения:

Далее мы производили замену переменных sи t. Однако давайте вместо этого просто поделим первые два уравнения на двойку, а третье – на (– 2):

В случае с последней формулой мы воспользовались правилом, по которому знак минус перед дробью можно убрать, если в числителе поменять местами вычитаемое и уменьшаемое.

Получили ф-лы, которые позволяют заменять произведение тригонометрических ф-ций их суммой.

Задание. Преобразуйте произведение в сумму:

Решение.

На этом наше знакомство с основными тригонометрическими формулами заканчивается. Ещё раз напомним, что в рамках школьного курса заучивать все ф-лы не нужно, можно при необходимости пользоваться смотреть в справочник. Тригон-кие преобразования помогут в будущем при решении сложных тригон-ких уравнений.

В самом конце приведем перечень всех формул, выведенными в этом уроке:

Что такое тангенс угла и как его найти

Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.

Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.

Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.

Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.

Тангенс угла

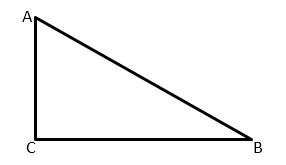
Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.

В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.

Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса (это что?), тангенса, котангенса.

Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.

Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.

Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.

Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).

Тангенс — это отношение…

Итак, есть два определения:

1. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

   Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.

2. Тангенс – это отношение синуса к косинусу.

   Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.

Приняты обозначения:

Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan⁡(α).

Как найти тангенс угла (формулы)

Первое свойство тангенса вытекает из его определения как отношения катетов.

Сумма двух непрямых углов прямоугольного треугольника равна 90º. Поэтому

Так как тангенс – это отношение катетов, то

Получается, что

Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.

В частности,

Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.

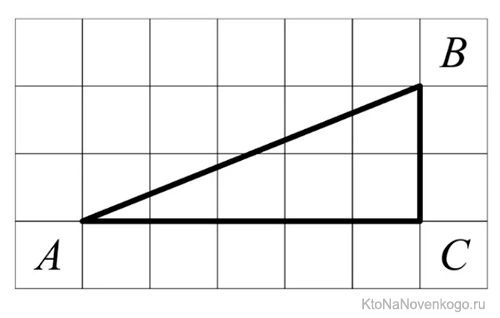
Как найти тангенс по клеточкам

Учитывая первое определение, можно определить, как найти его по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.

Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:

Из формулы тангенсов, записывающей кратко второе определение

и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.

Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится его зависимость от косинуса:

Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом: