Загрузить PDF
Загрузить PDF
Если вы умеете вычислять угловые коэффициенты (тангенс угла наклона) прямых, то на основании этих коэффициентов можно узнать другие параметры. Например, выяснить, параллельны ли прямые или же перпендикулярны, найти их точку пересечения и многие другие величины. Вычисление углового коэффициента — довольно простая задача. Прочитайте эту статью, чтобы узнать, как это сделать.
-
1
Угловой коэффициент (тангенс угла наклона) определяется как отношение изменения координаты «у» к изменению координаты «х».
Реклама
-
1
Рассмотрите любую прямую линию. Убедитесь, что линия прямая, так как угловой коэффициент вычисляется только для прямых линий.
-
2
Выберите любые две точки, лежащие на прямой. Запишите их координаты в виде (х,у). Не имеет значения, какие точки вы выберете (главное, чтобы они были разными и лежали на одной прямой).
-
3
Дайте обозначение выбранным точкам. Не имеет значения, какую из них вы обозначите первой, а какую – второй (главное — на протяжении всего процесса вычисления строго придерживаться выбранного обозначения). Координаты первой точки запишем как x1 и y1, а координаты второй точки как x2 и y2.
-
4
Подставьте координаты точек в формулу для вычисления углового коэффициента, приведенную выше.
-
5
Вычтите две координаты «у».
-
6
Вычтите две координаты «х».
-
7
Разделите результат разности координат «у» на результат разности координат «х». Сократите дробь, если возможно.
-
8
Проверьте полученный результат.
- Прямые, идущие вверх слева направо, всегда имеют положительный угловой коэффициент (даже если это дробь).
- Прямые, идущие вниз слева направо, всегда имеют отрицательный угловой коэффициент (даже если это дробь).
Реклама
Пример
- Дана прямая с точками A и B, лежащими на ней.
- Координаты точек: A(-2,0) и B(0,-2)
- (y2-y1): -2-0=-2; Изменение координаты «у» = -2
- (x2-x1): 0-(-2)=2; Изменение координаты «х» = 2
- Угловой коэффициент данной прямой равен -1.
Советы
- Как только вы обозначили координаты точек на прямой через (х1,у1) и (у1,у2), не меняйте эти обозначения, или вы получите неверный ответ.
- Вы нашли «m» в линейном уравнении вида y=mx+b, где «у» — координата «у», «m» – угловой коэффициент, «х» — координата «х», «b» – смещение прямой по оси Y (или значение координаты «у» при х=0).
- Для получения ответов на возникающие вопросы прочитайте школьный учебник или обратитесь к учителю.
Реклама
Предупреждения
- Не путайте формулу для вычисления углового коэффициента (тангенса угла наклона) прямой с любой другой формулой, например, с формулой для вычисления расстояния или формулой для вычисления средней точки.
Реклама
Что вам понадобится
- Миллиметровка (возможно).
- Координатная плоскость или прямая с координатами двух точек, лежащих на ней.
- Формула для вычисления углового коэффициента (тангенса угла наклона) прямой.
- Карандаш, бумага, линейка, калькулятор.
- Прямая.
- Координаты «х».
- Координаты «у».
Об этой статье
Эту страницу просматривали 103 403 раза.
Была ли эта статья полезной?
Как найти тангенс угла наклона
Под тангенсом угла наклона обычно понимают угловой коэффициент касательной прямой какой-либо функции. Однако вам может понадобиться также умение найти тангенс угла наклона обычной прямой, например, одной из сторон треугольника по отношению к другой. Определив, что вам надо найти, действуйте одним из следующих способов.

Инструкция
Если вам нужно посчитать угол наклона прямой к оси абсцисс, а вы не знаете уравнение прямой, опустите из любой точки этой прямой (кроме точки пересечения с осью) перпендикуляр на ось. Затем измерьте катеты полученного прямоугольного треугольника и найдите отношение прилежащего катета к противолежащему. Полученное число будет равно тангенсу угла наклона. Этот способ удобно использовать не только для изучения угла наклона прямой, но и для измерения любых углов, как на чертеже, так и в жизни (например, угол ската кровли).
Если вы знаете уравнение прямой, и вам нужно найти тангенс угла наклона этой прямой к оси абсцисс, выразите у через х. В результате вы получите выражение типа у=kх+b. Обратите внимание на коэффициент k – это и есть тангенс угла наклона между положительным направлением оси ох и лучом прямой, расположенным надо этой осью. Если же k=0, то тангенс также равен нулю, то есть прямая параллельна или совпадает с осью абсцисс.
Если вам дана сложная функция, например, квадратичная, и вам нужно найти тангенс угла наклона касательной к этой функции, или, по-другому, угловой коэффициент, вычислите производную. Затем вычислите значение производной в заданной точке, к которой будет проведена касательная. Полученное число и является тангенсом угла наклона касательной. Например, вам дана функция у=х^2+3х, посчитав ее производную, вы получите выражение у`=2х+3. Чтобы найти угловой коэффициент в точке х=3, подставьте это значение в уравнение. В результате несложных вычислений легко можно получить у=2*3+3=9, это и есть искомый тангенс.
Для того чтобы найти тангенс угла наклона одной из сторон треугольника к другой, поступите следующим образом. Найдите синус (sin) этого угла и разделите его на косинус (cos), в результате вы получите тангенс этого угла.
Источники:
- как найти тангенс по углу
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
7. Взаимосвязь функции и ее производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Угловой коэффициент касательной как тангенс угла наклона
(blacktriangleright) Если уравнение прямой задано в виде ({color{royalblue}{y=kx+b ;}}), то число (k) называется угловым коэффициентом.
(blacktriangleright) Угол (alpha) наклона прямой – это угол между этой прямой и положительным направлением оси (Ox) ((0leqslant
alpha< 180^circ)), лежащий в верхней полуплоскости.
(blacktriangleright) Основная формула. Угловой коэффициент прямой (y=kx+b) равен тангенсу угла наклона этой прямой:
[{large{color{royalblue}{k=mathrm{tg}, alpha}}}]
Т.к. касательная к графику некоторой функции — это и есть прямая, то для нее верны все эти утверждения.
Если (alpha<90^circ), то (k>0);
если (alpha>90^circ), то (k<0);
если (alpha=0^circ), то (k=0) (уравнение прямой имеет вид (y=b) и она параллельна оси (Ox));
если (alpha=90^circ), то уравнение прямой имеет вид (x=a) и она перпендикулярна оси (Ox).
Задание
1
#685
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = x), образует с положительным направлением оси (Ox) угол (alpha). Найдите (mathrm{tg}, alpha).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как для прямой (y = x) коэффициент (k) равен (1), то (mathrm{tg}, alpha = 1).
Ответ: 1
Задание
2
#686
Уровень задания: Легче ЕГЭ
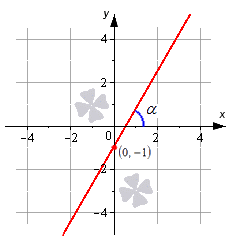
Прямая, заданная уравнением (y = 2x — 3), образует с положительным направлением оси (Ox) угол (alpha). Найдите (mathrm{tg}, alpha).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как для прямой (y = 2x — 3) коэффициент (k) равен (2), то (mathrm{tg}, alpha = 2).
Ответ: 2
Задание
3
#687
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = -x + 2), образует с положительным направлением оси (Ox) угол (alpha). Найдите (mathrm{tg}, alpha).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как для прямой (y = -x + 2) коэффициент (k) равен (-1), то (mathrm{tg}, alpha = -1).
Ответ: -1
Задание
4
#688
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = kx + 77), образует с положительным направлением оси (Ox) угол (alpha). Найдите (k), если (mathrm{tg}, alpha = 12).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как тангенс угла (alpha) между прямой (y = kx + 77) и положительным направлением оси (Ox) равен (12), то (k = mathrm{tg}, alpha = 12).
Ответ: 12
Задание
5
#689
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = kx + 0,2), образует с положительным направлением оси (Ox) угол (alpha). Найдите (k), если (mathrm{tg}, alpha = -3,3).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как тангенс угла (alpha) между прямой (y = kx + 0,2) и положительным направлением оси (Ox) равен (-3,3), то (k = mathrm{tg}, alpha = -3,3).
Ответ: -3,3
Задание
6
#690
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = kx), образует с положительным направлением оси (Ox) угол (alpha). Найдите (k), если (mathrm{tg}, alpha = 0).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как тангенс угла (alpha) между прямой (y = kx) и положительным направлением оси (Ox) равен (0), то (k = mathrm{tg}, alpha = 0).
Ответ: 0
Задание
7
#693
Уровень задания: Легче ЕГЭ
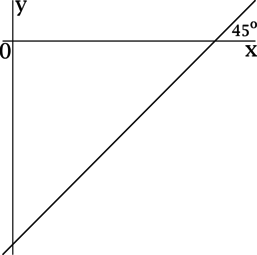
Прямая (y = kx — 2016) образует угол (45^{circ}) с положительным направлением оси (Ox). Найдите (k).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как угол между прямой (y = kx — 2016) и положительным направлением оси (Ox) равен (dfrac{pi}{4}), то (k = mathrm{tg}, dfrac{pi}{4} = 1).
Ответ: 1
Теме «Угловой коэффициент касательной как тангенс угла наклона» в аттестационном экзамене отводится сразу несколько заданий. В зависимости от их условия, от выпускника может требоваться как полный ответ, так и краткий. При подготовке к сдаче ЕГЭ по математике ученику обязательно стоит повторить задачи, в которых требуется вычислить угловой коэффициент касательной.
Сделать это вам поможет образовательный портал «Школково». Наши специалисты подготовили и представили теоретический и практический материал максимально доступно. Ознакомившись с ним, выпускники с любым уровнем подготовки смогут успешно решать задачи, связанные с производными, в которых требуется найти тангенс угла наклона касательной.
Основные моменты
Для нахождения правильного и рационального решения подобных заданий в ЕГЭ необходимо вспомнить базовое определение: производная представляет собой скорость изменения функции; она равна тангенсу угла наклона касательной, проведенной к графику функции в определенной точке. Не менее важно выполнить чертеж. Он позволит найти правильное решение задач ЕГЭ на производную, в которых требуется вычислить тангенс угла наклона касательной. Для наглядности лучше всего выполнить построение графика на плоскости ОХY.
Если вы уже ознакомились с базовым материалом на тему производной и готовы приступить к решению задач на вычисление тангенса угла наклона касательной, подобных заданиям ЕГЭ, сделать это можно в режиме онлайн. Для каждого задания, например, задач на тему «Связь производной со скоростью и ускорением тела», мы прописали правильный ответ и алгоритм решения. При этом учащиеся могут попрактиковаться в выполнении задач различного уровня сложности. В случае необходимости упражнение можно сохранить в разделе «Избранное», чтобы потом обсудить решение с преподавателем.

УСТАЛ? Просто отдохни
Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач
Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.
Угол наклона прямой и угловой коэффициент прямой
Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.
Угол наклона прямой к оси О х , расположенный в декартовой системе координат О х у на плоскости, это угол, который отсчитывается от положительного направления О х к прямой против часовой стрелки.
Когда прямая параллельна О х или происходит совпадение в ней, угол наклона равен 0 . Тогда угол наклона заданной прямой α определен на промежутке [ 0 , π ) .
Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.
Стандартное обозначение буквой k . Из определения получим, что k = t g α . Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.
Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.
Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.
Посчитать угловой коэффициент прямой при угле наклона равном 120 ° .
Из условия имеем, что α = 120 ° . По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k = t g α = 120 = — 3 .
Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k > 0 , тогда угол прямой острый и находится по формуле α = a r c t g k . Если k 0 , тогда угол тупой, что дает право определить его по формуле α = π — a r c t g k .
Определить угол наклона заданной прямой к О х при угловом коэффициенте равном 3 .
Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к О х меньше 90 градусов. Вычисления производятся по формуле α = a r c t g k = a r c t g 3 .
Ответ: α = a r c t g 3 .
Найти угол наклона прямой к оси О х , если угловой коэффициент = — 1 3 .
Если принять за обозначение углового коэффициента букву k , тогда α является углом наклона к заданной прямой по положительному направлению О х . Отсюда k = — 1 3 0 , тогда необходимо применить формулу α = π — a r c t g k При подстановке получим выражение:
α = π — a r c t g — 1 3 = π — a r c t g 1 3 = π — π 6 = 5 π 6 .
Ответ: 5 π 6 .
Уравнение с угловым коэффициентом
Уравнение вида y = k · x + b , где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой, непараллельной оси О у .
Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y = k · x + b . В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М , M 1 ( x 1 , y 1 ) , в уравнение y = k · x + b , тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.
Задана прямая с угловым коэффициентом y = 1 3 x — 1 . Вычислить, принадлежат ли точки M 1 ( 3 , 0 ) и M 2 ( 2 , — 2 ) заданной прямой.
Необходимо подставить координаты точки M 1 ( 3 , 0 ) в заданное уравнение, тогда получим 0 = 1 3 · 3 — 1 ⇔ 0 = 0 . Равенство верно, значит точка принадлежит прямой.
Если подставим координаты точки M 2 ( 2 , — 2 ) , тогда получим неверное равенство вида — 2 = 1 3 · 2 — 1 ⇔ — 2 = — 1 3 . Можно сделать вывод, что точка М 2 не принадлежит прямой.
Ответ: М 1 принадлежит прямой, а М 2 нет.
Известно, что прямая определена уравнением y = k · x + b , проходящим через M 1 ( 0 , b ) , при подстановке получили равенство вида b = k · 0 + b ⇔ b = b . Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y = k · x + b на плоскости определяет прямую, которая проходит через точку 0 , b . Она образует угол α с положительным направлением оси О х , где k = t g α .
Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y = 3 · x — 1 . Получим, что прямая пройдет через точку с координатой 0 , — 1 с наклоном в α = a r c t g 3 = π 3 радиан по положительному направлению оси О х . Отсюда видно, что коэффициент равен 3 .
Уравнение прямой с угловым коэффициентом, проходящей через заданную точку
Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M 1 ( x 1 , y 1 ) .
Равенство y 1 = k · x + b можно считать справедливым, так как прямая проходит через точку M 1 ( x 1 , y 1 ) . Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y — y 1 = k · ( x — x 1 ) . Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M 1 ( x 1 , y 1 ) .
Составьте уравнение прямой, проходящей через точку М 1 с координатами ( 4 , — 1 ) , с угловым коэффициентом равным — 2 .
Решение
По условию имеем, что x 1 = 4 , y 1 = — 1 , k = — 2 . Отсюда уравнение прямой запишется таким образом y — y 1 = k · ( x — x 1 ) ⇔ y — ( — 1 ) = — 2 · ( x — 4 ) ⇔ y = — 2 x + 7 .
Ответ: y = — 2 x + 7 .
Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М 1 с координатами ( 3 , 5 ) , параллельную прямой y = 2 x — 2 .
По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y = 2 x — 2 , отсюда следует, что k = 2 . Составляем уравнение с угловым коэффициентом и получаем:
y — y 1 = k · ( x — x 1 ) ⇔ y — 5 = 2 · ( x — 3 ) ⇔ y = 2 x — 1
Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно
Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.
Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x — x 1 a x = y — y 1 a y . Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y = k · x + b ⇔ y — b = k · x ⇔ k · x k = y — b k ⇔ x 1 = y — b k .
Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.
Привести уравнение прямой с угловым коэффициентом y = — 3 x + 12 к каноническому виду.
Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:
y = — 3 x + 12 ⇔ — 3 x = y — 12 ⇔ — 3 x — 3 = y — 12 — 3 ⇔ x 1 = y — 12 — 3
Ответ: x 1 = y — 12 — 3 .
Общее уравнение прямой проще всего получить из y = k · x + b , но для этого необходимо произвести преобразования: y = k · x + b ⇔ k · x — y + b = 0 . Производится переход из общего уравнения прямой к уравнениям другого вида.
Дано уравнение прямой вида y = 1 7 x — 2 . Выяснить, является ли вектор с координатами a → = ( — 1 , 7 ) нормальным вектором прямой?
Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:
y = 1 7 x — 2 ⇔ 1 7 x — y — 2 = 0
Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n → = 1 7 , — 1 , отсюда 1 7 x — y — 2 = 0 . Понятно, что вектор a → = ( — 1 , 7 ) коллинеарен вектору n → = 1 7 , — 1 , так как имеем справедливое соотношение a → = — 7 · n → . Отсюда следует, что исходный вектор a → = — 1 , 7 — нормальный вектор прямой 1 7 x — y — 2 = 0 , значит, считается нормальным вектором для прямой y = 1 7 x — 2 .
Решим задачу обратную данной.
Необходимо перейти от общего вида уравнения A x + B y + C = 0 , где B ≠ 0 , к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у. Получим A x + B y + C = 0 ⇔ — A B · x — C B .
Результат и является уравннием с угловым коэффициентом, который равняется — A B .
Задано уравнение прямой вида 2 3 x — 4 y + 1 = 0 . Получить уравнение данной прямой с угловым коэффициентом.
Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:
2 3 x — 4 y + 1 = 0 ⇔ 4 y = 2 3 x + 1 ⇔ y = 1 4 · 2 3 x + 1 ⇔ y = 1 6 x + 1 4 .
Ответ: y = 1 6 x + 1 4 .
Аналогичным образом решается уравнение вида x a + y b = 1 , которое называют уравнение прямой в отрезках, или каноническое вида x — x 1 a x = y — y 1 a y . Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:
x a + y b = 1 ⇔ y b = 1 — x a ⇔ y = — b a · x + b .
Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ ⇔ a x · y = a y · x — a y · x 1 + a x · y 1 ⇔ y = a y a x · x — a y a x · x 1 + y 1
Имеется прямая, заданная уравнением x 2 + y — 3 = 1 . Привести к виду уравнения с угловым коэффициентом.
Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на — 3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:
y — 3 = 1 — x 2 ⇔ — 3 · y — 3 = — 3 · 1 — x 2 ⇔ y = 3 2 x — 3 .
Ответ: y = 3 2 x — 3 .
Уравнение прямой вида x — 2 2 = y + 1 5 привести к виду с угловым коэффициентом.
Необходимо выражение x — 2 2 = y + 1 5 вычислить как пропорцию. Получим, что 5 · ( x — 2 ) = 2 · ( y + 1 ) . Теперь необходимо полностью его разрешить, для этого:
5 · ( x — 2 ) = 2 · ( y + 1 ) ⇔ 5 x — 10 = 2 y + 2 ⇔ 2 y = 5 x — 12 ⇔ y = 5 2 x
Ответ: y = 5 2 x — 6 .
Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.
Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x = λ y = — 1 + 2 · λ .
Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:
x = λ y = — 1 + 2 · λ ⇔ λ = x λ = y + 1 2 ⇔ x 1 = y + 1 2 .
Теперь необходимо разрешить данное равенство относительно y , чтобы получить уравнение прямой с угловым коэффициентом. для этого запишем таким образом:
x 1 = y + 1 2 ⇔ 2 · x = 1 · ( y + 1 ) ⇔ y = 2 x — 1
Отсюда следует, что угловой коэффициент прямой равен 2 . Это записывается как k = 2 .
Как найти тангенс угла наклона прямой
Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.
Угол наклона прямой и угловой коэффициент прямой
Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.
Угол наклона прямой к оси О х , расположенный в декартовой системе координат О х у на плоскости, это угол, который отсчитывается от положительного направления О х к прямой против часовой стрелки.
Когда прямая параллельна О х или происходит совпадение в ней, угол наклона равен 0 . Тогда угол наклона заданной прямой α определен на промежутке [ 0 , π ) .
Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.
Стандартное обозначение буквой k . Из определения получим, что k = t g α . Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.
Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.
Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.
Посчитать угловой коэффициент прямой при угле наклона равном 120 ° .
Из условия имеем, что α = 120 ° . По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k = t g α = 120 = — 3 .
Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k > 0 , тогда угол прямой острый и находится по формуле α = a r c t g k . Если k 0 , тогда угол тупой, что дает право определить его по формуле α = π — a r c t g k .
Определить угол наклона заданной прямой к О х при угловом коэффициенте равном 3 .
Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к О х меньше 90 градусов. Вычисления производятся по формуле α = a r c t g k = a r c t g 3 .
Ответ: α = a r c t g 3 .
Найти угол наклона прямой к оси О х , если угловой коэффициент = — 1 3 .
Если принять за обозначение углового коэффициента букву k , тогда α является углом наклона к заданной прямой по положительному направлению О х . Отсюда k = — 1 3 0 , тогда необходимо применить формулу α = π — a r c t g k При подстановке получим выражение:
α = π — a r c t g — 1 3 = π — a r c t g 1 3 = π — π 6 = 5 π 6 .
Ответ: 5 π 6 .
Уравнение с угловым коэффициентом
Уравнение вида y = k · x + b , где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой, непараллельной оси О у .
Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y = k · x + b . В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М , M 1 ( x 1 , y 1 ) , в уравнение y = k · x + b , тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.
Задана прямая с угловым коэффициентом y = 1 3 x — 1 . Вычислить, принадлежат ли точки M 1 ( 3 , 0 ) и M 2 ( 2 , — 2 ) заданной прямой.
Необходимо подставить координаты точки M 1 ( 3 , 0 ) в заданное уравнение, тогда получим 0 = 1 3 · 3 — 1 ⇔ 0 = 0 . Равенство верно, значит точка принадлежит прямой.
Если подставим координаты точки M 2 ( 2 , — 2 ) , тогда получим неверное равенство вида — 2 = 1 3 · 2 — 1 ⇔ — 2 = — 1 3 . Можно сделать вывод, что точка М 2 не принадлежит прямой.
Ответ: М 1 принадлежит прямой, а М 2 нет.
Известно, что прямая определена уравнением y = k · x + b , проходящим через M 1 ( 0 , b ) , при подстановке получили равенство вида b = k · 0 + b ⇔ b = b . Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y = k · x + b на плоскости определяет прямую, которая проходит через точку 0 , b . Она образует угол α с положительным направлением оси О х , где k = t g α .
Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y = 3 · x — 1 . Получим, что прямая пройдет через точку с координатой 0 , — 1 с наклоном в α = a r c t g 3 = π 3 радиан по положительному направлению оси О х . Отсюда видно, что коэффициент равен 3 .
Уравнение прямой с угловым коэффициентом, проходящей через заданную точку
Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M 1 ( x 1 , y 1 ) .
Равенство y 1 = k · x + b можно считать справедливым, так как прямая проходит через точку M 1 ( x 1 , y 1 ) . Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y — y 1 = k · ( x — x 1 ) . Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M 1 ( x 1 , y 1 ) .
Составьте уравнение прямой, проходящей через точку М 1 с координатами ( 4 , — 1 ) , с угловым коэффициентом равным — 2 .
Решение
По условию имеем, что x 1 = 4 , y 1 = — 1 , k = — 2 . Отсюда уравнение прямой запишется таким образом y — y 1 = k · ( x — x 1 ) ⇔ y — ( — 1 ) = — 2 · ( x — 4 ) ⇔ y = — 2 x + 7 .
Ответ: y = — 2 x + 7 .
Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М 1 с координатами ( 3 , 5 ) , параллельную прямой y = 2 x — 2 .
По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y = 2 x — 2 , отсюда следует, что k = 2 . Составляем уравнение с угловым коэффициентом и получаем:
y — y 1 = k · ( x — x 1 ) ⇔ y — 5 = 2 · ( x — 3 ) ⇔ y = 2 x — 1
Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно
Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.
Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x — x 1 a x = y — y 1 a y . Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y = k · x + b ⇔ y — b = k · x ⇔ k · x k = y — b k ⇔ x 1 = y — b k .
Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.
Привести уравнение прямой с угловым коэффициентом y = — 3 x + 12 к каноническому виду.
Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:
y = — 3 x + 12 ⇔ — 3 x = y — 12 ⇔ — 3 x — 3 = y — 12 — 3 ⇔ x 1 = y — 12 — 3
Ответ: x 1 = y — 12 — 3 .
Общее уравнение прямой проще всего получить из y = k · x + b , но для этого необходимо произвести преобразования: y = k · x + b ⇔ k · x — y + b = 0 . Производится переход из общего уравнения прямой к уравнениям другого вида.
Дано уравнение прямой вида y = 1 7 x — 2 . Выяснить, является ли вектор с координатами a → = ( — 1 , 7 ) нормальным вектором прямой?
Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:
y = 1 7 x — 2 ⇔ 1 7 x — y — 2 = 0
Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n → = 1 7 , — 1 , отсюда 1 7 x — y — 2 = 0 . Понятно, что вектор a → = ( — 1 , 7 ) коллинеарен вектору n → = 1 7 , — 1 , так как имеем справедливое соотношение a → = — 7 · n → . Отсюда следует, что исходный вектор a → = — 1 , 7 — нормальный вектор прямой 1 7 x — y — 2 = 0 , значит, считается нормальным вектором для прямой y = 1 7 x — 2 .
Решим задачу обратную данной.
Необходимо перейти от общего вида уравнения A x + B y + C = 0 , где B ≠ 0 , к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у. Получим A x + B y + C = 0 ⇔ — A B · x — C B .
Результат и является уравннием с угловым коэффициентом, который равняется — A B .
Задано уравнение прямой вида 2 3 x — 4 y + 1 = 0 . Получить уравнение данной прямой с угловым коэффициентом.
Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:
2 3 x — 4 y + 1 = 0 ⇔ 4 y = 2 3 x + 1 ⇔ y = 1 4 · 2 3 x + 1 ⇔ y = 1 6 x + 1 4 .
Ответ: y = 1 6 x + 1 4 .
Аналогичным образом решается уравнение вида x a + y b = 1 , которое называют уравнение прямой в отрезках, или каноническое вида x — x 1 a x = y — y 1 a y . Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:
x a + y b = 1 ⇔ y b = 1 — x a ⇔ y = — b a · x + b .
Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ ⇔ a x · y = a y · x — a y · x 1 + a x · y 1 ⇔ y = a y a x · x — a y a x · x 1 + y 1
Имеется прямая, заданная уравнением x 2 + y — 3 = 1 . Привести к виду уравнения с угловым коэффициентом.
Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на — 3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:
y — 3 = 1 — x 2 ⇔ — 3 · y — 3 = — 3 · 1 — x 2 ⇔ y = 3 2 x — 3 .
Ответ: y = 3 2 x — 3 .
Уравнение прямой вида x — 2 2 = y + 1 5 привести к виду с угловым коэффициентом.
Необходимо выражение x — 2 2 = y + 1 5 вычислить как пропорцию. Получим, что 5 · ( x — 2 ) = 2 · ( y + 1 ) . Теперь необходимо полностью его разрешить, для этого:
5 · ( x — 2 ) = 2 · ( y + 1 ) ⇔ 5 x — 10 = 2 y + 2 ⇔ 2 y = 5 x — 12 ⇔ y = 5 2 x
Ответ: y = 5 2 x — 6 .
Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.
Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x = λ y = — 1 + 2 · λ .
Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:
x = λ y = — 1 + 2 · λ ⇔ λ = x λ = y + 1 2 ⇔ x 1 = y + 1 2 .
Теперь необходимо разрешить данное равенство относительно y , чтобы получить уравнение прямой с угловым коэффициентом. для этого запишем таким образом:
x 1 = y + 1 2 ⇔ 2 · x = 1 · ( y + 1 ) ⇔ y = 2 x — 1
Отсюда следует, что угловой коэффициент прямой равен 2 . Это записывается как k = 2 .
Угловой коэффициент прямой. В этой статье мы с вами рассмотрим задачи связанные с координатной плоскостью включённые в ЕГЭ по математике. Это задания на:
— определение углового коэффициента прямой, когда известны две точки через которые она проходит;
— определение абсциссы или ординаты точки пересечения двух прямых на плоскости.
Что такое абсцисса и ордината точки было описано в прошлой статье данной рубрики. В ней мы уже рассмотрели несколько задач связанных с координатной плоскостью. Что необходимо понимать для рассматриваемого типа задач? Немного теории.
Уравнение прямой на координатной плоскости имеет вид:
где k – это и есть угловой коэффициент прямой.
Следующий момент! Угловой коэффициент прямой равен тангенсу угла наклона прямой. Это угол между данной прямой и осью ох.
Он лежит в пределах от 0 до 180 градусов.
То есть, если мы приведём уравнение прямой к виду y = kx + b, то далее всегда сможем определить коэффициент k (угловой коэффициент).
Так же, если мы исходя из условия сможем определить тангенс угла наклона прямой, то тем самым найдём её угловой коэффициент.
Следующий теоретический момент! Уравнение прямой походящей через две данные точки. Формула имеет вид:
Подробнее об этой формуле рассказано в этой статье !
Рассмотрим задачи (аналогичные задачам из открытого банка заданий):
Найдите угловой коэффициент прямой, проходящей через точки с координатами (–6;0) и (0;6).
В данной задаче самый рациональный путь решения это найти тангенс угла между осью ох и данной прямой. Известно, что он равен угловому коэффициенту. Рассмотрим прямоугольный треугольник образованный прямой и осями ох и оу:
Тангенсом угла в прямоугольном треугольнике является отношение противолежащего катета к прилежащему:
*Оба катета равны шести (это их длины).
Конечно, данную задачу можно решить используя формулу нахождения уравнения прямой проходящей через две данные точки. Но это будет более длительный путь решения.
Найдите угловой коэффициент прямой, проходящей через точки с координатами (5;0) и (0;5).
Формула уравнения прямой походящей через две данные точки имеет вид:
Наши точки имеют координаты (5;0) и (0;5). Значит,
Получили, что угловой коэффициент k = – 1.
Прямая a проходит через точки с координатами (0;6) и (8;0). Прямая b проходит через точку с координатами (0;10) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью оx.
В данной задаче можно найти уравнение прямой a, определить угловой коэффициент для неё. У прямой b угловой коэффициент будет такой же, так как они параллельны. Далее можно найти уравнение прямой b. А затем, подставив в него значение y = 0, найти абсциссу. НО!
В данном случае, проще использовать свойство подобия треугольников.
Прямоугольные треугольники, образованные данными (параллельными) прямыми о осями координат подобны, а это значит, что отношения их соответствующих сторон равны.
Искомая абсцисса равна 40/3.
Прямая a проходит через точки с координатами (0;8) и (–12;0). Прямая b проходит через точку с координатами (0; –12) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью оx.
Для данной задачи самый рациональный путь решения — это применение свойства подобия треугольников. Но мы решим её другим путём.
Нам известны точки, через которые проходит прямая а. Можем составить уравнение прямой. Формула уравнения прямой походящей через две данные точки имеет вид:
По условию точки имеют координаты (0;8) и (–12;0). Значит,
Получили, что угловой k = 2/3.
*Угловой коэффициент можно было найти через тангенс угла в прямоугольном треугольнике с катетами 8 и 12.
Известно, у параллельных прямых угловые коэффициенты равны. Значит уравнение прямой проходящей через точку (0;-12) имеет вид:
Найти величину b мы можем подставив абсциссу и ординату в уравнение:
Таким образом, прямая имеет вид:
Теперь чтобы найти искомую абсциссу точки пересечения прямой с осью ох, необходимо подставить у = 0:
Найдите ординату точки пересечения оси оy и прямой, проходящей через точку В(10;12) и параллельной прямой, проходящей через начало координат и точку А(10;24).
Найдём уравнение прямой проходящей через точки с координатами (0;0) и (10;24).
Формула уравнения прямой походящей через две данные точки имеет вид:
Наши точки имеют координаты (0;0) и (10;24). Значит,
Угловые коэффициенты параллельных прямых равны. Значит, уравнение прямой, проходящей через точку В(10;12) имеет вид:
Значение b найдём подставив в это уравнение координаты точки В(10;12):
Получили уравнение прямой:
Чтобы найти ординату точки пересечения этой прямой с осью оу нужно подставить в найденное уравнение х = 0:
*Самый простой способ решения. При помощи параллельного переноса сдвигаем данную прямую вниз вдоль оси оу до точки (10;12). Сдвиг происходит на 12 единиц, то есть точка А(10;24) «перешла» в точку В(10;12), а точка О(0;0) «перешла» в точку (0;–12). Значит, полученная прямая будет пересекать ось оу в точке (0;–12).
Искомая ордината равна –12.
Найдите ординату точки пересечения прямой, заданной уравнением
3х + 2у = 6 , с осью Oy .
Координата точки пересечения заданной прямой с осью оу имеет вид (0;у). Подставим в уравнение абсциссу х = 0, и найдём ординату:
Ордината точки пересечения прямой с осью оу равна 3.
Найдите ординату точки пересечения прямых, заданных уравнениями
3х + 2у = 6 и у = – х .
Когда заданны две прямые, и стоит вопрос о нахождении координат точки пересечения этих прямых, решается система из данных уравнений:
В первом уравнении подставляем – х вместо у:
Ордината равна минус шести.
Найдите угловой коэффициент прямой, проходящей через точки с координатами (–2;0) и (0;2).
Найдите угловой коэффициент прямой, проходящей через точки с координатами (2;0) и (0;2).
Прямая a проходит через точки с координатами (0;4) и (6;0). Прямая b проходит через точку с координатами (0;8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.
Прямая a проходит через точки с координатами (0;4) и (–6;0). Прямая b проходит через точку с координатами (0; –6) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.
Найдите ординату точки пересечения оси оy и прямой, проходящей через точку B (6;4) и параллельной прямой, проходящей через начало координат и точку A (6;8).
Найдите абсциссу точки пересечения прямой, заданной уравнением 2х + 2у = 6, с осью ох.
Найдите абсциссу точки пересечения прямых, заданных уравнениями 3х + 2у = 6 и у = х.
Конечно, некоторые задачи, которые мы рассмотрели можно было решить более рациональными способами. Но ставилась цель показать разные подходы к решению. Надеюсь, это удалось.
1. Необходимо чётко усвоить, что угловой коэффициент прямой равен тангенсу угла наклона прямой. Это поможет вам при решении многих задач данного типа.
2. Формулу нахождения прямой проходящей через две данные точки нужно понимать обязательно. С её помощью всегда найдёте уравнение прямой, если даны координаты двух её точек.
3. Помните о том, что угловые коэффициенты параллельных прямых равны.
4. Как вы поняли, в некоторых задачах удобно использовать признак подобия треугольников. Задачи решаются практически устно.
5. Задачи в которых даны две прямые и требуется найти абсциссу или ординату точки их пересечения можно решить графическим способом. То есть, построить их на координатной плоскости (на листе в клетку) и определить точку пересечения визуально. *Но этот способ применим не всегда.
6. И последнее. Если дана прямая и координаты точек её пересечения с осями координат, то в таких задачах удобно находить угловой коэффициент через нахождение тангенса угла в образованном прямоугольном треугольнике. Как «увидеть» этот треугольник при различных расположениях прямых на плоскости схематично показано ниже:
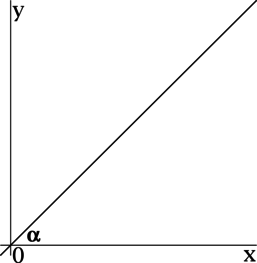
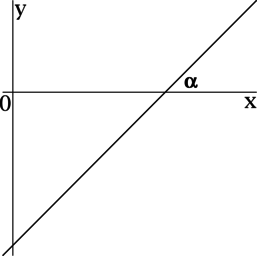
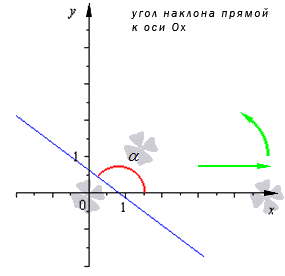
>> Угол наклона прямой от 0 до 90 градусов
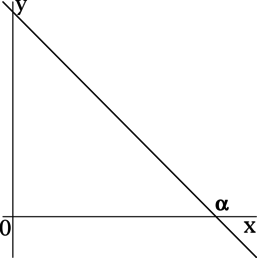
>> Угол наклона прямой от 90 до 180 градусов
В данных двух случаях, по свойству тангенса :
То есть, чтобы найти уголвой коэффициент прямой, необходимо вычислить тангенс бетта в полученном прямоугольном треугольнике и записать результат с отрицательным знаком.
В данной рубрике продолжим рассматривать задачи, не пропустите!
Функция НАКЛОН в Excel предназначена для определения угла наклона прямой, используемой для аппроксимации данных методом линейной регрессии, и возвращает значение коэффициента a из уравнения y=ax+b. Для определения наклона используются две любые точки на прямой. При этом вычисляется частное от деления длины отрезка, полученного при проецировании этих двух точек на ось Ординат (OY), на длину отрезка, образованного проекциями этих же двух точек на ось Абсцисс (OX).
Фактически, функция НАКЛОН вычисляет значение, которое характеризует скорость изменения данных вдоль линии регрессии. Зная наклон (коэффициент a) и значение коэффициента b можно рассчитать приближенные будущие значения какого-либо свойства y, которое меняется при изменении характеристики x.
Примеры использования функции НАКЛОН в Excel
Для расчета наклона линии регрессии используется уравнение:
- x_ср – среднее значение для диапазона известных значений независимой переменной;
- y_ср – среднее значение для диапазона известных значений зависимой переменной.
Функция НАКЛОН не может быть использована для анализа коллинеарных данных и будет возвращать код ошибки #ДЕЛ/0! в отличие от функции ЛИНЕЙН, которая использует иной алгоритм расчета и возвращает как минимум одно полученное значение.
Пример 1. Определить наклон аппроксимирующей прямой для показателей средней пенсии на протяжении нескольких лет.
Вид исходной таблицы данных:
Для нахождения наклона используем следующую формулу:
- B3:B13 – ссылка на диапазон ячеек, содержащих данные о средней пенсии, характеризующие зависимую переменную y;
- A3:A13 – диапазон ячеек с данными об отчетных периодах (годах), характеризующие независимую переменную x.
В результате вычислений получим:
Полученное значение свидетельствует о том, что на протяжении обозначенного периода размер пенсионных выплат в среднем увеличивался примерно на 560 рублей.
Прогноз объема продаж по линейно регрессии в Excel
Пример 2. В таблице Excel содержатся данные о прибыли за продажи некоторого продукта компании на протяжении последних нескольких дней. Рассчитать коэффициенты a и b уравнения прямой y=ax+b, аппроксимирующей данные. На основе полученного уравнения спрогнозировать данные о продажах для трех последующих дней.
Вид таблицы с данными:
Для нахождения коэффициента a используем следующую формулу:
Коэффициент b рассчитывается с помощью следующей функции:
Искомое уравнение имеет вид:
Для определения последующих значений y достаточно лишь подставить требуемое значение x. Выполним расчет предполагаемой прибыли для 13-го дня:
- D3 – полученное значение коэффициента a;
- A15 – новое значение x;
- E3 – значение коэффициента b.
Используем функцию автозаполнения чтобы получить значения для остальных дней:
Анализ корреляции спроса и объема производства в Excel
Пример 3. В таблице содержатся данные о количестве произведенной продукции за месяц, а также о числе приобретенных товаров данной марки покупателями. Отобразить взаимосвязь между данными графически, определить, целесообразно ли использовать уравнение линейно регрессии для описания корреляции между спросом и числом произведенных товаров.
Вид таблицы данных:
Для определения зависимости между двумя рядами числовых данных рассчитаем коэффициент корреляции по формуле:
Полученное значение (0,983) свидетельствует о том, что между двумя числовыми диапазонами существует сильная прямая взаимосвязь. Поэтому целесообразно использовать аппроксимирующую прямую, для нахождения коэффициентов уравнения которой используем формулы:
Для нахождения спроса на товары за июль при условии, что будет произведено, например, 2000 единиц продукции, используем полученное уравнение:
Альтернативным использованию функции НАКЛОН вариантом нахождения наклона в Excel является графический метод. Построим график на основе имеющихся данных, при этом для значений X выберем диапазон ячеек со значениями числа произведенных товаров, а для Y – с числом купленных товаров:
Отобразим на графике линию тренда:
В меню «Формат линии тренда» установим флажок напротив пункта «показывать уравнение на диаграмме»:
График примет следующий вид:
Как видно, найденные коэффициенты a и b соответствуют отображаемым на графике.
Особенности использования функции НАКЛОН в Excel
Функция имеет следующий синтаксис:
Описание аргументов (все являются обязательными для заполнения):
- известные_значения_y – аргумент, принимающий массив числовых значений или ссылку на диапазон ячеек, которые содержат числа, характеризующие значения зависимой переменной y, которые определены для известных значений x;
- известные_значения_x – аргумент, который может быть указан в виде массива чисел или ссылки на диапазон ячеек, содержащих числовые значения, которые характеризуют известные значения независимой переменной x.
- В качестве аргументов должны быть переданы массивы чисел либо ссылки на диапазоны ячеек с числовыми значениями или текстовыми строками, которые могут быть преобразованы к числам. Строки, не являющиеся текстовыми представлениями числовых данных, а также логические ИСТИНА и ЛОЖЬ в расчете не учитываются.
- Если в качестве аргументов были переданы массивы, содержащие разное количество элементов, или ссылки на диапазоны с разным количеством ячеек, функция НАКЛОН вернет код ошибки #Н/Д. Аналогичный код ошибки будет возвращен в случае, если оба аргумента принимают пустые массивы или ссылки на диапазоны пустых ячеек.
- Если оба аргумента ссылаются на нечисловые данные, функция НАКЛОН вернет код ошибки #ДЕЛ/0!.
- Если в диапазоне, переданном в качестве любого из аргументов, содержатся пустые ячейки, они игнорируются в расчете. Однако ячейки, содержащие значение 0 (нуль) будут учтены.
Love Soft
Инструменты пользователя
Инструменты сайта
Боковая панель
Навигация
Загрузки всякие
Связь
Содержание
Уравнение прямой
Прямая — ГМТ, равноудаленных от двух точек.
(I) Общее уравнение прямой на плоскости
Уравнение прямой имеет вид $Ax + By + C = 0$, где $A$, $B$ и $C$ — некоторые числа, причем $A$ и $B$ не равны 0 одновременно.
При $A=0$ прямая параллельна оси oX, при $B=0$ — параллельна оси oY.
При $C=0$ прямая проходит через начало координат.
Вектор с координатами $(A;B)$ называется нормальным вектором, он перпендикулярен прямой.
Также уравнение можно переписать в виде $$A(x-x_0) + B(y-y_0) = 0$$
(II) Уравнение прямой с угловым коэффициентом
Уравнением вида $y = kx + b$ можно задать не любую прямую — а именно, нельзя задать прямую, перпендикулярную оси абсцисс.
(III) Уравнение прямой в отрезках на осях
Если прямая пересекает оси OX и OY в точках с координатами (a, 0) и (0, b), то она может быть найдена используя формулу уравнения прямой в отрезках $$frac x a + frac = 1$$
В этом виде невозможно представить прямую, проходящую через начало координат.
(IV) Уравнение прямой, проходящей через две точки
Пусть даны две несовпадающие точки A(x1;y1) и B(x2;y2). Уравнение прямой, проходящей через точки A(x1;y1) и B(x2;y2) имеет вид:
(V) Каноническое уравнение прямой
Если известны координаты точки $P(x_0, y_0)$ лежащей на прямой и направляющего вектора $ vec v = (a; b)$, то уравнение прямой можно записать в каноническом виде, используя следующую формулу:
(VI) Параметрическое уравнение прямой
Параметрические уравнения прямой могут быть записаны следующим образом $$ x = a t + x_0, y = b t + y_0$$ где $(x_0, y_0)$ — координаты точки лежащей на прямой, $(a, b)$ — координаты направляющего вектора прямой.
(VII) Уравнение прямой в полярных координатах
Уравнение прямой с углом наклона $alpha$ в полярных координатах $r$ и $phi$: $$r cos(phi-alpha)=p$$
Калькулятор
Калькулятор для составления уравнения прямой — показывает ход решения
Переход к другой форме записи
От общего уравнения к уравнению с угловым коэффициентом
Выразить переменную y: $Ax + By + C = 0$
$y = -frac A B x- frac C B$
От уравнения с угловым коэффициентом к общему уравнению
Перенести все члены в левую часть уравнения
Угловой коэффициент прямой
Угловой коэффициент прямой $k$ = численно равен тангенсу угла между прямой и положительным направлением оси абсцисс.
Тангенс угла может рассчитываться как отношение противолежащего катета к прилежащему.
Slope — угловой коэффициент — наклон, склон холма, показатель насколько крутой холм или гора.
Чтобы найти наклон между двумя точками на плоскости используется формула:
Иногда горизонтальное изменение называют «пробег», а вертикальное изменение — «подъем» или «снижение, спад».
Наклон биссектрисы первого координатного угла равен 1, так как скорость изменения по оси X и по оси Y одинаковы.
Например, найдем наклон между точками (2, 1) и (-9, 7)
Найдем наклон между точками (-1, -3) и (1, 1)
Чем больше модуль числа, чем круче склон. Положительное число означает, что наклон идет вверх при движении слева направо (прямая возрастает). Отрицательное число означает, что наклон идет вниз при движении слева направо (прямая убывает).
Угол между двумя прямыми
Пусть две неперпендикулярные прямые представляются уравнениями $$y= a_1 x+ b_1 \ y= a_2 x+ b_2$$ Тогда угол между двумя прямыми найдется по формуле $$tg(θ)=frac<1+ a_1 cdot a_2>$$
Условие параллельности двух прямых
Две прямые параллельны (или совпадают), если равны их угловые коэффициенты.
Теорема. Прямые $y = k_1 x + b_1$ и $y = k_2 x + b_2$ параллельны тогда и только тогда, когда $k_1 = k_2$ и $b_1 ne b_2$.
Задача
Проверить, выполняется ли условие параллельности прямых $2x-3y+1=0$ и $4x-6y-5=0$.
Задача
Составить уравнение прямой линии, проходящей через точку $(1;2)$ параллельно прямой $2x-3y+1=0$.
Условие перпендикулярности двух прямых
Условие перпендикулярности прямых заключается в том, что произведение их угловых коэффициентов равно –1: $$k_1 cdot k_2=-1$$
Задача
При каком значении $k$ уравнение $y=kx+1$ определяет прямую, перпендикулярную к прямой $y=2x-1$?
Задача
Составить уравнение прямой линии, проходящей через точку $(-1;1)$ перпендикулярно к прямой $3x-y+2=0$.
Сводная таблица
| угловые коэффициенты | прямые |
|---|---|
| Если угловые коэффициенты двух линейных функций равны, то прямые, являющиеся их графиками, параллельны | Параллельные прямые имеют одинаковый наклон. |
| Если угловые коэффициенты двух линейных функций не равны, то прямые, являющиеся их графиками, пересекаются | Если прямые пересекаются, то их наклоны не равны |
| Если произведение угловых коэффициентов равно (-1), то прямые, являющиеся их графиками, перпендикулярны. | Если прямые перпендикулярны, то произведение их наклонов всегда = -1. |
| — | Если прямая параллельна оси ординат, то формула не применима (возникает деление на 0), и для таких прямых угловой коэффициент не определён. |
Задачи — угловой коэффициент на бумаге в клетку
Определить угловой коэффициент прямой:
Расстояние от точки до прямой
Когда прямая на плоскости задана уравнением $ax + by + c = 0$, где a, b и c — такие вещественные константы, что a и b не равны нулю одновременно, и расстояние от прямой до точки $(x_0,y_0)$ равно
Точка на прямой, наиболее близкая к $(x_0,y_0)$, имеет координаты
http://hd01.ru/info/kak-najti-tangens-ugla-naklona-prjamoj/
http://xlench.bget.ru/doku.php/mat/algebra/eq-line
Что такое линейная функция и как выглядит ее график мы подробно разбирали здесь.
В этой статье мы остановимся на том, как находить коэффициент наклона прямой.
Как мы знаем, уравнение прямой имеет вид 


Внимание! Не просто между прямой и осью 

Например, в прямой 



В уравнении прямой 





Если прямая наклонена вправо, то угол между прямой и положительным направлением оси 

Например:
Здесь 
Если прямая наклонена влево, то угол между прямой и положительным направлением оси 

Здесь 
Решим две задачи на нахождение коэффициента наклона прямой.
1. Найдите угловой коэффициент прямой, проходящей через точки с координатами (-1;-1) и (1;3).
Решим эту задачу двумя способами.
А). Так как прямая проходит через точки (-1;-1) и (1;3), координаты этих точек удовлетворяют уравнению прямой 
или
Вычтем из второго уравнения первое, и получим 

Б). Построим график этой функции. Для этого нанесем данные точки А(-1;-1) и В(1;3) на координатную плоскость и проведем через них прямую:
Коэффициент 


Чтобы найти 
Угол 


Отсюда
2. Найдите угловой коэффициент прямой, проходящей через точки с координатами (4;0) и (0;8).
Решение с помощью системы уравнений абсолютно аналогично решению предыдущей задачи, можете воспроизвести его самостоятельно.
Выполним это задание с помощью графика.
Нанесем данные токи на координатную плоскость и проведем через них прямую:


Коэффициент наклона прямой 

В этом прямоугольном треугольнике угол 




Еще раз! Если прямая наклонена влево, то коэффициент наклона прямой отрицательный.
И.В. Фельдман, репетитор по математике.