Вам необходимо найти Тангенс 3 градусов? Он же записывается как tg(3). Чему он равен? Ниже вы можете увидеть готовый ответ:
| Тангенс 3 градусов это | 1 |
tg(3) =
1
Результат для тангенса угла 3 градуса был взят из таблицы Брадиса..
Найти любой синус, косинус, тангенс, котангенс:
Еще примеры вычислений тангенсов разных углов:
Тангенс 80 градусов = 5.6712818196177.
Тангенс 133 градусов = -1.0723687100247.
Тангенс 240 градусов = 1.7320508075689.
Тангенс 286 градусов = -3.4874144438409.
Другие похожие материалы:
- Тангенс 13
- Тангенс 300
- Котангенс 0
- Синус 352
- Синус 212
- Тангенс 10
- Косинус 10
- Синус 319
Тангенс онлайн калькулятор
Введите число от 0 до 360.
(обязательное поле)
Введите число от 0 до 59.
(не обязательное поле, по умолчанию — 0)
Введите число от 0 до 59.
(не обязательное поле, по умолчанию — 0)
Математика, Геометрия 9 класс.
Тангенс 3 градусов таблица.
Тангенс 3 градусов 0 минут равен = 0.0524
Тангенс 3 градусов 1 минут равен = 0.0527
Тангенс 3 градусов 2 минут равен = 0.053
Тангенс 3 градусов 3 минут равен = 0.0533
Тангенс 3 градусов 4 минут равен = 0.0536
Тангенс 3 градусов 5 минут равен = 0.0539
Тангенс 3 градусов 6 минут равен = 0.0542
Тангенс 3 градусов 7 минут равен = 0.0544
Тангенс 3 градусов 8 минут равен = 0.0547
Тангенс 3 градусов 9 минут равен = 0.055
Тангенс 3 градусов 10 минут равен = 0.0553
Тангенс 3 градусов 11 минут равен = 0.0556
Тангенс 3 градусов 12 минут равен = 0.0559
Тангенс 3 градусов 13 минут равен = 0.0562
Тангенс 3 градусов 14 минут равен = 0.0565
Тангенс 3 градусов 15 минут равен = 0.0568
Математика, Геометрия 9 класс.
Тангенс угла 3 градусов
Тангенс 3 таблица.
Тангенс 3 градусов 16 минут равен = 0.0571
Тангенс 3 градусов 17 минут равен = 0.0574
Тангенс 3 градусов 18 минут равен = 0.0577
Тангенс 3 градусов 19 минут равен = 0.058
Тангенс 3 градусов 20 минут равен = 0.0582
Тангенс 3 градусов 21 минут равен = 0.0585
Тангенс 3 градусов 22 минут равен = 0.0588
Тангенс 3 градусов 23 минут равен = 0.0591
Тангенс 3 градусов 24 минут равен = 0.0594
Тангенс 3 градусов 25 минут равен = 0.0597
Тангенс 3 градусов 26 минут равен = 0.06
Тангенс 3 градусов 27 минут равен = 0.0603
Тангенс 3 градусов 28 минут равен = 0.0606
Тангенс 3 градусов 29 минут равен = 0.0609
Тангенс 3 градусов 30 минут равен = 0.0612
Математика, Геометрия 9 класс.
Тангенс 3 равен:
Таблица значений Тангенсов 3 градусов.
Тангенс 3 градусов 31 минут равен = 0.0615
Тангенс 3 градусов 32 минут равен = 0.0617
Тангенс 3 градусов 33 минут равен = 0.062
Тангенс 3 градусов 34 минут равен = 0.0623
Тангенс 3 градусов 35 минут равен = 0.0626
Тангенс 3 градусов 36 минут равен = 0.0629
Тангенс 3 градусов 37 минут равен = 0.0632
Тангенс 3 градусов 38 минут равен = 0.0635
Тангенс 3 градусов 39 минут равен = 0.0638
Тангенс 3 градусов 40 минут равен = 0.0641
Тангенс 3 градусов 41 минут равен = 0.0644
Тангенс 3 градусов 42 минут равен = 0.0647
Тангенс 3 градусов 43 минут равен = 0.065
Тангенс 3 градусов 44 минут равен = 0.0653
Тангенс 3 градусов 45 минут равен = 0.0655
Математика, Геометрия 9 класс.
Найти Тангенс 3 градусов:
Tg 3 градусов равен:
Тангенс 3 градусов 46 минут равен = 0.0658
Тангенс 3 градусов 47 минут равен = 0.0661
Тангенс 3 градусов 48 минут равен = 0.0664
Тангенс 3 градусов 49 минут равен = 0.0667
Тангенс 3 градусов 50 минут равен = 0.067
Тангенс 3 градусов 51 минут равен = 0.0673
Тангенс 3 градусов 52 минут равен = 0.0676
Тангенс 3 градусов 53 минут равен = 0.0679
Тангенс 3 градусов 54 минут равен = 0.0682
Тангенс 3 градусов 55 минут равен = 0.0685
Тангенс 3 градусов 56 минут равен = 0.0688
Тангенс 3 градусов 57 минут равен = 0.069
Тангенс 3 градусов 58 минут равен = 0.0693
Тангенс 3 градусов 59 минут равен = 0.0696
Тангенс 3 градусов 60 минут равен = 0.0699
Недавние расчеты
Тангенс 3 градусов 10 минут и 37 секунд равен = 0.055505035713547
(0.055448140708498 радиан)
Тангенс 3 градусов 29 минут и 58 секунд равен = 0.061152887610172
(0.061076827546179 радиан)
Тангенс 3 градусов 53 минут и 51 секунд равен = 0.068129324806457
(0.068024207596479 радиан)
Тангенс 3 градусов 33 минут и 55 секунд равен = 0.062306274503759
(0.062225835970409 радиан)
Тангенс 3 градусов 15 минут и 37 секунд равен = 0.056964076427344
(0.056902581751826 радиан)
Тангенс 3 градусов 1 минут и 55 секунд равен = 0.052966862724113
(0.052917413293106 радиан)
Тангенс 3 градусов 5 минут и 45 секунд равен = 0.054085129021234
(0.054032484759658 радиан)
Тангенс 3 градусов 17 минут и 9 секунд равен = 0.057411563734059
(0.057348610338447 радиан)
Тангенс 3 градусов 46 минут и 10 секунд равен = 0.065884297899663
(0.065789216526564 радиан)
Тангенс 3 градусов 48 минут и 0 секунд равен = 0.066419926714923
(0.066322511575785 радиан)
tg(0°)=tg(360°)=0 точная, но чуть более сложная таблица ( с точностью до 1′) здесь.
|
Углы |
Углы |
Углы |
Углы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
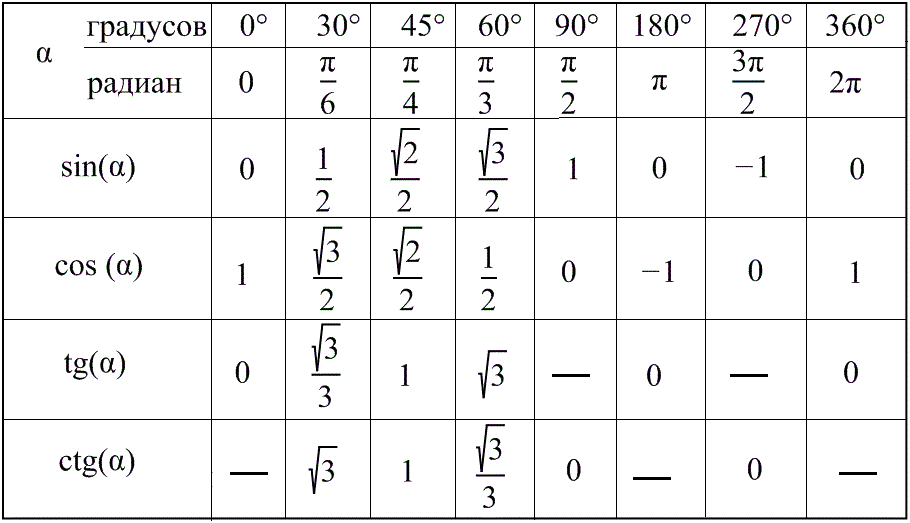
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π).
Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций
Доп. Инфо:
- Таблица косинусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений косинусов.
- Таблица синусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений синусов.
- Таблица синусов, она-же косинусов точная.
- Таблица тангенсов углов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений тангенса, tg
- Таблица котангенсов углов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений котангенса, ctg
- Таблица тангенсов, она же котангенсов точная.
- Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π).
Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций. - Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге.
- Определение и численные соотношения между единицами измерения углов в РФ.
Тысячные, угловые градусы, минуты, секунды, радианы, обороты. - Таблица соответствия угловых градусов, радиан, оборотов, тысячных (артиллерийских РФ). 0-360 градусов, 0-2π радиан.
| tg(3°0′0″) = 0.05240777928 | tg(3°20′0″) = 0.05824336747 | tg(3°40′0″) = 0.06408291178 |
| tg(3°1′0″) = 0.05269947089 | tg(3°21′0″) = 0.05853524741 | tg(3°41′0″) = 0.064375 |
| tg(3°2′0″) = 0.05299117145 | tg(3°22′0″) = 0.05882713729 | tg(3°42′0″) = 0.06466709917 |
| tg(3°3′0″) = 0.05328288099 | tg(3°23′0″) = 0.05911903716 | tg(3°43′0″) = 0.06495920933 |
| tg(3°4′0″) = 0.05357459958 | tg(3°24′0″) = 0.05941094707 | tg(3°44′0″) = 0.06525133053 |
| tg(3°5′0″) = 0.05386632726 | tg(3°25′0″) = 0.05970286706 | tg(3°45′0″) = 0.06554346282 |
| tg(3°6′0″) = 0.05415806409 | tg(3°26′0″) = 0.0599947972 | tg(3°46′0″) = 0.06583560624 |
| tg(3°7′0″) = 0.0544498101 | tg(3°27′0″) = 0.06028673753 | tg(3°47′0″) = 0.06612776086 |
| tg(3°8′0″) = 0.05474156536 | tg(3°28′0″) = 0.0605786881 | tg(3°48′0″) = 0.06641992671 |
| tg(3°9′0″) = 0.05503332991 | tg(3°29′0″) = 0.06087064895 | tg(3°49′0″) = 0.06671210386 |
| tg(3°10′0″) = 0.0553251038 | tg(3°30′0″) = 0.06116262015 | tg(3°50′0″) = 0.06700429235 |
| tg(3°11′0″) = 0.05561688709 | tg(3°31′0″) = 0.06145460174 | tg(3°51′0″) = 0.06729649222 |
| tg(3°12′0″) = 0.05590867981 | tg(3°32′0″) = 0.06174659376 | tg(3°52′0″) = 0.06758870354 |
| tg(3°13′0″) = 0.05620048202 | tg(3°33′0″) = 0.06203859628 | tg(3°53′0″) = 0.06788092635 |
| tg(3°14′0″) = 0.05649229378 | tg(3°34′0″) = 0.06233060933 | tg(3°54′0″) = 0.0681731607 |
| tg(3°15′0″) = 0.05678411513 | tg(3°35′0″) = 0.06262263297 | tg(3°55′0″) = 0.06846540663 |
| tg(3°16′0″) = 0.05707594612 | tg(3°36′0″) = 0.06291466725 | tg(3°56′0″) = 0.06875766421 |
| tg(3°17′0″) = 0.05736778679 | tg(3°37′0″) = 0.06320671223 | tg(3°57′0″) = 0.06904993348 |
| tg(3°18′0″) = 0.05765963721 | tg(3°38′0″) = 0.06349876794 | tg(3°58′0″) = 0.0693422145 |
| tg(3°19′0″) = 0.05795149742 | tg(3°39′0″) = 0.06379083444 | tg(3°59′0″) = 0.0696345073 |
Значения тангенса и котангенса на тригонометрическом круге
В прошлой статье мы познакомились с тригонометрическим кругом и научились находить значения синуса и косинуса основных углов.
Как же быть с тангенсом и котангенсом ? Об этом и поговорим сегодня.
Где же на тригонометрическом круге оси тангенсов и котангенсов?
Ось тангенсов параллельна оси синусов (имеет тоже направление, что ось синусов) и проходит через точку (1; 0).
Ось котангенсов параллельна оси косинусов (имеет тоже направление, что ось косинусов) и проходит через точку (0; 1).
На каждой из осей располагается вот такая цепочка основных значений тангенса и котангенса: Почему так?
Я думаю, вы легко сообразите и сами. 
Собственно, картинка за себя сама говорит.
Если не очень все же понятно, разберем примеры:
Пример 1.
Вычислить
Находим на круге . Эту точку соединяем с точкой (0;0) лучом (начало – точка (0;0)) и смотрим, где этот луч пересекает ось тангенсов. Видим, что
Ответ:
Пример 2.
Вычислить
Находим на круге . Точку (0;0) соединяем с указанной точкой лучом. И видим, что луч никогда не пересечет ось тангенсов.
не существует.
Ответ: не существует
Пример 3.
Вычислить
Находим на круге точку (это та же точка, что и ) и от нее по часовой стрелке (знак минус!) откладываем (). Куда попадаем? Мы окажемся в точке, что на круге у нас (см. рис.) названа как . Эту точку соединяем с точкой (0;0) лучом. Вышли на ось тангенсов в значение .
Так значит,
Ответ:
Пример 4.
Вычислить
Поэтому от точки (именно там будет ) откладываем против часовой стрелки .
Выходим на ось котангенсов, получаем, что
Ответ:
Пример 5.
Вычислить
Находим на круге . Эту точку соединяем с точкой (0; 0). Выходим на ось котангенсов. Видим, что
Ответ:
Теперь, умея находить по тригонометрическому кругу значения тригонометрических функций (а я надеюсь, что статья, где мы начинали знакомство с кругом и учились вычислять значения синусов и косинусов, вами прочитана…), вы можете пройт и тест по теме «Нахождение значений косинуса, синуса, тангенса и котангенса различных углов».
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
Тригонометрия простыми словами
Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».
Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике:
- Синус угла – отношение противолежащего катета к гипотенузе;
- Косинус угла – отношение прилежащего катета к гипотенузе;
- Тангенс угла – отношение противолежащего катета к прилежащему;
- Котангенс угла – отношение прилежащего катета к противолежащему.
Или в виде формул:
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
| 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|
| sin | 0 | 1 | √3 | – |
| ctg | – | √3 | 1 |
Принцип повтора знаков тригонометрических функцийУгол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону. В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ. Например, значения тригонометрических функций для углов 270° и -90° равны. Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно. Тригонометрический кругУглы в радианахДля математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан. Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π . Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций. источники: http://ege-study.ru/ru/ege/materialy/matematika/trigonometricheskij-krug/ http://matematika.club/articles/trigonometry/ |