Угол между касательными.
В этой статье мы рассмотрим, как решать задачи на нахождение угла между касательными.
Угол между касательными.
Пусть дана функция 

Угол между прямыми — это меньший из двух углов, образованных этими прямыми. В нашем случае это угол 
Чтобы найти угол 
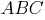
В треугольнике 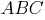


Но угол 



Угол 
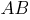


Итак,
Мы помним, что угол между прямыми всегда острый, и его тангенс должен быть больше нуля. В общем случае 
формула для нахождения тангенса угла между касательными 

Решим задачу:
Найти тангенс большего угла между касательными, проведенными из точки 

Заметим, что в этой задаче нужно найти тангенс большего угла между касательными, то есть тангенс тупого угла. Тангенсы смежных углов равны по модулю, но противоположны по знаку. Следовательно, нам нужно найти тангенс угла между касательными, и в ответе записать это значение со знаком «-«.
Нужно найти коэффициенты наклона касательных, проведенных к параболе из точки 


Вспомним, как находить уравнение касательной, проведенной к графику функции 
Пусть 
Уравнение касательной, проведенной из точки 
Подставим выражения для 


Решим это уравнение. Упростим правую часть:
Итак, мы нашли абсциссы точек касания:
Найдем коэффициенты наклона касательных, проведенных к параболе 
Тангенс большего угла между касательными равен
Ответ: -4
И.В. Фельдман, репетитор по математике.
7. Взаимосвязь функции и ее производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Угловой коэффициент касательной как тангенс угла наклона
(blacktriangleright) Если уравнение прямой задано в виде ({color{royalblue}{y=kx+b ;}}), то число (k) называется угловым коэффициентом.
(blacktriangleright) Угол (alpha) наклона прямой – это угол между этой прямой и положительным направлением оси (Ox) ((0leqslant
alpha< 180^circ)), лежащий в верхней полуплоскости.
(blacktriangleright) Основная формула. Угловой коэффициент прямой (y=kx+b) равен тангенсу угла наклона этой прямой:
[{large{color{royalblue}{k=mathrm{tg}, alpha}}}]
Т.к. касательная к графику некоторой функции — это и есть прямая, то для нее верны все эти утверждения.
Если (alpha<90^circ), то (k>0);
если (alpha>90^circ), то (k<0);
если (alpha=0^circ), то (k=0) (уравнение прямой имеет вид (y=b) и она параллельна оси (Ox));
если (alpha=90^circ), то уравнение прямой имеет вид (x=a) и она перпендикулярна оси (Ox).
Задание
1
#685
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = x), образует с положительным направлением оси (Ox) угол (alpha). Найдите (mathrm{tg}, alpha).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как для прямой (y = x) коэффициент (k) равен (1), то (mathrm{tg}, alpha = 1).
Ответ: 1
Задание
2
#686
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = 2x — 3), образует с положительным направлением оси (Ox) угол (alpha). Найдите (mathrm{tg}, alpha).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как для прямой (y = 2x — 3) коэффициент (k) равен (2), то (mathrm{tg}, alpha = 2).
Ответ: 2
Задание
3
#687
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = -x + 2), образует с положительным направлением оси (Ox) угол (alpha). Найдите (mathrm{tg}, alpha).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как для прямой (y = -x + 2) коэффициент (k) равен (-1), то (mathrm{tg}, alpha = -1).
Ответ: -1
Задание
4
#688
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = kx + 77), образует с положительным направлением оси (Ox) угол (alpha). Найдите (k), если (mathrm{tg}, alpha = 12).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как тангенс угла (alpha) между прямой (y = kx + 77) и положительным направлением оси (Ox) равен (12), то (k = mathrm{tg}, alpha = 12).
Ответ: 12
Задание
5
#689
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = kx + 0,2), образует с положительным направлением оси (Ox) угол (alpha). Найдите (k), если (mathrm{tg}, alpha = -3,3).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как тангенс угла (alpha) между прямой (y = kx + 0,2) и положительным направлением оси (Ox) равен (-3,3), то (k = mathrm{tg}, alpha = -3,3).
Ответ: -3,3
Задание
6
#690
Уровень задания: Легче ЕГЭ
Прямая, заданная уравнением (y = kx), образует с положительным направлением оси (Ox) угол (alpha). Найдите (k), если (mathrm{tg}, alpha = 0).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как тангенс угла (alpha) между прямой (y = kx) и положительным направлением оси (Ox) равен (0), то (k = mathrm{tg}, alpha = 0).
Ответ: 0
Задание
7
#693
Уровень задания: Легче ЕГЭ
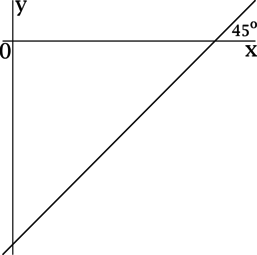
Прямая (y = kx — 2016) образует угол (45^{circ}) с положительным направлением оси (Ox). Найдите (k).
Для прямой, заданной уравнением (y = kx + b), коэффициент (k) есть значение тангенса угла между прямой (y = kx + b) и положительным направлением оси (Ox).
Так как угол между прямой (y = kx — 2016) и положительным направлением оси (Ox) равен (dfrac{pi}{4}), то (k = mathrm{tg}, dfrac{pi}{4} = 1).
Ответ: 1
Теме «Угловой коэффициент касательной как тангенс угла наклона» в аттестационном экзамене отводится сразу несколько заданий. В зависимости от их условия, от выпускника может требоваться как полный ответ, так и краткий. При подготовке к сдаче ЕГЭ по математике ученику обязательно стоит повторить задачи, в которых требуется вычислить угловой коэффициент касательной.
Сделать это вам поможет образовательный портал «Школково». Наши специалисты подготовили и представили теоретический и практический материал максимально доступно. Ознакомившись с ним, выпускники с любым уровнем подготовки смогут успешно решать задачи, связанные с производными, в которых требуется найти тангенс угла наклона касательной.
Основные моменты
Для нахождения правильного и рационального решения подобных заданий в ЕГЭ необходимо вспомнить базовое определение: производная представляет собой скорость изменения функции; она равна тангенсу угла наклона касательной, проведенной к графику функции в определенной точке. Не менее важно выполнить чертеж. Он позволит найти правильное решение задач ЕГЭ на производную, в которых требуется вычислить тангенс угла наклона касательной. Для наглядности лучше всего выполнить построение графика на плоскости ОХY.
Если вы уже ознакомились с базовым материалом на тему производной и готовы приступить к решению задач на вычисление тангенса угла наклона касательной, подобных заданиям ЕГЭ, сделать это можно в режиме онлайн. Для каждого задания, например, задач на тему «Связь производной со скоростью и ускорением тела», мы прописали правильный ответ и алгоритм решения. При этом учащиеся могут попрактиковаться в выполнении задач различного уровня сложности. В случае необходимости упражнение можно сохранить в разделе «Избранное», чтобы потом обсудить решение с преподавателем.

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Уравнение любой прямой в общем виде задается формулой:
$$y=kx+b;$$
Где (k) — это коэффициент наклона прямой, а (b) — свободный член.
Уравнение прямой в условии задачи выглядит так (y=-4). Сопоставьте это уравнение с общим видом прямой, и увидите, что у прямой из условия (k=0), а (b=-4).
Мы получили, что коэффициент наклона прямой из условия равен нулю! Значит у любой прямой, которая будет ей параллельна, коэффициент наклона тоже будет равен нулю. А раз коэффициент наклона ноль, то и производная тоже должна быть ноль.
Переформулируем условие задачи: необходимо найти на графике функции (f(x)) точки, в которых производная равна нулю.
Производная равна нулю в точках минимума и максимума: в «вершинах» и «впадинах». Нам остается только посчитать их количество на графике. Я их отметил красными точками:
Как найти тангенс угла наклона касательной
Геометрический смысл производной первого порядка функции F(х) представляет собой касательную прямую к ее графику, проходящую через заданную точку кривой и совпадающую с ней в этой точке. Причем значение производной в данной точке х0 является угловым коэффициентом или иначе – тангенсом угла наклона касательной прямой k = tg a = F`(х0). Вычисление данного коэффициента – одна из наиболее распространенных задач теории функций.

Инструкция
Запишите заданную функцию F(x), например F(x) = (x³ + 15х +26). Если в задаче явно указана точка, через которую проводится касательная, например, ее координата х0 = -2, можно обойтись без построения графика функции и дополнительных прямых на декартовой системе ОХY. Найдите производную первого порядка от заданной функции F`(x). В рассматриваемом примере F`(x) = (3x² + 15). Подставьте заданное значение аргумента х0 в производную функции и вычислите ее значение: F`(-2) = (3(-2)² + 15) = 27. Таким образом, вы нашли tg a = 27.
При рассмотрении задачи, где требуется определить тангенс угла наклона касательной к графику функции в точке пересечения этого графика с осью абсцисс, вам понадобится сначала найти числовое значение координат точки пересечения функции с ОХ. Для наглядности лучше всего выполнить построение графика функции на двухмерной плоскости ОХY.
Задайте координатный ряд для абсцисс, например, от -5 до 5 с шагом 1. Подставляя в функцию значения х, вычислите соответствующие им ординаты у и отложите на координатной плоскости полученные точки (х, у). Соедините точки плавной линией. Вы увидите на выполненном графике место пересечения функцией оси абсцисс. Ордината функции в данной точке равна нулю. Найдите численное значение соответствующего ей аргумента. Для этого заданную функцию, например F(x) = (4x² — 16), приравняйте к нулю. Решите полученное уравнение с одной переменной и вычислите х: 4x² — 16 = 0, x² = 4, х = 2. Таким образом, согласно условию задачи, тангенс угла наклона касательной к графику функции необходимо найти в точке с координатой х0 = 2.
Аналогично описанному ранее способу определите производную функции: F`(x) = 8*x. Затем вычислите ее значение в точке с х0 = 2, что соответствует точке пересечения исходной функции с ОХ. Подставьте полученное значение в производную функции и вычислите тангенс угла наклона касательной: tg a = F`(2) = 16.
При нахождении углового коэффициента в точке пересечения графика функции с осью ординат (ОY) выполните аналогичные действия. Только координату искомой точки х0 сразу следует принять равной нулю.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Геометрический смысл производной
Если плохо разбираешься в производной, то вот тебе полноценный гид по ней, с текстом, примерами и вебинарами: «Производная функции – геометрический смысл и правила дифференцирования»!
Рассмотрим график какой-то функции ( y=fleft( x right)):
Выберем на линии графика некую точку ( A). Пусть ее абсцисса ( {{x}_{0}}), тогда ордината равна ( fleft( {{x}_{0}} right)).
Затем выберем близкую к точке ( A) точку ( B) с абсциссой ( {{x}_{0}}+Delta x); ее ордината – это ( fleft( {{x}_{0}}+Delta x right)):
Проведем прямую через эти точки. Она называется секущей (прямо как в геометрии).
Обозначим угол наклона прямой к оси ( Ox) как ( alpha ).
Как и в тригонометрии, этот угол отсчитывается от положительного направления оси абсцисс против часовой стрелки.
Какие значения может принимать угол ( alpha )?
Как ни наклоняй эту прямую, все равно одна половина будет торчать вверх. Поэтому максимально возможный угол – ( 180{}^circ ), а минимально возможный – ( 0{}^circ ).
Значит, ( alpha in left[ 0{}^circ ;180{}^circ right)). Угол ( 180{}^circ ) не включается, поскольку положение прямой в этом случае в точности совпадает с ( 0{}^circ ), а логичнее выбирать меньший угол.
Возьмем на рисунке такую точку ( C), чтобы прямая ( AC) была параллельна оси абсцисс, а ( BC) – ординат:
По рисунку видно, что ( AC=Delta x), а ( BC=Delta f).
Тогда отношение приращений:
( frac{Delta f}{Delta x}=frac{BC}{AC}={tg}alpha )
(так как ( angle C=90{}^circ ), то ( triangle ABC) – прямоугольный).
Давай теперь уменьшать ( Delta x).
Тогда точка ( B) будет приближаться к точке ( A). Когда ( Delta x) станет бесконечно малым ( left( Delta xto 0 right)), отношение ( frac{Delta f}{Delta x}) станет равно производной функции в точке ( {{x}_{0}}).
Что же при этом станет с секущей?
Точка ( B) будет бесконечно близка к точке ( A), так что их можно будет считать одной и той же точкой.
Но прямая, имеющая с кривой только одну общую точку – это ни что иное, как касательная (в данном случае это условие выполняется только на небольшом участке – вблизи точки ( A), но этого достаточно).
Говорят, что при этом секущая занимает предельное положение.
Угол наклона секущей к оси ( displaystyle Ox) назовем ( varphi ). Тогда получится, что производная
( {f}’left( {{x}_{0}} right)underset{Delta xto 0}{mathop{=}},frac{Delta f}{Delta x}= {tg}varphi ),
то есть
Производная равна тангенсу угла наклона касательной к графику функции в данной точке
Поскольку касательная – это прямая, давай теперь вспомним уравнение прямой:
( y=kx+b).
За что отвечает коэффициент ( displaystyle k)? За наклон прямой. Он так и называется: угловой коэффициент.
Что это значит? А то, что равен он тангенсу угла между прямой и осью ( displaystyle Ox)!
То есть вот что получается:
( {f}’left( {{x}_{0}} right)= {tg}varphi =k).
Но мы получили это правило, рассматривая возрастающую функцию. А что изменится, если функция будет убывающей?
Посмотрим: Теперь углы ( alpha ) и ( displaystyle varphi ) тупые. А приращение функции ( Delta f) – отрицательное.
Снова рассмотрим ( triangle ABC): ( angle B=180{}^circ -alpha text{ }Rightarrow text{ } {tg}angle B=- {tg}alpha ).
С другой стороны, ( {tg}angle B=frac{AC}{BC}=frac{-Delta f}{Delta x}).
Получаем: ( frac{-Delta f}{Delta x}=- {tg}alpha text{ }Rightarrow text{ }frac{Delta f}{Delta x}= {tg}alpha ), то есть все, как и в прошлый раз.
Снова устремим точку ( displaystyle B) к точке ( displaystyle A), и секущая ( displaystyle AB) примет предельное положение, то есть превратится в касательную к графику функции в точке ( displaystyle A).
Итак, сформулируем окончательно полученное правило:
Производная функции в данной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или (что то же самое) угловому коэффициенту этой касательной:
( {f}’left( {{x}_{0}} right)= {tg}varphi =k)
Это и есть геометрический смысл производной.
Окей, все это интересно, но зачем оно нам? Вот пример:
На рисунке изображен график функции ( displaystyle y=mathsf{f}left( x right)) и касательная к нему в точке с абсциссой ( {{x}_{0}}).
Найдите значение производной функции ( displaystyle mathsf{f}left( x right)) в точке ( {{x}_{0}}).
Решение.
Как мы недавно выяснили, значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс:
( displaystyle f’left( x right)=k= {tg}varphi).
Значит, для нахождения значения производной нам нужно найти тангенс угла наклона касательной.
На рисунке у нас отмечено две точки, лежащие на касательной, координаты которых нам известны. Так давай достроим прямоугольный треугольник, проходящий через эти точки, и найдем тангенс угла наклона касательной!
Угол наклона касательной к оси ( displaystyle Ox) – это ( displaystyle angle BAC). Найдем тангенс этого угла:
( displaystyle {tg}angle BAC=frac{BC}{AC}=frac{6}{5}=1,2).
Таким образом, производная функции ( displaystyle mathsf{f}left( x right)) в точке ( {{x}_{0}}) равна ( displaystyle 1,2).
Ответ: ( displaystyle 1,2).
Теперь попробуй сам.
Уравнение касательной к графику функций
А сейчас сосредоточимся на произвольных касательных.
Предположим, у нас есть какая-то функция, например, ( fleft( x right)=left( {{x}^{2}}+2 right)). Мы нарисовали ее график и хотим провести касательную к нему в какой-нибудь точке ( {{x}_{0}}). Например, в точке ( {{x}_{0}}=2).
Берем линейку, пристраиваем ее к графику и чертим:
Что мы знаем об этой прямой? Что самое важное нужно знать о прямой на координатной плоскости?
Поскольку прямая – это изображение линейной функции, очень удобно было бы знать ее уравнение. То есть коэффициенты ( k) и ( b) в уравнении
( y=kx+b).
Но ведь ( k) мы уже знаем! Это угловой коэффициент касательной, который равен производной функции в этой точке:
( k={f}’left( {{x}_{0}} right)).
В нашем примере будет так:
( {f}’left( x right)={{left( {{x}^{2}}+2 right)}^{prime }}=2x;)
( k={f}’left( {{x}_{0}} right)={f}’left( 2 right)=2cdot 2=4.)
Теперь остается найти ( b) . Это проще простого: ведь ( b) – значение ( y) при ( displaystyle x=0).
Графически ( b) – это координата пересечения прямой с осью ординат (ведь ( displaystyle x=0) во всех точках оси ( displaystyle Oy)):
Проведём ( BCparallel Ox) (так, что ( triangle ABC) – прямоугольный).
Тогда ( angle ABC=alpha )(тому самому углу между касательной и осью абсцисс). Чему равны ( displaystyle AC) и ( displaystyle BC)?
По рисунку явно видно, что ( BC={{x}_{0}}), а ( AC=fleft( {{x}_{0}} right)-b). Тогда получаем:
( {f}’left( {{x}_{0}} right)= {tg}alpha =frac{AC}{BC}=frac{fleft( {{x}_{0}} right)-b}{{{x}_{0}}}text{ }Rightarrow text{ }b=fleft( {{x}_{0}} right)-{{x}_{0}}cdot {f}’left( {{x}_{0}} right)).
Соединяем все полученные формулы в уравнение прямой:
( y=kx+b={f}’left( {{x}_{0}} right)cdot x+fleft( {{x}_{0}} right)-{{x}_{0}}cdot {f}’left( {{x}_{0}} right);)
( y={f}’left( {{x}_{0}} right)cdot left( x-{{x}_{0}} right)+fleft( {{x}_{0}} right))
Это и есть уравнение касательной к графику функции ( fleft( x right)) в точке ( {{x}_{0}}).
Пример:
Найди уравнение касательной к графику функции ( fleft( x right)={{x}^{2}}-2x+3) в точке ( {{x}_{0}}=3).
Решение:
На этом примере выработаем простой…
Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике
ЕГЭ №7. Производная функции — геометрический смысл, дифференцирование
На этом видео мы вспомним, что такое функция и её график, научимся искать производную некоторых функций, например, такой: y = 2×3 – 3×2 + x + 5.
Мы разберём от А до Я все 7 типов задач, которые могут попасться в задаче №7 из ЕГЭ. Узнаем, на какие 3 фразы в условии задачи нужно обратить особое внимание, чтобы с лёгкостью решить задачу и не потерять баллы на ровном месте.
Разберём все возможные ошибки, которые можно допустить в этих задачах. Мы поймём, что многие из этих задач решаются обычным подсчётом клеточек на графике! Главное – не перепутать, что нужно считать.
P.S. Не забудьте потом посмотреть родственную тему: «Интегралы на ЕГЭ. Первообразные элементарных функций».