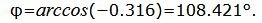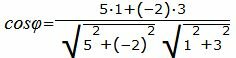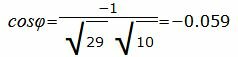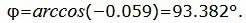Как найти тангенс угла между прямыми - Исправление недочетов и поиск решений вместе с Examum.ru

Угол между прямыми онлайн

С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

1. Угол между прямыми на плоскости

Прямые заданы каноническими уравнениями

1.1. Определение угла между прямыми

Пусть в двухмерном пространстве прямые L₁ и L₂ заданы каноническими уравнениями

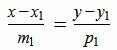(1.1)

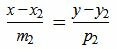(1.2)

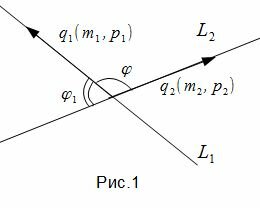
Задача об определении угла между прямыми L₁ и L₂ сводится к задаче об определении угла между направляющими векторами q₁ и q₂ (рис.1).

(1.3)

Из выражения (1.3) получим:

Таким образом, из формулы (1.4) можно найти угол между прямыми L₁ и L₂. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ₁. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L₁ и L₂: φ₁=180-φ.

Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

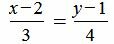(1.5)

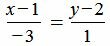(1.6)

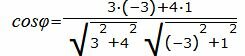
Упростим и решим:

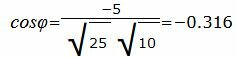
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

Угол между прямыми равен:

1.2. Условие параллельности прямых

Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:

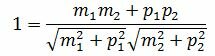(1.7)

Сделаем преобразования с выражением (1.7):

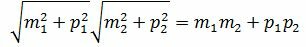
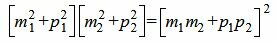
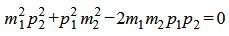
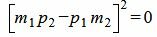
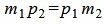(1.8)

Таким образом условие параллельности прямых L₁ и L₂ имеет вид (1.8). Если m₂≠0 и p₂≠0, то (1.8) можно записать так:

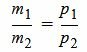(1.9)

Пример 2. Определить, параллельны ли прямые

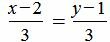(1.10)

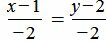(1.11)

Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.

Ответ. Прямые (1.10) и (1.11) параллельны.

1.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:

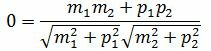(1.12)

Правая часть выражения (1.12) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L₁ и L₂ были перпендикулярны , должно выполняться условие

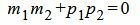(1.13)

Пример 3. Определить, перпендикулярны ли прямые

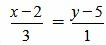(1.14)

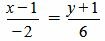(1.15)

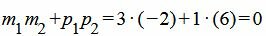(16)

Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.

Ответ. Прямые (1.14) и (1.15) перпендикулярны.

Прямые заданы общими уравнениями

1.4. Определение угла между прямыми

Пусть две прямые L₁ и L₂ заданы общими уравнениями

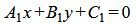(1.17)

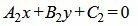(1.18)

Так как нормальным вектором прямой L₁ является n₁=(A₁, B₁), а нормальным вектором прямой L₂ является n₂=(A₂, B₂), то задача об определении угла между прямыми L₁ и L₂ сводится к определению угла φ между векторами n₁ и n₂ (Рис.2).

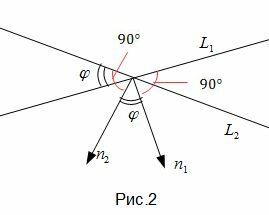
Из определения скалярного произведения двух векторов, имеем:

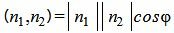(1.19)

Из уравнения (19) получим

Пример 4. Найти угол между прямыми

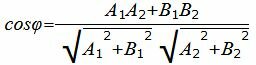(23)

Упростим и решим:

Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

1.5. Условие параллельности прямых

Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:

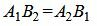(1.24)

С другой стороны условие параллельности прямых L₁ и L₂ эквивалентно условию коллинеарности векторов n₁ и n₂ и можно представить так:

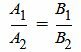(1.25)

Как видим уравнения (1.24) и (1.25) эквивалентны при A₂≠0 и B₂≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).

Пример 5. Определить, параллельны ли прямые

Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.

Ответ. Прямые (1.26) и (1.27) параллельны.

1.6. Условие перпендикулярности прямых

Условие перпендикулярности прямых L₁ и L₂ можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n₁,n₂)=0. Откуда

Таким образом условие перпендикулярности прямых определяется равенством (1.28).

Пример 6. Определить, перпендикулярны ли прямые

Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.

Ответ. Прямые (1.29) и (1.30) перпендикулярны.

2. Угол между прямыми в пространстве

2.1. Определение угла между прямыми

Пусть в пространстве прямые L₁ и L₂ заданы каноническими уравнениями

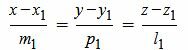(2.1)

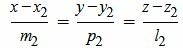(2.2)

Задача об определении угла между прямыми L₁ и L₂ сводится к задаче об определении угла между направляющими векторами q₁ и q₂ .

(2.3)

Из выражения (2.3) получим:

Таким образом, из формулы (2.4) можно найти угол между прямыми L₁ и L₂. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L₁ и L₂: φ₁=180-φ.

Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

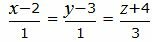(2.5)

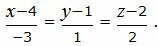(2.6)

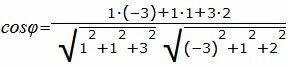
Упростим и решим:

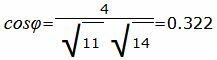
Угол между прямыми равен:

2.2. Условие параллельности прямых

Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q₁ и q₂, т.е. соответствующие координаты этих векторов пропорциональны. Пусть

m₁=αm₂, p₁=αp₂, l₁=αl₂

(2.7)

где α − некоторое число. Тогда соответствующие координаты векторов q₁ и q₂ пропорциональны, и, следовательно прямые L₁ и L₂ параллельны.

Условие параллельности прямых можно представить и так:

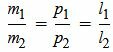(2.8)

Отметим, что любую пропорцию нужно понимать как равенство ad=bc.

Пример 2. Определить, параллельны ли прямые

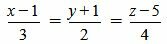(2.9)

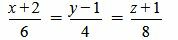(2.10)

Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.

Ответ. Прямые (2,9) и (2,10) параллельны.

Пример 3. Определить, параллельны ли прямые

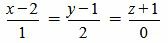(2.11)

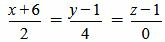(2.12)

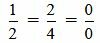(2.13)

Выражение (2.13) нужно понимать так:

Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.

Ответ. Прямые (2.11) и (2.12) параллельны.

2.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:

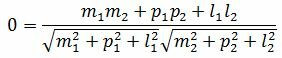(2.15)

Правая часть выражения (2.15) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L₁ и L₂ были перпендикулярны , должно выполняться условие

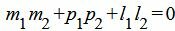(2.16)

Пример 3. Определить, перпендикулярны ли прямые

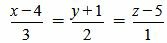(2.17)

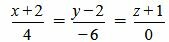(2.18)

Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.

Ответ. Прямые (2.17) и (2.18) перпендикулярны.

Угол между прямыми

Определение угла между прямыми

Угол между прямыми на плоскости

Угол между прямыми заданными уравнениями с угловым коэффициентом

то угол между ними можно найти, используя формулу:

Если знаменатель равен нулю (1 + k ₁· k ₂ = 0), то прямые перпендикулярны.

Соответственно легко найти угол между прямыми

tg γ = tg ( α — β ) = tg α — tg β 1 + tg α ·tg β = k ₁ — k ₂ 1 + k ₁· k ₂

Угол между прямыми через направляющие векторы этих прямых

cos φ = | a · b | | a | · | b |

Если уравнение прямой задано параметрически

x = l t + a y = m t + b

то вектор направляющей имеет вид

Если уравнение прямой задано как

то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = — C B значит точка на прямой имеет координаты K(0, — C B ), при y = 0 => x = — C A значит точка на прямой имеет координаты M(- C A , 0). Вектор направляющей KM = .

Если дано каноническое уравнение прямой

то вектор направляющей имеет вид

Если задано уравнение прямой с угловым коэффициентом

то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b ), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b ). Вектор направляющей KM =

Угол между прямыми через векторы нормалей этих прямых

cos φ = | a · b | | a | · | b |

Если уравнение прямой задано как

то вектор нормали имеет вид

Если задано уравнение прямой с угловым коэффициентом

то вектор нормали имеет вид

Угол между прямыми через направляющий вектор и вектор нормали этих прямых

sin φ = | a · b | | a | · | b |

Примеры задач на вычисления угла между прямыми на плоскости

Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:

tg γ = k ₁ — k ₂ 1 + k ₁· k ₂ = 2 — (-3) 1 + 2·(-3) = 5 -5 = 1

Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.

Для первой прямой направляющий вектор <1; 2>, для второй прямой направляющий вектор

cos φ = |1 · 2 + 2 · 1| 1 2 + 2 2 · 2 2 + 1 2 = 4 5 · 5 = 0.8

Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.

Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.

2 x + 3 y = 0 => y = — 2 3 x ( k ₁ = — 2 3 )

x — 2 3 = y 4 => y = 4 3 x — 8 3 ( k ₂ = 4 3 )

tg γ = k ₁ — k ₂ 1 + k ₁· k ₂ = — 2 3 — 4 3 1 + (- 2 3 )· 4 3 = — 6 3 1 — 8 9 = 18

Угол между прямыми в пространстве

cos φ = | a · b | | a | · | b |

Если дано каноническое уравнение прямой

то направляющий вектор имеет вид

Если уравнение прямой задано параметрически

x = l t + a y = m t + b z = n t + c

то направляющий вектор имеет вид

Решение: Так как прямые заданы параметрически, то <2; 1; -1>- направляющий вектор первой прямой, <1; -2; 0>направляющий вектор второй прямой.

cos φ = |2 · 1 + 1 · (-2) + (-1) · 0| 2 2 + 1 2 + (-1) 2 · 1 2 + (-2) 2 + 0 2 = 0 6 · 5 = 0

Решение: Для решения этой задачи найдем направляющие векторы этих прямых.

Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор <3; 4; 5>.

Преобразуем второе уравнение к каноническому вид.

1 — 3 y = 1 + y -1/3 = y — 1/3 -1/3

3 z — 5 2 = z — 5/3 2/3

Получено уравнение второй прямой в канонической форме

x — 2 -2 = y — 1/3 -1/3 = z — 5/3 2/3

<-2; — 1 3 ; 2 3 >- направляющий вектор второй прямой.

cos φ = 3·(-2) + 4·(- 1 3 ) + 5· 2 3 3 2 + 4 2 + 5 2 · (-2) 2 + (- 1 3 ) 2 + ( 2 3 ) 2 = -6 — 4 3 + 10 3 9 + 16 + 25 · 4 + 1 9 + 4 9 = -4 50 · 41/9 = 12 5 82 = 6 82 205

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Вычисление угла между двумя прямыми

Этот калькулятор онлайн вычисляет угол между двумя прямыми заданными в каноническом виде (для трехмерного пространства):

Онлайн калькулятор для вычисления расстояния от точки до плоскости не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.

Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac<2> <3>)

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac<5> <7>)

источники:

http://ru.onlinemschool.com/math/library/analytic_geometry/lines_angle/

http://www.math-solution.ru/math-task/lp-angle-line

Источник

Тангенс угла между прямыми, уравнения которых даны в общем виде:

l1: A1x + B1y + C1 = 0
l2: A2x + B2y + C2 = 0

определяется так:

tg α = (A1B2 — B1A2) / (A1A2 + B1B2).

Под этим углом понимается такой наименьший угол, на который нужно повернуть прямую l1 вокруг точки пересечения прямых против часовой стрелки, чтобы она совместилась с прямой l2.

В данном случае

А1 = 1, В1 = -2,
А2 = 0, В2 = 1.

Тогда tg α = (1*1 — (-2)*0) / (1*0 + (-2)*1) = 1/(-2) = -1/2

Можно поступить и проще, если заметить, что вторая прямая параллельна оси Ох, а первая прямая составляет в таком случае с ней тот же самый угол, что и с осью Ох. Уравнение же первой прямой можно переписать так: у = 0,5х — 2, угловой коэффициент этой прямой равен 0,5 — это тангенс угла наклона прямой — угла между прямой и осью Ох.

Источник

8. Геометрия в пространстве (стереометрия)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Нахождение угла между прямыми

(blacktriangleright) Угол между прямыми – это такой угол (alpha), что (0leqslant alphaleqslant 90^circ).

(blacktriangleright) В пространстве существует 4 типа взаимного расположения прямых: совпадают, пересекаются, параллельны, скрещиваются.

(blacktriangleright) Скрещивающиеся прямые – это прямые, через которые нельзя провести одну плоскость.

Признак скрещивающихся прямых: если первая прямая пересекает плоскость, в которой лежит вторая прямая, в точке, не лежащей на второй прямой, то такие прямые скрещиваются.

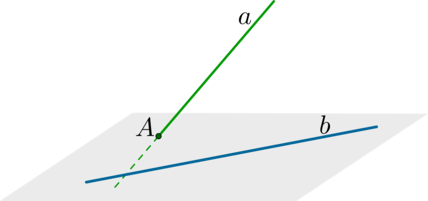
(blacktriangleright) Порядок нахождения угла между скрещивающимися прямыми:

Шаг 1: через одну из двух прямых (a) провести плоскость, параллельную второй прямой (b) (напомним признак: прямая параллельна плоскости, если она параллельна какой-нибудь прямой из этой плоскости);

Шаг 2: в этой плоскости найти прямую (c), параллельную прямой (b);

Шаг 3: тогда угол между прямыми (a) и (b) будет равен углу между прямыми (a) и (c).

Задание
1

#934

Уровень задания: Равен ЕГЭ

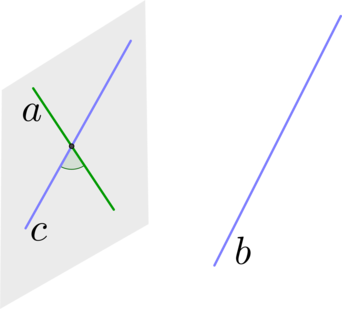
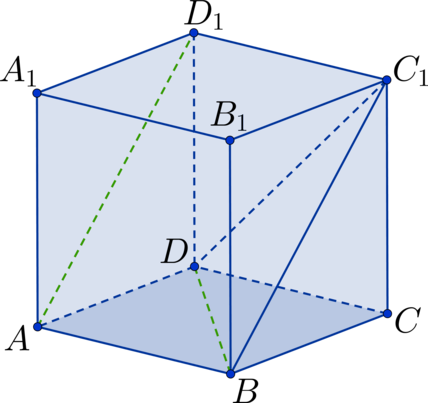
(ABCDA_1B_1C_1D_1) – куб. Найдите угол между прямыми, содержащими отрезки (AC) и (B_1D_1). Ответ дайте в градусах.

Прямая (BD) параллельна прямой (B_1D_1), тогда угол между (AC) и (B_1D_1) равен углу между (AC) и (BD), но (AC) и (BD) – диагонали квадрата, тогда они пересекаются под прямым углом, следовательно ответ (90^{circ}).

Ответ: 90

Задание
2

#2847

Уровень задания: Равен ЕГЭ

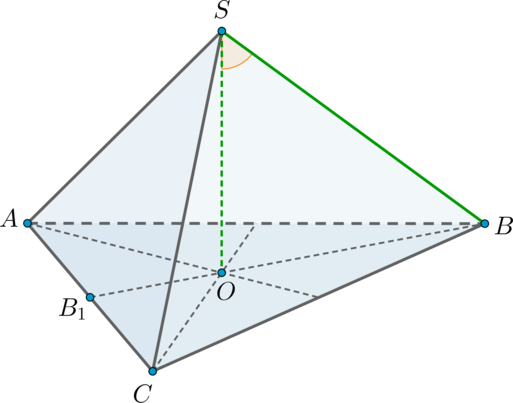
Дана правильная треугольная пирамида (SABC) с вершиной (S). Найдите угол между высотой пирамиды и ребром (SB), если высота пирамиды равна (2sqrt3), а сторона основания пирамиды равна (6). Ответ дайте в градусах.

Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, высота (SO) падает в точку пересечения медиан основания.

Пусть (BB_1) – медиана, а значит, и высота. По теореме Пифагора [BB_1=sqrt{BC^2-B_1C^2}=3sqrt3 quadRightarrowquad BO=dfrac23BB_1=2sqrt3,] так как медианы точкой пересечения делятся в отношении (2:1), считая от вершины.
Следовательно, прямоугольный (triangle SOB) является равнобедренным ((SO=BO=2sqrt3)), значит, острые углы равны по (45^circ).

Ответ: 45

Задание
3

#933

Уровень задания: Равен ЕГЭ

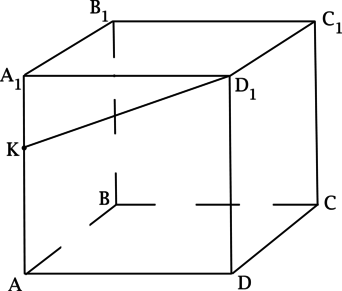
(ABCDA_1B_1C_1D_1) – куб. Точка (K) лежит на ребре (AA_1). Найдите угол между прямыми, содержащими отрезки (D_1K) и (AB). Ответ дайте в градусах.

Так как (ABCDA_1B_1C_1D_1) – куб, то (AB) перпендикулярен плоскости ((ADD_1)), тогда (AB) перпендикулярен любой прямой, лежащей в плоскости ((ADD_1)), следовательно, угол между прямыми, содержащими отрезки (D_1K) и (AB) равен (90^{circ}).

Ответ: 90

Задание
4

#2845

Уровень задания: Равен ЕГЭ

Дан правильный тетраэдр (SABC). Найдите квадрат тангенса угла между высотой грани (SAC), опущенной из вершины (S), и высотой грани (ABC), опущенной из вершины (B).

Пусть (SB_1) – высота грани (SAC). Так как тетраэдр правильный, то все его грани – равные правильные треугольники, то есть (SB_1) также является и медианой, значит, (AB_1=B_1C). Также у правильного тетраэдра высота из каждой вершины падает в точку пересечения медиан (биссектрис, высот) противоположной грани. Следовательно, если (SO) – высота, то (O) – точка пересечения медиан треугольника (ABC), а значит и высот, так как (triangle ABC) правильный. Следовательно, (BB_1) — медиана и высота.

Таким образом, необходимо найти (mathrm{tg}^2angle (SB_1,
BB_1)).
Пусть (a) – ребро тетраэдра. Тогда (BC=a, B_1C=0,5a), следовательно, по теореме Пифагора [BB_1=sqrt{BC^2-B_1C^2}=dfrac{sqrt3}2a] Так как (O) – точка пересечения медиан, а медианы точкой пересечения делятся в отношении (2:1), считая от вершины, то (OB_1=frac13BB_1=frac{sqrt3}6a).

Так как (triangle ABC=triangle SAC), то (SB_1=BB_1). Следовательно, из прямоугольного (triangle SB_1O): [cos
alpha=dfrac{OB_1}{SB_1}=dfrac13 quadRightarrowquad sin alpha
=sqrt{1-cos^2alpha}=dfrac{2sqrt2}3 quadRightarrowquad
mathrm{tg}^2alpha=(2sqrt2)^2=8.]

Ответ: 8

Задание
5

#1846

Уровень задания: Равен ЕГЭ

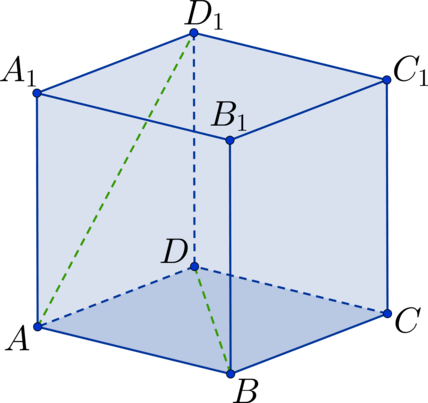
Дан куб (ABCDA_1B_1C_1D_1). Найдите угол между прямыми (AD_1) и (BD). Ответ дайте в градусах.

Заметим, что (BC_1 || AD_1), тогда рассмотрим треугольник (triangle BDC_1), в котором необходимо определить (angle DBC_1). Он состоит из диагоналей соответствующих квадратов. Так как квадраты между собой равны, то равны и диагонали (Rightarrow) (triangle BDC_1) – равносторонний треугольник (Rightarrow) (angle DBC_1 = 60^circ).

Ответ: 60

Задание
6

#1847

Уровень задания: Равен ЕГЭ

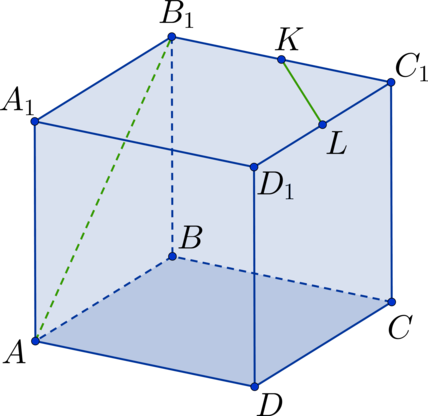
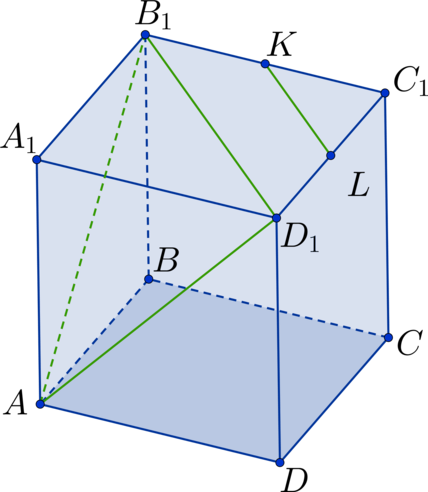
Дан куб (ABCDA_1B_1C_1D_1). Точка (K) – середина стороны (B_1C_1), а точка (L) – середина стороны (C_1D_1). Найдите угол между прямыми (AB_1) и (KL). Ответ дайте в градусах.

Проведем диагональ (B_1D_1) в квадрате (A_1B_1C_1D_1). Тогда (KL) – средняя линия в (triangle B_1C_1D_1) (Rightarrow) (KL || B_1D_1) (Rightarrow) (angle AB_1D_1) – искомый угол. Рассмотрим (triangle AB_1D_1). Он состоит из диагоналей соответствующих квадратов (Rightarrow) треугольник является равносторонним (Rightarrow) (angle AB_1D_1 = 60^circ).

Ответ: 60

Задание
7

#2846

Уровень задания: Сложнее ЕГЭ

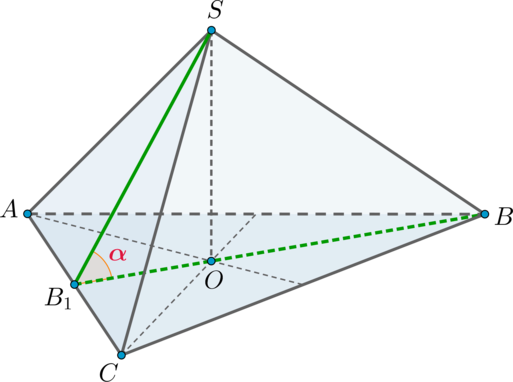
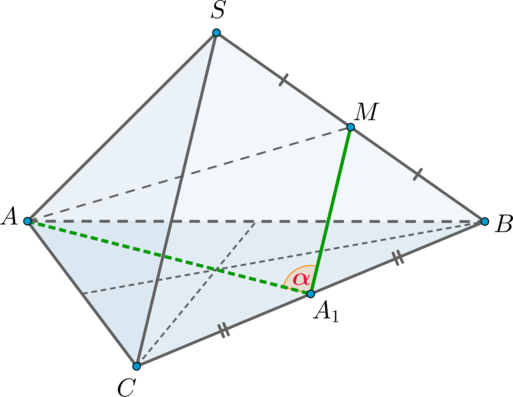
Дана правильная треугольная пирамида (SABC) с вершиной (S). Найдите косинус угла между высотой основания (AA_1) и ребром (SC), если сторона основания равна (sqrt3), а боковое ребро равно (2).

Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, (AA_1) также является и медианой.

Заметим, что прямые (AA_1) и (SC) скрещиваются. Проведем (A_1Mparallel SC), следовательно, (angle (AA_1, SC)=angle (AA_1,
A_1M)).
Так как (A_1Mparallel SC) и (A_1) – середина (BC), то (M) – середина (SB). Следовательно, (A_1M) – средняя линия и [A_1M=frac12SC=1.] По теореме Пифагора из (triangle ABA_1): [AA_1=sqrt{AB^2-A_1B^2}=dfrac32.] Медиану (AM) из (triangle SAB) можно найти по формуле медианы: [AM^2=dfrac{2AS^2+2AB^2-SB^2}4=dfrac52.] Следовательно, по теореме косинусов из (triangle AA_1M): [cos alpha=dfrac{AA_1^2+A_1M^2-AM^2}{2AA_1cdot A_1M}=dfrac14=0,25.]

Ответ: 0,25

Каждому школьнику, который готовится к ЕГЭ по математике, будет полезно повторить тему «Нахождение угла между прямыми». Как показывает статистика, при сдаче аттестационного испытания задачи по данному разделу стереометрии вызывают трудности у большого количества учащихся. При этом задания, требующие найти угол между прямыми, встречаются в ЕГЭ как базового, так и профильного уровня. Это значит, что уметь их решать должны все.

Основные моменты

В пространстве существует 4 типа взаимного расположения прямых. Они могут совпадать, пересекаться, быть параллельными или скрещивающимися. Угол между ними может быть острым или прямым.

Для нахождения угла между прямыми в ЕГЭ или, например, в решении задач по теореме о трех перпендикулярах, школьники Москвы и других городов могут использовать несколько способов решения задач по данному разделу стереометрии. Выполнить задание можно путем классических построений. Для этого стоит выучить основные аксиомы и теоремы стереометрии. Школьнику нужно уметь логически выстраивать рассуждение и создавать чертежи, для того чтобы привести задание к планиметрической задаче.

Также можно использовать векторно-координатный метод, применяя простые формулы, правила и алгоритмы. Главное в этом случае — правильно выполнить все вычисления. Отточить свои навыки решения задач по стереометрии и другим разделам школьного курса вам поможет образовательный проект «Школково».

УСТАЛ? Просто отдохни

Источник

Определение угла между прямыми

Две прямые называются пересекающимися, если они имеют единственную общую точку. Эта точка называется точкой пересечения прямых. Прямые разбиваются точкой пересечения на лучи, которые образуют четыре неразвернутых угла, среди которых две пары вертикальных углов и четыре пары смежных углов. Если известен размер одного из углов, образованных пересекающимися прямыми, то легко определить размер остальных углов. Если один из углов прямой, то все остальные тоже прямые, а прямые перпендикулярны.

Определение Угол между прямыми — размер наименьшего из углов, образованных этими прямыми.

Угол между прямыми на плоскости

Угол между прямыми заданными уравнениями с угловым коэффициентом

Если две прямые заданы уравнениями с угловым коэффициентом

y = k₁x + b₁,
y = k₂x + b₂,

то угол между ними можно найти, используя формулу:

Если знаменатель равен нулю (1 + k₁·k₂ = 0), то прямые перпендикулярны.

Доказательство. Если прямые заданы уравнениями с угловыми коэффициентами, то легко найти углы между этими прямыми и осью OX

tg α = k₁
tg β = k₂

Соответственно легко найти угол между прямыми

γ = α — β

tg γ = tg (α — β) = tg α — tg β1 + tg α ·tg β = k₁ — k₂1 + k₁·k₂

Угол между прямыми через направляющие векторы этих прямых

Если a — направляющий вектор первой прямой и b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

cos φ = |a · b||a| · |b|

Если уравнение прямой задано параметрически

x = l t + ay = m t + b

то вектор направляющей имеет вид {l; m}

Если уравнение прямой задано как

A x + B y + C = 0

то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = -CB значит точка на прямой имеет координаты K(0, -CB), при y = 0 => x = -CA значит точка на прямой имеет координаты M(-CA, 0). Вектор направляющей KM = {-CA; CB}.

Если дано каноническое уравнение прямой

x — x₀ l = y — y₀m

то вектор направляющей имеет вид {l; m}

Если задано уравнение прямой с угловым коэффициентом

y = kx + b

то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b). Вектор направляющей KM = {1; k}

Угол между прямыми через векторы нормалей этих прямых

Если a — вектор нормали первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

cos φ = |a · b||a| · |b|

Если уравнение прямой задано как

A x + B y + C = 0

то вектор нормали имеет вид {A; B}

Если задано уравнение прямой с угловым коэффициентом

y = kx + b

то вектор нормали имеет вид {1; —k}

Угол между прямыми через направляющий вектор и вектор нормали этих прямых

Если a — направляющий вектор первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

sin φ = |a · b||a| · |b|

Примеры задач на вычисления угла между прямыми на плоскости

Пример 1. Найти угол между прямыми y = 2x — 1 и y = -3x + 1.

Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:

tg γ =

k₁ — k₂1 + k₁·k₂

2 — (-3)1 + 2·(-3)

5-5

= 1

Ответ. γ = 45°

Пример 2. Найти угол между прямыми y = 2x — 1 и x = 2t + 1y = t.

Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.

Для первой прямой направляющий вектор {1; 2}, для второй прямой направляющий вектор {2; 1}

cos φ =

|1 · 2 + 2 · 1|1² + 2² · 2² + 1²

45 · 5

= 0.8

Ответ. φ ≈ 36.87°

Пример 3 Найти угол между прямыми 2x + 3y = 0 и

x — 23

Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.

Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.

2x + 3y = 0 => y = -23x (k₁ = -23)

x — 23 = y4 => y = 43x — 83 (k₂ = 43)

tg γ =

k₁ — k₂1 + k₁·k₂

-23 — 431 + (-23)·43

-631 — 89

= 18

Ответ. γ ≈ 86.82°

Угол между прямыми в пространстве

Если a — направляющий вектор первой прямой, а b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

cos φ = |a · b||a| · |b|

Если дано каноническое уравнение прямой

x — x₀ l = y — y₀m = z — z₀n

то направляющий вектор имеет вид {l; m; n}

Если уравнение прямой задано параметрически

x = l t + ay = m t + bz = n t + c

то направляющий вектор имеет вид {l; m; n}

Пример 4. Найти угол между прямыми

x = 2t + 1y = tz = -t — 1

x = t + 2y = -2t + 1z = 1

Решение: Так как прямые заданы параметрически, то {2; 1; -1} — направляющий вектор первой прямой, {1; -2; 0} направляющий вектор второй прямой.

cos φ =

|2 · 1 + 1 · (-2) + (-1) · 0|2² + 1² + (-1)² · 1² + (-2)² + 0²

06 · 5

= 0

Ответ. φ = 90°

Пример 5 Найти угол между прямыми

x — 23

z — 35

и —

x — 22

= 1 — 3y =

3z — 52

Решение: Для решения этой задачи найдем направляющие векторы этих прямых.

Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор {3; 4; 5}.

Преобразуем второе уравнение к каноническому вид.

—x — 22 = x — 2-2

1 — 3y = 1 + y-1/3 = y — 1/3-1/3

3z — 52 = z — 5/32/3

Получено уравнение второй прямой в канонической форме

x — 2-2 = y — 1/3-1/3 = z — 5/32/3

{-2; -13; 23} — направляющий вектор второй прямой.

cos φ =

3·(-2) + 4·(-13) + 5·233² + 4² + 5² · (-2)² + (-13)² + (23)²

-6 — 43 + 1039 + 16 + 25 · 4 + 19 + 49

-450 · 41/9

12582

682205

Ответ. φ ≈ 74.63°

Источник

Вычислить
тангенс острого угла между прямыми

,.
Ответ:

Ответ:

Световой луч,
падая из точки
и отражаясь от прямой,
проходит затем через точку.
Написать уравнение луча падающего
и луча отраженного.

Ответ:
,.

Основание
равнобедренного треугольника имеет
уравнение
.
Одна из боковых сторон имеет уравнение.
Найти уравнение другой боковой
стороны , если известно, что она
проходит через точку.

Ответ:
.

Даны уравнения
боковых сторон равнобедренного
треугольника
;и точкана его основании. Написать уравнение
его основания.Ответ:
.

Ответ:
,.

Точка
является вершиной квадрата, диагональ
которого лежит на прямойСоставить уравнения сторон и второй
диагонали этого квадрата.

Ответ:
,.

Даны
две противоположные вершины квадрата

и.
Составить уравнения его сторон.

Ответ:
,,,.

Точка
является
центром квадрата, одна из сторон
которого лежит на прямой.
Составить уравнения прямых, на
которых лежат остальные стороны
квадрата.

Ответ:
,,.

Из
точки
под углом
к оси
направлен луч света. Известно, что.
Дойдя до оси,
луч от нее отразился. Составить
уравнения прямых, на которых лежат
лучи падающий и отраженный.

Ответ:
,.

Даны
уравнения сторон треугольника
,,.
Доказать, что этот треугольник
равнобедренный. Решить задачу с
помощью сравнения углов треугольника.

§
3 Задачи, при решении которых используется

общее уравнение прямой.

СПИСОК ФОРМУЛ

Общее уравнение
прямой на плоскости имеет вид
.Само
это уравнение и все последующие формулы
выведены с использованием методов
векторной алгебры. Более того, решения
всех последующих задач будут проводиться
с использованием векторов и их свойств.
Переход от алгебраических уравнений
к векторам и обратно будет проводиться
автоматически, без оговорок.

Основной
вектор, вводимый по уравнению прямой

это нормальный (или перпендикулярный)
вектор прямой. В качестве его координат
берут коэффициенты при
ив уравнении,
т.е..
Второй вектор
это направляющий (или параллельный)
вектор прямой. Его координаты вводятся
по формуле
.