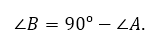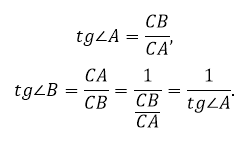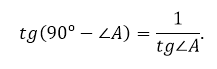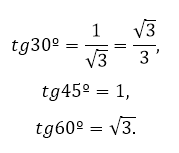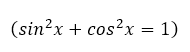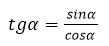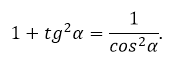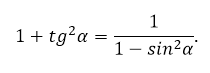Как найти тангенс угла огэ 9 класс

Всего: 40    1–20 | 21–40

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 40    1–20 | 21–40

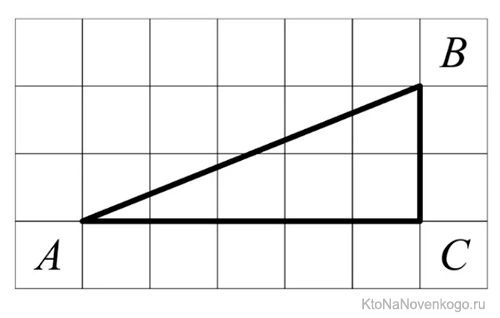
№8. Найдите тангенс угла AOB, изображенного на рисунке.

Решение:

Опустим перпендикуляр AH на сторону OB.

Рассмотрим прямоугольный △ A O H :

Тангенс угла – отношение противолежащего катета к прилежащему.

tg ∠ A O H = A H O H = 4 2 = 2

Ответ: 2

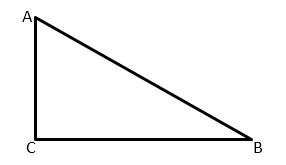
№9. Найдите тангенс угла A треугольника ABCб изображённого на рисунке.

Решение:

Тангенс угла – это отношение противолежащего катета к прилежащему.

tg ∠ B A C = B C A C = 2 5 = 0,4

Ответ: 0,4

№10. На рисунке изображена трапеция ABCD. Используя рисунок, найдите sin ∠ B A H .

Решение:

Рассмотрим прямоугольный △ A B H :

Синус угла – отношение противолежащего катета к гипотенузе.

sin ∠ A = B H A B

Найдем AB по теореме Пифагора:

A B 2 = A H 2 + B H 2

A B 2 = 3 2 + 4 2

A B 2 = 9 + 16 = 25

A B = ± 25 = [ − 5 не подходит 5 подходит

A B = 5

sin ∠ A = B H A B = 4 5 = 0,8

Ответ: 0,8

№11. На рисунке изображен ромб ABCD. Используя рисунок, найдите tg ∠ O B C .

Решение:

Тангенс угла – это отношение противолежащего катета к прилежащему.

tg ∠ O B C = O C B O = 3 4 = 0,75

Ответ: 0,75

№12. На рисунке изображена трапеция ABCD. Используя рисунок, найдите cos ∠ H B A .

Решение:

Рассмотрим прямоугольный △ A B H :

Косинус угла – отношение прилежащего катета к гипотенузе.

cos ∠ A B H = B H A B

Найдем A B по теореме Пифагора:

A B 2 = A H 2 + B H 2

A B 2 = 6 2 + 8 2

A B 2 = 36 + 64 = 100

A B = ± 100 = [ − 10 не подходит 10 подходит

A B = 10

cos ∠ A B H = B H A B = 8 10 = 0,8

Ответ: 0,8

№13. Найдите тангенс угла, изображенного на рисунке.

Решение:

tg β = tg ( 180 ° − α ) = − tg α

Рассмотрим прямоугольный △ B C H .

Тангенс угла – отношение противолежащего катета к прилежащему.

tg α = C H B H = 3 1

tg β = − tg α = − 3

Ответ: -3

№14. Найдите тангенс угла AOB.

Решение:

Опустим высоту BH на сторону OA.

Рассмотрим прямоугольный △ O B H :

tg ∠ O = B H O H

Найдем B H и O H по теореме Пифагора:

B H 2 = 2 2 + 8 2 = = 4 + 64 = 68

B H = ± 68   = ± 4 ⋅ 17 = ± 4 ⋅ 17 = ± 2 17 = [ − 2 17 не подходит 2 17 подходит

B H   =   2 17

O H 2 = 1 2 + 4 2 = 1 + 16 = 17

O H = ± 17 = [ − 17 не подходит 17 подходит

O H   =   17

tg ∠ O = B H O H = 2 17 17 = 2

Ответ: 2

Подготовка
к ОГЭ: нахождение тангенса угла по клеткам.

1. Источник: МА-9 ДЕМО 2017

Найдите тангенс угла АОВ треугольника,

изображённого на рисунке.

Решение:
Тангенсом
угла прямоугольного треугольника называется отношение противолежащего катета к
прилежащему. Воспользовавшись клеточками, нетрудно найти нужные величины: АВ=4    АО=2

 =  = 2

Ответ: 2

2. Источник: Открытый банк заданий по математике

 Прототип задания 12 (№
27450)

 

 

На клетчатой бумаге с размером клетки  

изображён угол. Найдите тангенс этого угла

Решение:
Находим прямоугольный треугольник

(как
показано  на рисунке). Далее по п1.

Ответ: 2,5

 

3. Источник: Открытый банк
заданий по математике

 Прототип задания 12 (№
27456)

На клетчатой бумаге с размером клетки  

изображён угол. Найдите тангенс этого угла

Решение:
Находим прямоугольный треугольник

(как
показано  на рисунке).

Находим по т. Пифагора
противолежащий катет

(красный треугольник),
прилежащий катет

(жёлтый треугольник).

 = 1

Замечание: обучающиеся
обычно решают это

задание следующим образом: кладут
снизу

клетчатый лист, чтобы на просвет
задача

стала аналогичной п.1.

(как показано  на рисунке).                         

   Ответ:
1

Геометрия. Урок 1. Задания. Часть 2.

№8. Найдите тангенс угла A O B , изображенного на рисунке.

Решение:

Опустим перпендикуляр A H на сторону O B .

Рассмотрим прямоугольный △ A O H :

Тангенс угла – отношение противолежащего катета к прилежащему.

tg ∠ A O H = A H O H = 4 2 = 2

№9. Найдите тангенс угла A треугольника A B C б изображённого на рисунке.

Решение:

Тангенс угла – это отношение противолежащего катета к прилежащему.

tg ∠ B A C = B C A C = 2 5 = 0,4

№10. На рисунке изображена трапеция A B C D . Используя рисунок, найдите sin ∠ B A H .

Решение:

Рассмотрим прямоугольный △ A B H :

Синус угла – отношение противолежащего катета к гипотенузе.

sin ∠ A = B H A B

Найдем A B по теореме Пифагора:

A B 2 = A H 2 + B H 2

A B 2 = 3 2 + 4 2

A B 2 = 9 + 16 = 25

A B = ± 25 = [ − 5 не подходит 5 подходит

sin ∠ A = B H A B = 4 5 = 0,8

№11. На рисунке изображен ромб A B C D . Используя рисунок, найдите tg ∠ O B C .

Решение:

Тангенс угла – это отношение противолежащего катета к прилежащему.

tg ∠ O B C = O C B O = 3 4 = 0,75

№12. На рисунке изображена трапеция A B C D . Используя рисунок, найдите cos ∠ H B A .

Решение:

Рассмотрим прямоугольный △ A B H :

Косинус угла – отношение прилежащего катета к гипотенузе.

cos ∠ A B H = B H A B

Найдем A B по теореме Пифагора:

A B 2 = A H 2 + B H 2

A B 2 = 6 2 + 8 2

A B 2 = 36 + 64 = 100

A B = ± 100 = [ − 10 не подходит 10 подходит

cos ∠ A B H = B H A B = 8 10 = 0,8

№13. Найдите тангенс угла, изображенного на рисунке.

Решение:

tg β = tg ( 180 ° − α ) = − tg α

Рассмотрим прямоугольный △ B C H .

Тангенс угла – отношение противолежащего катета к прилежащему.

tg α = C H B H = 3 1

tg β = − tg α = − 3

№14. Найдите тангенс угла A O B .

Решение:

Опустим высоту B H на сторону O A .

Рассмотрим прямоугольный △ O B H :

Найдем B H и O H по теореме Пифагора:

B H 2 = 2 2 + 8 2 = = 4 + 64 = 68

B H = ± 68 = ± 4 ⋅ 17 = ± 4 ⋅ 17 = ± 2 17 = [ − 2 17 не подходит 2 17 подходит

O H 2 = 1 2 + 4 2 = 1 + 16 = 17

O H = ± 17 = [ − 17 не подходит 17 подходит

Что такое тангенс угла и как его найти

Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.

Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.

Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.

Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.

Тангенс угла

Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.

В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.

Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса (это что?), тангенса, котангенса.

Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.

Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.

Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.

Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).

Тангенс — это отношение.

Итак, есть два определения:

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.

Тангенс – это отношение синуса к косинусу.

Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.

» alt=»»>

Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan⁡(α).

Как найти тангенс угла (формулы)

Первое свойство тангенса вытекает из его определения как отношения катетов.

Сумма двух непрямых углов прямоугольного треугольника равна 90º. Поэтому

Так как тангенс – это отношение катетов, то

Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.

Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.

Как найти тангенс по клеточкам

Учитывая первое определение, можно определить, как найти тангенс угла по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.

Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:

Из формулы тангенсов, записывающей кратко второе определение

и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.

Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится зависимость тангенса и косинуса:

Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом:

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (5)

Я Очень Люблю Правила, Теоремы, Формулы по Предмету «Математика», «Алгебра».

Прочитал статью и остался один главный вопрос, а собственно без вспомогательных таблиц найти угол В ГРАДУСАХ вообще возможно и есть ли у вас статья, где рассказыввается как это сделать? Спасибо.

Я ни разу не математик, но почему у вас сумма углов прямоугольного треугольника равна 90 градусов. А так все хорошо начиналось. Объясняете хорошо, но после таких ошибок у меня сомнения что информация верная.

Спасибо. Уточнил в тексте, что это сумма двух непрямых углов прямоугольного треугольника.

Пишу стихи. Востребован тангенс для решения жизненных ситуаций поскольку состоит из тех же функций,как-то, касающийся,прилежащий, трогающий. Куда без них денешься.

Подготовка к ОГЭ: нахождение тангенса угла.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Подготовка к ОГЭ: нахождение тангенса угла по клеткам.

1. Источник: МА-9 ДЕМО 2017

Найдите тангенс угла АОВ треугольника,

изображённого на рисунке.

Решение: Тангенсом угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему. Воспользовавшись клеточками, нетрудно найти нужные величины: АВ=4 АО=2

2. Источник: Открытый банк заданий по математике

Прототип задания 12 (№ 27450)

На клетчатой бумаге с размером клетки

изображён угол. Найдите тангенс этого угла

Решение: Находим прямоугольный треугольник

(как показано на рисунке). Далее по п1.

3. Источник: Открытый банк заданий по математике

Прототип задания 12 (№ 27456)

На клетчатой бумаге с размером клетки

изображён угол. Найдите тангенс этого угла

Решение: Находим прямоугольный треугольник

(как показано на рисунке).

Находим по т. Пифагора противолежащий катет

(красный треугольник), прилежащий катет

Замечание : обучающиеся обычно решают это

задание следующим образом: кладут снизу

клетчатый лист, чтобы на просвет задача

стала аналогичной п.1.

(как показано на рисунке).

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 958 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 310 человек из 70 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 679 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 553 785 материалов в базе

Другие материалы

• 27.07.2017
• 525
• 0

• 27.07.2017
• 1708
• 49

• 27.07.2017
• 1063
• 13

• 27.07.2017
• 2269
• 24

• 27.07.2017
• 638
• 0

• 27.07.2017
• 729
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 27.07.2017 4324
• DOCX 221.4 кбайт
• 19 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Медведкова Елена Алексеевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет и 3 месяца
• Подписчики: 0
• Всего просмотров: 6735
• Всего материалов: 6

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Общество «Знание» в 2022 году планирует запустить серию хакатонов и школу лекторов

Время чтения: 2 минуты

Минобрнауки подготовит государственный рейтинг университетов

Время чтения: 1 минута

В Египте нашли древние школьные «тетрадки»

Время чтения: 1 минута

Петербургская учительница уволилась после чтения на уроке Введенского и Хармса

Время чтения: 3 минуты

У 76% российских учителей оклад ниже МРОТ

Время чтения: 2 минуты

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

а) Для ответа подойдёт только десятичная дробь или целое число. В ответах не может быть обыкновенных дробей, округлённых примерных значений, то есть если в ответе у тебя получилась обыкновенная дробь, её обязательно надо превратить в десятичную. Если это не получается, ищи ошибку в решении. 

б) Десятичные дроби не получатся из несократимых обыкновенных дробей, у которых в знаменателе есть любые простые множители, кроме (2) и (5), т. к. в этом случае добиться того, чтоб в знаменателе было (10), (100), (1000), никак не получится. Если у тебя в ответе такая дробь — ищи ошибку.