Как найти тангенс угла в прямоугольном параллелепипеде - Исправление недочетов и поиск решений вместе с Examum.ru

Прямоугольный параллелепипед показан на рисунке.

Имеем b = 6 м, а = 8 м и с = 10м. Найти угол между диагональю параллелепипеда d =AG и плоскостью его основания ABCD, то есть угол между диагоналями AG и АС. (На рисунке диагональ АС не нарисована). Вначале найдем длину диагонали АС = sqrt(a^2 + b^2) = sqrt(8^2 + 6^2) = sqrt(64 + 36) = sqrt(100) = 10 м. (На рисунке диагональ АС не прочерчена, на своем рисунке прочертите ее для наглядности). Значок sqrt означает квадратный корень (от английских слов square root). Математический знак корня БВ не понимает, поэтому ставит вместо него знак вопроса ?). БВ не понимает ни греческие буквы, ни математические знаки, которых нет на клавиатуре. Итак, АС = 10 м. Имеем прямоугольный треугольник АСG. Теперь легко найти угол CAG в этом треугольнике CAG. Угол GCA будет прямоугольным (90°), так как ребро GC в параллелепипеде перпендикулярно основанию ADCB. Из прямоугольного треугольника AGC находим тангенс угла GAC. При этом заметим, GC = с = 10 м, так как оба эти катета – высота параллелепипеда. Имеем tg(GAC) = GC/AC = 10/10 = 1. А если тангенс равен 1, то это угол в 45°. Ответ 45°.

Источник

Задача 14 — стереометрия. Профиль.

Задача 1. В прямоугольном параллелепипеде у которого АВ=4, ВС=6, CC_1=4 , найдите тангенс угла между плоскостями CDD_1 и BDA_1 .

Очевидно, что, раз плоскости CDD_1 и ABA_1 параллельны, то можно найти тангенс угла между плоскостями BDA_1 и ABA_1 .

ster_1

Параллелепипед и плоскости

Заметим, что треугольник BDA_1 – равнобедренный: его боковые строны – диагонали равных прямоугольников ABCD и . Треугольник A_1AB также равнобедренный, так как грань параллелепипеда – квадрат. Тогда двугранный угол, тангенс которого мы ищем, равен линейному углу AOD , где – высота треугольника A_1AB , – высота треугольника BDA_1 .

ster_2

Вид сверху

Чтобы найти тангенс угла AOD в прямоугольном треугольнике AOD (прямой угол OAD – так как параллелепипед по условию прямоугольный) нужно найти отношение длин противолежащего катета к прилежащему .

AD=6 , – это половина диагонали квадрата со стороной 4. Тогда .

Ответ:

Задача 2. Длины всех ребер правильной четырехугольной пирамиды PABCD равны между собой. Найдите угол между прямыми PH и BM, если отрезок PH – высота данной пирамиды, точка М – середина ее бокового ребра PA.

Из точки М опустим перпендикуляр на основание пирамиды. Так как параллелен , то искомый угол – угол SMB .

ster_3

Пирамида

Его можно отыскать как арккосинус отношения к : .

Так как все ребра пирамиды равные (кстати, примем длину ребра за ), то найти длину отрезка несложно: это высота правильного треугольника со стороной , то есть

Треугольники AMS и APH подобны по двум углам: оба прямоугольные и имеют общий угол PAH . Коэффициент подобия равен {1/2} – так как по условию М – середина АР. Поэтому

Определим из треугольника PHK , в котором , а :

$PH=sqrt{PK^2-HK^2}=sqrt{a^2{3/4}-{a^2/4}}=sqrt{a^2/2}=a/{sqrt{2}}$

Тогда искомый угол:

Ответ:

Задача 3. Боковое ребро правильной треугольной пирамиды SABC равно 6, а косинус угла ASB при вершине боковой грани равен {1/9} . Точка М – середина ребра SC. Найдите косинус угла между прямыми BM и SA.

Проведем через точку М прямую, параллельную SA, и найдем косинус угла между этой прямой МТ и прямой SA.

ster_4

Правильная пирамида

Для этого можно воспользоваться теоремой косинусов, только потребуются длины МВ, МТ и ВТ.

Так как MT – средняя линия треугольника ASC, то ее длина 3.

Для определения длины ВТ найдем длину ребра основания пирамиды, опять же, применив теорему косинусов: $BC=AC=AB=sqrt{SC^2+SB^2-2*SC*SB*cos ASB}=sqrt{6^2+6^2-2*6*6*{1/9}}=sqrt{64}=8$

Тогда ВТ по теореме Пифагора: $BT=sqrt{BC^2-CT^2}=sqrt{64-16}=4sqrt{3}$

Для определения длины МВ снова применим ту же теорему косинусов:

$MB=sqrt{SM^2+SB^2-2*SM*SB*cos ASB}=sqrt{3^2+6^2-2*3*6*{1/9}}=sqrt{41}$

Ну и, наконец, снова теорема косинусов, но уже для треугольника МВТ (в котором нам известны все стороны), чтобы определить требуемый косинус угла между прямыми BM и SA:

$cos BMT={MT^2+MB^2- BT^2}/{2*MT*MB}$

$cos BMT={3^2+41- 48}/{2*3*sqrt{41}}=1/{3sqrt{41}}$

Ответ:

Задача 4. В конус, радиус основания которого равен 3, вписан шар радиуса 1,5.

а) Изобразите осевое сечение комбинации данных двух тел.

б) Найдите отношение площади полной поверхности конуса к площади поверхности шара.

Рисунок осевого сечения – несложный.

ster_5

Сечение конуса

Найти площадь поверхности шара, зная его радиус – тоже просто:

$S_{sf}=4{pi}r^2=4{pi}(1,5)^2=9{pi}$

А вот чтобы найти площадь поверхности конуса, нужно знать его образующую, на рисунке это отрезок ВС. Проведем радиусы шара OK и OS в точки касания шара и конуса. Отрезок KC – радиус основания конуса, он равен 3. Но тогда и отрезок SC равен 3, так как KC и SC – отрезки касательных, проведенных из одной точки. Найдем тангенс угла SCO:

Чтобы найти образующую конуса, нужен тангенс угла SCK, который вдвое больше угла SCO. Значит, нужно вспомнить формулу тангенса двойного угла:

$tg 2{alpha}={2tg{alpha}}/{1-tg^2 {alpha}}={2*{1/2}}/{1-{1/2}^2}=1/{3/4}=4/3=tg SCK$

Запишем теперь тангенс угла SCK как отношение высоты конуса к радиусу основания:

Отсюда высота конуса:

По теореме Пифагора определяем образующую конуса:

$BC=sqrt{BK^2+KC^2}=sqrt{4^2+3^2}=5$

Площадь поверхности конуса:

$S_{kon}={pi}r^2+{pi}rl=9{pi}+3*5*{pi}=24{pi}$

Отношение площадей: ${S_{kon}}/{ S_{sf}}={24{pi}}/{9{pi}}=24/9$

Ответ: б) 24/9

Задача 5. В правильной четырехугольной пирамиде PABCD, все ребра которой равны 4, точка К – середина ребра AP.

а) постройте сечение пирамиды плоскостью, проходящей через точку К и параллельной прямым PB и BC.

б) Найдите площадь сечения.

Так как площадь сечения должна быть параллельна прямой РВ, то через точку К проводим отрезок КМ, параллельный РВ. Через точку М проведем отрезок MN, параллельный ВС. Также проведем KL параллельно BC, после чего останется только соединить точки L и N – сечение построено. Оно представляет собой равнобокую трапецию.

ster_6

Сечение пирамиды плоскостью

б) Нижнее основание трапеции равно 4, а, так как верхнее основание и боковые стороны – средние линии треугольников APB, APD, и DPC, то длина KM, KL, LN равна 2.

ster_7

Вид сбоку

Найдем высоту трапеции: из треугольника LHN

$LH=sqrt{LN^2-NH^2}=sqrt{2^2-1}=sqrt{3}$

Площадь трапеции равна

$S_{LKMN}={{KL+MN}/2}*LH={{4+2}*sqrt{3}}/2=3sqrt{3}$

Ответ: б)

Источник

Презентация на тему: » 3 В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 АВ=АА 1 =4, AD=3. Найдите тангенс угла, который образует плоскость АСВ 1 с гранью СDD 1 C 1. 1).» — Транскрипт:

1

3 В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 АВ=АА 1 =4, AD=3. Найдите тангенс угла, который образует плоскость АСВ 1 с гранью СDD 1 C 1. 1). Я увидела, что плоскость CDD 1 можно заменить на параллельную плоскость ABB 1. D А В С А1А1 D1D1 С1С1 О В1В1 2). Я увидела ребро двугранного угла – это АВ 1. В грани АВВ 1 опускаю перпендикуляр ВА 1 на ребро (ведь эта грань квадрат) ). А вот дальше все не кажется мне очевидным. Я люблю наглядный очевидный чертеж. Поэтому я опрокину параллелепипед на грань АВВ 1 А 1. Посмотрим следующий слайд…

2

О 4 3 В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 АВ=АА 1 =4, AD=3. Найдите тангенс угла, который образует плоскость АСВ 1 с гранью СDD 1 C 1. 1). Плоскость CDD 1 можно заменить на параллельную плоскость ABB 1. A А1А1 В1В1 B D1D1 D С C1C1 2). Ребро двугранного угла – это АВ 1. В грани АВВ 1 опускаю перпендикуляр ВА 1 на ребро (ведь эта грань квадрат). 44 3). Обоснуем, что угол СОВ – линейный угол двугранного угла. Причем, можно сэкономить на теореме о трех перпендикулярах. АВС = В 1 ВС по катетам. Значит СО АВ 1. АС = СВ 1. АСВ 1 – равнобедренный. ВО АВ 1. В квадрате АВВ 1 А 1 : СОВ – линейный угол двугранного угла 22 3

Источник

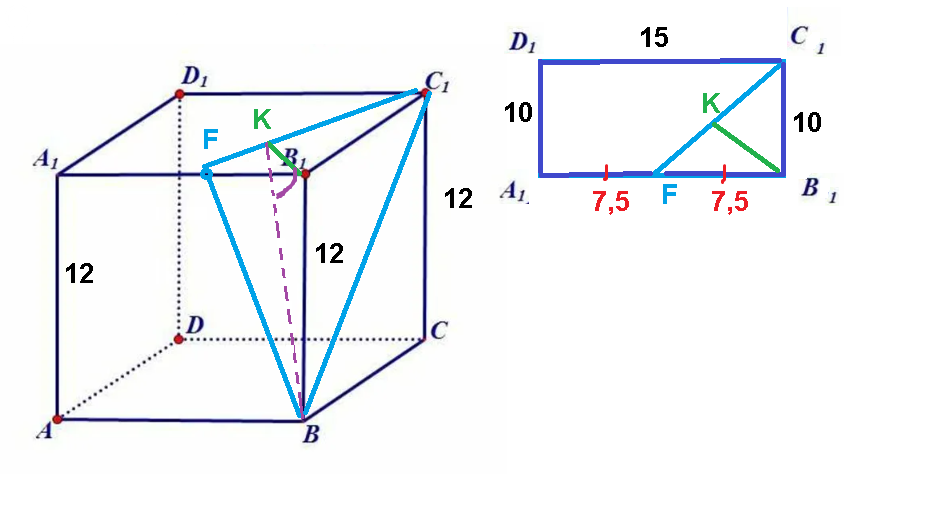
В прямоугольном параллелепипеде ABCDA1B1C1D1 точка F — середина ребра A1B1, AA1 = 12, AD = 10, AB = 15. Найдите тангенс угла между плоскостями BFC1 и АВС

математика 10-11 класс
3050

★

Пл АВС || пл. А_(1)В_(1)С_(1)

Угол между BFC_(1) и АВС равен углу между BFC_(1) и А_(1)В_(1)С_(1)

Угол между гранями BFC_(1) и А_(1)В_(1)С_(1) и есть двугранный угол

Двугранный угол измеряется линейным углом.

Две плоскости пересекаются по прямой. В нашем случае это прямая FС_(1)

Чтобы построить линейный угол двугранного угла надо из любой точки прямой FС_(1) провести перпендикуляры в каждой плоскости

В плоскости А_(1)В_(1)С_(1) проводим B_(1)K ⊥ FС_(1)

BB_(1) ⊥ пл. А_(1)В_(1)С_(1) ⇒ BB_(1) ⊥ FС_(1)

B_(1)K- проекция BK

По теореме о трех перпендикулярах BK⊥ FС_(1)

Провели два перпендикуляра к линии пересечения, а можно сказать, что из точки К прямой FС_(1) провели перпендикуляры в каждой плоскости

∠ BKB_(1)- линейный угол двугранного угла между BFC_(1) и А_(1)В_(1)С_(1)

Находим его из прямоугольного треугольника BKB_(1)

tg ∠ BKB_(1)=BB_(1)/B_(1)K

B_(1)K — высота прямоугольного треугольника FC_(1)B_(1), проведенная из вершины прямого угла

По теореме Пифагора

C_(1)F^2=10^2+7,5^2=100+56,25=156,25=12,5:2

C_(1)F=12,5

S_( Δ FC_(1)B_(1))=(1/2)FB_(1)*B_(1)C_(1)

S_( Δ FC_(1)B_(1))=(1/2)C_(1)F*B_(1)K

Приравниваем правые части

(1/2)FB_(1)*B_(1)C_(1) =(1/2)C_(1)F*B_(1)K

B_(1)K=FB_(1)*B_(1)C_(1) /C_(1)F

B_(1)K=7,5*10/12,5=[b]6[/b]

tg ∠ BKB_(1)=BB_(1)/B_(1)K=12/6=[b]2[/b]

Источник

Привет! Цель нашего проекта помочь тебе подготовиться к ЕГЭ (или ОГЭ).
У нас более 1000 заданий с подробным решением, сервис, запоминающий твои ответы, и удивительная система тестирования.
Обо всем по порядку расскажу тебе после быстрой регистрации.

Присоединиться к ExamMe