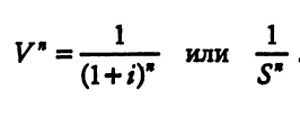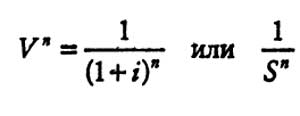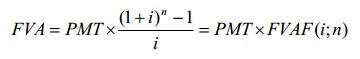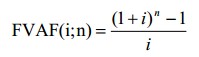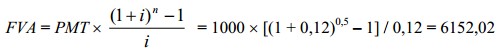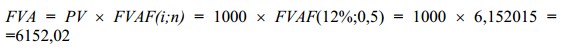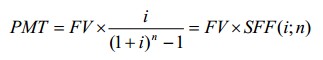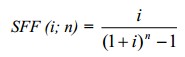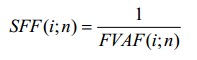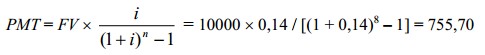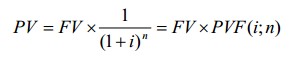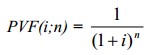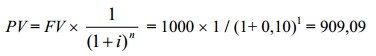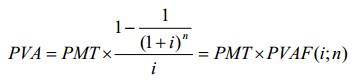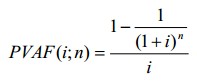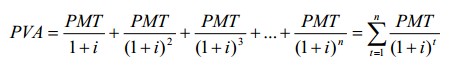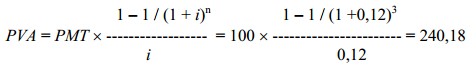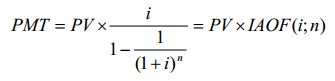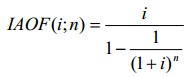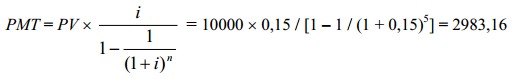Как найти текущую стоимость реверсии - Исправление недочетов и поиск решений вместе с Examum.ru

Текущая стоимость единицы (реверсии) — это величина, обратная накопленной сумме единицы. Это текущая стоимость одного доллара, который должен быть получен в будущем. Поскольку целью осуществления инвестиций является получение доходов в будущем, умножение фактора текущей стоимости реверсии на величину ожидаемого будущего дохода является важнейшим шагом в оценке инвестиций.

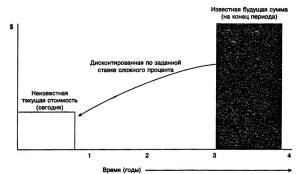
Рис. 3-6. Текущая стоимость реверсии — графическая иллюстрация

Текущая стоимость реверсии (V) описана графически на рис. 3-6. Данный коэффициент используется для оценки текущей стоимости известной (или прогнозируемой) суммы будущего единовременного поступления денежных средств с учетом заданного процента. При применении фактора текущей стоимости используются понятия дисконтирование (discounting) или ставка дисконта (discount rate), противоположные понятиям накопление (compounding) и ставка процента (interest rate), применяемым при расчете накопленной суммы единицы.

Поскольку деньги обладают стоимостью во времени, один доллар, который будет получен в будущем, стоит меньше доллара, получаемого сегодня. Насколько меньше (сумма дисконта), зависит от: а) разрыва во времени между оттоком и притоком денежных средств и б) необходимой ставки процента или дисконта.

Например, при 10%-ной ставке процента (ставке дисконта) текущая стоимость 100,00 долл., ожидаемых к получению через год, равна 90,91 долл. Арифметическая проверка: если сегодня инвестор вкладывает 90,91 долл. и в течение следующего года может получить чистый доход в 9,09 долл., то процент составит 9,09 долл.; поэтому через год основная сумма инвестиций, включая добавленный процент, будет равна 100,00 долл. (90,91 долл. + 9,09 долл. = 100,00 долл.).

Инвестор, который рассчитывает получить через два года 100,00 долл. и вкладывает сегодня 82,64 долл., получит 10%-ную годовую ставку. Проверка: при 10%-ной годовой ставке 82,64 долл. превратятся через год в 90,91 долл., а через 2 года — в 100,00 долл.

Смысл проведения подобных расчетов при работе с недвижимостью состоит в том, чтобы определить сумму, которую следует уплатить за землю сегодня с тем, чтобы перепродать ее с выигрышем в будущем. Например» инвестор, рассчитывающий перепродать собственность через 2 года за 10 000 долл., должен решить, сколько ему следует предложить эа землю сегодня. Если инвестор требует 10%-ную ставку дохода на вложенный капитал, то максимальная сумма, которую он сейчас может предложить продавцу — 8 264 долл. Более низкая цена повысит ставку дохода на инвестиции. Напротив, более высокая цена воспрепятствует достижению требуемой 10%-ной ставки дохода.

Формула расчета текущей стоимости реверсии

Формула расчета текущей стоимости реверсии имеет следующий вид:

Читатель видит, что данный фактор является обратной величиной от накопленной суммы единицы. Поэтому любая задача, которая может быть решена с использованием фактора накопленной суммы единицы, может быть также решена с применением фактора реверсии, однако не через умножение, а через деление.

Например, как показано ранее, 100,00 долл., накапливаемые по сложной ставке 10%, через пять лет возрастут до 161,05 долл. Поскольку 100,00 долл. через пять лет превратятся в 161,05 долл., то 62,05 долл. — это та сумма, которая за пять лет возрастет до 100,00 долл. Ниже показан анализ коэффициентов для данного примера:

Построение таблиц

Как и в случае с накопленной суммой единицы, регулярное и интенсивное использование в расчетах фактора текущей стоимости единицы вызвало необходимость построения стандартных таблиц. Текущая стоимость единицы приводится в колонке 4 многих таблиц сложного процента. Она рассчитывается по формуле, описанной ранее:

Поскольку это величина, обратная накопленной сумме единицы, таблицы могут быть построены соответствующим образом, как это показано в табл. 3-5:

Построение таблицы текущей стоимости реверсии (годовая ставка = 10%)

Год	Накопленная	Обратная величина	Текущая стоимость
	сумма		единицы
1	1,1	1/1,1	0,909091
2	1,21	1/1,21	0,826446
3	1,331	1/1,331	0,751315
4	1,4641	1/1,4641	0,683013
5	1,6105	1/1,6105	0,620921

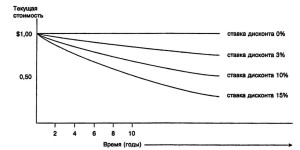
В некоторых таблицах на одной и той же странице приведены величины текущей стоимости единицы при различных ставках дисконта (процента). Такие таблицы могут быть удобны, например, для показа будущей покупательной способности 1 долл. при различных темпах инфляции. Табл. 3-6 показывает это при ставках 3, 6, 10 и 15%. Линия текущей стоимости единицы при различных ставках дисконта показана графически на рис. 3*7.

ТАБЛИЦА 3-6

Будущая покупательная способность 1,00 долл. при различных темпах инфляции

Индекс инфляции

3%	6%	10%	15%
0,9709	0,9434	0,9091	0,8690
0,9426	0,8900	0,8264	0,7561
0,9151	0,8396	0,7513	0,6575
0,8885	0,7921	0,6830	0,5718
0,8626	0,7473	0,6206	0,4972

Более частое дисконтирование

Как и в случае со сложным процентом, интервалы между периодами дисконтирования могут быть короче (более частыми), чем один год. В расчете текущей стоимости реверсии это учитывается так же, как и при накоплении процента. Номинальная ставка дисконта делится на частоту интервалов (например, при поквартальном дисконтировании делится на 4), а число периодов в году умножается на число лет.

Линии текущей стоимости при различных ставках дисконта

Применение финансового калькулятора

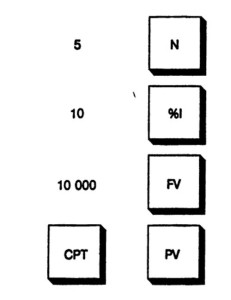
Для того чтобы с помощью калькулятора определить текущую стоимость известной будущей суммы, введите число временных периодов — N, периодическую ставку процента — %I и известную будущую стоимость — FV. Затем нажмите клавиши COMPUTE и PV. Дисплей покажет текущую стоимость. (На некоторых калькуляторах предварительно следует установить регистр CI.) Рис. 3-8 показывает, какие клавиши калькулятора необходимо использовать для определения текущей стоимости 10 000 долл., которые должны быть получены через пять лет при годовой ставке дисконта 10%.

Результат: 6209,21 (на дисплее)

Рис, 3-в. Клавиши калькулятора, используемые для расчета текущей стоимости реверсии при ставке дисконта 10%, ежегодном дисконтировании за 5 лет и будущей стоимости 10 000 долларов

Источник: Джек Фридман, Николас Орудей. Анализ и оценка приносящей доход недвижимости.

Источник

Основы теории стоимости денег во времени. Стандартные функции сложного процента

: 17.03.2015 11:00; 19069

Стандартные функции сложного процента

Применение стандартных функций сложного процента даёт возможность рассчитать величину любого из элементов, характеризующих распределенные во времени денежные потоки — стоимость, платеж, время, ставку, — при условии, что другие элементы известны.

Как правило, речь идет о 6 функциях сложного процента:

накопленная сумма единицы(её будущая стоимость),
накопление единицы за период,
взнос в формирование фонда возмещения,
реверсия (текущая стоимость единицы),
текущая стоимость обычного аннуитета,
взнос на амортизацию единицы

Поскольку эти функции применяют весьма широко и часто, разработаны стандартные таблицы, которые включают заранее рассчитанные факторы сложного процента. В данном контексте фактором называется одно из двух или более чисел, которые, будучи перемноженными, дают заданный результат. Все эти факторы созданы с применением базовой формулы (1 + i)n, дающей описание накопленной суммы единицы, и по сути, представляют собой производные от этого фактора.

Будущая стоимость единицы.

Будущая стоимость единицы – функция, которая определяет ее накопленную сумму спустя n периодов, если ставка дохода на капитал равна i. Функция подразумевает, что доход на капитал, полученный за период, вместе с первоначальным капиталом формирует базу, с которой будет определяться доход на капитал в следующий период.

Её рассчитывают по формуле:

где FV — будущая стоимость;
PV — текущая стоимость;
i — ставка дохода;
n — срок накопления (число периодов);
FVF(i;n) = (1 + i)n — фактор будущей стоимости единицы (накопленной суммы).

С помощью этой функции можно вычислить будущее значение денежной суммы, опираясь на ее текущее значение, размер ставки дохода на капитал и длительность срок накопления.

ПРИМЕР

В текущий момент стоимость земельного участка составляет 1000 долл., при уровне доходности 14%. Предполагается, что он будет продан через два года. При этом ни его характеристики, ни рыночные условия не изменятся. В данном случае будущая стоимость земельного участка станет равной 1300 долл.:

или, что одно и то же

Накопление единицы за период.

Накопление за период – функция, которая определяет будущую стоимость обычного аннуитета (то есть серии равновеликих периодических платежей и поступлений PMT) на протяжении n периодов при размере ставки дохода на капитал i.
Обычный аннуитет – это серия равновеликих периодических платежей и поступлений, причём первый из них производится в конце следующего, после текущего, периода. Если платежи производятся авансом, (в начале каждого периода), речь идёт об авансовом аннуитете.

Будущую стоимость обычного аннуитета рассчитывают по формуле:

4.3.04

где FVA — будущая стоимость обычного аннуитета
PMT – величина одного из серии равновеликих периодических платежей или поступлений
i — ставка дохода;
n — число периодов;

4.3.05

— фактор будущей стоимости обычного аннуитета.

ПРИМЕР

Нужно рассчитать будущую стоимость земельного участка, приобретенного при условии отсрочки платежа на полгода и компенсации 12% годовых. Платежи вносятся в конце каждого месяца — равными суммами по 1000 долл. В таком случае будущая стоимость земельного участка окажется равной 6152 долл.:

4.3.06

или, что то же самое

4.3.07

Взнос на формирование фонда возмещения.

Взносы на формирование фонда возмещения — функция, которой определяется величина платежей для обычного аннуитета, чья будущая стоимость через n периодов, при величине ставки i, равна 1.

Иначе говоря, с помощью функции взноса на формирование фонда возмещения можно определить размер равновеликого периодического платежа (регулярного дохода), нужного для накопления до конца установленного периода определенной суммы, с учетом накопленных процентов, при некоторой ставке дохода.

Расчет величины равновеликого периодического платежа осуществляется по формуле:

4.3.08

где PMT – величина равновеликого периодического платежа;
FV — будущая стоимость обычного аннуитета
i — ставка дохода;
n — число периодов;

4.3.09

— фактор фонда возмещения
SFF (i;n) (фактор фонда возмещения) является обратной величиной фактора будущей стоимости обычного аннуитета:

4.3.10

ПРИМЕР.

Нужно рассчитать величину ежегодных накоплений с целью равноценной замены существующего здания, которое приносит доход в 14%, с условием, что к окончанию периода экономической жизни (8 лет) затраты на замену здания составят 10000 долл. В данном случае величина ежегодных отчислений составит 755,70 долл.:

4.3.11

или

Текущая стоимость единицы (реверсии).

Текущая стоимость единицы (реверсии) – функция, которая определяет текущую стоимость будущей единицы, которую можно получить по истечении n периодов при заданной ставке дохода i. Данная функция позволяет осуществить оценку текущей стоимости дохода, который может быть получен от реализации объекта в конце периода при данной ставке дисконта.

Текущую стоимость единицы рассчитывают по формуле:

4.3.13

где PV — текущая стоимость;
FV — будущая стоимость;
i — ставка дохода (дисконта);
n — срок накопления (число периодов);

4.3.14

— фактор текущей стоимости единицы (реверсии).

В математическом смысле текущая стоимость единицы – это обратная величина функции ее будущей стоимости.

ПРИМЕР.

Требуется вычислить текущую стоимость земельного участка, который в конце года будет продан по цене 1000 долл. При ставке дисконта 10% в год текущая стоимость участка будет равной 909,09 долл.

4.3.15

или

Текущая стоимость обычного аннуитета.

Текущая стоимость обычного аннуитета – функция, которая определяет текущую стоимость серии будущих равновеликих периодических платежей (поступлений) PMT на протяжении n периодов при ставке дисконта i. Вычисление осуществляют по формуле:

4.3.17

где PVA — текущая стоимость обычного аннуитета
PMT — величина одного из серии равновеликих периодических платежей (поступлений)
i — ставка дохода (дисконта);
n — число периодов

4.3.18

— фактор текущей стоимости обычного аннуитета.

Текущая стоимость обычного аннуитета может быть определена как сумма текущих стоимостей всех платежей:

4.3.19

ПРИМЕР

Нужно определить текущую стоимость платежей по аренде, при условии, что земельный участок был сдан на три года, за ежегодную арендную плату 100 долл. Ставка дисконта равна 12%. Тогда текущая стоимость платежей составит 240,18 долл.:

4.3.20

или

Взнос на амортизацию единицы.

Взнос на амортизацию единицы – функция, при помощи которой определяют величину регулярного платежа (поступления), обеспечивающего доход на капитал и его возврат при ставке дисконта i за n периодов. Взнос на амортизацию единицы можно рассчитать по формуле:

4.3.22

где PMT — величина платежа для обычного аннуитета;
PV — текущая стоимость единицы,
i — ставка дисконта (дохода);
n — срок накопления (число периодов);

4.3.23

— фактор взноса на амортизацию единицы.

Эта функция, равно как и функция взноса на формирование фонда возмещения, даёт возможность определения платежа РМТ. Но в отличие от функции взноса на формирование фонда возмещения, связанной с платежом с целью накопления заданной суммы FV, функция взноса на амортизацию единицы имеет отношение к платежу, позволяющему вернуть заданную на текущий момент сумму PV. При этом платеж включает две составляющие: первая обеспечивает доход по заданной ставке i, вторая обеспечивает возврат капитала по норме возврата SFF(i; n) за n периодов.

Функция взноса на амортизацию единицы используется при определении регулярных равновеликих (аннуитетных) платежей в счет погашения кредита, если он выдан на некоторый период по заданной ставке по кредиту. При этом каждый платеж включает в себя и выплаты основной суммы долга, и начисленных процентов. Сами платежи при этом равновеликие, и от платежа к платежу соотношение доходной и возвратной составляющих меняется (уменьшается часть, с которой идёт выплата процентов, и увеличивается та часть, которая идёт на возврат принципала, то есть основной суммы кредита. То есть процент начисляется на невыплаченную сумму принципала и процентная ставка по кредиту, по мере его погашения, начисляется на меньшую сумму. Функция взноса на амортизацию единицы при этом обратна функции текущей стоимости обычного аннуитета.

ПРИМЕР.

Нужно рассчитать величину ежегодного дохода, который приходится на здание, которое будет эксплуатироваться в течение 5 лет, если его текущая стоимость равна 10000 долл., а ставка дисконта — 15%. При таких условиях размер ежегодного дохода составляет 2983,16 долл.:

4.3.24

или, что одно и то же

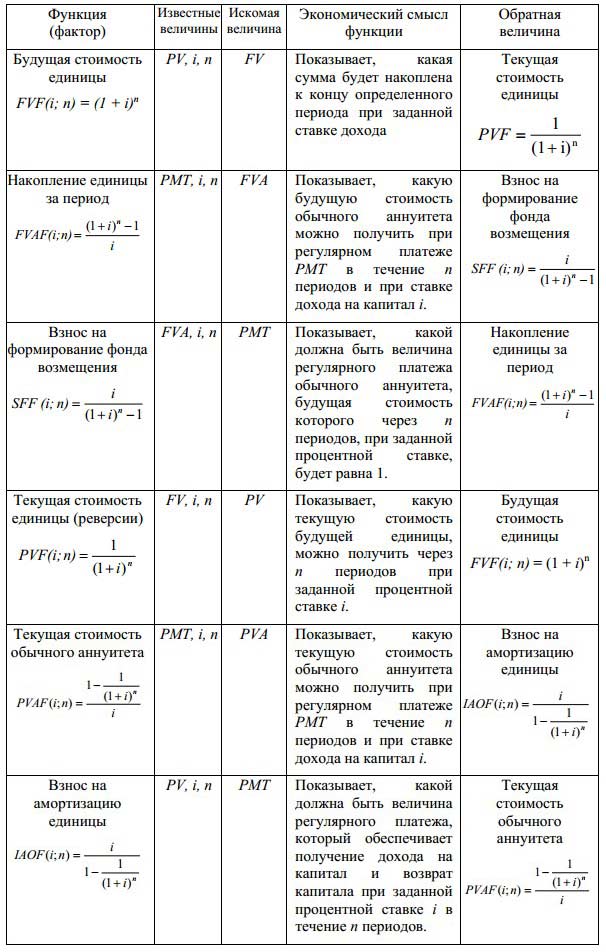
Используя взаимосвязь факторов шести функций сложного процента, можно предложить представить логику их построения и экономический смысл в табличной форме.

Взаимосвязь и экономический смысл стандартных функций сложного процента

4.3.26

Резюме

В оценке недвижимости важную роль играет теория стоимости денег во времени. С ее помощью объясняется такой значимый для оценки процесс, как дисконтирование, отражающий взаимосвязь между понятиями текущая стоимость, будущая стоимость, регулярный доход, время, ставка дохода.

Данная взаимосвязь реализуется на основе использования 6 функций сложного процента, позволяющих определить искомую величину на основе умножения известной величины на соответствующий фактор, значение которого может быть вычислено или взято из таблиц 6 функций сложного процента. Это существенно облегчает выполняемые при оценке многочисленные расчеты.

Источник

Стоимость
реверсии (остаточная
стоимость, стоимость постпрогнозного
периода, терминальная стоимость) —
это стоимость объекта в конце последнего
прогнозного года. Необходимость расчета
стоимости реверсии обусловлена
несовпадением длительности прогнозного
периода, используемого в методе
дисконтированных денежных потоков, с
остаточной экономической жизнью
оцениваемого объекта. Если рассматривать
стоимость недвижимости как сумму
дисконтированных будущих доходов, то
ограничение прогнозного периода не
позволяет использовать в расчетах все
потенциальные доходы. Для устранения
данного негативного положения
определяется стоимость реверсии, в
которой аккумулируются доходы,
которые оцениваемый объект принесет
в постпрогнозный период.

Методы
расчета стоимости реверсии определяются
экономическим положением объекта
на конец последнего прогнозного года.
Если экономическое состояние недвижимости
оценивается как благополучное, то
целесообразно рассчитывать стоимость
реверсии методом капитализации дохода
либо корректировкой стоимости
недвижимости, рассчитанной на дату
оценки, на величину возможного износа
за анализируемый период. Если на конец
прогнозного периода экономическое
положение оценивается как неблагоприятное,
то реверсия рассчитывается по
ликвидационной либо утилизационной
стоимости.

5
этап. Дисконтирование денежных потоков.
Поскольку денежные потоки и реверсия
рассчитывались для соответствующих
лет прогнозного периода, то для
определения рыночной стоимости
оцениваемой недвижимости их следует
привести к дате оценки или продисконтировать.
Текущие доходы (годовые денежные потоки)
и стоимость реверсии имеют различные
способы дисконтирования.

При
дисконтировании текущего дохода следует
учитывать момент возникновения денежного
потока.

1.
При авансовых арендных платежах
дисконтирование осуществляется на
начало периода.

2.
Если применяется последующий арендный
платеж, дисконтирование осуществляется
на конец периода.

3.
Если оцениваемая недвижимость
функционирует в составе имущественного
комплекса предприятия, то дисконтирование
осуществляется по факторам,
рассчитанным на середину периода:

где
R
—
ставка дисконтирования;

п
—
анализируемый прогнозный год.

Реверсия
всегда дисконтируется на конец последнего
прогнозного года.

6
этап. Расчет рыночной стоимости как
суммы дисконтированных денежных
потоков. Базовая
формула для расчета стоимости объектов
недвижимости в рамках метода
дисконтированных денежных потоков
выглядит следующим образом:

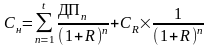
Где
С_н
— стоимость объекта недвижимости на
дату оценки;

ДП_n
— денежный поток;

R
— ставка
дисконтирования денежного потока
периода t;

С_R
— стоимость реверсии в конце прогнозного
периода.

Таким
образом, метод дисконтированных денежных
потоков при оценке недвижимости требует:

■ моделирования
денежных поступлений с учетом динамики
их изменения;

■ составления
прогноза относительно изменения
стоимости недвижимости в течение
установленного прогнозного периода;

■ оценки
риска, присущего объекту;

■ расчета
ставки доходности.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Навигация по разделу "движимое имущество:"общие темы, базовые понятия, затратный подход, сравнительный подход, доходный подход, оценка стоимости транспортных средств, источники, глоссарий - движимое

Содержание

1 5.1. Методы доходного подхода
2 5.2. Метод прямой капитализации
3 5.3. Метод дисконтирования денежных потоков
4 5.4. Потенциальный валовый доход
5 5.5. Действительный валовый доход
6 5.6. Операционные расходы
7 5.7. Операционные расходы
8 5.8. Чистый операционный доход
9 5.9. Реверсия (терминальная стоимость)
10 5.10. Ставка дисконтирования и капитализации, их взаимосвязь
11 5.11. Выбор периода дисконтирования
12 5.12. Норма возврата капитала (методы Ринга, Хоскольда, Инвуда)

5.1. Методы доходного подхода

5.1.1. Основные методы доходного подхода к оценке:

метод дисконтирования денежных потоков (см. тему 5.3);
метод капитализации;
метод равноэффективного функционального аналога.

5.1.2. Метод капитализации подразделяется на:

метод прямой капитализации (см. тему 5.2);
методы капитализации по расчетным моделям (см. тему 5.12).

5.1.3. Метод равноэффективного функционального аналога – метод доходного подхода, который позволяет оценить стоимость объекта, не прибегая к расчету его полного чистого операционного дохода.
${displaystyle S=(S_{b}+{frac {V_{z}d.b+I_{m}.b}{K_{a}.b+i}});times K_{p}rtimes ;K_{s}r-{frac {I_{m}+V_{z}d}{K_{a}+i}}}$

где:

– стоимость объекта оценки, ден. ед.;;

${displaystyle S_{b}}$

– стоимость базисного объекта, ден. ед.;

${displaystyle V_{z}d.b}$

– годовой валовой доход от здания, занимаемого базисным объектом (комплексом), ден. ед.;

${displaystyle I_{m}.b}$

– годовые операционные затраты при функционировании базисного объекта (без амортизации и затрат на содержание и эксплуатацию здания), ден. ед.;

${displaystyle K_{a}.b}$

– коэффициент амортизации базисного объекта, рассчитываемый по формуле третьей функции денежной единицы «Фактор фонда возмещения», доли ед.;

– ставка дисконта, доли ед.;

${displaystyle K_{p}r=Q/Q_{b}}$

– коэффициент, корректирующий различие производственной мощности оцениваемого и базисного объектов; Q и Qб – годовая производственная мощность соответственно оцениваемого и базисного объектов, доли ед.;

${displaystyle K_{s}r=((K_{a}.b+i))/({K_{a}+i})}$

– корректирующий коэффициент, учитывающий различие срока службы у оцениваемого и базисного объектов, доли ед.;

${displaystyle I_{m}}$

– годовые операционные затраты при функционировании оцениваемого объекта (без амортизации и затрат на содержание и эксплуатацию здания), ден.ед.;

${displaystyle V_{z}d}$

– годовой валовой доход от здания, занимаемого оцениваемым объектом, ден.ед.;

${displaystyle K_{a}}$

– коэффициент амортизации оцениваемого объекта, рассчитываемый по формуле третьей функции денежной единицы «Фактор фонда возмещения», доли ед.

5.2. Метод прямой капитализации

5.2.1. Метод прямой капитализации – частный случай метода дисконтирования денежных потоков. Применяется, когда объект оценки генерирует чистый операционный доход, величина которого либо относительно постоянна, либо изменяется равномерно (общая теория оценки).
Отметим, что применительно к оценке недвижимости в п.п. «в» п. 23 ФСО №7 указано, что метод применяется для оценки объектов, не требующих значительных капитальных вложений в их ремонт или реконструкцию, фактическое использование которых соответствует их наиболее эффективному использованию.

Сущность метода:

${displaystyle C={frac {CHOD}{R}}}$

где:

– рыночная стоимость объекта оценки, ден.ед.;

– чистый операционный доход, ден.ед./год (период);

– общая ставка капитализации, доли ед./год (период).

5.2.2. Отличие метода прямой капитализации от методов капитализации по расчетным моделям заключается в том, что:

в методах капитализации по расчетным моделям величина ставки капитализации рассчитывается на основе величины ставки дисконтирования и нормы возврата капитала, которая определяется, например, по моделям Ринга, Инвуда, Хоскольда;
в методе прямой капитализации величина ставки капитализации определяется напрямую, например, из объектов-аналогов методом рыночной экстракции.

5.3. Метод дисконтирования денежных потоков

5.3.1. Метод дисконтирования денежных потоков – метод расчета стоимости, основанный на приведении (дисконтировании) будущих денежных потоков доходов и расходов, связанных с объектом недвижимости, в том числе от его продажи в конце прогнозного периода, к дате, на которую определяется стоимость.

Дисконтирование денежных потоков – процесс определения стоимости денежных потоков на предыдущий момент (движение влево по оси времени).
Общая формула расчета имеет следующий вид (при возникновении денежных потоков в конце периода):

${displaystyle C;=;sum _{j=1}^{n}{frac {CF_{j}}{(1+i)^{j}}}+{frac {CF_{REV}}{(1+i)^{n}}}}$

где:	С –	стоимость объекта оценки, ден. ед.;
	CF_j –	денежный поток j-ого периода, ден. ед.;
	CF_РЕВ –	реверсия, ден.ед.;
	i –	cтавка дисконтирования, доли ед.;

Дисконтный множитель (фактор (коэффициент) дисконтирования) – коэффициент, умножение на который величины денежного потока будущего периода дает его текущую стоимость:

${displaystyle d=;{frac {1}{(1+i)^{t}}}}$

где:

d –

Дисконтный множитель, доли ед.

5.3.2. В случае, когда период генерации денежных потоков условно бесконечен, его разделяют на:

прогнозный период – период времени, в течение которого моделируются денежные потоки от объекта недвижимости. В качестве прогнозного периода могут рассматриваться типичный срок владения подобными активами, период до выхода объекта на стабильные потоки доходов и расходов;
постпрогнозный период – период времени, наступающий после прогнозного периода.

Для определения денежных потоков постпрогнозного периода может быть использована модель капитализации. Формула расчета (при возникновении денежных потоков в конце каждого периода):

${displaystyle PV;=;sum _{j=1}^{n}{frac {FV_{j}}{(1+i)^{j}}}+{frac {FV_{n+1}}{R}}times {frac {1}{(1+i)^{n}}}}$

где:	PV –	текущая стоимость денежных потоков прогнозного и постпрогнозного периодов, ден.ед.;
	FV_j –	денежный поток в j-ом периоде, ден. ед.;
	n–	продолжительность прогнозного периода, периодов;
	R–	ставка капитализации, доли ед.

5.3.3. Пример задачи. Определить текущую стоимость следующих денежных потоков. 1 год – 100 ед., 2 год – 150 ед., 3 год – 100 ед., 4 год (первый год постпрогнозного периода) – 120 ед. I = 15%, R = 20%. Дисконтирование выполнять на конец периода.

Решение:

Таблица 10.

Показатель	Значение
Прогнозный период	Первый год постпрогнозного периода
1 год	2 год	3 год
Денежный поток, ден.ед.	100	150	100	120
Период дисконтирования, лет	1	2	3	3
Ставка дисконтирования, %	15	15	15	15
Дисконтный множитель, доли ед.	0,8696	0,7561	0,6575	0,6575
Текущая стоимость, ден.ед.	87	113	66
Ставка капитализации, %				20
Будущая стоимость реверсии, ден.ед.				600
Текущая стоимость реверсии, ден.ед.	395
Текущая стоимость денежных потоков прогнозного и постпрогнозного периодов, ден.ед.	661

5.4. Потенциальный валовый доход

5.4.1. Потенциальный валовый доход (ПВД) – доход, который способен приносить объект при сдаче его или его элементов в аренду и получении арендной платы в полном объеме:

где:

– арендная ставка, ден.ед./ед.площади/год;

– Количественная характеристика объекта, например, ед., КВт.

5.4.2. Связь ПВД с другими уровнями дохода от эксплуатации объекта описывается следующими формулами:

${displaystyle PVD-NP-NZ+DX_{PR}=DVD}$

где:

– потенциальный валовый доход, ден.ед.;

– потери от неплатежей, ден.ед.;

– потери от недозагрузки, ден.ед.;

${displaystyle DX_{PR}}$

– прочие доходы от нормального рыночного использования объекта недвижимости, ден.ед.;

– действительный валовый доход, ден.ед.;

– операционные расходы, ден.ед.;

– расходы на замещение, ден.ед.;

– чистый операционный доход, ден.ед..

5.4.3. На что обратить внимание в оценочной практике: при определении дохода от сдачи машин и оборудования в аренду необходимо соблюдать соответствие между ставкой аренды и базой для ее начисления (ставке аренды за смену соответствует период времени в сменах, ставке аренды в сутках соответствует период времени в сутках и т.д.).

5.5. Действительный валовый доход

5.5.1. Действительный валовый доход (ДВД) – потенциальный валовый доход (ПВД) за вычетом потерь от недозагрузки, неплатежей арендаторов, а также с учетом дополнительных видов доходов.

5.5.2. Связь ДВД с другими уровнями дохода от эксплуатации объекта описывается следующими формулами:

${displaystyle PVD-NP-NZ+DX_{PR}=DVD}$

где:

– потенциальный валовый доход, ден.ед.;

– потери от неплатежей, ден.ед.;

– потери от недозагрузки, ден.ед.;

${displaystyle DX_{PR}}$

– прочие доходы от нормального рыночного использования объекта, ден.ед.;

– действительный валовый доход, ден.ед.;

– операционные расходы, ден.ед.;

– расходы на замещение, ден.ед.;

– чистый операционный доход, ден.ед..

5.5.3. На что обратить внимание в оценочной практике: при определении дохода от сдачи машин и оборудования в аренду необходимо соблюдать соответствие между ставкой аренды и базой для ее начисления (ставке аренды за смену соответствует период времени в сменах, ставке аренды в сутках соответствует период времени в сутках и т.д.).

5.6. Операционные расходы

5.6.1. Операционные расходы (ОР, операционные затраты) – операционные (производственные) затраты, связанные с владением и эксплуатацией объекта (без амортизационных отчислений), в том числе расходы на страхование, управление, электричество, техническое обслуживание, уборку, охрану, текущий ремонт и пр.

5.6.2. Связь ОР с различными уровнями дохода от эксплуатации недвижимости описывается следующими формулами:

${displaystyle PVD-NP-NZ+DX_{PR}=DVD}$

где:

– потенциальный валовый доход, ден.ед.;

– потери от неплатежей, ден.ед.;

– потери от недозагрузки, ден.ед.;

${displaystyle DX_{PR}}$

– прочие доходы от нормального рыночного использования объекта недвижимости, ден.ед.;

– действительный валовый доход, ден.ед.;

– операционные расходы, ден.ед.;

– расходы на замещение, ден.ед.;

– чистый операционный доход, ден.ед..

5.6.3. На что обратить внимание в оценочной практике: «неоценщики» (например, риэлторы, собственники объектов недвижимости) часто под ОР понимают расходы, которые понесет арендатор сверх выставленной ставки арендной платы. Например: арендатор уплачивает арендную плату + операционные расходы в составе платы за электричество и водоснабжение, определяемые по фактическим показаниям счетчика.

5.7. Операционные расходы

5.7.1. Постоянные расходы – не зависят от интенсивности эксплуатации машин и оборудования (например, арендные или страховые платежи).

5.7.2. Переменные расходы – зависят от интенсивности эксплуатации машин и оборудования (например, оплата электроэнергии).

5.8. Чистый операционный доход

5.8.1. Чистый операционный доход (ЧОД) – действительный валовый доход от приносящего доход актива за вычетом операционных расходов и расходов на замещение.

5.8.2. Связь ЧОД с другими уровнями дохода от эксплуатации объекта описывается следующими формулами:
${displaystyle PVD-NP-NZ+DH_{PR}=DVD}$

где:

– потенциальный валовый доход, ден.ед.;

– потери от неплатежей, ден.ед.;

– потери от недозагрузки, ден.ед.;

${displaystyle DH_{PR}}$

– прочие доходы от нормального рыночного использования объекта, ден.ед.;

– действительный валовый доход, ден.ед.;

– операционные расходы, ден.ед.;

– расходы на замещение, ден.ед.;

– чистый операционный доход, ден.ед..

5.9. Реверсия (терминальная стоимость)

5.9.1. Реверсия (синонимы: терминальная, продленная, постпрогнозная стоимость) – стоимость объекта на момент окончания периода прогнозирования денежных потоков от объекта.
5.9.2. Наиболее часто встречаются следующие варианты расчета величины реверсии:

капитализация денежного потока первого года постпрогнозного периода;
на основе сравнительного подхода (определение стоимости объекта на дату оценки с прогнозом ее изменения на конец прогнозного периода);

5.10. Ставка дисконтирования и капитализации, их взаимосвязь

5.10.1. Ставка дисконтирования:

процентная ставка, используемая для приведения прогнозируемых денежных потоков (доходов и расходов) к заданному моменту времени, например, к дате оценки;
процентная ставка, характеризующая требуемую инвестором доходность при инвестировании в объекты и проекты.

Синонимы – требуемая норма (ставка) доходности, норма отдачи на вложенный капитал. Размерность – проценты или доли единицы.
В зависимости от учета инфляционной составляющей выделяют реальную (очищенная от инфляционной составляющей) и номинальную (без очищения) ставку дисконтирования. Взаимосвязь между ними имеет следующий вид (формула Фишера):

${displaystyle i_{P}={frac {i_{H}-i_{INF}}{1+i_{INF}}},}$

где:

${displaystyle i_{P}}$

– реальная ставка дисконтирования, доли ед.

${displaystyle i_{H}}$

– Номинальная ставка дисконтирования, доли ед.;

${displaystyle i_{INF}}$

– Темп инфляции, доли ед.

5.10.2. Ставка капитализации (коэффициент капитализации) – выраженное в процентах отношение чистого операционного дохода объекта к его рыночной стоимости.

5.10.3. Метод кумулятивного построения – метод расчета ставки дисконтирования, учитывающий риски, связанные с инвестированием в объекты.

5.10.3.1. Ставка дисконтирования определяется как сумма «безрисковой» доходности, премии за низкую ликвидность, премии за риск вложения в объект.

${displaystyle i=i_{BR}+i_{NL}+i_{BH},}$

где:

– ставка дисконтирования, %;

${displaystyle i_{BR}}$

– безрисковая ставка, %;

${displaystyle i_{NL}}$

– премия за низкую ликвидность, %;

${displaystyle i_{BH}}$

– премия за риск вложения, %.

5.10.3.2. Безрисковая ставка (ставка безрисковой доходности) – процентная ставка доходности, которую инвестор может получить на свой капитал, при вложении в наиболее ликвидные активы, характеризующиеся отсутствием или минимальным возможным риском невозвращения вложенных средств.

5.10.3.3. Премия за низкую ликвидность – премия, учитывающая невозможность незамедлительного возврата вложенных в объект инвестиций. В заданиях квалификационного экзамена рассчитывается по формуле:

${displaystyle i_{BR}={frac {i_{B}R}{12}}times N,}$

где:

– срок экспозиции объекта на рынке, мес.;

${displaystyle i_{BR}}$

– безрисковая ставка, %;

Срок экспозиции объекта на открытом рынке (срок экспозиции) – период времени от выставления объекта на продажу до поступления денежных средств за проданный объект или типичный период времени, который необходим для того, чтобы объект был продан на открытом и конкурентном рынке при соблюдении всех рыночных условий.

5.10.3.4. Премия за риск вложений (инвестиций) в объект – премия на отраслевой риск инвестирования (инвестирование в объект).

5.10.4. Метод рыночной экстракции – метод определения коэффициента капитализации на основе анализа соотношения чистого арендного дохода и цен продаж по данным реальных сделок или соответствующим образом скорректированных цен предложений объектов при условии, что существующее использование объектов соответствует их наилучшему и наиболее эффективному использованию:

${displaystyle R={frac {CHOD}{C}},}$

где:

– общая ставка капитализации, доли ед.;

${displaystyle C_{BR}}$

– рыночная стоимость, ден.ед.;

– чистый операционный доход, ден.ед./год.

Результаты, полученные по различным аналогам, взвешиваются.

5.10.5. В рамках методов капитализации по расчетным моделям взаимосвязь ставки дисконтирования и капитализации имеет следующий вид:

${displaystyle R=i+i_{VOZVR},}$

где:

– ставка капитализации, доли ед. (%) / год (период);
– ставка дисконтирования, доли ед. (%) / год (период);
${displaystyle i_{VOZVR}}$ – норма возврата, доли ед. (%) / год (период).

5.10.6. На что обратить внимание в практической деятельности:

величины ставок дисконтирования и капитализации должны соответствовать типу денежного потока (например, в части учета инфляционной или налоговой составляющей);
в п. 5.10.3.1 структура рисковой составляющей приведена в соответствии с глоссарием Минэкономразвития. В реальной оценке она может быть другой.

5.11. Выбор периода дисконтирования

Формулировка вопроса допускает неоднозначное толкование – под «периодом дисконтирования» может подразумеваться продолжительность прогнозного периода или шаг дисконтирования.

5.11.1. Выбор продолжительности прогнозного периода осуществляется с учетом:

оставшегося срока экономической жизни объекта оценки;
прогнозной динамики изменения денежных потоков объекта оценки;
детальности исходной информации по денежным потокам объекта оценки.

Как правило, продолжительность прогнозного периода выбирается таким образом, чтобы к его концу денежные потоки объекта оценки стабилизировались.

5.11.2. Выбор шага дисконтирования осуществляется с учетом:

ставшегося срока экономической жизни объекта оценки;
периодичности генерации денежных потоков объектом оценки;
детальности исходной информации по денежным потокам объекта оценки.

Обычно в качестве шага дисконтирования используют: год, квартал, месяц.

5.12. Норма возврата капитала (методы Ринга, Хоскольда, Инвуда)

5.12.1. Методы капитализации по расчетным моделям – группа методов определения стоимости денежных потоков на предыдущую дату. Применяются в следующих условиях: генерация объектом оценки чистого операционного дохода, который либо относительно постоянен, либо изменяется линейно (равномерно снижается либо увеличивается).

Сущность методов:

${displaystyle C={frac {CHOD}{R}}={frac {CHOD}{ipm i_{VOZVR}}}}$

где:

– рыночная стоимость объекта оценки, ден.ед.;

– чистый операционный доход, ден.ед./год (период);

– ставка капитализации, доли ед./год (период);

– ставка дисконтирования, доли ед./год (период).

${displaystyle i_{VOZVR}}$

– норма возврата, доли ед./год (период).

5.12.2. Отличие методов капитализации по расчетным моделям от метода прямой капитализации заключается в том, что: • в методах капитализации по расчетным моделям величина ставки капитализации рассчитывается на основе величины ставки дисконтирования и нормы возврата капитала, определяемой, например, по моделям Ринга, Инвуда, Хоскольда; • в методе прямой капитализации величина ставки капитализации определяется напрямую, например, на основе данных по объектам-аналогам методом рыночной экстракции.

5.12.3. Норма возврата капитала (норма возврата) – величина ежегодной потери стоимости капитала за время ожидаемого периода использования объекта. Выделяют следующие основные методы расчета величины нормы возврата капитала: Ринга, Хоскольда, Инвуда.

5.12.4. Метод Ринга – метод расчета нормы возврата капитала. Предусматривается возмещение инвестированного капитала равными суммами:

${displaystyle i_{VOZVR}={frac {1}{T}}times 100%}$

где:

${displaystyle i_{VOZVR}}$

– норма возврата, %;

– оставшийся срок экономической жизни объекта оценки, лет.

5.12.5. Метод Хоскольда – метод расчета нормы возврата капитала. Для реинвестируемых средств предполагается получение дохода по безрисковой ставке:

${displaystyle i_{VOZVR}={begin{array}{l}\{frac {i_{BR}}{(1+i_{BR;})^{T}-1}}end{array}}}$

где:

${displaystyle i_{BR}}$

– безрисковая ставка доходности.

5.12.6. Метод Инвуда – метод расчета нормы возврата капитала. Для реинвестируемых средств предполагается получение дохода по ставке, равной требуемой норме доходности (норме отдачи) на собственный капитал:

${displaystyle i_{VOZVR}={begin{array}{l}\{frac {i}{(1+i)^{T}-1}}end{array}}}$

5.12.7. Пример задачи. Определить рыночную стоимость объекта оценки методом капитализации по расчетной модели при следующих условиях: ЧОД = 100 000 ден.ед., i = 15%, срок экономической жизни 10 лет, норму возврата определить по модели Инвуда. Решение:

${displaystyle i{VOZVR}={frac {CHOD}{R}}={frac {CHOD}{i+i{VOZVR}}}}$

${displaystyle i{VOZVR}={frac {0,15}{(1+0,15)^{T}-1}}approx 0,05.}$

${displaystyle PV={frac {CHOD}{i_{VOZVR}}}={frac {100000}{0,15+0,05}}={frac {100000}{0,2}}=500000}$

Навигация по разделу "движимое имущество:"общие темы, базовые понятия, затратный подход, сравнительный подход, доходный подход, оценка стоимости транспортных средств, источники, глоссарий - движимое

Источник