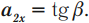Как найти тело отсчета

Относительность движения и система отсчета в физике

Тело отсчета и система координат

Тело отсчета выбирают произвольно. Следует отметить, что движущееся тело и тело отсчета равноправны. Каждое из них при расчете движения в случае необходимости можно рассматривать или как тело отсчета, или как тело движущееся. Например, человек стоит на Земле и наблюдает, как по дороге едет автомобиль. Человек неподвижен относительно Земли и считает Землю телом отсчета, самолет и автомобиль в этом случае тела движущиеся. Однако, пассажир автомобиля, который говорит, что дорога убегает из-под колес, тоже прав. Он считает телом отсчета автомобиль (он неподвижен относительно автомобиля), Земля при этом – тело движущееся.

Чтобы фиксировать изменение положение тела в пространстве, с телом отсчета нужно связать систему координат. Система координат – это способ задания положения объекта в пространстве.

При решении физических задач наиболее распространенной является декартова прямоугольная система координат с тремя взаимно перпендикулярными прямолинейными осями – абсциссой (), ординатой () и аппликатой (). Масштабной единицей измерения длины в СИ является метр.

При ориентировании на местности пользуются полярной системой координат. По карте определяют расстояние до нужного населенного пункта. Направление движения определяют по азимуту, т.е. углу, который составляет нулевое направление с линией, соединяющей человека с нужным пунктом. Таким образом, в полярной системе координат координатами являются расстояние и угол .

В географии, астрономии и при расчетах движений спутников и космических кораблей положение всех тел определяется относительно центра Земли в сферической системе координат. Для определения положения точки в пространстве в сферической системе координат задают расстояние до начала отсчета и углы и — углы, которые составляет радиус-вектор с плоскостью нулевого гринвичского меридиана (долгота) и плоскостью экватора (широта).

Система отсчета

Система координат, тело отсчета, с которым она связана, и прибор для измерения времени образуют систему отсчета, относительно которой рассматривается движение тела.

При решении любой задачи о движении прежде всего должна быть указана та система отсчета, в которой будет рассматриваться движение.

При рассмотрении движения относительно подвижной системы отсчета справедлив классический закон сложения скоростей: скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной:

   

Примеры решения задач по теме «Относительность движения»

Кинематика

Механика — это раздел физики, изучающий механическое движение тел.

Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.

Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если

• расстояние, которое проходит тело, много больше его размера;
• расстояние от данного тела до другого тела много больше его размера;
• тело движется поступательно.

Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.

Важно! 
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.

Основная задача механики — определить положение тела в пространстве в любой момент времени.

Механическое движение и его виды

Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение может быть:
1. по характеру движения

• поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
• вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
• колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;

2. по виду траектории

• прямолинейным — это движение, траектория которого прямая линия;
• криволинейным — это движение, траектория которого кривая линия;

3. по скорости

• равномерным — движение, при котором скорость тела с течением времени не изменяется;
• неравномерным — это движение, при котором скорость тела с течением времени изменяется;

4. по ускорению

• равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
• равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.

Относительность механического движения

Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.

Правило сложения перемещений

Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:

где ​( S )​ — перемещение тела относительно неподвижной системы отсчета;
​( S_1 )​ — перемещение тела относительно подвижной системы отсчета;
​( S_2 )​ — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.

Правило сложения скоростей

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:

где ​( v )​ — скорость тела относительно неподвижной системы отсчета;
​( v_1 )​ — скорость тела относительно подвижной системы отсчета;
​( v_2 )​ — скорость подвижной системы отсчета относительно неподвижной системы отсчета.

Относительная скорость

Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.

Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_{12} ):

Определим скорость второго тела относительно первого ( v_{21} ):

Следует помнить, что траектория движения тела и пройденный путь тоже относительны.

Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:

Если скорости направлены под углом ​( alpha )​ друг к другу, то относительная скорость рассчитывается по теореме косинусов:

Скорость

Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.

Обозначение — ​( v )​, единицы измерения — ​м/с (км/ч)​.

Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:

Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:

Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.

Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.

Ускорение

Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.

Обозначение — ​( a )​, единица измерения — м/с².
В векторном виде:

где ​( v )​ – конечная скорость; ​( v_0 )​ – начальная скорость;
​( t )​ – промежуток времени, за который произошло изменение скорости.

В проекциях на ось ОХ:

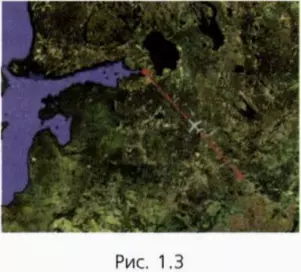
где ​( a_n )​ – нормальное ускорение, ​( a_{tau} )​ – тангенциальное ускорение.

Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:

Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:

Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.

Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_{tau} ) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_{tau} ) = 0, ( a_n ) = 0, ​( v )​ ≠ 0, то тело движется равномерно по прямой;
если ( a_{tau} ) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_{tau} ) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_{tau} ) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.

Равномерное движение

Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.

Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

Проекция вектора скорости на ось ОХ:

Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:

График скорости (проекции скорости)

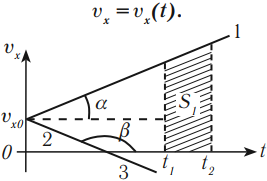
График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ​( t )​, тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ​( t )​, тело движется против оси ОХ.

Перемещение при равномерном движении – это величина, равная произведению скорости на время:

Проекция вектора перемещения на ось ОХ:

График перемещения (проекции перемещения)

График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:

График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.

По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Координата тела при равномерном движении рассчитывается по формуле:

График координаты представляет собой зависимость координаты от времени: ​( x=x(t) )​.

График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:

График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:

Прямолинейное равноускоренное движение

Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:

При движении с ускорением скорость может как увеличиваться, так и уменьшаться.

Скорость тела при равноускоренном движении рассчитывается по формуле:

При разгоне (в проекциях на ось ОХ):

При торможении (в проекциях на ось ОХ):

График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:

График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ​( a_x )​ > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) < 0.

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равноускоренном движении – прямая.
График 1 направлен вверх, тело движется равноускоренно в положительном направлении оси ОХ, ​( v_{0x} )​ > 0, ​( a_x )​ > 0.

График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) < 0,

График 3 направлен вниз, тело движется равноускоренно против оси ОХ, ( v_{0x} ) < 0, ( a_x ) < 0. По графику зависимости скорости от времени можно определить перемещение, пройденное телом за промежуток времени ​( t_2-t_1 )​. Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Перемещение при равноускоренном движении рассчитывается по формулам:

Перемещение в ​( n )​-ую секунду при равноускоренном движении рассчитывается по формуле:

Координата тела при равноускоренном движении рассчитывается по формуле:

Свободное падение (ускорение свободного падения)

Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.

Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).

Обозначение – ​( g )​, единицы измерения – м/с².

Важно! ( g ) = 9,8 м/с², но при решении задач считается, что ( g ) = 10 м/с².

Движение тела по вертикали

Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

Если тело падает вниз без начальной скорости, то ​( v_0 )​ = 0.
Время падения рассчитывается по формуле:

Тело брошено вверх:

Если брошенное вверх тело достигло максимальной высоты, то ​( v )​ = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально

Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали со скоростью ​( v_0=v_{0x} )​;
2. равноускоренного движения по вертикали с ускорением свободного падения ​( g )​ и без начальной скорости ​( v_{0y}=0 )​.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Дальность полета:

Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали;
2. равноускоренного движения по вертикали с ускорением свободного падения.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:

Время полета:

Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ​( v_0 )​, с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ​( alpha )​, под которым тело брошено, будет равен углу, под которым оно упадет.

При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

Движение по окружности с постоянной по модулю скоростью

Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.

Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ​( a_{цс} )​, единицы измерения – ​м/с^2​.

Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ​( T )​, единицы измерения – с.

где ​( N )​ – количество оборотов, ​( t )​ – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ​( nu )​, единицы измерения – с^–1 (Гц).

Период и частота – взаимно обратные величины:

Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ​( v )​, единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:

Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ​( omega )​, единицы измерения – рад/с .

Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:

Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:

Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:

Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ​( v_1 )​, и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ), то относительно дороги мгновенная скорость разных точек колеса различна.

Мгновенная скорость нижней точки ​( (m) )​ равна нулю, мгновенная скорость в верхней точке ​( (n) )​ равна удвоенной скорости ​( v_1 )​, мгновенная скорость точки ​( (p) )​, лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ​( (c) )​ – по теореме косинусов.

Основные формулы по теме «Кинематика»

Механика изучает механическое движение, то есть изменение положения тел друг относительно друга с течением времени. Основная задача механики – определение положения тел в заданный момент времени, если известны положение и скорость тел в начальный момент.

Движение тел зависит от взаимодействия между ними. Но для изучения взаимодействий тел нужно овладеть понятиями, с помощью которых описывают движение тела. Это – траектория движения тела, его перемещение, скорость и ускорение. Раздел механики, в котором рассматривают описание движения тел, называют кинематикой.

1. Система отсчёта

Из курса физики основной школы вы знаете, что движение относительно. Например, сидящий в кресле пассажир летящего самолета (рис. 1.1) покоится относительно самолета, однако относительно Земли он движется, причем довольно быстро. Кроме того, он движется относительно стюардессы, идущей вдоль рядов кресел.

Поэтому, прежде чем описывать движение тел, мы должны выбрать тело, относительно которого будем рассматривать положение всех тел в данной задаче. Это тело называют телом отсчета.

Иногда тело отсчета не указывают явно (когда из-за этого не может возникнуть недоразумений).

? 1. Что принято за тело отсчета в следующих случаях?
а) Автомобиль едет со скоростью 100 км/ч.
б) Стюардесса идет со скоростью 1 м/с.
в) Скорость Луны равна 1 км/с.

С телом отсчета связывают систему координат (рис. 1.2). Кроме того, для описания движения нужны часы.

Тело отсчета, связанная с ним система координат и часы образуют систему отсчета.

2. Материальная точка

Часто для описания движения тела достаточно задать движение только одной его точки. В таком случае тело мысленно заменяют одной точкой.

Тело, размерами которого в данной задаче можно пренебречь,называют материальной точкой.

Тело можно считать материальной точкой в следующих случаях.

а) Когда размеры тела малы по сравнению с расстоянием, пройденным телом. В этом случае различие в движении разных точек тела несущественно.

Например, самолет можно считать материальной точкой, если надо найти время его перелета между двумя городами (рис. 1.3). Но его нельзя считать материальной точкой при рассмотрении фигур высшего пилотажа.

б) При поступательном движении тела. Так называют движение тела, при котором все его точки движутся одинаково, поэтому для описания движения тела можно задать движение только одной его точки. При поступательном движении отрезок, соединяющий любые две точки тела, остается параллельным самому себе.

При поступательном движении тело может двигаться вдоль прямой – например, соскальзывать с наклонной плоскости. Но оно может двигаться и по кривой линии. Так, поступательно движется кабинка колеса обозрения (рис. 1.4), если она не вращается вокруг своей оси. Отрезок, соединяющий середину пола кабинки с серединой ее крыши, остается все время вертикальным (на фотографии он показан красным).

? 2. Приведите пример задачи, в которой Землю можно считать материальной точкой, и задачи, в которой нельзя.

3. Траектория, путь и перемещение

В дальнейшем мы будем рассматривать в основном такие задачи, в которых тело можно считать материальной точкой.

Когда тело движется, соответствующая ему материальная точка описывает в пространстве некоторую воображаемую линию, которую называют траекторией движения тела (или, для краткости, просто траекторией). Если тело оставляет за собой след, траектория тела становится видимой (рис. 1.5).

На рисунке 1.5, а изображена траектория прямолинейного движения тела, а на рисунке 1.5, б – криволинейного.

Если конечная точка траектории совпадает с начальной, траекторию называют замкнутой.

? 3. Приведите свои примеры прямолинейного и криволинейного движения, а также движения по замкнутой траектории.

Зависит ли форма траектории от выбора системы отсчета?

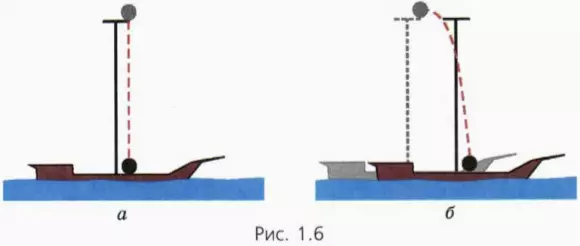
Рассмотрим пример, предложенный Галилеем.

С вершины мачты плывущего корабля на палубу падает ядро. В системе отсчета, связанной с кораблем, траектория движения ядра – прямолинейный вертикальный отрезок (рис. 1.6, а). В системе же отсчета, связанной с Землей, ядро движется по кривой линии – параболе (рис. 1.6, б).

Итак, форма траектории движения тела зависит от выбора системы отсчета.

Длину траектории называют путем, пройденным телом.

Если тело проходит какой-то участок траектории несколько раз, то путь равен длине этого участка, умноженной на число, показывающее, сколько раз тело прошло этот участок. Например, если автомобиль делает три круга по шоссе длиной 100 км, то пройденный им путь равен 300 км.

Путь является скалярной величиной (то есть характеризуется только числовым значением). Будем обозначать путь буквой l.

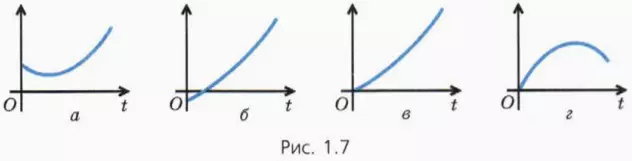
? 4. Какие из графиков, приведенных на рисунке 1.7, не могут отображать зависимость пути от времени? Почему?

Если за любые равные промежутки времени тело проходит равные пути, движение тела называют равномерным. Оно может быть как прямолинейным, так и криволинейным.

Если же пути, проходимые телом за равные промежутки времени, не одинаковы, движение называют неравномерным.

? 5. Приведите примеры равномерного и неравномерного движения – как прямолинейного, так и криволинейного.

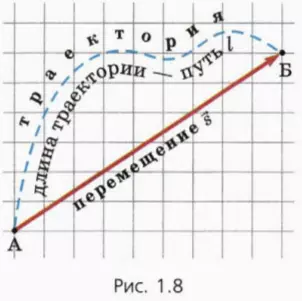
Пусть тело (материальная точка), двигаясь по некоторой траектории, переместилось из начального положения А в положение Б (рис. 1.8).

Направленный отрезок, проведенный от начального положения тела к его положению в данный момент времени, называют перемещением 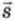тела.

Перемещение является векторной величиной, которая характеризуется неотрицательным числовым значением (модулем) и направлением.

? 6. Используя рисунок 1.8, найдите модуль перемещения материальной точки (масштаб на чертеже 1:1). Придумайте, как измерить пройденный путь, и найдите его значение.
? 7. Как движется тело, если:
а) модуль его перемещения равен пройденному пути?
б) перемещение равно нулю, но путь не равен нулю?
? 8. Изобразите в тетради как можно более простую траекторию движения, для которой:
а) путь в 3 раза больше модуля перемещения;
б) путь в π/2 раз больше модуля перемещения.
? 9. Длина минутной и секундной стрелок часов равна 10 см. В начальный момент концы стрелок совпадают.
а) Чему равны модули перемещений концов этих стрелок за 20 мин?
б) Какой путь прошел конец каждой стрелки за это время?

4. Действия с векторными величинами

Векторные величины (часто для краткости их называют просто векторами) широко используют в физике: это, например, перемещение, скорость, ускорение. Векторную величину обозначают буквой со стрелкой над ней, а модуль этой величины – той же буквой, но без стрелки. Например, перемещение обозначают 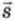, а модуль перемещения – s.

Напомним действия с векторами, уже знакомые вам из курса математики.

а) Умножение вектора на число

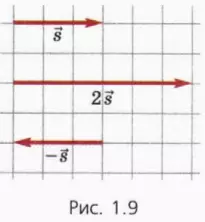
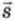
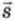
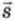
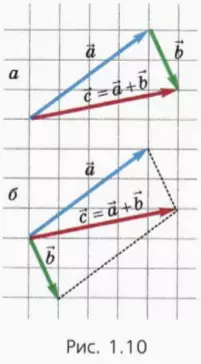
При умножении вектора на число его модуль умножают на это число. Важно помнить: если это число отрицательно, то направление вектора изменяется на противоположное. На рисунке 1.9 изображены векторы , 2 и –.

б) Сложение векторов

Две векторные величины складывают по правилу треугольника (рис. 1.10, а) или по правилу параллелограмма (рис. 1.10, б). Результат сложения один и тот же, поэтому при выборе правила сложения исходят из соображений удобства.

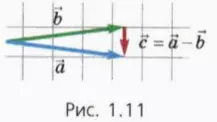
в) Вычитание векторов

Чтобы вычесть из вектора вектор , можно отложить эти векторы из одной точки и соединить направленным отрезком конец вектора с концом вектора (рис. 1.11). Этот направленный отрезок и есть вектор = – . Действительно, из рисунка 1.11 видно, что = + .

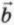
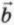
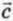
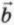
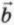
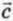
Мы намеренно выбрали случай, когда векторы и равны по модулю. Обратите внимание на то, что при малом угле между такими векторами их разность представляет собой вектор, почти перпендикулярный векторам и . Это замечание пригодится нам в дальнейшем.

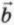
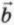
? 10. Вектор направлен вертикально вверх, а вектор по горизонтали вправо. Модуль вектора равен 4, а модуль вектора равен 3. Постройте вектор = – . Чему равен его модуль?

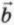
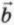
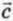
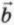
Проекции векторных величин

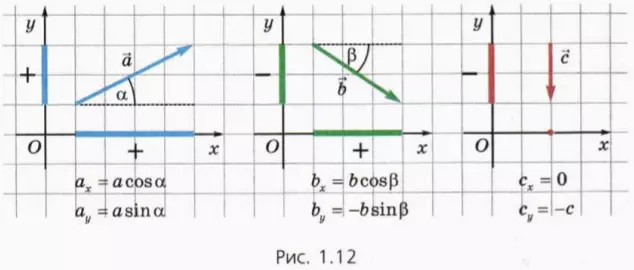
Действия с векторными величинами часто упрощаются, если использовать проекции этих величин на оси координат. (В школьном курсе геометрии проекции вектора называют координатами вектора.) Проекцию вектора обозначают той же буквой, что и сам вектор, но без стрелки и с индексом внизу, указывающим ось координат. Например, проекцию вектора на ось x обозначают a_x.

Чтобы найти проекцию вектора на ось координат, проецируют изображающий этот вектор отрезок на данную ось, а затем приписывают проекции знак «+» или «–» в зависимости от того, как направлен данный вектор относительно выбранной оси. На рисунке 1.12 показано, как находить проекции векторов на оси координат x и y.

Обратите внимание, что проекция вектора может быть положительной, отрицательной или равной нулю.

При умножении вектора на число все проекции этого вектора умножаются на то же число.

При сложении векторов их проекции складываются, а при вычитании – вычитаются.

Например, если = + , то a_x = b_x + c_x; a_y = b_y + c_y.

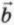
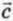
? 11. Изобразите на чертеже в тетради:
а) вектор, у которого обе проекции на оси координат x, y отрицательны;
б) два вектора с общим началом, модули которых не равны, а проекции на ось x равны;
в) два вектора с общим началом, модули которых равны, а проекции на ось y не равны.

Дополнительные вопросы и задания

12. Корабль совершил кругосветное путешествие за полгода. Является ли его траектория замкнутой в системе отсчета, связанной: а) с Землей? б) с Солнцем? Как изменились бы ответы, если бы путешествие длилось точно год?

13. Велосипедист едет по прямой дороге. Изобразите в тетради приблизительный вид траектории точки колеса велосипеда в системе отсчета, связанной: а) с велосипедистом; б) с дорогой.

14. Реактивный самолет А оставляет в небе след (см. рис. 1.5, а). Является ли этот след траекторией движения самолета А в системе отсчета, связанной: а) с Землей? б) с самолетом Б, летящим рядом с самолетом А? Поясните свои ответы.

15. Автомобиль поворачивает на 90º вправо по дуге окружности. При этом его левое переднее колесо прошло путь l_л. Выразите путь l_п, который прошло правое колесо, через l_л и расстояние между колесами d. Найдите числовое значение l_п, если l_л = 10 м, d = 1,5 м. Сделайте пояснительный чертеж.

16. Вектор имеет проекции a_x = 3 см, a_y = 5 см, а проекции вектора равны b_x = 4 см, b_y = –2 см. Изобразите эти векторы и найдите графически вектор = – . Чему равны проекции этого вектора?

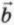
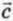
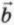
17. Полярник вышел из палатки, расположенной точно на Северном полюсе, прошел 5 км по прямой, затем в направлении точно на восток 15,71 км, после этого повернул налево и шел по прямой еще 5 км. Какова форма траектории полярника? Чему равен модуль перемещения? Сделайте в тетради пояснительный чертеж.

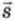
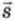
18. Турист переместился из пункта А в пункт В, а затем – в пункт С. Известно, что s_AB = 5 км, s_AC = 4 км, причем _BC ⊥ _AC. Чему равен s_BC? Сделайте в тетради пояснительный чертеж.

План урока:

Механическое движение. Система отсчёта. Закон относительности движения

Уравнения движения. Радиус-вектор. Проекция вектора

Траектория. Путь. Перемещение

Равномерное прямолинейное движение: скорость и уравнение движения

Механическое движение. Система отсчёта. Закон относительности движения

Механическим движением в физике называется изменение с течением времени положения тела (или его частей) в пространстве относительно других тел.

То есть, чтобы сказать, что тело или система совершает механическое движение, нам необходимо: 1) наблюдать его во времени; 2) сравнивать его положение с положением какого-то другого тела (относительно этого тела).

Например, пассажир в едущем автомобиле неподвижен относительно кресла, на котором он сидит, но он движется относительно людей, стоящих на автобусной остановке и самой остановки. А сама автобусная остановка неподвижна относительно стоящих людей, ждущих автобус (см. рисунок 1). Однако она движется относительно проезжающих мимо машин. В первом случае наблюдаемым объектом был человек в машине, а точкой отсчета кресло и люди на остановке. Во втором случае наблюдаемой была автобусная остановка, а точками отсчета – люди на остановке и проезжающие мимо машины.

Рисунок 1 – Иллюстрация к примеру

Из примеров можно сделать вывод, что важно, какой именно объект находится под наблюдением и относительно какого объекта – тела отсчета – рассматривается его движение. Отсюда можно сформулировать закон относительности движения: характер движения тела зависит от того, относительно какого объекта мы рассматриваем данное движение.

Тело (или точка) отсчета, связанная с ним система координат и часы, вместе образуют систему отсчета. То есть все сказанное выше можно переформулировать в одно предложение: для наблюдения механического движения важно в какой системе отсчета будет происходить наблюдение.

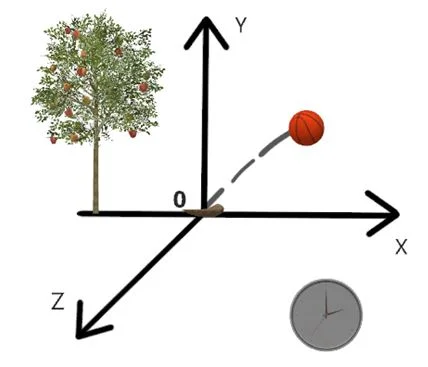
Рисунок 2 – Пример системы отсчета (наблюдаемы объект – летящий мяч, тело отсчета – камень, лежащий в начале координат, система координат и секундомер для отсчета времени)

Однако объекты могут быть очень сложными для наблюдения. Например, автомобиль едет по прямой несколько километров и необходимо описать его движение относительно камня на обочине. Казалось бы, все просто. Но как именно описать движение автомобиля, если корпус его движется по прямой, а колеса совершают вращательные движения.

Для удобства решения подобных задач принято упрощение: если размер и форма тела в данной задаче не играют важной роли для наблюдателя, можно считать это тело за материальную точку.

Материальная точка – это такое тело, размером и формой которого в условиях данной задачи можно пренебречь.

Приведем пример: когда автобус едет из города А в город Б, его можно рассматривать как  материальную точку. Когда пассажир идет из одного конца этого автобуса в другой, считать автобус материальной точкой нельзя. В общем случае можно сказать, что тело можно считать материальной точкой, если его размеры значительно меньше расстояния, на которое оно перемещается.

Уравнения движения. Радиус-вектор. Проекция вектора

Для описания движения тела необходимо уметь рассчитывать его положение в каждый момент времени. Как это сделать?

Самый очевидный способ – координатный. Если вернуться к примеру на рисунке 2, можно увидеть, что летящий мяч в каждый момент времени имеет три координаты по осям OX, OY и OZ. Эти координаты являются функциями времени (т.е. они зависят от времени), а значит, их можно записать в виде системы:

Вид этих уравнений будет зависеть от многих вещей: от того, с какой силой бросили мяч в начале, от массы мяча, под каким углом его бросили и так далее. В любом случае, если эти уравнения заданы, можно найти координаты (то есть положение) тела в любой момент времени. Поиск этих уравнений – основная задача кинематики.

Эта система является кинематическими уравнениями движения тела или материальной точки, записанными в координатной форме. Повторим: если вид уравнений движения задан, можно узнать координату движущейся точки в любой момент времени.

В общем случае, координат три, но иногда можно обойтись двумя или даже одной координатой. Например, для описания движения бильярдного шара достаточно двух координат (так как шар не может двигаться вверх и вниз), а для описания движения шарика, катящегося по прямому горизонтальному желобку достаточно одной координаты (шарик не может двигаться вверх-вниз и вправо-влево).

Еще один способ описания движения – векторный.

*Перед дальнейшим прочтением данной статьи желательно вспомнить основную теорию по теме «Векторы» и «Метод координат»

Вектор, проведенный из начала координат к материальной точке, называется радиус-вектором (см. рисунок 3).

Рисунок 3 – Радиус-вектор (серой линией изображены траектория движения материальной точки, r₁ и r₂* радиус-векторы, проведенные к этой материальной точке в разные моменты времени)

Радиус-вектор проведенный к материальной точке в разные моменты времени будет разным. Значит, его тоже можно представить, как функцию времени:

r = r(t)

Такая функция и будет уравнением движения в векторной форме. Если ее вид задан, можно описать движение тела с той же полнотой, как и при координатной записи.

Еще раз обозначим отличия: при записи уравнения движения в координатной форме в каждый момент времени наблюдающий будет знать три координаты тела; при записи в векторной форме в каждый момент времени известен радиус-вектор (его модуль и направление). Обе записи равносильны.

*На письме векторы обычно обозначаются стрелкой сверху, над величиной. Однако в печатном тексте не всегда удобно нагромождать формулы дополнительными знаками, поэтому в печати векторные величины пишут просто жирным шрифтом. В данной статье далее жирным шрифтом будут написаны только векторные величины.

Покажем, что векторная и координатная записи равносильны. Для этого необходимо вспомнить, как построить проекцию вектора на ось (см. рисунок 4).

Рисунок 4 – Построение проекции вектора на ось

Чтобы построить проекцию вектора на ось, необходимо опустить перпендикуляра из начала и конца вектора на эту ось. Длина получившегося отрезка между проекциями начала и конца вектора, взятая со знаком «+», если вектор а сонаправлен с осью Х, или со знаком «-», если вектор а противонаправлен оси Х, — это и есть искомая проекция.

Если вектор выходит из начала координат, задача облегчается – необходимо опустить перпендикуляр только из конца вектора.

Напоминания из геометрии:

• два вектора равны, если они параллельны или лежат на одной прямой, сонаправлены, а их модули равны;

• проекции равных векторов равны.

Рассмотрим пример (см. рисунок 5)

Рисунок 5 – Задача на нахождение проекции векторов

Предлагаем читателю самому подумать, а затем сравнить свои рассуждения с приведенными ниже.

Итак, вектор а: его начала соответствует координате х_н=1, а конец х_к = 4. Значит a_x = х_к – х_н = 4-1 = 3. Вектор b: его начало лежит в точке х_н=2, а конец х_к =0. Значит b_x = х_к – х_н = 0-2 = -2.

В двумерном случае, проецировать нужно на две оси, но принцип остается тем же.

Иногда еще нужно находить составляющие компоненты вектора а_х и а_у. Рассмотрим пример, для простоты возьмем вектор, выходящий из начал координат (см. рисунок 6).

Сумма векторов а_х и а_у равна а. Модули векторов а_х и а_у численно равны координатам точек, куда попали перпендикуляры, опущенные из конца вектора а на оси ОХ и ОУ.

Еще следует отметить, что, если известен угол β между вектором а и осью ОХ, воспользовавшись основами тригонометрии, можно найти величины проекций:

а_х = а*cos(β);

а_y = а*sin(β).

Если бы вектор а совпадал с радиус-вектором какой-нибудь точки, то величины а_х и а_у совпадали бы с координатами тела по осям ОХ и ОY.

Способ с использованием тригонометрических функций удобен, когда координата конца вектора попадает в нецелое число и опустив перпендикуляр на ось его трудно найти точно. В физических задачах такое часто случается.

Рисунок 6 – Нахождение компонент вектора а

Рассмотрим пример (см. рисунок 7). Модуль вектора r равен 2. Сам вектор направлен под углом в 45 градусов к оси ОХ. Необходимо найти величины проекций (они же координаты) этого вектора на оси ОХ и ОУ.

Рисунок 7 – Задача на нахождение проекций вектора в двумерном пространстве

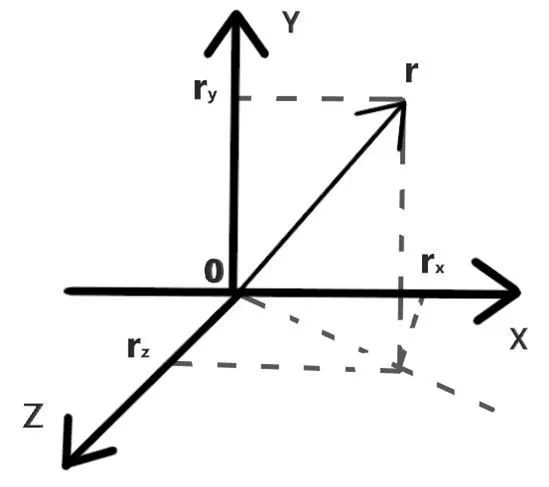
В общем случае радиус-вектор находится в трехмерном пространстве (см. рисунок 8). Построение проекции осуществляется по тому же принципу, что и в рассмотренных выше примерах. Когда строятся проекции на оси ОХ и ОУ, перпендикуляр сначала опускается на плоскость, в которой лежат оси ОХ и ОУ, а затем точка, в которую упал перпендикуляр к плоскости, проецируется на оси ОХ и ОУ.

Точки, в которые попал перпендикуляры к осям – r_x, r_y, r_z – это и есть координаты x, y, z тела в текущий момент времени.

Следует оговориться, что большинство задач 10-го класса будут ограничиваться двумерным пространством.

Рисунок 8 – Построение проекций радиус-вектора

Траектория. Путь. Перемещение

Траектория – это линия, вдоль которой движется тело.

Траектория движения может быть прямолинейной, если тело движется по прямой линии, и криволинейной, если тело движется по кривой.

Путь (S), пройденный телом, равен длине траектории.

Перемещение (r)* – это вектор, проведенный из начала пути в конец.

В случае прямолинейного движения путь и модуль перемещения тела совпадают (см. рисунок 9а). В случае криволинейного – путь и перемещение различаются (см. рисунок 9б), так как длина линии движения тела больше длины вектора, соединяющего начало и конец траектории.

Рисунок 9 – Путь (S) и перемещение (r) при прямолинейном (а) и криволинейном (б) движении

*Иногда перемещение так же, как и путь, называют буквой S — (на письме с вектором над ней, при печати  — жирным шрифтом, так как это векторная величина). В данной статье, чтобы не путаться, перемещение называется только буквой r. В целом, обозначения равноправны, поэтому при решении задач можно использовать то, которое удобнее. Однако не стоит забывать отмечать, что именно обозначено под той или иной буквой.

Равномерное прямолинейное движение: скорость и уравнение движения

Путь и перемещение при равномерном прямолинейном движении

Прямолинейное равномерное движение уже рассматривалось в курсе физики ранее, однако приведем основные определения.

Прямолинейное движение – это движение по прямой линии. Равномерное движение – такое, в процессе которого тело за равные временные промежутки проходит один и тот же путь. Если объединить эти два определения получится третье:

• равномерное прямолинейное движение – это такое движение, в ходе которого 1) тело совершает движение по прямой линии; 2) за одинаковые временные промежутки проходит одинаковый путь.

Зная определения пути и перемещения, это определение можно упростить: прямолинейное равномерное движение тела – это такое движение, в процессе которого тело за одинаковые временные промежутки совершает равные перемещения.

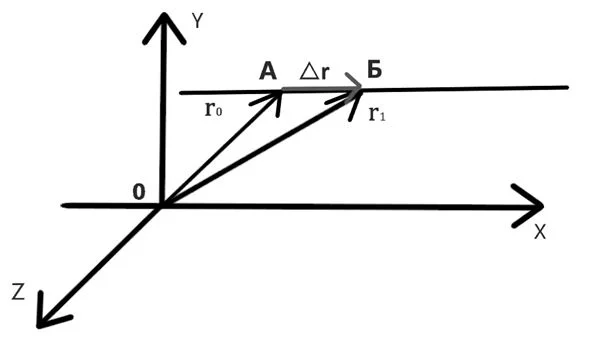
Важной характеристикой является скорость механического движения. Предположим, что при равномерном прямолинейном движении тело за промежуток времени △t перемещается из точки А в точку Б (см. рисунок 8). Радиус-вектор, проведенный в точку A обозначим r₀, а радиус-вектор в точку Б обозначим r₁. Изменение радиус-вектора назовем △r – нетрудно заметить, что это есть перемещение тела за время △t.

Рисунок 8 – Поиск перемещения тела через радиус-векторы при равномерном прямолинейном движении

Тогда скорость движения (v) будет вычисляться по формуле:

Так как △r – вектор, △t – скаляр, скорость v тоже будет вектором, сонаправленным перемещению.

Если тело начинает двигаться в момент начала отсчета, то △t = t*. Из правила сложения векторов следует, что △r = r₁ — r₀. Тогда выражение для скорости можно переписать в виде:

Из этого выражения следует:

r₁ = r₀ + v*t.

Это выражение можно применить к любому произвольно взятому моменту времени, поэтому можно опустить индекс в левой части и переписать:

r = r₀ + v*t.

Данное уравнение является уравнением движения при прямолинейном равномерном движении.

*Напоминание: символом △ (дельта) обозначают изменение какой-нибудь величины. Например △t = t – t₁, где t – конечный момент времени, t₁ – начальный. Если же начальный момент времени совпадает с началом отсчета t₁ = 0, то △t = t – 0 = t_.

Фактически уравнение равномерного прямолинейного движения означает, что радиус-вектор в произвольный момент времени t можно посчитать, сложив начальный радиус-вектор и приращение v*t.

Найдя проекции радиус-вектора и вектора скорости, можно разложить уравнение движения тела на три составляющие вдоль осей ОX, ОY и ОZ.

r_x = r_0x + v_x*t;

r_y = r_0y + v_y*t;

r_z = r_0z + v_z*t.

В этих выражениях r_0x, r_0y, r_0z  и v_x, v_y, v_z – это компоненты изначальных векторов r₀ и v вдоль осей ОХ, ОY и ОZ соответственно. И теперь можно перейти к скалярному виду:

r_x = r_0x + v_x*t;

r_y = r_0y + v_y*t;

r_z = r_0z + v_z*t.

Стоит отметить, что при проецировании какие-то компоненты вектора могут стать отрицательными, тогда знаки в выражениях поменяются на противоположные.

В рассмотренном выше примере движение происходит только вдоль оси ОХ (остальные координаты не изменяются). На рисунке 9 приведены проекции начальной (х₀) и конечной (х₁) точки на ось ОХ.

Рисунок 9 – Перемещение тела в координатном представлении

Уравнение координаты (х) движения будет выглядеть:

x(t) = x₀ + v*t.

А это уже похоже на знакомую из прошедшего курса физики формулу для нахождения пути:

S(t) = S₀ + v*t.

Если точка начала двигаться из начала отсчета S₀ = 0, можно переписать эту формулу в виде:

S(t) = v*t.

Отсюда следуют известные уже формулы для нахождения скорости и времени при равномерном прямолинейном движении:

Приведем последний в этой статье пример: известно, что тело движется вдоль оси ОХ, начиная из точки x₀ = 3 см. Скорость тела равна v = 5 м/с и направлена вдоль оси ОХ. Необходимо записать уравнение движения по координате х для этого тела.

Итак, для начала приведем все единицы измерения к СИ:

x₀ = 3 см = 0,03 м.

Теперь можно записывать уравнение для координаты х:

x(t) = x₀ + v*t = 0,03 + 5*t.

Из этого уравнения можно найти координату тела в любой момент времени. Например, через 2 секунды после начала отсчета тело находилось в точке:

x(2) = 0,03 + 5*2 = 10, 03.

А какой путь прошло тело к этому моменту? В начале оно находилось в точке x(2)  = 0,03 м, а через 2 секунды оно стало находиться в точке x(2) = 10, 03. Значит за 2 секунды тело прошло:

S = x(2) – x₀ = 10, 03 – 0,03 = 10 м.

А если скорость тела была направлена противоположно оси ОХ, как тогда выглядело бы уравнение движения?

Тогда проекция вектора скорости на ось ОХ была бы отрицательной и в уравнении знак перед скоростью поменялся бы на противоположный:

x(t) = x₀ — v*t = 0,03 — 5*t.