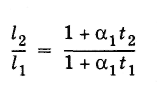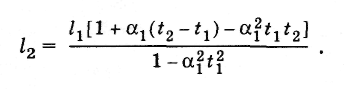Как найти температурный коэффициент линейного расширения - Исправление недочетов и поиск решений вместе с Examum.ru

Термическим расширением называется изменение размеров и объёма тела под воздействием температуры.

При изменении температуры изменяются размеры твёрдых тел. Расширение под воздействием температуры характеризуется коэффициентом линейного термического расширения.

Изменение линейных размеров тела описывается формулой:

l=l0(1+α⋅Δt)

, где:

— первоначальная длина тела;

— коэффициент линейного термического расширения;

ΔT=Δt

— разница температур.

Коэффициент линейного термического расширения показывает, на какую часть первоначальной длины или ширины изменится размер тела, если его температура повысится на (1) градус.

Рис. (1). Удлинения различных материалов

Если рассматривать стержень твёрдого вещества длиной (1) метр, то при повышении температуры на один градус длина стержня изменится на такое число метров, которое равно коэффициенту линейного расширения

Пример:

(10) км железнодорожного пути при увеличении температуры воздуха на (9) градусов (например, от (-5) до (+4)) удлиняются на

10000⋅0,000012⋅9=1,08

метра. По этой причине между участками рельсов оставляют промежутки.

Рис. (2). Поведение рельсов

На этом рисунке видно, что происходит в жаркую погоду, если между участками рельсов оставлены неверные промежутки

Термическое расширение надо учитывать и в трубопроводах, там используются компенсаторы — изогнутые трубы, которые при изменении температуры воздуха при необходимости могут сгибаться. На рисунке видно, что произойдёт, если не будет компенсатора.

Рис. (3). Трубопровод

Инженерам, проектирующим мосты, оборудование, здания, которые подвержены изменениям температуры, необходимо знать, какие материалы можно соединять, чтобы не образовались трещины.

Электрикам, которые протягивают линии электропередачи, необходимо знать, каким изменениям температуры будут подвержены провода. Если летом провода натянуты, то зимой они оборвутся.

При термическом расширении металлов используют автоматические выключатели тепловых приборов. Этот выключатель состоит из двух плотно соединённых пластин различных металлов (с различными термическими коэффициентами). Биметаллические пластины под воздействием температуры сгибаются или выпрямляются, замыкая или размыкая электрическую цепь.

Рис. (4). Биметаллические пластины, поведение при изменении температуры

………………………………………………………………………….. Биметаллические пластины состоят из двух металлов с различными коэффициентами линейного расширения. При изменении температуры длина каждой пластины изменяется по-разному, в зависимости от этого пластины выгибаются либо вверх, либо вниз

С изменением линейных размеров изменяется также и объём тела. Изменение объёма тела описывается формулой, похожей на формулу линейного расширения, только вместо коэффициента линейного термического расширения используется коэффициент объёмного термического расширения.

Изменение объёма тела под воздействием температуры описывается формулой:

V=V0(1+β⋅Δt)

, где:

— первоначальный объём тела;

— коэффициент объёмного термического расширения;

ΔT=Δt

— разница температур.

Коэффициент объёмного термического расширения показывает, на какую часть первоначального объёма изменится объём тела после повышения температуры на (1) градус.

Вещество	Коэффициент объёмного расширения β, K−1
Бензин	(0,001100)
Ртуть…	(0,000181)
Эфир	(0,001650)
Глицерин	(0,000505)
Нефть	(0,000850)
Керосин	(0,000900)
Спирт	(0,001100)
Вода	(0,000208)

Пример:

если объём спирта при температуре

−30°C

равен

500л

, то при температуре

25°C

его объём увеличится на

500⋅0,00011⋅(25−(−30))=3,025л.

Из формулы изменения объёма следует, что при повышении температуры объём жидкости увеличивается, но вода в очередной раз отличилась своими уникальными свойствами, так как при нагревании воды до определённой температуры она не расширяется, а сжимается.

Рис. (5). Изменение объёма в зависимости от температуры

При нагревании воды с температуры таяния льда вначале у неё уменьшается объём, и только после

4°C

её объём начинает увеличиваться

Источники:

Рис. 4. Биметаллические пластины, поведение при изменении температуры. © ЯКласс.
Рис. 5. Изменение объёма в зависимости от температуры. © ЯКласс.

Источник

Содержание:

Тепловое расширение твердых и жидких тел
Зависимость объёма тел от температуры
Линейное расширение твёрдых тел
Объёмное расширение твёрдых тел
Учёт теплового расширения в технике
Терморегулятор
Тепловое расширение жидкостей

Тепловое расширение – это изменение размеров и формы тел при изменении температуры. Математически можно высчитать объемный коэффициент расширения, позволяющий спрогнозировать поведение газов и жидкостей в изменяющихся внешних условиях. Чтобы получить такие же результаты для твердых тел, необходимо учитывать коэффициент линейного расширения.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Тепловое расширение твердых и жидких тел

Тепловое расширение (также используется термин «термическое расширение») — это изменение линейных размеров и формы тела при изменении его температуры. Количественно тепловое расширение жидкостей и газов при постоянном давлении характеризуется изобарным коэффициентом расширения (объёмным коэффициентом теплового расширения). Для характеристики теплового расширения твёрдых тел дополнительно вводят коэффициент линейного теплового расширения.

Зависимость объёма тел от температуры

Частицы твёрдого тела занимают друг относительно друга определённые положения, но не остаются в покое, а совершают колебания. При нагревании тела увеличивается средняя скорость движения частиц. Средние расстояния между частицами при этом увеличиваются, поэтому увеличиваются линейные размеры тела, а следовательно, увеличивается и объём тела.

При охлаждении линейные размеры тела сокращаются, и объём его уменьшается.

При нагревании, как известно, тела расширяются, а при охлаждении сжимаются. Качественная сторона этих явлений была уже рассмотрена в начальном курсе физики.

Наша задача теперь — ознакомиться с количественными законами этих явлений.

Линейное расширение твёрдых тел

Твёрдое тело при данной температуре имеет определённую форму и определённые линейные размеры. Увеличение линейных размеров тела при нагревании называется тепловым линейным расширением.

Измерения показывают, что одно и то же тело расширяется при различных температурах по-разному: при высоких температурах обычно сильнее, чем при низких. Но это различие в расширении столь невелико, что при сравнительно небольших изменениях температуры им можно пренебречь и считать, что изменение размеров тела пропорционально изменению температуры.

В начальном курсе физики было установлено, что различные вещества по-разному расширяются при нагревании: одни сильнее, другие слабее; железо, например, расширяется сильнее стекла и слабее меди.

Чтобы количественно характеризовать это важное тепловое свойство тел, введена особая величина, называемая коэффициентом линейного расширения.

Пусть твёрдое тело при температуре 0°С имеет длину а при температуре t° его длина становится Значит, при изменении температуры на t° длина тела увеличивается на Предполагая, что увеличение длины при нагревании на каждый градус идёт равномерно, находим, что при нагревании на 1°С вся длина тела увеличилась на каждая единица длины на

(1)

Величина (греч. «бэта»), характеризующая тепловое расширение тела, называется коэффициентом линейного расширения.

Формула (1) показывает, что при t = 1°С и = 1 ед. длины величина равна т. е. коэффициент линейного расширения численно равен удлинению, которое получает при нагревании на 1°С стержень, имевший при 0°С длину, равную единице длины.

Из формулы (1) следует, что наименованием коэффициента является

Формулу (1) можно записать в следующем виде:

Отсюда легко определить длину тела при любой температуре, если известны его начальная длина и коэффициент линейного расширения.

Ниже в таблице приведены коэффициенты линейного расширения некоторых веществ, определённые на опыте.

Объёмное расширение твёрдых тел

При тепловом расширении твёрдого тела с увеличением линейных размеров тела увеличивается и его объём. Аналогично коэффициенту линейного расширения для характеристики объёмного расширения можно ввести коэффициент объёмного расширения. Опыт показывает, что так же, как и в случае линейного расширения, можно без большой ошибки принять, что приращение объёма тела пропорционально повышению температуры.

Обозначив объём тела при 0°С через V₀ , объём при температуре t⁰ через V_t а коэффициент объёмного расширения через найдём:

(2)

При V₀ = 1 ед. объёма и t = 1°С величина а равна V_t— V₀, т. е. коэффициент объёмного расширения численно равен приросту объёма тела при нагревании на 1°С, если при 0°С объём был равен единице объёма.

По формуле (2), зная объём тела при температуре 0°С, можно вычислить объём его при любой температуре t°:

Установим соотношение между коэффициентами объёмного и линейного расширения.

Допустим, что имеем кубик, ребро которого при 0° С равно 1 см. При нагревании на 1°С ребро станет равным см, а объём кубика увеличится на см³.

Можно написать следующее равенство:

Но

В этой формуле величины и настолько малы, что ими можно пренебречь и написать:

Коэффициент объёмного расширения твёрдого тела равен утроенному коэффициенту линейного расширения.

Учёт теплового расширения в технике

Из таблицы на странице 124 видно, что коэффициенты расширения твёрдых тел очень малы. Однако самые незначительные, изменения размеров тел при изменении температуры вызывают появление огромных сил.

Опыт показывает, что даже для небольшою удлинения твёрдого тела требуются огромные внешние силы. Так, например, чтобы увеличить длину стального стержня сечением в 1 см² приблизительно на 0,0005 его первоначальной длины, необходимо приложить силу в 1000 кГ. Но такой же величины расширение этого стержня получается при нагревании его на 50°С. Ясно поэтому, что, расширяясь при нагревании (или сжимаясь при охлаждении) на 50°С, стержень будет оказывать давление около 1000 на те тела, которые будут препятствовать его расширению (сжатию).

Огромные силы, возникающие при расширении и сжатии твёрдых тел, учитываются в технике. Так, например, один из концов моста не закрепляют неподвижно, а устанавливают на катках; железнодорожные рельсы не укладывают вплотную, а оставляют между ними просвет; паропроводы подвешивают на крюках, а между отдельными трубами устанавливают компенсаторы, изгибающиеся при удлинении труб паропровода. По этой же причине котёл паровоза закрепляется только на одном конце, другой же его конец может свободно перемещаться.

Огромное значение имеет расширение от нагревания при точных измерениях. В самом деле, если масштабная линейка или калибр, которыми проверяются размеры изготовленной части машины, значительно изменяют свою величину, то необходимой точности при измерении не получится. Для избежания грубых ошибок при измерении или контроле изготовленные изделия заблаговременно приносят в помещение, где производятся измерения, чтобы они успели принять температуру калибров. Самые калибры и измерительные инструменты делают из материала с очень малым коэффициентом расширения. Таким материалом, например, является особая железо-никелевая сталь — инвар, с коэффициентом расширения 0,0000015.

Рис. 132а. Схема устройства металлического термометра.

Как показывает таблица на странице 124, платина и стекло имеют одинаковый коэффициент расширения; поэтому можно вплавлять платину в стекло, причём после охлаждения не происходит ни ослабления связи обоих веществ, ни растрескивания стекла. В электрических лампочках в стекло вплавляется железо-никелевая проволока, имеющая такой же коэффициент расширения, как и стекло. Заслуживает внимания очень малый коэффициент расширения у кварцевого стекла. Такое стекло выдерживает, не лопаясь и не растрескиваясь, неравномерное нагревание или охлаждение. Так, например, в раскалённую докрасна колбочку из кварцевого стекла можно вливать холодную воду, тогда как колба из обычного стекла при таком опыте лопается. Указанная особенность кварцевого стекла является следствием малости его коэффициента теплового расширения.

Терморегулятор

Две одинаковые полоски из разных металлов, например из железа и латуни, склёпанные вместе, образуют так называемую биметаллическую пластинку. При нагревании такие пластинки изгибаются вследствие того, что одна расширяется больше другой. Та из полосок, которая расширяется больше, оказывается всегда с выпуклой стороны. Это свойство биметаллических пластинок широко используется для измерения температуры и её регулирования.

1. Металлический термометр. Этот прибор представляет собой биметаллическую дугу (рис. 132, а), конец которой A прочно закреплён, а конец В свободен. Дуга соединена в В со стрелкой С. При изменении температуры дуга закручивается или раскручивается, двигая соответственно стрелку. Шкала проградуирована по обыкновенному термометру. Если к концу стрелки прикрепить перо, то колебания температуры можно записывать на специальной бумажной ленте. По такому принципу устроен термограф.

2. Термостат. Так называется прибор для установления постоянной температуры.

Рас. 1326. Принцип устройства регулятора температуры с биметаллической пластинкой.

На рисунке 132б изображён принцип устройства одного из типов регуляторов температуры. Биметаллическая дуга С при изменении температуры закручивается или раскручивается. К её свободному концу прикреплена металлическая пластинка М, которая при раскручивании дуги прикасается к контакту К, а при закручивании отходит от него. Если, например, контакт К и пластинка М присоединены к концам электрической цепи АА₁ содержащей нагревательный прибор, то при соприкосновении К и М электрическая цепь замкнётся; прибор начнёт нагревать помещение. Биметаллическая дуга С при нагревании начнёт закручиваться и при определённой температуре отсоединит пластинку М от контакта К цепь разорвётся, нагревание прекратится. При охлаждении дуга С, раскручиваясь, снова заставит включиться нагревательный прибор: таким образом, температура помещения будет поддерживаться на заданном уровне.

Рис. 132в. Прибор для определения коэффициента расширения жидкостей.

Тепловое расширение жидкостей

В отношении жидкостей имеет смысл говорить лишь об объёмном расширении. У жидкостей оно значительно больше, чем у твёрдых тел. Как показывает опыт, зависимость объёма жидкости от температуры выражается такой же формулой, что и для твёрдых тел.

Если при 0°С жидкость занимает объём V₀, то при температуре t её объём V_t будет:

Для измерения коэффициента расширения жидкости применяется стеклянный сосуд термометрической формы, объём которого известен (рис. 132в). Шарик с трубкой наполняют доверху жидкостью и нагревают весь прибор до определённой температуры; при этом часть жидкости выливается из сосуда. Затем сосуд с жидкостью охлаждают в тающем льду до 0°. При этом жидкость наполнит уже не весь сосуд, и незаполненный объём покажет, на сколько жидкость расширилась при нагревании. Зная коэффициент расширения стекла, можно довольно точно вычислить и коэффициент расширения жидкости.

Коэффициент расширения некоторых жидкостей:

Эфир…………….0,00166 Вода (от 20°С и выше) . . . .0,00020

Спирт……………0,00110 Вода (от 5 до 8°С)…….0,00002

Керосин…………..0,00100 Ртуть…………….0,00018

Расширение воды при нагревании отличается от расширения других жидкостей. Если нагревать воду от 0°С, то можно заметить, что при нагревании до 4°С её объём не увеличивается, а уменьшается. При нагревании же выше 4°С объём воды увеличивается.

Наибольшую плотность, равную 1 вода имеет при 4°С. Изменение плотности воды в зависимости от температуры изображено графически на рисунке 133.

Рис. 133. График изменения плотности воды в зависимости от температуры.

Особенностью расширения воды объясняется то, что вода в прудах и озёрах не промерзает зимой до дна. При охлаждении воды осенью верхние остывшие слои опускаются на дно, а на их место снизу поступают более тёплые слои. Такое перемещение слоёв происходит только до тех пор, пока вода не примет температуру 4°С. При дальнейшем охлаждении верхние слои не опускаются вниз, а, постепенно охлаждаясь, остаются наверху и, наконец, замерзают.

Услуги по физике:

Заказать физику
Заказать контрольную работу по физике
Помощь по физике

Лекции по физике:

Физические величины и их измерение
Основные законы механики
Прямолинейное равномерное движение
Прямолинейное равнопеременное движение
Сила
Масса
Взаимодействия тел
Механическая энергия
Импульс
Вращение твердого тела
Криволинейное движение тел
Колебания
Колебания и волны
Механические колебания и волны
Бегущая волна
Стоячие волны
Акустика
Звук
Звук и ультразвук
Движение жидкости и газа
Молекулярно-кинетическая теория
Молекулярно-кинетическая теория строения вещества
Молекулярно — кинетическая теория газообразного состояния вещества
Теплота и работа
Температура и теплота
Термодинамические процессы
Идеальный газ
Уравнение состояния идеального газа
Изменение внутренней энергии
Переход вещества из жидкого состояния в газообразное и обратно
Кипение, свойства паров, критическое состояние вещества
Водяной пар в атмосфере
Плавление и кристаллизация
Тепловое расширение тел
Энтропия
Процессы перехода из одного агрегатного состояния в другое
Свойства газов
Свойства жидкостей
Свойства твёрдых тел
Изменение агрегатного состояния вещества
Тепловые двигатели
Электрическое поле
Постоянный ток
Переменный ток
Магнитное поле
Электромагнитное поле
Электромагнитное излучение
Электрический заряд (Закон Кулона)
Электрический ток в металлах
Электрический ток в электролитах
Электрический ток в газах и в вакууме
Электрический ток в полупроводниках
Электромагнитная индукция
Работа, мощность и тепловое действие электрического тока
Термоэлектрические явления
Распространение электромагнитных волн
Интерференционные явления
Рассеяние
Дифракция рентгеновских лучей на кристалле
Двойное лучепреломление
Магнитное поле и электромагнитная индукция
Электромагнитные колебания и волны
Природа света
Распространение света
Отражение и преломление света
Оптические приборы и зрение
Волновые свойства света
Действия света
Линзы и получение изображений с помощью линз
Оптические приборы и глаз
Фотометрия
Излучение и спектры
Квантовые свойства излучения
Специальная теория относительности в физике
Теория относительности
Квантовая теория и природа поля
Строение и свойства вещества
Физика атомного ядра
Строение атома

Источник

Линейное тепловое расширение

Если

l₁	начальная длина тела при температуре t₁,	метр
l₂	конечная длина тела при температуре t₂,	метр
Δl	удлинение тела l₂-l₁,	метр
Δt	разность температур t₂-t₁,	метр
α	коэффициент линейного расширения (линейный коэффициент теплового расширения),	1/К

то в хорошем приближении справедливы равенства

[ Δl = l_1 α Δt ]

[ l_2 = l_1 + Δl = l_1 + l_1 α Δt ]

[ l_2 = l_1 ( 1 + α Δt ) ]

Коэффициент линейного расширения (линейный коэффициент теплового расширения)

Коэффициент линейного расширения α равен отношению относительного удлинения Δl/l к разности температур Δt.

[ α = frac{Δl}{l_1 Δt} ]

Линейное тепловое расширение	стр. 516

Источник

Применительно
к твердым телам, форма которых при
изменении температуры (при равномерном
нагревании или охлаждении) не меняется,
различают изменение линейных размеров
(длины, диаметра и т. п.) — линейное
расширение и изменение объема —
объемное
расширение. У жидкостей при нагревании
форма может меняться (например, в
термометре ртуть входит в капилляр).
Поэтому в случае жидкостей имеет смысл
говорить только об объемном расширении.

Опыт
показывает, что при небольших изменениях
температуры изменение линейных размеров
твердого тела прямо пропорционально
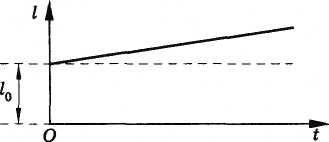
изменению температуры (рис. 9.3). Так как
удлинение при нагревании (или укорочение
при охлаждении) зависит также от
первоначальной длины тела, удобнее
рассматривать не само удлинение тела,
а относительное удлинение: отношение
увеличения длины Δl
= l
— l₀
к
первоначальной длине l₀.
Относительное
удлинение
пропорционально изменению температурыΔt
= t
— t₀:

(9.2.1)

Рис. 9.3

Коэффициент
пропорциональности α₁
называют температурным
коэффициентом линейного расширения.
Он показывает, на какую долю своего
первоначального значения изменяются
линейные размеры тела при нагревании
его на 1 К. Коэффициент линейного
расширения зависит от природы вещества,
а также от температуры. Однако, если
рассматривать изменения температуры
в не слишком широких пределах, зависимостью
α₁
от температуры можно пренебречь и
считать температурный коэффициент
линейного расширения величиной постоянной
для данного вещества. Для большинства
веществ этот коэффициент мал, его
значения составляют 10^-5—10^-6К^-1.

Особенно мал
коэффициент линейного расширения в
диапазоне температур от -30 до +100 °С у
инвара (сплав железа и никеля). Поэтому
инвар применяют для изготовления точных
инструментов, используемых при определении
размеров тел. Линейные размеры самого
инструмента из инвара мало зависят от
колебаний температуры.

Линейные размеры
тела, как вытекает из формулы (9.2.1),
зависят от изменения температуры
следующим образом:

(9.2.2)

В
формулах (9.2.1) и (9.2.2) обычно начальное
значение температуры полагают равным
нулю (t₀
= 0
°С) и соответственно l₀
считают
длиной тела при этой температуре. На
практике же начальная температура тела
далеко не всегда бывает равна 0 °С. Тогда
расчет длины тела при любой температуре
можно выполнить так. Пусть при температуре
t₁
длина
тела равна l₁
а
при температуре t₂
она
равна l₂.
Тогда,
считая начальную температуру t₀
= 0
°С, имеем:

Отсюда

(9.2.3)

Однако,
учитывая, что значение α₁
очень
мало, формулу (9.2.3) можно упростить.
Умножив числитель и знаменатель на 1—
α₁t₁,
получим:

Ввиду
малости коэффициента ах члены, содержащие
α₁,
малы
по сравнению с членом, в который входит
α₁
в
первой степени (точнее, α₁t
››
t²).
Поэтому
их можно отбросить. В результате формула
для вычисления длины 12
оказывается
более простой и достаточно точной для
инженерной практики:

или

(9.2.4)

Решая задачи с
учетом теплового линейного расширения
тел, необходимо иметь в виду, что при
изменении температуры меняется не
только длина, но и все другие линейные
размеры тела. Так, у круглого стержня
при нагревании увеличивается диаметр,
и притом во столько раз, во сколько
увеличивается длина стержня. У пластинки
в одно и то же число раз увеличиваются
длина, ширина и толщина. Если начертить
на пластинке какую-нибудь линию, то
длина этой линии при нагревании увеличится
в такое же число раз. У окружности
увеличатся ее длина и диаметр.

При нагревании
пластинки, имеющей круглое отверстие,
диаметр отверстия тоже увеличится. Дело
в том, что при равномерном нагревании
в теле не возникают силы упругости.
Поэтому расширение происходит так, как
если бы пластинка была сплошной. Точно
так же увеличивается при нагревании
диаметр гайки, размеры раковины в толще
металлической отливки и т. д.

В справедливости
сказанного можно убедиться на опыте с
металлическим шаром, о котором уже шла
речь в § 9.1. Шар застревает в кольце, если
его нагреть, и проходит с большим зазором,
если нагреть кольцо. Наоборот, при
охлаждении кольца шар застревает, а
охлаждение шара увеличивает зазор между
ним и кольцом.

Линейные размеры,
твердых тел увеличиваются прямо
пропорционально росту температуры.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник