Температурный коэффициент сопротивления (ТКС) — величина, равная относительному изменению удельного сопротивления вещества при изменении температуры на единицу.
ТКС характеризует зависимость сопротивления проводника от изменении его температуры.Как правило применяют температурный коэффициент сопротивления металлов.
Формула температурного коэффициента сопротивления через относительное изменение сопротивления
{alpha = dfrac{R_2-R_1}{R_1(T_2-T_1)}}
Формула температурного коэффициента сопротивления через удельное сопротивление
{alpha = dfrac{rho_2-rho_1}{rho_1(T_2-T_1)}}
Таблица «Температурный коэффициент сопротивления»
| Проводник | α (10-3/K) |
|---|---|
|
Алюминий температурный коэффициент сопротивления алюминия |
4,2 |
|
Вольфрам температурный коэффициент сопротивления вольфрама |
5 |
|
Железо температурный коэффициент сопротивления железа |
6 |
|
Золото температурный коэффициент сопротивления золота |
4 |
|
Константан (сплав Ni-Cu + Mn) температурный коэффициент сопротивления константина |
0,05 |
|
Латунь температурный коэффициент сопротивления латуни |
0,1-0,4 |
|
Магний температурный коэффициент сопротивления магния |
3,9 |
|
Манганин (сплав меди марганца и никеля — приборный) температурный коэффициент сопротивления манганин |
0,01 |
|
Марганец температурный коэффициент сопротивления марганца |
0,02 |
|
Медь температурный коэффициент сопротивления меди |
4,3 |
|
Нейзильбер температурный коэффициент сопротивления нейзильбера |
0,25 |
|
Никелин (сплав меди и никеля) температурный коэффициент сопротивления никелина |
0,1 |
|
Никель температурный коэффициент сопротивления никеля |
6,5 |
|
Нихром (сплав никеля хрома железы и марганца) температурный коэффициент сопротивления нихрома |
0,1 |
|
Олово температурный коэффициент сопротивления олова |
4,4 |
|
Платина температурный коэффициент сопротивления платины |
3,9 |
|
Ртуть температурный коэффициент сопротивления ртути |
1 |
|
Свинец температурный коэффициент сопротивления свинца |
3,7 |
|
Серебро температурный коэффициент сопротивления серебра |
4,1 |
|
Сталь температурный коэффициент сопротивления стали |
1-4 |
|
Фехраль (Cr (12—15 %); Al (3,5—5,5 %); Si (1 %); Mn (0,7 %); + Fe) температурный коэффициент сопротивления фехраля |
0,1 |
|
Цинк температурный коэффициент сопротивления цинка |
4,2 |
|
Чугун температурный коэффициент сопротивления чугуна |
1 |
Содержание
- Термин: Зависимость электрического сопротивления от температуры (ТКС)
- Электрическое сопротивление
- Электрическое сопротивление проводника в общем случае зависит от материала проводника
- Определение и формула температурного коэффициента сопротивления
- Единицы
- Примеры решения задач
- Расчет сопротивления электрического проводника
- Расчет длины электрического проводника
- Расчет сечения электрического проводника
- Температурный коэффициент объемного расширения
- Температурный коэффициент линейного расширения
- Зависимость сопротивлений от температуры
- Как рассчитать температурный коэффициент реакции?
- Температурный коэффициент электрического сопротивления металлов α
Термин: Зависимость электрического сопротивления от температуры (ТКС)
Зависимость электрического сопротивления провода от температуры приходится учитывать в различных схемах измерений, поскольку эта зависимость может оказывать существенное влияние на дополнительную погрешность измерения.
Зависимость сопротивления R(t) провода от температуры t задаётся температурным коэффициентом сопротивления (ТКС) провода α и описывается формулой:
R(t) = R20 (1 + α (t — 20) ),
где температура t задаётся в градусах Цельсия; R20 – это сопротивление провода при 20°С, а ТКС α – это константа с размерностью 1/°С, зависящая от материала провода. Приблизительные ТКС некоторых проводников приводим в таблице ниже.
Проводник α (ТКС), 1/°С
| Алюминий | 4,2*10-3 |
| Вольфрам | 5*10-3 |
| Железо | 6*10-3 |
| Золото | 4*10-3 |
| Латунь | (0,1 — 0,4)*10-3 |
| Магний | 3,9*10-3 |
| Медь | 4,3*10-3 |
| Никель | 6,5*10-3 |
| Нихром | 0,1*10-3 |
| Олово | 4,4*10-3 |
| Платина | 3,9*10-3 |
| Серебро | 4,1*10-3 |
| Сталь | (1 — 4)*10-3 |
Абсолютное изменение сопротивления проводника ∆R при изменении температуры ∆t и начальном сопротивлении R рассчитывается по формуле:
∆R = R*α*∆t.
Относительное изменение сопротивления проводника ∆R/R при изменении температуры ∆t рассчитывается по формуле: ∆R/R = α*∆t.
К схемам измерений, в которых существенное влияние отказывает ТКС проводов, относят: полномостовые четырёхпроводные балансные схемы и полумостовые трёхпроводные схемы. Эти схемы применяют в тензометрии, и здесь существенное влияние на шкалу (масштаб) измерения оказывают ТКС проводов питания.
Существуют также балансные мостовые схемы, в которых существенное влияние отказывает не собственный ТКС проводов, а различия ТКС проводов, которыми подключен мост. К такому случаю относят трёхпроводную четверьмостовую схему. В то же время, существуют схемы измерений, в которых ТКС проводов не оказывает никакого влияния на измерения, например, в случае питания тензомоста от источника стабильного тока.
Термин ТКС (англ: TCR temperature coefficient of resistance) широко применяют также к резисторам (и к элементам, проявляющим резистивные свойства) для описания их температурной зависимости с размерностью 10-6/°С или ppm/°С. При этом, ТКС реальных резистивных элементов может быть как положительным, так и отрицательным, но, кроме того, в зависимости от технологии этих элементов, их ТКС может быть разным при разной температуре.
Большое абсолютное значение ТКС в сочетанием фактором самонагрева резистивного элемента из-за протекающего тока может рассматриваться как проявление нелинейного сопротивления на интервалах времени значительно больших, чем время самонагрева.
На интервалах времени значительно меньших, чем время самонагрева резистивного элемента, большое абсолютное значение ТКС будет восприниматься как дрейф (нестабильность) сопротивления по причине самонагрева.
Электрическое сопротивление
Электрическое сопротивление — это физическая величина , характеризующая противодействие проводника или электрической цепи электрическому току . Физика 7,8,9,10,11 класс, ЕГЭ, ГИА Копировать ссылку Распечатать
Электрическое сопротивление — это физическая величина, характеризующая противодействие проводника или электрической цепи электрическому току.
Электрическое сопротивление определяется как коэффициент пропорциональности R между напряжением U и Iсилой постоянного тока в законе Ома для участка цепи.
Единица сопротивления называется омом (Ом) в честь немецкого ученого Г. Ома, который ввел это понятие в физику. Один ом (1 Ом) — это сопротивление такого проводника, в котором при напряжении 1В сила тока равна 1А.
Электрическое сопротивление проводника в общем случае зависит от материала проводника
от его длины и от поперечного сечения, или более кратко — от удельного сопротивления и от геометрических размеров проводника. Данная зависимость общеизвестна и выражается формулой:
Известен каждому и закон Ома для однородного участка электрической цепи, из которого видно, что ток тем меньше, чем сопротивление выше. Таким образом, если сопротивление проводника постоянно, то с ростом приложенного напряжения ток должен бы линейно расти. Но в реальности это не так. Сопротивление проводников не постоянно.
За примерами далеко ходить не надо. Если к регулируемому блоку питания (с вольтметром и амперметром) подключить лампочку, и постепенно повышать напряжение на ней, доводя до номинала, то легко заметить, что ток растет не линейно: с приближением напряжения к номиналу лампы, ток через ее спираль растет все медленнее, причем лампочка светится все ярче.
Нет такого, что с увеличением вдвое приложенного к спирали напряжения, вдвое возрос и ток. Закон Ома как-будто не выполняется. На самом деле закон Ома выполняется, и точно, просто сопротивление нити накала лампы непостоянно, оно зависит температуры.
Вспомним, с чем связана высокая электрическая проводимость металлов. Она связана с наличием в металлах большого количества носителей заряда — составных частей тока — электронов проводимости. Это электроны, образующиеся из валентных электронов атомов металла, которые для всего проводника являются общими, они не принадлежат каждый отдельному атому.
Под действием приложенного к проводнику электрического поля, свободные электроны проводимости переходят из хаотичного в более-менее упорядоченное движение — образуется электрический ток. Но электроны на своем пути встречают препятствия, неоднородности ионной решетки, такие как дефекты решетки, неоднородная структура, вызванные ее тепловыми колебаниями.
Электроны взаимодействуют с ионами, теряют импульс, их энергия передается ионам решетки, переходит в колебания ионов решетки, и хаос теплового движения самих электронов усиливается, от того проводник и нагревается при прохождении по нему тока.
В диэлектриках, полупроводниках, электролитах, газах, неполярных жидкостях — причина сопротивления может быть иной, однако закон Ома, очевидно, не остается постоянно линейным.
Таким образом, для металлов, рост температуры приводит к еще большему возрастанию тепловых колебаний кристаллической решетки, и сопротивление движению электронов проводимости возрастает. Это видно по эксперименту с лампой: яркость свечения увеличилась, но ток возрос слабее. То есть изменение температуры повлияло на сопротивление нити накаливания лампы.
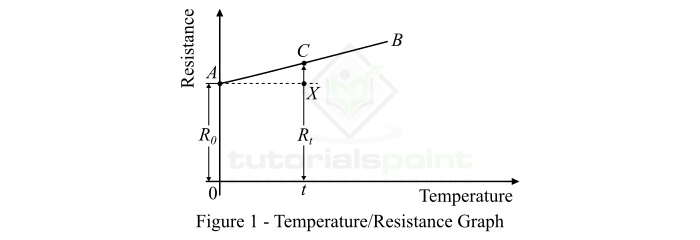
В итоге становится ясно, что сопротивление металлических проводников зависит почти линейно от температуры. А если принять во внимание, что при нагревании геометрические размеры проводника меняются слабо, то и удельное электрическое сопротивление почти линейно зависит от температуры. Зависимости эти можно выразить формулами:
Обратим внимание на коэффициенты. Пусть при 0°C сопротивление проводника равно R0, тогда при температуре t°C оно примет значение R(t), и относительное изменение сопротивления будет равно α*t°C. Вот этот коэффициент пропорциональности α и называется температурным коэффициентом сопротивления. Он характеризует зависимость электрического сопротивления вещества от его текущей температуры.
Данный коэффициент численно равен относительному изменению электрического сопротивления проводника при изменении его температуры на 1К (на один градус Кельвина, что равноценно изменению температуры на один градус Цельсия).
Для металлов ТКС (температурный коэффициент сопротивления α) хоть и относительно мал, но всегда больше нуля, ведь при прохождении тока электроны тем чаще сталкиваются с ионами кристаллической решетки, чем выше температура, то есть чем выше тепловое хаотичное их движение и чем выше их скорость. Сталкиваясь в хаотичном движении с ионами решетки, электроны металла теряют энергию, что мы и видим в результате — сопротивление при нагревании проводника возрастает. Данное явление используется технически в термометрах сопротивления.
Итак, температурный коэффициент сопротивления α характеризует зависимость электрического сопротивления вещества от температуры и измеряется в 1/К — кельвин в степени -1. Величину с обратным знаком называют температурным коэффициентом проводимости.
Что касается чистых полупроводников, то для них ТКС отрицателен, то есть сопротивление снижается с ростом температуры, это связано с тем, что с ростом температуры все больше электронов переходят в зону проводимости, растет при этом и концентрация дырок. Этот же механизм свойственен для жидких неполярных и твердых диэлектриков.
Полярные жидкости свое сопротивление резко уменьшают с ростом температуры из-за снижения вязкости и роста диссоциации. Это свойство применяется для защиты электронных ламп от разрушительного действия больших пусковых токов.
У сплавов, легированных полупроводников, газов и электролитов тепловая зависимость сопротивления более сложна чем у чистых металлов. Сплавы с очень малым ТКС, такие как манганин и константан, применяют в электроизмерительных приборах.
Определение и формула температурного коэффициента сопротивления
Сопротивление проводника (R) (удельное сопротивление) ()
зависит от температуры. Эту зависимость при незначительных изменениях температуры
представляют в виде функции:
где
— удельное сопротивление проводника при температуре равной 0oC;
— температурный коэффициент сопротивления.
ОПРЕДЕЛЕНИЕ Температурным коэффициентом электрического сопротивления () называют физическую величину, равную относительному приращению (R) участка цепи (или удельного сопротивления среды (
), которое происходит при нагревании проводника на 1oС. Математически определение температурного коэффициента сопротивления можно представить как:
Величина
служит характеристикой связи электросопротивления с температурой.
При температурах, принадлежащих диапазону
у большинства металлов рассматриваемый коэффициент
остается постоянным. Для чистых металлов температурный коэффициент сопротивления часто принимают равным
Иногда говорят о среднем температурном коэффициенте сопротивления, определяя его как:
где
— средняя величина температурного коэффициента в заданном интервале температур
Основной единицей измерения температурного коэффициента сопротивления в системе СИ является:
Единицы
Тепловой коэффициент электрическая цепь части иногда указываются как промилле/°C, или же промилле/K. Он определяет долю (выраженную в миллионных долях), на которую его электрические характеристики будут отклоняться при достижении температуры выше или ниже Рабочая Температура.
Примеры решения задач
ПРИМЕР 1
| Задание | Лампа накаливания, имеющая спираль из вольфрама включена в сеть с напряжением B, по ней идет ток А. Какой будет температура спирали, если при температуре oС она имеет сопротивление Ом? Температурный коэффициент сопротивления вольфрама . |
| Решение | В качестве основы для решения задачи используем формулу зависимости сопротивления от температуры вида:
где По закону Ома для участка цепи имеем: Вычислим Запишем уравнение связывающее сопротивление Проведем вычисления: |
| Ответ | K |
ПРИМЕР 2
| Задание | При температуре сопротивление реостата равно , сопротивление амперметра равно и он показывает силу тока Реостат, сделан из железной проволоки, он последовательно соединен с амперметром (рис.1). Каким будет сила тока течь через амперметр, если реостат нагреть до температуры ? Считать температурный коэффициент сопротивления железа равным .  Рис. 1 Рис. 1 |
| Решение | Закон Ома для участка цепи при температуре 0oC можно записать как:
После нагревания сопротивление реостата стало равно R, тогда через амперметр течет ток равный: Сопротивление зависит от температуры: Подставим выражения (2.3) и (2.1) в уравнение (2.2), получим: |
| Ответ |
Расчет сопротивления электрического проводника
Сопротивление электрического проводника рассчитываем по формуле:
R = ρ * L / S
- R — сопротивление электрического проводника
- ρ — удельное сопротивление проводника
вычисляется по формуле (1): ρ = ρ20[1 + α(t — 20)]- ρ20 — удельное сопротивление проводника при температуре t = 20°C (Таблица 1)
- t — температура проводника
- α — температурный коэффициент электрического сопротивления (Таблица 1)
- L — длина электрического проводника
- S — сечение электрического проводника
Расчет длины электрического проводника
Длину электрического проводника рассчитываем по формуле:
L = R * S / ρ
- L — длина электрического проводника
- R — сопротивление электрического проводника
- S — сечение электрического проводника
- ρ — удельное сопротивление проводника
вычисляется по формуле (1): ρ = ρ20[1 + α(t — 20)]- ρ20 — удельное сопротивление проводника при температуре t = 20°C (Таблица 1)
- t — температура проводника
- α — температурный коэффициент электрического сопротивления (Таблица 1)
Расчет сечения электрического проводника
Минимальное сечение электрического проводника при допустимых потерях напряжения рассчитываем по формуле:
S = I * ρ * L / ΔU
- S — сечение электрического проводника
- I — сила тока в электрической цепи
- L — длина электрического проводника
при двухпроводной линии, длина проводника (значение L) удваивается - ΔU — допустимые потери напряжения
- ρ — удельное сопротивление проводника
вычисляется по формуле (1): ρ = ρ20[1 + α(t — 20)]- ρ20 — удельное сопротивление проводника при температуре t = 20°C (Таблица 1)
- t — температура проводника
- α — температурный коэффициент электрического сопротивления (Таблица 1)
Температурный коэффициент объемного расширения
Температурным коэффициентом объемного расширения тела является физическая величина, которая характеризует относительное изменение объема тела
которое происходит при нагревании тела на 1 K и неизменном давлении:
Температурный коэффициент линейного расширения
ОПРЕДЕЛЕНИЕ Температурный коэффициент линейного расширения
— это физическая величина, которая характеризует изменение линейных размеров твердого тела с ростом или уменьшением его температуры.
где
— начальная длина тела,
— увеличение длины тела (удлинение) при росте температуры тела на
Зависимость сопротивлений от температуры
С повышением температуры сопротивление металлов возрастает. Однако существуют сплавы, сопротивление которых почти не меняется при повышении температуры (например, константан, манганин и др.). Сопротивление же электролитов с повышением температуры уменьшается.
Температурным коэффициентом сопротивления проводника называется отношение величины изменения сопротивления проводника при нагревании на 1 °С к величине его сопротивления при 0 ºС:
Зависимость удельного сопротивления проводников от температуры выражается формулой:
В общем случае α зависит от температуры, но если интервал температур невелик, то температурный коэффициент можно считать постоянным. Для чистых металлов α = (1/273)К-1. Для растворов электролитов α < 0. Например, для 10% раствора поваренной соли α = -0,02 К-1. Для константана (сплава меди с никелем) α = 10-5 К-1.
Зависимость сопротивления проводника от температуры используется в термометрах сопротивления.
Как рассчитать температурный коэффициент реакции?
Что такое температурный коэффициент?
Во-первых, при повышении температуры скорость реакции возрастает. Всё логично
Значит, температурный коэффициент- это число, которое показывает, во сколько раз увеличилась скорость реакции, когда мы повысим температуру на 10 градусов
Вот такая страшная формула( но только на первый взгляд)
γ-это и есть наш температурный коэффициент
Следовательно, чтобы его расчитать, нужно знать
2 скорости (до и после повышения температуры на 10 градусов)
2 константы (у каждой реакции они свои. Обычно их пишут в условии задачи)
Температурный коэффициент электрического сопротивления металлов α
- В разумных температурных пределах вокруг некоторой точки зависимость удельного сопротивления металлов от температуры описывается как:
- ΔR = α*R*ΔT, где α — температурный коэффициент электрического сопротивления.
- Ниже приведена таблица значений α для ряда металлов в диапазоне температур от 0 до 100 ° C.
Зависимость сопротивления металлов от температуры. Температурный коэффициент электрического сопротивления металлов α .
| Проводник | Удельное сопротивление ρ, Ом*мм2/м |
α, 10 -3*C-1(или K -1) |
| Алюминий | 0,028 | 4,2 |
| Бронза | 0,095 — 0,1 | — |
| Висмут | 1,2 | — |
| Вольфрам | 0,05 | 5 |
| Железо | 0,1 | 6 |
| Золото | 0,023 | 4 |
| Иридий | 0,0474 | — |
| Константан ( сплав Ni-Cu + Mn) | 0,5 | 0,05! |
| Латунь | 0,025 — 0,108 | 0,1-0,4 |
| Магний | 0,045 | 3,9 |
| Манганин (сплав меди марганца и никеля — приборный) | 0,43 — 0,51 | 0,01!! |
| Медь | 0,0175 | 4,3 |
| Молибден | 0,059 | — |
| Нейзильбер (сплав меди цинка и никеля) | 0,2 | 0,25 |
| Натрий | 0,047 | — |
| Никелин ( сплав меди и никеля) | 0,42 | 0,1 |
| Никель | 0,087 | 6,5 |
| Нихром ( сплав никеля хрома железы и марганца) | 1,05 — 1,4 | 0,1 |
| Олово | 0,12 | 4,4 |
| Платина | 0.107 | 3,9 |
| Ртуть | 0,94 | 1,0 |
| Свинец | 0,22 | 3,7 |
| Серебро | 0,015 | 4,1 |
| Сталь | 0,103 — 0,137 | 1-4 |
| Титан | 0,6 | — |
| Фехраль (Cr (12—15 %); Al (3,5—5,5 %); Si (1 %); Mn (0,7 %); + Fe) | 1,15 — 1,35 | 0,1 |
| Хромаль | 1,3 — 1,5 | — |
| Цинк | 0,054 | 4,2 |
| Чугун | 0,5-1,0 | 1,0 |
Источники
- https://www.lcard.ru/lexicon/wire_tcr
- https://www.calc.ru/Elektricheskoye-Soprotivleniye.html
- http://ElectricalSchool.info/main/osnovy/1873-temperaturnyjj-kojefficient.html
- http://ru.solverbook.com/spravochnik/koefficienty/temperaturnyj-koefficient-soprotivleniya/
- https://wikiaro.ru/wiki/Temperature_coefficient
- https://www.axwap.com/kipia/docs/elektrika/provodnik.htm
- http://ru.solverbook.com/spravochnik/koefficienty/temperaturnyj-koefficient/
- https://yandex.ru/q/question/kak_rasschitat_temperaturnyi_koeffitsient_26938630/
- https://dpva.ru/Guide/GuidePhysics/ElectricityAndMagnethism/ElectricalResistanceAndConductivity/MetalsElResHeatCoef/
Помогла ли вам статья?
Содержание
- Температурные коэффициенты для кабеля
- Температура окружающей среды при проверке проводов и кабелей по нагреву
- Температура воздуха
- Температура почвы
- Пример определения поправочного коэффициента по температуре
- ПУЭ: Глава 1.3. Выбор проводников по нагреву, экономической плотности тока и по условиям короны
- Область применения
- Выбор сечений проводников по нагреву
- Таблица 1.3.1. Допустимая кратковременная перегрузка для кабелей напряжением до 10 кВ с бумажной пропитанной изоляцией
- Таблица 1.3.2. Допустимая на период ликвидации послеаварийного режима перегрузка для кабелей напряжением до 10 кВ с бумажной изоляцией
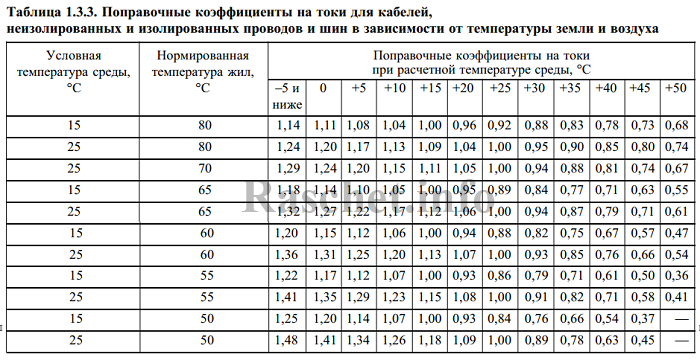
- Таблица 1.3.3. Поправочные коэффициенты на токи для кабелей, неизолированных и изолированных проводов и шин в зависимости от температуры земли и воздуха
- Допустимые длительные оки для проводов, шнуров и кабелей с резиновой или пластмассовой изоляцией
- Таблица 1.3.4. Допустимый длительный ток для проводов и шнуров с резиновой и поливинилхлоридной изоляцией с медными жилами
- Таблица 1.3.5. Допустимый длительный ток для проводов с резиновой и поливинилхлоридной изоляцией с алюминиевыми жилами
- Таблица 1.3.6. Допустимый длительный ток для проводов с медными жилами с резиновой изоляцией в металлических защитных оболочках и кабелей с медными жилами с резиновой изоляцией в свинцовой, поливинилхлоридной, найритовой или резиновой оболочке, бронированных и небронированных
- Таблица 1.3.7. Допустимый длительный ток для кабелей с алюминиевыми жилами с резиновой или пластмассовой изоляцией в свинцовой, поливинилхлоридной и резиновой оболочках, бронированных и небронированных
- Таблица 1.3.8. Допустимый длительный ток для переносных шланговых легких и средних шнуров, переносных шланговых тяжелых кабелей, шахтных гибких шланговых, прожекторных кабелей и переносных проводов с медными жилами
- Таблица 1.3.9. Допустимый длительный ток для переносных шланговых с медными жилами с резиновой изоляцией кабелей для торфопредприятий
- Таблица 1.3.10. Допустимый длительный ток для шланговых с медными жилами с резиновой изоляцией кабелей для передвижных электроприемников
- Таблица 1.3.11. Допустимый длительный ток для проводов с медными жилами с резиновой изоляцией для электрифицированного транспорта 1,3 и 4 кВ
- Таблица 1.3.12. Снижающий коэффициент для проводов и кабелей, прокладываемых в коробах
- Допустимые длительные токи для кабелей с бумажной пропитанной изоляцией
- 1.3.12. Допустимые длительные токи для кабелей напряжением до 35 кВ с изоляцией из пропитанной кабельной бумаги в свинцовой, алюминиевой или поливинилхлоридной оболочке приняты в соответствии с допустимыми температурами жил кабелей:
- Таблица 1.3.13. Допустимый длительный ток для кабелей с медными жилами с бумажной пропитанной маслоканифольной и нестекающей массами изоляцией в свинцовой оболочке, прокладываемых в земле
- Таблица 1.3.14. Допустимый длительный ток для кабелей с медными жилами с бумажной пропитанной маслоканифольной и нестекающей массами изоляцией в свинцовой оболочке, прокладываемых в воде
- Таблица 1.3.15. Допустимый длительный ток для кабелей с медными жилами с бумажной пропитанной маслоканифольной и нестекающей массами изоляцией в свинцовой оболочке, прокладываемых в воздухе
- Таблица 1.3.16. Допустимый длительный ток для кабелей с алюминиевыми жилами с бумажной пропитанной маслоканифольной и нестекающей массами изоляцией в свинцовой или алюминиевой оболочке, прокладываемых в земле
- Таблица 1.3.17. Допустимый длительный ток для кабелей с алюминиевыми жилами с бумажной пропитанной маслоканифольной и нестекающей массами изоляцией в свинцовой оболочке, прокладываемых в воде
- Таблица 1.3.18. Допустимый длительный ток для кабелей с алюминиевыми жилами с бумажной пропитанной маслоканифольной и нестекающей массами изоляцией в свинцовой или алюминиевой оболочке, прокладываемых в воздухе
- Таблица 1.3.19. Допустимый длительный ток для трехжильных кабелей напряжением 6 кВ с медными жилами с обедненнопропитанной изоляцией в общей свинцовой оболочке, прокладываемых в земле и воздухе
- Таблица 1.3.20. Допустимый длительный ток для трехжильных кабелей напряжением 6 кВ с алюминиевыми жилами с обедненнопропитанной изоляцией в общей свинцовой оболочке, прокладываемых в земле и воздухе
- Таблица 1.3.21. Допустимый длительный ток для кабелей с отдельно освинцованными медными жилами с бумажной пропитанной маслоканифольной и нестекающей массами изоляцией, прокладываемых в земле, воде, воздухе
- Таблица 1.3.22. Допустимый длительный ток для кабелей с отдельно освинцованными алюминиевыми жилами с бумажной пропитанной маслоканифольной и нестекающей массами изоляцией, прокладываемых в земле, воде, воздухе
- Таблица 1.3.23. Поправочный коэффициент на допустимый длительный ток для кабелей, проложенных в земле, в зависимости от удельного сопротивления земли
- Таблица 1.3.24. Допустимый длительный ток для одножильных кабелей с медной жилой с бумажной пропитанной маслоканифольной и нестекающей массами изоляцией в свинцовой оболочке, небронированных, прокладываемых в воздухе
- Таблица 1.3.25. Допустимый длительный ток для одножильных кабелей с алюминиевой жилой с бумажной пропитанной маслоканифольной и нестекающей массами изоляцией в свинцовой или алюминиевой оболочке, небронированных, прокладываемых в воздухе
- Таблица 1.3.26. Поправочный коэффициент на количество работающих кабелей, лежащих рядом в земле (в трубах или без труб)
- Таблица 1.3.27. Допустимый длительный ток для кабелей, кВ с медными или алюминиевыми жилами сечением 95 мм², прокладываемых в блоках
- Таблица 1.3.28. Поправочный коэффициент a на сечение кабеля
- Допустимые длительные токи для неизолированных проводов и шин
- Таблица 1.3.29. Допустимый длительный ток для неизолированных проводов по ГОСТ 839-80
- Таблица 1.3.30. Допустимый длительный ток для шин круглого и трубчатого сечений
- Таблица 1.3.31. Допустимый длительный ток для шин прямоугольного сечения
- Таблица 1.3.32. Допустимый длительный ток для неизолированных бронзовых и сталебронзовых проводов
- Таблица 1.3.33. Допустимый длительный ток для неизолированных стальных проводов
- Таблица 1.3.34. Допустимый длительный ток для четырехполосных шин с расположением полос но сторонам квадрата («полый пакет»)
- Таблица 1.3.35. Допустимый длительный ток для шин коробчатого сечения
- Выбор сечения проводов по экономической плотности тока
- Таблица 1.3.36. Экономическая плотность тока
- ПРОВЕРКА ПРОВОДНИКОВ ПО УСЛОВИЯМ КОРОНЫ И РАДИОПОМЕХ
Температурные коэффициенты для кабеля
Для приведения при необходимости измеренных значений сопротивление шлейфа (Ом км) и сопротивления изоляции при температуре +20° на один км однородной линии, как это задаётся нормами, следует пользоваться формулами:
Где R шл.Т ; R из.Т — измеренные значения соответственно сопротивления шлейфа и сопротивления изоляции при температуре, отличной от 20°С, К 1 и К 2 поправочные температурные коэффициенты для приведения Rшл. И Rиз. к температуре +20°С l — длина линии.
Примечания: 1. В кабелях с полиэтиленовой или полистирольной изоляцией жил в интервале температур ±30° С величина сопротивления изоляции практически остается постоянной и поэтому при обработке результатов измерений К 2 в указанном интервале принимается равным 1.
2. При температурах, отличающихся от приведенных в таблице коэффициенты К 1 и К 2 рассчитываются по приведенным ниже формулам:

где α 1 -температурный коэффициент для кабелей из медных жил, равный 0,004;

где α 2 — температурный коэффициент для кабелей с воздушно бумажной изоляцией жил. равный 0,06.
Взято из общей инструкции по строительству ЛС ГТС 1978 год
Источник
Температура окружающей среды при проверке проводов и кабелей по нагреву
В данной статье будет рассматриваться выбор температуры окружающей среды при проверке проводов и кабелей по нагреву.
Будут представлены таблицы с температурой воздуха и почвы согласно нормативных документов.
Для многих инженеров кто впервые столкнулся с проверкой проводов и кабелей по нагреву, возникает много вопросов в части температуры окружающей среды.
Этот момент достаточно важен, так как при снижении температуры окружающей среды допускаемая нагрузка на провод (кабель) повышается и наоборот при повышении температуры окружающей среды допускаемая нагрузка на провод (кабель) понижается.
В справочных таблицах ПУЭ приводятся значения допустимых длительных токов, составленные для различных марок проводов и кабелей исходя из средних значений температуры окружающей среды и температуры жил.
Ниже приведены сами пункты ПУЭ:
1. ПУЭ п.1.3.10, 1.3.11 для проводов, шнуров и кабелей с резиновой или пластмассовой изоляцией:
2. ПУЭ п.1.3.12 — 1.3.16 для кабелей с бумажной пропитанной изоляцией:
3. ПУЭ п.1.3.22 для неизолированных проводов и шин:
В зависимости от районов сооружения воздушных линий, средние значения температур окружающего воздуха могут колебаться от +15 °С в северных районах РФ до +35 °С в южных. При наличии длительных наблюдений по данному району следует в качестве расчетной температуры принимать среднемесячную температуру в 13 ч за наиболее жаркий месяц [Л1, с.99].
Для кабелей, прокладываемых в земле, на воздухе или воде, среднюю температуру следует принимать равной среднесуточной для данной местности за наиболее жаркий месяц [Л1, с.99].
Расчетные температуры среды для проводов и кабелей представлены в таблице 2-9 [Л2. с 55].
Соответственно, если температура среды прокладываемых кабелей, проводов и шин отличается от принятых температур в ПУЭ для которых приведены значения длительно допустимых токов, тогда нужно применять поправочные коэффициенты, согласно ПУЭ таблица 1.3.3.
Температура воздуха
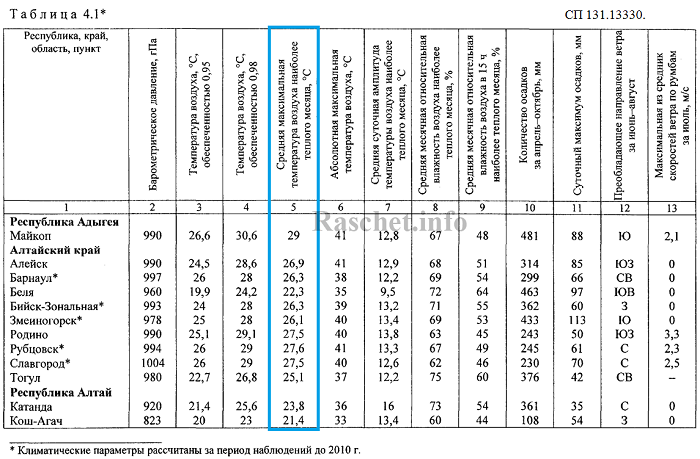
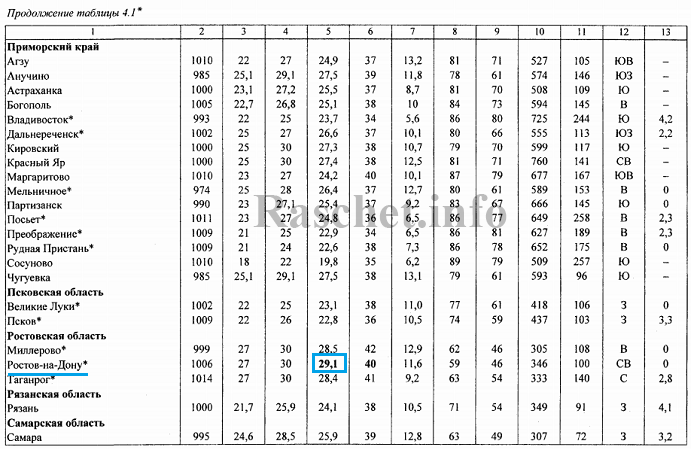
Для определения средней максимальной температуры воздуха наиболее жаркого месяца, можно воспользоваться СП 131.13330.2018 (СНиП 23-01—99) таблица 4.1 (РФ) и ДСТУ-Н Б В.1.1-27:2010 таблица 2 (Украина).
Есть один нюанс — значение среднесуточной температуры за наиболее жаркий месяц в СП 131.13330.2018 не приводится. Для ориентировочных расчетов за расчетную температуру вместо суточной температуры, можно применить значение средней максимальной температуры воздуха наиболее теплого месяца.
Для того чтобы понимать терминологию климатических параметров, которая используется в СП 131.13330.2018 таблице 4.1 привожу трактовку их:
Температура почвы
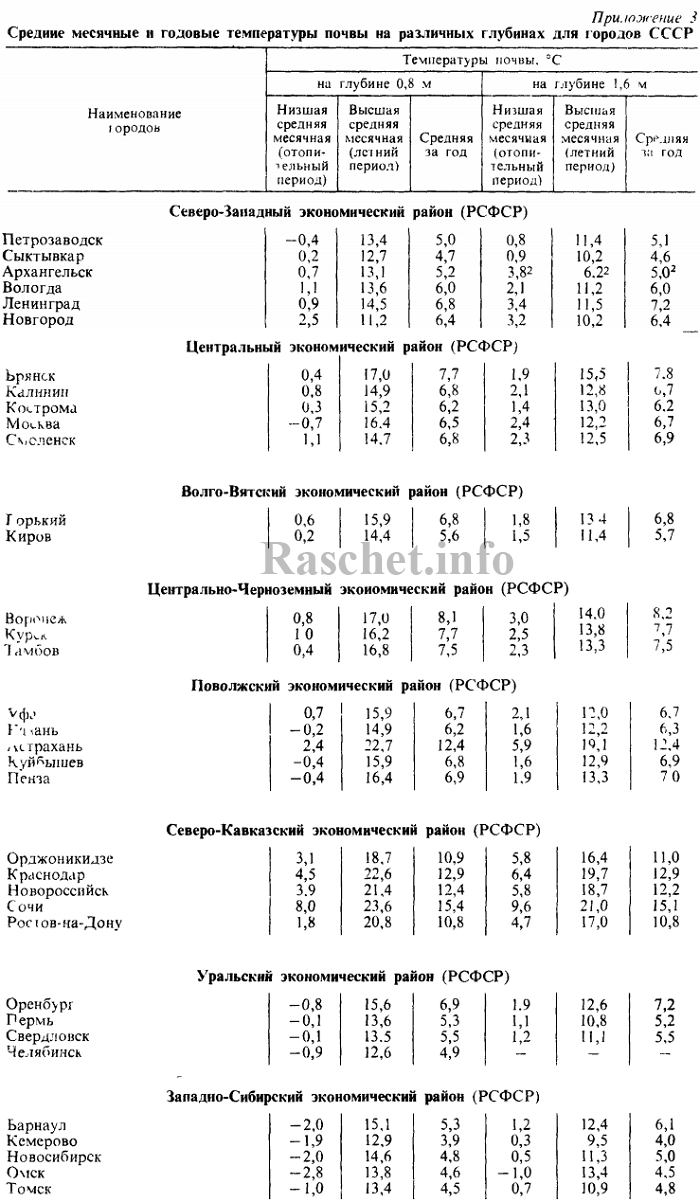
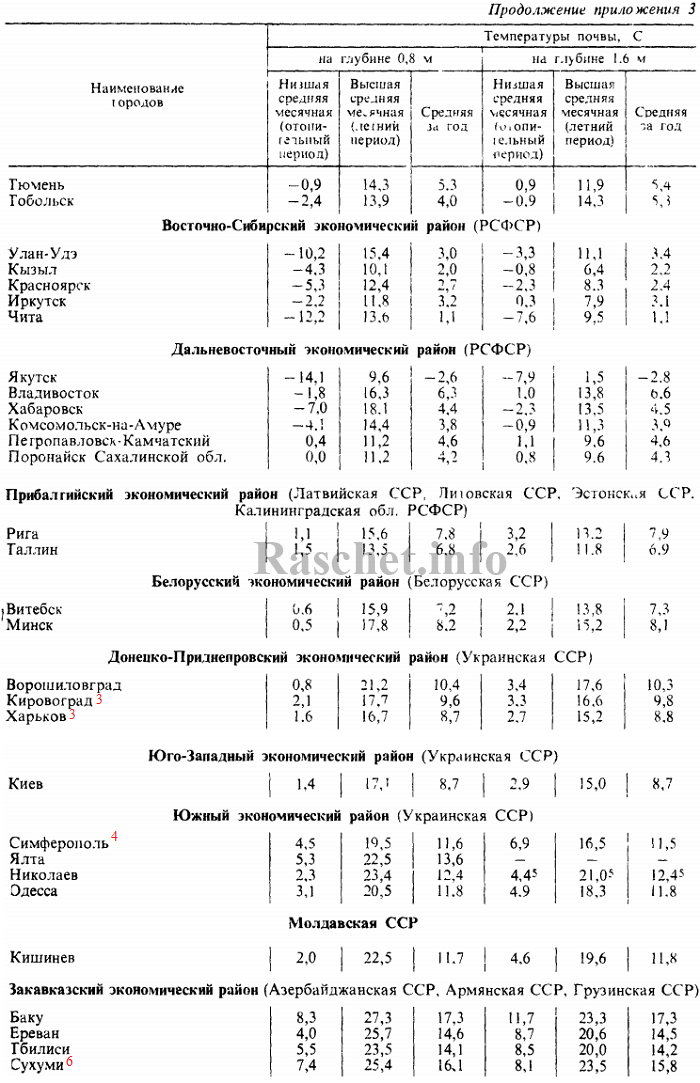
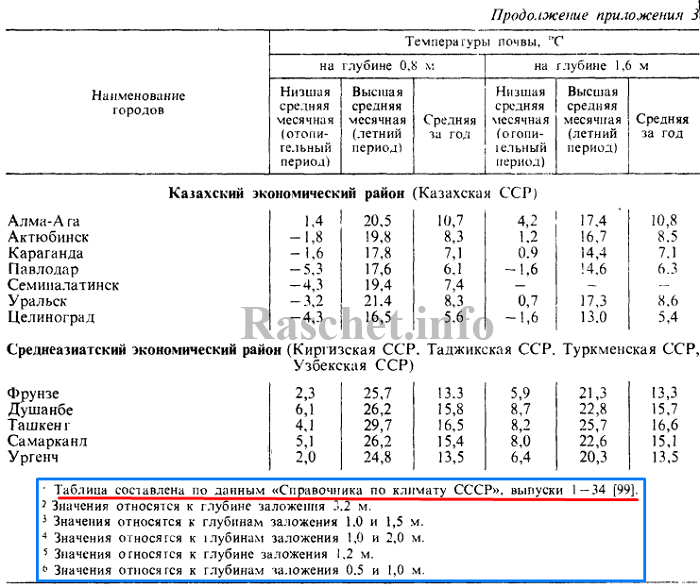
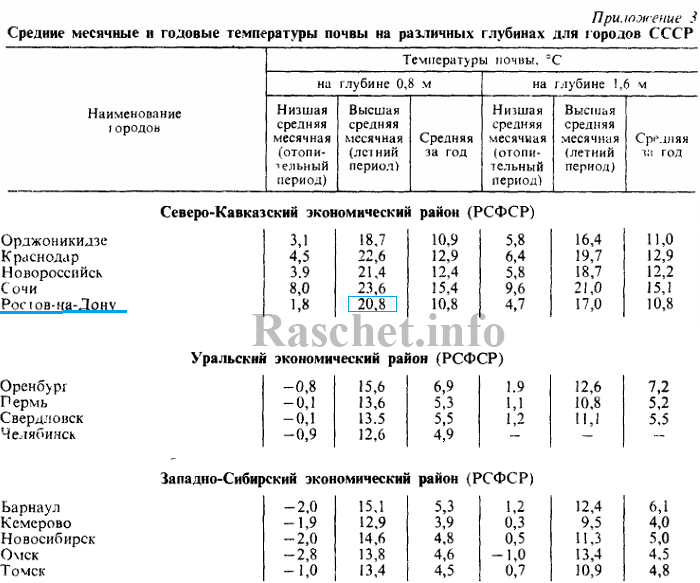
Средние месячные и годовые температуры почвы на глубине 0,8 м и 1,6 м для городов СССР приведены в справочном пособие по проектированию «Водяные тепловые сети» Н.К. Громова. 1988 г Приложение 3.
Также информацию о температуре почвы и не только, вы сможете найти в «Справочнике по климату СССР», выпуски 1 – 34.
Для получения же более точных значений климатических параметров, советую использовать сайт «Федеральной службы по гидрометеорологии и мониторингу окружающей среды», где представлено более 600 станций, так как в основном справочник по климату СССР – в настоящее время не актуален.
Данные на данном сайте предоставляются бесплатно, нужно только зарегистрироваться.
Пример определения поправочного коэффициента по температуре
Требуется определить поправочный коэффициент по температуре (kcp) для кабеля марки АВВГнг 3х16+1х10 прокладываемый внутри здания на воздухе и в траншее глубиной 0,7 м в Ростове-на-Дону.
Согласно ПУЭ п.1.3.10 для кабелей с поливинилхлоридной изоляцией и оболочкой, допустимые длительные токи приняты для температур: жил +65, окружающего воздуха +25 и земли +15°С.
1. Определяем по СП 131.13330.2018 таблица 4.1 расчетную температуру воздуха (средняя максимальная температуры воздуха наиболее жаркого месяца): +29,1°С.
2. Определяем по справочному пособию по проектированию «Водяные тепловые сети» расчетную температуру почвы: +20,8°С.
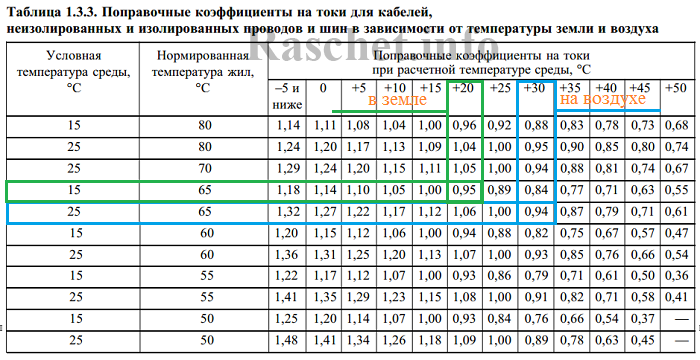
3. Определяем поправочный коэффициент (kср) учитывающий температуру среды, отличную от расчетной по ПУЭ таблица 1.3.3.
- для кабеля прокладываемого внутри здания на воздухе kср = 0,94.
- для кабеля, прокладываемого в траншее kср = 0,95.
Все материалы, которые использовались при написании данной статьи, вы сможете найти в архиве:
- Справочник по климату СССР, выпуски 1 – 34 (Отсутствуют выпуски: 5, 7, 30, 31).
- Справочное пособие по проектированию «Водяные тепловые сети» Н.К. Громова. 1988 г.
- Электрические сети энергетических систем. Боровиков В.А. 1977 г.
- Проектирование кабельных сетей и проводок. Хромченко Г.Е. 1980 г.
- Электрические сети энергетических систем. Боровиков В.А. 1977 г.
- Проектирование кабельных сетей и проводок. Хромченко Г.Е. 1980 г.
Источник
ПУЭ: Глава 1.3. Выбор проводников по нагреву, экономической плотности тока и по условиям короны
Область применения
1.3.1. Настоящая глава Правил распространяется на выбор сечений электрических проводников (неизолированные и изолированные провода, кабели и шины) по нагреву, экономической плотности тока и по условиям короны. Если сечение проводника, определенное по этим условиям, получается меньше сечения, требуемого по другим условиям (термическая и электродинамическая стойкость при токах КЗ, потери и отклонения напряжения, механическая прочность, защита от перегрузки), то должно приниматься наибольшее сечение, требуемое этими условиями.
Выбор сечений проводников по нагреву
1.3.2. Проводники любого назначения должны удовлетворять требованиям в отношении предельно допустимого нагрева с учетом не только нормальных, но и послеаварийных режимов, а также режимов в период ремонта и возможных неравномерностей распределения токов между линиями, секциями шин и т. п. При проверке на нагрев принимается получасовой максимум тока, наибольший из средних получасовых токов данного элемента сети.
1.3.3. При повторно-кратковременном и кратковременном режимах работы электроприемников (с общей длительностью цикла до 10 мин и длительностью рабочего периода не более 4 мин) в качестве расчетного тока для проверки сечения проводников по нагреву следует принимать ток, приведенный к длительному режиму. При этом:
1) для медных проводников сечением до 6 мм², а для алюминиевых проводников до 10 мм² ток принимается как для установок с длительным режимом работы;
2) для медных проводников сечением более 6 мм², а для алюминиевых проводников более 10 мм² ток определяется умножением допустимого длительного тока на коэффициент 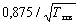
1.3.4. Для кратковременного режима работы с длительностью включения не более 4 мин и перерывами между включениями, достаточными для охлаждения проводников до температуры окружающей среды, наибольшие допустимые токи следует определять по нормам повторно — кратковременного режима (см. 1.3.3). При длительности включения более 4 мин, а также при перерывах недостаточной длительности между включениями наибольшие допустимые токи следует определять как для установок с длительным режимом работы.
1.3.5. Для кабелей напряжением до 10 кВ с бумажной пропитанной изоляцией, несущих нагрузки меньше номинальных, может допускаться кратковременная перегрузка, указанная в табл. 1.3.1.
1.3.6. На период ликвидации послеаварийного режима для кабелей с полиэтиленовой изоляцией допускается перегрузка до 10%, а для кабелей с поливинилхлоридной изоляцией до 15% номинальной на время максимумов нагрузки продолжительностью не более 6 ч в сутки в течение 5 сут., если нагрузка в остальные периоды времени этих суток не превышает номинальной.
На период ликвидации послеаварийного режима для кабелей напряжением до 10 кВ с бумажной изоляцией допускаются перегрузки в течение 5 сут. в пределах, указанных в табл. 1.3.2.
Таблица 1.3.1. Допустимая кратковременная перегрузка для кабелей напряжением до 10 кВ с бумажной пропитанной изоляцией
| Коэффициент предварительной нагрузки |
Вид прокладки |
Допустимая перегрузка по отношению к номинальной в течение, ч | ||
|---|---|---|---|---|
| 0,5 | 1,0 | 3,0 | ||
| 0,6 | В земле | 1,35 | 1,30 | 1,15 |
| В воздухе | 1,25 | 1,15 | 1,10 | |
| В трубах (в земле) | 1,20 | 1,0 | 1,0 | |
| 0,8 | В земле | 1,20 | 1,15 | 1,10 |
| В воздухе | 1,15 | 1,10 | 1,05 | |
| В трубах (в земле) | 1,10 | 1,05 | 1,00 |
Таблица 1.3.2. Допустимая на период ликвидации послеаварийного режима перегрузка для кабелей напряжением до 10 кВ с бумажной изоляцией
| Коэффициент предварительной нагрузки |
Вид прокладки |
Допустимая перегрузка по отношению к номинальной при длительности максимума, ч |
||
|---|---|---|---|---|
| 1 | 3 | 6 | ||
| 0,6 | В земле | 1,5 | 1,35 | 1,25 |
| В воздухе | 1,35 | 1,25 | 1,25 | |
| В трубах (в земле) | 1,30 | 1,20 | 1,15 | |
| 0,8 | В земле | 1,35 | 1,25 | 1,20 |
| В воздухе | 1,30 | 1,25 | 1,25 | |
| В трубах (в земле) | 1,20 | 1,15 | 1,10 |
Для кабельных линий, находящихся в эксплуатации более 15 лет, перегрузки должны быть понижены на 10%.
Перегрузка кабельных линий напряжением 20-35 кВ не допускается.
1.3.7. Требования к нормальным нагрузкам и послеаварийным перегрузкам относятся к кабелям и установленным на них соединительным и концевым муфтам и концевым заделкам.
1.3.8. Нулевые рабочие проводники в четырехпроводной системе трехфазного тока должны иметь проводимость не менее 50% проводимости фазных проводников; в необходимых случаях она должна быть увеличена до 100% проводимости фазных проводников.
1.3.9. При определении допустимых длительных токов для кабелей, неизолированных и изолированных проводов и шин, а также для жестких и гибких токопроводов, проложенных в среде, температура которой существенно отличается от приведенной в 1.3.12-1.3.15 и 1.3.22, следует применять коэффициенты, приведенные в табл. 1.3.3.
Таблица 1.3.3. Поправочные коэффициенты на токи для кабелей, неизолированных и изолированных проводов и шин в зависимости от температуры земли и воздуха
| Условная температура среды, °С | Нормированная температура жил, °С | Поправочные коэффициенты на токи при расчетной температуре среды, °С | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| -5 и ниже | 0 | +5 | +10 | +15 | +20 | +25 | +30 | +35 | +40 | +45 | +50 | ||
| 15 | 80 | 1,14 | 1,11 | 1,08 | 1,04 | 1,00 | 0,96 | 0,92 | 0,88 | 0,83 | 0,78 | 0,73 | 0,68 |
| 25 | 80 | 1,24 | 1,20 | 1,17 | 1,13 | 1,09 | 1,04 | 1,00 | 0,95 | 0,90 | 0,85 | 0,80 | 0,74 |
| 25 | 70 | 1,29 | 1,24 | 1,20 | 1,15 | 1,11 | 1,05 | 1,00 | 0,94 | 0,88 | 0,81 | 0,74 | 0,67 |
| 15 | 65 | 1,18 | 1,14 | 1,10 | 1,05 | 1,00 | 0,95 | 0,89 | 0,84 | 0,77 | 0,71 | 0,63 | 0,55 |
| 25 | 65 | 1,32 | 1,27 | 1,22 | 1,17 | 1,12 | 1,06 | 1,00 | 0,94 | 0,87 | 0,79 | 0,71 | 0,61 |
| 15 | 60 | 1,20 | 1,15 | 1,12 | 1,06 | 1,00 | 0,94 | 0,88 | 0,82 | 0,75 | 0,67 | 0,57 | 0,47 |
| 25 | 60 | 1,36 | 1,31 | 1,25 | 1,20 | 1,13 | 1,07 | 1,00 | 0,93 | 0,85 | 0,76 | 0,66 | 0,54 |
| 15 | 55 | 1,22 | 1,17 | 1,12 | 1,07 | 1,00 | 0,93 | 0,86 | 0,79 | 0,71 | 0,61 | 0,50 | 0,36 |
| 25 | 55 | 1,41 | 1,35 | 1,29 | 1,23 | 1,15 | 1,08 | 1,00 | 0,91 | 0,82 | 0,71 | 0,58 | 0,41 |
| 15 | 50 | 1,25 | 1,20 | 1,14 | 1,07 | 1,00 | 0,93 | 0,84 | 0,76 | 0,66 | 0,54 | 0,37 | — |
| 25 | 50 | 1,48 | 1,41 | 1,34 | 1,26 | 1,18 | 1,09 | 1,00 | 0,89 | 0,78 | 0,63 | 0,45 | — |
Допустимые длительные оки для проводов, шнуров и кабелей с резиновой или пластмассовой изоляцией
1.3.10. Допустимые длительные токи для проводов с резиновой или поливинилхлоридной изоляцией, шнуров с резиновой изоляцией и кабелей с резиновой или пластмассовой изоляцией в свинцовой, поливинилхлоридной и резиновой оболочках приведены в табл. 1.3.4-1.3.11. Они приняты для температур: жил +65, окружающего воздуха +25 и земли + 15°С.
При определении количества проводов, прокладываемых в одной трубе (или жил многожильного проводника), нулевой рабочий проводник четырехпроводной системы трехфазного тока, а также заземляющие и нулевые защитные проводники в расчет не принимаются.
Данные, содержащиеся в табл. 1.3.4 и 1.3.5, следует применять независимо от количества труб и места их прокладки (в воздухе, перекрытиях, фундаментах).
Допустимые длительные токи для проводов и кабелей, проложенных в коробах, а также в лотках пучками, должны приниматься: для проводов — по табл. 1.3.4 и 1.3.5 как для проводов, проложенных в трубах, для кабелей — по табл. 1.3.6-1.3.8 как для кабелей, проложенных в воздухе. При количестве одновременно нагруженных проводов более четырех, проложенных в трубах, коробах, а также в лотках пучками, токи для проводов должны приниматься по табл. 1.3.4 и 1.3.5 как для проводов, проложенных открыто (в воздухе), с введением снижающих коэффициентов 0,68 для 5 и 6; 0,63 для 7-9 и 0,6 для 10-12 проводников.
Для проводов вторичных цепей снижающие коэффициенты не вводятся.
Таблица 1.3.4. Допустимый длительный ток для проводов и шнуров с резиновой и поливинилхлоридной изоляцией с медными жилами
| Сечение токопроводящей жилы, мм² | Ток, А, для проводов, проложенных | |||||
|---|---|---|---|---|---|---|
| открыто | в одной трубе | |||||
| двух одножильных | трех одножильных | четырех одножильных | одного двухжильного | одного трехжильного | ||
| 0,5 | 11 | — | — | — | — | — |
| 0,75 | 15 | — | — | — | — | — |
| 1 | 17 | 16 | 15 | 14 | 15 | 14 |
| 1,2 | 20 | 18 | 16 | 15 | 16 | 14,5 |
| 1,5 | 23 | 19 | 17 | 16 | 18 | 15 |
| 2 | 26 | 24 | 22 | 20 | 23 | 19 |
| 2,5 | 30 | 27 | 25 | 25 | 25 | 21 |
| 3 | 34 | 32 | 28 | 26 | 28 | 24 |
| 4 | 41 | 38 | 35 | 30 | 32 | 27 |
| 5 | 46 | 42 | 39 | 34 | 37 | 31 |
| 6 | 50 | 46 | 42 | 40 | 40 | 34 |
| 8 | 62 | 54 | 51 | 46 | 48 | 43 |
| 10 | 80 | 70 | 60 | 50 | 55 | 50 |
| 16 | 100 | 85 | 80 | 75 | 80 | 70 |
| 25 | 140 | 115 | 100 | 90 | 100 | 85 |
| 35 | 170 | 135 | 125 | 115 | 125 | 100 |
| 50 | 215 | 185 | 170 | 150 | 160 | 135 |
| 70 | 270 | 225 | 210 | 185 | 195 | 175 |
| 95 | 330 | 275 | 255 | 225 | 245 | 215 |
| 120 | 385 | 315 | 290 | 260 | 295 | 250 |
| 150 | 440 | 360 | 330 | — | — | — |
| 185 | 510 | — | — | — | — | — |
| 240 | 605 | — | — | — | — | — |
| 300 | 695 | — | — | — | — | — |
| 400 | 830 | — | — | — | — | — |
Таблица 1.3.5. Допустимый длительный ток для проводов с резиновой и поливинилхлоридной изоляцией с алюминиевыми жилами
| Сечение токопроводящей жилы, мм² | Ток, А, для проводов, проложенных | |||||
|---|---|---|---|---|---|---|
| открыто | в одной трубе | |||||
| двух одножильных | трех одножильных | четырех одножильных | одного двухжильного | одного трехжильного | ||
| 2 | 21 | 19 | 18 | 15 | 17 | 14 |
| 2,5 | 24 | 20 | 19 | 19 | 19 | 16 |
| 3 | 27 | 24 | 22 | 21 | 22 | 18 |
| 4 | 32 | 28 | 28 | 23 | 25 | 21 |
| 5 | 36 | 32 | 30 | 27 | 28 | 24 |
| 6 | 39 | 36 | 32 | 30 | 31 | 26 |
| 8 | 46 | 43 | 40 | 37 | 38 | 32 |
| 10 | 60 | 50 | 47 | 39 | 42 | 38 |
| 16 | 75 | 60 | 60 | 55 | 60 | 55 |
| 25 | 105 | 85 | 80 | 70 | 75 | 65 |
| 35 | 130 | 100 | 95 | 85 | 95 | 75 |
| 50 | 165 | 140 | 130 | 120 | 125 | 105 |
| 70 | 210 | 175 | 165 | 140 | 150 | 135 |
| 95 | 255 | 215 | 200 | 175 | 190 | 165 |
| 120 | 295 | 245 | 220 | 200 | 230 | 190 |
| 150 | 340 | 275 | 255 | — | — | — |
| 185 | 390 | — | — | — | — | — |
| 240 | 465 | — | — | — | — | — |
| 300 | 535 | — | — | — | — | — |
| 400 | 645 | — | — | — | — | — |
Таблица 1.3.6. Допустимый длительный ток для проводов с медными жилами с резиновой изоляцией в металлических защитных оболочках и кабелей с медными жилами с резиновой изоляцией в свинцовой, поливинилхлоридной, найритовой или резиновой оболочке, бронированных и небронированных
| Сечение токопроводящей жилы, мм² | Ток *, А, для проводов и кабелей | |||
|---|---|---|---|---|
| одножильных | двухжильных | трехжильных | ||
| при прокладке | ||||
| в воздухе | в воздухе | в земле | в воздухе | в земле |
| __________________ |
* Токи относятся к проводам и кабелям как с нулевой жилой, так и без нее.
1,5 23 19 33 19 27 2,5 30 27 44 25 38 4 41 38 55 35 49 6 50 50 70 42 60 10 80 70 105 55 90 16 100 90 135 75 115 25 140 115 175 95 150 35 170 140 210 120 180 50 215 175 265 145 225 70 270 215 320 180 275 95 325 260 385 220 330 120 385 300 445 260 385 150 440 350 505 305 435 185 510 405 570 350 500 240 605 — — — —
Таблица 1.3.7. Допустимый длительный ток для кабелей с алюминиевыми жилами с резиновой или пластмассовой изоляцией в свинцовой, поливинилхлоридной и резиновой оболочках, бронированных и небронированных
| Сечение токопроводящей жилы, мм² | Ток, А, для кабелей | ||||
|---|---|---|---|---|---|
| одножильных | двухжильных | трехжильных | |||
| при прокладке | |||||
| в воздухе | в воздухе | в земле | в воздухе | в земле | |
| 2,5 | 23 | 21 | 34 | 19 | 29 |
| 4 | 31 | 29 | 42 | 27 | 38 |
| 6 | 38 | 38 | 55 | 32 | 46 |
| 10 | 60 | 55 | 80 | 42 | 70 |
| 16 | 75 | 70 | 105 | 60 | 90 |
| 25 | 105 | 90 | 135 | 75 | 115 |
| 35 | 130 | 105 | 160 | 90 | 140 |
| 50 | 165 | 135 | 205 | 110 | 175 |
| 70 | 210 | 165 | 245 | 140 | 210 |
| 95 | 250 | 200 | 295 | 170 | 255 |
| 120 | 295 | 230 | 340 | 200 | 295 |
| 150 | 340 | 270 | 390 | 235 | 335 |
| 185 | 390 | 310 | 440 | 270 | 385 |
| 240 | 465 | — | — | — | — |
Примечание. Допустимые длительные токи для четырехжильных кабелей с пластмассовой изоляцией на напряжение до 1 кВ могут выбираться по табл. 1.3.7, как для трехжильных кабелей, но с коэффициентом 0,92.
Таблица 1.3.8. Допустимый длительный ток для переносных шланговых легких и средних шнуров, переносных шланговых тяжелых кабелей, шахтных гибких шланговых, прожекторных кабелей и переносных проводов с медными жилами
| Сечение токопроводящей жилы, мм² | Ток *, А, для шнуров, проводов и кабелей | |
|---|---|---|
| одножильных | двухжильных | трехжильных |
| __________________ |
* Токи относятся к шнурам, проводам и кабелям с нулевой жилой и без нее.
0,5 — 12 — 0,75 — 16 14 1,0 — 18 16 1,5 — 23 20 2,5 40 33 28 4 50 43 36 6 . 65 55 45 10 90 75 60 16 120 95 80 25 160 125 105 35 190 150 130 50 235 185 160 70 290 235 200
Таблица 1.3.9. Допустимый длительный ток для переносных шланговых с медными жилами с резиновой изоляцией кабелей для торфопредприятий
| Сечение токопроводящей жилы, мм² | Ток *, А, для кабелей напряжением, кВ | |
|---|---|---|
| 0,5 | 3 | 6 |
| __________________ |
* Токи относятся к кабелям с нулевой жилой и без нее.
6 44 45 47 10 60 60 65 16 80 80 85 25 100 105 105 35 125 125 130 50 155 155 160 70 190 195 —
Таблица 1.3.10. Допустимый длительный ток для шланговых с медными жилами с резиновой изоляцией кабелей для передвижных электроприемников
| Сечение токопроводящей жилы, мм² | Ток *, А, для кабелей напряжением, кВ | Сечение токопроводящей жилы, мм² | Ток *, А, для кабелей напряжением, кВ |
|---|---|---|---|
| 3 | 6 | 3 | 6 |
| __________________ |
* Токи относятся к кабелям с нулевой жилой и без нее.
16 85 90 70 215 220 25 115 120 95 260 265 35 140 145 120 305 310 50 175 180 150 345 350
Таблица 1.3.11. Допустимый длительный ток для проводов с медными жилами с резиновой изоляцией для электрифицированного транспорта 1,3 и 4 кВ
| Сечение токопроводящей жилы, мм² | Ток, А | Сечение токопроводящей жилы, мм² | Ток, А | Сечение токопроводящей жилы, мм² | Ток, А |
|---|---|---|---|---|---|
| 1 | 20 | 16 | 115 | 120 | 390 |
| 1,5 | 25 | 25 | 150 | 150 | 445 |
| 2,5 | 40 | 35 | 185 | 185 | 505 |
| 4 | 50 | 50 | 230 | 240 | 590 |
| 6 | 65 | 70 | 285 | 300 | 670 |
| 10 | 90 | 95 | 340 | 350 | 745 |
Таблица 1.3.12. Снижающий коэффициент для проводов и кабелей, прокладываемых в коробах
| Способ прокладки | Количество проложенных проводов и кабелей | Снижающий коэффициент для проводов, питающих | ||
|---|---|---|---|---|
| одножильных | многожильных | отдельные электроприемники с коэффициен том использования до 0,7 | группы электроприемников и отдельные приемники с коэффициентом использования более 0,7 | |
| Многослойно и пучками | — | До 4 | 1,0 | — |
| 2 | 5-6 | 0,85 | — | |
| 3-9 | 7-9 | 0,75 | — | |
| 10-11 | 10-11 | 0,7 | — | |
| 12-14 | 12-14 | 0,65 | — | |
| 15-18 | 15-18 | 0,6 | — | |
| Однослойно | 2-4 | 2-4 | — | 0,67 |
| 5 | 5 | — | 0,6 |
1.3.11. Допустимые длительные токи для проводов, проложенных в лотках, при однорядной прокладке (не в пучках) следует принимать, как для проводов, проложенных в воздухе.
Допустимые длительные токи для проводов и кабелей, прокладываемых в коробах, следует принимать по табл. 1.3.4-1.3.7 как для одиночных проводов и кабелей, проложенных открыто (в воздухе), с применением снижающих коэффициентов, указанных в табл. 1.3.12.
При выборе снижающих коэффициентов контрольные и резервные провода и кабели не учитываются.
Допустимые длительные токи для кабелей с бумажной пропитанной изоляцией
1.3.12. Допустимые длительные токи для кабелей напряжением до 35 кВ с изоляцией из пропитанной кабельной бумаги в свинцовой, алюминиевой или поливинилхлоридной оболочке приняты в соответствии с допустимыми температурами жил кабелей:
1.3.13. Для кабелей, проложенных в земле, допустимые длительные токи приведены в табл. 1.3.13, 1.3.16, 1.3.19-1.3.22. Они приняты из расчета прокладки в траншее на глубине 0,7-1,0 м не более одного кабеля при температуре земли +15°С и удельном сопротивлении земли 120 см·К/Вт.
Таблица 1.3.13. Допустимый длительный ток для кабелей с медными жилами с бумажной пропитанной маслоканифольной и нестекающей массами изоляцией в свинцовой оболочке, прокладываемых в земле
| Сечение токопроводящей жилы, мм² | Ток, А, для кабелей | |||||
|---|---|---|---|---|---|---|
| одножильных до 1 кВ | двухжильных до 1 кВ | трехжильных напряжением, кВ | четырехжильных до 1 кВ | |||
| до 3 | 6 | 10 | ||||
| 6 | — | 80 | 70 | — | — | — |
| 10 | 140 | 105 | 95 | 80 | — | 85 |
| 16 | 175 | 140 | 120 | 105 | 95 | 115 |
| 25 | 235 | 185 | 160 | 135 | 120 | 150 |
| 35 | 285 | 225 | 190 | 160 | 150 | 175 |
| 50 | 360 | 270 | 235 | 200 | 180 | 215 |
| 70 | 440 | 325 | 285 | 245 | 215 | 265 |
| 95 | 520 | 380 | 340 | 295 | 265 | 310 |
| 120 | 595 | 435 | 390 | 340 | 310 | 350 |
| 150 | 675 | 500 | 435 | 390 | 355 | 395 |
| 185 | 755 | — | 490 | 440 | 400 | 450 |
| 240 | 880 | — | 570 | 510 | 460 | — |
| 300 | 1000 | — | — | — | — | — |
| 400 | 1220 | — | — | — | — | — |
| 500 | 1400 | — | — | — | — | — |
| 625 | 1520 | — | — | — | — | — |
| 800 | 1700 | — | — | — | — | — |
Таблица 1.3.14. Допустимый длительный ток для кабелей с медными жилами с бумажной пропитанной маслоканифольной и нестекающей массами изоляцией в свинцовой оболочке, прокладываемых в воде
| Сечение токопроводящей жилы, мм² | Ток, А, для кабелей | |||
|---|---|---|---|---|
| трехжильных напряжением, кВ | четырех- жильных до 1 кВ | |||
| до 3 | 6 | 10 | ||
| 16 | — | 135 | 120 | — |
| 25 | 210 | 170 | 150 | 195 |
| 35 | 250 | 205 | 180 | 230 |
| 50 | 305 | 255 | 220 | 285 |
| 70 | 375 | 310 | 275 | 350 |
| 95 | 440 | 375 | 340 | 410 |
| 120 | 505 | 430 | 395 | 470 |
| 150 | 565 | 500 | 450 | — |
| 185 | 615 | 545 | 510 | — |
| 240 | 715 | 625 | 585 | — |
Таблица 1.3.15. Допустимый длительный ток для кабелей с медными жилами с бумажной пропитанной маслоканифольной и нестекающей массами изоляцией в свинцовой оболочке, прокладываемых в воздухе
| Сечение токопроводящей жилы, мм² | Ток, А, для кабелей | |||||
|---|---|---|---|---|---|---|
| одножильных до 1кВ | двухжильных до 1кВ | трехжильных напряжением, кВ | четырехжильных до 1 кВ | |||
| до 3 | 6 | 10 | ||||
| 6 | — | 55 | 45 | — | — | — |
| 10 | 95 | 75 | 60 | 55 | — | 60 |
| 16 | 120 | 95 | 80 | 65 | 60 | 80 |
| 25 | 160 | 130 | 105 | 90 | 85 | 100 |
| 35 | 200 | 150 | 125 | 110 | 105 | 120 |
| 50 | 245 | 185 | 155 | 145 | 135 | 145 |
| 70 | 305 | 225 | 200 | 175 | 165 | 185 |
| 95 | 360 | 275 | 245 | 215 | 200 | 215 |
| 120 | 415 | 320 | 285 | 250 | 240 | 260 |
| 150 | 470 | 375 | 330 | 290 | 270 | 300 |
| 185 | 525 | — | 375 | 325 | 305 | 340 |
| 240 | 610 | — | 430 | 375 | 350 | — |
| 300 | 720 | — | — | — | — | — |
| 400 | 880 | — | — | — | — | — |
| 500 | 1020 | — | — | — | — | — |
| 625 | 1180 | — | — | — | — | — |
| 800 | 1400 | — | — | — | — | — |
Таблица 1.3.16. Допустимый длительный ток для кабелей с алюминиевыми жилами с бумажной пропитанной маслоканифольной и нестекающей массами изоляцией в свинцовой или алюминиевой оболочке, прокладываемых в земле
| Сечение токопроводящей жилы, мм² | Ток, А, для кабелей | |||||
|---|---|---|---|---|---|---|
| одножильных до 1кВ | двухжильных до 1кВ | трехжильных напряжением, кВ | четырехжильных до 1 кВ | |||
| до 3 | 6 | 10 | ||||
| 6 | — | 60 | 55 | — | — | — |
| 10 | 110 | 80 | 75 | 60 | — | 65 |
| 16 | 135 | 110 | 90 | 80 | 75 | 90 |
| 25 | 180 | 140 | 125 | 105 | 90 | 115 |
| 35 | 220 | 175 | 145 | 125 | 115 | 135 |
| 50 | 275 | 210 | 180 | 155 | 140 | 165 |
| 70 | 340 | 250 | 220 | 190 | 165 | 200 |
| 95 | 400 | 290 | 260 | 225 | 205 | 240 |
| 120 | 460 | 335 | 300 | 260 | 240 | 270 |
| 150 | 520 | 385 | 335 | 300 | 275 | 305 |
| 185 | 580 | — | 380 | 340 | 310 | 345 |
| 240 | 675 | — | 440 | 390 | 355 | — |
| 300 | 770 | — | — | — | — | — |
| 400 | 940 | — | — | — | — | — |
| 500 | 1080 | — | — | — | — | — |
| 625 | 1170 | — | — | — | — | — |
| 800 | 1310 | — | — | — | — | — |
Таблица 1.3.17. Допустимый длительный ток для кабелей с алюминиевыми жилами с бумажной пропитанной маслоканифольной и нестекающей массами изоляцией в свинцовой оболочке, прокладываемых в воде
| Сечение токопроводящей жилы, мм² | Ток, А, для кабелей | |||
|---|---|---|---|---|
| трехжильных напряжением, кВ | четырех- жильных до 1 кВ | |||
| до 3 | 6 | 10 | ||
| 16 | — | 105 | 90 | — |
| 25 | 160 | 130 | 115 | 150 |
| 35 | 190 | 160 | 140 | 175 |
| 50 | 235 | 195 | 170 | 220 |
| 70 | 290 | 240 | 210 | 270 |
| 95 | 340 | 290 | 260 | 315 |
| 120 | 390 | 330 | 305 | 360 |
| 150 | 435 | 385 | 345 | — |
| 185 | 475 | 420 | 390 | — |
| 240 | 550 | 480 | 450 | — |
Таблица 1.3.18. Допустимый длительный ток для кабелей с алюминиевыми жилами с бумажной пропитанной маслоканифольной и нестекающей массами изоляцией в свинцовой или алюминиевой оболочке, прокладываемых в воздухе
| Сечение токопроводящей жилы, мм² | Ток, А, для кабелей | |||||
|---|---|---|---|---|---|---|
| одножильных до 1 кВ | двухжильных до 1 кВ | трехжильных напряжением, кВ | четырехжильных до 1 кВ | |||
| до 3 | 6 | 10 | ||||
| 6 | — | 42 | 35 | — | — | — |
| 10 | 75 | 55 | 46 | 42 | — | 45 |
| 16 | 90 | 75 | 60 | 50 | 46 | 60 |
| 25 | 125 | 100 | 80 | 70 | 65 | 75 |
| 35 | 155 | 115 | 95 | 85 | 80 | 95 |
| 50 | 190 | 140 | 120 | 110 | 105 | 110 |
| 70 | 235 | 175 | 155 | 135 | 130 | 140 |
| 95 | 275 | 210 | 190 | 165 | 155 | 165 |
| 120 | 320 | 245 | 220 | 190 | 185 | 200 |
| 150 | 360 | 290 | 255 | 225 | 210 | 230 |
| 185 | 405 | — | 290 | 250 | 235 | 260 |
| 240 | 470 | — | 330 | 290 | 270 | — |
| 300 | 555 | — | — | — | — | — |
| 400 | 675 | — | — | — | — | — |
| 500 | 785 | — | — | — | — | — |
| 625 | 910 | — | — | — | — | — |
| 800 | 1080 | — | — | — | — | — |
Таблица 1.3.19. Допустимый длительный ток для трехжильных кабелей напряжением 6 кВ с медными жилами с обедненнопропитанной изоляцией в общей свинцовой оболочке, прокладываемых в земле и воздухе
| Сечение токопроводящей жилы, мм² | Ток, А, для кабелей проложенных | Сечение токопроводящей жилы, мм² | Ток, А, для кабелей проложенных | ||
|---|---|---|---|---|---|
| в земле | в воздухе | в земле | в воздухе | ||
| 16 | 90 | 65 | 70 | 220 | 170 |
| 25 | 120 | 90 | 95 | 265 | 210 |
| 35 | 145 | 110 | 120 | 310 | 245 |
| 50 | 180 | 140 | 150 | 355 | 290 |
Таблица 1.3.20. Допустимый длительный ток для трехжильных кабелей напряжением 6 кВ с алюминиевыми жилами с обедненнопропитанной изоляцией в общей свинцовой оболочке, прокладываемых в земле и воздухе
| Сечение токопроводящей жилы, мм² | Ток, А, для кабелей проложенных | Сечение токопроводящей жилы, мм² | Ток, А, для кабелей проложенных | ||
|---|---|---|---|---|---|
| в земле | в воздухе | в земле | в воздухе | ||
| 16 | 70 | 50 | 70 | 170 | 130 |
| 25 | 90 | 70 | 95 | 205 | 160 |
| 35 | 110 | 85 | 120 | 240 | 190 |
| 50 | 140 | 110 | 150 | 275 | 225 |
Таблица 1.3.21. Допустимый длительный ток для кабелей с отдельно освинцованными медными жилами с бумажной пропитанной маслоканифольной и нестекающей массами изоляцией, прокладываемых в земле, воде, воздухе
| Сечение токопроводящей жилы, мм² | Ток, А, для трехжильных кабелей напряжением, кВ | |||||
|---|---|---|---|---|---|---|
| 20 | 35 | |||||
| при прокладке | ||||||
| в земле | в воде | в воздухе | в земле | в воде | в воздухе | |
| 25 | 110 | 120 | 85 | — | — | — |
| 35 | 135 | 145 | 100 | — | — | — |
| 50 | 165 | 180 | 120 | — | — | — |
| 70 | 200 | 225 | 150 | — | — | — |
| 95 | 240 | 275 | 180 | — | — | — |
| 120 | 275 | 315 | 205 | 270 | 290 | 205 |
| 150 | 315 | 350 | 230 | 310 | — | 230 |
| 185 | 355 | 390 | 265 | — | — | — |
Таблица 1.3.22. Допустимый длительный ток для кабелей с отдельно освинцованными алюминиевыми жилами с бумажной пропитанной маслоканифольной и нестекающей массами изоляцией, прокладываемых в земле, воде, воздухе
| Сечение токопроводящей жилы, мм² | Ток, А, для трехжильных кабелей напряжением, кВ | |||||
|---|---|---|---|---|---|---|
| 20 | 35 | |||||
| при прокладке | ||||||
| в земле | в воде | в воздухе | в земле | в воде | в воздухе | |
| 25 | 85 | 90 | 65 | — | — | — |
| 35 | 105 | 110 | 75 | — | — | — |
| 50 | 125 | 140 | 90 | — | — | — |
| 70 | 155 | 175 | 115 | — | — | — |
| 95 | 185 | 210 | 140 | — | — | — |
| 120 | 210 | 245 | 160 | 210 | 225 | 160 |
| 150 | 240 | 270 | 175 | 240 | — | 175 |
| 185 | 275 | 300 | 205 | — | — | — |
Таблица 1.3.23. Поправочный коэффициент на допустимый длительный ток для кабелей, проложенных в земле, в зависимости от удельного сопротивления земли
При удельном сопротивлении земли, отличающемся от 120 см·К/Вт, необходимо к токовым нагрузкам, указанным в упомянутых ранее таблицах, применять поправочные коэффициенты, указанные в табл. 1.3.23.
1.3.14. Для кабелей, проложенных в воде, допустимые длительные токи приведены в табл. 1.3.14, 1.3.17, 1.3.21, 1.3.22. Они приняты из расчета температуры воды +15°С.
1.3.15. Для кабелей, проложенных в воздухе, внутри и вне зданий, при любом количестве кабелей и температуре воздуха +25°С допустимые длительные токи приведены в табл. 1.3.15, 1.3.18-1.3.22, 1.3.24, 1.3.25.
1.3.16. Допустимые длительные токи для одиночных кабелей, прокладываемых в трубах в земле, должны приниматься как для тех же кабелей, прокладываемых в воздухе, при температуре, равной температуре земли.
Таблица 1.3.24. Допустимый длительный ток для одножильных кабелей с медной жилой с бумажной пропитанной маслоканифольной и нестекающей массами изоляцией в свинцовой оболочке, небронированных, прокладываемых в воздухе
| Характеристика земли | Удельное сопротивление см·К/Вт | Поправочный коэффициент |
|---|---|---|
| Сечение токопроводящей жилы, мм² | Ток *, А, для кабелей напряжением, кВ | |
|---|---|---|
| до 3 | 20 | 35 |
| __________________ |
* В числителе указаны токи для кабелей, расположенных в одной плоскости с расстоянием в свету 35-125 мм, в знаменателе — для кабелей, расположенных вплотную треугольником.
10 85/- — — 16 120/- — — 25 145/- 105/110 — 35 170/- 125/135 — 50 215/- 155/165 — 70 260/- 185/205 — 95 305/- 220/255 — 120 330/- 245/290 240/265 150 360/- 270/330 265/300 185 385/- 290/360 285/335 240 435/- 320/395 315/380 300 460/- 350/425 340/420 400 485/- 370/450 — 500 505/- — — 625 525/- — — 800 550/- — —
1.3.17. При смешанной прокладке кабелей допустимые длительные токи должны приниматься для участка трассы с наихудшими условиями охлаждения, если длина его более 10 м. Рекомендуется применять в указанных случаях кабельные вставки большего сечения.
1.3.18. При прокладке нескольких кабелей в земле (включая прокладку в трубах) допустимые длительные токи должны быть уменьшены путем введения коэффициентов, приведенных в табл. 1.3.26. При этом не должны учитываться резервные кабели.
Прокладка нескольких кабелей в земле с расстояниями между ними менее 100 мм в свету не рекомендуется.
1.3.19. Для масло- и газонаполненных одножильных бронированных кабелей, а также других кабелей новых конструкций допустимые длительные токи устанавливаются заводами-изготовителями.
1.3.20. Допустимые длительные токи для кабелей, прокладываемых в блоках, следует определять по эмпирической формуле
где I0 — допустимый длительный ток для трехжильного кабеля напряжением 10 кВ с медными или алюминиевыми жилами, определяемый по табл. 1.3.27; a — коэффициент, выбираемый по табл. 1.3.28 в зависимости от сечения и расположения кабеля в блоке; b — коэффициент, выбираемый в зависимости от напряжения кабеля:
c — коэффициент, выбираемый в зависимости от среднесуточной загрузки всего блока:
Таблица 1.3.25. Допустимый длительный ток для одножильных кабелей с алюминиевой жилой с бумажной пропитанной маслоканифольной и нестекающей массами изоляцией в свинцовой или алюминиевой оболочке, небронированных, прокладываемых в воздухе
| Сечение токопроводящей жилы, мм2 | Ток *, А, для кабелей напряжением, кВ | |
|---|---|---|
| до 3 | 20 | 35 |
| __________________ |
* В числителе указаны токи для кабелей, расположенных в одной плоскости с расстоянием в свету 35-125 мм, в знаменателе — для кабелей, расположенных вплотную треугольником.
10 65/- — — 16 90/- — — 25 110/- 80/85 — 35 130/- 95/105 — 50 165/- 120/130 — 70 200/- 140/160 — 95 235/- 170/195 — 120 255/- 190/225 185/205 150 275/- 210/255 205/230 185 295/- 225/275 220/255 240 335/- 245/305 245/290 300 355/- 270/330 260/330 400 375/- 285/350 — 500 390/- — — 625 405/- — — 800 425/- — —
Таблица 1.3.26. Поправочный коэффициент на количество работающих кабелей, лежащих рядом в земле (в трубах или без труб)
| Расстояние между кабелями в свету, мм | Коэффициент при количестве кабелей | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 100 | 1,00 | 0,90 | 0,85 | 0,80 | 0,78 | 0,75 |
| 200 | 1,00 | 0,92 | 0,87 | 0,84 | 0,82 | 0,81 |
| 300 | 1,00 | 0,93 | 0,90 | 0,87 | 0,86 | 0,85 |
Таблица 1.3.27. Допустимый длительный ток для кабелей, кВ с медными или алюминиевыми жилами сечением 95 мм², прокладываемых в блоках
| Группа | Конфигурация блоков | № канала | Ток I, А для кабелей | |
|---|---|---|---|---|
| медных | алюминиевых | |||
| I |  |
1 | 191 | 147 |
| II |     |
2 | 173 | 133 |
| 3 | 167 | 129 | ||
| III |   |
2 | 154 | 119 |
| IV |   |
2 | 147 | 113 |
| 3 | 138 | 106 | ||
| V |      |
2 | 143 | 110 |
| 3 | 135 | 104 | ||
| 4 | 131 | 101 | ||
| VI |  |
2 | 140 | 103 |
| 3 | 132 | 102 | ||
| 4 | 118 | 91 | ||
| VII |  |
2 | 136 | 105 |
| 3 | 132 | 102 | ||
| 4 | 119 | 92 | ||
| VIII |         |
2 | 135 | 104 |
| 3 | 124 | 96 | ||
| 4 | 104 | 80 | ||
| IX |        |
2 | 135 | 104 |
| 3 | 118 | 91 | ||
| 4 | 100 | 77 | ||
| X |  |
2 | 133 | 102 |
| 3 | 116 | 90 | ||
| 4 | 81 | 62 | ||
| XI |      |
2 | 129 | 99 |
| 3 | 114 | 88 | ||
| 4 | 79 | 55 |
Таблица 1.3.28. Поправочный коэффициент a на сечение кабеля
| Сечение токопроводящей жилы, мм2 | Коэффициент для номера канала в блоке | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| 25 | 0,44 | 0,46 | 0,47 | 0,51 |
| 35 | 0,54 | 0,57 | 0,57 | 0,60 |
| 50 | 0,67 | 0,69 | 0,69 | 0,71 |
| 70 | 0,81 | 0,84 | 0,84 | 0,85 |
| 95 | 1,00 | 1,00 | 1,00 | 1,00 |
| 120 | 1,14 | 1,13 | 1,13 | 1,12 |
| 150 | 1,33 | 1,30 | 1,29 | 1,26 |
| 185 | 1,50 | 1,46 | 1,45 | 1,38 |
| 240 | 1,78 | 1,70 | 1,68 | 1,55 |
Резервные кабели допускается прокладывать в незанумерованных каналах блока, если они работают, когда рабочие кабели отключены.
1.3.21. Допустимые длительные токи для кабелей, прокладываемых в двух параллельных блоках одинаковой конфигурации, должны уменьшаться путем умножения на коэффициенты, выбираемые в зависимости от расстояния между блоками:
Допустимые длительные токи для неизолированных проводов и шин
1.3.22. Допустимые длительные токи для неизолированных проводов и окрашенных шин приведены в табл. 1.3.29-1.3.35. Они приняты из расчета допустимой температуры их нагрева +70°С при температуре воздуха +25°С.
Для полых алюминиевых проводов марок ПА500 и ПА600 допустимый длительный ток следует принимать:
1.3.23. При расположении шин прямоугольного сечения плашмя токи, приведенные в табл. 1.3.33, должны быть уменьшены на 5% для шин с шириной полос до 60 мм и на 8% для шин с шириной полос более 60 мм.
1.3.24. При выборе шин больших сечений необходимо выбирать наиболее экономичные по условиям пропускной способности конструктивные решения, обеспечивающие наименьшие добавочные потери от поверхностного эффекта и эффекта близости и наилучшие условия охлаждения (уменьшение количества полос в пакете, рациональная конструкция пакета, применение профильных шин и т.п.).
Таблица 1.3.29. Допустимый длительный ток для неизолированных проводов по ГОСТ 839-80
| Номинальное сечение, мм² | Сечение (алюминий/ сталь), мм2 | Ток, А, для проводов марок | |||||
|---|---|---|---|---|---|---|---|
| АС, АСКС, АСК, АСКП | М | А и АКП | М | А и АКП | |||
| вне помещений | внутри помещений | вне помещений | внутри помещений | ||||
| 10 | 10/1,8 | 84 | 53 | 95 | — | 60 | — |
| 16 | 16/2,7 | 111 | 79 | 133 | 105 | 102 | 75 |
| 25 | 25/4,2 | 142 | 109 | 183 | 136 | 137 | 106 |
| 35 | 35/6,2 | 175 | 135 | 223 | 170 | 173 | 130 |
| 50 | 50/8 | 210 | 165 | 275 | 215 | 219 | 165 |
| 70 | 70/11 | 265 | 210 | 337 | 265 | 268 | 210 |
| 95 | 95/16 | 330 | 260 | 422 | 320 | 341 | 255 |
| 120 | 120/19 | 390 | 313 | 485 | 375 | 395 | 300 |
| 120/27 | 375 | — | |||||
| 150 | 150/19 | 450 | 365 | 570 | 440 | 465 | 355 |
| 150/24 | 450 | 365 | |||||
| 150/34 | 450 | — | |||||
| 185 | 185/24 | 520 | 430 | 650 | 500 | 540 | 410 |
| 185/29 | 510 | 425 | |||||
| 185/43 | 515 | — | |||||
| 240 | 240/32 | 605 | 505 | 760 | 590 | 685 | 490 |
| 240/39 | 610 | 505 | |||||
| 240/56 | 610 | — | |||||
| 300 | 300/39 | 710 | 600 | 880 | 680 | 740 | 570 |
| 300/48 | 690 | 585 | |||||
| 300/66 | 680 | — | |||||
| 330 | 330/27 | 730 | — | — | — | — | — |
| 400 | 400/22 | 830 | 713 | 1050 | 815 | 895 | 690 |
| 400/51 | 825 | 705 | |||||
| 400/64 | 860 | — | |||||
| 500 | 500/27 | 960 | 830 | — | 980 | — | 820 |
| 500/64 | 945 | 815 | |||||
| 600 | 600/72 | 1050 | 920 | — | 1100 | — | 955 |
| 700 | 700/86 | 1180 | 1040 | — | — | — | — |
Таблица 1.3.30. Допустимый длительный ток для шин круглого и трубчатого сечений
| Диам, мм | Круглые шины | Медные трубы | Алюминиевые трубы | Стальные трубы | ||||
|---|---|---|---|---|---|---|---|---|
| Ток *, А | Внутр. и наружн. диам., мм | Ток, А | Внутр. и наружн. диам., мм | Ток, А | Условн. проход, мм | Толщ. стенки, мм | Наружн. диаметр, мм | Переменный ток, А |
| медные | алюм. | без разреза | с продолн. разрезом | |||||
| __________________ |
* В числителе приведены нагрузки при переменном токе, в знаменателе — при постоянном.
6 155/155 120/120 12/15 340 13/16 295 8 2,8 13,5 75 — 7 195/195 150/150 14/18 460 17/20 345 10 2,8 17,0 90 — 8 235/235 180/180 16/20 505 18/22 425 15 3,2 21.3 118 — 10 320/320 245/245 18/22 555 27/30 500 20 3,2 26,8 145 — 12 415/415 320/320 20/24 600 26/30 575 25 4,0 33,5 180 — 14 505/505 390/390 22/26 650 25/30 640 32 4,0 42,3 220 — 15 565/565 435/435 25/30 830 36/40 765 40 4,0 48,0 255 — 16 610/615 475/475 29/34 925 35/40 850 50 4,5 60,0 320 — 18 720/725 560/560 35/40 1100 40/45 935 65 4,5 75,5 390 — 19 780/785 605/610 40/45 1200 45/50 1040 80 4,5 88,5 455 — 20 835/840 650/655 45/50 1330 50/55 1150 100 5,0 114 670 770 21 900/905 695/700 49/55 1580 54/60 1340 125 5,5 140 800 890 22 955/965 740/745 53/60 1860 64/70 1545 150 5,5 165 900 1000 25 1140/1165 885/900 62/70 2295 74/80 1770 — — — — — 27 1270/1290 980/1000 72/80 2610 72/80 2035 — — — — — 28 1325/1360 1025/1050 75/85 3070 75/85 2400 — — — — — 30 1450/1490 1120/1155 90/95 2460 90/95 1925 — — — — — 35 1770/1865 1370/1450 95/100 3060 90/100 2840 — — — — — 38 1960/2100 1510/1620 — — — — — — — — — 40 2080/2260 1610/1750 — — — — — — — — — 42 2200/2430 1700/1870 — — — — — — — — — 45 2380/2670 1850/2060 — — — — — — — — —
Таблица 1.3.31. Допустимый длительный ток для шин прямоугольного сечения
| Разм., мм | Медные шины | Алюминиевые шины | Стальные шины | ||||
|---|---|---|---|---|---|---|---|
| Ток *, А, при количестве полос на полюс или фазу | Разм., мм | Ток *, А | |||||
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| __________________ |
* В числителе приведены значения переменного тока, в знаменателе — постоянного.
15х3 210 — — — 165 — — — 16х2,5 55/70 20х3 275 — — — 215 — — — 20х2,5 60/90 25х3 340 — — — 265 — — — 25х2,5 75/110 30х4 475 — — — 365/370 — — — 20х3 65/100 40х4 625 -/1090 — — 480 -/855 — — 25х3 80/120 40х5 700/705 -/1250 — — 540/545 -/965 — — 30х3 95/140 50х5 860/870 -/1525 -/1895 — 665/670 -/1180 -/1470 — 40х3 125/190 50х6 955/960 -/1700 -/2145 — 740/745 -/1315 -/1655 — 50х3 155/230 60х6 1125/1145 1740/1990 2240/2495 — 870/880 1350/1555 1720/1940 — 60х3 185/280 80х6 1480/1510 2110/2630 2720/3220 — 1150/1170 1630/2055 2100/2460 — 70х3 215/320 100х6 1810/1875 2470/3245 3170/3940 — 1425/1455 1935/2515 2500/3040 — 75х3 230/345 60х8 1320/1345 2160/2485 2790/3020 — 1025/1040 1680/1840 2180/2330 — 80х3 245/365 80х8 1690/1755 2620/3095 3370/3850 — 1320/1355 2040/2400 2620/2975 — 90х3 275/410 100х8 2080/2180 3060/3810 3930/4690 — 1625/1690 2390/2945 3050/3620 — 100х3 305/460 120х8 2400/2600 3400/4400 4340/5600 — 1900/2040 2650/3350 3380/4250 — 20х4 70/115 60х10 1475/1525 2560/2725 3300/3530 — 1155/1180 2010/2110 2650/2720 — 22х4 75/125 80х10 1900/1990 3100/3510 3990/4450 — 1480/1540 2410/2735 3100/3440 — 25х4 85/140 100х10 2310/2470 3610/4325 4650/5385 5300/ 6060 1820/1910 2860/3350 3650/4160 4150/ 4400 30х4 100/165 120х10 2650/2950 4100/5000 5200/6250 5900/ 6800 2070/2300 3200/3900 4100/4860 4650/ 5200 40х4 130/220 — 50х4 165/270 60х4 195/325 70х4 225/375 80х4 260/430 90х4 290/480 100х4 325/535
Таблица 1.3.32. Допустимый длительный ток для неизолированных бронзовых и сталебронзовых проводов
| Провод | Марка провода | Ток *, А |
|---|---|---|
| __________________ |
* Токи даны для бронзы с удельным сопротивлением 
Бронзовый Б-50 215 Б-70 265 Б-95 330 Б-120 380 Б-150 430 Б-185 500 Б-240 600 Б-300 700 Сталебронзовый БС-185 515 БС-240 640 БС-300 750 БС-400 890 БС-500 980
Таблица 1.3.33. Допустимый длительный ток для неизолированных стальных проводов
| Марка провода | Ток, А | Марка провода | Ток, А |
|---|---|---|---|
| ПСО-3 | 23 | ПС-25 | 60 |
| ПСО-3,5 | 26 | ПС-35 | 75 |
| ПСО-4 | 30 | ПС-50 | 90 |
| ПСО-5 | 35 | ПС-70 | 125 |
| — | ПС-95 | 135 |
Таблица 1.3.34. Допустимый длительный ток для четырехполосных шин с расположением полос но сторонам квадрата («полый пакет»)
| Размеры, мм | Поперечное сечение четырехполосной шины, мм² | Ток, А, на пакет шин | ||||
|---|---|---|---|---|---|---|
| h | b | h1 | H | медных | алюминиевых | |
| 80 | 8 | 140 | 157 | 2560 | 5750 | 4550 |
| 80 | 10 | 144 | 160 | 3200 | 6400 | 5100 |
| 100 | 8 | 160 | 185 | 3200 | 7000 | 5550 |
| 100 | 10 | 164 | 188 | 4000 | 7700 | 6200 |
| 120 | 10 | 184 | 216 | 4800 | 9050 | 7300 |
Таблица 1.3.35. Допустимый длительный ток для шин коробчатого сечения
| Размеры, мм | Поперечное сечение одной шины, мм² | Ток, А, на две шины | ||||
|---|---|---|---|---|---|---|
| a | b | c | r | медные | алюминиевые | |
| 75 | 35 | 4 | 6 | 520 | 2730 | — |
| 75 | 35 | 5,5 | 6 | 695 | 3250 | 2670 |
| 100 | 45 | 4,5 | 8 | 775 | 3620 | 2820 |
| 100 | 45 | 6 | 8 | 1010 | 4300 | 3500 |
| 125 | 55 | 6,5 | 10 | 1370 | 5500 | 4640 |
| 150 | 65 | 7 | 10 | 1785 | 7000 | 5650 |
| 175 | 80 | 8 | 12 | 2440 | 8550 | 6430 |
| 200 | 90 | 10 | 14 | 3435 | 9900 | 7550 |
| 200 | 90 | 12 | 16 | 4040 | 10500 | 8830 |
| 225 | 105 | 12,5 | 16 | 4880 | 12500 | 10300 |
| 250 | 115 | 12,5 | 16 | 5450 | — | 10800 |
Выбор сечения проводов по экономической плотности тока
1.3.25. Сечения проводников должны быть проверены по экономической плотности тока. Экономически целесообразное сечение S, мм², определяется из соотношения
где I — расчетный ток в час максимума энергосистемы, А; Jэк — нормированное значение экономической плотности тока, А/мм², для заданных условий работы, выбираемое по табл. 1.3.36.
Сечение, полученное в результате указанного расчета, округляется до ближайшего стандартного сечения. Расчетный ток принимается для нормального режима работы, т. е. увеличение тока в послеаварийных и ремонтных режимах сети не учитывается.
1.3.26. Выбор сечений проводов линий электропередачи постоянного и переменного тока напряжением 330 кВ и выше, а также линий межсистемных связей и мощных жестких и гибких токопроводов, работающих с большим числом часов использования максимума, производится на основе технико-экономических расчетов.
1.3.27. Увеличение количества линий или цепей сверх необходимого по условиям надежности электроснабжения в целях удовлетворения экономической плотности тока производится на основе технико-экономического расчета. При этом во избежание увеличения количество линий или цепей допускается двукратное превышение нормированных значений, приведенных в табл. 1.3.36.
Таблица 1.3.36. Экономическая плотность тока
В технико-экономических расчетах следует учитывать все вложения в дополнительную линию, включая оборудование и камеры распределительных устройств на обоих концах линий. Следует также проверять целесообразность повышения напряжения линии.
Данными указаниями следует руководствоваться также при замене существующих проводов проводами большего сечения или при прокладке дополнительных линий для обеспечения экономической плотности тока при росте нагрузки. В этих случаях должна учитываться также полная стоимость всех работ по демонтажу и монтажу оборудования линии, включая стоимость аппаратов и материалов.
1.3.28. Проверке по экономической плотности тока не подлежат:
сети промышленных предприятий и сооружений напряжением до 1 кВ при числе часов использования максимума нагрузки предприятий до 4000-5000;
ответвления к отдельным электроприемникам напряжением до 1 кВ, а также осветительные сети промышленных предприятий, жилых и общественных зданий;
сборные шины электроустановок и ошиновка в пределах открытых и закрытых распределительных устройств всех напряжений;
проводники, идущие к резисторам, пусковым реостатам и т. п.;
сети временных сооружений, а также устройства со сроком службы 3-5 лет.
1.3.29. При пользовании табл. 1.3.36 необходимо руководствоваться следующим (см. также 1.3.27):
1. При максимуме нагрузки в ночное время экономическая плотность тока увеличивается на 40%.
2. Для изолированных проводников сечением 16 мм²и менее экономическая плотность тока увеличивается на 40%.
3. Для линий одинакового сечения с n ответвляющимися нагрузками экономическая плотность тока в начале линии может быть увеличена в kp раз, причем kp определяется из выражения
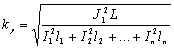
где I1, I2, . In — нагрузки отдельных участков линии; l1, l2, . ln — длины отдельных участков линии; L — полная длина линии.
4. При выборе сечений проводников для питания n однотипных, взаиморезервируемых электроприемников (например, насосов водоснабжения, преобразовательных агрегатов и т. д.), из которых m одновременно находятся в работе, экономическая плотность тока может быть увеличена против значений, приведенных в табл. 1.3.36, в kn раз, где knравно:
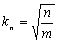
1.3.30. Сечение проводов ВЛ 35 кВ в сельской местности, питающих понижающие подстанции 35/6 — 10 кВ с трансформаторами с регулированием напряжения под нагрузкой, должно выбираться по экономической плотности тока. Расчетную нагрузку при выборе сечений проводов рекомендуется принимать на перспективу в 5 лет, считая от года ввода ВЛ в эксплуатацию. Для ВЛ 35 кВ, предназначенных для резервирования в сетях 35 кВ в сельской местности, должны применяться минимальные по длительно допустимому току сечения проводов, исходя из обеспечения питания потребителей электроэнергии в послеаварийных и ремонтных режимах.
1.3.31. Выбор экономических сечений проводов воздушных и жил кабельных линий, имеющих промежуточные отборы мощности, следует производить для каждого из участков, исходя из соответствующих расчетных токов участков. При этом для соседних участков допускается принимать одинаковое сечение провода, соответствующее экономическому для наиболее протяженного участка, если разница между значениями экономического сечения для этих участков находится в пределах одной ступени по шкале стандартных сечений. Сечения проводов на ответвлениях длиной до 1 км принимаются такими же, как на ВЛ, от которой производится ответвление. При большей длине ответвления экономическое сечение определяется по расчетной нагрузке этого ответвления.
1.3.32. Для линий электропередачи напряжением 6-20 кВ приведенные в табл. 1.3.36 значения плотности тока допускается применять лишь тогда, когда они не вызывают отклонения напряжения у приемников электроэнергии сверх допустимых пределов с учетом применяемых средств регулирования напряжения и компенсации реактивной мощности.
ПРОВЕРКА ПРОВОДНИКОВ ПО УСЛОВИЯМ КОРОНЫ И РАДИОПОМЕХ
1.3.33. При напряжении 35 кВ и выше проводники должны быть проверены по условиям образования короны с учетом среднегодовых значений плотности и температуры воздуха на высоте расположения данной электроустановки над уровнем моря, приведенного радиуса проводника, а также коэффициента негладкости проводников.
При этом наибольшая напряженность поля у поверхности любого из проводников, определенная при среднем эксплуатационном напряжении, должна быть не более 0,9 начальной напряженности электрического поля, соответствующей появлению общей короны.
Проверку следует проводить в соответствии с действующими руководящими указаниями.
Кроме того, для проводников необходима проверка по условиям допустимого уровня радиопомех от короны.
Источник
Adblock
detector
| Проводники | Экономическая плотность тока, А/мм², при числе часов использования максимума нагрузки в год | |
|---|---|---|
| более 1000 до 3000 | более 3000 до 5000 | более 5000 |
The electrical and electronic components such as resistors, capacitors, inductors, wires,
cables, insulators, etc. are made up of different types of material. We generally refer all these
materials as engineering materials. Based on electrical resistivity, the engineering materials
are categorized into three categories namely – conductors, semiconductors, and insulators.
Since every material present in the nature possess a finite amount of electrical resistance.
Also, this resistance can change with the variation in the temperature. The following points
briefly explain the variation in resistance of the different types of materials with the change in
temperature −
- The resistance of conductors increases with the rise in its temperature.
- The resistance of semiconductors decrease with the increase in temperature.
- The resistance of insulating materials also decrease with the increase in temperature.
The change in the resistance of a material with the change in its temperature is expressed in
terms of the temperature coefficient of resistance.
In this article, we will discuss the temperature coefficient of resistance, its definition,
derivation, formula, and examples. So let’s begin with the definition of temperature
coefficient of resistance.
What is the Temperature Coefficient of Resistance?
The measure of change in the electrical resistance of a material with per unit change in the
temperature is referred to as the temperature coefficient of resistance. It is denoted by the
Greek letter alpha (α).
Experimentally, it has been found that in the normal range of temperatures −
- The change in resistance is directly proportional to the initial resistance, i.e.,
$$mathrm{Delta Rpropto R_{0}}$$
Where,
$$mathrm{Delta R=R_{t}- R_{0}}$$
And, 𝑅0 is the initial resistance of the material, and Rt is the resistance of the material
at any t °C.
- The change in resistance is directly proportional to the rise in temperature, i.e.,
$$mathrm{Delta Rpropto t-0=t}$$
- The change in resistance depends upon the nature the material.
Combining the first two points, we have,
$$mathrm{Delta Rpropto R_{0}t}$$
$$mathrm{Rightarrow Delta R=alpha _{0} R_{0}t: cdot cdot cdot left ( 1 right )}$$
Also,
$$mathrm{R_{t}-R_{0}=alpha _{0}R_{0}t: cdot cdot cdot left ( 2 right )}$$
Or,
$$mathrm{R_{t}=R_{0}left ( 1+alpha _{0}t right ): cdot cdot cdot left ( 3 right )}$$
Where, α0 is a constant of proportionality, and is called the temperature coefficient of
resistance of material at 0 °C.
On rearranging the equation (2), we get,
$$mathrm{alpha _{0}=frac{R_{t}-R_{0}}{R_{0}t}: cdot cdot cdot left ( 4 right )}$$
Hence, the temperature coefficient of resistance of a material is the change in resistance per
ohm original resistance per °C change in temperature. The unit of temperature coefficient is
per degree Celsius (/°C).
Since, the value of temperature coefficient of resistance at 0 °C (α0) is different for different
materials. Thus, the change in resistance of different materials is different for the same
change in the temperature. That is why, conductors, semiconductors, and insulators shows
different variations in resistance with the same change in the temperature.
In case of conductors, the value of ΔR is positive, i.e. the resistance of conductors increase
with rise in temperature. Thus, the temperature coefficient of resistance for conductors is
positive. But, in the resistance of semiconductors and insulators decrease with the increase in
temperature. Thus, the temperature coefficient of resistance for semiconductors and insulators
is negative.
Graphical Determination of Temperature Coefficient of Resistance
We can also determine the value of temperature coefficient of resistance graphically with the
help of temperature-resistance graph of a substance. Consider a typical temperatureresistance
graph for a conductor as shown in Figure-1.
For conductors, the plot of the temperature-resistance graph is a straight line. Here, the
resistance of the conductor is 𝑅0 at 0 °C as represented by OA. The resistance of conductor at
temperature t °C is Rt.
Thus, by the definition of the temperature coefficient of resistance, we have,
$$mathrm{alpha _{0}=frac{R_{t}-R_{0}}{R_{0}times t}}$$
From the temperature-resistance graph,
$$mathrm{R_{t}-R_{0}=XC}$$
And,
$$mathrm{Rise: in: temp.=t=AX}$$
Therefore, the temperature coefficient of resistance of the conductor at 0 °C is,
$$mathrm{alpha _{0}=frac{XC}{R_{0}times AX}}$$
But, the slope of the temperature-resistance graph is,
$$mathrm{Slope: of: graph=frac{XC}{AX}}$$
Therefore,
$$mathrm{alpha _{0}=frac{Slope: of: temp.: resistance graph}{Initial: reisstance}: cdot cdot cdot left ( 5 right )}$$
Hence, the temperature coefficient of resistance of a substance at 0 °C is the slope of the
temperature-resistance graph divided by the initial resistance of the substance (or the
resistance at 0 °C, i.e., 𝑅0).
Temperature Coefficient of Resistance at any Temperature
For a material, if the temperature coefficient of resistance at 0 °C (i.e., 𝛼0) is known. Then,
we can determine the value of temperature coefficient of resistance of the material at any
temperature by using the following expression,
$$mathrm{alpha _{t}=frac{alpha _{0}}{1+alpha _{0}t}: cdot cdot cdot left ( 6 right )}$$
Where, 𝛼0 is the temperature coefficient of resistance at t °C.
Note − The temperature coefficient of resistance helps us to determine the value of resistance
of the material at different temperatures. Let 𝑅1 and 𝑅2 are the resistances of a material at
𝑡1°C and 𝑡2°C respectively. If α1 is the temperature coefficient of resistance at 𝑡1°C. Then, the
resistance of the material R2 is given by,
$$mathrm{R_{2}=R_{1}left [ 1+alpha _{1}left ( t_{2}-t_{1} right ) right ]: cdot cdot cdot left ( 7 right )}$$
Temperature Coefficient of Resistance of Some Materials
The following table gives the value of the temperature coefficient of resistance of some
materials at standard temperature (20 °C), which are used in electrical, electronics and other
engineering fields −
| S. No. | Material | Temperature Coefficient of Resistance at 20 °C (in /°C) |
|---|---|---|
| 6. | Iron (Fe) | 0.00651 |
| 12. | Nickel (Ni) | 0.00641 |
| 5. | Tungsten (W) | 0.0045 |
| 4. | Aluminium (Al) | 0.00429 |
| 13. | Tin (Sn) | 0.0042 |
| 7. | Platinum (Pt) | 0.003927 |
| 2. | Copper (Cu) | 0.00386 |
| 1. | Silver (Ag) | 0.0038 |
| 3. | Gold (Au) | 0.0034 |
| 8. | Mercury (Hg) | 0.0009 |
| 14. | Nichrome (Ni-Cr-Fe) | 0.0004 |
| 16. | Constantan (Cu-Ni) | 0.00003 |
| 15. | Manganin (Cu-Mn-Ni) | 0.000002 |
| 9. | Carbon (C) | -0.0005 |
| 10. | Germanium (Ge) | -0.05 |
| 11. | Silicon (Si) | -0.07 |
Numerical Example (1)
The field winding of an electric motor has a resistance of 15 Ω at 0 °C and 18 Ω at 30 °C.
Find the temperature coefficient of resistance of the field winding at 0 °C.
Solution
Given data,
- 𝑅0 = 15 Ω
- 𝑅30 = 18 Ω
Since, the temperature coefficient of resistance at 0 °C is given by,
$$mathrm{alpha _{0}=frac{R_{t}-R_{0}}{R_{0}times t}}$$
In this case, t = 30 °C, thus,
$$mathrm{alpha _{0}=frac{R_{30}-R_{0}}{R_{0}times 30}=frac{18-15}{15times 30}}$$
$$mathrm{therefore alpha _{0}=0.00667: _{}^{circ }textrm{C}^{-1}}$$
Numerical Example (2)
The shunt winding of a DC generator is made up of copper wire and has a temperature
coefficient of resistance 0.00426 /°C at 0 °C. Determine the temperature coefficient of
resistance of the winding at 27 °C.
Solution
Given data,
- 𝛼0 = 0.00426
The temperature coefficient of resistance at 27 °C is given by,
$$mathrm{ alpha _{27}=frac{alpha _{0}}{1+27alpha _{0}}}$$
$$mathrm{Rightarrow alpha _{27}=frac{0.00426}{1+left ( 27times 0.00426 right )}}$$
$$mathrm{therefore alpha _{27}=0.00382, _{}^{circ }textrm{C}^{-1}}$$
Numerical Example (3)
The stator winding of a motor has a resistance of 90 Ω at 17 °C. Find its resistance at 50 °C,
if its temperature coefficient of resistance is 0.003 at 17 °C.
Solution
Given data,
- 𝑅17 = 90 Ω
- 𝛼17 = 0.003
Then, the resistance of the winding at 50 °C is given by,
$$mathrm{R_{50}=R_{17}left [ 1+alpha _{17}left ( 50-17 right ) right ]}$$
$$mathrm{Rightarrow R_{50}=90times left [ 1+0.003times 33 right ]}$$
$$mathrm{therefore R_{50}=98.91, Omega }$$
Conclusion
We will conclude this article with the following points −
-
The electrical resistance of materials changes with the variation in temperature.
-
The change in resistance of materials is described by a factor known as temperature coefficient of resistance of the material.
-
The temperature coefficient of resistance helps us in selecting a material suitable for a particular application.
-
The temperature coefficient of resistance can also be used to determine the resistance of a material at a particular temperature.
-
For metals, the temperature coefficient of resistance is positive, which indicates that the resistance of metals increases with the increase in temperature and vice-versa.
For semiconductors and insulators, the temperature coefficient of resistance is negative,
which indicates that the resistance of semiconductors and insulators decreases with the
increase in temperature and vice-versa.
Что такое температурный коэффициент сопротивления
На основании закона Ома и измерения удельного электрического сопротивления ряда материалов, в частности сопротивления металлов, было выявлено, что данный параметр не постоянен и меняется при изменении температуры. Как правило, при нагреве их проводимость ухудшается.
Убедиться на практике в наличии данного явления можно, включив лампочку накаливания. В момент включения уже горящие лампочки на короткое время уменьшают яркость своего свечения. Это свидетельствует о том, что холодная лампочка (спираль которой выполнена из металла вольфрама) потребляет больший ток от сети, чем разогретая, и «просаживает» напряжение. Следовательно, холодная лампочка проводит электрический ток значительно лучше разогретой.
Как определяется температурный коэффициент сопротивления
Количественной мерой изменения электрического сопротивления проводника служит температурный коэффициент удельного сопротивления (ТКС). Ввиду малости значений ТКС выражается в особых единицах — миллионных долях на один Кельвин или градус Цельсия и обозначается ppm/°C или К-1.
Чтобы рассчитать температурный коэффициент сопротивления меди или любого другого материала, применяют метод, основанный на измерении электрического сопротивления при различных температурных показателях. Затем используется формула:
Температурный коэффициент сопротивлений обозначают буквой α. Его можно выразить через удельное сопротивление:
Исходя из этого, для расчета сопротивления резистора R или любого другого проводника применяется следующее выражение:
Знак ТКС
Чтобы определить температурный коэффициент сопротивления вольфрама или температурный коэффициент сопротивления алюминия, никеля, серебра и пр. материалов и сплавов, нужно знать проводимость исследуемого материала. Она измеряется при разной температуре. TКС характеризует средний наклон графика сопротивления проводника в исследуемом температурном интервале. Если наклон линии зависимости сопротивления от температуры постоянен, зависимость называется линейной. Но для многих материалов, например, для нихромовой проволоки свойственна нелинейная форма температурной зависимости сопротивления. Поэтому важно указывать, какая температура соответствует определенному значению ТКС. Например, температурный коэффициент сопротивления платины равен 3900 при температуре 20 градусов.
ТКС материала может быть положительным или отрицательным по знаку. Плюсовое значение показывает, что с увеличением нагрева сопротивление также увеличивается. Отрицательный коэффициент означает, что с ростом температуры сопротивление уменьшается. Следует также знать, что в разных температурных интервалах знак может отличаться.
ТКС чистых металлов обычно имеет положительное значение, например, температурный коэффициент сопротивления никеля никогда не бывает отрицательным. Материалы с большим (по модулю) параметром используются для измерения температуры в составе датчиков температуры. Резисторы для подобных применений называют терморезисторами или термисторами.
У электролитов ТКС отрицательный. Это связано с тем, что при нагреве в растворе увеличивается количество обеспечивающих электрическая проводимость свободных ионов. Таким образом, электролиты при нагревании начинают проводить лучше, но характер этой зависимости резко нелинейный.
Отрицателен этот параметр и у чистых (беспримесных) полупроводников. Связано это с тем, что при нагреве в зону проводимости переходит большее количество электронов, тем самым увеличивая концентрацию дырок в полупроводнике.
Материалами для изготовления эталонных (образцовых) сопротивлений (резисторов) служат сплавы с равным или очень близким к нулю ТКС. Одним из таких сплавов является проволока из манганина (сплава на основе меди с добавкой марганца и никеля).
ТКС можно узнать из справочной литературы. Например, таблица, представленная ниже, позволяет определить температурный коэффициент сопротивления железа или сопротивления нихрома, а также серебра, меди, алюминия и прочих материалов.
Термин ТКС был введен с целью обозначения термической стабильности резисторов, поскольку удельное сопротивление их резистивного слоя под воздействием температуры может меняться. Температурную зависимость сопротивления используют в устройствах, называемых термометрами сопротивления. Основным их элементом является проволока из меди или платины, намотанная на жесткий каркас из диэлектрика. Платиновый термометр обычно используется для измерения температуры от +263 до 1064, а медный — 180…–50 градусов.
Если при создании электроизмерительных приборов требуются проводники с сопротивлением, мало зависящим от температурных показателей, используют специальные сплавы, такие как манганин или константан. Например, ТКС последнего в 820 раз меньше, чем температурный коэффициент сопротивления серебра.