Температурный коэффициент сопротивления (ТКС) — величина, равная относительному изменению удельного сопротивления вещества при изменении температуры на единицу.
ТКС характеризует зависимость сопротивления проводника от изменении его температуры.Как правило применяют температурный коэффициент сопротивления металлов.
Формула температурного коэффициента сопротивления через относительное изменение сопротивления
{alpha = dfrac{R_2-R_1}{R_1(T_2-T_1)}}
Формула температурного коэффициента сопротивления через удельное сопротивление
{alpha = dfrac{rho_2-rho_1}{rho_1(T_2-T_1)}}
Таблица «Температурный коэффициент сопротивления»
| Проводник | α (10-3/K) |
|---|---|
|
Алюминий температурный коэффициент сопротивления алюминия |
4,2 |
|
Вольфрам температурный коэффициент сопротивления вольфрама |
5 |
|
Железо температурный коэффициент сопротивления железа |
6 |
|
Золото температурный коэффициент сопротивления золота |
4 |
|
Константан (сплав Ni-Cu + Mn) температурный коэффициент сопротивления константина |
0,05 |
|
Латунь температурный коэффициент сопротивления латуни |
0,1-0,4 |
|
Магний температурный коэффициент сопротивления магния |
3,9 |
|
Манганин (сплав меди марганца и никеля — приборный) температурный коэффициент сопротивления манганин |
0,01 |
|
Марганец температурный коэффициент сопротивления марганца |
0,02 |
|
Медь температурный коэффициент сопротивления меди |
4,3 |
|
Нейзильбер температурный коэффициент сопротивления нейзильбера |
0,25 |
|
Никелин (сплав меди и никеля) температурный коэффициент сопротивления никелина |
0,1 |
|
Никель температурный коэффициент сопротивления никеля |
6,5 |
|
Нихром (сплав никеля хрома железы и марганца) температурный коэффициент сопротивления нихрома |
0,1 |
|
Олово температурный коэффициент сопротивления олова |
4,4 |
|
Платина температурный коэффициент сопротивления платины |
3,9 |
|
Ртуть температурный коэффициент сопротивления ртути |
1 |
|
Свинец температурный коэффициент сопротивления свинца |
3,7 |
|
Серебро температурный коэффициент сопротивления серебра |
4,1 |
|
Сталь температурный коэффициент сопротивления стали |
1-4 |
|
Фехраль (Cr (12—15 %); Al (3,5—5,5 %); Si (1 %); Mn (0,7 %); + Fe) температурный коэффициент сопротивления фехраля |
0,1 |
|
Цинк температурный коэффициент сопротивления цинка |
4,2 |
|
Чугун температурный коэффициент сопротивления чугуна |
1 |
Что такое температурный коэффициент сопротивления
На основании закона Ома и измерения удельного электрического сопротивления ряда материалов, в частности сопротивления металлов, было выявлено, что данный параметр не постоянен и меняется при изменении температуры. Как правило, при нагреве их проводимость ухудшается.
Убедиться на практике в наличии данного явления можно, включив лампочку накаливания. В момент включения уже горящие лампочки на короткое время уменьшают яркость своего свечения. Это свидетельствует о том, что холодная лампочка (спираль которой выполнена из металла вольфрама) потребляет больший ток от сети, чем разогретая, и «просаживает» напряжение. Следовательно, холодная лампочка проводит электрический ток значительно лучше разогретой.
Как определяется температурный коэффициент сопротивления
Количественной мерой изменения электрического сопротивления проводника служит температурный коэффициент удельного сопротивления (ТКС). Ввиду малости значений ТКС выражается в особых единицах — миллионных долях на один Кельвин или градус Цельсия и обозначается ppm/°C или К-1.
Чтобы рассчитать температурный коэффициент сопротивления меди или любого другого материала, применяют метод, основанный на измерении электрического сопротивления при различных температурных показателях. Затем используется формула:
Температурный коэффициент сопротивлений обозначают буквой α. Его можно выразить через удельное сопротивление:
Исходя из этого, для расчета сопротивления резистора R или любого другого проводника применяется следующее выражение:
Знак ТКС
Чтобы определить температурный коэффициент сопротивления вольфрама или температурный коэффициент сопротивления алюминия, никеля, серебра и пр. материалов и сплавов, нужно знать проводимость исследуемого материала. Она измеряется при разной температуре. TКС характеризует средний наклон графика сопротивления проводника в исследуемом температурном интервале. Если наклон линии зависимости сопротивления от температуры постоянен, зависимость называется линейной. Но для многих материалов, например, для нихромовой проволоки свойственна нелинейная форма температурной зависимости сопротивления. Поэтому важно указывать, какая температура соответствует определенному значению ТКС. Например, температурный коэффициент сопротивления платины равен 3900 при температуре 20 градусов.
ТКС материала может быть положительным или отрицательным по знаку. Плюсовое значение показывает, что с увеличением нагрева сопротивление также увеличивается. Отрицательный коэффициент означает, что с ростом температуры сопротивление уменьшается. Следует также знать, что в разных температурных интервалах знак может отличаться.
ТКС чистых металлов обычно имеет положительное значение, например, температурный коэффициент сопротивления никеля никогда не бывает отрицательным. Материалы с большим (по модулю) параметром используются для измерения температуры в составе датчиков температуры. Резисторы для подобных применений называют терморезисторами или термисторами.
У электролитов ТКС отрицательный. Это связано с тем, что при нагреве в растворе увеличивается количество обеспечивающих электрическая проводимость свободных ионов. Таким образом, электролиты при нагревании начинают проводить лучше, но характер этой зависимости резко нелинейный.
Отрицателен этот параметр и у чистых (беспримесных) полупроводников. Связано это с тем, что при нагреве в зону проводимости переходит большее количество электронов, тем самым увеличивая концентрацию дырок в полупроводнике.
Материалами для изготовления эталонных (образцовых) сопротивлений (резисторов) служат сплавы с равным или очень близким к нулю ТКС. Одним из таких сплавов является проволока из манганина (сплава на основе меди с добавкой марганца и никеля).
ТКС можно узнать из справочной литературы. Например, таблица, представленная ниже, позволяет определить температурный коэффициент сопротивления железа или сопротивления нихрома, а также серебра, меди, алюминия и прочих материалов.
Термин ТКС был введен с целью обозначения термической стабильности резисторов, поскольку удельное сопротивление их резистивного слоя под воздействием температуры может меняться. Температурную зависимость сопротивления используют в устройствах, называемых термометрами сопротивления. Основным их элементом является проволока из меди или платины, намотанная на жесткий каркас из диэлектрика. Платиновый термометр обычно используется для измерения температуры от +263 до 1064, а медный — 180…–50 градусов.
Если при создании электроизмерительных приборов требуются проводники с сопротивлением, мало зависящим от температурных показателей, используют специальные сплавы, такие как манганин или константан. Например, ТКС последнего в 820 раз меньше, чем температурный коэффициент сопротивления серебра.
Видео по теме
The electrical and electronic components such as resistors, capacitors, inductors, wires,
cables, insulators, etc. are made up of different types of material. We generally refer all these
materials as engineering materials. Based on electrical resistivity, the engineering materials
are categorized into three categories namely – conductors, semiconductors, and insulators.
Since every material present in the nature possess a finite amount of electrical resistance.
Also, this resistance can change with the variation in the temperature. The following points
briefly explain the variation in resistance of the different types of materials with the change in
temperature −
- The resistance of conductors increases with the rise in its temperature.
- The resistance of semiconductors decrease with the increase in temperature.
- The resistance of insulating materials also decrease with the increase in temperature.
The change in the resistance of a material with the change in its temperature is expressed in
terms of the temperature coefficient of resistance.
In this article, we will discuss the temperature coefficient of resistance, its definition,
derivation, formula, and examples. So let’s begin with the definition of temperature
coefficient of resistance.
What is the Temperature Coefficient of Resistance?
The measure of change in the electrical resistance of a material with per unit change in the
temperature is referred to as the temperature coefficient of resistance. It is denoted by the
Greek letter alpha (α).
Experimentally, it has been found that in the normal range of temperatures −
- The change in resistance is directly proportional to the initial resistance, i.e.,
$$mathrm{Delta Rpropto R_{0}}$$
Where,
$$mathrm{Delta R=R_{t}- R_{0}}$$
And, 𝑅0 is the initial resistance of the material, and Rt is the resistance of the material
at any t °C.
- The change in resistance is directly proportional to the rise in temperature, i.e.,
$$mathrm{Delta Rpropto t-0=t}$$
- The change in resistance depends upon the nature the material.
Combining the first two points, we have,
$$mathrm{Delta Rpropto R_{0}t}$$
$$mathrm{Rightarrow Delta R=alpha _{0} R_{0}t: cdot cdot cdot left ( 1 right )}$$
Also,
$$mathrm{R_{t}-R_{0}=alpha _{0}R_{0}t: cdot cdot cdot left ( 2 right )}$$
Or,
$$mathrm{R_{t}=R_{0}left ( 1+alpha _{0}t right ): cdot cdot cdot left ( 3 right )}$$
Where, α0 is a constant of proportionality, and is called the temperature coefficient of
resistance of material at 0 °C.
On rearranging the equation (2), we get,
$$mathrm{alpha _{0}=frac{R_{t}-R_{0}}{R_{0}t}: cdot cdot cdot left ( 4 right )}$$
Hence, the temperature coefficient of resistance of a material is the change in resistance per
ohm original resistance per °C change in temperature. The unit of temperature coefficient is
per degree Celsius (/°C).
Since, the value of temperature coefficient of resistance at 0 °C (α0) is different for different
materials. Thus, the change in resistance of different materials is different for the same
change in the temperature. That is why, conductors, semiconductors, and insulators shows
different variations in resistance with the same change in the temperature.
In case of conductors, the value of ΔR is positive, i.e. the resistance of conductors increase
with rise in temperature. Thus, the temperature coefficient of resistance for conductors is
positive. But, in the resistance of semiconductors and insulators decrease with the increase in
temperature. Thus, the temperature coefficient of resistance for semiconductors and insulators
is negative.
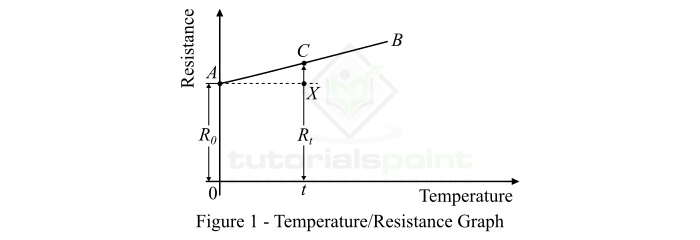
Graphical Determination of Temperature Coefficient of Resistance
We can also determine the value of temperature coefficient of resistance graphically with the
help of temperature-resistance graph of a substance. Consider a typical temperatureresistance
graph for a conductor as shown in Figure-1.
For conductors, the plot of the temperature-resistance graph is a straight line. Here, the
resistance of the conductor is 𝑅0 at 0 °C as represented by OA. The resistance of conductor at
temperature t °C is Rt.
Thus, by the definition of the temperature coefficient of resistance, we have,
$$mathrm{alpha _{0}=frac{R_{t}-R_{0}}{R_{0}times t}}$$
From the temperature-resistance graph,
$$mathrm{R_{t}-R_{0}=XC}$$
And,
$$mathrm{Rise: in: temp.=t=AX}$$
Therefore, the temperature coefficient of resistance of the conductor at 0 °C is,
$$mathrm{alpha _{0}=frac{XC}{R_{0}times AX}}$$
But, the slope of the temperature-resistance graph is,
$$mathrm{Slope: of: graph=frac{XC}{AX}}$$
Therefore,
$$mathrm{alpha _{0}=frac{Slope: of: temp.: resistance graph}{Initial: reisstance}: cdot cdot cdot left ( 5 right )}$$
Hence, the temperature coefficient of resistance of a substance at 0 °C is the slope of the
temperature-resistance graph divided by the initial resistance of the substance (or the
resistance at 0 °C, i.e., 𝑅0).
Temperature Coefficient of Resistance at any Temperature
For a material, if the temperature coefficient of resistance at 0 °C (i.e., 𝛼0) is known. Then,
we can determine the value of temperature coefficient of resistance of the material at any
temperature by using the following expression,
$$mathrm{alpha _{t}=frac{alpha _{0}}{1+alpha _{0}t}: cdot cdot cdot left ( 6 right )}$$
Where, 𝛼0 is the temperature coefficient of resistance at t °C.
Note − The temperature coefficient of resistance helps us to determine the value of resistance
of the material at different temperatures. Let 𝑅1 and 𝑅2 are the resistances of a material at
𝑡1°C and 𝑡2°C respectively. If α1 is the temperature coefficient of resistance at 𝑡1°C. Then, the
resistance of the material R2 is given by,
$$mathrm{R_{2}=R_{1}left [ 1+alpha _{1}left ( t_{2}-t_{1} right ) right ]: cdot cdot cdot left ( 7 right )}$$
Temperature Coefficient of Resistance of Some Materials
The following table gives the value of the temperature coefficient of resistance of some
materials at standard temperature (20 °C), which are used in electrical, electronics and other
engineering fields −
| S. No. | Material | Temperature Coefficient of Resistance at 20 °C (in /°C) |
|---|---|---|
| 6. | Iron (Fe) | 0.00651 |
| 12. | Nickel (Ni) | 0.00641 |
| 5. | Tungsten (W) | 0.0045 |
| 4. | Aluminium (Al) | 0.00429 |
| 13. | Tin (Sn) | 0.0042 |
| 7. | Platinum (Pt) | 0.003927 |
| 2. | Copper (Cu) | 0.00386 |
| 1. | Silver (Ag) | 0.0038 |
| 3. | Gold (Au) | 0.0034 |
| 8. | Mercury (Hg) | 0.0009 |
| 14. | Nichrome (Ni-Cr-Fe) | 0.0004 |
| 16. | Constantan (Cu-Ni) | 0.00003 |
| 15. | Manganin (Cu-Mn-Ni) | 0.000002 |
| 9. | Carbon (C) | -0.0005 |
| 10. | Germanium (Ge) | -0.05 |
| 11. | Silicon (Si) | -0.07 |
Numerical Example (1)
The field winding of an electric motor has a resistance of 15 Ω at 0 °C and 18 Ω at 30 °C.
Find the temperature coefficient of resistance of the field winding at 0 °C.
Solution
Given data,
- 𝑅0 = 15 Ω
- 𝑅30 = 18 Ω
Since, the temperature coefficient of resistance at 0 °C is given by,
$$mathrm{alpha _{0}=frac{R_{t}-R_{0}}{R_{0}times t}}$$
In this case, t = 30 °C, thus,
$$mathrm{alpha _{0}=frac{R_{30}-R_{0}}{R_{0}times 30}=frac{18-15}{15times 30}}$$
$$mathrm{therefore alpha _{0}=0.00667: _{}^{circ }textrm{C}^{-1}}$$
Numerical Example (2)
The shunt winding of a DC generator is made up of copper wire and has a temperature
coefficient of resistance 0.00426 /°C at 0 °C. Determine the temperature coefficient of
resistance of the winding at 27 °C.
Solution
Given data,
- 𝛼0 = 0.00426
The temperature coefficient of resistance at 27 °C is given by,
$$mathrm{ alpha _{27}=frac{alpha _{0}}{1+27alpha _{0}}}$$
$$mathrm{Rightarrow alpha _{27}=frac{0.00426}{1+left ( 27times 0.00426 right )}}$$
$$mathrm{therefore alpha _{27}=0.00382, _{}^{circ }textrm{C}^{-1}}$$
Numerical Example (3)
The stator winding of a motor has a resistance of 90 Ω at 17 °C. Find its resistance at 50 °C,
if its temperature coefficient of resistance is 0.003 at 17 °C.
Solution
Given data,
- 𝑅17 = 90 Ω
- 𝛼17 = 0.003
Then, the resistance of the winding at 50 °C is given by,
$$mathrm{R_{50}=R_{17}left [ 1+alpha _{17}left ( 50-17 right ) right ]}$$
$$mathrm{Rightarrow R_{50}=90times left [ 1+0.003times 33 right ]}$$
$$mathrm{therefore R_{50}=98.91, Omega }$$
Conclusion
We will conclude this article with the following points −
-
The electrical resistance of materials changes with the variation in temperature.
-
The change in resistance of materials is described by a factor known as temperature coefficient of resistance of the material.
-
The temperature coefficient of resistance helps us in selecting a material suitable for a particular application.
-
The temperature coefficient of resistance can also be used to determine the resistance of a material at a particular temperature.
-
For metals, the temperature coefficient of resistance is positive, which indicates that the resistance of metals increases with the increase in temperature and vice-versa.
For semiconductors and insulators, the temperature coefficient of resistance is negative,
which indicates that the resistance of semiconductors and insulators decreases with the
increase in temperature and vice-versa.
Удельные сопротивления и температурный коэффициент сопротивления металлов и сплавов
|
Металл |
Удельное |
Температурный |
|
Медь |
0.0175=1/57 |
0.004 |
|
Бронза |
0.020÷0.028 |
0.001 |
|
Алюминий |
0.033=1/30 |
0.0037 |
|
Железо |
0.13÷0.18 |
0.0048 |
|
Латунь |
0.07÷0.08 |
0.0015 |
|
Нихром |
1.0÷1.1 |
— |
|
Константан |
0.5 |
— |
|
Манганин |
0.42 |
— |
|
Серебро |
0.016 |
0.0038 |
|
Платина |
0.094 |
0.0024 |
|
Графит |
50÷100 |
— |
Температурный
коэффициент сопротивления α показывает
на сколько увеличивается сопротивление
проводника в 1 Ом при увеличении
температуры (нагревании проводника)
на 1 ºС.
Сопротивление
проводника при температуре t
рассчитывается по формуле:
rt
= r20
+ α*
r20*(t
— 20 ºС)
или
rt
= r20
*[1 + α*(t
– 20 ºС)],
где r20
– сопротивление проводника при
температуре 20 ºС, rt
– сопротивление проводника при
температуре t.
Плотность
тока
Задача 1.
Через медный
проводник с площадью поперечного сечения
S
= 4 мм² протекает ток I
= 10 А. Какова плотность тока?
Решение
Плотность тока J
= I/S
= 10 А/4 мм² = 2.5 А/мм².
[По площади
поперечного сечения 1 мм² протекает
ток I
= 2.5 А; по всему поперечному сечению S
протекает ток I
= 10 А].
Задача 2.
По шине
распределительного устройства
прямоугольного поперечного сечения
(20х80) мм² проходит ток I
= 1000 А. Какова плотность тока в шине?
Решение
Площадь поперечного
сечения шины S
= 20х80 = 1600 мм². Плотность тока
J
= I/S
= 1000 A/1600
мм² = 0.625 А/мм².
Задача 3.
У катушки провод
имеет круглое сечение диаметром 0.8 мм
и допускает плотность тока 2.5 А/мм².
Какой допустимый ток можно пропустить
по проводу (нагрев не должен превысить
допустимый)?
Решение
Площадь поперечного
сечения провода S
= π * d²/4
= 3/14*0.8²/4 ≈ 0.5 мм².
Допустимый ток I
= J*S
= 2.5 А/мм² * 0.5 мм² = 1.25 А.
Задача 4.
Допустимая плотность
тока для обмотки трансформатора J
= 2.5 А/мм². Через обмотку проходит ток I
= 4 А. Каким должно быть поперечное сечение
(диаметр) круглого сечения проводника,
чтобы обмотка не перегревалась?
Решение
Площадь поперечного
сечения S
= I/J
= (4 А) / (2.5 А/мм²) = 1.6 мм²
Этому сечению
соответствует диаметр провода 1.42 мм.
Задача 5.
По изолированному
медному проводу сечением 4 мм² проходит
максимально допустимый ток 38 А (см.
таблицу). Какова допустимая плотность
тока? Чему равны допустимые плотности
тока для медных проводов сечением 1, 10
и 16 мм²?
Решение
1). Допустимая
плотность тока
J
= I/S
= 38 А / 4мм² = 9.5 А/мм².
2). Для сечения 1
мм² допустимая плотность тока (см. табл.)
J
= I/S
= 16 А / 1 мм² = 16 А/мм².
3). Для сечения 10
мм² допустимая плотность тока
J
= 70 A
/ 10 мм² = 7.0 А/мм²
4). Для сечения 16
мм² допустимая плотность тока
J = I/S =
85 А / 16 мм²
= 5.3 А/мм².
Допустимая плотность
тока с увеличением сечения падает. Табл.
действительна для электрических проводов
с изоляцией класса В.
Задачи для
самостоятельного решения
-
Через обмотку
трансформатора должен протекать ток
I
= 4 А. Какое должно быть сечение обмоточного
провода при допустимой плотности тока
J
= 2.5 А/мм²? (S
= 1.6
мм²) -
По проводу диаметром
0.3 мм проходит ток 100 мА. Какова плотность
тока? (J
= 1.415 А/мм²) -
По обмотке
электромагнита из изолированного
провода диаметром
d
= 2.26 мм (без учёта изоляции) проходит ток
10 А. Какова плотность
тока? (J
= 2.5 А/мм²).
4. Обмотка
трансформатора допускает плотность
тока 2.5 А/мм². Ток в обмотке равен 15 А.
Какое наименьшее сечение и диаметр
может иметь круглый провод (без учёта
изоляции)? (в мм²; 2.76 мм).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Термин: Зависимость электрического сопротивления от температуры (ТКС)
- Электрическое сопротивление
- Электрическое сопротивление проводника в общем случае зависит от материала проводника
- Определение и формула температурного коэффициента сопротивления
- Единицы
- Примеры решения задач
- Расчет сопротивления электрического проводника
- Расчет длины электрического проводника
- Расчет сечения электрического проводника
- Температурный коэффициент объемного расширения
- Температурный коэффициент линейного расширения
- Зависимость сопротивлений от температуры
- Как рассчитать температурный коэффициент реакции?
- Температурный коэффициент электрического сопротивления металлов α
Термин: Зависимость электрического сопротивления от температуры (ТКС)
Зависимость электрического сопротивления провода от температуры приходится учитывать в различных схемах измерений, поскольку эта зависимость может оказывать существенное влияние на дополнительную погрешность измерения.
Зависимость сопротивления R(t) провода от температуры t задаётся температурным коэффициентом сопротивления (ТКС) провода α и описывается формулой:
R(t) = R20 (1 + α (t — 20) ),
где температура t задаётся в градусах Цельсия; R20 – это сопротивление провода при 20°С, а ТКС α – это константа с размерностью 1/°С, зависящая от материала провода. Приблизительные ТКС некоторых проводников приводим в таблице ниже.
Проводник α (ТКС), 1/°С
| Алюминий | 4,2*10-3 |
| Вольфрам | 5*10-3 |
| Железо | 6*10-3 |
| Золото | 4*10-3 |
| Латунь | (0,1 — 0,4)*10-3 |
| Магний | 3,9*10-3 |
| Медь | 4,3*10-3 |
| Никель | 6,5*10-3 |
| Нихром | 0,1*10-3 |
| Олово | 4,4*10-3 |
| Платина | 3,9*10-3 |
| Серебро | 4,1*10-3 |
| Сталь | (1 — 4)*10-3 |
Абсолютное изменение сопротивления проводника ∆R при изменении температуры ∆t и начальном сопротивлении R рассчитывается по формуле:
∆R = R*α*∆t.
Относительное изменение сопротивления проводника ∆R/R при изменении температуры ∆t рассчитывается по формуле: ∆R/R = α*∆t.
К схемам измерений, в которых существенное влияние отказывает ТКС проводов, относят: полномостовые четырёхпроводные балансные схемы и полумостовые трёхпроводные схемы. Эти схемы применяют в тензометрии, и здесь существенное влияние на шкалу (масштаб) измерения оказывают ТКС проводов питания.
Существуют также балансные мостовые схемы, в которых существенное влияние отказывает не собственный ТКС проводов, а различия ТКС проводов, которыми подключен мост. К такому случаю относят трёхпроводную четверьмостовую схему. В то же время, существуют схемы измерений, в которых ТКС проводов не оказывает никакого влияния на измерения, например, в случае питания тензомоста от источника стабильного тока.
Термин ТКС (англ: TCR temperature coefficient of resistance) широко применяют также к резисторам (и к элементам, проявляющим резистивные свойства) для описания их температурной зависимости с размерностью 10-6/°С или ppm/°С. При этом, ТКС реальных резистивных элементов может быть как положительным, так и отрицательным, но, кроме того, в зависимости от технологии этих элементов, их ТКС может быть разным при разной температуре.
Большое абсолютное значение ТКС в сочетанием фактором самонагрева резистивного элемента из-за протекающего тока может рассматриваться как проявление нелинейного сопротивления на интервалах времени значительно больших, чем время самонагрева.
На интервалах времени значительно меньших, чем время самонагрева резистивного элемента, большое абсолютное значение ТКС будет восприниматься как дрейф (нестабильность) сопротивления по причине самонагрева.
Электрическое сопротивление
Электрическое сопротивление — это физическая величина , характеризующая противодействие проводника или электрической цепи электрическому току . Физика 7,8,9,10,11 класс, ЕГЭ, ГИА Копировать ссылку Распечатать
Электрическое сопротивление — это физическая величина, характеризующая противодействие проводника или электрической цепи электрическому току.
Электрическое сопротивление определяется как коэффициент пропорциональности R между напряжением U и Iсилой постоянного тока в законе Ома для участка цепи.
Единица сопротивления называется омом (Ом) в честь немецкого ученого Г. Ома, который ввел это понятие в физику. Один ом (1 Ом) — это сопротивление такого проводника, в котором при напряжении 1В сила тока равна 1А.
Электрическое сопротивление проводника в общем случае зависит от материала проводника
от его длины и от поперечного сечения, или более кратко — от удельного сопротивления и от геометрических размеров проводника. Данная зависимость общеизвестна и выражается формулой:
Известен каждому и закон Ома для однородного участка электрической цепи, из которого видно, что ток тем меньше, чем сопротивление выше. Таким образом, если сопротивление проводника постоянно, то с ростом приложенного напряжения ток должен бы линейно расти. Но в реальности это не так. Сопротивление проводников не постоянно.
За примерами далеко ходить не надо. Если к регулируемому блоку питания (с вольтметром и амперметром) подключить лампочку, и постепенно повышать напряжение на ней, доводя до номинала, то легко заметить, что ток растет не линейно: с приближением напряжения к номиналу лампы, ток через ее спираль растет все медленнее, причем лампочка светится все ярче.
Нет такого, что с увеличением вдвое приложенного к спирали напряжения, вдвое возрос и ток. Закон Ома как-будто не выполняется. На самом деле закон Ома выполняется, и точно, просто сопротивление нити накала лампы непостоянно, оно зависит температуры.
Вспомним, с чем связана высокая электрическая проводимость металлов. Она связана с наличием в металлах большого количества носителей заряда — составных частей тока — электронов проводимости. Это электроны, образующиеся из валентных электронов атомов металла, которые для всего проводника являются общими, они не принадлежат каждый отдельному атому.
Под действием приложенного к проводнику электрического поля, свободные электроны проводимости переходят из хаотичного в более-менее упорядоченное движение — образуется электрический ток. Но электроны на своем пути встречают препятствия, неоднородности ионной решетки, такие как дефекты решетки, неоднородная структура, вызванные ее тепловыми колебаниями.
Электроны взаимодействуют с ионами, теряют импульс, их энергия передается ионам решетки, переходит в колебания ионов решетки, и хаос теплового движения самих электронов усиливается, от того проводник и нагревается при прохождении по нему тока.
В диэлектриках, полупроводниках, электролитах, газах, неполярных жидкостях — причина сопротивления может быть иной, однако закон Ома, очевидно, не остается постоянно линейным.
Таким образом, для металлов, рост температуры приводит к еще большему возрастанию тепловых колебаний кристаллической решетки, и сопротивление движению электронов проводимости возрастает. Это видно по эксперименту с лампой: яркость свечения увеличилась, но ток возрос слабее. То есть изменение температуры повлияло на сопротивление нити накаливания лампы.
В итоге становится ясно, что сопротивление металлических проводников зависит почти линейно от температуры. А если принять во внимание, что при нагревании геометрические размеры проводника меняются слабо, то и удельное электрическое сопротивление почти линейно зависит от температуры. Зависимости эти можно выразить формулами:
Обратим внимание на коэффициенты. Пусть при 0°C сопротивление проводника равно R0, тогда при температуре t°C оно примет значение R(t), и относительное изменение сопротивления будет равно α*t°C. Вот этот коэффициент пропорциональности α и называется температурным коэффициентом сопротивления. Он характеризует зависимость электрического сопротивления вещества от его текущей температуры.
Данный коэффициент численно равен относительному изменению электрического сопротивления проводника при изменении его температуры на 1К (на один градус Кельвина, что равноценно изменению температуры на один градус Цельсия).
Для металлов ТКС (температурный коэффициент сопротивления α) хоть и относительно мал, но всегда больше нуля, ведь при прохождении тока электроны тем чаще сталкиваются с ионами кристаллической решетки, чем выше температура, то есть чем выше тепловое хаотичное их движение и чем выше их скорость. Сталкиваясь в хаотичном движении с ионами решетки, электроны металла теряют энергию, что мы и видим в результате — сопротивление при нагревании проводника возрастает. Данное явление используется технически в термометрах сопротивления.
Итак, температурный коэффициент сопротивления α характеризует зависимость электрического сопротивления вещества от температуры и измеряется в 1/К — кельвин в степени -1. Величину с обратным знаком называют температурным коэффициентом проводимости.
Что касается чистых полупроводников, то для них ТКС отрицателен, то есть сопротивление снижается с ростом температуры, это связано с тем, что с ростом температуры все больше электронов переходят в зону проводимости, растет при этом и концентрация дырок. Этот же механизм свойственен для жидких неполярных и твердых диэлектриков.
Полярные жидкости свое сопротивление резко уменьшают с ростом температуры из-за снижения вязкости и роста диссоциации. Это свойство применяется для защиты электронных ламп от разрушительного действия больших пусковых токов.
У сплавов, легированных полупроводников, газов и электролитов тепловая зависимость сопротивления более сложна чем у чистых металлов. Сплавы с очень малым ТКС, такие как манганин и константан, применяют в электроизмерительных приборах.
Определение и формула температурного коэффициента сопротивления
Сопротивление проводника (R) (удельное сопротивление) (
)
зависит от температуры. Эту зависимость при незначительных изменениях температуры 
представляют в виде функции:
![[rho ={rho }_0left(1+alpha tright), R=R_0left(1+alpha tright) qquad (1)]](https://radiofiles.ru/images/wp-content/ql-cache/quicklatex.com-30de519b2aa19e453e771c5258527457_l3.png "Rendered by QuickLaTeX.com")
где 
— удельное сопротивление проводника при температуре равной 0oC; 
— температурный коэффициент сопротивления.
ОПРЕДЕЛЕНИЕ Температурным коэффициентом электрического сопротивления () называют физическую величину, равную относительному приращению (R) участка цепи (или удельного сопротивления среды (), которое происходит при нагревании проводника на 1oС. Математически определение температурного коэффициента сопротивления можно представить как:
![[alpha =frac{1}{R}frac{dR}{dT}; alpha =frac{1}{rho }frac{drho }{dT} qquad (2)]](https://radiofiles.ru/images/wp-content/ql-cache/quicklatex.com-bd1deb5ea647a068141abd156ba9e07b_l3.png "Rendered by QuickLaTeX.com")
Величина
служит характеристикой связи электросопротивления с температурой.
При температурах, принадлежащих диапазону
у большинства металлов рассматриваемый коэффициент
остается постоянным. Для чистых металлов температурный коэффициент сопротивления часто принимают равным 
Иногда говорят о среднем температурном коэффициенте сопротивления, определяя его как:
![[leftlangle alpha rightrangle =frac{1}{rho }frac{triangle rho }{triangle T} qquad (3)]](https://radiofiles.ru/images/wp-content/ql-cache/quicklatex.com-9c4e2e22c34d6b57d93c0785fd8bc305_l3.png "Rendered by QuickLaTeX.com")
где 
— средняя величина температурного коэффициента в заданном интервале температур 
Основной единицей измерения температурного коэффициента сопротивления в системе СИ является:
![[left[alpha right]=frac{1}{K}]](https://radiofiles.ru/images/wp-content/ql-cache/quicklatex.com-45d81646f4b962e88927a680d2ceea08_l3.png "Rendered by QuickLaTeX.com")
Единицы
Тепловой коэффициент электрическая цепь части иногда указываются как промилле/°C, или же промилле/K. Он определяет долю (выраженную в миллионных долях), на которую его электрические характеристики будут отклоняться при достижении температуры выше или ниже Рабочая Температура.
Примеры решения задач
ПРИМЕР 1
| Задание | Лампа накаливания, имеющая спираль из вольфрама включена в сеть с напряжением  B, по ней идет ток  А. Какой будет температура спирали, если при температуре  oС она имеет сопротивление  Ом? Температурный коэффициент сопротивления вольфрама  . |
| Решение | В качестве основы для решения задачи используем формулу зависимости сопротивления от температуры вида:
где
По закону Ома для участка цепи имеем:
Вычислим
Запишем уравнение связывающее сопротивление
Проведем вычисления:
|
| Ответ |  K |
![[R_{20}=R_0left(1+бat_{20}right) qquad left(1.1right),]](https://radiofiles.ru/images/wp-content/ql-cache/quicklatex.com-ca884b97696fae6379f2edba6a3da6ed_l3.png "Rendered by QuickLaTeX.com")
![[R_0=frac{R_{20}}{1+alpha t_{20}}=frac{35,8}{1+4,6cdot {10}^{-3}cdot 20}=32,8 left(Omright)]](https://radiofiles.ru/images/wp-content/ql-cache/quicklatex.com-ff8b4877644c5a5df3371df648ad3aed_l3.png "Rendered by QuickLaTeX.com")
![[I=frac{U}{R_2}to R_2=frac{U}{I} qquad left(1.2right)]](https://radiofiles.ru/images/wp-content/ql-cache/quicklatex.com-1c88c94847257c30be6d95252a84f134_l3.png "Rendered by QuickLaTeX.com")
![[R_2=frac{120}{0,33}=364 left(Omright)]](https://radiofiles.ru/images/wp-content/ql-cache/quicklatex.com-b7930dff9dc252cb0b6763688d93a3cf_l3.png "Rendered by QuickLaTeX.com")
![[R_2=R_0left(1+alpha t_2right) to t_2=frac{R_2-R_0}{{alpha R}_0} qquad left(1.3right)]](https://radiofiles.ru/images/wp-content/ql-cache/quicklatex.com-4fc500fb9ee4fdaf37d85ee99ae62ac4_l3.png "Rendered by QuickLaTeX.com")
![[t_2=frac{364-32,8}{4,6cdot {10}^{-3}cdot 32,8}=2195 (K)]](https://radiofiles.ru/images/wp-content/ql-cache/quicklatex.com-fd13ff5a476f22354a994bf3cfbd7fc8_l3.png "Rendered by QuickLaTeX.com")
ПРИМЕР 2
| Задание | При температуре  сопротивление реостата равно  , сопротивление амперметра равно  и он показывает силу тока  Реостат, сделан из железной проволоки, он последовательно соединен с амперметром (рис.1). Каким будет сила тока течь через амперметр, если реостат нагреть до температуры  ? Считать температурный коэффициент сопротивления железа равным .  Рис. 1 |
| Решение | Закон Ома для участка цепи при температуре 0oC можно записать как:
После нагревания сопротивление реостата стало равно R, тогда через амперметр течет ток равный:
Сопротивление зависит от температуры:
Подставим выражения (2.3) и (2.1) в уравнение (2.2), получим:
|
| Ответ |  |
![[I_0=frac{U}{R_0+R_{A0}}to U=I_0(R_0+R_{A0}) qquad left(2.1right)]](https://radiofiles.ru/images/wp-content/ql-cache/quicklatex.com-602f870109785aaf8456b1f19dc65631_l3.png "Rendered by QuickLaTeX.com")
![[I=frac{U}{R+R_{A0}} qquad left(2.2right)]](https://radiofiles.ru/images/wp-content/ql-cache/quicklatex.com-c38e506a3c34de131f27f9b56d349335_l3.png "Rendered by QuickLaTeX.com")
![[R=R_0left(1+alpha tright) qquad left(2.3right)]](https://radiofiles.ru/images/wp-content/ql-cache/quicklatex.com-ae8456c540f371f0e2b9c67df9ba4252_l3.png "Rendered by QuickLaTeX.com")
![[I=frac{I_0(R_0+R_{A0})}{R_0left(1+alpha tright)+R_{A0}}]](https://radiofiles.ru/images/wp-content/ql-cache/quicklatex.com-cce0de116f0ac897cd6293e6506bd42f_l3.png "Rendered by QuickLaTeX.com")
Расчет сопротивления электрического проводника
Сопротивление электрического проводника рассчитываем по формуле:
R = ρ * L / S
- R — сопротивление электрического проводника
- ρ — удельное сопротивление проводника
вычисляется по формуле (1): ρ = ρ20[1 + α(t — 20)]- ρ20 — удельное сопротивление проводника при температуре t = 20°C (Таблица 1)
- t — температура проводника
- α — температурный коэффициент электрического сопротивления (Таблица 1)
- L — длина электрического проводника
- S — сечение электрического проводника
Расчет длины электрического проводника
Длину электрического проводника рассчитываем по формуле:
L = R * S / ρ
- L — длина электрического проводника
- R — сопротивление электрического проводника
- S — сечение электрического проводника
- ρ — удельное сопротивление проводника
вычисляется по формуле (1): ρ = ρ20[1 + α(t — 20)]- ρ20 — удельное сопротивление проводника при температуре t = 20°C (Таблица 1)
- t — температура проводника
- α — температурный коэффициент электрического сопротивления (Таблица 1)
Расчет сечения электрического проводника
Минимальное сечение электрического проводника при допустимых потерях напряжения рассчитываем по формуле:
S = I * ρ * L / ΔU
- S — сечение электрического проводника
- I — сила тока в электрической цепи
- L — длина электрического проводника
при двухпроводной линии, длина проводника (значение L) удваивается - ΔU — допустимые потери напряжения
- ρ — удельное сопротивление проводника
вычисляется по формуле (1): ρ = ρ20[1 + α(t — 20)]- ρ20 — удельное сопротивление проводника при температуре t = 20°C (Таблица 1)
- t — температура проводника
- α — температурный коэффициент электрического сопротивления (Таблица 1)
Температурный коэффициент объемного расширения
Температурным коэффициентом объемного расширения тела является физическая величина, которая характеризует относительное изменение объема тела 
которое происходит при нагревании тела на 1 K и неизменном давлении:
![[{alpha }_V=frac{1}{V_0}frac{Delta V}{Delta T} qquad (5)]](https://radiofiles.ru/images/wp-content/ql-cache/quicklatex.com-d1d1ffe185ecfb8ec8fda0b79f3763c0_l3.png "Rendered by QuickLaTeX.com")
Температурный коэффициент линейного расширения
ОПРЕДЕЛЕНИЕ Температурный коэффициент линейного расширения 
— это физическая величина, которая характеризует изменение линейных размеров твердого тела с ростом или уменьшением его температуры.
![[{alpha }_l=frac{1}{l_0}frac{Delta l}{Delta T} qquad (4)]](https://radiofiles.ru/images/wp-content/ql-cache/quicklatex.com-17c6840015dc6f628632fb6203bf036d_l3.png "Rendered by QuickLaTeX.com")
где 
— начальная длина тела, 
— увеличение длины тела (удлинение) при росте температуры тела на 
Зависимость сопротивлений от температуры
С повышением температуры сопротивление металлов возрастает. Однако существуют сплавы, сопротивление которых почти не меняется при повышении температуры (например, константан, манганин и др.). Сопротивление же электролитов с повышением температуры уменьшается.
Температурным коэффициентом сопротивления проводника называется отношение величины изменения сопротивления проводника при нагревании на 1 °С к величине его сопротивления при 0 ºС:
Зависимость удельного сопротивления проводников от температуры выражается формулой:
В общем случае α зависит от температуры, но если интервал температур невелик, то температурный коэффициент можно считать постоянным. Для чистых металлов α = (1/273)К-1. Для растворов электролитов α < 0. Например, для 10% раствора поваренной соли α = -0,02 К-1. Для константана (сплава меди с никелем) α = 10-5 К-1.
Зависимость сопротивления проводника от температуры используется в термометрах сопротивления.
Как рассчитать температурный коэффициент реакции?
Что такое температурный коэффициент?
Во-первых, при повышении температуры скорость реакции возрастает. Всё логично
Значит, температурный коэффициент- это число, которое показывает, во сколько раз увеличилась скорость реакции, когда мы повысим температуру на 10 градусов
Вот такая страшная формула( но только на первый взгляд)
γ-это и есть наш температурный коэффициент
Следовательно, чтобы его расчитать, нужно знать
2 скорости (до и после повышения температуры на 10 градусов)
2 константы (у каждой реакции они свои. Обычно их пишут в условии задачи)
Температурный коэффициент электрического сопротивления металлов α
- В разумных температурных пределах вокруг некоторой точки зависимость удельного сопротивления металлов от температуры описывается как:
- ΔR = α*R*ΔT, где α — температурный коэффициент электрического сопротивления.
- Ниже приведена таблица значений α для ряда металлов в диапазоне температур от 0 до 100 ° C.
Зависимость сопротивления металлов от температуры. Температурный коэффициент электрического сопротивления металлов α .
| Проводник | Удельное сопротивление ρ, Ом*мм2/м |
α, 10 -3*C-1(или K -1) |
| Алюминий | 0,028 | 4,2 |
| Бронза | 0,095 — 0,1 | — |
| Висмут | 1,2 | — |
| Вольфрам | 0,05 | 5 |
| Железо | 0,1 | 6 |
| Золото | 0,023 | 4 |
| Иридий | 0,0474 | — |
| Константан ( сплав Ni-Cu + Mn) | 0,5 | 0,05! |
| Латунь | 0,025 — 0,108 | 0,1-0,4 |
| Магний | 0,045 | 3,9 |
| Манганин (сплав меди марганца и никеля — приборный) | 0,43 — 0,51 | 0,01!! |
| Медь | 0,0175 | 4,3 |
| Молибден | 0,059 | — |
| Нейзильбер (сплав меди цинка и никеля) | 0,2 | 0,25 |
| Натрий | 0,047 | — |
| Никелин ( сплав меди и никеля) | 0,42 | 0,1 |
| Никель | 0,087 | 6,5 |
| Нихром ( сплав никеля хрома железы и марганца) | 1,05 — 1,4 | 0,1 |
| Олово | 0,12 | 4,4 |
| Платина | 0.107 | 3,9 |
| Ртуть | 0,94 | 1,0 |
| Свинец | 0,22 | 3,7 |
| Серебро | 0,015 | 4,1 |
| Сталь | 0,103 — 0,137 | 1-4 |
| Титан | 0,6 | — |
| Фехраль (Cr (12—15 %); Al (3,5—5,5 %); Si (1 %); Mn (0,7 %); + Fe) | 1,15 — 1,35 | 0,1 |
| Хромаль | 1,3 — 1,5 | — |
| Цинк | 0,054 | 4,2 |
| Чугун | 0,5-1,0 | 1,0 |
Источники
- https://www.lcard.ru/lexicon/wire_tcr
- https://www.calc.ru/Elektricheskoye-Soprotivleniye.html
- http://ElectricalSchool.info/main/osnovy/1873-temperaturnyjj-kojefficient.html
- http://ru.solverbook.com/spravochnik/koefficienty/temperaturnyj-koefficient-soprotivleniya/
- https://wikiaro.ru/wiki/Temperature_coefficient
- https://www.axwap.com/kipia/docs/elektrika/provodnik.htm
- http://ru.solverbook.com/spravochnik/koefficienty/temperaturnyj-koefficient/
- https://yandex.ru/q/question/kak_rasschitat_temperaturnyi_koeffitsient_26938630/
- https://dpva.ru/Guide/GuidePhysics/ElectricityAndMagnethism/ElectricalResistanceAndConductivity/MetalsElResHeatCoef/
Помогла ли вам статья?