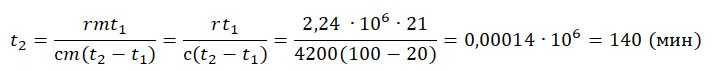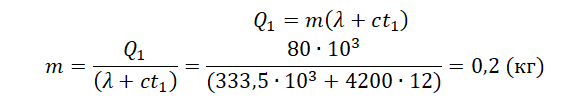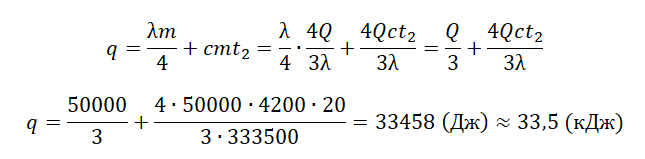Тела, температура которых отличается, могут обмениваться тепловой энергией. То есть, между телами будет происходить теплообмен. Самостоятельно тепловая энергия переходит от более нагретых тел к менее нагретым.
Что такое теплообмен и при каких условиях он происходит
Тела, имеющие различные температуры, будут обмениваться тепловой энергией. Этот процесс называется теплообменом.
Теплообмен – процесс обмена тепловой энергией между телами, имеющими различные температуры.
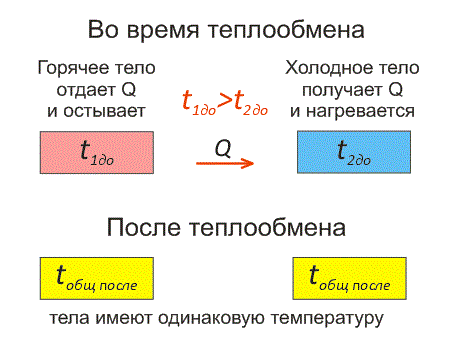
Рассмотрим два тела, имеющие различные температуры (рис. 1).
Тело, имеющее более высокую температуру, будет остывать и отдавать тепловую энергию телу, имеющему низкую температуру. А тело с низкой температурой будет получать количество теплоты и нагреваться.
Рис.1. Два тела во время теплообмена и после
На рисунке, горячее тело имеет розовый оттенок, а холодное изображено голубым цветом.
Когда температуры тел выравниваются, теплообмен прекращается.
Чтобы теплообмен происходил, нужно, чтобы тела имели различные температуры.
Когда температура тел выравняется, теплообмен прекратится.
Тепловое равновесие — это состояние, при котором тела имеют одинаковую температуру.
Уравнение теплового баланса и сохранение тепловой энергии
Когда тело остывает, оно отдает тепловую энергию (теплоту). Утерянное количество теплоты Q имеет знак «минус».
А когда тело нагревается – оно получает тепловую энергию. Приобретенное количество теплоты Q имеет знак «плюс».
Эти факты отражены на рисунке 2.
Рис. 2. Полученное количество теплоты имеет знак «+», а отданное Q – знак «-»
Закон сохранения тепловой энергии: Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом.
Примечание: Существует и другая формулировка закона сохранения энергии: Энергия не появляется сама собой и не исчезает бесследно. Она переходит из одного вида в другой.
Уравнение теплового баланса
Тот факт, что тепловая энергия сохраняется, можно записать с помощью математики в виде уравнения. Такую запись называют уравнением теплового баланса.
Запишем уравнение теплового баланса для двух тел, обменивающихся тепловой энергией:
[large boxed{ Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 }]
(large Q_{text{остывания горяч}} left( text{Дж} right) ) – это количество теплоты горячее тело теряет.
(large Q_{text{нагревания холод}} left( text{Дж} right) ) – это количество теплоты холодное тело получает.
В левой части уравнения складываем количество теплоты каждого из тел, участвующих в теплообмене.
Записываем ноль в правой части уравнения, когда теплообмен с окружающей средой отсутствует. То есть, теплообмен происходит только между рассматриваемыми телами.
В некоторых учебниках применяют сокращения:
[large Q_{1} + Q_{2} = 0 ]
Примечание: Складывая два числа мы получим ноль, когда эти числа будут:
- равными по модулю и
- имеют различные знаки (одно число — знак «плюс», а второе – знак «минус»).
Если несколько тел участвуют в процессе теплообмена
Иногда в процессе теплообмена участвуют несколько тел. Тогда, для каждого тела нужно записать формулу количества теплоты Q. А потом все количества теплоты подставить в уравнение для теплового баланса:
[large boxed{ Q_{1} + Q_{2} + Q_{3} + ldots + Q_{n} = 0 } ]
При этом:
- Q для каждого нагреваемого тела будет обладать знаком «+»,
- Q для каждого охлаждаемого тела — знаком «-».
Пример расчетов для теплообмена между холодным и горячим телом
К горячей воде, массой 200 грамм, имеющей температуру +80 градусов Цельсия, добавили холодную воду, в количестве 100 грамм при температуре +15 градусов Цельсия. Какую температуру будет иметь смесь после установления теплового равновесия? Считать, что окружающая среда в теплообмене не участвует.
Примечание: Здесь мы рассматриваем упрощенную задачу, для того, чтобы облегчить понимание закона сохранения энергии. Мы не учитываем в этой задаче, что вода содержится в емкости. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.
При решении других задач обязательно учитывайте, что емкость, в которой будет содержаться вещество, имеет массу. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.
Решение:
В условии сказано, что окружающая среда в теплообмене не участвует. Поэтому, будем считать рассматриваемую систему замкнутой. А в замкнутых системах выполняются законы сохранения. Например, закон сохранения энергии.
Иными словами, с сосудом и окружающим воздухом теплообмен не происходит и, все тепловая энергия, отданная горячей водой, будет получена холодной водой.
1). Запишем уравнение теплового баланса, в правой части которого можно записать ноль:
[large Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 ]
2). Теперь запишем формулу для каждого количества теплоты:
[large Q_{text{остывания горяч}} = c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) ]
[large Q_{text{нагревания холодн}} = c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) ]
Примечания:
- (large c_{text{воды}} ) – удельную теплоемкость воды находим в справочнике;
- Массу воды переводим в килограммы;
- Горячая вода остывает и отдает тепловую энергию. Поэтому, разность (large (t_{text{общ}} — t_{text{горяч}} ) ) будет иметь знак «минус», потому, что конечная температура горячей воды меньше ее начальной температуры;
- Холодная вода получает тепловую энергию и нагревается. Из-за этого, разность (large (t_{text{общ}} — t_{text{холодн}} ) ) будет иметь знак «плюс», потому, что конечная температура холодной воды больше ее начальной температуры;
3). Подставим выражения для каждого Q в уравнение баланса:
[large c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) + c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) = 0 ]
4). Для удобства, заменим символы числами:
[large 4200 cdot 0,2 cdot (t_{text{общ}} — 80 ) + 4200 cdot 0,1 cdot (t_{text{общ}} — 15 ) = 0 ]
Проведем упрощение:
[large 840 cdot (t_{text{общ}} — 80 ) + 420 cdot (t_{text{общ}} — 15 ) = 0 ]
Раскрыв скобки и решив это уравнение, получим ответ:
[large t_{text{общ}} = 58,33 ]
Ответ: Температура смеси после прекращения теплообмена будет равна 58,33 градуса Цельсия.
Задача для самостоятельного решения:
В алюминиевом калориметре массой 100 грамм находится керосин массой 250 грамм при температуре +80 градусов Цельсия. В керосин поместили свинцовый шарик, массой 300 грамм. Начальная температура шарика +20 градусов Цельсия. Найдите температуру тел после установления теплового равновесия. Внешняя среда в теплообмене не участвует.
Примечание к решению: В левой части уравнения теплового баланса теперь будут находиться три слагаемых. Потому, что мы учитываем три количества теплоты:
- (large Q_{1} ) – охлаждение алюминия от температуры +80 градусов до конечной температуры;
- (large Q_{2} ) – охлаждение керосина от температуры +80 градусов до конечной температуры;
- (large Q_{3} ) – нагревание свинца от температуры +20 градусов до конечной температуры;
А справа в уравнение теплового баланса запишем ноль. Так как внешняя среда в теплообмене не участвует.
Выводы
- Если тела имеют различную температуру, то между ними возможен обмен тепловой энергией, т. е. теплообмен;
- Когда тела будут иметь равную температуру, теплообмен прекратится;
- Тело с высокой температурой, отдает тепловую энергию (теплоту) и остывает. Отданное количество теплоты Q имеет знак «минус»;
- А тело с низкой температурой получает тепловую энергию и нагревается. Полученное количество теплоты Q имеет знак «плюс»;
- Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом. Это – закон сохранения тепловой энергии;
- Сохранение тепловой энергии можно записать в виде уравнения теплового баланса;
- В левой части уравнения складываем количества теплоты (всех тел, участвующих в теплообмене);
- В правой части уравнения записываем ноль, когда теплообмен с окружающей средой отсутствует.
Общие сведения
Баланс в переводе на русский язык означает равновесие. Когда теплоизолированная система приходит в состояние теплового равновесия, то температура всех тел, образующих эту совокупность, становится одинаковой. Такую ситуацию называют законом теплового равновесия или нулевым уравнением термодинамики.
Впервые с уравнением теплового баланса знакомят в средней школе на уроке физики. Ученикам в седьмом классе предлагается решить несколько простых заданий, используя равенство. Формула и определение даётся без доказательства, так как для понимания процесса нужно знать понятия, которые разбираются в выпускных классах школы. Например, то, что теплоёмкость не является характеристикой вещества, при этом она может быть разной в зависимости от проходящих процессов.
Закон теплового баланса позволяет утверждать, что когда в изолированной системе физических тел происходит только теплообмен, то часть тепла, переданного телами, внутреннее состояние энергии которых уменьшается, численно равняется теплу, полученному объектами с возрастающей внутренней энергии. Математически уравнение записывается в виде следующей формулы: Q 1 + Q 2 + Q 3 + …+ Qn = 0, где:
- n — число тел, находящихся в теплоизолированной системе;
- Q — полученное количество теплоты.
Если предположить, что имеется совокупность, состоящая из двух тел, из которых одно отдаёт тепло, а другое принимает его, то справедливо будет записать: Q1 = Q2. Таким образом, теплоотдача всегда равняется теплоприёму. Поэтому этот закон и называют правилом сохранения энергии в тепловых процессах.
Когда тела два, то понять, какое из них отдаёт тепло, а какое получает, несложно. То, что имеет большее нагревание, — будет отдавать. Если же объектов три и более, и некоторые из них имеют промежуточную температуру, определить, какие из них принимают тепло, довольно сложно. Вот тут на помощь и приходит уравнение термодинамики.
Изменение внутренней энергии объясняется теплопередачей, то есть случаем, когда работа не совершается. Поэтому в физике уравнение теплового баланса используется при анализе процессов теплопередачи, нахождении КПД. Это равенство можно применять как при рассмотрении твёрдых тел, так и жидкости.
Суть уравнения
Следует рассмотреть процесс установления теплового равновесия в теплоизолированной системе. Это такая совокупность, в которой объекты взаимодействуют только друг с другом. Простейшая система будет состоять из двух тел. Например, в термос налит сок и в него вброшен лёд. В этом случае термос является изолятором от внешнего воздействия. Пусть первое тело имеет температуру t1, а второе t2. Допустим, что t1 больше t2. Это допущение не является принципиальным, поэтому его можно использовать.
В начальный момент времени тела находятся далеко друг от друга и теплообмен между ними не происходит. Как только, они соприкоснутся — начнётся взаимодействие. Так как температура первого тела больше, то оно начнёт остывать, а второе нагреваться. Происходит теплопередача. В какой-то момент времени она прекратится и наступит тепловое равновесие. То есть температура двух тел станет одинаковой: t1 = t2.
Получившаяся температура называется равновесной. Обозначается она греческой буквой тета — θ. Так как раньше первое тело имело большую температуру, то получается, что в процессе взаимодействия оно отдало тепло. Записать это можно как Q1— — количество теплоты, отданное первым телом. Второй же объект в процессе подогрелся — увеличил температуру. Обозначить это можно как +Q2 — количество теплоты, полученное вторым телом.
Получить тепло второй объект мог только от первого тела, так как рассматриваемая система изолированная. Соответственно, и отдать определённое количество теплоты первое тело могло только второму. Отсюда можно сделать вывод, что если система теплоизолированная, то эти два количества теплоты одинаковы: Q1— = +Q2. Фактически это есть уравнение баланса.
Такая запись даётся в школьных учебниках. Но профессиональные физики записывают его в другой форме. Для термодинамики неважно, какой объект отдаёт, а какой получает тепло. Наука изучает только количество теплоты, полученное в процессе. Взяв простую аналогию с весом, когда о похудевшем человеке на два килограмма можно сказать, что он поправился на минус два кило, будет верным записать: Q1— = -Q1 или -Q1 = Q2.
Если собрать два слагаемых таким образом, чтобы они находились с одной стороны знака равенства, то можно записать: Q1 + Q2 = 0.
Суммарное количество теплоты, образуемое при теплообмене тел в теплоизолированной системе, равно нулю. При этом это правило будет справедливо и для энного количества объектов.
Доказательство закона
Пусть имеется теплоизолированная система, состоящая из нескольких помещённых в неё объектов. Сами тела могут обмениваться теплом только друг с другом. Первый закон термодинамики для системы в целом можно записать как Q = А’ + Δ U. То есть количество теплоты, полученное всей системой, равняется суммарной работе, совершённой всеми телами в совокупности над внешним миром, складывающейся с изменением энергии всех тел внутри системы.
По условию задачи внутренняя энергия меняется не за счёт совершения работы. Поэтому А’ = 0. С другой же стороны, теплоизоляция обозначает, что Q = 0. Иными словами, количество энергии, поступающее из окружения Земли, равняется нулю. Следовательно, изменение внутренней энергии всех тел в системе будет нулевым: Δ U = 0.
Энергия системы состоит из внутренних энергий каждого из входящих в неё тел: U = U1 + U2 +…+ Un. Изменение же её Δ U = Δ U 1 + Δ U 2 + … + Δ Un. Отсюда следует, что если внутренняя энергия остаётся неизменной, то сумма Δ U будет нулевой: Δ U 1 + Δ U 2 + … + Δ Un = 0.
Первый закон термодинамики персонально для каждого из тел входящих в систему можно записать как следующую систему:
{Q1 = А 1′ + Δ U1;
{Q2 = А 2′ + Δ U2;
… ;
{Qn = А n’ + Δ Un.
Все уравнения, входящие в неё, можно сложить почленно. При этом распределив слагаемые для удобства дальнейшего анализирования: Q1 + Q2 +…+ Q n = (А n1′ + А n2′ + … + А n’) + (Δ U1 + Δ U2 + … + Δ Un). Из полученного выражения можно сделать вывод, что сумма дельт второго члена в правой части равняется нулю. В первом же члене с правой стороны каждое слагаемое также равняется нулю. Поэтому можно записать: Q1 + Q2 +…+ Q n = 0. Что и следовало доказать.
Для решения задач полезно вспомнить, на что может идти полученное тепло. К таким частным случаям относят:
- Процессы, при которых нет фазовых переходов. В таком случае полученное количество идёт на увеличение теплоты потенциальной и кинетической энергии: Q = c * m * ΔT (изохорная теплоёмкость).
- Плавление. Например, есть тающий лёд, к которому подводят тепло, при этом кинетическая энергия остаётся постоянной. Значит, изменяется только потенциальная мощность. В этом случае происходит превращение льда в воду. Это действие называют плавлением — переход кристаллического вещества из твёрдого состояния в жидкое: Q = λ * m.
- Парообразование. Выделение из жидкости пара: Q = L * m.
Типовое задание
Явление теплового баланса используется как в изучении процессов при переходе из одного агрегатного состояния в другое, так и для твёрдых или жидких тел, не изменяющих решётку. Существуют типовые задания, входящие в школьную программу. Ученик, решая их, научится находить удельные параметры и сможет понять всю важность выражения теплового баланса.
В латунный котёл массой 128 граммов, содержащий 240 граммов воды, при 8,4 градусах опущено металлическое тело массой 192 грамма, нагретое до 120 градусов Цельсия. Окончательная установившаяся температура составила 21,5 градус. Определить удельную теплоёмкость рассматриваемого тела. Для решения задачи необходимо из справочника взять значение энергетической теплоёмкости латуни. Она составляет 400 Дж/ кг *С0. При этом нужно учитывать, что котёл теплоизолирован.
Температуру, которая установилась через время, обозначают буквой θ. Решение подобных задач начинают с установления количества тел, участвующих в теплообмене. В этом примере их три: вода, котёл, испытываемое тело. Количество тепла, полученное всеми тремя объектами, согласно закону, будет равняться нулю: Qв + Qк +Qт = 0. Теперь следует каждое слагаемое расписать отдельно:
- Qв = mв * cв * Св (θ — Tв).
- Qк = mк * cл * (θ — Tв).
- Qт = mт * cт * (θ — Tк).
Полученные формулы нужно подставить в исходное уравнение. При этом следует обратить внимание, что при подстановке образуется общий множитель (θ — T в), который можно вынести за скобки: (m в * c в + m к * c л) * (θ — T в) + m т * c т * (θ — T к) = 0.
Из условия задачи известно, что у тела температура 100 градусов, а равновесная температура меньше. Поэтому последняя скобка будет отрицательной. Значит, есть смысл перенести это слагаемое вправо, поменяв местами вычитаемое и уменьшаемое: (m в * c в + m к * c л) * (θ — T в) = m т * c т * (T к — θ). Отсюда можно выразить удельную теплоёмкость массы тела. Она будет равняться: C т = (m в * c в + m к * c л) * (θ — T в) / m т * (T к — θ) .
Все данные, используемые в формуле, известны. Остаётся только провести расчёты, подставив значения: Cт = (0,24 кг * 4,2 кДж/кг*С + 0,128 кг * 0,4 кДж/кг*С *(21,5 — 8,4) С) / 0,192 кг * (100 — 21,5)С = 0,921 кДж/ кг *С0. Полученное вещество является алюминием.
Примеры высокого уровня
Эти задачи рассчитаны на подготовленных учащихся, понимающих суть процессов и знающих уравнение баланса. Например, электрическая установка с мощностью P = 350 Вт не может нагреть воду массой 0,6 кг до кипения. Убедившись в этом, её выключают. Нужно определить, каким останется конечный нагрев воды через 15 секунд.
Из условия можно утверждать, что мощность теплопотерь равняется мощности нагревателя: Pпот = P. По сути, мощность теплопотерь это количество тепла, отдаваемое телом в единицу времени. То есть: P пот = Q— / ΔT. С другой стороны, отданное тепло находится из формулы: Q — = c * m * (-ΔT). Отсюда можно записать: P = — c * m * ΔT / Δt. Из последнего выражения легко выразить искомый параметр: ΔT = -(P * Δt) / (c * m). Все необходимые данные есть в условии и их необходимо просто подставить: ΔT = — 350 Вт * 15 с / 4200 Дж * 0,6 кг = — 2,1 С0. Минус в ответе показывает, что температура понижается. Задача решена.
Вот ещё одна задача, для решения которой необходимо вначале исследовать ситуацию. В ёмкость поместили смесь, состоящую из пяти килограммов воды и трёх килограммов льда. Затем туда пустили 0,2 кг водяного пара при температуре 1000С. Нужно определить, что произойдёт.
По условию задачи даны три массы mв, mл, mп. Можно предположить, что при смешении в момент запуска пара температура в системе была нулевой. Это исходит из того, что в ёмкости одновременно находится лёд и вода. Поступающий пар конденсирует, и из него образуется вода. Через время она остывает до нуля. Поэтому в начальный момент выделившаяся энергия идёт только на таяние льда. Cуществует три варианта развития события:
- Лёд не растает ( θ =00С).
- Лёд полностью растает (0 < θ < 1000С).
- Вода начнёт кипеть ( θ = 1000С) .
Для того чтобы выяснить, какой вариант верный, нужно найти выделившуюся энергию: Qпл = λ * m = 330 * 3 = 990 кДж. Получается, чтобы растопить лёд, нужно 990 кДж теплоты. Пар, вступая в реакцию, отдаёт: Q- = L* m + cв * mв (Tпар – Tпл) = 2300 + 0,2 + 4,2 * 0,2 * 100 = 544 кДж. Учитывая два полученных результата, можно утверждать, что при конденсации основного пара выделившейся теплоты будет недостаточно для расплавления льда. Следовательно θ = 00С.
Лицей естественных
наук г. Кирова
Г.Г. Самарин
Решение
задач на теплообмен
с использованием уравнения
теплового баланса
(методические рекомендации)
Киров
2002
ББК
74.204.2
С
17
Печатается
по решению редакционно-издательского совета Лицея естественных наук г. Кирова
Рецензент: К.А. Коханов, кандидат
педагогических наук, старший преподаватель кафедры дидактики физики Вятского
государственного гуманитарного университета, заместитель заведующего кафедрой
дидактики физики.
С 17 Самарин Г.Г. Решение задач на теплообмен с использованием уравнения теплового
баланса: Методические рекомендации. – Киров: Издательство Лицея естественных
наук, 2002. – 35 с.
Пособие рекомендовано учащимся,
желающим получить практические навыки в решении задач на теплообмен, и может
быть полезным для учителей и абитуриентов.
©
Лицей естественных наук, 2002
©
Г.Г. Самарин, 2002
При соприкосновении тел, имеющих
разные температуры, между этими телами происходит теплообмен. С точки зрения молекулярно-кинетической
теории, это объясняется так: молекулы более нагретого тела имеют большую
кинетическую энергию, чем молекулы тела, менее нагретого. При «столкновениях»
молекул соприкасающихся тел происходит процесс выравнивания их средних кинетических
энергий. Молекулы более нагретого тела теряют часть своей кинетической энергии,
при этом нагретое тело будет остывать. Кинетическая энергия молекул холодного
тела возрастает, поэтому температура этого тела будет увеличиваться. В
конечном итоге кинетические энергии молекул обоих тел сравняются, и температуры
тел станут одинаковыми. На этом теплообмен прекращается.
Энергию, которую тело получает
или отдаёт в процессе теплообмена, называют количеством теплоты (Q).
Количество теплоты, как и все другие
виды энергии, измеряется в системе СИ в Джоулях: [Q] = Дж. *
Нагревание или охлаждение
При нагревании или охлаждении тела
количество теплоты, поглощаемое или выделяемое им, рассчитывается по формуле:
Q = сm(t2 – t1), (1)
где m – масса тела, кг;
(t2 – t1) – разность
температур тела,°С (или К);
с – удельная теплоёмкость вещества, из
которого состоит тело,
или
.
Удельная теплоёмкость вещества – это количество теплоты, которое нужно
сообщить одному килограмму данного вещества, чтобы увеличить его температуру на
1°С (или
это количество теплоты, которое выделяет один килограмм данного вещества,
остывая на 1°С).
Например, Своды = 4200, Сльда, водяного пара =
2100, Ссвинца = 140
, Смеди = 380
, Сжелеза, стали = 460
, Салюминия = 920
.
Значения удельных теплоемкостей других
веществ можно найти в справочниках, а также в школьном учебнике или задачнике.
При нагревании тела его внутренняя
энергия увеличивается. Это требует притока энергии к телу от других тел.
Значит, оно поглощает некоторое количество теплоты, принимая его от других тел,
участвующих в теплообмене.
При охлаждении тела его внутренняя
энергия уменьшается. Поэтому остывающее тело отдаёт кому-либо некоторое
количество теплоты.
Обычно конечную температуру,
установившуюся в результате теплообмена, обозначают греческой буквой q (тэта).
В формуле (1) произведение cm для каждого конкретного тела есть величина постоянная. Её называют теплоёмкостью
тела и обозначают С:
C
= c×m.(2)
Размерность теплоемкости: [С] = . Теплоемкость
тела показывает, сколько энергии нужно подвести к данному телу, чтобы нагреть
его на 1°С
(или сколько энергии выделяет это тело, остывая на 1°С).
Теплообмен между телами, имеющими
одинаковые температуры, не происходит, даже если контактируют вещества,
находящиеся в разных агрегатных состояниях. Например, при температуре
плавления (0°С) лёд и вода могут находиться бесконечно долго, при этом количество
льда и количество воды останутся неизменными. Аналогично ведут себя пар и
жидкость, находящиеся при температуре кипения. Теплообмен между ними не
происходит.
Плавление или кристаллизация
Если при нагревании тела его
температура достигнет температуры плавления, то начинает происходить процесс
перехода этого вещества из твердого состояния в жидкое. При этом идут изменения
в расположении и характере взаимодействия молекул. Температура при плавлении
не изменяется. Это означает, что средние кинетические энергии молекул жидкости
и твердого тела при температуре плавления одинаковы. Однако внутренняя энергия
тела при плавлении возрастает за счет увеличения энергии взаимодействия
молекул. Количество теплоты, поглощаемое телом при плавлении, рассчитывается по
формуле
Q = l×m(3),
где m
– масса тела, кг;
l – удельная
теплота плавления, .
При кристаллизации, наоборот,
внутренняя энергия тела уменьшается на величину Q = l×m, и
эта теплота данным телом выделяется. Она поглощается другими телами,
участвующими в теплообмене.
Удельная теплота плавления показывает, сколько энергии нужно сообщить одному килограмму данного
вещества, взятого при температуре плавления, чтобы полностью превратить его при
этой температуре в жидкость (или сколько энергии выделяет 1
кг жидкости, взятой при температуре кристаллизации, если вся она при этой
температуре полностью превратится в твёрдое тело).
Удельную теплоту плавления любого
вещества можно найти в справочниках. Для льда же l = 3,4×105 .
Температура плавления у каждого
вещества своя. Её также можно найти в справочниках. Важно подчеркнуть, что
температура плавления вещества равна температуре кристаллизации этого же
вещества. У льда tпл = 0°С.
Кипение или конденсация
При достижении жидкостью температуры
кипения начинает происходить другой фазовый переход – кипение, при котором
расстояния между молекулами значительно увеличиваются, а силы взаимодействия
молекул уменьшаются. Вся подводимая к жидкости теплота идет на разрыв связей
между молекулами. При конденсации пара в жидкость, наоборот, расстояния между
молекулами значительно сокращаются, а силы взаимодействия молекул
увеличиваются. Для кипения жидкости энергию к жидкости нужно подводить, при
конденсации пара энергия выделяется. Количество теплоты, поглощаемое при
кипении или выделяемое при конденсации, рассчитывается по формуле:
Q = L×m (4),
где m – масса тела, кг;
L – удельная теплота парообразования, .
Удельная теплота парообразования показывает, сколько энергии нужно сообщить одному килограмму жидкости,
взятой при температуре кипения, чтобы при этой температуре полностью превратить
её в пар (для конденсации: сколько энергии выделяет один килограмм пара,
взятого при температуре конденсации, полностью превращаясь в жидкость).
При одинаковом давлении температура
кипения и температура конденсации одного и того же вещества одинаковы.
Температуры кипения и удельные теплоты
парообразования также можно найти в справочниках. Для воды же они
соответственно равны: tкип = 100°С, L = 2,3×106 (при нормальном атмосферном
давлении).
Уравнение теплового баланса
Тела, участвующие в теплообмене,
представляют собой термодинамическую систему. Термодинамическая система
называется теплоизолированной, если она не получает энергию извне и не
отдаёт её; теплообмен происходит только между телами, входящими в эту систему.
Для любой теплоизолированной системы тел справедливо следующее утверждение: количество
теплоты, отданное одними телами, равно количеству теплоты, принимаемому другими
телами.
Qотд. = Qполуч.(5)
Это утверждение описывает частный
случай закона сохранения и превращения энергии в применении к процессу
теплообмена. А формула (5) является одним из видов уравнения теплового баланса.
При решении задач с помощью данного
вида уравнения теплового баланса в формуле (1) в качестве t2 следует брать большую температуру, а в
качестве t1 – меньшую.
Тогда разность (t2 – t1) будет положительна и всё произведение cm(t2–t1) также будет положительным. Все теплоты,
отданные и полученные, будут положительными.
Уравнение теплового баланса можно
записать и в таком виде:
Q1+ Q2+…+ Qn=
0,(6)
Где n –
количество тел системы.
Алгебраическая сумма всех
количеств теплоты (поглощенных и выделенных) в теплоизолированной системе
равна нулю.
Q1, Q2, …, Qn –
это теплоты, поглощаемые или выделяемые участниками теплообмена. Очевидно, что
в этом случае какие-то теплоты должны быть положительны, а какие-то –
отрицательны. При записи уравнения теплового баланса в виде (6) всегда t2 – конечная температура, а t1 – начальная.
Если тело нагревается, то разность (t2 – t1) положительна и все произведение cm(t2 – t1) положительно. То есть Q > 0 тогда, когда
теплота к данному телу подводится.
А если t2 < t1 (тело
остывает), то разность (t2
– t1) отрицательна, то
есть Q < 0. В этом случае тело энергию выделяет.
Если при фазовом переходе энергия к
телу подводится (плавление, кипение), то Q > 0; если
тело выделяет энергию (кристаллизация, конденсация), то Q
< 0.
В принципе уравнения (5) и (6)
равносильны. Результат решения задачи не зависит от того, каким видом уравнения
пользуемся. Выбор способа решения – за читателем.
Применим уравнение теплового баланса
для решения ряда задач.
Задача 1
В медном калориметре массой 100
г находится 1 кг воды при температуре 20°С. В воду опускают свинцовую
деталь массой 2 кг, имеющую температуру 90°С. До какой температуры
нагреется вода? Потерями теплоты пренебречь.*
Решение
|
с1= 380 Дж/(кг×0С) t2 = 20°С m2 = 1 кг с2=4200 Дж/(кг×0С) m3 = 2 кг с3= 140 Дж/(кг×0С) t3 = 90°С q – ? |
Проведём анализ: Вода и калориметр находились в тепловом При опускании в воду с температурой 20°С свинцового тела с температурой 90°С между водой и свинцом будет происходить |
|
|
Изменение температур тел с течением Отрезок АВ соответствует графику изменения |
|
Два параллельных отрезка СВ соответствуют графикам изменения |
|
|
Решим задачу с использованием уравнения Q1 + Q2 = Q3, c1m1(q — t1) + c2m2(q — t2) = c3m3(t3 Выражаем температуру q: q = |
Решим
задачу с использованием уравнения теплового баланса в виде (6):
Q1 + Q2 + Q3 = 0,
c1m1(q — t1) + c2m2(q — t2) + c3m3(q — t3) = 0.
q = 
Ответ: Вода нагреется до 24 °С.
Предлагаю читателю
самостоятельно сделать проверку размерности.
Задача
2

кг и температуру t1 = 100°С,
железную (m2 = 1,2 кг, t2 = 150°С)
и алюминиевую (m3 = 0,8 кг, t3 = 80°С)
сложили вплотную (см рис). Какую температуру будут иметь пластины, когда
теплообмен прекратится? Потерями теплоты в окружающую среду пренебречь.
|
m1 = 1 кг с1= 380 Дж/(кг×0С) t1 = 100°С m2 = 1,2 кг с2= 460 Дж/(кг×0С) t2 = 150°С m3 = 0,8 кг с3= 920 Дж/(кг×0С) t3 = 80°С |
РешениеРешим задачу с
|
|
q — ? |
t =
2. Теперь медная пластина вступает в
теплообмен с железной и алюминиевой. Медная будет нагреваться от температуры t1 до температуры q, а железная и алюминиевая –
остывать от температуры t до температуры q. Тогда:

= Q2‘+ Q3‘,
c1m1(q — t1) = (c2m2
+ c3m3)(t —
q),
c1m1q – c1m1t1 = (c2m2
+ c3m3)t – (c2m2 + c3m3)q
q
=
3. Решим
задачу, применив уравнение теплового баланса в виде (6):
Q1 + Q2 + Q3 = 0,
c1m1(q — t1) + c2m2(q – t2) + c3m3(q — t3)
= 0,
q = 
Ответ: Пластины будут иметь температуру 108 °С.
Как видим,
второй способ оказался и в данном случае более рациональным. Однако, первый
способ зачастую оказывается более понятным, особенно при наличии фазовых
переходов. Поэтому в дальнейшем автор будет придерживаться первого способа
решения задач. Желательно, чтобы читатель пробовал решать их и вторым
способом.
Задача
3
В
железном ведре массой 1,2 кг находится 5
кг воды при температуре 20°С. Сколько льда температурой –10°С надо положить в
ведро, чтобы температура воды понизилась до 12°С? Теплообменом с окружающей
средой пренебречь.
|
m1 = 1,2 кг с1=460 Дж/(кг×0С) m2 = 5 кг с2=4200 Дж/(кг×0С) t1 = t2 = 20°С t3 = —10°С с3=2100 Дж/(кг×0С)
q = |
Решение Известна конечная температура, Значит, анализ ситуации довольно поглощая теплоту Q4, а затем вода, образовавшаяся из льда, Так как иных участников теплообмена нет, то можно Q1 + Q2 = Q3 + Q4 (c1m1 + c2m2)(t1 = c3m3(t4 — t3) + lm3 + c2m3(q — t4) |
|
|
Ответ: Потребуется 0,4
кг льда.
Задача
4
В алюминиевую кастрюлю массой 200
г, содержащую 3 кг воды при 20°С,
поместили стальную деталь массой 0,5 кг, нагретую до 500°С. При этом часть воды выкипела, а оставшаяся
вода нагрелась до 22°С.
Сколько воды выкипело?
|
с1=4200Дж/(кг°С) m2 = с2 =920 t1 = q = 22°С m3 = с3 = 460 t3 = L = 2,3×106 Дж/кг |
Решение 1. Q3 2. Часть воды массой m0 нагрелась до температуры кипения (100оС) Q1 = c1m0(100 — t1) 3. Оставшаяся в кастрюле вода массой (m1 — m0) и сама кастрюля массой m2 нагрелись от 200С до 22°С. При этом была поглощена теплота Q2 |
|
|
m0 |
||
|
4. Так как потерь тепла нет, то записываем уравнение теплового Q1 + Q2 = Q3, c1m0(100 — t1) + c2m2(q — t2) = c3m3(t3 5. Решая это уравнение, находим m0: m0 m0 = |
Ответ: Выкипело 32
г воды.
Задача
5
Комок мокрого снега массой 400
г опустили в медный таз массой 500 г, содержащий 2
кг воды при температуре 20°С. После установления теплового равновесия температура воды в тазу
стала 10°С. Сколько воды было в комке снега?
|
l = 3,4×105 t1 = t3 = m1 = с1 = 380 m2 = с2=4200Дж/(кг×0С) q = 10°С |
Решение 1. Медный таз и вода находятся в тепловом Q1 + Q2 = c1m1(t1 2. Мокрый снег – это снег, содержащий воду. |
|
|
mв |
||
|
Итак, начальная температура мокрого снега 0°С. 3. На пути к температуре 10°С снег массой m3—mв будет сначала таять. Для этого требуется теплота Q3 4. Так как нет потерь тепла, то можно Q1 + Q2 = Q3 + Q4, с1m1(t1 — q) + c2m2(t2 — q) = l(m3 5. Решая это уравнение, находим mв: mв mв Ответ: В комке |
Задача
6
В холодную воду массой 2
кг, имеющую температуру 10°С, находящуюся в кастрюле, влили 3
кг горячей воды при температуре 80°С. До какой температуры нагреется холодная вода,
если известно, что 25% теплоты, отданной горячей водой, пошло на нагревание
кастрюли? Какова теплоемкость кастрюли?
|
M1 = t1 = m2 = t2 = h1=0,25 (25%) |
Решение Так как 25% h2 = Здесь Qполез — теплота, идущая на нагревание холодной воды: Qполез Qзатр — теплота, отданная
|
|
q — ? С — ? |
q =
q =
Так как 25% теплоты, отданной горячей водой, пошло на
нагревание кастрюли, то можно говорить и о КПД процесса нагревания кастрюли:

откуда:
Ответ: Холодная вода нагреется до температуры 47°С. Теплоемкость кастрюли 2809 Дж/0С.
Задача
7
Сколько керосина нужно сжечь, чтобы превратить
в пар 1 кг льда, взятого при температуре —40°С?
КПД нагревательного устройства равен 60%, удельная теплота сгорания керосина
46 МДж/кг.
|
t1 = с1 =2100Дж/(кг×0С) l = 3,4×105 с2 =4200Дж/(кг×0С) L = 2,3×106 h = 0,6 (60%) |
Решение 1. Изобразим на графике t(t) процессы: нагревание льда, плавление льда, 2. Применим формулу КПД нагревателя: h = Здесь Qполез = Q1 + Q2 + Q3 + Q4 = = m1[c1(0 — t1) + l + c2(100 а Qзатр = qm2. Получаем: h = откуда: m2 = m2 = = 114 |
|
m2 |
Ответ: Нужно сжечь 114
г керосина.
Задача 8
Сколько
водяного пара, имеющего температуру 120°С, надо впустить в калориметр,
содержащий 800 г льда при температуре —20°С, чтобы температура
образовавшейся воды оказалась 20°С? Теплоёмкостью калориметра пренебречь.
|
t1 = с1 = с2 Дж/(кг×0С) t2 = с3 =4200Дж/(кг×0С) q = 20°С |
Решение1. Так как теплоемкостью калориметра можно пренебречь, то систему 2. Получают теплоту тела: — — — 3. Отдают теплоту тела: — — — 4. Других участников теплообмена нет, поэтому Q1 + Q2 + Q3 = Q4 c1m1(0 – t1) + lm1 + c3m1(q — 0) = c2m2(t2 — 100) + + Lm2 + c3m2(100 |
|
m2-? |
Ответ: Потребуется 140 г водяного пара.
Часто при
решении задач можно встретиться со следующей проблемой. В теплообмене участвуют
вещества, находящиеся в различных агрегатных состояниях, и конечная температура
теплообмена не известна. Тогда уравнение теплового баланса сразу написать не
удастся, так как его вид зависит от того, в каких агрегатных состояниях будут
находиться конечные продукты. В этом случае последовательность решения задачи
немного изменяется. Сначала нужно сделать предварительные расчеты: сколько
теплоты выделит или поглотит каждое вещество в предполагаемом процессе,
сравнить эти теплоты и сделать вывод о том, в каких агрегатных состояниях будут
находиться продукты теплообмена. И только после этого можно записывать
уравнение теплового баланса. Такие задачи значительно сложнее задач, в которых
конечная температура известна. Рассмотрим ряд таких задач.
Задача
9
В калориметр, содержащий воду массой 0,5
кг при температуре 25°С, впускают водяной пар массой 50
г при температуре 120°С. Какая температура установится в калориметре, если его теплоёмкость
1200 Дж/оС?
 |
|
m1 = 0,5 кг с1 =4200 t1 = 25°С m2 = 0,05 кг t2 = 120°С c2=2100 Дж/(кг×0С) С = 1200 Дж/0С L = 2,3×106 |
Решение 1. Если в конечном итоге весь пар остынет от 120°С до 100°С, затем пара вода |
|
q-? |
|
|
|
2. Если Здесь m¢ — масса сконденсировавшегося |
|
|
3. Пар Уравнение
|
|
Каким из трёх уравнений пользоваться? Cделаем предварительные расчёты. Вычислим: а) сколько Q1 = c1m1(100 — t1) + C(100 — t1) = 4200×0,5×75+1200×75 = 247500 (Дж). б) сколько в) сколько Q3 = Lm2 = 2300000×0,05 = 115000 (Дж). |
Выделяющаяся
теплота Q2 + Q3 = 2100 Дж + 115000 Дж = 117100 Дж при
охлаждении пара и его конденсации меньше теплоты, которая требуется для
нагревания «холодной» воды и калориметра. Значит, чтобы вода вместе с
калориметром смогла нагреться до 100°С, ей нужно больше энергии, чем может отдать пар,
остывая и конденсируясь. Поэтому 117100 Дж пар отдаст, став при этом «горячей»
водой при 100°С, а «холодная» вода при этом до 100°С ещё не нагреется. Тогда в
калориметре будут одновременно находиться сконденсировавшаяся из пара вода при
100°С и
подогретая «холодная» вода. В результате дальнейшего теплообмена «горячая»
вода остынет, а «холодная» нагреется. И в итоге в калориметре будет вода,
температура которой ниже 1000С, но выше 250С.
Уравнение
теплового баланса будет иметь вид (1):
c1m1(q — t1) + C(q — t1) = c2m2(t2 — 100) + Lm2 + c1m2(100 — q), откуда
c1m1q — c1m1t1 + Сq
— Сt1 = 117100 + c1m2×100
— c1m2q.
Ответ: В
калориметре установится температура 63°С.
Задача 10
В калориметре
находится вода массой 0,8 кг при температуре 20°С. В воду опустили 2
кг льда при температуре —30°С. Что будет в калориметре после того, как теплообмен прекратится?
Теплоёмкостью калориметра пренебречь.
1) Весь лёд нагреется до температуры 0°С, весь расплавится и
образуется из льда вода, которая нагреется с 0°С до температуры q:
Уравнение
теплового баланса:
c1m1(t1—q)=c2m2(0-t2)+lm2+c1m²¢(q-0)
Тогда в
калориметре будет вода при температуре q.
|
с1=4200 Дж/(кг×0С) t1 = 20°С m2 = 2 кг t2 = —30°С c2=2100 l = 3,4×105 Дж/кг |
Решение Рассмотрим 1. А опущенный Уравнение c1m1(t1 — 0) + lm1 |
|
|
2. Вода остынет от 20°С до 0°С, часть её замёрзнет и станет льдом при 0°С, остальная –
останется водой при 0°С.
Лёд при этом нагреется от —30°С до 0°С (см. график). И тогда в калориметре будет
находиться смесь воды со льдом при температуре 0°С. Уравнение
теплового баланса запишется так:

в лед воды.
3. Вода
остынет от 20°С до 0°С. Лёд при этом нагреется от —30°С до 0°С, затем частично или полностью расплавится и станет водой при 0°С. В калориметре
будет смесь воды и льда при температуре 0°С. Уравнение теплового
баланса запишется так:
c1m1(t1 — 0) = c2m2(0 — t2) + lm², где m² — масса
превратившегося в воду льда.
4. Лёд нагреется от —30°С до 0°С, расплавится, и образовавшаяся из льда вода нагреется от 0°С до температуры q. А вода массой m1 при этом остынет от 20°С до температуры q. Тогда в калориметре
будет находиться вода при температуре q. Уравнение теплового баланса запишется так:
c1m1(t1 — q) = c2m2(0 — t2) + lm2 + c1m2(q —
0).
Проведем численный анализ ситуации. Сколько теплоты:
а) выделит вода при остывании от 20°С до 0°С:
Q1 = c1m1(t1
— 0) = 4200×0,8×20
= 67200 (Дж);
б) выделит вода при превращении в лед при 0°С:
Q2 = lm1 = 340000×0,8 = 272000 (Дж);
в) нужно получить льду, чтобы нагреться от —30°С до 0°С:
Q3 = c2m2(0
— t2) = 2100×2×30
= 126000 (Дж);
г) нужно получить льду, чтобы полностью
расплавиться при температуре 0°С:
Q4 = lm2 = 340000×2 = 680000 (Дж).
Получаем: чтобы весь лёд нагрелся от —30°С до 0°С, ему нужно передать
126000 Дж теплоты, а вода при этом, остывая от 20°С до 0°С, может дать только 67200
Дж. Значит, лёд эти 67200 Дж у воды «возьмет», но ему ещё не будет хватать Q¢ = 126000 Дж — 67200 Дж = 58800 Дж,
чтобы нагреться до 0°С. Он их «возьмёт» у превращающейся в лед воды (если бы вода
полностью превратилась в лед, то она бы выделила 272000 Дж, а это больше, чем
«нужно» льду):
Q¢ = lm¢ Þ m¢ = Q¢/l = 58800/340000 » 0,2 (кг), где
m¢ — это масса воды, обратившейся в лёд при температуре 0°С.
Как только лёд
нагреется до 0°С, теплообмен между льдом и водой прекратится, так как они будут иметь
одинаковые температуры.
Итак, получили:
вода остынет до 0°С, часть её (а именно m¢ = 0,2 кг) замёрзнет и станет льдом при 0°С, а лёд нагреется до 0°С. И в результате в
калориметре будет находиться смесь воды и льда при 0°С. При этом масса воды
будет равна:
mв = m1 — m¢= 0,8
кг — 0,2
кг = 0,6 кг,
а масса льда
равна: mл = m2 + m¢ = 2 кг + 0,2 кг = 2,2 кг.
Ответ: В калориметре
при 0°С
находится смесь воды (0,6 кг) и льда (2,2
кг).
Задача 11
В калориметр,
содержащий 1 кг льда при —20°С, впускают 200 г водяного пара при 120°С. Что будет в калориметре,
когда теплообмен прекратится? Теплоёмкостью калориметра пренебречь.
|
m1 = 1 кг с1 = c2 t1 = —20°С m2 = 0,2 кг t2 = 120°С L = 2,3×106 Дж/кг l = 3,4×105 с3 =4200Дж/(кг×0С) |
Решение 1. Q1¢ = 2. Q1² = lm1 = 340000×1 = 340000 (Дж); 3. Q1²¢ = c3m1(100 — 0) = 4200×1×100 = 420000 (Дж); 4. Q2¢ = 5. Q2² = 6. Рассчитаем, сколько теплоты может выделить вода, образовавшаяся Q2²¢ = c3m3(100 — 0) = 4200×0,2×100 = 84000 (Дж). |
|
q – mв – ? mл |
|
Проведем анализ ситуации:
а) льду надо
получить 42000 Дж, чтобы нагреться от —20°С до 0°С, а пар, остывая от 120°С до 100°С, может отдать только 8400 Дж. Значит, лёд «возьмёт» у пара 8400 Дж,
но ещё не нагреется до 0°С. Льду не достает еще 42000 Дж – 8400 Дж = 33600 Дж, чтобы нагреться
до 0°С;
б)
недостающая энергия может быть получена от конденсации пара. Пар будет
конденсироваться при 100°С и выделит при этом 460000 Дж. Лёд за счёт этого сначала нагреется до
0°С, а
затем будет плавиться. Для этого ему нужна энергия: 33600 Дж + 340000 Дж =
373600 Дж. Это меньше, чем выделит пар, превращаясь в воду;
в) значит,
лед растает и станет водой при 0°С. А у пара еще «останется» 460000 Дж – 373600 Дж = 86400 (Дж). Но
этого не хватит, чтобы вода, образующаяся из льда, нагрелась до 100°С. Но на сколько-то
она все же нагреется. Поэтому можно сделать вывод: в калориметре будет
находиться только вода. Она будет состоять из воды, образованной из льда, и
воды, образованной из пара. Её масса: mв = m1 + m2 = 1,2
кг.
Конечную
температуру воды q будем искать из уравнения теплового баланса:
c1m1(0 —
t1) + lm1 + c3m1(q —
0) =c2m2(t2 — 100) + Lm2 + c3m3(100 — q).
Используем результаты сделанных ранее вычислений:
c3m1(q — 0) — c3m2(100 — q) = 86400,
c3m1q — c3m2100 + c3m2q = 86400,
q = 
Ответ: В калориметре будет находиться 1,2
кг воды при температуре 17°С.
Иногда в задачах говорится о
веществах, находящихся при указанных температурах в таких агрегатных
состояниях, которые не соответствуют указанной температуре. Например,
перегретая жидкость – жидкость, находящаяся при температуре выше температуры
кипения (при обычном давлении); переохлаждённая жидкость – жидкость,
находящаяся при температуре ниже температуры замерзания, но остающаяся ещё
жидкостью. Такое возможно в условиях, когда нет центров парообразования или
центров кристаллизации. При малейшем возмущении эти вещества самопроизвольно и
очень быстро переходят в то агрегатное состояние, которое соответствует
указанной температуре. В таких веществах энергия, необходимая для того или
иного процесса, заключена в самом веществе. При решении подобных задач строить
графики нет необходимости.
Задача 12
Колбу , содержащую 120
г перегретой воды при температуре 118°С и нормальном атмосферном
давлении, слегка встряхивают, отчего происходит бурное вскипание воды. Сколько
воды останется в колбе? Теплоёмкостью колбы и теплообменом с окружающей средой
пренебречь.
|
m = 0,12 t1 = 118°С t2 = 100°С с = 4200 Дж/(кг×0С) L = 2,3×106 Дж/кг |
Решение Обозначим: m1 – Q1 = Lm1 – энергия, необходимая для превращения в пар воды массой m1. Этот переход обычно происходит при 100°С. а вся вода Значит, вся вода остывает до 100°С, выделяя при этом теплоту Уравнение теплового баланса: Q1 = Q2 Lm1 = cm(t1 — t2) Þ m1 = m m – m1 = m – m = 0,12(1 — |
|
(m – m1) — ? |
Ответ: В колбе останется 116
г воды.
Задача 13
Пробирку, содержащую 100
г воды, переохлаждённой до температуры —10°С, слегка
встряхивают, отчего вода превращается в лёд с температурой 0°С. Какова масса
образовавшегося льда? Теплоёмкость пробирки мала.
|
m = 0,1 с =4200 Дж/(кг×0С) l = 3,4×105 t1 = —10°С t2 = 0°С |
Решение Вся вода нагревается от —10°С до 0°С, получая энергию Q за |
|
m1 |
Получается, что вся вода нагревается за счет теплоты,
выделяющейся при кристаллизации своей части. Поэтому:
Q = Q1,
cm(t2 — t1)
= lm1,
m1 = 
m1 = .
Ответ: Масса образовавшегося льда равна 12
г.
Задачи для самостоятельного
решения
1.
Для приготовления ванны ёмкостью 100
л смешали холодную воду, имеющую температуру 12°С, и горячую, имеющую
температуру 72°С. Сколько той и другой воды надо взять, чтобы температура воды в ванне
была 36°С?*
2.
Когда в 2
кг воды, находящейся в калориметре при 20°С, опустили алюминиевое тело
массой 0,8 кг, имеющее температуру 100°С, температура воды поднялась до 25°С. Определить
теплоёмкость калориметра.
3.
В 2 кг воды, имеющей температуру 20°С, опустили сначала
медное тело массой 2 кг, имеющее температуру 80°С. После того, как
температура перестала меняться, в воду опустили железное тело массой 3
кг, имеющее температуру —20°С. Какой после этого стала температура воды? Теплоёмкостью сосуда
пренебречь.
4.
После опускания в воду, имеющую температуру 100°С, тела с
температурой 20°С, установилась общая температура 80°С. Какой станет температура
воды, если, не вынимая первого тела, в нее опустить ещё два таких же тела,
имеющих температуру 20°С?
5.
В чайник налили воду при температуре 200С
и поставили на электроплитку. Через 13 минут вода закипела. Через какое время
половина воды выкипит?
6.
Для того, чтобы на спиртовом нагревателе, с КПД
70%, нагреть до кипения 1,4 кг воды и половину ее превратить в пар, израсходовали
100 г спирта. Какова начальная температура воды? Удельная теплота сгорания
спирта 29×106 Дж/кг.
7.
В калориметре находится лёд массой 500
г при температуре 0°С. В калориметр впускают водяной пар температурой 100°С. Сколько воды
окажется в калориметре, когда весь лёд растает, а температура образовавшейся
воды будет равна 0°С?
8.
В калориметр, содержащий 400
г воды и 200 г льда при 0°С, впустили водяной пар с температурой 100°С. Сколько пара было впущено
в калориметр, если в калориметре установилась температура 20°С? Теплоёмкость
калориметра 1000 Дж/0С.
9.
В сосуд теплоёмкостью 1000 Дж/0С,
содержащий 5 кг воды при температуре 20°С, положили лёд, имеющий температуру —40°С. Температура
образовавшейся смеси оказалась равна —2°С. Сколько льда было положено в сосуд?
10.
В алюминиевом калориметре массой 200
г находится кусок льда с температурой —20°С. В калориметр впустили водяной пар, имеющий температуру 100°С. Когда температура
калориметра стала равна 20°С, измерили массу его содержимого. Она оказалась равной 400
г. Найти массу льда, находящегося в калориметре, и массу сконденсировавшегося
пара.
11.
В калориметр, содержащий 3
кг воды при температуре 20°С, опустили 2 кг льда, имеющего температуру —10°С. Что будет в калориметре,
когда теплообмен прекратится? Теплоемкостью калориметра пренебречь.
12.
В калориметр, содержащий 1
кг льда и 800 г воды при 0°С впускают 100 г водяного пара при 100°С. Что будет в калориметре,
когда теплообмен прекратится? Теплоемкостью калориметра пренебречь.
13.
В калориметре находится вода массой 600
г при температуре 5°С. К ней долили ещё 300 г воды с температурой 10°С и положили 600
г льда с температурой —60°С. Что будет в калориметре после того, как теплообмен прекратится?
Теплоемкостью калориметра пренебречь.
14.
В теплоизолированном медном сосуде массой 400
г находятся 2 кг льда при температуре —10°С. В сосуд помещают 400 г водяного пара при температуре 110°С. Что будет в сосуде
после того, как теплообмен прекратится?
15.
В колбе находятся 200
г воды при температуре 0°С. Откачиванием паров всю воду в колбе заморозили. Сколько получилось
льда?
Ответы и решения
1. 60 л холодной и 40
л горячей воды.
|
t2 = 72°С q = 36°С V = 100 |
Решение Q1 = cm1(q — t1) – теплота, которую получит холодная Q2 = c(m — m1)(t2 — q) – теплота, которую отдаст |
|
V1 — V2 |
Q1 = Q2,
cm1(q — t1) = c(m — m1)(t2 — q),
m1(q — t1) + m1(t2 — q) = m(t2 — q),
rV1(q —
t1 + t2 — q) = rV (t2 — q),
V1 = V×
V1 = 100×
V2 = V — V1 = 100 – 60 = 40 (л).
2. 2640 .
|
t1 = 20°С с1=4200 Дж/(кг×0С) m2 = 0,8 t2 = 100°С с2 = 920 Дж/(кг×0С) q = 25°С_______ Ск — ? |
Решение Q2 = Q + Q1, где Q2 – теплота, отданная алюминиевым телом; Q1 – теплота, полученная водой, Q — теплота, полученная c2m2(t2 — q) = (Cк + Cк = Cк = |
3. 190С.
|
m1 = 2 кг c1=4200 Дж/(кг×0С) t1 = 20°С m2 = 2 кг c2 = 380 Дж/(кг×0С) t2 = 80°С m3 = 3 кг c3 = 460 Дж/(кг×0С) t3 = —20°С |
Решение Здесь удобнее пользоваться уравнением Q1 + Q2 + Q3 = 0, c1m1(q q =
|
|
q – ? |
4. 53°С
|
С1– теплоёмкость воды; t1 = 100°С С2– теплоёмкость тела; t2 = 20°С t3 = 80°С |
Решение 1. При опускании в воду с температурой t1 первого тела: С1(t1 — t3) = С2(t3 — t2). (1) 2. При опускании в воду с температурой t2 сразу трех тел: С1(t1 — t4) = 3С2(t4 — t2). (2) 3. Делим уравнение (1) на уравнение (2) и получаем:
Решая это уравнение, находим, что : t4 » 53 °С. |
|
t4 — ? |
5. 44,5 мин.
|
t1 t1 = 20°С t2 = 100°С m2 = m1/2 с = 4200 Дж/(кг×0С) L = 2,3×106 Дж/кг |
|
t2 |
Решение
Мощность электроплитки подразумеваем
постоянной. Поэтому:


откуда:
6. 29°С
 |
|
m1 = 1,4 кг с1=4200 Дж/(кг×0С) t2 = 100°С h = 0,7 m2 = 0,1 кг q = 29×106 |
Решение h = Qполез = Q1 + Q2 = = cm1(t2 — t1) + L Qзатр = qm2. Тогда h = |
|
t1-? |
Выражаем t1: t1 = t2 –
t1 =
100 — 
7. 563
г.
|
m1 = 0,5кг l = 3,4×105 Дж/кг t1 = 0°С с = 4200 Дж/(кг×0С) L = 2,3×106 t2 = 100°С |
Q1 = Q2 + Q3, lm1 = Lm2 + cm2(t2 — t1), m2 = m2 = |
|
m |
= 0,063 (кг) = 63
г
В итоге: m = m1 + m2 = 500 +63 = 563 (г).
8. 65 г
|
m2 = 0,2 кг l = 3,4×105 Дж/кг t1 c =4200Дж/(кг×0С) t2 = 100°С L = 2,3×106 q = 20°С C = 1000 Дж/0С |
РешениеQ1 + Q2 + Q3 = lm2 + c(m1 + m2)(0 — t1) + C(q — t1) = Lm3 + cm3(t2 — q), m3 = |
|
m3 – ? |
9. 27,1 кг.
 |
|
C = 1000 Дж/0С m1 = 5 кг c1=4200 Дж/(кг×0С) t1 = 20°С t2 = —40°С c2=2100 Дж/(кг×0С) l = 3,4×105 Дж/кг q = —2°С |
РешениеQ1 + Q2 + Q3 + Q2 + Q4 = C(t1 — q) – теплота, отданная калориметром; Q1 + Q3 + Q5 = c1m1(t1 — 0) + lm1 + c2m1(0 Q6 = c2m2(q — t2) – теплота, принятая льдом. |
|
m2 – ? |
|
Тогда m2
= 
m2 =

10. 340
г льда и 60 г пара.
|
m1 = 0,2 кг t1 = t2 = —20°С c2=2100 Дж/(кг×0С) t3 = 100°С L = 2,3×106 l = 3,4×105 Дж/кг c3=4200 Дж/(кг×0С) q = 20°С m = 0,4 |
РешениеQ1 + Q2 + Q3 + Q4 = Q6 + Q7. Q2, Q3, Q4 – Q1, Q5 – теплоты, Q6, Q7 – теплоты, отданные c1m1(q — t1) + c2m2(0 — t2) = L(m — m2) Масса льда: |
|
m2 – ? m3 – ? |
m2 =
m2 =

Масса пара: m3 = m – m2 = 0,4 кг – 0,34 кг = 0,06 кг.
11. Смесь, состоящая из 1,4 кг льда и 3,6
кг воды при температуре 00С.
|
m1 = 3 кг t1 = 20°С c1= 4200 m2 = 2 кг t2 = —10°С c2= 2100 Дж/(кг×0С) l = 3,4×105 Дж/кг |
Решение1. Q1 = c1m1(t1 2. Q2 = c2m2(0 — t2) = 2100×2×10 = 42000 (Дж) – нужно льду, чтобы нагреться от –10°С до 0°С. 3. Q3 = lm2 = 340000×2 = 680000 (Дж) – нужно льду, чтобы полностью 4. Q1 — Q2 < Q3 – значит, у воды |
|
m¢1 m¢2 q – ? |
Вывод: лёд растает не весь, и
в калориметре будет находиться смесь воды со льдом при температуре 0°С.
Сколько растает льда?
lm¢ = Q1
— Q2 Þ m¢ = 
Тогда останется льда: m¢2 = m2 — m¢ = 2 кг – 0,6
кг = 1,4 кг.
Масса воды: m¢1 = m1
+ m¢ = 3
кг + 0,6 кг =
3,6 кг
12. 0,2
кг льда и 1,7 кг воды при температуре 00С.
|
m1 = 1 кг m2 = 0,8 кг t1 = t2 = 0°С l = 3,4×105 Дж/кг c = 4200 Дж/(кг×0С) m3 = 0,1 кг t3 = 100°С L = 2,3×106 |
Решение1. Q1 = lm1 = 340000×1 = 340000 (Дж) – нужно льду, чтобы полностью растаять при 00С. 2. Q2 = Lm3 = 2300000×0,1 = 3. Q3 = cm3(t3 — t1) = 4200×0,1×100 = 42000 (Дж) – может отдать пар, остывая от 1000С Поэтому лёд растает не весь, пар весь |
|
q – ? m¢1 m¢2 |
Сколько льда растает?
lm¢ = Q2 + Q3 Þ m¢ = 
В калориметре останется льда: m¢1
= m1
— m¢ = 1 кг – 0,8
кг = 0,2 кг .
Масса воды: m¢2 =
m2
+ m¢ + m3 = (0,8 + 0,8 + 0,1) кг = 1,7 (кг)
Полученная смесь находится при температуре 0°С.
13. Смесь воды (750
г) и льда (750 г) при 00С.
|
m1 = 0,6 кг c1= 4200 Дж/(кг×0С) t1 = 5°С m2 = 0,3 кг t2 = 10°С m3 = 0,6 кг t3 = —600С с2= 2100 Дж/(кг×0С) l = 3,4×105 Дж/кг |
Решение 1. Q1 = c1m1(t1 — 2. Q2 = c1m2(t2 — Q1 3. Q3 = c2m3(0 — t3) = 2100×0,6×60 = 75600 (Дж) – нужно льду, чтобы нагреться от Q3 > Q1 + Q2 Þ вся вода DQ = Q3 |
|
q – ? mводы – ? mльда – ? |
lm¢ = DQ Þ
m¢ = =

Итак, в калориметре будет находиться
смесь воды со льдом при температуре 0°С:
mводы = m1 + m2 — m¢ = 0,6 + 0,3 — 0,15 = 0,75 (кг),
mльда = m3 + m¢ =
0,6 + 0,15 = 0,75 (кг)
14. 2,4
кг воды при температуре 360С.
|
m1 = 0,4 кг c1 = 380 Дж/(кг×0С) m2 = 2 кг c2= 2100 Дж/(кг×0С) t1 = t2 = —10°С l = 3,4×105 Дж/кг m3 = 0,4 кг t3 = 110°С с3= 2100 Дж/(кг×0С) L = 2,3×106 Дж/кг c4= 4200 Дж/(кг×0С) |
Решение 1. Q1 = c1m1(0 — t1) = 380×0,4×10 = 1520 (Дж) – нужно получить медному сосуду, 2. Q2 = c2m2(0 — t1) = 2100×2×10 = 42000 (Дж) – нужно получить льду, чтобы он —10°С 3. Q3 = lm2 = Q1 4. Q4 = c3m3(t3 — 5. Q5 = Lm3 = 2300000×0,4 = |
|
q – ? m – ? |
|
Q4 + Q5 = 8400 + 920000 = 928400 (Дж) – может отдать пар, превращаясь в пар с
температурой 100°С;
DQ = (Q4 + Q5) — (Q1 + Q2 + Q3) = 928400 – 723520 = 204880 (Дж) –
столько энергии останется у пара, когда он станет водой при 1000С,
(лед при этом превратится в воду при 0°С).
Проверим, хватит ли этой энергии,
чтобы вода, образовавшаяся из льда, нагрелась вместе с сосудом от 0°С до 100°С?
Q6 =
(c1m1 + c2m2)(100 — 0) = (380×0,4 + 4200×2)×100 = 855200 (Дж).
Это больше, чем 204880 Дж. Значит,
вода, образовавшаяся из льда, нагреется не до 100°С. Найдем, до какой
температуры нагреются вода и сосуд:
Q1 + Q2 + Q3 + (c1m1
+ c4m2)(q — 0) = Q4 + Q5 + c4m3(100
— q),
c1m1q + c4m2q + c4m3q = c4m3×100 + 204880,
q = 
15. 174
г.
|
l = 3,4×105 Дж/кг L = 2,3×106 |
Решение |
|
m1 — ? |
Q1 = lm1 – энергия,
которая выделяется при замерзании воды массой m1.
Q2 = L(m – m1) – энергия, которая необходима для превращения оставшейся воды в пар.
Q1 = Q2,
lm1
= L(m — m1)
m1 = m×
m1 = (кг) = 0,174 кг = 174 г.
Учебное издание
Самарин Григорий Геннадьевич
Решение задач на теплообмен с использованием уравнения теплового
баланса
(методические рекомендации)
Редактор
– Г. Д. Попырина
Компьютерная
верстка – К. В. Маренин
Подписано
в печать:
Бумага
типографская
Условных
печатных листов – 2,25
Тираж
– 100 экз.
Заказ
–
Цена
договорная.
Лицей естественных наук
610006, г. Киров, ул. Возрождения, 6
Уравнение теплового баланса

4.5
Средняя оценка: 4.5
Всего получено оценок: 89.
4.5
Средняя оценка: 4.5
Всего получено оценок: 89.
Решение задач термодинамики заключается в нахождении неизвестных величин в процессе обмена теплом внутри рассматриваемой системы. Важнейшим этапом решения является составление уравнения теплового баланса. Далее с помощью обычных математических правил находятся неизвестные величины. Рассмотрим порядок построения этого уравнения.
Теплообмен в системе
В соответствии с положениями молекулярно-кинетической теории (МКТ), температура тела – это количественная характеристика энергии молекул тела. Каждая молекула обладает некоторой кинетической энергией, и средняя энергия молекулы пропорциональна температуре ($k$ – постоянная Больцмана):
$$E_{ср}={3over2}kT$$
В равновесном состоянии температура тела во всех точках системы одинакова, и, следовательно, средняя энергия также одинакова. При столкновениях молекулы обмениваются энергией, однако, в среднем, каждая молекула получает от соседних ту же энергию, что и отдает им.
Что произойдет, если система будет образована с телами разной температуры ?
Разная температура тел означает, что молекулы этих тел имеют разную среднюю энергию. При столкновениях молекул более энергичные молекулы горячего тела будут отдавать молекулам холодного тела гораздо больше энергии, чем молекулы холодного тела смогут отдать молекулам горячего. При этом сами молекулы горячего тела, отдавая энергию, теряют скорость (а значит, и температуру), а молекулы холодного тела – скорость увеличивают (а значит, и температуру).
Такой процесс передачи энергии молекул от горячего тела к холодному называется теплообменом.
Уравнение теплового баланса
Поскольку количество молекул пропорционально массе тела, а средняя энергия молекулы пропорциональна температуре, то количество тепла, отданное или принятое телом, пропорционально массе и разности температур до и после обмена:
$$Q thicksim mΔt$$
При этом величина $Δt$ (а значит, и $Q$) будет положительна, если тело нагревается, и отрицательна, если тело охлаждается. Для окончательного нахождения количества тепла, принятого или отданного телом, необходимо ввести коэффициент пропорциональности, физический смысл которого состоит в том, что это количество энергии, необходимое, чтобы нагреть 1кг вещества на 1К. Данный коэффициент называется удельной теплоемкостью, обозначается латинской буквой «c», и имеет размерность в $Дж over кг × К$.
Таким образом, количество тепла, переданное n-му телу, равно:
$$Q_n = c_n m_n Δt_n$$
Поскольку система замкнута, то, согласно Закону сохранения энергии, общее количество энергии в системе остается постоянным. Теплообмен состоит лишь в том, чтобы энергия распределилась по системе равномерно. То есть, сумма количества тепла, переданного или принятого каждым телом в системе равна нулю:
$$Q_1+Q_2+ Q_3+…=0$$
В результате мы получили формулу уравнения теплового баланса. Подставив значения количества тепла, полученное или отданное каждым телом в системе, и решив получившееся уравнение, можно найти неизвестные величины.
Подчеркнем, что система должна быть замкнутой – то есть теплоизолированной от внешнего мира. Обычно изоляция осуществляется с помощью специального теплообменного аппарата – калориметра.
Порядок составления уравнения теплового баланса
Для составления уравнения теплового баланса необходимо рассмотреть все тела в представленной системе. Каждое тело обладает определенной массой $m_n$ и теплоемкостью $c_n$.
Кроме того, в начальный момент каждое тело имело некоторую температуру $t_n$, а в после теплообмена во всей системе установилась новая температура $t_{рез}$. Следовательно, у каждого из тел надо определить разность температур $Δt_n = t_{рез}-t_n$ (эта величина будет положительной для нагреваемых тел, и отрицательной для охлаждаемых).
Подставляя эти три параметра (теплоемкость, массу и разность температур) в формулу количества тепла для каждого тела, получаем выражения для $Q_1$,$Q_2$,$Q_3$…, сумма этих составляющих по Закону сохранения энергии равна нулю. В результате имеем готовое уравнение теплового баланса для данной системы, из которого возможно определение неизвестной величины.
Что мы узнали?
Уравнение теплового баланса следует из закона сохранения энергии. Оно означает, что сумма тепла, полученная нагреваемыми телами равна сумме тепла, отданного охлаждаемыми, общее количество переданного тепла всеми телами равно нулю. Составив уравнение теплового баланса для системы, можно найти неизвестную величину.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.5
Средняя оценка: 4.5
Всего получено оценок: 89.
А какая ваша оценка?
Фазовые переходы — это термодинамические процессы, приводящие к изменению агрегатного состояния вещества.
Плавление и отвердевание
ОпределениеПлавление — переход вещества из твердого состояния в жидкое.
Для расчета количества теплоты, необходимого для процесса плавления, следует применять формулу:
Q=λm
m — масса вещества, λ (Дж/кг) — удельная теплота плавления.
Плавление каждого вещества происходит при определенной температуре, которую называют температурой плавления. Все проводимое тепло идет на разрушение кристаллической решетки, при этом увеличивается потенциальная энергия молекул. Кинетическая энергия остается без изменения и температура в процессе плавления не изменяется.
Удельная теплота плавления показывает, какое количество теплоты необходимо сообщить 1 кг данного вещества, чтобы перевести его из твердого состояния в жидкое при условии, что оно уже нагрето до температуры плавления. В процессе отвердевания 1 кг данной жидкости, охлажденной до температуры отвердевания, выделится такое же количество теплоты.
Внимание! Удельная теплота плавления — табличная величина.
ОпределениеОтвердевание, или кристаллизация — переход состояния из жидкого состояния в твердое (это процесс, обратный плавлению).
Отвердевание происходит при той же температуре, что и плавление. В процессе отвердевания температура также не изменяется. Количество теплоты, выделяемое в процессе отвердевания:
Q=−λm
Парообразование и конденсация
ОпределениеПарообразование, или кипение — переход вещества из жидкого состояния в газообразное.
Количество теплоты, необходимое для процесса кипения, вычисляют по формуле:
Q=rm
m — масса вещества, r (Дж/кг) — удельная теплота парообразования.
Парообразование происходит при определенной температуре, которую называют температурой кипения. В отличие от испарения, процесс парообразования идет со всего объема жидкости. Несмотря на то, что к кипящему веществу подводят тепло, температура не изменяется. Все затраты энергии идут на увеличение промежутком между молекулами. Температура кипения зависит от рода вещества и внешнего атмосферного давления.
Удельная теплота парообразования показывает, какое количество теплоты необходимо затратить, чтобы перевести в пар 1 кг жидкости, нагретой до температуры кипения. Такое же количество теплоты выделится в процессе конденсации 1 кг пара, охлажденного до температуры конденсации.
Внимание! Удельная теплота парообразования — табличная величина.
ОпределениеКонденсация — процесс, обратный кипению. Это переход вещества из газообразного состояния в жидкое.
Конденсация происходит при температуре кипения, которая также не изменяется во время всего процесса. Количество теплоты, выделяемое в процессе конденсации:
Q=−rm
Тепловые процессы при нагревании и охлаждении
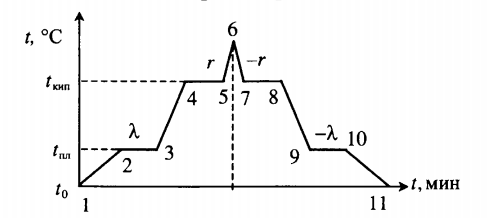
Все фазовые переходы, а также процессы нагревания и остывания вещества можно отобразить графически. Посмотрите на график фазовых переходов вещества:
Он показывает зависимость температуры вещества от времени в процессе его нагревания и остывания. Опишем процессы, отображаемые на графике, в таблице.
| Процесс | Что происходит | Количество выделенной теплоты |
| 1–2 | Нагревание твердого тела |
Q=cтm(tпл−t0) ст — удельная теплоемкость вещества в твердом состоянии. |
| 2–3 | Плавление при температуре плавления (tпл) |
Q=λm |
| 3–4 | Нагревание жидкости |
Q=cжm(tкип−tпл) сж — удельная теплоемкость вещества в жидком состоянии. |
| 4–5 | Кипение при температуре кипения (tкип) |
Q=rm |
| 5–6 | Нагревание пара |
Q=cпm(t−tкип) сп — удельная теплоемкость вещества в газообразном состоянии. |
| 6–7 | Охлаждение пара |
Q=cпm(tкип−t) |
| 7–8 | Кипение при температуре кипения (tкип) |
Q=−rm |
| 8–9 | Охлаждение жидкости |
Q=cжm(tпд−tкип) |
| 9–10 | Отвердевание при температуре плавления (tпл) |
Q=−λm |
| 10–11 | Охлаждение твердого тела |
Q=cтm(t0−tпл) |
Внимание! На участках 2–3 и 9–10 вещество частично находится в жидком и твердом состояниях, а на 4–5 и 7–8 — в жидком и газообразном.
Частные случаи тепловых процессов
| Что происходит | График | Формула количества теплоты |
| Полностью растопили лед, имеющий отрицательную температуру. | 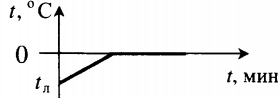 |
Q=cлm(tпл−tл)+λm cл — удельная теплоемкость льда, tл — начальная температура льда. |
| Лед, взятый при отрицательной температуре, превратили в воду при комнатной температуре. | 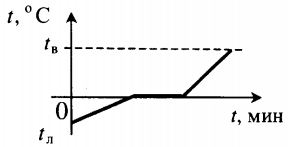 |
Q=cлm(tпл−tл)+λm+cвm(tв−tпл) cв — удельная теплоемкость воды. |
| Взяли лед при температуре 0 оС и полностью испарили. | 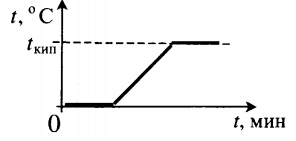 |
Q=λm+cвm(tкип−tпл)+rm |
| Взяли воду при комнатной температуре и половину превратили в пар. | 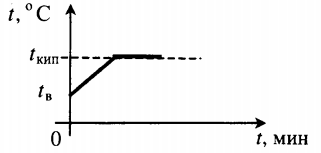 |
Q=cвm(tкип−tв)+rm2 |
Подсказки к задачам
| Единицы измерения | Температуру можно оставлять в градусах Цельсия, так как изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах. |
| Кипяток | Вода, которая при нормальном атмосферном давлении имеет температуру в 100 оС. |
| Объем воды 5 л | m = 5 кг, так как:
m=ρV=103· Внимание! Равенство V (л) = m (кг) справедливо только для воды. |
Пример №1. Какое количество теплоты нужно сообщить льду массой 2 кг, находящемуся при температуре –10 оС, чтобы превратить его в воду и нагреть ее до температуры +30 оС?
Можно выделить три тепловых процесса:
- Нагревание льда до температуры плавления.
- Плавление льда.
- Нагревание воды до указанной температуры.
Поэтому количество теплоты будет равно сумме количеств теплоты для каждого из этих процессов:
Q=Q1+Q2+Q3
Q=cлm(0−t1)+λm+cвm(t2−0)
Удельные теплоемкости и удельную теплоту плавления смотрим в таблицах:
- Удельная теплоемкость льда = 2050 Дж/(кг∙К).
- Удельная теплоемкость воды = 4200 Дж/(кг∙К).
- Удельная теплота плавления льда = 333,5∙103 Дж/кг.
Отсюда:
Q=2050·2(0−(−10))+333,5·103·2+4220·2·30=961200 (дж)=961,2 (кДж)
Уравнение теплового баланса
Суммарное количество теплоты, которое выделяется в теплоизолированной системе равно количеству теплоты (суммарному), которое в этой системе поглощается.
Математически уравнение теплового баланса с учетом знаков количества теплоты записывается так:
Qотд=−Qпол
Отданное количество теплоты меньше нуля (Qотд < 0), а полученное количество теплоты положительно (Qполуч > 0).
Подсказки к задачам на уравнение теплового баланса
| Теплообмен происходит в калориметре | Потерями энергии можно пренебречь. |
| Жидкость нагревают в некотором сосуде | Начальные и конечные температуры жидкости и сосуда совпадают. |
| В жидкость опускают термометр | Через некоторое время он покажет конечную температуру жидкости и термометра. |
| Мокрый снег | Содержит воду и лед при 0 оС. Учтите, что лед плавится, если он находится при температуре 0 оС и получает энергию от более нагретого тела. Вода кристаллизируется при температуре 0 оС, если она отдает энергию более холодному телу. Если лед и вода находятся при температуре 0 оС, то никаких агрегатных переходов между ними не происходит. |
Частные случаи теплообмена
| В воду комнатной температуры бросили ком снега, содержащий некоторое количество воды, после чего установилась некоторая положительная температура. | 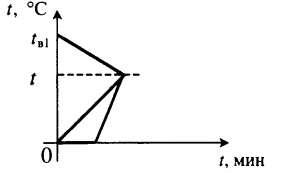
Уравнение теплового баланса: Q1+Q2+Q3=0 cвmв1(t−tв1)+cвmв2(t−0)+λmл+cвmл(t−0)=0 |
| Для получения некоторой положительной температуры воды используют горячую воду и лед, имеющий отрицательную температуру. | 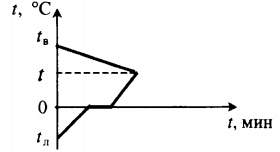
Уравнение теплового баланса: Q1+Q2=0 cвmв(t−tв)+cлmл(0−tл)+λmл+cвmл(t−0)=0 |
| В воду комнатной температуры бросают раскаленное твердое тело, в результате часть воды испаряется. | 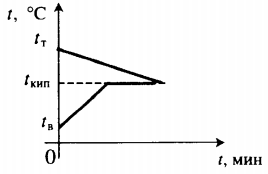
Уравнение теплового баланса: Q1+Q2=0 cтmт(100−tт)+cвmв(100−tв)+rmп=0 |
| Воду комнатной температуры нагревают до кипения, вводя пар при t = 100 оС. | 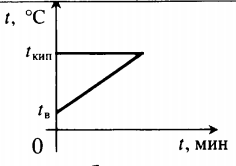
Уравнение теплового баланса: Q1+Q2=0 −rmп+cвmв(100−tв)=0 |
| Лед, имеющий температуру плавления, нагревают до положительной температуры, вводя пар при t = 100 оС. | 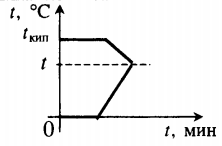
Уравнение теплового баланса: Q1+Q2=0 −rmп+cвmп(t−tкип)+λmл+cвmл(t−tпл)=0 |
Пример №2. В кастрюлю, где находится вода объемом 2 л при температуре 25 оС, долили 3 л кипятка. Какая температура воды установилась?
2 л = 2 кг
3 л = 3 кг
Количество теплоты, отданное кипятком, равно количеству теплоты, принятому более прохладной водой. Поэтому:
cm1(t−t0)=−cm2(t−tкип)
Или:
m1(t−t0)=−m2(t−tкип)
m1t+m2t=m1t0+m2tкип
(m1+m2)t=m1t0+m2tкип
t=m1t0+m2tкипm1+m2
t=2·25+3·1002+3=3505=70 (°C)
Взаимные превращения механической и внутренней энергии
Если в тексте задачи указан процент одного вида энергии, перешедший в другой, то он указывается в виде десятичной дроби перед этой энергией, которой тело обладало вначале.
Частные случаи закона сохранения энергии
| При неупругом ударе о стенку пуля нагрелась |
mv22=cmΔt |
| Тело падает с некоторой высоты и в момент падения нагревается |
mgh=cmΔt |
| В результате того, что пуля пробивает стену, ее скорость уменьшается, 50% выделившейся при этом энергии идет на нагревание пули |
0,5(mv202−mv22)=cmΔt |
| Летящая пуля при ударе о стенку расплавилась. Начальная температура пули меньше температуры плавления |
mv22=cmΔt+λm |
| Капля воды, падая с некоторой высоты, в момент удара испарилась. Температура капли у поверхности земли меньше температуры кипения. На нагрев пошло 60% выделившейся механической энергии |
0,6mgh=cmΔt+rm |
| Вследствие сгорания топлива ракета поднялась на некоторую высоту |
qmтоп=mрgh |
| Вследствие сгорания топлива снаряд приобрел некоторую скорость, и на это было затрачено 25% энергии |
0,25qmтопmсv22 |
Пример №3. Свинцовая дробинка, летящая со скоростью 100 м/с, попадает в доску и входит в нее. 52% кинетической энергии дробинки идет на ее нагревание. На сколько градусов нагрелась дробинка? Удельная теплоемкость свинца 130 Дж/(кг∙К).
Запишем закон сохранения энергии для этого случая:
0,52mv22=cmΔt
Δt=0,52v22c=0,52·10022·130=20 (К)
Примеры КПД
| Устройство | Полезная энергия (работа), затраченная энергия (полная работа) | КПД |
| Электронагреватель, электроплитка, электрочайник, кипятильник. |
Qполезн=cmΔT Иногда: Qполезн=cmΔT+rm Wзатр=Pt (произведение мощности на время) |
η=cmΔTPt100% |
| Газовая горелка, паровая турбина, спиртовка, плавильная печь. |
Qполезн=cmΔT Qзатр=qmтоп |
η=cmΔTqmтоп100% |
| Двигатель автомобиля, самолета. |
Aполезн=Nt=Nsv Qзатр=qmтоп |
η=cmΔTvqmтоп100 |
| Ружье с пороховым зарядом, пушка |
Eполезн=mv22 Qзатр=qmпор |
η=mv22qmпор100 |
Внимание! Если в задаче указано время, в течение которого происходит один тепловой процесс, а спрашивают о времени протекания другого, то считайте, что мощность нагревателя или холодильника постоянна:
Q1t1=Q2t2
Пример №4. Для нагревания на электроплитке некоторого количества воды от 20 до 100 оС потребовалась 21 минута. Сколько времени после этого необходимо для полного испарения воды? Удельная теплоемкость воды 4200 Дж (кг∙К), удельная теплота парообразования 2,24 МДж/кг.
Будем считать, что мощность электроплитки постоянна. Поэтому:
Q1t1=Q2t2
Количество теплоты, сообщенное воде при нагревании:
Q1=сm(t2−t1)
Количество теплоты, которое нужно сообщить, чтобы вода полностью испарилась:
Q1=rm
Отсюда:
сm(t2−t1)t1=rmt2
Задание EF17544
Кусок льда, имеющий температуру 0°С, помещён в калориметр с электронагревателем. Чтобы превратить этот лёд в воду с температурой 12°С, требуется количество теплоты 80 кДж. Какая температура установится внутри калориметра, если лёд получит от нагревателя количество теплоты 60 кДж? Теплоёмкостью калориметра и теплообменом с внешней средой пренебречь.
Ответ:
а) 0°С
б) 4°С
в) 6°С
г) 9°С
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать уравнение теплового баланса для первого случая.
Решение
Запишем исходные данные:
• Начальная температура льда: t0 = 0 oC.
• Конечная температура воды в первом случае: t1 = 12 oC.
• Количество теплоты, выделенное электронагревателем в первом случае: Q1 = 80 кДж.
• Количество теплоты, выделенное электронагревателем во втором случае: Q2 = 60 кДж.
Составим уравнение теплового баланса для первого случая:
Q1=λm+cmt1
Внимание! Вместо разности температур используется значение только конечной температуры, так как начальная температура равна 0.
Найдем массу льда из уравнения теплового баланса для первого случая. Учтем что:
• Удельная теплоемкость воды: c = 4200 Дж/(кг∙К).
• Удельная теплота плавления льда: λ = 333,5 кДж/(кг∙К).
Отсюда:
Чтобы расплавить кусок льда массой 0,5 кг, нужно затратить следующее количество теплоты:
Лед не расплавится весь, так как ему будет сообщено лишь 60 кДж теплоты. Поэтому в калориметре температура будет равна 0 оС.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18791
Внимательно прочитайте текст задания и выберите верный ответ из списка
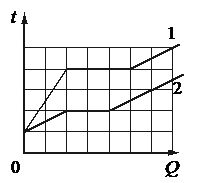
Используя данные графиков, выберите из предложенного перечня два верных утверждения и укажите их номера.
Ответ:
а) Температура плавления первого тела в 1,5 раза больше, чем второго.
б) Тела имеют одинаковую удельную теплоёмкость в твёрдом агрегатном состоянии.
в) Удельная теплоёмкость второго тела в твёрдом агрегатном состоянии
в 3 раза больше, чем первого.
г) Оба тела имеют одинаковую удельную теплоту плавления.
д) Тела имеют одинаковую удельную теплоёмкость в жидком агрегатном состоянии.
Алгоритм решения
- Проанализировать каждое из утверждений.
- Проверить истинность утверждений с помощью графика.
- Выбрать и записать верные утверждения.
Решение
Проверим первое утверждение, согласно которому, температура плавления первого тела в 1,5 раза больше, чем второго.
Если это было бы так, то количество клеток до горизонтального участка графика 1 относилось к количеству клеток до горизонтального участка графика 2 как 3 к 2. Но мы видим, что до 1 графика 4 клетки, до 1 — 2. Следовательно, температура плавления первого тела в 2 раза больше, чем второго.
Первое утверждение неверно.
Проверим второе утверждение, согласно которому тела имеют одинаковую удельную теплоёмкость в твёрдом агрегатном состоянии.
Если бы это было так, то соответствующие участки графиков совпадали бы. Только в таком случае температура тел увеличивалась на одну и ту же температуру при получении одного и того же количества теплоты. Но мы видим, что это не так.
Второе утверждение неверно.
Проверим третье утверждение, согласно которому удельная теплоёмкость второго тела в твёрдом агрегатном состоянии в 3 раза больше, чем первого.
Если это было бы так, то первое тело при сообщении телам одинакового количества теплоты нагревалось бы втрое быстрее второго. И это действительно так, потому что температура второго во время нагревания в твердом состоянии увеличилась только на 1 клетку, в то время как температура первого тела — на 2 клетки.
Третье утверждение верно.
Проверим четвертое утверждение, согласно которому оба тела имеют одинаковую удельную теплоту плавления.
Если это было бы так, то протяженность горизонтальных участков обоих графиков была бы одинаковой. Но это не так. Протяженность этого участка для тела 1 составляет 3 клетки, для тела 2 — 2 клетки.
Четвертое утверждение верно.
Проверим пятое утверждение, согласно которому тела имеют одинаковую удельную теплоёмкость в жидком агрегатном состоянии.
Если бы это было так, то соответствующие участки графиков были параллельными. Только при таком условии при повышении температуры на одно и то же количество градусов тела бы получли одинаковое количество теплоты. И это действительно так.
Пятое утверждение верно.
Вывод: верным утверждения «в» и «д».
Ответ: вд
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22685
В сосуде лежит кусок льда. Температура льда t1 = 0 °C. Если сообщить ему количество теплоты Q = 50 кДж, то 3/4 льда растает. Какое количество теплоты q надо после этого сообщить содержимому сосуда дополнительно, чтобы весь лёд растаял и образовавшаяся вода нагрелась до температуры t2 = 20 °C? Тепловыми потерями на нагрев сосуда пренебречь.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать уравнение теплового баланса.
3.Выполнить решение в общем виде.
4.Определить и вычислить искомую величину.
Решение
Запишем исходные данные:
• Начальная температура льда: t1 = 0 oC.
• Конечная температура воды: t2 = 20 oC.
• Количество теплоты, переданное льду изначально: Q = 50 кДж.
• Удельная теплоемкость воды: c = 4200 Дж/(кг∙К).
• Удельная теплота плавления льда: λ = 333,5 кДж/(кг∙К).
50 кДж = 50000 Дж
333,5 кДж = 333500 Дж
Составим уравнение теплового баланса:
Qобщ=Q+q
где q — количество теплоты, необходимое для того, чтобы окончательно растопить лед и нагреть воду:
q=Q2+Q3
Мы знаем, что изначально было растоплено 3/4 льда. Поэтому:
Q=3λm4
Отсюда масса льда равна:
m=4Q3λ
На растопку оставшегося льда уйдет следующее количество теплоты:
Q2=λm4
На нагревание воды уйдет следующее количество теплоты:
Q3=cmt2
Внимание! Вместо разности температур используется значение только конечной температуры, так как начальная температура равна 0.
Отсюда:
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 13.2k