Физика, 10 класс
Урок №19. Температура. Энергия теплового движения молекул
На уроке рассматриваются понятия: температура и тепловое равновесие; шкалы Цельсия и Кельвина; абсолютная температура как мера средней кинетической энергии теплового движения частиц вещества, зависимость давления от концентрации молекул и температуры.
Глоссарий по теме:
Макроскопические параметры — величины объём V, давление p и температура t, характеризующие состояние макроскопических тел без учёта их молекулярного строения.
Температура характеризует степень нагретости тела (холодное, тёплое, горячее).
Температура (от лат. temperatura — надлежащее смешение, соразмерность, нормальное состояние) — физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы.
Тепловым равновесием называют – такое состояние тел, при котором температура во всех точках системы одинакова.
Тепловым или термодинамическим равновесием, изолированной системы тел, называют состояние, при котором все макроскопические параметры в системе остаются неизменными.
Термометр — это прибор для измерения температуры путём контакта с исследуемым телом. Различают жидкостные, газовые термометры, термопары, термометры сопротивления.
Абсолютная температура Т прямо пропорциональна температуре Θ (тета), выражаемой в энергетических единицах (Дж).
Абсолютный нуль — предельная температура, при которой давление идеального газа обращается в нуль при фиксированном объёме или объём идеального газа стремится к нулю при неизменном давлении.
Абсолютный нуль – температура, при которой прекращается тепловое движение молекул.
Абсолютная шкала температур (Шкала Кельвина) – здесь нулевая температура соответствует абсолютному нулю, а каждая единица температуры равна градусу по шкале Цельсия.
Кельвин — единица абсолютной температуры в Международной системе измерений (СИ).
Постоянная Больцмана – коэффициент
Абсолютная температура есть мера средней кинетической энергии молекул.
Давление газа прямо пропорционально концентрации его молекул и абсолютной температуре Т.
Закон Авогадро – в равных объёмах газов при одинаковых температурах и давлениях содержится одинаковое число молекул
Обязательная литература:
- Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 195 – 203.
Дополнительная литература:
- Смородинский Я.А. Температура. — 3-е издание. — М.: Бюро Квантум, 2007. (Библиотечка «Квант». Вып. 103. Приложение к журналу «Квант» № 5/2007.) С. 5— 25.
- Кирик Л.А., Генденштейн Л.Э., Гельфгат И.М.. Задачи по физике. 10-11 классы для профильной школы. – М.: Илекса, 2010. – С. 111-115.
- Рымкевич А.П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. — С. 65 – 67.
- Орлов В.А., Сауров Ю.А. Практика решения физических задач. 10-11классы. – М.: Вентана-Граф, 2014. – С. 98-99.
- http://kvant.mccme.ru/1991/09/idealnyj_gaz_-_universalnaya_f.htm
Теоретический материал для самостоятельного изучения
Измеряя расположение звёзд на небе, расстояния на земле, время, люди знали, для чего они это делают и изобретали, телескопы, часы, прототипы современных линеек. О температуре такого же сказать было нельзя. О том, что такое тепловое равновесие и что означает степень нагрева тела (температура), существовали разные мнения. Но человек с незапамятных времен точно знал, что, когда два тела плотно соприкасаются, между ними устанавливается, выражаясь современным языком, тепловое равновесие.
Любое макроскопическое тело или группа макроскопических тел при неизменных внешних условиях самопроизвольно переходят в состояние теплового равновесия.
Тепловым равновесием называют такое состояние тел, при котором температура во всех точках системы одинакова.
Температура (от лат. temperatura — надлежащее смешение, соразмерность, нормальное состояние) — физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы.
К числу характеристик состояния макроскопических тел (твёрдых тел, жидкостей, газов) и процессов изменения их состояний, относят объём, давление и температуру. Эти величины описывают в целом тела, состоящие из большого числа молекул, а не отдельные молекулы. При этом микроскопические процессы внутри тела не прекращаются при тепловом равновесии: расположения молекул всё время меняются и меняются их скорости при столкновениях.
Величины объём, давление и температуру, характеризующие состояние макроскопических тел без учёта их молекулярного строения, называют макроскопическими параметрами.
Тепловым или термодинамическим равновесием, изолированной системы тел, называют состояние, при котором все макроскопические параметры в системе остаются неизменными.
Для точной характеристики нагретости тела, необходим прибор, способный измерить температуры тел и дать возможности их сравнения.
Термометр — это прибор для измерения температуры путём контакта с исследуемым телом. Различают жидкостные, газовые термометры, термопары, термометры сопротивления.
В 1597 году Галилей создал термоскоп, в собственных сочинениях учёного нет описания этого прибора, но его ученики засвидетельствовали этот факт. Аппарат представлял собой устройство для поднятия воды при помощи нагревания.
Изобретение термометра, данные которого не зависели бы от перепадов атмосферного давления, произошли благодаря экспериментам физика Э. Торричелли, ученика Галилея.
Во всех приборах, изобретённых в XVIII веке, измерение температуры было относительно расширению столбика воды, спирта или ртути и произвольности выбора начала отсчёта, т.е. нулевой температуры. Наполняющие их вещества замерзали или кипели и этими термометрами нельзя было измерять очень низкие или очень высокие температуры. Необходимо было изобрести такую шкалу, чтобы избавиться от зависимости выбранного вещества, на основе которого формировалось градуирование.
Шкала, предложенная шведским учёным Андерсом Цельсием в 1742 г., точно устанавливала положение двух точек: 0 и 100 градусов. По шкале Цельсия температура обозначается буквой t, измеряется в градусах Цельсия (ºС).
На территории Англии и США используется шкала Фаренгейта. Такая шкала была предложена немецким учёным Даниелем Габриелем Фаренгейтом в 1724 г.: 0 °F — температура смеси снега с нашатырём или поваренною солью, 96 °F —температура здорового человеческого тела, во рту или под мышкой.
Рене Антуан де Реомюр не одобрял применения ртути в термометрах вследствие малого коэффициента расширения ртути. В 1730 году изобрёл водно-спиртовой термометр и предложил шкалу от 0 до 80°.
Шкала Реомюра очень долго использовалась на родине учёного во Франции вплоть до настоящего времени.
Различные жидкости при нагревании расширяются не одинаково. Поэтому расстояния на шкале между нулевой отметкой 0 °C и 100 °C будут разными.
Однако существует способ создать тело, которое приближенно обладает нужными качествами. Это идеальный газ. Было замечено, что в отличие от жидкостей все разряжённые газы – водород, гелий, кислород – расширяются при нагревании одинаково и одинаково меняют своё давление при изменении температуры. Это свойство газов позволяет избавиться в термометрах от одного существенного недостатка шкалы Цельсия – произвольности выбора начала отсчёта, то есть нулевой температуры.
При тепловом равновесии, если давление и объём газа массой m постоянны, то средняя кинетическая энергия молекул газа должна иметь строго определённое значение, как и температура.
Практически такую проверку произвести непосредственно невозможно, но с помощью основного уравнения молекулярно-кинетической теории её можно выразить через макроскопические параметры:




Если кинетическая энергия действительно одинакова для всех газов в состоянии теплового равновесия, то и значение давления р должно быть тоже одинаково для всех газов при постоянном значении отношения объёма к числу молекул. Подтвердить или опровергнуть данное предположение может только опыт.
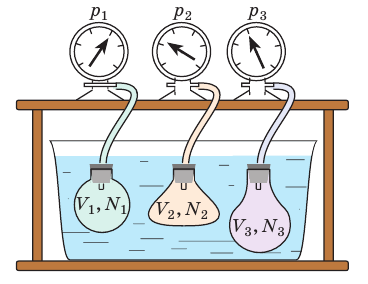
Возьмём несколько сосудов, заполненных различными газами, например, водородом, гелием и кислородом. Сосуды имеют определённые объёмы и снабжены манометрами, для измерения давления газов в сосудах. Массы газов известны, тем самым известно число молекул в каждом сосуде. Приведём газы в состояние теплового равновесия. Для этого поместим их в тающий лёд и подождём, пока не установится тепловое равновесие и давление газов перестанет меняться.
Здесь устанавливается тепловое равновесие и все газы имеют одинаковую температуру 0 °С. При этом показания манометра показывают разное давление р, объёмы сосудов V изначально были разными и число молекул N различно, так как газы, закаченные в баллоны разные. Найдём отношение для водорода всех параметров для одного моля вещества:
Такое значение отношения произведения давления газа на его объём к числу молекул получается для всех газов при температуре тающего льда. Обозначим это отношение через Θ0 (тета нулевое):
Таким образом, предположение, что средняя кинетическая энергия, а также давление р в состоянии теплового равновесия одинаковы для всех газов, если их объёмы и количества вещества одинаковы или если отношение
Если же сосуды с газами поместить в кипящую воду при нормальном атмосферном давлении, то согласно эксперименту, отношение макроскопических параметров будет также одинаковым для всех газов, но значение будет больше предыдущего
Отсюда следует, что величина Θ растёт с повышением температуры и не зависит от других параметром, кроме температуры. Этот опытный факт позволяет рассматривать величину Θ тета как естественную меру температуры и измерять в энергетических единицах — джоулях.
А теперь вместо энергетической температуры введём температуру, которая будет измеряться в градусах. Будем считать величину тета Θ прямо пропорциональной температуре Т, где k- коэффициент пропорциональности
Так как 
По этой формуле вводится температура, которая даже теоретически не может быть отрицательной, так как все величины левой части этого равенства больше или равны нулю. Следовательно, наименьшим значением этой температуры является нуль, при любом другом параметре p, V, N равным нулю.
Предельную температуру, при которой давление идеального газа обращается в нуль при фиксированном объёме или при которой объём идеального газа стремится к нулю при неизменном давлении, называют абсолютным нулём температуры.
Тепловое движение молекул непрерывно и бесконечно, а при абсолютном нуле молекулы поступательно не двигаются. Следовательно, абсолютный нуль температур при наличии молекул вещества не может быть достигнут. Абсолютный нуль температур — это самая низкая температурная граница, верхней не существует, та «наибольшая или последняя степень холода», существование которой предсказывал М.В. Ломоносов.
В 1848 г. английскому физику Вильяму Томсону (лорд Кельвин) удалось построить абсолютную температурную шкалу (её в настоящее время называют шкалой Кельвина), которая имеет две основные точки 0 К (или абсолютный нуль) и 273К, точка в которой вода существует в трёх состояниях (в твёрдом, жидком и газообразном).
Абсолютная температурная шкала — шкала температур, в которой за начало отсчёта принят абсолютный нуль. Температура здесь обозначается буквой T и измеряется в кельвинах (К).
На шкале Цельсия, есть две основные точки: 0°С (точка, в которой тает лёд) и 100°С (кипение воды). Температура, которую определяют по шкале Цельсия, обозначается t. Шкала Цельсия имеет как положительные, так и отрицательные значения.
Из опыта мы определили значения величины Θ (тета) при 0 °С и 100 °С. Обозначим абсолютную температуру при 0 °С через Т1, а при 100 °С через Т2. Тогда согласно формуле:
Отсюда можно вычислить коэффициент k, который связывает температуру в Θ энергетических единицах (Дж) с абсолютной температурой Т (К)
k = 1,38 • 10-23 Дж/К — постоянная Больцмана.
Зная постоянную Больцмана, можно найти значение абсолютного нуля по шкале Цельсия. Для этого найдём сначала значение абсолютной температуры, соответствующее 0°С:

Один кельвин и один градус шкалы Цельсия совпадают. Поэтому любое значение абсолютной температуры Т будет на 273 градуса выше соответствующей температуры t по Цельсию:

Теперь выведем ещё одну зависимость температуры от средней кинетической энергии молекул. Из основного уравнения молекулярно-кинетической теории и уравнения для определения абсолютной температуры

Здесь видно, что левые части этих уравнений равны, значит правые равны тоже.
Средняя кинетическая энергия хаотического поступательного движения молекул газа пропорциональна абсолютной температуре.
Абсолютная температура есть мера средней кинетической энергии движения молекул.
Из выведенных формул мы можем получить выражение, которое показывает зависимость давления газа от концентрации молекул и температуры


Из этой зависимости вытекает, что при одинаковых давлениях и температурах концентрация молекул у всех газов одна и та же. Отсюда следует закон Авогадро, известный нам из курса химии.
Закон Авогадро: в равных объёмах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.
Рассмотрим задачи тренировочного блока урока.
1. При температуре _______ (370C; 2830C; 270C) средняя кинетическая энергия поступательного движения молекул равна 6,21·10-21Дж.
Дано:
k = 1,38 • 10-23 Дж/К — постоянная Больцмана
t -?
Решение:
Запишем значение средней кинетической энергии хаотического поступательного движения молекул с зависимостью от абсолютной температуры:
Отсюда выразим Т:
Соотношение между абсолютной температурой и температурой в градусах Цельсия:
Подставим значение абсолютной температуры:
Правильный вариант ответа:
2. При температуре 290 К и давлении 0,8 МПа, средняя кинетическая энергия молекул равна __________ Дж, а концентрация составляет молекул ___________ м-3.
Дано:
Т = 290К
р = 0,8 МПа =0,8·106 Па
k = 1,38 • 10-23 Дж/К — постоянная Больцмана
Ек -? n — ?
Решение:
Значение средней кинетической энергии хаотического поступательного движения молекул:
Подставив значение абсолютной температуры, найдём ответ:
Определим концентрацию газа из соотношения:
Правильный вариант ответа: 6·10-21; 2·1026 м-3.
Содержание:
Температура:
Перед тем как, например, пойти на пляж, многие интересуются прогнозом погоды. И если ожидается температура воздуха 10 °С, то, скорее всего, планы будут изменены. А стоит ли отказываться от прогулки, если прогнозируется температура 300 К (кельвинов)? И что на самом деле вкладывают физики в понятие «температура»?
Что такое температура
Эксперименты показывают, что макроскопическая система может переходить из одного состояния в другое. Например, если в морозный день занести в комнату шарик, наполненный гелием, то гелий в шарике будет нагреваться и при этом будут изменяться давление, объем и некоторые другие параметры газа. После того как шарик пробудет в комнате некоторое время, изменения прекратятся. Один из постулатов молекулярной физики и термодинамики — его еще называют нулевое начало термодинамики — гласит: любое макроскопическое тело или система тел при неизменных внешних условиях самопроизвольно переходит в термодинамическое равновесное состояние (состояние теплового равновесия), после достижения которого все части системы имеют одинаковую температуру. Нулевое начало термодинамики фактически вводит и определяет понятие температуры.
Температура — физическая величина, характеризующая состояние теплового равновесия макроскопической системы.
Состояние теплового равновесия — это такое состояние макроскопической системы, при котором все макроскопические параметры системы остаются неизменными сколь угодно долго.
В состоянии теплового равновесия все части системы имеют одинаковую температуру; другие макроскопические параметры неизменны, но могут быть разными. Вспомните пример с шариком: после того как установится тепловое равновесие, температура окружающего воздуха и температура гелия в шарике будут одинаковыми, а давление, плотность и объем — разными.
Как работают термометры
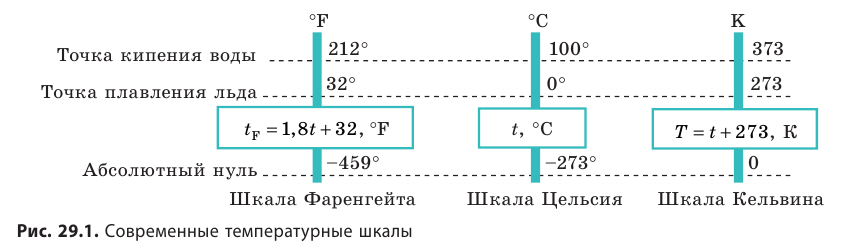
Температура — это физическая величина, и ее можно измерять. Для этого нужно установить шкалу температур. Самые распространенные температурные шкалы — шкалы Цельсия, Кельвина, Фаренгейта (рис. 29.1).
Построение шкалы температур начинается с выбора реперных (опорных) точек, которые должны быть однозначно связаны с какими-либо физическими процессами, которые легко воспроизвести. Например, за нулевую точку температурной шкалы Цельсия принята температура таяния льда при нормальном атмосферном давлении ( t = 0 °С). Температуре кипения воды при нормальном атмосферном давлении приписывают значение t =100 °С. Единица температуры по шкале Цельсия — градус Цельсия: 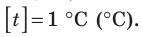
Рис. 29.2. различные виды термометров: а — жидкостный (принцип действия: изменение объема жидкости при изменении температуры); б — термометр сопротивления (изменение электрического сопротивления проводника при изменении температуры); в — биметаллический деформационный (изменение длин двух разных металлических пластин при изменении температуры)
Приборы для измерения температуры — термометры (рис. 29.2). Основные части любого термометра — термометрическое тело (ртуть или спирт в жидкостном термометре, биметаллическая пластина в металлическом деформационном термометре и т. д.) и шкала. Если термометрическое тело привести в контакт с телом, температуру которого нужно измерить, система придет в неравновесное состояние. При переходе в равновесное состояние будут изменяться некоторые параметры термометрического тела (объем, сопротивление и т. п.). Зная, как эти параметры зависят от температуры, определяют температуру тела.
Обратите внимание!
- Термометр фиксирует собственную температуру, равную температуре тела, с которым термометр находится в термодинамическом равновесии.
- Термометрическое тело не должно быть массивным, иначе оно существенно изменит температуру тела, с которым контактирует.
Температура и средняя кинетическая энергия молекул
То, что температура тела должна быть связана с кинетической энергией его молекул, следует из простых соображений. Например, с увеличением температуры увеличивается скорость движения броуновских частиц, ускоряется диффузия, повышается давление газа, а это значит, что молекулы движутся быстрее и их кинетическая энергия становится больше. Можно предположить: если газы находятся в состоянии теплового равновесия, средние кинетические энергии молекул этих газов одинаковы. Но как это доказать, ведь непосредственно измерить эти энергии невозможно?
Обратимся к основному уравнению МКТ идеального газа: 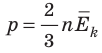
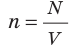
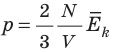
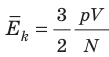
Таким образом, чтобы экспериментально убедиться в равенстве средних кинетических энергий молекул различных газов при одинаковой температуре, нужно измерить объемы (V), давления (p) и массы (m) газов и, зная их молярную массу (M), найти число молекул каждого газа (N) по формуле 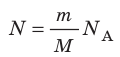
Чтобы обеспечить одинаковую температуру, можно, например, погрузить баллоны с различными газами в сосуд с водой и дождаться состояния теплового равновесия (рис. 29.3).
Рис. 29.3. опыт, позволяющий установить связь между температурой и средней кинетической энергией поступательного движения молекул газа. Газы в сосудах находятся в состоянии теплового равновесия со средой, а следовательно, и друг с другом
Эксперименты показывают, что для всех газов в состоянии теплового равновесия отношение 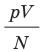
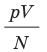
Например, при температуре 0 °С (сосуды с газами погрузили в тающий лед) 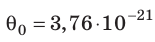
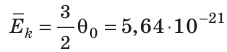
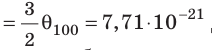
Абсолютная шкала температур
Понятно, что в джоулях представлять температуру неудобно (прежде всего потому, что значения θ очень малы), к тому же неудобно полностью отказываться от шкалы Цельсия. В 1848 г. английский физик Уильям Томсон (лорд Кельвин) (1824–1907) предложил абсолютную шкалу температур (сейчас ее называют шкалой Кельвина).
Температуру Т, измеренную по шкале кельвина, называют абсолютной температурой.
Единица абсолютной температуры — кельвин — основная единица СИ: [T] = 1 К (К).
Шкала Кельвина построена следующим образом:
- изменение температуры по шкале Кельвина равно изменению температуры по шкале Цельсия: ∆ = T t ∆ , то есть цена деления шкалы Кельвина равна цене деления шкалы Цельсия: 1 °С = 1 К; температуры, измеренные по шкалам Кельвина и Цельсия, связаны соотношениями:
- температура по шкале Кельвина связана с величиной
соотношением θ = kT, где k — постоянная Больцмана — коэффициент пропорциональности, не зависящий ни от температуры, ни от состава и количества газа:
- абсолютная температура имеет глубокий физический смысл: средняя кинетическая энергия поступательного движения молекул идеального газа прямо пропорциональна абсолютной температуре:
(1) То есть, если газ охладить до температуры T= 0 К, движение его молекул должно прекратиться (
). Таким образом, нулевая точка шкалы Кельвина — это самая низкая теоретически возможная температура. На самом деле движение молекул не прекращается никогда, поэтому достичь температуры 0 К (–273 °С) невозможно.
Абсолютный нижний предел температуры, при котором движение молекул и атомов должно прекратиться, называют абсолютным нулем температуры. Давление p газа полностью определяется его абсолютной температурой T и концентрацией n молекул газа: p=nkT (2).
Выводы:
- Физическая величина, характеризующая состояние теплового равновесия макроскопической системы, называется температурой. Абсолютный нижний предел температуры, при котором движение молекул и атомов должно прекратиться, называют абсолютным нулем температуры. Шкала, за нулевую точку которой взят абсолютный нуль температуры, называется абсолютной шкалой температур (шкалой Кельвина). Единица абсолютной температуры — кельвин (К) — основная единица СИ. Температуры по шкале Кельвина и Цельсия связаны соотношением: T=t + 273; t=T – 273.
- Средняя кинетическая энергия поступательного движения молекул идеального газа прямо пропорциональна абсолютной температуре, а давление газа определяется абсолютной температурой и концентрацией молекул газа:
— постоянная Больцмана.
- Парообразование и конденсация
- Тепловое равновесие в физике
- Изопроцессы в физике
- Твердые тела и их свойства в физике
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
- Уравнение состояния идеального газа
Абсолютная температура. Температура — мера средней кинетической энергии молекул
- Подробности
- Обновлено 04.10.2018 16:54
- Просмотров: 772
«Физика — 10 класс»
Абсолютная температура.
Вместо температуры Θ, выражаемой в энергетических единицах, введём температуру, выражаемую в привычных для нас градусах.
Будем считать величину Θ прямо пропорциональной температуре Т, измеряемой в градусах:
Θ = kТ, (9.12)
где k — коэффициент пропорциональности.
>Определяемая равенством (9.12) температура называется абсолютной.
Такое название, как мы сейчас увидим, имеет достаточные основания. Учитывая определение (9.12), получим
По этой формуле вводится температурная шкала (в градусах), не зависящая от вещества, используемого для измерения температуры.
Температура, определяемая формулой (9.13), очевидно, не может быть отрицательной, так как все величины, стоящие в левой части этой формулы, заведомо положительны. Следовательно, наименьшим возможным значением температуры Т является значение Т = 0, если давление р или объём V равны нулю.
Предельную температуру, при которой давление идеального газа обращается в нуль при фиксированном объёме или при которой объём идеального газа стремится к нулю при неизменном давлении, называют абсолютным нулём температуры.
Это самая низкая температура в природе, та «наибольшая или последняя степень холода», существование которой предсказывал Ломоносов.
Английский учёный У. Томсон (лорд Кельвин) (1824—1907) ввёл абсолютную шкалу температур. Нулевая температура по абсолютной шкале (её называют также шкалой Кельвина) соответствует абсолютному нулю, а каждая единица температуры по этой шкале равна градусу по шкале Цельсия.
Единица абсолютной температуры в СИ называется кельвином (обозначается буквой К).
Постоянная Больцмана.
Определим коэффициент k в формуле (9.13) так, чтобы изменение температуры на один кельвин (1 К) было равно изменению температуры на один градус по шкале Цельсия (1 °С).
Мы знаем значения величины Θ при 0 °С и 100 °С (см. формулы (9.9) и (9.11)). Обозначим абсолютную температуру при 0 °С через Т1, а при 100 °С через Т2. Тогда согласно формуле (9.12)
Θ100 — Θ0 = k(T2 -T1),
Θ100 — Θ0 = k • 100 K = (5,14 — 3,76) • 10-21 Дж.
Отсюда
Коэффициент
k = 1,38 • 10-23 Дж/К (9.14)
называется постоянной Больцмана в честь Л. Больцмана, одного из основателей молекулярно-кинетической теории газов.
Постоянная Больцмана связывает температуру Θ в энергетических единицах с температурой Т в кельвинах.
Это одна из наиболее важных постоянных в молекулярно-кинетической теории.
Зная постоянную Больцмана, можно найти значение абсолютного нуля по шкале Цельсия. Для этого найдём сначала значение абсолютной температуры, соответствующее 0 °С. Так как при 0 °С kT1 = 3,76 • 10-21 Дж, то
Один кельвин и один градус шкалы Цельсия совпадают. Поэтому любое значение абсолютной температуры Т будет на 273 градуса выше соответствующей температуры t по Цельсию:
Т (К) = (f + 273) (°С). (9.15)
Изменение абсолютной температуры ΔТ равно изменению температуры по шкале Цельсия Δt: ΔТ(К) = Δt (°С).
На рисунке 9.5 для сравнения изображены абсолютная шкала и шкала Цельсия. Абсолютному нулю соответствует температура t = -273 °С.
В США используется шкала Фаренгейта. Точка замерзания воды по этой шкале 32 °F, а точка кипения 212 °Е Пересчёт температуры из шкалы Фаренгейта в шкалу Цельсия производится по формуле t(°C) = 5/9 (t(°F) — 32).
Отметим важнейший факт: абсолютный нуль температуры недостижим!
Температура — мера средней кинетической энергии молекул.
Из основного уравнения молекулярно-кинетической теории (9.8) и определения температуры (9.13) вытекает важнейшее следствие:
абсолютная температура есть мера средней кинетической энергии движения молекул.
Докажем это.
Из уравнений (9.7) и (9.13) следует, что 
Средняя кинетическая энергия хаотичного поступательного движения молекул газа пропорциональна абсолютной температуре.
Чем выше температура, тем быстрее движутся молекулы. Таким образом, выдвинутая ранее догадка о связи температуры со средней скоростью молекул получила надёжное обоснование. Соотношение (9.16) между температурой и средней кинетической энергией поступательного движения молекул установлено для идеальных газов.
Однако оно оказывается справедливым для любых веществ, у которых движение атомов или молекул подчиняется законам механики Ньютона. Оно верно для жидкостей, а также и для твёрдых тел, где атомы могут лишь колебаться возле положений равновесия в узлах кристаллической решётки.
При приближении температуры к абсолютному нулю энергия теплового движения молекул приближается к нулю, т. е. прекращается поступательное тепловое движение молекул.
Зависимость давления газа от концентрации его молекул и температуры. Учитывая, что 
Из формулы (9.17) вытекает, что при одинаковых давлениях и температурах концентрация молекул у всех газов одна и та же.
Отсюда следует закон Авогадро, известный вам из курса химии.
Закон Авогадро:
В равных объёмах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Основные положения МКТ. Тепловые явления — Физика, учебник для 10 класса — Класс!ная физика
Почему тепловые явления изучаются в молекулярной физике —
Основные положения молекулярно-кинетической теории. Размеры молекул —
Примеры решения задач по теме «Основные положения МКТ» —
Броуновское движение —
Силы взаимодействия молекул. Строение газообразных, жидких и твёрдых тел —
Идеальный газ в МКТ. Среднее значение квадрата скорости молекул —
Основное уравнение молекулярно-кинетической теории газов —
Примеры решения задач по теме «Основное уравнение молекулярно-кинетической теории» —
Температура и тепловое равновесие —
Определение температуры. Энергия теплового движения молекул —
Абсолютная температура. Температура — мера средней кинетической энергии молекул —
Измерение скоростей молекул газа —
Примеры решения задач по теме «Энергия теплового движения молекул» —
Уравнение состояния идеального газа —
Примеры решения задач по теме «Уравнение состояния идеального газа» —
Газовые законы —
Примеры решения задач по теме «Газовые законы» —
Примеры решения задач по теме «Определение параметров газа по графикам изопроцессов»
На прошлом уроке мы с вами говорили о температуре и тепловом
равновесии. Давайте вспомним, что температура является характеристикой
состояния теплового равновесия системы, а все тела, входящие в систему, имеют
одинаковую температуру. При этом любое макроскопическое тело (или группа тел)
при неизменных внешних условиях будет самопроизвольно переходить в состояние
теплового равновесия. Пользуясь молекулярно-кинетическими представлениями,
можно дать более наглядное толкование этого состояния. Предположим, что у нас
есть некий сосуд, разделённый перегородкой на две равные части. Пусть в одной
части сосуда находится, например, аргон, а во второй — гелий, температура
которого гораздо больше, чем у аргона. Следовательно, и средняя кинетическая
энергия молекул гелия будет в несколько раз больше (вспомните: чем быстрее
движутся молекулы в веществе, тем больше его температура). Приведём в
соприкосновение наши газы, убрав разделяющую их перегородку. Если бы смогли
наблюдать за процессами, происходящими в сосуде, то увидели бы, как молекулы,
движущиеся с большими скоростями, сталкиваясь с молекулами другого газа,
передают им часть своей энергии, ускоряя их. Сами же они при этом будут
замедляться.
И такая передача энергии будет происходить до тех пор, пока средние
кинетические энергии молекул обоих газов не выровняются. Это и есть состояние
теплового равновесия, при котором переход внутренней энергии от одного газа к
другому прекращается, хотя столкновения беспорядочно движущихся молекул обоих
газов будут продолжаться.
Таким образом, получается, что при соприкосновении двух тел
происходит выравнивание и температур, и средних кинетических энергий молекул. Тогда
естественно предположить, что температура может служить мерой средней
кинетической энергии поступательного движения молекул.
Мы уже с вами знаем, что газ, находящийся в сосуде, будет
создавать давление, значение которого прямо пропорционально средней
кинетической энергии поступательного движения молекул:
В записанной формуле n — это
концентрация молекул, то есть их число в единице объёма:
При этом общее число молекул мы можем легко рассчитать по
формулам для количества вещества:
Перепишем основное уравнение МКТ с учётом наших рассуждений:
И преобразуем его так, как это показано на экране:
Из полученного нами уравнения следует, что при тепловом
равновесии (при условии, что масса газа, его давление и объём постоянны и
известны) средняя кинетическая энергия поступательного движения молекул газа
должна иметь строго определённое значение, как и температура. Но тогда и
значение давления должно быть тоже одинаково для всех газов при постоянном
отношении объёма газа к числу молекул в нём.
Чтобы проверить это предположение, проведём такой опыт.
Возьмём три сосуда известных объёмов (0,3 м3, 0,1 м3, 0,2
м3), снабжённые манометрами. Пусть в каждом сосуде находится по
одному молю разных газов (например, водорода, неона и гелия). Опустим баллоны с
газом в тающий лёд и подождём, пока давление газов перестанет меняться и в
сосудах не установится тепловое равновесие. Теперь все газы имеют одинаковую
температуру 0 оС. При этом давление газов и их объёмы различны.
Давайте найдём отношения произведения давления и объёма газов
к числу их молекул:
Как видим эти отношения одинаковы для всех газов:
Даже если мы увеличим объёмы сосудов в k
раз, то число молекул в них тоже увеличится в k
раз. Однако отношение PV/NA останется
неизменным.
Таким образом, средняя кинетическая энергия поступательного
движения молекул, а также давление в состоянии теплового равновесия одинаковы
для всех газов, если их объёмы и количества вещества одинаковы или если
отношение произведения давления газа на его объём к числу молекул остаётся
неизменным.
Продолжим опыт и поместим наши баллоны с газами в кипящую
воду при нормальном атмосферном давлении. Подождём, пока не установится
тепловое равновесие в сосудах.
И вновь определим отношения произведений давления и объёмов
газов к числу их молекул:
Как видим, наши отношения хоть и увеличились, но они по-прежнему
равны между собой:
Тогда можно утверждать, что величина Θ с ростом
температуры газа увеличивается и ни от чего, кроме температуры, не зависит.
Этот опытный факт позволяет рассматривать эту величину как естественную меру
температуры, как параметр газа, определяемый через другие макроскопические
параметры. В принципе, можно было бы считать температурой и саму величину Θ
и измерять температуру в энергетических единицах, то есть в джоулях. Однако,
во-первых, это неудобно для практического применения. Только представьте: вы
приходите к врачу на приём и после всех процедур он вам говорит: «Да вы,
батенька, больной. У вас же средняя кинетическая энергия поступательного
движения молекул тела равна 6,64 ∙ 10–21 Дж», что
соответствует температуре в 38 оС.
А во-вторых, и это самое важное, уже давно температуру
принято выражать в градусах.
Поэтому нам с вами нужно как-то перейти от температуры,
выражаемой в джоулях, к температуре, выражаемой в привычных нам градусах. Это
сделать достаточно просто. Мы уже с вами показали, что величина Θ зависит
только от температуры, причём, как показали опыты, эта зависимость является
линейной:
Коэффициент пропорциональности, входящий в формулу, является
одной из важных констант в МКТ и носит название постоянной Больцмана, в
честь одного из основателей МКТ Людвига Больцмана. Её значение вы сейчас видите
на экране:
Постоянная Больцмана связывает температуру в
энергетических единицах с температурой в кельвинах.
Теперь можно записать, что отношение произведения давления
газа на его объём к числу молекул прямо пропорционально температуре:
Эта формула позволяет создать температурную шкалу, не
зависящую от рода вещества. Такую шкалу, называемую абсолютной (или
термодинамической) шкалой температур, предложил ещё в 1848 году выдающийся
английский физик Уильям Томсон, удостоенный за работы в области физики в 1892
году титула лорда Кельвина. Поэтому эту шкалу обычно называют шкалой
Кельвина.
Нулевая точка в ней соответствует самой низкой теоретически
возможной температуре, называемой абсолютным нулём температуры. При этой
предельной температуре давление идеального газа обращается в ноль при
фиксированном объёме или стремится к нулю объём газа при постоянном давлении.
Сразу отметим, что такие условия недостижимы.
Единица температуры по абсолютной шкале 1 К является основной
единицей температуры в СИ и совпадает с 1 оС. Поэтому разность
температур по шкале Кельвина и по шкале Цельсия одинакова:
∆T = ∆t.
Зная постоянную Больцмана, можно найти значение абсолютного
нуля по шкале Цельсия. Для этого сначала определим значение абсолютной температуры
для тающего льда, воспользовавшись данными из наших прошлых опытов: …
А так как один кельвин и один градус шкалы Цельсия совпадают,
то любое значение абсолютной температуры будет на 273 градуса выше
соответствующей температуры по Цельсию (а если совсем точно, то на 273,15
градуса).
Следовательно, абсолютному нулю соответствует температура в –273,15
oC.
Мы уже знаем, что молекулы в веществе движутся тем быстрее,
чем выше температура вещества. Следовательно, должна существовать связь между
средней скоростью поступательного движения молекул, а значит, и с их средней
кинетической энергией, и температурой. Чтобы эту связь найти, запишем основное уравнение
МКТ (уравнение Клаузиуса):
А теперь сравним эту формулу с уравнением для абсолютной
температуры:
Таким образом, получается, что абсолютная температура является
мерой средней кинетической энергии поступательного движения молекул.
С учётом этой формулы основное уравнение МКТ можно записать в
виде:
Из уравнения видно, что при одинаковых значениях температуры
и концентрации частиц давления любых газов одинаковы, независимо от того, из
каких частиц они состоят.
Отсюда следует известный вам из курса химии закон
Авогадро: в равных объёмах газов при одинаковых температурах и давлениях
содержится одинаковое число молекул.
Для закрепления материала решим с вами такую задачу. В
баллоне вместимостью 10 л находится газ при температуре 17 оС.
Расходуя газ, из баллона выпустили 1022 молекул. Если через
некоторый промежуток времени температура газа увеличилась до первоначального
значения, то на сколько уменьшилось давление газа в баллоне?
Скачать материал

Скачать материал


- Сейчас обучается 71 человек из 42 регионов


- Сейчас обучается 34 человека из 20 регионов


- Сейчас обучается 110 человек из 46 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Определение температуры. Энергия теплового движения молекул
Федоров А.М. – учитель физики Кюкяйской СОШ Сунтарского улуса Республики Саха -
2 слайд
Газы в состоянии теплового равновесия
Возьмём несколько сосудов, заполненных различными газами, например, водородом, гелием и кислородом. Приведём газы в состояние теплового равновесия при температуре тающего льда. Найдём отношение 𝒑𝑽 𝑵 для водорода:Такое значение отношения 𝒑𝑽 𝑵 получим и для других газов.
-
3 слайд
Определение температуры
Обозначим это отношение через Θ 0 . Тогда:Если же сосуды поместить в кипящую воду при н. а. д., то согласно эксперименту отношение 𝒑𝑽 𝑵 по-прежнему будет одним и тем же для всех газов, но больше, чем предыдущее:
Можно, следовательно утверждать, что величина Θ растёт с повышением температуры. Величину Θ можно рассматривать как естественную меру температуры, как параметр газа. В принципе можно было бы считать температурой и саму величину Θ и измерять температуру в энергетических единицах – джоулях. (Но это неудобно!)
-
4 слайд
Абсолютная температура
Уже давно температуру принято выражать в градусах. Вместо температуры Θ , выражаемой в энергетических единицах, введём температуру, выражаемую в градусах.
Будем считать величину Θ прямо пропорциональной температуре Т, измеряемой в градусах:
Θ = kT,
k- коэффициент пропорциональности. Температура Т – абсолютная температура.𝑝𝑉 𝑁 = kT.
Температура, определяемая этой формулой, не может быть отрицательной.
Предельную температуру, при которой давление идеального газа обращается в нуль при фиксированном объёме или при которой объём идеального газа стремится к нулю при неизменном давлении, называют абсолютным нулём температуры. -
5 слайд
Шкала Кельвина
Английский учёный У. Томсон(лорд Кельвин) ввёл абсолютную шкалу температур. Нулевая температура по абсолютной шкале соответствует абсолютному нулю, а каждая единица температуры по этой шкале равна градусу по шкале Цельсия.
Единица абсолютной температуры в СИ называется кельвином(обозначается буквой К).
Определим коэффициент k в формуле
𝒑𝑽 𝑵 = kT.коэффициент k = 1,38· 10¯²³ Дж/К
называется постоянной Больцмана в честь Л. Больцмана, одного из основателей МКТ газов.
У. Томсон -
6 слайд
Физический смысл постоянной Больцмана
Постоянная Больцмана связывает температуру Θ в энергетических единицах с температурой Т в кельвинах.
Зная k, можно найти значение абсолютного нуля по шкале Цельсия. Для этого найдём значение абсолютной температуры, соответствующее 0°С. Так как при 0°С kT =3,76*10⁻²¹ Дж, то
Т = 3,76∗10⁻²¹ 1,38· 10¯²³ К = 273 К.
Один кельвин и один градус шкалы Цельсия совпадают.
Т(К) = (t + 273) (°C).
Изменение абсолютной температуры ∆Т равно изменению температуры по шкале Цельсия ∆t : ∆Т (K) = ∆t (°C). -
7 слайд
Шкалы температур для сравнения
Абсолютному нулю соответствует температура t = -273°C.
Пример: 1. Температура воды 12°С. Перевести температуру в абсолютную шкалу.
2. Температура газа по абсолютной шкале 300 К. Перевести в шкалу Цельсия.
В США используется шкала Фаренгейта. Точка замерзания воды по этой шкале 32°F, а точка кипения 212°F. Пересчёт температуры из шкалы Фаренгейта в шкалу Цельсия производится по формуле t(°C) =
5/9(t(°F) – 32).
! Абсолютный нуль недостижим! -
8 слайд
Температура – мера средней кинетической энергии молекул
Абсолютная температура есть мера средней кинетической энергии движения молекул.
Из уравнений p = 3 2 kT и 𝑝𝑉 𝑁 = kT следует, что 𝑝𝑉 𝑁 = 2 3 Е . Отсюда вытекает связь между средней кинетической энергией поступательного движения молекулы и температурой:𝑬 = 𝟑 𝟐 kT .
Средняя кинетическая энергия хаотического поступательного движения молекул газа пропорциональна абсолютной температуре.
При приближении к абсолютному нулю энергия теплового движения молекул приближается к нулю, т.е. прекращается поступательное тепловое движение молекул. -
9 слайд
Зависимость давления газа от концентрации его молекул и температуры
Учитывая, что 𝑁 𝑉 = n, получим выражение, показывающее зависимость давления газа от концентрации молекул и температуры:
p = nkT.
При одинаковых давлениях и температурах концентрация молекул у всех газов одна и та же.
Отсюда следует закон Авогадро, известный вам из курса химии.
В равных объёмах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.
В частности, при нормальных условиях, то есть при 0 °C (273,15 К) и 101,325 кПа, объём 1 моля газа равен 22,413 962(13) л. Эту физическую константу называют стандартным молярным объёмом идеального газа и обозначают Vm. -
-
11 слайд
Упражнения
Определить концентрацию молекул однородного газа при температуре 300 К и давлении 1 МПа. Газ считать идеальным.
Решение:2. В сосуде вместимостью V = 10 л находится одноатомный газ, количество вещества которого ν = 2,0 моль и давление p = 6,0 · 105 Па. Определите среднюю кинетическую энергию теплового движения атомов этого газа.
Решение: -
-
13 слайд
Домашнее задание
Как определяют шкалу температур по Цельсию?
Укажите температурный диапазон по шкале Кельвина для вашего города летом и зимой.
Воздух состоит в основном из азота и кислорода. Кинетическая энергия молекул какого газа больше?
Какова температура кипения воды при нормальном атмосферном давлении по абсолютной шкале температур?
Значение температуры по шкале Цельсия, соответствующее абсолютной температуре 20 K, равно: ….
Цинк кипит при температуре 906°С. Чему равна температура кипения цинка при её измерении по шкале Кельвина? -
14 слайд
Использованные ссылки
https://upload.wikimedia.org/wikipedia/commons/thumb/a/a0/Lord_Kelvin_photograph.jpg/274px-Lord_Kelvin_photograph.jpg
https://cdn3.static1-sima-land.com/items/512950/0/1600.jpg?v=1518527847
http://znakka4estva.ru/uploads/category_items/sources/20dae20c2ad7d93b496239e33cc43e95.jpg
http://profil.adu.by/mod/book/view.php?id=3185&chapterid=9210
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 267 013 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-
«Физика (базовый уровень)», Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. / Под ред. Парфентьевой Н.А.
Тема
§ 65. Определение температуры
Больше материалов по этой теме
Другие материалы
- 26.01.2022
- 107
- 0
- 26.01.2022
- 147
- 3

- 26.01.2022
- 130
- 1
- 26.01.2022
- 72
- 0
- 26.01.2022
- 79
- 0


- 26.01.2022
- 153
- 0
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
-
Курс повышения квалификации «Методика написания учебной и научно-исследовательской работы в школе (доклад, реферат, эссе, статья) в процессе реализации метапредметных задач ФГОС ОО»
-
Курс повышения квалификации «Педагогическая риторика в условиях реализации ФГОС»
-
Курс повышения квалификации «Основы местного самоуправления и муниципальной службы»
-
Курс повышения квалификации «Организация научно-исследовательской работы студентов в соответствии с требованиями ФГОС»
-
Курс профессиональной переподготовки «Клиническая психология: организация реабилитационной работы в социальной сфере»
-
Курс профессиональной переподготовки «Клиническая психология: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Логистика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «ЕГЭ по физике: методика решения задач»
-
Курс профессиональной переподготовки «Организация деятельности секретаря руководителя со знанием английского языка»
-
Курс профессиональной переподготовки «Управление сервисами информационных технологий»
-
Курс профессиональной переподготовки «Информационная поддержка бизнес-процессов в организации»
-
Курс профессиональной переподготовки «Стратегическое управление деятельностью по дистанционному информационно-справочному обслуживанию»

































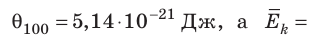
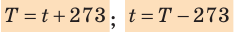
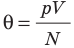 соотношением θ = kT, где k — постоянная Больцмана — коэффициент пропорциональности, не зависящий ни от температуры, ни от состава и количества газа:
соотношением θ = kT, где k — постоянная Больцмана — коэффициент пропорциональности, не зависящий ни от температуры, ни от состава и количества газа: 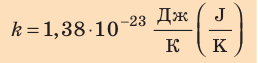
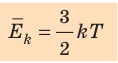 (1) То есть, если газ охладить до температуры T= 0 К, движение его молекул должно прекратиться (
(1) То есть, если газ охладить до температуры T= 0 К, движение его молекул должно прекратиться (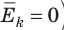 ). Таким образом, нулевая точка шкалы Кельвина — это самая низкая теоретически возможная температура. На самом деле движение молекул не прекращается никогда, поэтому достичь температуры 0 К (–273 °С) невозможно.
). Таким образом, нулевая точка шкалы Кельвина — это самая низкая теоретически возможная температура. На самом деле движение молекул не прекращается никогда, поэтому достичь температуры 0 К (–273 °С) невозможно.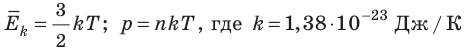 — постоянная Больцмана.
— постоянная Больцмана.



















