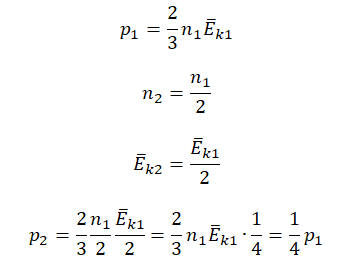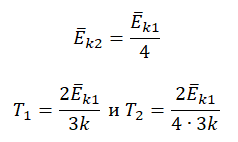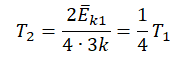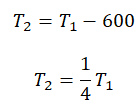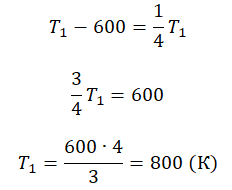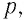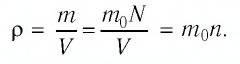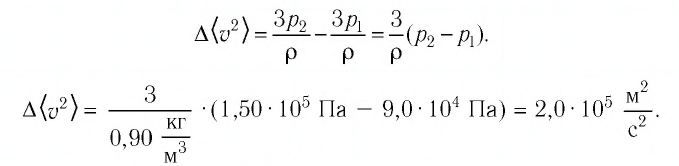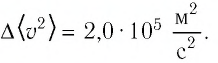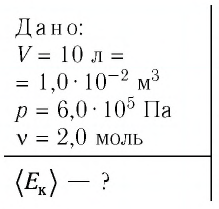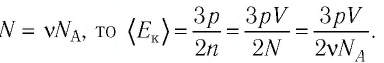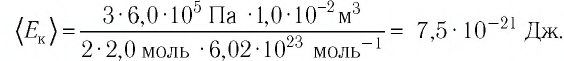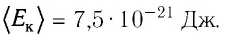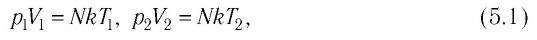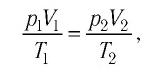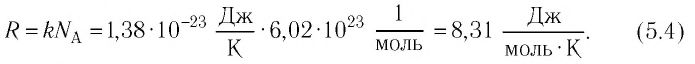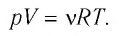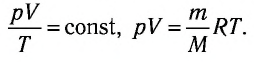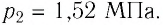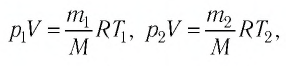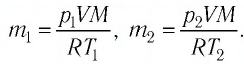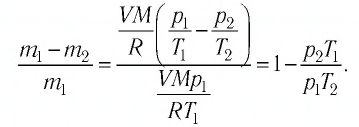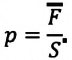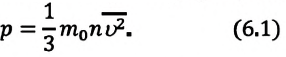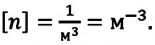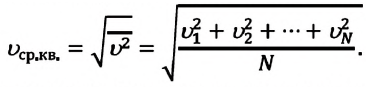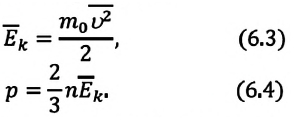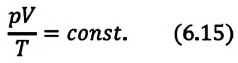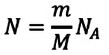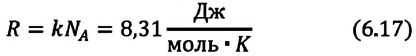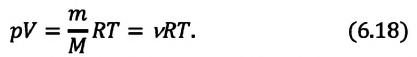Идеальный газ — газ, удовлетворяющий трем условиям:
- Молекулы — материальные точки.
- Потенциальная энергия взаимодействия молекул пренебрежительно мала.
- Столкновения между молекулами являются абсолютно упругими.
Реальный газ с малой плотностью можно считать идеальным газом.
Измерение температуры
Температуру можно измерять по шкале Цельсия и шкале Кельвина. По шкале Цельсия за нуль принимается температура, при которой происходит плавление льда. По шкале Кельвина за нуль принимается абсолютный нуль — температура, при котором давление идеального газа равно нулю, и его объем тоже равен нулю.
Обозначение температуры
- По шкале Цельсия — t. Единица измерения — 1 градус Цельсия (1 oC).
- По шкале Кельвина — T. Единица измерения — 1 Кельвин (1 К).
Цена деления обеих шкал составляет 1 градус. Поэтому изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах:
∆t = ∆T
При решении задач в МКТ используют значения температуры по шкале Кельвина. Если в условиях задачи температура задается в градусах Цельсия, нужно их перевести в Кельвины. Это можно сделать по формуле:
T = t + 273
Если особо важна точность, следует использовать более точную формулу:
T = t + 273,15
Пример №1. Температура воды равна oC. Определить температуру воды в Кельвинах.
T = t + 273 = 2 + 273 = 275 (К)
Основное уравнение МКТ идеального газа
Давление идеального газа обусловлено беспорядочным движением молекул, которые сталкиваются друг с другом и со стенками сосуда. Основное уравнение МКТ идеального газа связывает давление и другие макропараметры (объем, температуру и массу) с микропараметрами (массой молекул, скоростью молекул и кинетической энергией).
Основное уравнение МКТ
Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.
p=23n−Ek
p — давление идеального газа, n — концентрация молекул газа, −Ek — средняя кинетическая энергия поступательного движения молекул.
Выражая физические величины друг через друга, можно получить следующие способы записи основного уравнения МКТ идеального газа:
|
p=13m0n−v2 |
m0— масса одной молекулы газа; n — концентрация молекул газа; −v2 — среднее значение квадрата скорости молекул газа. Среднее значение квадрата скорости не следует путать со среднеквадратичной скоростью v, которая равна корню из среднего значения квадрата скорости: v=√−v2 |
|
p=13ρ−v2 |
ρ — плотность газа |
|
p=nkT |
k — постоянная Больцмана (k = 1,38∙10–3 Дж/кг) T — температура газа по шкале Кельвина |
Пример №2. Во сколько раз уменьшится давление идеального одноатомного газа, если среднюю кинетическую энергию теплового движения молекул и концентрацию уменьшить в 2 раза?
Согласно основному уравнению МКТ идеального газа, давление прямо пропорционально произведению средней кинетической энергии теплового движения молекул и концентрации его молекул. Следовательно, если каждая из этих величин уменьшится в 2 раза, то давление уменьшится в 4 раза:
Следствия из основного уравнения МКТ идеального газа
Через основное уравнение МКТ идеального газа можно выразить скорость движения молекул (частиц газа):
v=√3kTm0=√3RTM
R — универсальная газовая постоянная, равная произведения постоянной Авогадро на постоянную Больцмана:
R=NAk=8,31 Дж/К·моль
Температура — мера кинетической энергии молекул идеального газа:
−Ek=32kT
T=2−Ek3k
Полная энергия поступательного движения молекул газа определяется формулой:
E=N−Ek
Пример №3. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?
Запишем формулу, связывающую температуру со средней кинетической энергией теплового движения молекул, для обоих случаев, с учетом что:
Следовательно:
Составим систему уравнений:
Отсюда:
Задание EF19012

Алгоритм решения
1.Указать, в каких координатах построен график.
2.На основании основного уравнения МКТ идеального газа и уравнения Менделеева — Клапейрона выяснить, как меняются указанные физические величины во время процессов 1–2 и 2–3.
Решение
График построен в координатах (V;Ek). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:
T=2−Ek3
Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.
Запишем уравнение Менделеева — Клапейрона:
pV=νRT
Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:
νR=p1V1T1=p2V2T2
Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.
Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.
Ответ:
• Участок 1–2 — изобарный процесс. Температура увеличивается, давление постоянно.
• Участок 2–3 — изотермический процесс. Температура постоянно, давление увеличивается.
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17560
Первоначальное давление газа в сосуде равнялось р1. Увеличив объём сосуда, концентрацию молекул газа уменьшили в 3 раза, и одновременно в 2 раза увеличили среднюю энергию хаотичного движения молекул газа. В результате этого давление р2 газа в сосуде стало равным
Ответ:
а) 13p1
б) 2p1
в) 23p1
г) 43p1
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для состояний 1 и 2.
4.Выразить искомую величину.
Решение
Исходные данные:
• Начальное давление: p0.
• Начальная концентрация молекул: n1 = 3n.
• Конечная концентрация молекул: n2 = n.
• Начальная средняя энергия хаотичного движения молекул: Ek1 = Ek.
• Конечная средняя энергия хаотичного движения молекул: Ek2 = 2Ek.
Основное уравнение МКТ:
p=23n−Ek
Составим уравнения для начального и конечного состояний:
p1=23n1−Ek1=233n−Ek=2n−Ek
p2=23n2−Ek2=23n2−Ek=43n−Ek
Отсюда:
n−Ek=p12=3p24
p2=4p16=23p1
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18416
Цилиндрический сосуд разделён неподвижной теплоизолирующей перегородкой. В одной части сосуда находится кислород, в другой – водород, концентрации газов одинаковы. Давление кислорода в 2 раза больше давления водорода. Чему равно отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода?
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для обоих газов.
4.Найти отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода.
Решение
Анализируя условия задачи, можно выделить следующие данные:
• Концентрации кислорода и водорода в сосуде равны. Следовательно, n1 = n2 = n.
• Давление кислорода вдвое выше давления водорода. Следовательно, p1 = 2p, а p2 = p.
Запишем основное уравнение идеального газа:
p=23n−Ek
Применим его для обоих газов и получим:
p1=23n1−Ek1 или 2p=23n−Ek1
p2=23n2−Ek2 или p=23n−Ek2
Выразим среднюю кинетическую энергию молекул газа из каждого уравнения:
−Ek1=3pn
−Ek2=3p2n
Поделим уравнения друг на друга и получим:
−Ek1−Ek2=3pn·2n3p=2
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18824
В одном сосуде находится аргон, а в другом – неон. Средние кинетические энергии теплового движения молекул газов одинаковы. Давление аргона в 2 раза больше давления неона. Чему равно отношение концентрации молекул аргона к концентрации молекул неона?
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для обоих газов.
4.Найти отношение концентрации молекул аргона к концентрации молекул неона.
Решение
Анализируя условия задачи, можно выделить следующие данные:
• Средние кинетические энергии теплового движения молекул газов одинаковы. Следовательно, −Ek1=−Ek2=−Ek.
• Давление аргона в 2 раза больше давления неона. Следовательно, p1 = 2p, а p2 = p.
Запишем основное уравнение идеального газа:
p=23n−Ek
Применим его для обоих газов и получим:
p1=23n1−Ek1 или 2p=23n1−Ek
p2=23n2−Ek2 или p=23n2−Ek
Выразим концентрации молекул газа из каждого уравнения:
n1=3p−Ek
n2=3p2−Ek
Поделим уравнения друг на друга и получим:
n1n2=3p−Ek·2−Ek3p=2
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 10.9k
Содержание:
Идеальный газ:
Наиболее простым из всех агрегатных состояний вещества является газообразное. Поэтому изучение свойств веществ начинают с газов. Газ (греч. chaos — хаос) — такое агрегатное состояние вещества, когда составляющие его частицы почти свободно и хаотически движутся между соударениями, во время которых происходит резкое изменение их скорости. Термин «газ» предложил в начале XVII в. нидерландский химик Ян Батист ван Гельмонт (1579— 1644).
Макро- и микропараметры:
При изучении механики в 9-м классе вы познакомились с понятием «состояние механической системы тел». Параметрами этого состояния являются координаты, скорости или импульсы тел. В тепловых процессах основными физическими величинами, характеризующими состояние макроскопических тел без учёта их молекулярного строения, являются давление
Одна из важнейших задач молекулярно-кпнетической теории состоит в установлении связи между макроскопическими и микроскопическими параметрами.
Идеальный газ
Для теоретического объяснения свойств газов используют их упрощённую модель — идеальный газ.
Идеальный газ — модель газа, удовлетворяющая следующим условиям: 1) молекулы газа можно считать материальными точками, которые хаотически движутся; 2) силы взаимодействия между молекулами идеального газа практически отсутствуют (потенциальная энергия их взаимодействия равна нулю); силы действуют только во время столкновений молекул, причём это силы отталкивания.
Поведение молекул идеального газа можно описать, используя законы Ньютона и учитывая, что между соударениями молекулы движутся практически равномерно и прямолинейно.
Модель идеального газа можно использовать в ограниченном диапазоне температур и при достаточно малых давлениях. Так, например, свойства водорода и гелия при нормальном атмосферном давлении и комнатной температуре близки к свойствам идеального газа.
Изучая физику в 7-м классе, вы узнали, что давление газа на стенки сосуда, в котором он находится, как и на любое тело, помещённое внутрь сосуда, создаётся в результате ударов частиц, образующих газ (рис. 14). Вследствие хаотичности их движения усреднённое по времени давление газа в любой части сосуда одинаково, и его можно определить по формуле
Выражение (3.1) называют основным уравнением молекулярно-кинетической теории идеального газа. Это уравнение позволяет рассчитать макроскопический параметр давление р идеального газа через массу 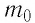
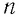
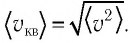
Зависимость давления газа от среднего значения квадрата скорости 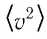
Обозначим через 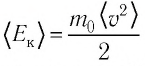
Из выражения (3.2) следует, что давление идеального газа зависит от средней кинетической энергии поступательного движения его молекул и их концентрации.
Пример №1
Баллон электрической лампы наполнен газом, плотность которого 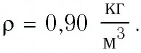
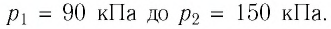
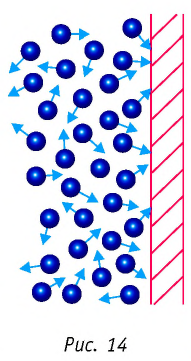
Решение. Покажем, что между плотностью р газа и концентрацией 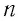
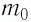
Тогда основное уравнение молекулярно-кинетической теории можно записать в виде: 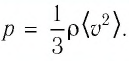
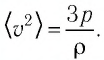
Ответ:
Пример №2
В сосуде вместимостью 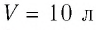
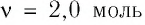
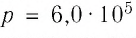
Решение. Из основного уравнения молекулярно-кинетической теории, записанного в виде 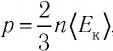
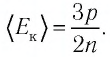
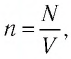
Ответ:
Уравнение состояния идеального газа
Выясним, как связаны между собой макроскопические параметры идеального газа, которые характеризуют его равновесное состояние: давление, масса всего газа, объём, предоставленный ему, и температура.
Состояние макроскопической системы полностью определено, если известны её макроскопические параметры — давление р, масса 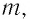
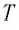
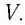
Если при переходе идеального газа из одного состояния в другое число его т
молекул 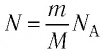
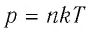
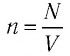
где 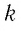
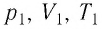
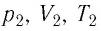
или
При неизменных массе и молярной массе идеального газа отношение произведения его давления и объёма к абсолютной температуре является величиной постоянной.
Уравнение (5.2) связывает два рассматриваемых состояния идеального газа независимо от того, каким образом газ перешёл из одного состояния в другое.
Уравнение состояния в виде (5.2) впервые вывел в 1834 г. французский физик Бенуа Клапейрон (1799—1864), поэтому его называют уравнением Клапейрона.
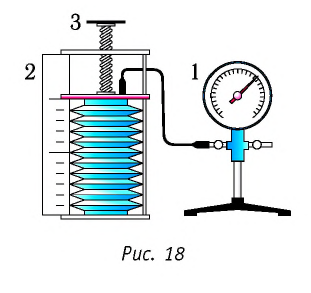
В справедливости уравнения состояния можно убедиться, воспользовавшись установкой, изображённой на рисунке 18. Манометром 1, соединённым с герметичным гофрированным сосудом, регистрируют давление газа внутри сосуда. Объём газа в сосуде можно рассчитать, используя линейку 2. Температура газа в сосуде равна температуре окружающей среды и может быть измерена термометром.
Измерив параметры газа 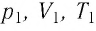
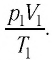
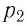
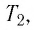
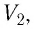
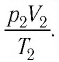
Уравнение состояния (5.2) можно применять для газов при следующих условиях:
- не очень большие давления (пока собственный объём всех молекул газа пренебрежимо мал по сравнению с предоставленным ему объёмом);
- не слишком низкие или же высокие температуры (пока абсолютное значение потенциальной энергии межмолекулярного взаимодействия пренебрежимо мало по сравнению с кинетической энергией теплового движения молекул).
Поскольку число частиц 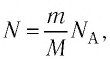
Величину, равную произведению постоянной Больцмана 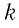
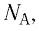
С учётом выражения (5.4) уравнение (5.3) примет вид:
Поскольку количество вещества 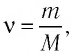
Уравнение состояния в виде (5.5) впервые получил русский учёный Д. И. Менделеев (1834—1907) в 1874 г., поэтому его называют уравнением Клапейрона—Менделеева.
Отметим, что уравнение Клапейрона—Менделеева связывает между собой макроскопические параметры конкретного состояния идеального газа. Используя уравнение Клапейрона-Менделеева, можно описать различные процессы, происходящие в идеальном газе.
Давление смеси газов
В повседневной жизни часто приходится иметь дело не с газом, состоящим из одинаковых молекул, а со смесью нескольких разнородных газов, не вступающих в химические реакции при рассматриваемых условиях. Например, воздух в комнате является смесью азота, кислорода, инертных газов и водорода, а также некоторых других газов.
Вследствие теплового движения частиц каждого газа, входящего в состав газовой смеси, они равномерно распределяются по всему предоставленному смеси объёму. Столкновения частиц обеспечивают в смеси тепловое равновесие.
Каждый газ вносит свой вклад в суммарное давление, производимое газовой смесью, создавая давление, называемое парциальным.
Парциальное давление — давление газа, входящего в состав газовой смеси, если бы он один занимал весь объём, предоставленный смеси, при той же температуре.
Смесь идеальных газов принимают за идеальный газ.
Из истории физики:
Фундаментальные исследования газовых смесей провёл английский учёный Джон Дальтон (1766-1844). Им сформулирован закон независимости парциальных давлений компонентов смеси (1801-1802). В 1802 г. на несколько месяцев раньше французского учёного Жозефа Гей-Люссака (1778-1850) Дальтон установил закон теплового расширения газов, а также ввёл понятие атомного веса.
При постоянных массе и молярной массе отношение произведения давления идеального газа и его объёма к абсолютной температуре является величиной постоянной (уравнение состояния идеального газа):
Парциальное давление — давление газа, входящего в состав газовой смеси, если бы он один занимал весь объём, предоставленный смеси, при той же температуре.
Пример №3
Баллон с газом, давление которого 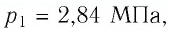
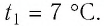
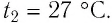
Решение. Если пренебречь тепловым расширением баллона, то его вместимость не изменяется. Запишем уравнение Клапейрона—Менделеева для начального и конечного состоянии газа, считая его идеальным:
откуда
Тогда
Ответ:
Основное уравнение молекулярно-кинетической теории идеального газа
В молекулярной физике изучаются свойства вещества во всех агрегатных состояниях, в том числе и газообразном. В природе почти нет отдельно взятого газа, реальный газ атмосферы представляют собой сложную систему разных газов.
Основная задача молекулярно-кинетической теории — установление связи между макроскопическими и микроскопическими параметрами, характеризующими свойства этой сложной системы. С этой целью реальный газ сложного состава заменяется упрощенной, идеализированной моделью.
Идеальный газ:
Первый шаг в создании любой физической теории состоит в построении идеализированной модели реального объекта. Такая модель всегда имеет упрощенный вид действительности, и с ее помощью изучаются количественные и качественные закономерности и свойства реального объекта с учетом определенных ограничений.
Для изучения свойств газов в молекулярно-кинетической теории применяется идеализированная модель — «идеальный газ».
Идеальный газ — это газ, удовлетворяющий следующим условиям:
- — линейные размеры молекул во много раз меньше расстояний между ними и не принимаются во внимание. Поэтому можно сказать, что молекулы идеального газа не взаимодействуют друг с другом, то есть потенциальная энергия взаимодействия молекул идеального газа равна нулю:
Поэтому идеальный газ можно сколько угодно сжимать; —только при соударении молекул друг с другом или со стенками сосуда между ними возникают силы отталкивания;
- — соударения молекул абсолютно упругие;
- — скорость молекул может иметь произвольные значения, движение каждой молекулы подчиняется законам классической механики.
Свойства идеального газа характеризуются микроскопическими и макроскопическими параметрами и связями между ними.
Микроскопические параметры газа — это параметры, характеризующие движение молекул газа. К ним относятся масса молекулы, его скорость, импульс и кинетическая энергия поступательного движения молекулы.
Макроскопическими являются такие параметры газа, как ее давление, объем и температура, определяющие свойства газа в целом.
Основной задачей молекулярно-кинетической теории является установление взаимной связи между микроскопическими параметрами, характеризующими молекулы газа, и макроскопическими (измеряемыми) величинами, характеризующими газ.
Основное уравнение молекулярно-кинетической теории идеального газа:
Известно, что давление газа возникает в результате многочисленных непрерывных и беспорядочных соударений молекул газа о стенки сосуда, в котором он находится. Это давление равно среднему значению модуля равнодействующей силы, приходящейся на единицу площади:
В 1857 г. немецкий физик Рудольф Клаузиус (1822-1888), используя модель идеального газа, определил уравнение для давления газа, называемое основным уравнением молекулярно-кинетической теории идеального газа.
Основное уравнение молекулярно-кинетической теории идеального газа — это уравнение, связывающее макроскопический параметр газа — его давление, с микроскопическими параметрами, характеризующими молекулы газа:
Где 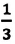
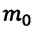
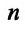
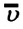
Концентрация молекул — это число молекул в единице объема:
Единица концентрации в СИ:
Средняя квадратичная скорость молекул равна корню квадратному из средней арифметической величины квадратов скоростей отдельных молекул:
Так как среднее значение квадрата скорости молекул связано со средним значением кинетической энергии их поступательного движения, то, следовательно, и давление идеального газа зависит от среднего значения кинетической энергии молекул:
Давление идеального газа прямо пропорционально концентрации молекул и среднему значению кинетической энергии молекул.
Если принять во внимание, что плотность газа 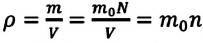
Вы исследовали идеальный газ с позиций MKT и определили связь между его макроскопическими и микроскопическими параметрами.
Уравнение Клапейрона
Связь между тремя макроскопическими параметрами (давление, объем и температура), характеризующими состояние идеального газа, определяет уравнение состояние идеального газа.
Уравнение состояния идеального газа — это уравнение, описывающее состояние газа и устанавливающее связь между параметрами его начального и конечного состояний.
Если число молекул идеального газа остается постоянным, то есть масса и молярная масса не меняются, то при переходе идеального газа из одного состояния в другое, из формул (6.2) и (6.9) имеем для этих состояний:
Где 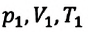
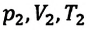
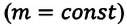
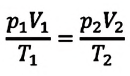
Это уравнение (6.15), характеризующее состояние идеального газа, впервые в 1834 году получил французский физик Бенуа Клапейрон (1799-1864), поэтому его назвали уравнением Клапейрона.
Отношение произведения давления идеального газа данной массы на его объем к абсолютной температуре является постоянной величиной.
Уравнение Менделеева-Клапейрона:
Приняв во внимание формулу, связывающую число частичек вещества, общую массу вещества, молярную массу и число Авогадро,
в формуле (6.14), получим:
Произведение постоянной Больцмана на постоянную Авогадро также является постоянной величиной. Оно называется универсальной газовой постоянной, обозначается буквой 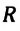
Приняв во внимание выражение (6.17) в (6.16), получаем выражение, характеризующее состояние идеального газа и называемое уравнением Менделеева-Клапейрона.
Физический смысл универсальной газовой постоянной определяется из последнего выражения.
Универсальная газовая постоянная равна отношению произведения давления и объема к абсолютной температуре одного моля любого газа.
Уравнение Менделеева-Клапейрона можно записать и в таком виде:
Где 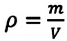
- Уравнение МКТ идеального газа
- Уравнение состояния идеального газа
- Температура в физике
- Парообразование и конденсация
- Зависимость веса тела от вида движения
- Движение тел под воздействием нескольких сил
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
Модель идеального газа в МКТ
Идеальный газ — это теоретическая модель газа, в которой пренебрегают размерами и взаимодействиями частиц газа и учитывают лишь их упругие столкновения.
Другими словами, предполагается, что внутренняя энергия идеального газа определяется лишь кинетической энергией его частиц (т. е. потенциальной энергией взаимодействия молекул пренебрегают).
Модель идеального газа была предложена в 1847 г. Дж. Герапатом. На основе этой модели были теоретически выведены газовые законы (закон Бойля—Мариотта, закон Гей-Люссака, закон Шарля, закон Авогадро), которые ранее были установлены экспериментально. Модель идеального газа была положена в основу молекулярно-кинетической теории газа.
Основными законами идеального газа являются уравнение состояния и закон Авогадро, в которых впервые были связаны макрохарактеристики газа (давление, температура, масса) с массой молекулы (уравнение Менделеева-Клапейрона, или уравнение состояния идеального газа).
В современной физике ее используют также для описания ансамблей любых слабовзаимодействующих частиц. Модель идеального газа справедлива для реальных классических газов при достаточно высоких температурах и разрежениях, когда среднее расстояние между молекулами много больше размеров самих молекул. В этом случае силами притяжения можно пренебречь. Силы же отталкивания проявляются лишь при столкновении друг с другом в течение ничтожно малых интервалов времени.
В простейшей модели газа молекулы рассматриваются как очень маленькие твердые шарики, обладающие массой. Движение отдельных молекул подчиняется законам механики Ньютона. Конечно, не все процессы в разреженных газах можно объяснить с помощью такой модели, однако давление газа вычислить с ее помощью можно.
Основное уравнение МКТ (давление газа)
Основное уравнение молекулярно-кинетической теории устанавливает связь между давлением идеального газа и средней кинетической энергией его молекул.
Вывод основного уравнения МКТ основывается на допущениях модели идеального газа и утверждении: давление газа является результатом ударов молекул о стенку сосуда.
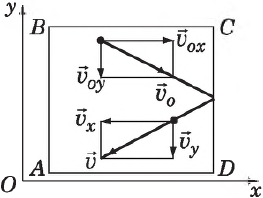
Определим давление газа на стенку площадью $S$ сосуда $ABCD$.
Каждая молекула массой $m_0$, отскакивая от стенки после упругого соударения со стенкой, передает ей импульс $2m_{0}υ_x$, где $υ_x$ — проекция скорости молекулы $υ↖{→}$ на ось $О_х$, перпендикулярную стенке. Всего за одну секунду суммарный импульс, получаемый стенкой от всех молекул, равен $2m_{0}υ_{x}Z$, где $Z$ — число таких столкновений (за $1$ с) всех молекул. Очевидно, что $Z=n={N}/{V}$, где $n$ — концентрация молекул в единице объема; $N$ — число всех молекул. Число $Z$ пропорционально также скорости молекул $υ_x$ и площади стенки $S:Z∼nυ_{x}S$. Поскольку все направления при хаотичном движении молекул газа равновероятны, то из всех молекул, имеющих составляющую скорости $υ_x$, только половина движется в сторону стенки $CD$ вторая половина — в сторону $АВ$ (т. е. в обратную). Поэтому $Z={1}/{2}nυ_{x}S$, а полный импульс, переданный стенке за $1$ с, равен $2m_{0}nυ_x^{2}S$. Поскольку изменение импульса точки (тела) за единицу времени равно действующей на него силе $F={∆(mυ)}/{∆t}$, то $F=m_{0}nυ_x^{2}S$. В действительности, поскольку речь идет о большом количестве молекул, движущихся с разными скоростями, силу следует усреднить: $F↖{-}={m_{0}nυ_x^{2}S}↖{-}$.
Сила эта зависит, таким образом, от среднего квадрата скорости ${υ_x^{2}}↖{-}$.
Поскольку вследствие хаотичности движения все направления равноправны, то
${υ_x^{2}}↖{-}={υ_y^{2}}↖{-}={υ_z^{2}}↖{-}$
С другой стороны, известно, что квадрат модуля любого вектора равен сумме квадратов его проекций на оси координат, поэтому:
$υ^2=υ_x^{2}+υ_y^{2}+υ_z^{2}$
Усредняя это выражение по всем молекулам и учитывая $υ^2=υ_x^{2}+υ_y^{2}+υ_z^{2}$, получим:
${υ^2}↖{-}={υ_x^{2}}↖{-}+{υ_y^{2}}↖{-}+{υ_z^{2}}↖{-}=3{υ_x^{2}}↖{-}$
Отсюда:
${υ_x^{2}}↖{-}={1}/{3}{υ_^2}↖{-}$
С учетом последней формулы $F↖{-}={1}/{3}m_{0}n{υ^2}↖{-}$
Следовательно, давление на стенку сосуда равно:
$p={F}/{S}={1}/{3}m_{0}n{υ^2}↖{-}$
Это основное уравнение молекулярно-кинетической теории. Это уравнение — первое количественное соотношение, полученное в МКТ.
Уравнение $p={F}/{S}={1}/{3}m_{0}n{υ^2}↖{-}$ позволяет получить связь между давлением и средней кинетической энергией молекул ${E_k}↖{-}={m_{0}{υ^2}↖{-}}/{2}:$
$p={2}/{3}n{E_k}↖{-}$
Давление идеального газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.
Важно подчеркнуть, что здесь речь идет о средней кинетической энергии молекул газа. Это означает, что давление газа — величина, органически связанная с тем, что газ состоит из большого числа молекул. Нет смысла говорить о давлении, создаваемом несколькими молекулами. Давление газа — понятие, имеющее статистический характер (так называют понятия, имеющие смысл только для систем с очень большим числом частиц).
Абсолютная температура
Согласно основному уравнению МКТ, давление $р$ прямо пропорционально средней кинетической энергии $E↖{-}$ поступательного движения молекул:
$p={2}/{3}n{E}↖{-}$
где $n$ — объемная концентрация молекул. Заменив в $p={2}/{3}n{E}↖{-}$ $n$ отношением числа молекул $N$ к объему газа $V(n={N}/{V})$, получим:
${pV}/{N}={2}/{3}{E}↖{-}$
В состоянии теплового равновесия при постоянном объеме средняя кинетическая энергия данной массы газа должна иметь вполне определенное значение, как и температура. Согласно формуле ${pV}/{N}={2}/{3}{E}↖{-}$, это означает, что отношение ${pV}/{N}$ для данной температуры должно быть одним и тем же для любых идеальных газов. То, что это действительно так, было подтверждено экспериментально для разных газов, находящихся в условиях теплового равновесия при постоянном объеме (измерялось давление).
Таким образом, величина $Θ={pV}/{N}$, которую, в отличие от микропараметра ${E}↖{-}$, легко измерить, является вполне однозначной характеристикой теплового состояния газа, как и температура. Измеряется $Θ$ (как и энергия) в джоулях. Зависит она только от температуры и может рассматриваться как естественная мера температуры. Однако в силу укоренившейся привычки измерять температуру в градусах был введен коэффициент пропорциональности $k$ между температурой $Θ$, выраженной в энергетических единицах, и температурой $Т$, выраженной в градусах:
$Θ=kT$
или
${pV}/{N}=kT$
Температура $Т$, определяемая равенством $Θ=kT$, называется абсолютной температурой.
Значения температуры, определенной по формуле ${pV}/{N}={2}/{3}{E}↖{-}$, всегда положительны в силу положительности $Θ={pV}/{N}$ (ни давление, ни объем, ни число частиц отрицательными быть не могут). Поэтому минимальным значением температуры является нуль. Температура может равняться нулю, если давление либо объем равны нулю. Из принятого определения температуры следует, что нулем температуры является температура, при которой прекращается хаотическое движение молекул. Она называется абсолютным нулем температуры.
Температура, как и давление, определяется средней кинетической энергией молекул идеального газа. Поэтому температура, как и давление, является статистической величиной (статистической называется величина, имеющая смысл только для систем, содержащих очень большое число частиц). Нельзя говорить о температуре одной или нескольких молекул.
Абсолютную шкалу температур ввел английский ученый У. Кельвин в 1850 г. Нулевая температура по абсолютной шкале (ее называют также шкалой Кельвина) соответствует абсолютному нулю, а каждая единица температуры по этой шкале равна градусу по шкале Цельсия.
Единица абсолютной температуры является одной из семи основных единиц СИ и измеряется в кельвинах (обозначается буквой $К$).
Связь между температурами, измеренными по шкалам Цельсия $t$ и Кельвина $Т$, описывается формулой:
$T(K)=t(°C)+273.15K$
Абсолютный нуль равен $-273.15°$С. Как правило, при расчетах пользуются округленным значением абсолютного нуля ($-273°$С).
Коэффициент пропорциональности к в формуле $Θ=kT$ называется постоянной Больцмана в честь Л. Больцмана — одного из основателей молекулярно-кинетической теории газа. Этот коэффициент составляет $k=1.38^{-23}$ Дж/К.
Постоянная Больцмана связывает температуру $Θ$ в энергетических единицах с температурой $Т$ в кельвинах. Это одна из наиболее важных постоянных в молекулярно-кинетической теории.
Температура как мера кинетической энергии
Из основного уравнения молекулярно-кинетической теории, записанного в форме $p={2}/{3}{E}↖{-}$
${pv}/{N}={2}/{3}{E}↖{-}$
и определения абсолютной температуры согласно ${pV}/{N}=kt$
${pv}/{N}=kT$
получим:
$E↖{-}={3}/{2}kT$
Средняя кинетическая энергия хаотического поступательного движения молекул газа пропорциональна абсолютной температуре.
Из полученного результата однозначно следует, что абсолютная температура есть мера средней кинетической энергии движения молекул.
Соотношение между температурой и кинетической энергией справедливо не только для разреженных газов (идеальных газов), но также для любых тел, подчиняющихся законам механики Ньютона. Оно справедливо и для жидкостей, и для твердых тел, атомы которых колеблются около положения равновесия.
Уравнение $р = nkТ$
Из формулы $p={2}/{3}n{E_k}↖{-}$ может быть получена зависимость давления газа от абсолютной температуры $Т$ и концентрации его молекул, если воспользоваться выражением для средней кинетической энергии:
$p=nkT$
где $k$ — постоянная Больцмана.
Из формулы $p=nkT$ очевидно, что при одинаковых давлениях и температурах концентрация молекул у всех газов одинакова.
Отсюда следует известный закон Авогадро: в равных объемах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.
Средняя скорость теплового движения молекул может быть также выражена через абсолютную температуру, если в формуле $E↖{-}={3}/{2}kT$ заменить $E↖{-}$ на ${m_{0}{υ^2}↖{-}}/{2}$:
${m_{0}{υ^2}↖{-}}/{2}={3}/{2}kT→{υ^2}↖{-}=3{kT}/{m_0}$
Квадратный корень из этой величины называется средней квадратичной скоростью:
$υ↖{-}=√{{3kT}/{m_0}}$
Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа)
Уравнение состояния идеального газа — это зависимость между параметрами идеального газа — давлением $р$, объемом $V$ и абсолютной температурой $Т$, определяющими его состояние:
$pV=BT$
где $В$ зависит от массы газа $m$ и его молекулярной массы $М$. В таком виде уравнения впервые получено в 1834 г. французским ученым Б. П. Э. Клапейроном и называется уравнением Клапейрона.
В 1874 г. Д. И. Менделеев вывел уравнение состояния для одного моля идеального газа: $pV=RT$, где $R$ — универсальная газовая постоянная. Если молярная масса газа $М$, то
$pV={m}/{M}RT$
Уравнение состояния в форме $pV={m}/{M}RT$ называется уравнением Клапейрона-Менделеева. Оно объединяет газовые законы Гей-Люссака, Бойля—Мариотта, Авогадро, Шарля.
Уравнение состояния $pV={m}/{M}RT$ может быть получено из зависимости давления от температуры $p=nkT$, если в нее подставить концентрацию молекул $n$ из выражения
$n={N}/{V}={1}/{V}·{m}/{M}N_A$
где $N_А$ — постоянная Авогадро, $N$ — число молекул в теле.
В результате получим:
$pV={m}/{M}kN_{A}T$
где $kN_A=R$ — универсальная газовая постоянная, равная $8.31$ Дж/моль$·$К; $k$ — постоянная Больцмана, равная $1.38·10^{-23}$ Дж/К. Заменив в $pV={m}/{M}kN_{A}T$ $kN_A$ на $R$, получаем уравнение состояния в виде $pV={m}/{M}RT$. Отношение уравнений $pV={m}/{M}RT$ или $pV=BT$ при двух наборах параметров $p_1,V_1,T_1$ и $p_2,V_2,T_2$ дает:
${p_1V_1}/{T_1}={p_2V_2}/{T_2}=const$
Внутренняя энергия идеального одноатомного газа
Поскольку молекулы идеального газа не взаимодействуют друг с другом, их потенциальная энергия считается равной нулю. Внутренняя энергия идеального газа определяется только кинетической энергией беспорядочного поступательного движения его молекул. Для ее вычисления нужно умножить среднюю кинетическую энергию одного атома $E↖{-}={3}/{2}kT$ на число атомов $N={m}/{M}N_A$.
Учитывая, что $kN_A=R$, получим значение внутренней энергии идеального газа:
$U={3}/{2}·{m}/{M}RT$
Внутренняя энергия идеального одноатомного газа прямо пропорциональна его температуре.
Если воспользоваться уравнением Клапейрона-Менделеева, то выражение для внутренней энергии идеального газа можно представить в виде:
$U={3}/{2}pV$
Следует отметить, что, согласно выражению для средней кинетической энергии одного атома $(E↖{-}={3}/{2}kT)$ и в силу хаотичности движения, на каждое из трех возможных направлении движения или каждую степень свободы по оси $X,Y$ и $Z$ приходится одинаковая энергия ${kT}/{2}$.
Число степеней свободы — это число возможных независимых направлений движения молекулы.
Газ, каждая молекула которого состоит из двух атомов, называется двухатомным. Каждый атом может двигаться по трем направлениям, поэтому общее число возможных направлений движения — $6$. За счет связи между молекулами число степеней свободы уменьшается на одну, поэтому число степеней свободы для двухатомной молекулы равно пяти.
Средняя кинетическая энергия двухатомной молекулы равна ${5}/{2}kT$. Соответственно внутренняя энергия идеального двухатомного газа равна:
$U={5}/{2}·{m}/{M}RT={5}/{2}pV$
Формулы для внутренней энергии идеального газа можно обобщить:
$U={i}/{2}·{m}/{M}RT={i}/{2}pV$
где $i$ — число степеней свободы молекул газа ($i = 3$ для одноатомного и $i=5$ для двухатомного газа).
Для идеальных газов внутренняя энергия зависит только от одного макроскопического параметра — температуры и не зависит от объема, т. к. потенциальная энергия равна нулю (объем определяет среднее расстояние между молекулами).
Для реальных газов потенциальная энергия не равна нулю. Поэтому внутренняя энергия в термодинамике в общем случае однозначно определяется параметрами, характеризующими состояние этих тел: объемом ($V$) и температурой ($Т$).
Закон Дальтона
Закон Дальтона для смеси идеальных газов гласит: давление смеси газов равно сумме парциальных давлений ее компонент.
Парциальным давлением какого-либо газа — компонента газовой смеси называется давление, которое оказывал бы этот газ, если бы он один занимал весь объем, занимаемый смесью.
Для доказательства закона Дальтона перепишем уравнение $p=nkT$ в виде:
$pV=NkT$
Рассмотрим сосуд объемом $V$, в котором имеется смесь нереагирующих химически газов, находящихся в состоянии теплового равновесия. Уравнение состояния для такой смеси имеет вид:
$pV=(N_{1}+N_{2}+N_{3}+…)kT$
где $N_{1},N_{2},N_{3}…$ — числа компонент смеси.
Очевидно, что
$N_{1},N_{2},N_{3}+…=N$
где $N$ — общее число молекул в сосуде.
Давление смеси газа получим, поделив обе части $pV=(N_{1}+N_{2}+N_{3}+…)kT$ на объем $V$:
$p={N_1}/{V}kT+{N_2}/{V}kT+{N_3}/{V}kT+…$
Слагаемые этой суммы представляют собой давления каждой из компонент смеси, занимающей объем $V$, т. е. являются парциальными давлениями компонент смеси $р_1 р_2, р_3, …$ что и утверждает закон Дальтона:
$p=р_1+р_2+р_3+…$
То, что каждая группа молекул оказывает давление, не зависящее от давления, оказываемого другими группами, обусловлено отсутствием взаимодействия между молекулами. Последнее реально выполняется только для газов при невысоких давлениях, которые приближаются к идеальному газу.
Уравнение состояния идеального газа
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: модель идеального газа, связь между давлением и средней кинетической энергией теплового движения молекул идеального газа, связь температуры газа со средней кинетической энергией его частиц, уравнение  , уравнение Менделеева—Клапейрона.
, уравнение Менделеева—Клапейрона.
Из трёх агрегатных состояний вещества наиболее простым для изучения является газообразное. В достаточно разреженных газах расстояния между молекулами намного больше размеров самих молекул (тогда как в жидкостях и твёрдых телах молекулы «упакованы» весьма плотно).Поэтому силы взаимодействия между молекулами таких газов очень малы.
Для описания разреженных газов в физике используется модель идеального газа. В рамках этой модели делаются следующие допущения.
1. Пренебрегаем размерами молекул. Иными словами, молекулы газа считаются материальными точками.
2. Пренебрегаем взаимодействием молекул на расстоянии.
3. Соударения молекул друг с другом и со стенками сосуда считаем абсолютно упругими.
Таким образом, идеальный газ — это газ, частицы которого являются не взаимодействующими на расстоянии материальными точками и испытывают абсолютно упругие соударения друг с другом и со стенками сосуда.
Средняя кинетическая энергия частиц газа
Оказывается, что ключевую роль в описании идеального газа играет средняя кинетическая энергия его частиц.
Частицы газа двигаются с разными скоростями. Пусть в газе содержится частиц, скорости которых равны
. Масса каждой частицы равна
. Кинетические энергии частиц:
Средняя кинетическая энергия частиц газа это среднее арифметическое их кинетических энергий:
Последний множитель — это средний квадрат скорости, обозначаемый просто :
Тогда формула для средней кинетической энергии приобретает привычный вид:
(1)
Корень из среднего квадрата скорости называется средней квадратической скоростью:
Основное уравнение МКТ идеального газа
Cвязь между давлением газа и средней кинетической энергией его частиц называется основным уравнением молекулярно-кинетической теории идеального газа. Эта связь выводится из законов механики и имеет вид:
(2)
где — концентрация газа (число частиц в единице объёма). С учётом (1) имеем также:
(3)
Что такое ? Произведение массы частицы на число частиц в единице объёма даёт массу единицы объёма, то есть плотность:
. Получаем третью разновидность основного уравнения:
(4)
Энергия частиц и температура газа
Можно показать, что при установлении теплового равновесия между двумя газами выравниваются средние кинетические энергии их частиц. Но мы знаем, что при этом становятся равны и температуры газов. Следовательно, температура газа — это мера средней кинетической энергии его частиц.
Собственно, ничто не мешает попросту отождествить эти величины и сказать, что температура газа — это средняя кинетическая энергия его молекул. В продвинутых курсах теоретической физики так и поступают. Определённая таким образом температура измеряется в энергетических единицах — джоулях.
Но для практических задач удобнее иметь дело с привычными кельвинами. Связь средней кинетической энергии частиц и абсолютной температуры газа даётся формулой:
(5)
где Дж/К — постоянная Больцмана.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Уравнение состояния идеального газа» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
В прошлой заметке я рассказывал о том, какие вопросы возникали у меня при чтении книжек о физике (в частности — книги Айзека Азимова «Understanding Physics»). Вот те из них, которые возникли у меня при чтении разделов, касающихся газов, температуры, теплоты и термодинамики:
- Что такое температура
- Уравнение состояния идеального газа
- 2-е начало термодинамики и что такое энтропия
Здесь обсужу первые два, последний оставлю для отдельной заметки.
Что такое температура
Первое, от чего принято отталкиваться, давая определение понятия «температура», — это субъективное ощущение «тепло, холодно», которое возникает у нас, когда мы прикасаемся к тому или иному предмету. Второе: существует корреляция между субъективным ощущением человека и измеримыми свойствами различных тел. Причем, насколько я понимаю, таким свойством, которое используется для определения меры нагретости тела является главным образом объем. Тела при нагревании расширяются, то есть тело становясь субъективно более «горячим» увеличивается в размерах, и это увеличение можно считать объективной мерой нагретости тела. Далее мы постулируем, что тела, которые находятся в тепловом контакте друг с другом (т. е. могут обмениваться теплом) достаточно долгое время, имеют одинаковую степень нагретости — т. е. находятся в тепловом равновесии. И оказывается, что если нагревать два тела, находящиеся в тепловом равновесии друг с другом и состоящие из разных веществ, то отношение приращений их размеров будет одинаковым независимо от степени их нагретости (абсолютные величины этих приращений будут разными). Это позволяет ввести физическую величину, которую называют температурой, и сказать, что расширение тел пропорционально ее изменению. Соответствующий коэффициент пропорциональности называется коэффициентом теплового расширения. Таким образом, любое тело можно использовать в качестве термометра: каждому значению объема тела можно приписать определенное значение температуры. Однако на объем тела может влиять не только степень его нагретости, но и, например, давление. Значит давление (и какие-то другие параметры, влияющие на объем тела) надо зафиксировать, и тогда тело можно использовать в качестве термометра. Итак, определение температуры: температура тела — это то, что измеряет термометр, находящийся в тепловом равновесии с телом. Причем, если термометр находится в тепловом равновесии одновременно с телом A и с телом B, то тело A находится в тепловом равновесии с телом B. Последнее утверждение называется нулевым началом термодинамики.
Физический смысл изменения температуры более или менее ясен, но не столь ясен смысл ее абсолютного значения. Существуют разные температурные шкалы, например, Цельсия и Фаренгейта. Градуировка этих шкал выбиралась их авторами произвольно. Например, Цельсий выбрал в качестве нулевой температуры точку замерзания воды при атмосферном давлении, а в качестве температуры 100 градусов — точку кипения воды опять же при атмосферном давлении. Фаренгейт в качестве нуля температуры выбрал точку замерзания раствора, состоящего из воды, льда и хлорида аммония (-17.8 градусов Цельсия), а в качестве 100 градусов — примерную температуру человеческого тела (37.8 градусов Цельсия).
И последнее: молекулярно-кинетическая теория устанавливает, что средняя кинетическая энергия поступательного движения молекул идеального газа прямо пропорциональна температуре, и коэффициент пропорциональности является константой. Т. е. можно сказать, что температура идеального газа — это мера средней кинетической энергии поступательного движения молекул идеального газа.
Уравнение состояния идеального газа
Уравнение состояния идеального газа получено из обобщения трех экспериментальных закономерностей. Все эти закономерности, как я подозреваю, можно получить при помощи одного и того же устройства — J-образной трубки, закрытой с одного конца и открытой с другого (см. рис. 1). В закрытом конце трубки заперт газ. Газ заперт при помощи столба ртути. Давление газа, если измерять его в мм. рт. ст., равно разности высот столбиков ртути в закрытом и открытом концах плюс атмосферное давление, равное как известно 750 мм. рт. ст. Перепад высот столбика ртути можно регулировать, изменяя таким образом давление и/или объем газа. И наконец, газ можно нагревать, т. е. изменять его температуру.
Закон Бойля-Мариотта
Английский физик Роберт Бойль в 1662 г. установил, что объем газа обратно пропорционален его давлению. Бойль изменял давление газа при помощи столба ртути (рис. 1). Французский физик Эдм Мариотт в 1676 г. независимо от Бойля открыл ту же закономерность, однако особо отметил тот факт, что температура в таком эксперименте должна быть постоянной.
Закон Шарля (2-й закон Гей-Люссака)
Француз Жак Шарль в 1787 г., по его собственному утверждению, установил, что при постоянном давлении изменение объема газа прямо пропорционально изменению его температуры. Однако он не опубликовал этот результат. В 1802 г. ту же закономерность установил Жозеф Гей-Люссак. Причем было замечено, что температура, при которой объем газа должен был бы стать нулевым соответствует -273 градусам Цельсия. В 1848 г. англичанин Уильям Томсон (который позднее стал лордом Кельвином) предположил, что температура -273 градуса Цельсия является минимальной возможной температурой.
Закон Гей-Люссака
Между 1800 и 1802 гг. Жозеф Гей-Люссак установил, что при постоянном объеме изменение давления газа прямо пропорционально изменению его температуры.
Гипотеза Авогадро
Из трех газовых законов следует, что PV~T. Очевидно также, что произведение PV пропорционально количеству газа. Но в чем выражается это количество? Итальянский ученый Амедео Авогадро в 1811 г. предположил, при одинаковом давлении и температуре равные объемы разных газов содержат равное число молекул. Это предположение называется гипотезой Авогадро и из нее следует, что коэффициент пропорциональности в выражении PV~T зависит только от числа молекул в исследуемом объеме газа. Но как это проверить? Нельзя же взять и подсчитать число молекул. Можно воспользоваться тем, что если взять количество граммов вещества, численно равное относительной относительной молекулярной массе вещества (это количество называется моль), то мы получим одно и то же число молекул независимо от вещества. Таким образом, если гипотеза Авогадро верна, то при одинаковых давлении и температуре равные объемы газа будут весить пропорционально их относительным молекулярным массам. Однако, чтобы это проверить, надо знать относительные молекулярные массы различных веществ, и эту проблему решали в XIX веке химики, о чем можно прочитать в еще одной книге Айзека Азимова — Краткая история химии. Развитие идей и представлений в химии.
Уравнение состояния идеального газа вместе с тремя газовыми законами представлено на рис. 2. Здесь NA — число Авогадро (число молекул в одном моле вещества), R — универсальная газовая постоянная, k — постоянная Больцмана, n — число молей в объеме газа.
Молекулярно-кинетическая теория
В 1860-х гг. Джеймс Клерк Максвелл и Людвиг Больцман развили теорию — молекулярно-кинетическую теорию — которая позволила интерпретировать температуру как меру средней кинетической энергии поступательного движения молекул газа. Соответствующие математические выкладки представлены на рис. 3. Интересно, что температура почему-то отражает энергию именно поступательного движения молекул газа, и не отражает энергию их вращательного и/или колебательного движения.