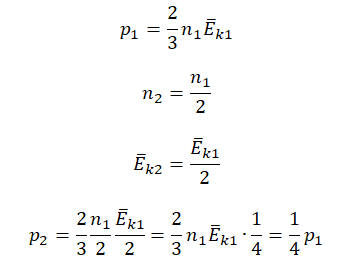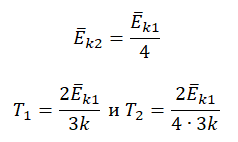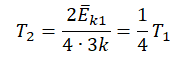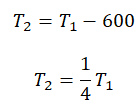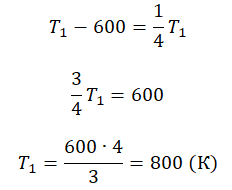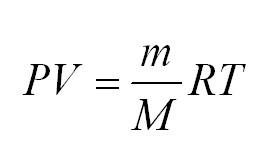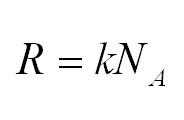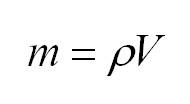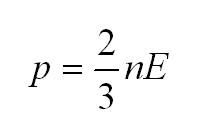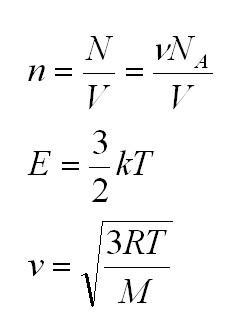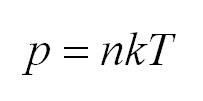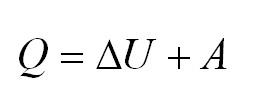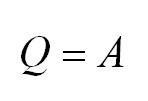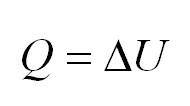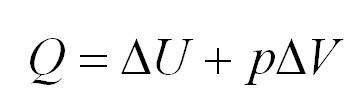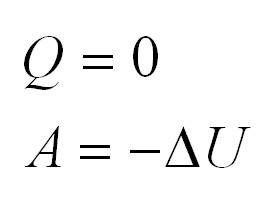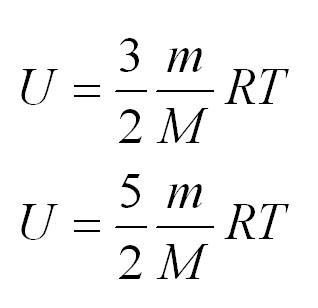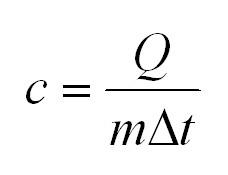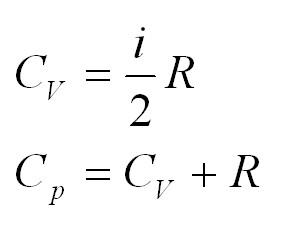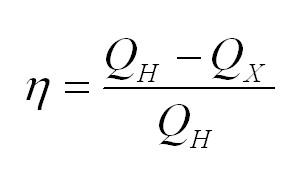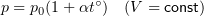Как найти температуру в молекулярной физике формула

Определение

Идеальный газ — газ, удовлетворяющий трем условиям:

• Молекулы — материальные точки.
• Потенциальная энергия взаимодействия молекул пренебрежительно мала.
• Столкновения между молекулами являются абсолютно упругими.

Реальный газ с малой плотностью можно считать идеальным газом.

Измерение температуры

Температуру можно измерять по шкале Цельсия и шкале Кельвина. По шкале Цельсия за нуль принимается температура, при которой происходит плавление льда. По шкале Кельвина за нуль принимается абсолютный нуль — температура, при котором давление идеального газа равно нулю, и его объем тоже равен нулю.

Обозначение температуры

1. По шкале Цельсия — t. Единица измерения — 1 градус Цельсия (1 ^oC).
2. По шкале Кельвина — T. Единица измерения — 1 Кельвин (1 К).

Цена деления обеих шкал составляет 1 градус. Поэтому изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах:

∆t = ∆T

При решении задач в МКТ используют значения температуры по шкале Кельвина. Если в условиях задачи температура задается в градусах Цельсия, нужно их перевести в Кельвины. Это можно сделать по формуле:

T = t + 273

Если особо важна точность, следует использовать более точную формулу:

T = t + 273,15

Пример №1. Температура воды равна ^oC. Определить температуру воды в Кельвинах.

T = t + 273 = 2 + 273 = 275 (К)

Основное уравнение МКТ идеального газа

Давление идеального газа обусловлено беспорядочным движением молекул, которые сталкиваются друг с другом и со стенками сосуда. Основное уравнение МКТ идеального газа связывает давление и другие макропараметры (объем, температуру и массу) с микропараметрами (массой молекул, скоростью молекул и кинетической энергией).

Основное уравнение МКТ

Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

p=23n−Ek

p — давление идеального газа, n — концентрация молекул газа, −Ek — средняя кинетическая энергия поступательного движения молекул.

Выражая физические величины друг через друга, можно получить следующие способы записи основного уравнения МКТ идеального газа:

p=13m0n−v2	m0— масса одной молекулы газа; n — концентрация молекул газа; −v2 — среднее значение квадрата скорости молекул газа. Среднее значение квадрата скорости не следует путать со среднеквадратичной скоростью v, которая равна корню из среднего значения квадрата скорости: v=√−v2
p=13ρ−v2	ρ — плотность газа
p=nkT	k — постоянная Больцмана (k = 1,38∙10–3 Дж/кг) T — температура газа по шкале Кельвина

Пример №2. Во сколько раз уменьшится давление идеального одноатомного газа, если среднюю кинетическую энергию теплового движения молекул и концентрацию уменьшить в 2 раза?

Согласно основному уравнению МКТ идеального газа, давление прямо пропорционально произведению средней кинетической энергии теплового движения молекул и концентрации его молекул. Следовательно, если каждая из этих величин уменьшится в 2 раза, то давление уменьшится в 4 раза:

Следствия из основного уравнения МКТ идеального газа

Через основное уравнение МКТ идеального газа можно выразить скорость движения молекул (частиц газа):

v=√3kTm0=√3RTM

R — универсальная газовая постоянная, равная произведения постоянной Авогадро на постоянную Больцмана:

R=NAk=8,31 Дж/К·моль

Температура — мера кинетической энергии молекул идеального газа:

−Ek=32kT

T=2−Ek3k

Полная энергия поступательного движения молекул газа определяется формулой:

E=N−Ek

Пример №3. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?

Запишем формулу, связывающую температуру со средней кинетической энергией теплового движения молекул, для обоих случаев, с учетом что:

Следовательно:

Составим систему уравнений:

Отсюда:

Задание EF19012

На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

---

Алгоритм решения

1.Указать, в каких координатах построен график.

2.На основании основного уравнения МКТ идеального газа и уравнения Менделеева — Клапейрона выяснить, как меняются указанные физические величины во время процессов 1–2 и 2–3.

Решение

График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

T=2−Ek3

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

pV=νRT

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

νR=p1V1T1=p2V2T2

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

Ответ:

• Участок 1–2 — изобарный процесс. Температура увеличивается, давление постоянно.

• Участок 2–3 — изотермический процесс. Температура постоянно, давление увеличивается.

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17560

Первоначальное давление газа в сосуде равнялось р₁. Увеличив объём сосуда, концентрацию молекул газа уменьшили в 3 раза, и одновременно в 2 раза увеличили среднюю энергию хаотичного движения молекул газа. В результате этого давление р₂ газа в сосуде стало равным

Ответ:

а) 13p1

б) 2p1

в) 23p1

г) 43p1

---

Алгоритм решения

1.Записать исходные данные.

2.Записать основное уравнение МКТ идеального газа.

3.Составить уравнения для состояний 1 и 2.

4.Выразить искомую величину.

Решение

Исходные данные:

• Начальное давление: p₀.

• Начальная концентрация молекул: n₁ = 3n.

• Конечная концентрация молекул: n₂ = n.

• Начальная средняя энергия хаотичного движения молекул: E_k1 = E_k.

• Конечная средняя энергия хаотичного движения молекул: E_k2 = 2E_k.

Основное уравнение МКТ:

p=23n−Ek

Составим уравнения для начального и конечного состояний:

p1=23n1−Ek1=233n−Ek=2n−Ek

p2=23n2−Ek2=23n2−Ek=43n−Ek

Отсюда:

n−Ek=p12=3p24

p2=4p16=23p1

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18416

Цилиндрический сосуд разделён неподвижной теплоизолирующей перегородкой. В одной части сосуда находится кислород, в другой – водород, концентрации газов одинаковы. Давление кислорода в 2 раза больше давления водорода. Чему равно отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода?

---

Алгоритм решения

1.Записать исходные данные.

2.Записать основное уравнение МКТ идеального газа.

3.Составить уравнения для обоих газов.

4.Найти отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода.

Решение

Анализируя условия задачи, можно выделить следующие данные:

• Концентрации кислорода и водорода в сосуде равны. Следовательно, n₁ = n₂ = n.

• Давление кислорода вдвое выше давления водорода. Следовательно, p₁ = 2p, а p₂ = p.

Запишем основное уравнение идеального газа:

p=23n−Ek

Применим его для обоих газов и получим:

p1=23n1−Ek1 или 2p=23n−Ek1 

p2=23n2−Ek2 или p=23n−Ek2 

Выразим среднюю кинетическую энергию молекул газа из каждого уравнения:

−Ek1=3pn

−Ek2=3p2n

Поделим уравнения друг на друга и получим:

−Ek1−Ek2=3pn·2n3p=2

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18824

В одном сосуде находится аргон, а в другом – неон. Средние кинетические энергии теплового движения молекул газов одинаковы. Давление аргона в 2 раза больше давления неона. Чему равно отношение концентрации молекул аргона к концентрации молекул неона?

---

Алгоритм решения

1.Записать исходные данные.

2.Записать основное уравнение МКТ идеального газа.

3.Составить уравнения для обоих газов.

4.Найти отношение концентрации молекул аргона к концентрации молекул неона.

Решение

Анализируя условия задачи, можно выделить следующие данные:

• Средние кинетические энергии теплового движения молекул газов одинаковы. Следовательно, −Ek1=−Ek2=−Ek.

• Давление аргона в 2 раза больше давления неона. Следовательно, p₁ = 2p, а p₂ = p.

Запишем основное уравнение идеального газа:

p=23n−Ek

Применим его для обоих газов и получим:

p1=23n1−Ek1 или 2p=23n1−Ek 

p2=23n2−Ek2 или p=23n2−Ek 

Выразим концентрации молекул газа из каждого уравнения:

n1=3p−Ek

n2=3p2−Ek

Поделим уравнения друг на друга и получим:

n1n2=3p−Ek·2−Ek3p=2

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 11k

Основные формулы термодинамики и молекулярной физики, которые вам пригодятся. Еще один отличный день для практических занятий по физике. Сегодня мы соберем вместе формулы, которые чаще всего используются при решении задач в термодинамике и молекулярной физике.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Итак, поехали. Попытаемся изложить законы и формулы термодинамики кратко.

Идеальный газ

Идеальный газ – это идеализация, как и материальная точка. Молекулы такого газа являются материальными точками, а соударения молекул – абсолютно упругие. Взаимодействием же молекул на расстоянии пренебрегаем. В задачах по термодинамике реальные газы часто принимаются за идеальные. Так гораздо легче жить, и не нужно иметь дела с массой новых членов в уравнениях.

Итак, что происходит с молекулами идеального газа? Да, они движутся! И резонно спросить, с какой скоростью? Конечно, помимо скорости молекул нас интересует еще и общее состояние нашего газа. Какое давление P он оказывает на стенки сосуда, какой объем V занимает, какая у него температура T.

Для того, чтобы узнать все это, есть уравнение состояния идеального газа, или уравнение Клапейрона-Менделеева

Здесь m – масса газа, M – его молекулярная масса (находим по таблице Менделеева), R – универсальная газовая постоянная, равная 8,3144598(48) Дж/(моль*кг).

Универсальная газовая постоянная может быть выражена через другие константы (постоянная Больцмана и число Авогадро)

Массу, в свою очередь, можно вычислить, как произведение плотности и объема.

Основное уравнение молекулярно-кинетической теории (МКТ)

Как мы уже говорили, молекулы газа движутся, причем, чем выше температура – тем быстрее. Существует связь между давлением газа и средней кинетической энергией E его частиц. Эта связь называется основным уравнением молекулярно-кинетической теории и имеет вид:

Здесь n – концентрация молекул (отношение их количества к объему), E – средняя кинетическая энергия. Найти их, а также среднюю квадратичную скорость молекул можно, соответственно, по формулам:

Подставим энергию в первое уравнение, и получим еще один вид основного уравнения МКТ

Первое начало термодинамики. Формулы для изопроцессов

Напомним Вам, что первый закон термодинамики гласит: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа U и на совершение газом работы A. Формула первого закона термодинамики записывается так:

Как известно, с газом что-то происходит, мы можем сжать его, можем нагреть. В данном случае нас интересуют такие процессы, которые протекают при одном постоянном параметре. Рассмотрим, как выглядит первое начало термодинамики в каждом из них.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы. 

Изотермический процесс протекает при постоянной температуре. Тут работает закон Бойля-Мариотта: в изотермическом процессе давление газа обратно пропорционально его объёму. В изотермическом процессе:

Изохорный процесс протекает при постоянном объеме. Для этого процесса характерен закон Шарля: При постоянном объеме давление прямо пропорционально температуре. В изохорном процессе все тепло, подведенное к газу, идет на изменение его внутренней энергии.

Изобарный процесс идет при постоянном давлении. Закон Гей-Люссака гласит, что при постоянном давлении газа его объём прямо пропорционален температуре. При изобарном процессе тепло идет как на изменение внутренней энергии, так и на совершение газом работы.

Адиабатный процесс. Адиабатный процесс – это такой процесс, который проходит без теплообмена с окружающей средой. Это значит, что формула первого закона термодинамики для адиабатного процесса выглядит так:

Внутренняя энергия одноатомного и двухатомного идеального газа

Теплоемкость

Удельная теплоемкость равна количеству теплоты, которое необходимо для нагревания одного килограмма вещества на один градус Цельсия.

Помимо удельной теплоемкости, есть молярная теплоемкость (количество теплоты, необходимое для нагревания одного моля вещества на один градус) при постоянном объеме, и молярная теплоемкость при постоянном давлении. В формулах ниже, i – число степеней свободы молекул газа. Для одноатомного газа i=3, для двухатомного – 5.

Тепловые машины. Формула КПД в термодинамике

Тепловая машина, в простейшем случае, состоит из нагревателя, холодильника и рабочего тела. Нагреватель сообщает тепло рабочему телу, оно совершает работу, затем охлаждается холодильником, и все повторяется вновь. Типичным примером тепловой машины является двигатель внутреннего сгорания.

Коэффициент полезного действия тепловой машины вычисляется по формуле

Вот мы и собрали основные формулы термодинамики, которые пригодятся в решении задач. Конечно, это не все все формулы из темы термодинамика, но их знание действительно может сослужить хорошую службу. А если возникнут вопросы  – помните о студенческом сервисе, специалисты которого готовы в любой момент прийти на выручку.

Молекулярная физика Основные формулы

1. Основы молекулярно-кинетической теории. Газовые законы

1.1 Количество вещества

m — масса;

μ — молярная масса вещества;

N — число молекул;

N_A = 6,02·10²³ моль^-1 — число Авогадро

1.2 Основное уравнение молекулярно-кинетической теории идеального газа

p — давление идеального газа;

m — масса одной молекулы;

n = N/V — концентрация молекул;

V — объем газа;

N — число молекул;

— среднее значение квадрата скорости молекул.

1.3 Средняя квадратичная скорость молекул идеального газа

k = 1,38·10^-23 Дж/К — постоянная Больцмана;

R = kN_A = 8,31 Дж/(моль·К) — универсальная газовая постоянная;

T = t+273 — абсолютная температура;

t — температура по шкале Цельсия.

1.4 Средняя кинетическая энергия молекулы одноатомного газа

1.5 Давление идеального газа

n — концентрация молекул;

k — постоянная Больцмана;

T — абсолютная температура.

1.6 Закон Бойля-Мариотта

p — давление;

V — объем газа.

1.7 Закон Шарля

p₀ — давление газа при 0 °С;

α = 1/273 °C^-1 — температурный коэффициент давления.

1.8 Закон Гей-Люссака

V₀ — объем газа при 0 °С.

1.9 Уравнение Менделеева-Клапейрона

1.10 Объединенный закон газового состояния (уравнение Клапейрона)

1.11 Закон Дальтона

p_i — парциальное давление i-й компоненты смеси газов.

2. Основы термодинамики

2.1 Внутренняя энергия идеального одноатомного газа

ν — количество вещества;

R = 8,31 Дж/(моль·К) — универсальная газовая постоянная;

T — абсолютная температура.

2.2 Элементарная работа, совершаемая газом,

при изменении объема на бесконечно малую величину dV

p — давление газа.

При изменении объема от V₁ до V₂

2.3 Первый закон термодинамики

ΔQ — количество подведенной теплоты;

ΔA — работа, совершаемая веществом;

ΔU — изменение внутренней энергии вещества.

2.4 Теплоемкость идеального газа

ΔQ — количество переданной системе теплоты на участке процесса;

ΔT — изменение температуры на этом участке процесса.

Представляем формулу основного уравнения молекулярно-кинетической теории (МКТ) газов:

(где n=NV – это концентрация частиц в газе, N – это число частиц, V – это объем газа, 〈E〉 – это средняя кинетическая энергия поступательного движения молекул газа, υkv – это средняя квадратичная скорость, m0 – это масса молекулы) связывает давление – макропараметр, достаточно просто измеряющийся с такими микропараметрами, как средняя энергия движения отдельной молекулы (или в другом выражении), как масса частицы и ее скорость. Но находя только лишь давление, нельзя установить кинетические энергии частиц отдельно от концентрации. Поэтому для нахождения в полном объеме микропараметров нужно знать еще какую-то физическую величину, связанную с кинетической энергией частиц, составляющих газ. За данную величину можно взять термодинамическую температуру.

Газовая температура

Для определения газовой температуры нужно вспомнить важное свойство, которое сообщает о том, что в условиях равновесия средняя кинетическая энергия молекул в смеси газов одинаковая для различных компонентов данной смеси. Из данного свойства следует то, что если 2 газа в различных сосудах находятся в тепловом равновесии, тогда средние кинетические энергии молекул данных газов одинаковые. Это свойство мы и будем использовать. К тому же в ходе экспериментов доказано, что для любых газов (при неограниченном числе), которые находятся в состоянии теплового равновесия, справедливо следующее выражение:

С учетом вышесказанного, используем (1) и (2) и получаем:

Из уравнения (3) следует, что величина θ, которой мы обозначили температуру, вычисляется в Дж, в чем измеряется также и кинетическая энергия. В лабораторных работах температура в системе измерения вычисляется в кельвинах. Поэтому введем коэффициент, который уберет данное противоречие. Он обозначается k, измеряется в ДжК и равняется 1,38·10-23. Данный коэффициент называется постоянной Больцмана. Таким образом:

θ=kT (4), где T – это термодинамическая температура в кельвинах.

Связь термодинамической температуры и средней кинетической энергией теплового движения молекул газа выражается формулой:

E=32kT (5).

Из уравнения (5) видно, что средняя кинетическая энергия теплового движения молекул прямо пропорциональна температуре газа. Температура является абсолютной величиной. Физический смысл температуры заключается в том, что она, с одной стороны, определяется средней кинетической энергией, которая приходится на 1 молекулу. А с другой стороны, температура – это характеристика системы в целом. Таким образом, уравнение (5) показывает связь параметров макромира с параметрами микромира.

Известно, что температура – это мера средней кинетической энергии молекул.

Можно установить температуру системы, а затем рассчитать энергию молекул.

Абсолютный ноль температур

В условиях термодинамического равновесия все составляющие системы характеризуются одинаковой температурой.

Температура, при которой средняя кинетическая энергия молекул равняется 0, давление идеального газа равняется 0, называется абсолютным нулем температур. Абсолютная температура никогда не является отрицательной.

Основное уравнение мкт газов. Температура

Простейшей моделью
молекулярно-кинетической теории является
модель идеального газа. В кинетической
модели идеального газа молекулы
рассматриваются как идеально упругие
шарики, взаимодействующие между собой
и со стенками только во время упругих
столкновений. Суммарный объем всех
молекул предполагается малым по сравнению
с объемом сосуда, в котором находится
газ. Модель идеального газа достаточно
хорошо описывает поведение реальных
газов в широком диапазоне давлений и
температур. Задача молекулярно-кинетической
теории состоит в том, чтобы установить
связь между микроскопическими
(масса, скорость, кинетическая энергия
молекул) и макроскопическими параметрами
(давление, газ, температура).

В результате каждого
столкновения между молекулами и молекул
со стенкой скорости молекул могут
изменяться по модулю и по направлению;
на интервалах между последовательными
столкновениями молекулы движутся
равномерно и прямолинейно. В модели
идеального газа предполагается, что
все столкновения происходят по законам
упругого удара, то есть подчиняются
законам механики Ньютона.

Используя модель
идеального газа, вычислим давление
газа на стенку сосуда. В процессе
взаимодействия молекулы со стенкой
сосуда между ними возникают силы,
подчиняющиеся третьему закону Ньютона.
В результате проекция υ_x скорости
молекулы, перпендикулярная стенке,
изменяет свой знак на противоположный,
а проекция υ_y скорости, параллельная
стенке, остается неизменной (рис. 1.3.3).

1

Рисунок 1.3.3. Упругое столкновение молекулы со стенкой.

Поэтому изменение
импульса молекулы будет равно 2m₀υ_x,
где m₀ – масса молекулы.

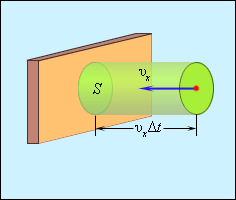
Выделим на стенке
некоторую площадку S (рис. 1.3.4). За
время Δt с этой площадкой столкнутся
все молекулы, имеющие проекцию скорости
υ_x, направленную в сторону стенки,
и находящиеся в цилиндре с основанием
площади S и высотой υ_xΔt.

2

Рисунок 1.3.4. Определение числа столкновений молекул с площадкой S.

Пусть в единице объема
сосуда содержатся n молекул; тогда число
молекул в объеме цилиндра равно nSυ_xΔt.
Но из этого числа лишь половина движется
в сторону стенки, а другая половина
движется в противоположном направлении
и со стенкой не сталкивается. Следовательно,
число ударов молекул о площадку S за
время Δt равно
Поскольку
каждая молекула при столкновении со
стенкой изменяет свой импульс на величину
2m₀υ_x, то полное изменение
импульса всех молекул, столкнувшихся
за время Δt с площадкой S, равно
По
законам механики это изменение импульса
всех столкнувшихся со стенкой молекул
происходит под действием импульса силы
FΔt, где F – некоторая средняя сила,
действующая на молекулы со стороны
стенки на площадке S. Но по 3-му закону
Ньютона такая же по модулю сила действует
со стороны молекул на площадку S. Поэтому
можно записать:

Разделив обе части на
SΔt, получим:

где p – давление газа
на стенку сосуда. 

При выводе этого
соотношения предполагалось, что все n
молекул, содержащихся в единице объема
газа, имеют одинаковые проекции скоростей
на ось X. На самом деле это не так.

В результате
многочисленных соударений молекул газа
между собой и со стенками в сосуде,
содержащем большое число молекул,
устанавливается некоторое статистическое
распределение молекул по скоростям.
При этом все направления векторов
скоростей молекул оказываются
равноправными (равновероятными), а
модули скоростей и их проекции на
координатные оси подчиняются определенным
закономерностям. Распределение молекул
газа по модулю скоростей называется
распределением Максвелла (1860 г.).
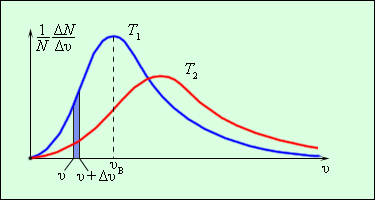
Дж. Максвелл вывел закон
распределения молекул газа по скоростям,
исходя из основных положений
молекулярно-кинетической теории. На
рис. 3.2.3 представлены типичные кривые
распределения молекул по скоростям. По
оси абсцисс отложен модуль скорости, а
по оси ординат – относительное число
молекул, скорости которых лежат в
интервале от υ до υ + Δυ. Это число
равно площади выделенного на рис. 1.3.5
столбика.

3

Рисунок 1.3.5. Распределение молекул по скоростям. T2 > T1.

Характерными параметрами
распределения Максвелла являются
наиболее вероятная скорость υ_в,
соответствующая максимуму кривой
распределения, и среднеквадратичная
скорость
где

–
среднее значение квадрата скорости.

С ростом температуры
максимум кривой распределения смещается
в сторону больших скоростей, при этом
υ_в и υ_кв увеличиваются.

ВЕРОЯТНОСТЬЮ Р_i
получения некоторого результата
измерения называется предел отношения
количества измерений, давших этот
результат, (N_i)
к полному числу измерений N,
когда N 
.

ЭЛЕМЕНТАРНОЙ вероятностью
dP_V
при измерении величины скорости v
называется вероятность наличия скорости
величиной от v до v
+ dv. Эта вероятность
пропорциональна приращению скорости
dv: dP_V
= F(v) dv,
где коэффициент пропорциональности
F(v) называется
ФУНКЦИЕЙ РАСПРЕДЕЛЕНИЯ молекул по
величине скорости. Она может быть
выражена через другие функции распределения

F(v)
= (v_X)(v_Y)(v_Z)4v²
= f(v)4v²
, где (v_X),
(v_Y)
и(v_Z)
— функции распределения для соответствующих
проекций скоростей молекул, а f(v)
— их произведение.

В §98
вы можете найти вывод формул, в частности

.

СреднЯЯ
скорость
,

СреднЯЯ
квадратичная скорость v_ср.кв
=
.

Наивероятнейшей
называется скорость v_ВЕР,
при которой F(v)
имеет максимум: v_ВЕР
=
.

Чтобы уточнить формулу
для давления газа на стенку сосуда,
предположим, что все молекулы, содержащиеся
в единице объема, разбиты на группы,
содержащие n₁, n₂, n₃ и
т. д. молекул с проекциями скоростей
υ_x1, υ_x2, υ_x3 и т. д.
соответственно. При этом
Каждая
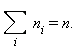
группа молекул вносит свой вклад
в
давление газа. В результате соударений
со стенкой молекул с различными значениями
проекций υ_xi скоростей возникает
суммарное давление

Входящая в это выражение
сумма – это сумма квадратов проекций
υ_x всех n молекул в единичном объеме
газа. Если эту сумму разделить на n, то
мы получим среднее значение
квадрата
проекции
скорости
молекул:

Теперь формулу для
давления газа можно записать в виде

Так как все направления
для векторов скоростей молекул
равновероятны, среднее значение квадратов
их проекций на координатные оси равны
между собой:

Последнее равенство
вытекает из формулы:

Формула для среднего
давления газа на стенку сосуда запишется
в виде

Это уравнение
устанавливает связь между давлением p
идеального газа, массой молекулы m₀,
концентрацией молекул n, средним значением
квадрата скорости
и
средней кинетической энергией

поступательного
движения молекул. Его называют основным
уравнением молекулярно-кинетической
теории газов.

Таким образом, давление
газа равно двум третям средней кинетической
энергии поступательного движения
молекул, содержащихся в единице объема.

В основное уравнение
молекулярно-кинетической теории газов
входит произведение концентрации
молекул n на среднюю кинетическую энергию

поступательного
движения. Если предположить, что газ
находится в сосуде неизменного объема
V, то
(N
– число молекул в сосуде). В этом случае
изменение давления Δp пропорционально
изменению
средней
кинетической энергии.

Возникают вопросы:
каким образом можно на опыте изменять
среднюю кинетическую энергию движения
молекул в сосуде неизменного объема?
Какую физическую величину нужно изменить,
чтобы изменилась средняя кинетическая
энергия
Такой
величиной в физике является температура.

Понятие температуры
тесно связано с понятием теплового
равновесия. Тела, находящиеся в
контакте друг с другом, могут обмениваться
энергией. Энергия, передаваемая одним
телом другому при тепловом контакте,
называется количеством теплоты.

Тепловое равновесие
– это такое состояние системы тел,
находящихся в тепловом контакте, при
котором не происходит теплопередачи
от одного тела к другому, и все
макроскопические параметры тел остаются
неизменными. Температура – это физический
параметр, одинаковый для всех тел,
находящихся в тепловом равновесии.
Возможность введения понятия температуры
следует из опыта и носит название
нулевого закона термодинамики.

Для измерения температуры
используются физические приборы –
термометры, в которых о величине
температуры судят по изменению какого-либо
физического параметра. Для создания
термометра необходимо выбрать
термометрическое вещество (например,
ртуть, спирт) и термометрическую
величину, характеризующую свойство
вещества (например, длина ртутного или
спиртового столбика). В различных
конструкциях термометров используются
разнообразные физические свойства
вещества (например, изменение линейных
размеров твердых тел или изменение
электрического сопротивления проводников
при нагревании).

Термометры должны
быть откалиброваны. Для этого их приводят
в тепловой контакт с телами, температуры
которых считаются заданными. Чаще всего
используют простые природные системы,
в которых температура остается неизменной,
несмотря на теплообмен с окружающей
средой – это смесь льда и воды и смесь
воды и пара при кипении при нормальном
атмосферном давлении. По температурной
шкале Цельсия точке плавления льда
приписывается температура 0 °С, а
точке кипения воды – 100 °С. Изменение
длины столба жидкости в капиллярах
термометра на одну сотую длины между
отметками 0 °С и 100 °С принимается
равным 1 °С. В ряде стран (США) широко
используется шкала Фаренгейта (T_F),
в которой температура замерзающей воды
принимается равной 32 °F, а температура
кипения воды равной 212 °F. Следовательно,

Особое место в физике
занимают газовые термометры
(рис. 1.3.6), в которых термометрическим
веществом является разреженный газ
(гелий, воздух) в сосуде неизменного
объема (V = const), а термометрической
величиной – давление газа p. Опыт
показывает, что давление газа (при
V = const) растет с ростом температуры,
измеренной по шкале Цельсия.

Рисунок 1.3.6. Газовый термометр с постоянным объемом.

Чтобы проградуировать
газовый термометр постоянного объема,
можно измерить давление при двух
значениях температуры (например, 0 °C
и 100 °C), нанести точки p₀ и p₁₀₀
на график, а затем провести между ними
прямую линию (рис. 1.3.7). Используя
полученный таким образом калибровочный
график, можно определять температуры,
соответствующие другим значениям
давления. Экстраполируя график в область
низких давлений, можно определить
некоторую «гипотетическую» температуру,
при которой давление газа стало бы
равным нулю. Опыт показывает, что эта
температура равна –273,15 °С и не зависит
от свойств газа. Невозможно на опыте
получить путем охлаждения газ в состоянии
с нулевым давлением, так как при очень
низких температурах все газы переходят
в жидкие или твердые состояния.

5

Рисунок 1.3.7. Зависимость давления газа от температуры при V = const.

Английский физик
У. Кельвин (Томсон) в 1848 г. предложил
использовать точку нулевого давления
газа для построения новой температурной
шкалы (шкала Кельвина). В этой шкале
единица измерения температуры такая
же, как и в шкале Цельсия, но нулевая
точка сдвинута:

TК = TС + 273,15.

В системе СИ принято
единицу измерения температуры по шкале
Кельвина называть кельвином и
обозначать буквой К. Например, комнатная
температура T_С = 20 °С по
шкале Кельвина равна T_К = 293,15 К.

Температурная шкала
Кельвина называется абсолютной шкалой
температур. Она оказывается наиболее
удобной при построении физических
теорий.

Нет необходимости
привязывать шкалу Кельвина к двум
фиксированным точкам – точке плавления
льда и точке кипения воды при нормальном
атмосферном давлении, как это принято
в шкале Цельсия.

Кроме точки нулевого
давления газа, которая называется
абсолютным нулем температуры,
достаточно принять еще одну фиксированную
опорную точку. В шкале Кельвина в качестве
такой точки используется температура
тройной точки воды (0,01 °С), в которой
в тепловом равновесии находятся все
три фазы – лед, вода и пар. По шкале
Кельвина температура тройной точки
принимается равной 273,16 К.

Газовые термометры
громоздки и неудобны для практического
применения: они используются в качестве
прецизионного стандарта для калибровки
других термометров.

Таким образом, давление
разреженного газа в сосуде постоянного
объема V изменяется прямо пропорционально
его абсолютной температуре: p ~ T.
С другой стороны, опыт показывает, что
при неизменных объеме V и температуре
T давление газа изменяется прямо
пропорционально отношению количества
вещества ν в данном сосуде к объему V
сосуда

где N – число молекул
в сосуде, N_А – постоянная Авогадро,
n = N / V – концентрация молекул
(то есть число молекул в единице объема
сосуда). Объединяя эти соотношения
пропорциональности, можно записать:

p = nkT,

где k – некоторая
универсальная для всех газов постоянная
величина. Ее называют постоянной
Больцмана, в честь австрийского физика
Л. Больцмана (1844–1906 гг.), одного из
создателей молекулярно-кинетической
теории. Постоянная Больцмана – одна из
фундаментальных физических констант.
Ее численное значение в СИ равно:

k = 1,38·10–23 Дж/К.

Сравнивая соотношения
p = nkT с основным уравнением
молекулярно-кинетической теории газов,
можно получить:

Средняя кинетическая
энергия хаотического движения молекул
газа прямо пропорциональна абсолютной
температуре.

Таким образом,
температура есть мера средней
кинетической энергии поступательного
движения молекул.

Следует обратить
внимание на то, что средняя кинетическая
энергия поступательного движения
молекулы не зависит от ее массы.
Броуновская частица, взвешенная в
жидкости или газе, обладает такой же
средней кинетической энергией, как и
отдельная молекула, масса которой на
много порядков меньше массы броуновской
частицы. Этот вывод распространяется
и на случай, когда в сосуде находится
смесь химически невзаимодействующих
газов, молекулы которых имеют разные
массы. В состоянии равновесия молекулы
разных газов будут иметь одинаковые
средние кинетические энергии теплового
движения, определяемые только температурой
смеси. Давление смеси газов на стенки
сосуда будет складываться из парциальных
давлений каждого газа:

p = p1 + p2 + p3 + … = (n1 + n2 + n3 + …)kT.

В этом соотношении
n₁, n₂, n₃, … – концентрации
молекул различных газов в смеси. Это
соотношение выражает на языке
молекулярно-кинетической теории
экспериментально установленный в начале
XIX столетия закон Дальтона: давление
в смеси химически невзаимодействующих
газов равно сумме их парциальных
давлений.