Теорема Гаусса выражает связь между потоком вектора напряженности электрического поля через замкнутую поверхность и алгебраической суммой зарядов, заключенных в объеме, ограниченном этой поверхностью. О примерах использования теоремы Гаусса на практике поговорим в этой статье.
Присоединяйтесь к нам в телеграме, чтобы не только решать задачи, но и быть в курсе актуальных новостей для студентов всех специальностей.
Задачи на теорему Гаусса с решением
Если вам нужно сначала освежить теоретические знания, читайте подробную теорию по теореме Гаусса в нашем справочнике. Ну а перед решением задач не забудьте повторить памятку и на всякий случай держите под рукой полезные формулы.
Кстати, при решении задач на теорему Гаусса придется довольно часто брать интегралы. Хотите научиться делать это по-быстрому? У нас уже есть отдельная статья и видео на эту тему.
Задача на теорему Гаусса №1: напряженность поля плоскости
Условие
Определите напряженность поля бесконечной заряженной плоскости. Поверхностная плотность заряда сигма.
Решение
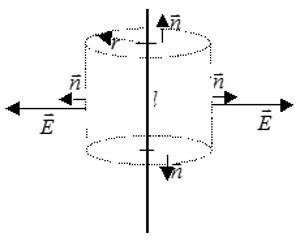
Линии напряженности перпендикулярны рассматриваемой плоскости и направлены в обе стороны от неё. Выберем в качестве гауссовой поверхности цилиндр с основанием, параллельным плоскости:
По теореме Гаусса:
Поток сквозь цилиндр равен сумме потоков сквозь боковую поверхность цилиндра и потокам сквозь оба его основания. Поток сквозь боковую поверхность равен нулю, так как линии напряженности параллельны ей:
Согласно теореме Гаусса:
Отсюда:
Ответ: см. выше.
Задача на теорему Гаусса №2: напряженность поля двух пластин
Условие
Электрическое поле создано двумя параллельными заряженными тонкими пластинами с поверхностными плотностями заряда + сигма и -2 сигма. Площадь каждой пластины S, расстояние между пластинами d можно считать значительно меньшим их продольных размеров. Какова напряженность электрического поля, созданного этими пластинами?
Решение
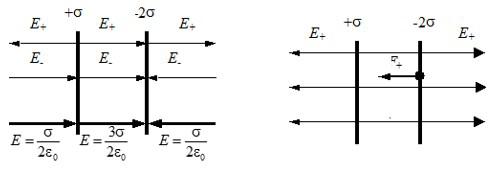
Для электрического поля действует принцип суперпозиции: результирующее поле равно векторной сумме отдельных полей каждой пластины. Из предыдущей задачи мы знаем формулу, по которой вычисляется напряженность поля тонкой заряженной пластины, запишем для каждой из них:
Векторы напряженности между пластинами совпадают по направлению, результирующая напряженность равна:
Справа и слева от пластин, во внешней области, векторы направлены в разные стороны:
Для наглядности приведем рисунок:
Ответ: см. выше.
Задача на теорему Гаусса №3: напряженность электрического поля бесконечной нити
Условие
Определить напряженность электрического поля, создаваемую бесконечной тонкой нитью, равномерно заряженной с линейной плотностью заряда лямбда.
Решение
Напряженность будем искать при помощи теоремы Гаусса. Наша задача – определить зависимость напряженности от расстояния от нити. В качестве поверхности выберем цилиндр с боковыми стенками, параллельными нити. Будем учитывать только поток вектора напряженности через боковую поверхность, так как поток через основания цилиндра равен нулю:
Заряд нити внутри рассматриваемой поверхности равен заряду отрезка нити длиной l:
По теореме Гаусса:
Отсюда:
Ответ: см. выше.
Задача с применением теоремы Гаусса №4
Условие
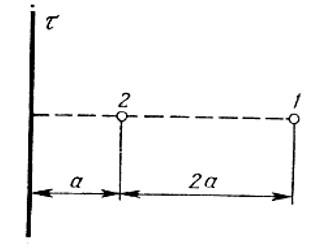
Электрическое поле создано бесконечной заряженной прямой линией с равномерно распределённым зарядом (τ = 10 нКл/м). Определить кинетическую энергию Т2 электрона в точке 2, если в точке 1 его кинетическая энергия Т1 = 200 эВ. Расстояние точки 2 от линии равно а = 0,5 см, точки 1 – b=1,5 см.
Решение
Ранее рассмотренные задачи были примерами вычисления полей с помощью теоремы Гаусса. Теперь рассмотрим задачу, которая решается сиспользованием этой информации. Из предыдущей задачи возьмем выражение для напряженности поля заряженной нити:
Разность потенциалов поля в двух точках будет равна:
При прохождении этой разницы потенциалов электрон приобретёт кинетическую энергию:
Конечная энергия частицы будет равна:
Получим:
Ответ: 397.6 эВ.
Задача на теорему Гаусса №5: поток электрического поля
Условие
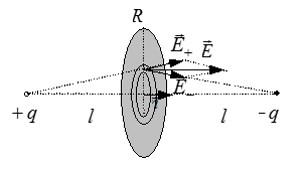
Два точечных заряда q и –q расположены на расстоянии 2l друг от друга. Найти поток вектора напряженности через круг радиуса R. Плоскость круга проходит через его середину и перпендикулярна отрезку прямой, соединяющей заряды.
Решение
Рассмотрим элементарный поток результирующего электрического поля через бесконечно малую кольцевую зону круга:
В записи потока учтено, что вектор напряженности перпендикулярен поверхности круга. Выразим напряженность электрического поля через «ро», используя подобие треугольников, показанных на рисунке:
Вычисление потока сводится к взятию интеграла:
Ответ: см. выше.
Примеры применения теоремы Гаусса можно найти не только в электростатике, но и в других областях физики.
Вопросы на теорему Гаусса
Вопрос 1. Сформулируйте теорему Гаусса.
Ответ. Теорема Гаусса гласит:
Поток вектора напряженности электростатического поля через замкнутую поверхность равен алгебраической сумме зарядов внутри поверхности, деленной на эпсилон нулевое (электрическую постоянную).
Вопрос 2. Что такое поток вектора напряженности?
Ответ. Поток вектора напряженности – скалярная физическая величина, определяемая как число линий вектора напряженности, пронизывающих некоторую поверхность S. Поток напряженности электрического поля через поверхность S конечного размера определяется как алгебраическая сумма элементарных потоков:
Вопрос 3. Что такое силовые линии напряженности?
Ответ. Это линии, с помощью которых используются для графического представления поля:
- касательная к силовой линии в каждой точке пространства направлена вдоль вектора поля;
- густота силовых линий пропорциональна напряженности поля в данной точке;
- поток вектора напряженности пропорционален числу силовых линий, пронизывающих поверхность.
Вопрос 4. Где начинаются и где заканчиваются силовые линии?
Ответ. Силовые линии начинаются и заканчиваются на зарядах, оставаясь непрерывными в пустом пространстве.
Вопрос 5. Верно ли утвержление: теорема Гаусса справедлива только для неподвижных зарядов.
Ответ. Нет, так как заряд частицы не зависит от ее скорости.
Нужна помощь в решении задач и других студенческих заданий? Обратитесь в профессиональный студенческий сервис за качественным решением проблем.
Карл Фридрих Гаусс – немецкий математик, основатель одноименного метода решения СЛАУ
Карл Фридрих Гаусс – был известным великим математиком и его в своё время признали «королём математики». Хотя название «метод Гаусса» является общепринятым, Гаусс не является его автором: метод Гаусса был известен задолго до него. Первое его описание имеется в китайском трактате «Математика в девяти книгах», который составлен между II в. до н. э. и I в. н. э. и представляет собой компиляцию более ранних трудов, написанных примерно в X в. до н. э.
Метод Гаусса – последовательное исключение неизвестных. Этот метод используется для решения квадратных систем линейных алгебраических уравнений. Хотя уравнения при помощи метода Гаусса решаются легко, но всё же студенты часто не могут найти правильное решение, так как путаются в знаках (плюсы и минусы). Поэтому во время решения СЛАУ необходимо быть предельно внимательным и только тогда можно легко, быстро и правильно решить даже самое сложное уравнение.
У систем линейных алгебраических уравнений есть несколько преимуществ: уравнение не обязательно заранее на совместность; можно решать такие системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равняется нулю; есть возможность при помощи метода Гаусса приводить к результату при сравнительно небольшом количестве вычислительных операций.
Определения и обозначения
Как уже говорилось, метод Гаусса вызывает у студентов некоторые сложности. Однако, если выучить методику и алгоритм решения, сразу же приходит понимание в тонкостях решения.
Для начала систематизируем знания о системах линейных уравнений.
СЛАУ в зависимости от её элементов может иметь:
- Одно решение;
- много решений;
- совсем не иметь решений.
В первых двух случаях СЛАУ называется совместимой, а в третьем случае – несовместима. Если система имеет одно решение, она называется определённой, а если решений больше одного, тогда система называется неопределённой.
Метод Крамера и матричный способ не подходят для решения уравнений, если система имеет бесконечное множество решений. Вот поэтому нам и нужен метод Гаусса, который поможет нам в любом случае найти правильное решение. К элементарным преобразованиям относятся:
- перемена мест уравнений системы;
- почленное умножение обеих частей на одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами;
- сложение к обеим частям одного из уравнений определённых частей другого уравнения.
Итак, когда мы знаем основные правила и обозначения, можно приступать к решению.
Теперь рассмотрим, как решаются системы методом Гаусса на простом примере:
где а, в, с – заданные коэффициенты, d – заданные свободные члены, x, y, z – неизвестные. Коэффициенты и свободные члены уравнения можно называть его элементами.
Если =
=
=
, тогда система линейных алгебраических уравнений называется однородной, в другом случае – неоднородной.
Множественные числа ,
,
называются решением СЛАУ, если при подстановке
,
,
в СЛАУ получим числовые тождества.
Система, которую мы написали выше имеет координатную форму. Если её переделать в матричную форму, тогда система будет выглядеть так:
– это основная матрица СЛАУ.
– матрица столбец неизвестных переменных.
– матрица столбец свободных членов.
Если к основной матрице добавить в качестве
– ого столбца матрицу-столбец свободных членов, тогда получится расширенная матрица систем линейных уравнений. Как правило, расширенная матрица обозначается буквой
, а столбец свободных членов желательно отделить вертикальной линией от остальных столбцов. То есть, расширенная матрица выглядит так:
Если квадратная матрица равна нулю, она называется вырожденная, а если – матрица невырожденная.
Если с системой уравнений:
Произвести такие действия:
тогда получается эквивалентная система, у которой такое же решение или нет решений совсем.
Теперь можно перейти непосредственно к методу Гаусса.
Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать работу
Простейшие преобразования элементов матрицы
Мы рассмотрели основные определения и уже понимаем, чем нам поможет метод Гаусса в решении системы. Теперь давайте рассмотрим простую систему уравнений. Для этого возьмём самое обычное уравнение, где и используем решение методом Гаусса:
Из уравнения запишем расширенную матрицу:
Из данной матрицы видно, по какому принципу она записана. Вертикальную черту не обязательно ставить, но просто так удобнее решать систему.
Матрица системы – это матрица, которая составляется исключительно с коэффициентами при неизвестных. Что касается расширенной матрицы системы, так, это такая матрица, в которой кроме коэффициентов записаны ещё и свободные члены. Любую из этих матриц называют просто матрицей.
На матрице, которая написана выше рассмотрим, какие существуют элементарные преобразования:
1. В матрице строки можно переставлять местами. Например, в нашей матрице спокойно можно переставить первую и вторую строки:
.
2. Если в матрице имеются (или появились) пропорциональные строки (одинаковые), тогда необходимо оставить всего лишь одну строку, а остальные убрать (удалить).
3. Если в ходе преобразований в матрице появилась строка, где находятся одни нули, тогда такую строку тоже нужно удалять.
4. Строку матрицы можно умножать (делить) на любое число, которое отличное от нуля. Такое действие желательно проделывать, так как в будущем проще преобразовывать матрицу.
5. Сейчас рассмотрим преобразование, которое больше всего вызывает затруднение у студентов. Для этого возьмём изначальную нашу матрицу:
Для удобства умножаем первую строку на (-3):
Теперь ко второй строке прибавляем первую строку, которую умножали на -3. Вот что у нас получается:
В итоге получилось такое преобразование:
Теперь для проверки можно разделить все коэффициенты первой строки на те же и вот что получается:
В матрице верхняя строка преобразовалась:
Первую строку делим на и преобразовалась нижняя строка:
И верхнюю строку поделили на то же самое число :
Как вы можете убедиться, в итоге строка, которую мы прибавляли ни капельки не изменилась, а вот вторая строка поменялась. ВСЕГДА меняется только та строка, к которой прибавляются коэффициенты.
Мы расписали в таких подробностях, чтобы было вам понятно, откуда какая цифра взялась. На практике, например, на контрольной или экзамене матрица так подробно не расписывается. Как правило, в задании решение матрицы оформляется так:
.
Если в примере приведены десятичные дроби, метод Гаусса в этом случае также поможет решить систему линейных алгебраических уравнений. Однако, не стоит забывать, что следует избегать приближённых вычислений, так как ответ будет неверным. Лучше всего использовать десятичные дроби, а от них переходить к обыкновенным дробям.
Алгоритм решения методом Гаусса пошагово
После того, как мы рассмотрели простейшие преобразования, в которых на помощь пришёл метод Гаусса, можем вернуться к нашей системе, которую уже разложили по полочкам и пошагово распишем:
Шаг 1. Переписываем систему в виде матрицы
Записываем матрицу:
Шаг 2. Преобразовываем матрицу: вторую строку в первом столбце приводим к нулю
Как мы привели вторую строку в первом столбце к нулю описано выше. Напомним, что первую строку умножали на и вторую строку прибавили к первой , умноженной на
.
Шаг 3. Приводим матрицу к ступенчатому виду
Теперь вторую строку можно поделить на 2 и получается:
Верхнюю строку делим на и приводим матрицу к ступенчатому виду:
Когда оформляют задание, так и отчёркивают простым карандашом для упрощения работы, а также обводят те числа, которые стоят на “ступеньках”. Хотя в учебниках и другой литературе нет такого понятия, как ступенчатый вид. Как правило, математики такой вид называют трапециевидным или треугольным.
Шаг 4. Записываем эквивалентную систему
После наших элементарных преобразований получилась эквивалентная система:
Шаг 5. Производим проверку (решение системы обратным путём)
Теперь систему нужно решить в обратном направлении, то есть обратным ходом, начиная с последней строки.:
находим :
,
,
.
После находим
:
,
.
Тогда:
.
Как видим, уравнение решено правильно, так как ответы в системе совпадают.
Решение систем линейных уравнений методом Гаусса, в которых основная матрица невырожденная, а количество в ней неизвестных равняется количеству уравнений
Как мы уже упоминали, невырожденная матрица бывает тогда, когда . Разберём систему уравнений невырожденной матрицы, где уравнений по количеству столько же, сколько и неизвестных. Эту систему уравнений решим другим способом.
Дана система уравнений:
Для начала нужно решить первое уравнение системы относительно неизвестной переменной . Далее подставим полученное выражение сначала во второе уравнение, а затем в третье, чтобы исключить из них эту переменную.
Теперь переходим ко второму уравнению системы относительно и полученный результат подставим в третье уравнение.. Это нужно для того, чтобы исключить неизвестную переменную
:
Из последнего, третьего уравнения мы видим, что . Из второго уравнения находим
. И последнее, находим первое уравнение
.
Итак, мы нашли все три неизвестных при помощи последовательного исключения. Такой процесс называют – прямой ход метода Гаусса. Когда последовательно находятся неизвестные переменные, начиная с последнего уравнения, называется обратным ходом метода Гаусса.
Когда выражается через
и
в первом уравнении, а затем подставляется полученное выражение во второе или третье уравнения, тогда, чтобы привести в к такому же результату, необходимо проделать такие действия:
И действительно, благодаря такой процедуре у нас есть возможность исключать неизвестную переменную со второго и третьего уравнения системы:
Возникают нюансы с исключением неизвестных переменных тогда, когда в уравнении системы нет каких-либо неизвестных переменных. Рассмотрим такую систему:
В этой системе в первом уравнении нет переменной и поэтому у нас нет возможности решить первое уравнение системы относительно
, чтобы исключить данную переменную из остальных уравнений. В таком случае выход есть. Нужно всего лишь уравнения переставить местами.
Так как мы описываем уравнения системы, в которых определитель основных матриц отличен от нуля, тогда всегда есть такое уравнение, в котором есть необходимая нам переменная и это уравнение мы можем поставить туда, куда нам нужно.
В примере, который мы рассматриваем, достаточно всего лишь поменять местами первое и второе уравнение.
Теперь мы можем спокойно разрешить первое уравнение относительно переменной и убрать (исключить) из остальных уравнений в системе. Вот и весь принцип работы с такими, на первый взгляд, сложными системами.
Решение систем линейных уравнений методом Гаусса, в которых основная матрица вырожденная, а количество в ней неизвестных не совпадает с количеством уравнений
Метод Гаусса помогает решать системы уравнений, у которых основная матрица прямоугольная или квадратная, но основная вырожденная матрица может совсем не иметь решений, иметь бесконечное множество решений или иметь всего лишь одно единственное решение.
Рассмотрим, как при помощи метода Гаусса устанавливается совместность или несовместность систем линейных уравнений. В случае, если есть совместность определим все решения или одно решение.
В принципе, исключать неизвестные переменные можно точно так, как описано выше. Однако, есть некоторые непонятные ситуации, которые могут возникнуть в ходе решения:
1. На некоторых этапах в момент исключения неизвестных переменных некоторые уравнения могут обратиться в тождества . В данном случае такие уравнения лишние в системе и их можно смело полностью убирать, а затем продолжать решать уравнение методом Гаусса.
Например, вам попалась подобная система:
У нас получается такая ситуация
Как видим, второе уравнение . Соответственно, данное уравнение мы можем из системы удалить, так как оно без надобности.
Дальше можно продолжать решение системы линейных алгебраических уравнений уравнений традиционным методом Гаусса.
2. При решении уравнений прямым ходом методом Гаусса могут принять не только одно, но и несколько уравнений такой вид: , где
– число, которое отличное от нуля. Это говорит о том, что такое уравнение никогда не сможет превратиться в тождество даже при любых значениях неизвестных переменных. То есть, можно выразить по-другому. Если уравнение приняло
вид, значит система несовместна, то есть, не имеет решений. Рассмотрим на примере:
Для начала необходимо исключить неизвестную переменную из всех уравнений данной системы, начиная со второго уравнения. Для этого нужно прибавить к левой и правой частям второго, третьего, четвёртого уравнения части (левую и правую) первого уравнения, которые соответственно, умножаются на (-1), (-2), (-3). Получается:
В третьем уравнении получилось равенство . Оно не подходит ни для каких значений неизвестных переменных
,
и
, и поэтому, у данной системы нет решений. То есть, говорится, что система не имеет решений.
3. Допустим, что при выполнении прямого хода методом Гаусса нам нужно исключить неизвестную переменную , и ранее, на каком-то этапе у нас уже исключалась вместе с переменной
. Как вы поступите в таком случае? При таком положении нам нужно перейти к исключению переменной
. Если же
уже исключались, тогда переходим к
,
и т. д.
Рассмотрим систему уравнений на таком этапе, когда уже исключилась переменная :
Такая система уравнений после преобразования выглядит так:
Вы наверное уже обратили внимание, что вместе с исключились
и
. Поэтому решение методом Гаусса продолжаем исключением переменной
из всех уравнений системы, а начнём мы с третьего уравнения:
Чтобы завершить уравнение прямым ходом метода Гаусса, необходимо исключить последнюю неизвестную переменную из последнего уравнения:
Допусти, что система уравнений стала:
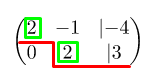
В этой системе нет ни одного уравнения, которое бы сводилось к . В данном случае можно было бы говорить о несовместности системы. Дальше непонятно, что же делать? Выход есть всегда. Для начала нужно выписать все неизвестные, которые стоят на первом месте в системе:
В нашем примере это ,
и
. В левой части системы оставим только неизвестные, которые выделены зелёным квадратом а в правую перенесём известные числа, но с противоположным знаком. Посмотрите на примере, как это выглядит:
Можно придать неизвестным переменным с правой части уравнений свободные (произвольные) значения: ,
,
, где
,
,
– произвольные числа.
Теперь в правых частях уравнений нашей системы имеются числа и можно приступать к обратному ходу решения методом Гаусса.
В последнем уравнении системы получилось: , и теперь мы легко найдём решение в предпоследнем уравнении:
, а из первого уравнения получаем:
=
=
В итоге, получился результат, который можно и записать.
Ответ
,
,
,
,
,
.
Примеры решения методом Гаусса
Выше мы подробно расписали решение системы методом Гаусса. Чтобы закрепить материал, решим несколько примеров, в которых опять нам поможет метод Гаусса. Соответственно, начнём с самой простой системы.
Задача
Решить систему линейных алгебраических уравнений методом Гаусса:
Решение
Выписываем матрицу, куда добавляем столбец свободных членов:
Прежде всего мы смотрим на элемент, который находится в матрице в левом верхнем углу (первая строка, первый столбец). Для наглядности выделим цифру зелёным квадратом. На этом месте практически всегда стоит единица:
Так как мы должны использовать подходящее элементарное преобразование строк и сделать так, чтобы элемент, который находится в матрице под выделенной цифрой
превратился в
. Для этого можно ко второй строке прибавить первую строку и умножить на
.Однако, не сильно хочется работать с дробями, поэтому давайте постараемся этого избежать. Для этого нужно вторую строку умножить на
(разрешающий элемент данного шага).
Соответственно, первая строка остаётся неизменной, а вторая поменяется:
Подбираем такое элементарное преобразование строк, чтобы во второй строке в первом столбце образовался . Для этого первую строку нужно умножить на
и только после этого ко второй строке прибавить изменённую после умножения на
вторую строку. Вот что получилось:
. Теперь прибавляем со второй строки
первую строку
. У нас получился
, который записываем во вторую строку в первый столбец. Также решаем и остальные элементы матрицы. Вот что у нас получилось:
Как всегда у нас первая строка осталась без изменений, а вторая с новыми числами.
Итак, у нас получился ступенчатый вид матрицы:
Записываем новую систему уравнений:
Для проверки решаем систему обратным ходом. Для этого находим сначала :
Так как найден, находим
:
.
Подставляем в изначальную нашу систему уравнений найденные и
:
и
.
Как видите из решения, система уравнений решена верно. Запишем ответ.
Ответ
Выше мы решали систему уравнений в двумя неизвестными, а теперь рассмотрим систему уравнений с тремя неизвестными.
Задача
Решить систему уравнений методом Гаусса:
Решение
Составляем матрицу, куда вписываем и свободные члены:
Что нам надо? Чтобы вместо цифры 2 появился 0. Для этого подбираем ближайшее число. Например, можно взять цифру -2 и на неё перемножить все элементы первой строки. Значит, умножаем , а потом прибавляем, при этом задействуем вторую строку:
. В итоге у нас получился нуль, который записываем во вторую строку в первый столбец. Затем
, и
. Аналогично,
и
. И умножаем свободный член
. Так и запишем следующую матрицу. Не забывайте, что первая строка остаётся без изменений:
Дальше необходимо проделать те же самые действия по отношению к третьей строке. То есть, первую строку нужно умножать не на (-2), а на цифру 3, так как и в третьей строке нужно коэффициенты привести у нулю. Также первую строку умножаем на 3 и прибавляем третью строку. Получается так:
Теперь нужно обнулить элемент 7, который стоит в третьей строке во втором столбце. Для этого выбираем цифру (-7) и проделываем те же действия. Однако, необходимо задействовать вторую строку. То есть, вторую строку умножаем на (-7) и прибавляем с третьей строкой. Итак, . Записываем результат в третью строку. Такие же действия проделываем и с остальными элементами. Получается новая матрица:
В результате получилась ступенчатая система уравнений:
Сначала находим :
,
.
Обратный ход:
Итак, уравнение системы решено верно.
Ответ
,
,
.
Система с четырьмя неизвестными более сложная, так как в ней легко запутаться. Попробуем решить такую систему уравнений.
Задача
Решите систему уравнений методом Гаусса:
Решение
В уравнении , то есть
– ведущий член и пусть
≠ 0
Из данного уравнения составим расширенную матрицу:
Теперь нужно умножить последние три строки (вторую, третью и четвёртую) на: ,
,
. Затем прибавим полученный результат ко второй, третьей и четвёртой строкам исключаем переменную
из каждой строки, начиная не с первой, а не со второй. Посмотрите, как изменилась наша новая матрица и в
теперь стоит 0.
Поменяем вторую и третью строку местами и получим:
Получилось так, что =
b и тогда, умножая вторую строку на (-7/4) и результат данной строки, прибавляя к четвёртой, можно исключить переменную
из третьей и четвёртой строк:
Получилась такая матрица:
Также, учитывая, что =
, умножим третью строку на: 13,5/8 = 27/16, и, полученный результат прибавим к четвёртой, чтобы исключить переменную
и получаем новую систему уравнений:
Теперь необходимо решить уравнение обратным ходом и найдём из последнего, четвёртого уравнения ,
из третьего: =
=
=
второе уравнение находим: =
=
= 2,
из первого уравнения: =
.
Значит, решение системы такое: (1, 2, -1, -2).
Ответ
,
,
,
.
Добавим ещё несколько примеров для закрепления материла, но без такого подробного описания, как предыдущие системы уравнений.
Задача
Решить систему уравнений методом Гаусса:
Решение
Записываем расширенную матрицу системы:
Сначала смотрим на левое верхнее число:
Как выше уже было сказано, на этом месте должна стоять единица, но не обязательно. Производим такие действия: первую строку умножаем на -3, а потом ко второй строке прибавляем первую:
Производим следующие действия: первую строку умножаем на -1. Затем к третьей строки прибавляем вторую:
Теперь вторую строку умножаем на 1, а затем к третьей строке прибавляем вторую:
Получился ступенчатый вид уравнения:
Проверяем:
,
,
,
,
.
.
Ответ
,
,
.
Заключение
Итак, вы видите, что метод Гаусса – интересный и простой способ решения систем линейных алгебраических уравнений. Путём элементарных преобразований нужно из системы исключать неизвестные переменные, чтобы систему превратить в ступенчатый вид. Данный метод удобен тем, что всегда можно проверить, правильно ли решено уравнение. Нужно просто подставить найденные неизвестные в изначальную систему уравнений.
Если элементы определителя не равняются нулю, тогда лучше обратиться к методу Крамера, а если же элементы нулевые, тогда такие системы очень удобно решать благодаря методу Гаусса.
Предлагаем ещё почитать учебники, в которых также описаны решения систем методом Гаусса.
Литература для общего развития:
Умнов А. Е. Аналитическая геометрия и линейная алгебра, изд. 3: учеб. пособие – М. МФТИ – 2011 – 259 с.
Карчевский Е. М. Лекции по линейной алгебре и аналитической геометрии, учеб. пособие – Казанский университет – 2012 – 302 с.
Когда
зарядов много, при расчётах полей
возникают некоторые трудности.

их помогает теорема Гаусса. Суть теоремы
Гаусса
сводится к следующему: если произвольное
количество зарядов мысленно окружить
замкнутой поверхностью S,
то поток напряжённости электрического
поля через элементарную площадку dS
можно записать как dФ
= Есоsα۰dS
где α
— угол между нормалью к плоскости и
вектором напряжённости .
(рис.12.7)
Полный
же поток через всю поверхность будет
равен сумме потоков от всех зарядов,
произвольным образом распределённых
внутри её и пропорционально величине
этого заряда
(12.9)

поток вектора напряжённости сквозь
сферическую поверхность радиуса r,
в центре которой расположен точечный
заряд +q
(рис.12.8). Линии напряжённости перпендикулярны
поверхности сферы, α =0, следовательно
соsα
= 1. Тогда
или
Если
поле образовано системой зарядов, то
Теорема
Гаусса:
поток вектора напряжённости
электростатического поля в вакууме
сквозь любую замкнутую поверхность
равен алгебраической сумме зарядов,
заключенных внутри этой поверхности,
делённой на электрическую постоянную.
(12.10)
Если
внутри сферы зарядов нет, то Ф = 0.
Теорема
Гаусса позволяет сравнительно просто
рассчитать электрические поля при
симметрично распределённых зарядов.
Введём
понятие о плотности распределенных
зарядов.
-
Линейная
плотность обозначается τ и характеризует
заряд q,
приходящийся на единицу длины ℓ. В
общем виде может быть рассчитана по
формуле
(12.11)
При
равномерном распределении зарядов
линейная плотность равна
-
Поверхностная
плотность обозначается σ и характеризует
заряд q,
приходящийся на единицу площади S.
В общем виде определяется по формуле
(12.12)
При
равномерном распределении зарядов по
поверхности поверхностная плотность
равна
-
Объёмная
плотность обозначается ρ, характеризует
заряд q,
приходящийся на единицу объёма V.
В общем виде определяется по формуле
(12.13)
При
равномерном распределении зарядов она
равна .
-
Н
апряжённость
электростатического поля равномерно
заряженной сферы
(рис.12.9),
имеющей радиус r0.
Найдём модуль вектора
в какой-либо точке А, находящейся на
расстоянии r1
от центра
этой сферы.
Так
как заряд q
располагается на сфере равномерно, то
σ
= const.
Применим теорему Гаусса. Проведём сферу
радиусом через точку А. Поток вектора
напряжённости рис.12.9 сквозь
сферическую поверхность радиуса равен
соsα
= 1, так как α
= 0. По теореме Гаусса, .
или
(12.14)
Из
выражения (12.14) следует, что напряжённость
поля вне заряженной сферы такая же, как
напряжённость поля точечного заряда,
помещённого в центре сферы. На поверхности
сферы, т.е. r1
= r0
, напряжённость .
Внутри
сферы r1
< r0
(рис.12.9) напряжённость Е = 0, так как сфера
радиусом r2
внутри
никаких зарядов не содержит и, по теореме
Гаусса, поток вектора сквозь такую
сферу равен нулю.
-
Н
апряжённость
поля, создаваемого равномерно заряженным
бесконечно длинным цилиндром
Цилиндр
радиусом r0
равномерно
заряжен с поверхностной плотностью σ
(рис.12.10). Определим напряжённость поля
в произвольно выбранной точке А. Проведём
через точку А воображаемую цилиндрическую
поверхность радиусом R
и длиной ℓ. Вследствие симметрии поток
будет выходить только через боковые
поверхности цилиндра, так как заряды
на цилиндре радиуса r0
распределены по его поверхности
равномерно, т.е. линии напряжённости
будут радиальными прямыми, перпендикулярными
боковым поверхностям обоих цилиндров.
Так как поток через основание цилиндров
равен нулю (cos
α
= 0), а боковая поверхность цилиндра
перпендикулярна силовым линиям (cos
α
= 1), то
или
(12.15)
Выразим
величину Е через σ — поверхностную
плотность. По определению,
следовательно,
Подставим
значение q
в формулу (12.15)
(12.16)
По
определению линейной плотности,
, откуда ;
подставляем это выражение в формулу
(12.16):
(12.17)
т.е.
напряжённость поля, создаваемого
бесконечно длинным заряженным цилиндром,
пропорциональна линейной плотности
заряда и обратно пропорциональна
расстоянию.
-
Напряжённость
поля, создаваемого бесконечной
равномерно заряженной плоскостью
напряжённость поля, создаваемого
бесконечной равномерно заряженной
плоскостью в точке А. Пусть поверхностная
плотность заряда плоскости равна σ. В
качестве замкнутой поверхности удобно
выбрать цилиндр, ось которого
перпендикулярна плоскости, а правое
основание содержит точку А. Плоскость
делит цилиндр пополам. Очевидно, что
силовые линии перпендикулярны плоскости
и параллельны боковой поверхности
цилиндра, поэтому весь поток проходит
только через основания цилиндра. На
обоих основаниях напряжённость поля
одинакова, т.к. точки А и В симметричны
относительно плоскости. Тогда поток,
через основания цилиндра равен
Согласно
теореме Гаусса,
Так
как ,
то ,
откуда
(12.18)
Таким
образом, напряжённость поля бесконечной
заряженной плоскости пропорциональна
поверхностной плотности заряда и не
зависит от расстояния до плоскости.
Следовательно, поле плоскости является
однородным.
-
Напряжённость
поля, создаваемого двумя разноименно
равномерно заряженными параллельными
плоскостями

поле, создаваемое двумя плоскостями,
определяется по принципу суперпозиции
полей:
(рис.12.12). Поле, создаваемое каждой
плоскостью, является однородным,
напряжённости этих полей равны по
модулю, но противоположны по направлению:
.
По принципу суперпозиции напряжённость
суммарного поля вне плоскости равна
нулю:
Между плоскостями
напряжённости полей имеют одинаковые
направления, поэтому результирующая
напряжённость равна
(12.19)
Таким
образом, поле между двумя разноименно
равномерно заряженными плоскостями
однородно и его напряжённость в два
раза больше, чем напряжённость поля,
создаваемого одной плоскостью. Слева
и справа от плоскостей поле отсутствует.
Такой же вид имеет и поле конечных
плоскостей, искажение появляется только
вблизи их границ. С помощью полученной
формулы можно рассчитать поле между
обкладками плоского конденсатора.
Соседние файлы в папке Физика
- #
- #
- #
- #
- #
- #
- #
- #
This article is about Gauss’s law concerning the electric field. For analogous laws concerning different fields, see Gauss’s law for magnetism and Gauss’s law for gravity. For the Ostrogradsky–Gauss theorem, a mathematical theorem relevant to all of these laws, see Divergence theorem.
Gauss’s law in its integral form is most useful when, by symmetry reasons, a closed surface (GS) can be found along which the electric field is uniform. The electric flux is then a simple product of the surface area and the strength of the electric field, and is proportional to the total charge enclosed by the surface. Here, the electric field outside (r > R) and inside (r < R) of a charged sphere is being calculated (see Wikiversity).
In physics and electromagnetism, Gauss’s law, also known as Gauss’s flux theorem, (or sometimes simply called Gauss’s theorem) is a law relating the distribution of electric charge to the resulting electric field. In its integral form, it states that the flux of the electric field out of an arbitrary closed surface is proportional to the electric charge enclosed by the surface, irrespective of how that charge is distributed. Even though the law alone is insufficient to determine the electric field across a surface enclosing any charge distribution, this may be possible in cases where symmetry mandates uniformity of the field. Where no such symmetry exists, Gauss’s law can be used in its differential form, which states that the divergence of the electric field is proportional to the local density of charge.
The law was first[1] formulated by Joseph-Louis Lagrange in 1773,[2] followed by Carl Friedrich Gauss in 1835,[3] both in the context of the attraction of ellipsoids. It is one of Maxwell’s equations, which forms the basis of classical electrodynamics.[note 1] Gauss’s law can be used to derive Coulomb’s law,[4] and vice versa.
Qualitative description[edit]
In words, Gauss’s law states:
- The net electric flux through any hypothetical closed surface is equal to 1/ε0 times the net electric charge enclosed within that closed surface. The closed surface is also referred to as Gaussian surface.[5]
Gauss’s law has a close mathematical similarity with a number of laws in other areas of physics, such as Gauss’s law for magnetism and Gauss’s law for gravity. In fact, any inverse-square law can be formulated in a way similar to Gauss’s law: for example, Gauss’s law itself is essentially equivalent to the Coulomb’s law, and Gauss’s law for gravity is essentially equivalent to the Newton’s law of gravity, both of which are inverse-square laws.
The law can be expressed mathematically using vector calculus in integral form and differential form; both are equivalent since they are related by the divergence theorem, also called Gauss’s theorem. Each of these forms in turn can also be expressed two ways: In terms of a relation between the electric field E and the total electric charge, or in terms of the electric displacement field D and the free electric charge.[6]
Equation involving the E field[edit]
Gauss’s law can be stated using either the electric field E or the electric displacement field D. This section shows some of the forms with E; the form with D is below, as are other forms with E.
Integral form[edit]
Electric flux through an arbitrary surface is proportional to the total charge enclosed by the surface.
No charge is enclosed by the sphere. Electric flux through its surface is zero.
Gauss’s law may be expressed as:[6]
where ΦE is the electric flux through a closed surface S enclosing any volume V, Q is the total charge enclosed within V, and ε0 is the electric constant. The electric flux ΦE is defined as a surface integral of the electric field:
where E is the electric field, dA is a vector representing an infinitesimal element of area of the surface,[note 2] and · represents the dot product of two vectors.
In a curved spacetime, the flux of an electromagnetic field through a closed surface is expressed as
where 





Since the flux is defined as an integral of the electric field, this expression of Gauss’s law is called the integral form.
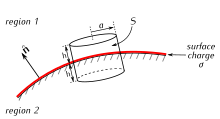
A tiny Gauss’s box whose sides are perpendicular to a conductor’s surface is used to find the local surface charge once the electric potential and the electric field are calculated by solving Laplace’s equation. The electric field is perpendicular, locally, to the equipotential surface of the conductor, and zero inside; its flux πa2·E, by Gauss’s law equals πa2·σ/ε0. Thus, σ = ε0E.
In problems involving conductors set at known potentials, the potential away from them is obtained by solving Laplace’s equation, either analytically or numerically. The electric field is then calculated as the potential’s negative gradient. Gauss’s law makes it possible to find the distribution of electric charge: The charge in any given region of the conductor can be deduced by integrating the electric field to find the flux through a small box whose sides are perpendicular to the conductor’s surface and by noting that the electric field is perpendicular to the surface, and zero inside the conductor.
The reverse problem, when the electric charge distribution is known and the electric field must be computed, is much more difficult. The total flux through a given surface gives little information about the electric field, and can go in and out of the surface in arbitrarily complicated patterns.
An exception is if there is some symmetry in the problem, which mandates that the electric field passes through the surface in a uniform way. Then, if the total flux is known, the field itself can be deduced at every point. Common examples of symmetries which lend themselves to Gauss’s law include: cylindrical symmetry, planar symmetry, and spherical symmetry. See the article Gaussian surface for examples where these symmetries are exploited to compute electric fields.
Differential form[edit]
By the divergence theorem, Gauss’s law can alternatively be written in the differential form:
where ∇ · E is the divergence of the electric field, ε0 is the vacuum permittivity, 
Equivalence of integral and differential forms[edit]
The integral and differential forms are mathematically equivalent, by the divergence theorem. Here is the argument more specifically.
Outline of proof
The integral form of Gauss’ law is:
for any closed surface S containing charge Q. By the divergence theorem, this equation is equivalent to:
for any volume V containing charge Q. By the relation between charge and charge density, this equation is equivalent to:
for any volume V. In order for this equation to be simultaneously true for every possible volume V, it is necessary (and sufficient) for the integrands to be equal everywhere. Therefore, this equation is equivalent to:
Thus the integral and differential forms are equivalent.
Equation involving the D field[edit]
Free, bound, and total charge[edit]
The electric charge that arises in the simplest textbook situations would be classified as «free charge»—for example, the charge which is transferred in static electricity, or the charge on a capacitor plate. In contrast, «bound charge» arises only in the context of dielectric (polarizable) materials. (All materials are polarizable to some extent.) When such materials are placed in an external electric field, the electrons remain bound to their respective atoms, but shift a microscopic distance in response to the field, so that they’re more on one side of the atom than the other. All these microscopic displacements add up to give a macroscopic net charge distribution, and this constitutes the «bound charge».
Although microscopically all charge is fundamentally the same, there are often practical reasons for wanting to treat bound charge differently from free charge. The result is that the more fundamental Gauss’s law, in terms of E (above), is sometimes put into the equivalent form below, which is in terms of D and the free charge only.
Integral form[edit]
This formulation of Gauss’s law states the total charge form:
where ΦD is the D-field flux through a surface S which encloses a volume V, and Qfree is the free charge contained in V. The flux ΦD is defined analogously to the flux ΦE of the electric field E through S:
Differential form[edit]
The differential form of Gauss’s law, involving free charge only, states:
where ∇ · D is the divergence of the electric displacement field, and ρfree is the free electric charge density.
Equivalence of total and free charge statements[edit]
Proof that the formulations of Gauss’s law in terms of free charge are equivalent to the formulations involving total charge.
In this proof, we will show that the equation
is equivalent to the equation
Note that we are only dealing with the differential forms, not the integral forms, but that is sufficient since the differential and integral forms are equivalent in each case, by the divergence theorem.
We introduce the polarization density P, which has the following relation to E and D:
and the following relation to the bound charge:
Now, consider the three equations:
The key insight is that the sum of the first two equations is the third equation. This completes the proof: The first equation is true by definition, and therefore the second equation is true if and only if the third equation is true. So the second and third equations are equivalent, which is what we wanted to prove.
Equation for linear materials[edit]
In homogeneous, isotropic, nondispersive, linear materials, there is a simple relationship between E and D:
where ε is the permittivity of the material. For the case of vacuum (aka free space), ε = ε0. Under these circumstances, Gauss’s law modifies to
for the integral form, and
for the differential form.
Interpretations[edit]
In terms of fields of force[edit]
Gauss’s theorem can be interpreted in terms of the lines of force of the field as follows:
The flux through a closed surface is dependent upon both the magnitude and direction of the electric field lines penetrating the surface. In general a positive flux is defined by these lines leaving the surface and negative flux by lines entering this surface. This results in positive charges causing a positive flux and negative charges creating a negative flux. These electric field lines will extend to infinity decreasing in strength by a factor of one over the distance from the source of the charge squared. The larger the number of field lines emanating from a charge the larger the magnitude of the charge is, and the closer together the field lines are the greater the magnitude of the electric field. This has the natural result of the electric field becoming weaker as one moves away from a charged particle, but the surface area also increases so that the net electric field exiting this particle will stay the same. In other words the closed integral of the electric field and the dot product of the derivative of the area will equal the net charge enclosed divided by permittivity of free space.
Relation to Coulomb’s law[edit]
Deriving Gauss’s law from Coulomb’s law[edit]
Strictly speaking, Gauss’s law cannot be derived from Coulomb’s law alone, since Coulomb’s law gives the electric field due to an individual, electrostatic point charge only. However, Gauss’s law can be proven from Coulomb’s law if it is assumed, in addition, that the electric field obeys the superposition principle. The superposition principle states that the resulting field is the vector sum of fields generated by each particle (or the integral, if the charges are distributed smoothly in space).
Outline of proof
Coulomb’s law states that the electric field due to a stationary point charge is:
where
- er is the radial unit vector,
- r is the radius, |r|,
- ε0 is the electric constant,
- q is the charge of the particle, which is assumed to be located at the origin.
Using the expression from Coulomb’s law, we get the total field at r by using an integral to sum the field at r due to the infinitesimal charge at each other point s in space, to give
where ρ is the charge density. If we take the divergence of both sides of this equation with respect to r, and use the known theorem[9]
where δ(r) is the Dirac delta function, the result is
Using the «sifting property» of the Dirac delta function, we arrive at
which is the differential form of Gauss’ law, as desired.
Since Coulomb’s law only applies to stationary charges, there is no reason to expect Gauss’s law to hold for moving charges based on this derivation alone. In fact, Gauss’s law does hold for moving charges, and in this respect Gauss’s law is more general than Coulomb’s law.
Proof (without Dirac Delta)
Let 
be the electric field, with 
It is true for all 

Consider now a compact set 



But because 
for the argument above (

Therefore the flux through a closed surface generated by some charge density outside (the surface) is null.
Now consider 




Let 

,
and
The last equality follows by observing that 
The RHS is the electric flux generated by a charged sphere, and so:
with
Where the last equality follows by the mean value theorem for integrals. Using the squeeze theorem and the continuity of 
Deriving Coulomb’s law from Gauss’s law[edit]
Strictly speaking, Coulomb’s law cannot be derived from Gauss’s law alone, since Gauss’s law does not give any information regarding the curl of E (see Helmholtz decomposition and Faraday’s law). However, Coulomb’s law can be proven from Gauss’s law if it is assumed, in addition, that the electric field from a point charge is spherically symmetric (this assumption, like Coulomb’s law itself, is exactly true if the charge is stationary, and approximately true if the charge is in motion).
Outline of proof
Taking S in the integral form of Gauss’ law to be a spherical surface of radius r, centered at the point charge Q, we have
By the assumption of spherical symmetry, the integrand is a constant which can be taken out of the integral. The result is
where r̂ is a unit vector pointing radially away from the charge. Again by spherical symmetry, E points in the radial direction, and so we get
which is essentially equivalent to Coulomb’s law. Thus the inverse-square law dependence of the electric field in Coulomb’s law follows from Gauss’ law.
See also[edit]
- Method of image charges
- Uniqueness theorem for Poisson’s equation
- List of examples of Stigler’s law
Notes[edit]
- ^ The other three of Maxwell’s equations are: Gauss’s law for magnetism, Faraday’s law of induction, and Ampère’s law with Maxwell’s correction
- ^ More specifically, the infinitesimal area is thought of as planar and with area dN. The vector dR is normal to this area element and has magnitude dA.[7]
Citations[edit]
- ^ Duhem, Pierre (1891). Leçons sur l’électricité et le magnétisme (in French). Paris Gauthier-Villars. vol. 1, ch. 4, p. 22–23. shows that Lagrange has priority over Gauss. Others after Gauss discovered «Gauss’ Law», too.
- ^ Lagrange, Joseph-Louis (1773). «Sur l’attraction des sphéroïdes elliptiques». Mémoires de l’Académie de Berlin (in French): 125.
- ^ Gauss, Carl Friedrich (1877). Theoria attractionis corporum sphaeroidicorum ellipticorum homogeneorum methodo nova tractata (in Latin). (Gauss, Werke, vol. V, p. 1). Gauss mentions Newton’s Principia proposition XCI regarding finding the force exerted by a sphere on a point anywhere along an axis passing through the sphere.
- ^ Halliday, David; Resnick, Robert (1970). Fundamentals of Physics. John Wiley & Sons. pp. 452–453.
- ^ Serway, Raymond A. (1996). Physics for Scientists and Engineers with Modern Physics (4th ed.). p. 687.
- ^ a b Grant, I. S.; Phillips, W. R. (2008). Electromagnetism. Manchester Physics (2nd ed.). John Wiley & Sons. ISBN 978-0-471-92712-9.
- ^ Matthews, Paul (1998). Vector Calculus. Springer. ISBN 3-540-76180-2.
- ^ Fedosin, Sergey G. (2019). «On the Covariant Representation of Integral Equations of the Electromagnetic Field». Progress in Electromagnetics Research C. 96: 109–122. arXiv:1911.11138. Bibcode:2019arXiv191111138F. doi:10.2528/PIERC19062902. S2CID 208095922.
- ^ See, for example, Griffiths, David J. (2013). Introduction to Electrodynamics (4th ed.). Prentice Hall. p. 50.
References[edit]
- Gauss, Carl Friedrich (1867). Werke Band 5. Digital version
- Jackson, John David (1998). Classical Electrodynamics (3rd ed.). New York: Wiley. ISBN 0-471-30932-X. David J. Griffiths (6th ed.)
External links[edit]
Media related to Gauss’ Law at Wikimedia Commons
- MIT Video Lecture Series (30 x 50 minute lectures)- Electricity and Magnetism Taught by Professor Walter Lewin.
- section on Gauss’s law in an online textbook
- MISN-0-132 Gauss’s Law for Spherical Symmetry (PDF file) by Peter Signell for Project PHYSNET.
- MISN-0-133 Gauss’s Law Applied to Cylindrical and Planar Charge Distributions (PDF file) by Peter Signell for Project PHYSNET.
До того, как мы рассмотрим теорему Гаусса, поговорим о том, кто же ее открыл и применил на практике.
Карл Фридрих Гаусс 1777-1855 г. Немецкий математик — один из великих, который не уступает Ньютону и Архимеду. Родился в Брауншвейге, в крестьянской семье.
Гениальная способность к математике проявилась уже в детстве и, пораженный чудесным талантом, учитель начальных классов убеждал родителей Карла не отдавать мальчика в ремесленную школу, а предоставить возможность продолжить образование. В четырнадцать лет Гаусс буквально удивился своим обширным знанием графа Брауншвейгского, и он дал юноше стипендию.
Большую часть своих важных математических исследований Гаусс сделал до того, как в 1799 г. он получил ученую степень доктора наук в Гёттингенском университете, а через два года выпустил свой фундаментальный труд «Трактат о математике», посвященный его влиятельному покровителю.
первый крупный труд 24-летнего немецкого математика К.Ф. Гаусса
В трактате речь шла об арифметике — разделе математики, который занимается, прежде всего, натуральными числами и отношениями между ним, например, такими как Великая теорема Ферма. Впоследствии Гаусс не оставил свои занятия математикой, формулируя ряд принципов теоретической вероятности и математики, в том числе распределения случайной величины вокруг средней величины, которое было названо распределением Гаусса.
В 1801 г., когда был открыт первый астероид Церера, Гаусс обратился к астрологии. Чтобы рассчитать параметры орбиты, он разработал методику наименьшего квадрата, которая позволяет полностью рассчитывать орбиту солнечного спутника по результатам только трех измерений положения его места на орбите около Солнца. Через пять лет ученый был назначен директором Гёттингенской обсерватория и остался на этом посту до конца своей жизни. К тому же Гаусс был первым, кто всерьёз занимался изучением земной магнетизма, и именно в честь него названа единица магнитной напряженности.
В науке нередко бывает так, что один и тот же закон может быть сформулирован по-разному. В большинстве случаев формулировка закона не меняет ничего в плане его действий, но новые формулировки помогают теоретикам чуть иначе трактовать его и проверять его в отношении новых природных явлений. Именно таким образом можно рассмотреть теорему Гаусса — это, по сути, обобщение закона Кулона, который, в своей очередь, был обобщением всех знаний ученых об электростатических зарядах.
В математике, физике, астрономии найдется немного областей, развитию которых не посодействовал замечательный гений Карла Фридриха Гаусса.
В 1831 г. вместе с юным коллегой Вильгельмом Вебером (1804-1891 г.) он начал изучать электричество и магнетизм, вскоре сформулировав и доказав теорему, которая носит его имя. Для понимания её смысла представьте изолированный точечный электрический заряд Q. А сейчас представьте себе, что его окружает замкнутая поверхность. В теореме форма поверхности не важна – это может оказаться даже сдутым воздушным шариком.
В каждой точке окружающей заряд поверхности, наблюдается электрическое поле, образованное зарядом, а произведение напряженности этого электрического поля на сколь угодно малую единицу площади окружающей заряд поверхности, через которую проходят силовые линии поля, называется потоком напряженности электрического поля, и можно рассчитать поток напряженности, приходящийся на каждый элемент поверхности. В теореме Гаусса говорится, что общий поток электрической напряженности, проходящий по окружающей поверхности заряда, пропорционален величине зарядов.
Связь между законом Кулона и теоремой Гаусса можно рассмотреть на простом примере. Предположим, что заряд q окружен сферой радиуса r. На удалении r от заряда напряженность электрического поля, которая определяется силой притяжения или отталкивания единичного заряда, помещенного в соответствующую точку, составит, согласно закону Кулона:
Формула
[E=k q / r^{2}]
И то же самое значение мы получим для любой точки сферы заданного радиуса. Следовательно, суммарный поток напряженности электрического поля будет равен значению напряженности поля на удалении r от заряда, помноженному на площадь сферы (которая, как известно, равняется 4πr2). Иными словами, суммарный поток будет равен:
Формула
Формула теоремы Гаусса
[4 pi r^{2} times k q / r^{2}=4 pi k q]
Применение формулы Гаусса
Формула применяется для преобразования объемного интеграла в интеграл на замкнутую поверхность и обратно. В математическом анализе формула Теоремы Остроградского — Гаусса применяется для расчета дифференциации, т.е. потока вектора по поверхности окружающей среды внешними направлениями.
Принимая во внимание то, что поток векторного поля через замкнутую поверхность δδ в направлении внешней единичной нормали n0¯¯¯¯¯n0¯ равен дивергенции данного поля, вычисленной по телу TT, которое эта поверхность.
Нет времени решать самому?
Наши эксперты помогут!
Применение теоремы Гаусса для электростатического поля
Теорема Остроградского-Гаусса применяется для расчета электростатического поля для тех задач, где поле имеет специальную симметрию. Например, плоскую, цилиндрическую или сферическую. В данном случае на эффективность применения теоремы влияют симметрия и конфигурация поля, которые должны соответствовать двум условиям:
- заряженное тело должно быть окружено простой замкнутой поверхностью;
- вычисление потока вектора напряженности необходимо свести к умножению ЕЕ (или EnEn) на площадь поверхности SS или часть нее.
Если исходные данные не соответствуют условиям, то при решении задачи необходимо использовать другие методы.
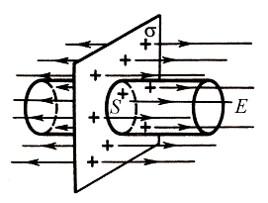
Рассмотрим применение теоремы для равномерно заряженной плоскости.
Задача
Предположим, что заряд положительный, а плоскость заряжена с постоянной поверхностной плотностью, что выражается в формуле δ=dqdSδ=dqdS. Благодаря симметрии можно сделать вывод, что напряженность в любой точке поля обладает направлением, перпендикулярным плоскости. Из этого же можно сделать вывод, что во всех точках, симметричных плоскости, напряженность поля одинакова, но ее направление противоположно.
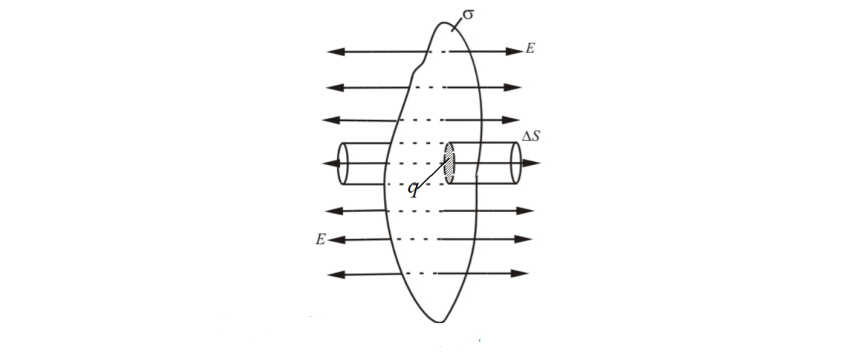
Отметим на заряженной плоскости площадь △S△S. Определим вокруг площадки замкнутую цилиндрическую поверхность (рисунок 3) так, чтобы ее образующие основания были перпендикулярны плоскости, располагались симметрично, относительно нее и имели величину △S△S.
А теперь используем теорему Остроградского-Гаусса: ∮SEndS=1ε0∑q1∮SEndS=1ε0∑q1. Так как в этом случае En=0En=0 в каждой точке, через боковую часть потока не будет. В случае оснований En=EEn=E, а исходя из этого совокупный поток через поверхность равен 2E△S2E△S.
Посмотрим теперь внутрь поверхности. Там заключен заряд δ△Sδ△S. В соответствии с теоремой Остроградского-Гаусса, должно быть выполнено условие: 2E△S=δ△Sε02E△S=δ△Sε0, из чего следует E=δ2ε0E=δ2ε0.
Так как напряженность поля равна на любых расстояниях от плоскости, в вычисления не нужно включать длину цилиндра. Если плоскость заряжена, то направление векторов изменяется на противоположное.
Поток вектора напряженности в теореме Гаусса
Поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме всех зарядов, расположенных внутри поверхности, деленной на ε0 (поток вектора напряженности электрического поля равен числу линий напряженности, пересекающих поверхность S.)
С помощью дифференциальной формы теоремы можно рассчитать электростатическое поле при произвольном пространственном распределении зарядов. В ней установлена связь между объемной плотностью заряда ρ и изменением Е в окрестности данной точки пространства.

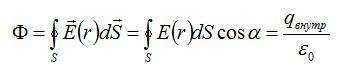
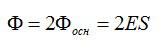
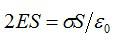
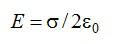
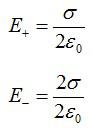
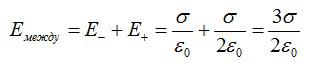
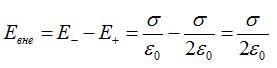
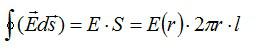
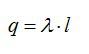
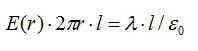
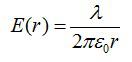
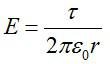
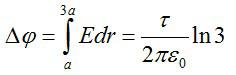
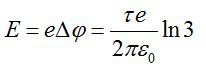
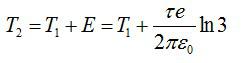
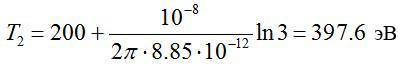
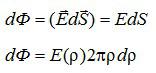
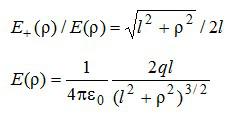
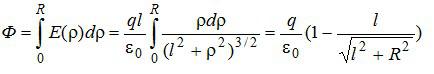
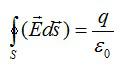
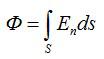

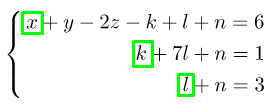
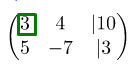
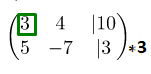
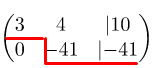

 апряжённость
апряжённость апряжённость
апряжённость