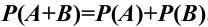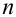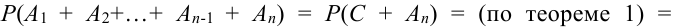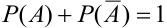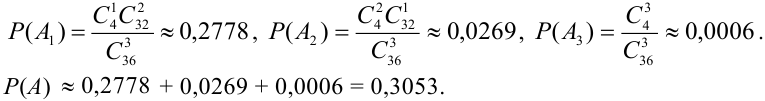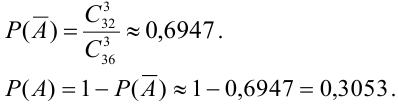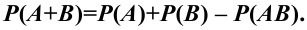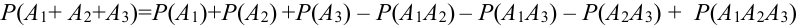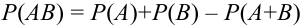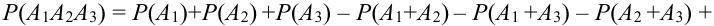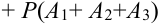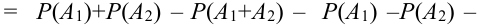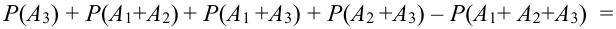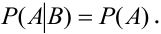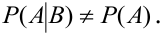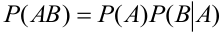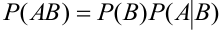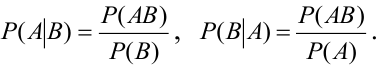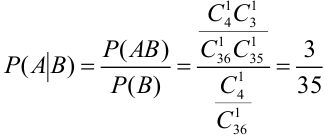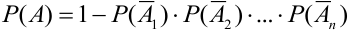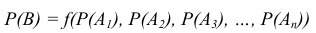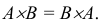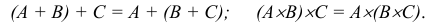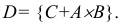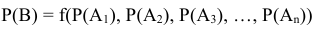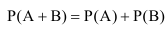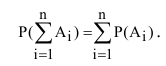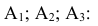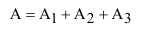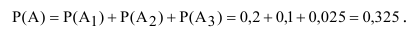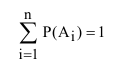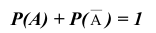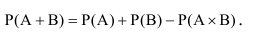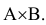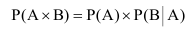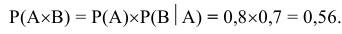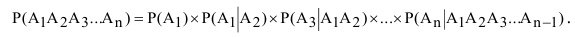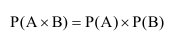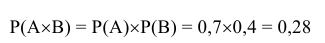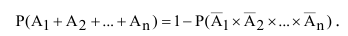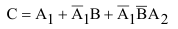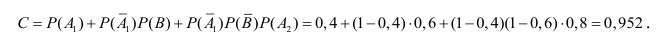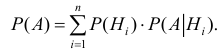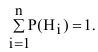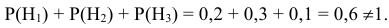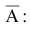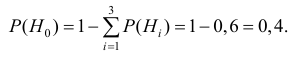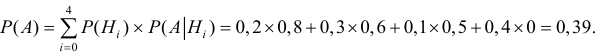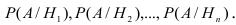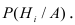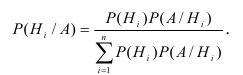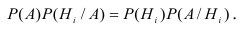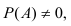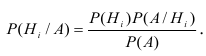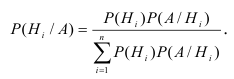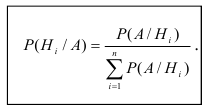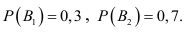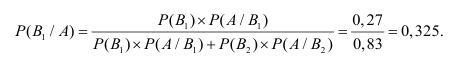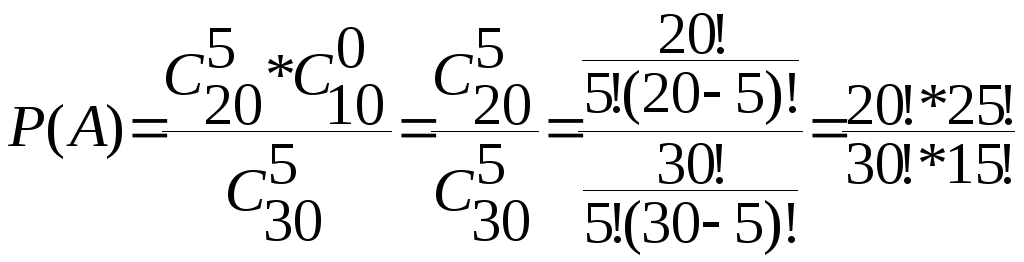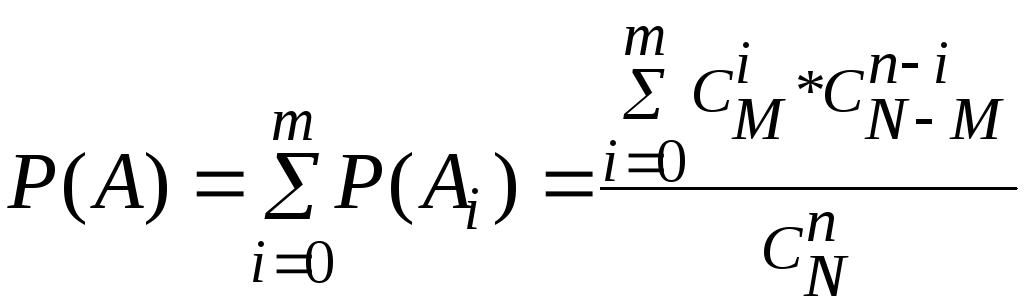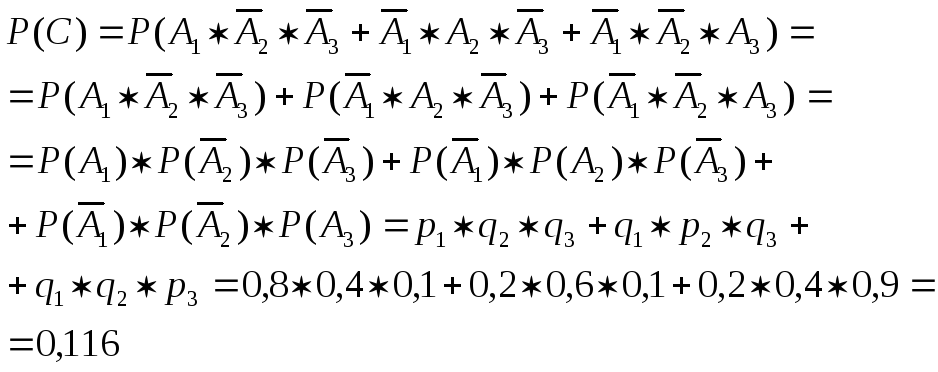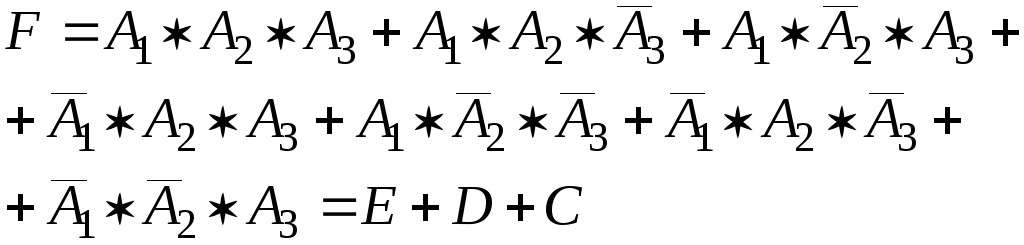Как найти теорему вероятности

Содержание:

Основные теоремы теории вероятностей:

Теоремы сложения вероятностей

Теорема 1. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: Теоремы теории вероятностей - определение и вычисление с примерами решения

Доказательство.

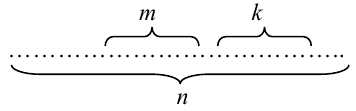
Докажем теорему для схемы случаев. Пусть всевозможные исходы опыта сводятся к совокупности случаев, которые можно наглядно изобразить в виде Теоремы теории вероятностей - определение и вычисление с примерами решения

Теоремы теории вероятностей - определение и вычисление с примерами решения

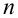
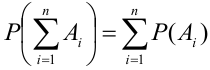
Теорема 1 (Обобщенная теорема сложения несовместных событий) Вероятность суммы Теоремы теории вероятностей - определение и вычисление с примерами решения несовместных событий равна сумме вероятностей этих событий: Теоремы теории вероятностей - определение и вычисление с примерами решения.

Доказательство (методом математической индукции).

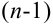
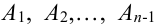
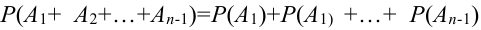
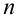
Предположим, что теорема справедлива для Теоремы теории вероятностей - определение и вычисление с примерами решения несовместного события: Теоремы теории вероятностей - определение и вычисление с примерами решения, т.е. справедливо равенство: Теоремы теории вероятностей - определение и вычисление с примерами решения. Докажем, что теорема будет справедлива для Теоремы теории вероятностей - определение и вычисление с примерами решения несовместных событий.

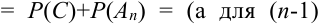
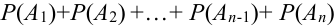
Обозначим Теоремы теории вероятностей - определение и вычисление с примерами решения.

Имеем Теоремы теории вероятностей - определение и вычисление с примерами решенияТеоремы теории вероятностей - определение и вычисление с примерами решения несовместного события теорема доказана) = Теоремы теории вероятностей - определение и вычисление с примерами решения. (что и треб. доказать)

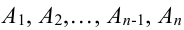
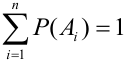
Следствие 1. Если события Теоремы теории вероятностей - определение и вычисление с примерами решения образуют полную группу несовместных событий, то сумма их вероятностей равна единице: Теоремы теории вероятностей - определение и вычисление с примерами решения.

Доказательство.

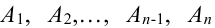
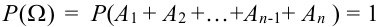
Т.к. события Теоремы теории вероятностей - определение и вычисление с примерами решения образуют полную группу несовместных событий, то, по определению, появление хотя бы одного из них — достоверное событие: Теоремы теории вероятностей - определение и вычисление с примерами решения.

Т.к. события несовместные, то к ним применима обобщенная теорема сложения:

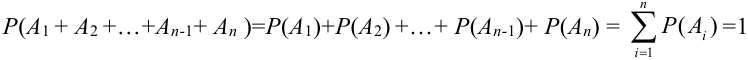
Теоремы теории вероятностей - определение и вычисление с примерами решения, (что и треб, доказать).

Следствие 2. Сумма вероятностей противоположных событий равна единице: Теоремы теории вероятностей - определение и вычисление с примерами решения

Доказательство.

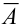
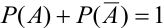
События А, Теоремы теории вероятностей - определение и вычисление с примерами решения — противоположные, т.е. по определению образуют полную группу несовместных событий, тогда по следствию 1, Теоремы теории вероятностей - определение и вычисление с примерами решения.

Замечание. Следствие 2 — частный случай следствия 1. На практике весьма часто оказывается легче вычислить вероятность противоположного события, чем прямого.

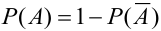
Теоремы теории вероятностей - определение и вычисление с примерами решения.

В формулировке таких задач встречаются слова «хотя бы», «не менее», «по крайней мере» и др.

Пример:

Из колоды карт (36) наудачу вынимают 3 карты. Найти вероятность того, что среди них окажется хотя бы один туз.

Решение.

1 способ (по теореме 1′).

Событие А = {из 3 карт окажется хотя бы один туз}.

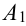
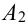
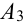
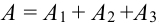
Хотя бы один — это либо один, либо два, либо три, т.е. событие А может быть представлено в виде суммы трех событий: Теоремы теории вероятностей - определение и вычисление с примерами решения = {из 3 карт окажется один туз}, Теоремы теории вероятностей - определение и вычисление с примерами решения = {из 3 карт окажется два туза}, Теоремы теории вероятностей - определение и вычисление с примерами решения = {из 3 карт окажется три туза}.

Теоремы теории вероятностей - определение и вычисление с примерами решения.

Т.к. события несовместны, то по теореме 1′: 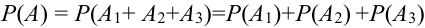Теоремы теории вероятностей - определение и вычисление с примерами решения.

Найдем отдельно вероятности событий.

Теоремы теории вероятностей - определение и вычисление с примерами решения

2 способ (по следствию 2).

Событие 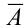Теоремы теории вероятностей - определение и вычисление с примерами решения = {из 3 вынутых карт не окажется ни одного туза}.

Теоремы теории вероятностей - определение и вычисление с примерами решения

Теорема 2. Вероятность суммы двух совместных событий равна сумме вероятностей этих

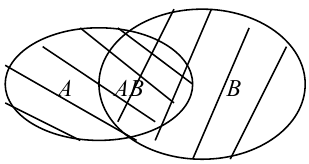
событий без вероятности    их произведения (совместного осуществления): Теоремы теории вероятностей - определение и вычисление с примерами решения

Доказательство (геометрическое)

Теоремы теории вероятностей - определение и вычисление с примерами решения

События отождествляют с множествами. Два раза накладываем «лепесток» друг на друга, поэтому и отнимаем его. (что и треб. доказать)

Теорема 2 ( Обобщенная теорема сложения совместных событий).

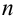
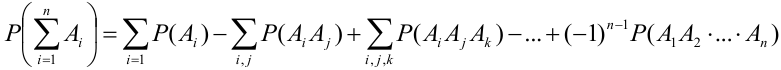
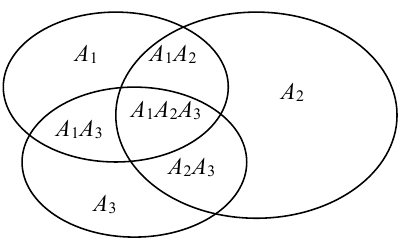
Вероятность суммы Теоремы теории вероятностей - определение и вычисление с примерами решения совместных событий равна Теоремы теории вероятностей - определение и вычисление с примерами решения, где суммы распространяются на различные значения индексов.

Для трех совместных событий теорема запишется в виде:

Теоремы теории вероятностей - определение и вычисление с примерами решения

Доказательство для трех событий (геометрическое):

Теоремы теории вероятностей - определение и вычисление с примерами решения

События отождествляют с множествами (см. рис.). (что и треб. доказать)

Замечание. Аналогичную формулу можно написать для произведения совместных событий:

Теоремы теории вероятностей - определение и вычисление с примерами решения

Теоремы теории вероятностей - определение и вычисление с примерами решенияТеоремы теории вероятностей - определение и вычисление с примерами решения

Пример:

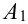
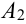
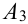
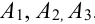
Для поражения самолета необходимо, чтобы были поражены оба двигателя (события Теоремы теории вероятностей - определение и вычисление с примерами решения и Теоремы теории вероятностей - определение и вычисление с примерами решения) или была поражена кабина пилота (событие Теоремы теории вероятностей - определение и вычисление с примерами решения). Требуется выразить вероятность поражения самолета (событие А) через вероятности событий Теоремы теории вероятностей - определение и вычисление с примерами решения.

Решение.

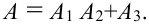
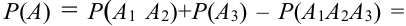
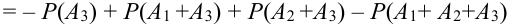
Теоремы теории вероятностей - определение и вычисление с примерами решения Т.к. события совместны, то по теореме 2 следует, что

Теоремы теории вероятностей - определение и вычисление с примерами решения (по замечанию) =Теоремы теории вероятностей - определение и вычисление с примерами решенияТеоремы теории вероятностей - определение и вычисление с примерами решенияТеоремы теории вероятностей - определение и вычисление с примерами решения.

Теоремы умножения вероятностей

Определение 21. Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.

Определение 22. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Примеры:

1) А = {появление решки на первой монете}, В = {появление решки на второй монете}. А и В — независимы.

2) А = {рождение мальчика у Тани}, В = {рождение мальчика у Лены}. А и В — независимы.

3) В урне 2 белых и 1 черный шар. Двое Таня и Ваня вынимают из урны по одному шару. Зависимы или независимы события: А = {появление белого шара у Тани}, В = {появление белого шара у Вани}?

Решение.

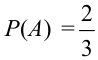
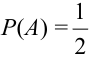
Найдем вероятности событий. Теоремы теории вероятностей - определение и вычисление с примерами решения до известия о событии В. После известия о событии В данная вероятность Теоремы теории вероятностей - определение и вычисление с примерами решения. Следовательно, А и В зависимые.

Определение 23. Два события называются независимыми, если появление одного из них не изменяет вероятности появления другого.

Определение 24. Несколько событий называются независимыми, если любое из них не зависит от любой совокупности остальных.

Определение 25. Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается 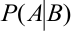Теоремы теории вероятностей - определение и вычисление с примерами решения.

В Примере 3): 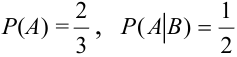Теоремы теории вероятностей - определение и вычисление с примерами решения.

Условие независимости события А от события В: Теоремы теории вероятностей - определение и вычисление с примерами решения

Условие зависимости события А от события В: Теоремы теории вероятностей - определение и вычисление с примерами решения

Теорема 3. Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место.

Теоремы теории вероятностей - определение и вычисление с примерами решения

Доказательство.

Докажем для схемы урн истинность тождества формулы.

Пусть всевозможные исходы опыта сводятся к 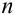Теоремы теории вероятностей - определение и вычисление с примерами решения случаям, которые изобразим в виде точек:

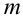
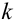
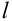
Пусть событию А благоприятствует Теоремы теории вероятностей - определение и вычисление с примерами решения случаев, событию В — Теоремы теории вероятностей - определение и вычисление с примерами решения случаев, а т.к. события А и В совместны (мы не предполагали их несовместность), то событиям А и В одновременно благоприятствует Теоремы теории вероятностей - определение и вычисление с примерами решения случаев.

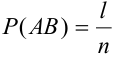
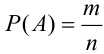
Тогда, вероятности данных событий равны: Теоремы теории вероятностей - определение и вычисление с примерами решения, Теоремы теории вероятностей - определение и вычисление с примерами решения.

Теоремы теории вероятностей - определение и вычисление с примерами решения

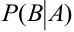
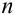
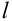
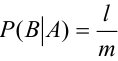
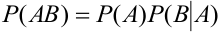
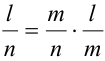
Вычислим условную вероятность Теоремы теории вероятностей - определение и вычисление с примерами решения, т.е. условную вероятность события В в предположении, что А имело место. Если известно, что А произошло, то из ранее возможных Теоремы теории вероятностей - определение и вычисление с примерами решения случаев остаются возможными только те, которые благоприятствовали событию А. Из них Теоремы теории вероятностей - определение и вычисление с примерами решения случаев благоприятны событию В, следовательно, Теоремы теории вероятностей - определение и вычисление с примерами решения, т.е.

Теоремы теории вероятностей - определение и вычисление с примерами решения — истинно, т.к. Теоремы теории вероятностей - определение и вычисление с примерами решения — истинное тождество. (что и треб, доказать).

Замечание 1. При применении теоремы вполне безразлично, какое из событий А или В считать первым, а какое вторым, т.е. теорему можно записать в виде: Теоремы теории вероятностей - определение и вычисление с примерами решения

Замечание 2. В общем случае при 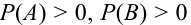Теоремы теории вероятностей - определение и вычисление с примерами решения условная вероятность выражается формулой: Теоремы теории вероятностей - определение и вычисление с примерами решения

Следствие 1. Если событие А не зависит от события В, то и событие В не зависит от события А.

Замечание 3. Зависимость и независимость событий всегда взаимны.

Замечание 4. Условные вероятности обладают всеми свойствами, присущими обычным вероятностям:

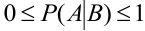
1. Теоремы теории вероятностей - определение и вычисление с примерами решения,

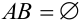
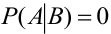
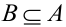
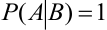
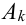
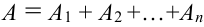
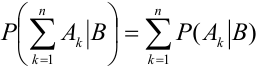
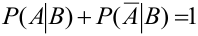
2. если наступление события В исключает возможность осуществления А, т.е. Теоремы теории вероятностей - определение и вычисление с примерами решения, то Теоремы теории вероятностей - определение и вычисление с примерами решения если событие В ведет к обязательному осуществлению А, т.е. Теоремы теории вероятностей - определение и вычисление с примерами решения, то Теоремы теории вероятностей - определение и вычисление с примерами решения.

3. Если Теоремы теории вероятностей - определение и вычисление с примерами решения— несовместные события, т.е. Теоремы теории вероятностей - определение и вычисление с примерами решения, то Теоремы теории вероятностей - определение и вычисление с примерами решения.

4. Теоремы теории вероятностей - определение и вычисление с примерами решения.

Замечание 5. Если А и В независимы, то независимы также события 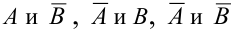Теоремы теории вероятностей - определение и вычисление с примерами решения.

Теорема 3. ( Обобщенная теорема умножения зависимых событий).

Вероятность произведения нескольких зависимых событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что всс предыдущие имели место:

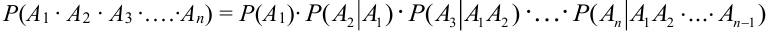
Теоремы теории вероятностей - определение и вычисление с примерами решения.

Теорема 4. {теорема умножения независимых событий).

Вероятность произведения двух независимых событий равна произведению вероятностей этих событий: 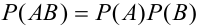Теоремы теории вероятностей - определение и вычисление с примерами решения.

Теорема 4. ( Обобщенная теорема умножения независимых событий).

Вероятность произведения нескольких независимых событий равна произведению вероятностей этих событий:

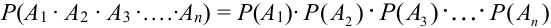
Теоремы теории вероятностей - определение и вычисление с примерами решения.

Пример:

Из колоды карт последовательно вынуты две карты. Найти: а) вероятность того, что вторая карта окажется тузом (неизвестно, какая карта была вынута вначале), б) вероятность того, что вторая карта будет тузом, если первоначально тоже был вынут туз.

Решение.

Обозначим А = {появление туза вторым}, В = {появление туза первым}.

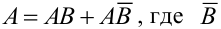
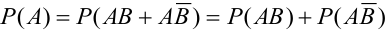
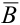
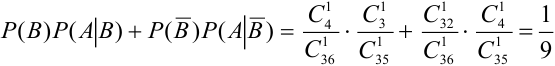
а) Теоремы теории вероятностей - определение и вычисление с примерами решения = {появление первым не туза}. События АВ и АВ — несовместны, тогда по теореме 1 следует, что Теоремы теории вероятностей - определение и вычисление с примерами решения = (события А и В, А и Теоремы теории вероятностей - определение и вычисление с примерами решения — зависимые, применим теорему 3) = Теоремы теории вероятностей - определение и вычисление с примерами решения.

б) Если вынутая первая карта — туз , то в колоде осталось 35 карт и среди них только три туза, следовательно, 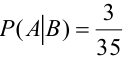Теоремы теории вероятностей - определение и вычисление с примерами решения.

Или можно было найти эту вероятность, используя формулу условной вероятности: 

Теоремы теории вероятностей - определение и вычисление с примерами решения

Пример:

В урне 2 белых и 3 черных шара. Из урны вынимают подряд 2 шара. Найти вероятность того, что а) оба белые, б) оба белые, если после первого вынимания шар возвращают обратно в урну, и шары перемешиваются.

Решение.

Обозначим: А = {появление двух белых шаров}, В = {появление белого шара при первом вынимании}, С = {появление белого шара при втором вынимании}.

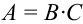
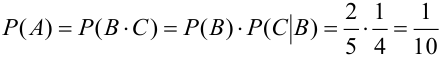
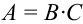
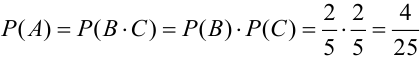
а) Теоремы теории вероятностей - определение и вычисление с примерами решения. События В и С — зависимы, тогда по теореме 3 следует, что

Теоремы теории вероятностей - определение и вычисление с примерами решения.

б) Теоремы теории вероятностей - определение и вычисление с примерами решения. События В и С — независимы, тогда по теореме 4 следует, что Теоремы теории вероятностей - определение и вычисление с примерами решения.

Теорема 5. Вероятность наступления события А, состоящего в появлении хотя бы одного из событий 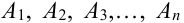Теоремы теории вероятностей - определение и вычисление с примерами решения, независимых в совокупности, равна разности между 1 и произведением вероятностей противоположных событий: Теоремы теории вероятностей - определение и вычисление с примерами решения

Если все 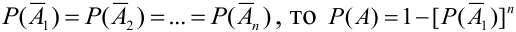Теоремы теории вероятностей - определение и вычисление с примерами решения.

Пример:

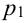
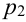
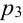
Производится три выстрела по одной и той же мишени. Вероятности попадания при первом, втором и третьем выстрелах равны соответственно Теоремы теории вероятностей - определение и вычисление с примерами решения = 0,4; Теоремы теории вероятностей - определение и вычисление с примерами решения = 0,5; Теоремы теории вероятностей - определение и вычисление с примерами решения = 0,7. Найти вероятность того, что в результате этих трех выстрелов в мишени будет хотя бы одна пробоина.

Решение.

Обозначим А = {хотя бы одно попадание в цель}.

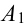
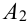
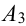
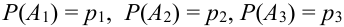
Теоремы теории вероятностей - определение и вычисление с примерами решения = {попадание в цель при первом выстреле}, Теоремы теории вероятностей - определение и вычисление с примерами решения = {попадание в цель при втором выстреле}, Теоремы теории вероятностей - определение и вычисление с примерами решения = {попадание в цель при третьем выстреле}. Теоремы теории вероятностей - определение и вычисление с примерами решения.

Можно расписать в алгебре событий данное событие в виде суммы произведений: 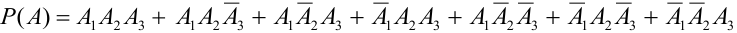Теоремы теории вероятностей - определение и вычисление с примерами решения и найти вероятности слагаемых, где множители — независимые события. Но это нецелесообразно.

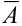
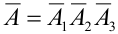
Перейдем от прямого события к противоположному: Теоремы теории вероятностей - определение и вычисление с примерами решения = { ни одного попадания в цель}:

Теоремы теории вероятностей - определение и вычисление с примерами решения,

где 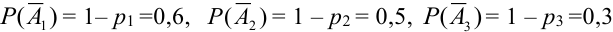Теоремы теории вероятностей - определение и вычисление с примерами решения.

Тогда по теореме 5:

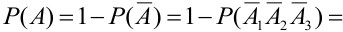
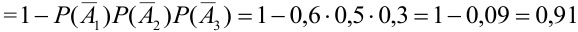
Теоремы теории вероятностей - определение и вычисление с примерами решения (т.к. события независимые, то по теореме 4) = Теоремы теории вероятностей - определение и вычисление с примерами решения.

Основные формулы для вычисления вероятностей

Ограниченность классического и статистического способов определения вероятности событий, приемлемых, главным образом, для определения вероятности простых событий, приводит к тому, что в подавляющем большинстве случаев ни один из этих способов в чистом виде для решения задачи определения наступления событий применить не удаётся.

Например, требуется определить вероятность поражения движущегося танка. Определить эту вероятность по частоте наступления события на практике невозможно — необходимо провести большое число стрельб. При этом надо не только определить вероятность попадания в движущийся танк (что сделать не сложно), но и определить вероятность поражения его экипажа, если будет иметь место попадание в танк (а это выполнить на практике невозможно).

Факт сложности или невозможности определения вероятности сложных событий явился стимулом разработки аппарата теории вероятностей, с помощью которого вероятность определяется не прямым, а косвенным методом через вероятность более простых событий.

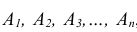
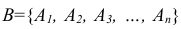
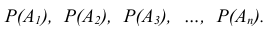
Сущность косвенного метода определения вероятности сложного события заключается в следующем: вначале анализируют условия испытания и устанавливают события Теоремы теории вероятностей - определение и вычисление с примерами решения от которых зависит наступление события В, как комбинацию Теоремы теории вероятностей - определение и вычисление с примерами решения. Определяют вероятности наступления простых событий Теоремы теории вероятностей - определение и вычисление с примерами решения. После чего определяют вероятности интересующего события В как функцию известных или заданных вероятностей.

Теоремы теории вероятностей - определение и вычисление с примерами решения

Однако определению вероятности наступления сложного события как комбинации более простых событий должны предшествовать твёрдые знания правил применения рассмотренных в лекции теорем сложения (объединения) и умножения (пересечения) событий.

Этому вопросу и будет посвящён вопрос нашего занятия.

Пример:

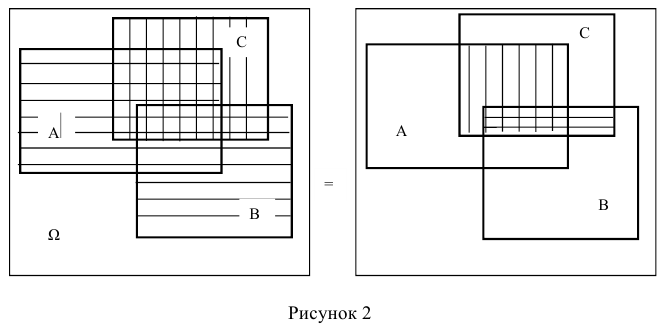
Для того что бы вывести из строя артиллерийскую батарею необходимо поразить либо два взвода с орудиями либо центр управления огнём. Используя операции сложения (объединения) и умножения (пересечения) событий представим сложное событие D={ поражение артиллерийской батареи} как комбинацию простых событий. Результат проиллюстрируем диаграммой Эйлера-Венна.

Решение:

Обозначим через событие А = {поражение первого взвода орудий}, через событие В = {поражение второго взвода орудий}, С = {поражение центра управления огнём}. Тогда событие D = {поражение артиллерийской батареи} определится как поражение либо центра управления огнём (событие С) либо одновременно первого взвода орудий (событие А) и второго взвода орудий (событие В), т.е. будет иметь место следующая комбинация событий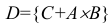Теоремы теории вероятностей - определение и вычисление с примерами решения (рисунок 1).

Теоремы теории вероятностей - определение и вычисление с примерами решения
Для решения такого типа задач необходимо усвоить ряд основных свойств, которыми обладают действия над событиями.

Операции сложения (объединения) и умножения (пересечения) событий обладают рядом свойств, аналогичным свойствам сложения и умножения чисел.

1.    Переместительное свойство:

А + В = В + А;    Теоремы теории вероятностей - определение и вычисление с примерами решения

2.    Сочетательное свойство:

Теоремы теории вероятностей - определение и вычисление с примерами решения

3.    Распределительное свойство:

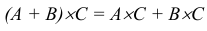
Теоремы теории вероятностей - определение и вычисление с примерами решения (рисунок 2).

Теоремы теории вероятностей - определение и вычисление с примерами решения
 

4.    Операции прибавления пустого множества и умножения на пустое множество аналогичны операциям над числами, если считать пустое множество за ноль.Теоремы теории вероятностей - определение и вычисление с примерами решения

Ряд операций над событиями уже не обладают свойствами по аналогии с арифметическими действиями, например:

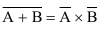
5.    Теоремы теории вероятностей - определение и вычисление с примерами решения (рисунок 3)

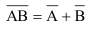
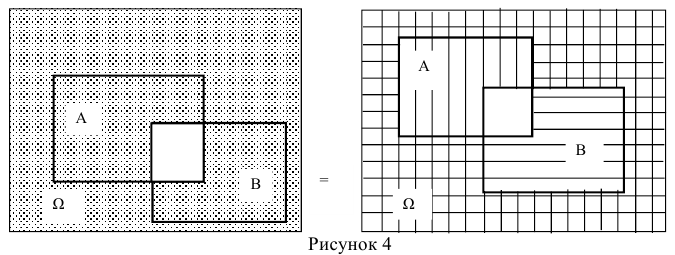
Теоремы теории вероятностей - определение и вычисление с примерами решения

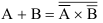
6. Теоремы теории вероятностей - определение и вычисление с примерами решения (рисунок 4).

 Теоремы теории вероятностей - определение и вычисление с примерами решения                           

7. Теоремы теории вероятностей - определение и вычисление с примерами решения (рисунок 5)

Теоремы теории вероятностей - определение и вычисление с примерами решения

Основные теоремы теории вероятностей: сложение, умножение, формула полной вероятности

На предыдущей лекции мы говорили о том, что достаточно часто определить вероятность сложного события трудно или вообще невозможно. Для чего научились представлять события, как комбинацию других более простых событий используя понятия суммы (объединения) или произведения (пересечения) событий.

Вспомним пример, рассматриваемый нами на предыдущей лекции:

Для того что бы вывести из строя артиллерийскую батарею необходимо поразить либо два взвода с орудиями либо центр управления огнём. Используя для решения задачи правила сложения и умножения событий сложное событие — поражение артиллерийской батареи, заключающееся в поражении либо двух взводов орудий либо центра управления огнём, было представлено как следующая комбинация событий Теоремы теории вероятностей - определение и вычисление с примерами решения

На сегодняшнем занятии мы ответим на следующий вопрос: как определить вероятность сложного события представляющего собой функцию известных или заданных вероятностей

Теоремы теории вероятностей - определение и вычисление с примерами решения

При определении вероятностей сложных событий пользуются теоремами сложения и умножения вероятностей. Эти теоремы теоретически могут быть доказаны только для таких событий, вероятность появления которых может быть определена классическим способом. Для других событий эти теоремы принимаются как аксиомы. Поэтому мы не будем показывать доказательство этих теорем, а ограничимся только понятием «правила», понимая при этом ряд теорем и следствий из них, с помощью которых определяется вероятность комбинации событий.

Правила сложения вероятностей

Аксиома: Вероятность суммы или наступления хотя бы одного из двух несовместных событий равна сумме вероятностей этих событий (аддитивность Р):

Теоремы теории вероятностей - определение и вычисление с примерами решения

Данную аксиому иногда называют «теоремой сложения», так как для опытов, сводящихся к «схеме случаев», она может быть доказана.

Эта аксиома легко обращается на любое число несовместных событий: вероятность суммы несовместных событий равна сумме вероятностей этих событий:

Теоремы теории вероятностей - определение и вычисление с примерами решения

Пример №1

Вероятность попадания в башню танка при одном выстреле- 0,2, в его корпус — 0,1, в ходовую часть — 0,025. Найти вероятность попадания в танк при одном выстреле.

Решение:

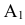
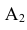
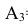
Обозначим интересующее нас событие через А = {попадание в танк}, тогда Теоремы теории вероятностей - определение и вычисление с примерами решения = {попадание в башню танка}, Теоремы теории вероятностей - определение и вычисление с примерами решения = {попадание в корпус танка}, Теоремы теории вероятностей - определение и вычисление с примерами решения={попадание в ходовую часть}.

Очевидно, что попадание в танк наступит тогда, когда снаряд попадёт либо в башню, либо в корпус, либо в ходовую часть танка. Таким образом, интересующее нас событие А будет являться суммой событий Теоремы теории вероятностей - определение и вычисление с примерами решения

Теоремы теории вероятностей - определение и вычисление с примерами решения

А так как события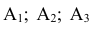Теоремы теории вероятностей - определение и вычисление с примерами решения несовместные (наступление одного из них исключает появление другого), то вероятность наступления события А определится как:

Теоремы теории вероятностей - определение и вычисление с примерами решения

Вывод:    полученный результат означает, что при проведении достаточно большого числа стрельб в аналогичных условиях в среднем в 325 случаях из 1000 будет получено попадание в танк.

Из данной аксиомы вытекают два важных следствия.

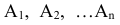
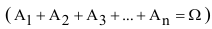
Следствие 1. Если события Теоремы теории вероятностей - определение и вычисление с примерами решенияобразуют полную группу несовместных событий Теоремы теории вероятностей - определение и вычисление с примерами решения, то сумма их вероятностей равна единице.

Теоремы теории вероятностей - определение и вычисление с примерами решения

Следствие 2. Сумма вероятностей противоположных событий равна 1.

Теоремы теории вероятностей - определение и вычисление с примерами решения

Для совместных событий аксиома примет следующий вид:

Вероятность суммы, или наступление хотя бы одного из двух совместных событий, равна сумме вероятности этих событий без вероятности произведения этих событий:

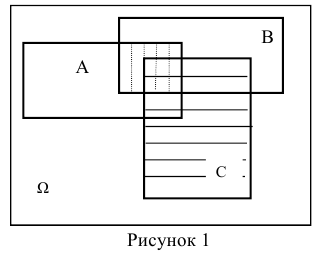
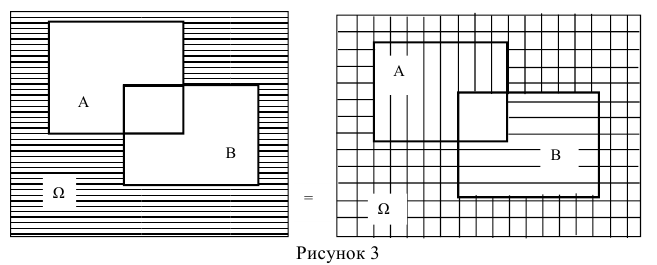
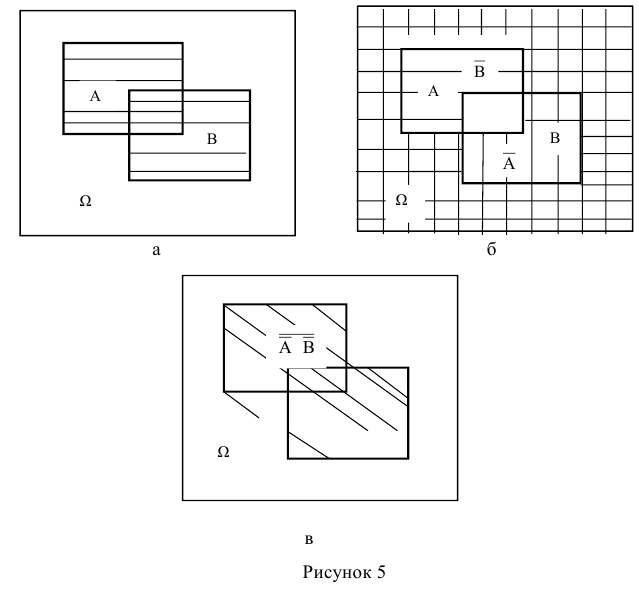
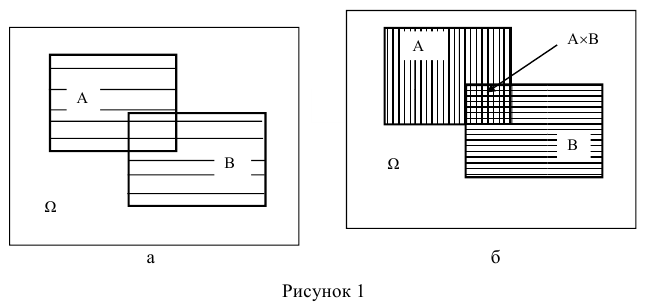
Теоремы теории вероятностей - определение и вычисление с примерами решения

Справедливость этого тождества наглядно следует из его геометрической интерпретации (рисунок 1).

Теоремы теории вероятностей - определение и вычисление с примерами решения

На диаграмме Эйлера-Венна вероятность наступления событий А (или

В) по существу есть площадь области, при попадании случайной точки в которую, наступает событие А (или В). Тогда вероятность комбинации А + В будет соответствовать площади заштрихованной области (рисунок 1 .а). Чтобы получить такую же по площади область, необходимо из площади областей наступления событий А и В вычесть площадь их совместного появления АхВ (рисунок 1.6).

Пример №2

Вероятность подавления батареи противника из-за потерь только в личном составе составляет 0,15; вследствие повреждения материальной части — 0,45; а из-за потерь одновременно в личном составе и материальной части — 0,25. Какова вероятность подавления артиллерийской батареи?

Решение: Пусть событие А = {подавление личного состава батареи}, а событие В= {повреждения материальной части}. Тогда одновременное подавление личного состава и повреждение материальной части будут являться совместным наступлением событий А и В или Теоремы теории вероятностей - определение и вычисление с примерами решения

Вероятность наступления события А по условию задачи равна 0,15 (Р(А)=0,15), вероятность наступления события В равна 0,45 (Р(В)=0,45), вероятность совместного наступления события А и В равна 0,25 (Р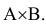Теоремы теории вероятностей - определение и вычисление с примерами решения)=0,25).

Требуется найти вероятность события С ={подавления батареи противника}, которое будет заключаться либо в подавлении личного состава батареи, либо в повреждении материальной части либо того и другого, или Р(А+В).

Применив теорему сложения вероятностей, получим:

Р(С) = Р(А + В) = Р(А) + Р(В) — Р(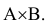Теоремы теории вероятностей - определение и вычисление с примерами решения) = 0,15 + 0,45 — 0,25 = 0,35.

Вывод: Полученный результат означает, что при проведении достаточно большого числа стрельб в аналогичных условиях в среднем в 35 случаях из 100 батарея противника будет подавлена, т.е. поражён либо личный состав, либо повреждена техника, либо и то и другое.

Правила умножения вероятностей

Перед рассмотрением правил умножения вероятностей введём ряд новых понятий, которые необходимы для логического понимания производимых над событиями действий.

Событие А называется независимым от события В, если вероятность наступления события А не зависит от того, произошло ли событие В.

Событие А называется зависимым от события В, если вероятность наступления события А меняется в зависимости от того, произошло событие В или нет.

Факт зависимости или независимости события устанавливают из анализа условий испытания. В теории вероятностей под зависимостью случайных событий понимают не причинную зависимость, при которой два события выступают по отношению друг к другу как причина и следствие, а вероятностную или стохастическую зависимость (стохастическая зависимость [stochastic dependence] — зависимость между случайными величинами, проявляющаяся в том, что изменение закона распределения одной из них происходит под влиянием изменения закона распределения другой). Смысл вероятностной или стохастической зависимости двух событий состоит в том, что при наступлении одного из них другое наступает чаще или реже, чем наступает вообще при реализации данного комплекса условий.

В качестве примеров зависимых событий можно привести следующие:

Пример №3

Реализация комплекса условий: выстрел по танку; событие А= {попадание в танк}; реализация комплекса условий — попадание в танк; событие В = {поражение экипажа танка}.

Для появления интересующего события В = {поражение экипажа танка} при реализации комплекса условий — выстрел по танку необходимо появления события А = {попадание в танк}, в то же время при реализации комплекса условий события А = {попадание в танк} не всегда может наступить событие В = {поражение экипажа танка}.

Раз нам требуется определить вероятность совместного наступления двух зависимых событий, одно из которых может наступить только при том условии, что имело место другое из них, введём понятие условной вероятности события.

Вероятность события В, вычисленная при условии, что имело место другое событие А называется условной вероятностью события В по отношению к событию А (обозначается 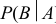Теоремы теории вероятностей - определение и вычисление с примерами решения)).

Теорема: Вероятность произведения или совместного наступления двух любых случайных событий равна произведению вероятностей одного из них на условную вероятность другого, вычисленную при условии, что первое имело место.

Теоремы теории вероятностей - определение и вычисление с примерами решения

Пример №4

Вероятность попадания в танк при одном выстреле равна 0,8; вероятность поражения экипажа танка при попадании в танк равна 0,7. Определить вероятность поражения экипажа танка при одном выстреле.

Решение:

Пусть событие А = {попадание в танк при одном выстреле}, а событие В = {поражение экипажа танка}. Интересующее нас событие С = {поражение экипажа танка при одном выстреле} будет иметь место только в том случае, если наступит событие А, при этом наступление события С возможно только тогда, когда одновременно наступят события А и В.

Вероятность наступления события А по условию задачи равна 0,8 (Р(А)=0,8); вероятность наступления события В равна 0,7 (Р(В)=0,7).

Требуется найти вероятность поражения экипажа танка при одном выстреле, которая будет являться произведением вероятностей попадания в танк при одном выстреле и поражении экипажа танка при условии что имело место попадание в него, т.е. Р(С)=Р(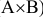Теоремы теории вероятностей - определение и вычисление с примерами решения).

Применив теорему умножения вероятностей, получим:

Теоремы теории вероятностей - определение и вычисление с примерами решения

Вывод:    полученный результат означает, что при проведении

достаточно большого числа стрельб в аналогичных условиях по одному выстрелу в каждом в среднем в 56 случаях из 100 экипаж танка будет поражён.

Правило умножения вероятностей легко обращается на случай произвольного числа событий:

Теоремы теории вероятностей - определение и вычисление с примерами решения

Из данной теоремы вытекает ряд важных следствий.

Следствие 1. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий.

Теоремы теории вероятностей - определение и вычисление с примерами решения

Пример №5

По цели в тире производят по одному выстрелу два студента. Вероятность попадания в цель первого студента равна 0,7, второго — 0,4. Найти вероятность того, что в цель попадут оба студента.

Решение:

Пусть событие А={попадание в цель первым студентом}, а событие В={попадание в цель вторым студентом}, тогда интересующее нас событие С={попадание в цель и первым и вторым студентом}.

Вероятность наступления события А по условию задачи равна 0,7 (Р(А)=0,7), вероятность наступления события В равна 0,4 (Р(В)=0,4).

Попадание в цель вторым студентом не зависит от того, попадёт ли в цель первый студент и наоборот, а следовательно события А и В -независимы. Применив следствие из теоремы умножения для независимых событий, получим:

Теоремы теории вероятностей - определение и вычисление с примерами решения

Вывод:    полученный результат означает, что при проведении

достаточно большого числа стрельб в аналогичных условиях в среднем в 28 случаях из 100 в цель попадут оба студента.

Зависимость и независимость событий всегда взаимны. Если событие А не зависит от события В, то и событие В не зависит от события А. Таким образом, можно уточнить данное ранее определение независимых событий. Два события называются независимыми, если появление одного из них не изменяет вероятности появления другого.

Из рассмотренных выше правил сложения и умножения вероятностей вытекает ещё одно очень важное следствие: если противоположное событие распадается на меньшее число вариантов, чем прямое событие, то имеет смысл при вычислении вероятностей переходить к противоположному событию:

Теоремы теории вероятностей - определение и вычисление с примерами решения

Пример №6

Два орудия, начиная с первого, ведут последовательно огонь по цели до получения первого попадания. При этом первое орудие может произвести два выстрела, а второе — только один. Вероятность попадания в цель при первом выстреле первого орудия — 0,4; вторым выстрелом — 0,8; вероятность попадания в цель вторым орудием — 0,6. Чему равна вероятность поражения цели?

Решение:

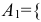
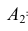
Обозначим за событие Теоремы теории вероятностей - определение и вычисление с примерами решенияпопадание в танк первым орудием с первого выстрела}, за событиеТеоремы теории вероятностей - определение и вычисление с примерами решения= {попадание в танк первым орудием со второго выстрела};В={ попадание в танк вторым орудием}. Тогда интересующее нас событие С={поражение танка} определится как:

Теоремы теории вероятностей - определение и вычисление с примерами решения

Так как события 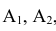Теоремы теории вероятностей - определение и вычисление с примерами решения В несовместны и независимы, то вероятность наступления события С будет равна:

Теоремы теории вероятностей - определение и вычисление с примерами решения

Вывод: полученный результат означает, что при проведении достаточно большого числа испытаний в аналогичных условиях в среднем в 95 случаях из 100, танк будет поражён.

Формула полной вероятности

При изложении третьего вопроса лекции преподаватель на примере поражения    движущегося танка обозначает проблему определения вероятности сложного события (давая при этом понятие гипотезы).

После чего преподаватель доводит условие задачи (Пример 7), формулу для вычисления полной вероятности события (без её вывода) и условия её применения.

При постановке задачи и пояснения физической сущности вопроса преподаватель использует оверхэд-проектор и подготовленные слайды.

Решение задачи преподаватель проводит на доске, особое внимание при этом обращая на методику её решения и порядок записи. В заключении решения задачи преподаватель под запись доводит вывод, отражающий физическую сущность полученного результата.

При решении ряда практических задач вычисление вероятности некоторого сложного события можно существенно облегчить, если связать наступление этого события с наступлением единственно возможных и несовместных событий, под которыми понимаются гипотезы о всех возможных исходах испытаний.

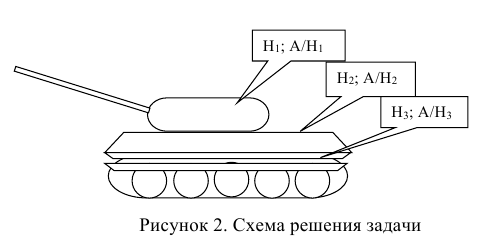
Пусть, например, производится выстрел по танку (рисунок 2).

Теоремы теории вероятностей - определение и вычисление с примерами решения

Известно, что башня танка, его корпус или ходовая часть имеют не только различные размеры, форму и т.д., что усложняет попадание, но и различную степень уязвимости. Первое приводит к тому, что вероятность попадания в различные отсеки танка будет различной, а второе — к тому, что различной будет и вероятность поражения танка при попадании в его башню, корпус или ходовую часть, а, следовательно, и вероятность поражения танка в целом. Поэтому для облегчения вычисления вероятности поражения танка Р(А) представляется целесообразным ввести гипотезы о возможном исходе стрельбы.

Дадим определение:

Под гипотезами понимают полную группу единственно возможных несовместных событий, которые могут наступить в результате проведения испытаний.

В условиях нашей задачи гипотезы о возможном исходе стрельбы будут следующие:

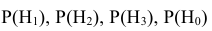
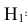
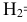
Вероятности этих гипотез Теоремы теории вероятностей - определение и вычисление с примерами решения можно определить и не проводя стрельбу по танку, достаточно, например, провести стрельбу  его макету. Далее можно поставить задачу определения условных вероятностей поражения танка при попадании в различные его отсеки, т.е. поставить задачу определения условных вероятностей поражения танка при реализации выбранных гипотез: Теоремы теории вероятностей - определение и вычисление с примерами решения={npH попадании в башню танка}; Теоремы теории вероятностей - определение и вычисление с примерами решения={при попадании в корпус танка}; Нз= {при попадании в ходовую часть танка}:

Указанные условные вероятности возможно определить опытным путём, проводя полигонные стрельбы по танку.

Пример №7

Ведётся стрельба из орудия по танку. Известно, что при попадании снаряда в башню вероятность поражения танка равна 0,8; при попадании в корпус — 0,6; при попадании в ходовую часть — 0,5.

Известны также вероятности попадания снаряда в каждый из отсеков танка. Вероятность попадания в башню танка равна 0,2. Вероятность попадания в корпус равна 0,3; вероятность попадания в ходовую часть равна 0,1.

Требуется определить вероятность поражения танка при одном выстреле.

Вычислить вероятность наступления интересующего нас события позволяет формула, получившая особое название формулы полной вероятности.

Полная вероятность события равна сумме парных произведений вероятностей каждой из гипотез на отвечающие им условные вероятности наступления этого события.

Теоремы теории вероятностей - определение и вычисление с примерами решения

Данная формула является следствием из обеих теорем — теорем сложения и умножения вероятностей.

При определении полной вероятности необходимо следить, чтобы были учтены все гипотезы о возможном исходе испытания, при которых может наступить интересующее нас событие, т.е. гипотезы должны составлять полную группу несовместных событий. Свидетельством полного учёта всех гипотез является выполнение равенства

Теоремы теории вероятностей - определение и вычисление с примерами решения

Если данное равенство не выполняется, то это означает, что учтены не все гипотезы о возможных исходах испытания.

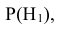
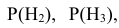
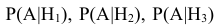
Таким образом оказывается, что знания вероятностей гипотез Теоремы теории вероятностей - определение и вычисление с примерами решения Теоремы теории вероятностей - определение и вычисление с примерами решения о возможных исходах стрельбы и условных вероятностей наступления интересующего нас события А — поражение танка при осуществлении этих гипотезТеоремы теории вероятностей - определение и вычисление с примерами решения является достаточным для вычисления вероятности поражения танка, т.е. наступления интересующего нас события А.

Вернёмся к решению примера.

Решение:

Таким образом, возможные гипотезы об исходах стрельбы:

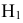
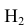
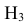
Теоремы теории вероятностей - определение и вычисление с примерами решения = {попадание в башню танка};

Теоремы теории вероятностей - определение и вычисление с примерами решения= {попадание в корпус танка};

Теоремы теории вероятностей - определение и вычисление с примерами решения = {попадание в ходовую часть}.

По условию задачи вероятности гипотез будут равны:

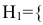
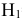
гипотеза Теоремы теории вероятностей - определение и вычисление с примерами решенияпопадания в башню танка} — равна 0,2 (Р(Теоремы теории вероятностей - определение и вычисление с примерами решения) = 0,2);

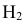
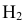
гипотеза Теоремы теории вероятностей - определение и вычисление с примерами решения ={попадание в корпус танка} — равна 0,3 (Р(Теоремы теории вероятностей - определение и вычисление с примерами решения) = 0,3);

гипотеза Нз ={попадание в ходовую часть} — равна 0,1 (Р(Нз) = 0,1).

Интересующее нас событие А = {поражение танка}. По условию задачи вероятность поражения танка при реализации гипотез:

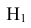
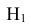
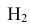
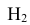
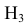
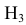
Теоремы теории вероятностей - определение и вычисление с примерами решения = {попадание в башню танка} равна 0,8 (Р(А|Теоремы теории вероятностей - определение и вычисление с примерами решения) = 0,8);

Теоремы теории вероятностей - определение и вычисление с примерами решения = {попадание в корпус танка} равна 0,6 (Р(А|Теоремы теории вероятностей - определение и вычисление с примерами решения) = 0,6);

Теоремы теории вероятностей - определение и вычисление с примерами решения = {попадание в ходовую часть} равна 0,5 (Р(А|Теоремы теории вероятностей - определение и вычисление с примерами решения) = 0,5).

Проверим, все ли гипотезы об исходах стрельбы учтены:

Теоремы теории вероятностей - определение и вычисление с примерами решения

Следовательно, имеющиеся гипотезы не составляют полной группы событий и не учтено событие 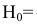Теоремы теории вероятностей - определение и вычисление с примерами решения{промах}, вероятность которого можно определить как вероятность противоположного попаданию в танк события -промаху — Теоремы теории вероятностей - определение и вычисление с примерами решения

Теоремы теории вероятностей - определение и вычисление с примерами решения

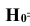
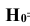
Таким образом, вероятность гипотезы Теоремы теории вероятностей - определение и вычисление с примерами решения={промах} равна 0,4. (Р|Теоремы теории вероятностей - определение и вычисление с примерами решения) =0,4).

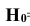
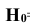
Вероятность поражения танка при реализации гипотезы Теоремы теории вероятностей - определение и вычисление с примерами решения={промах} равна 0. (Р(А|Теоремы теории вероятностей - определение и вычисление с примерами решения) = 0).

Применяя формулу полной вероятности для решения задачи получим:

Теоремы теории вероятностей - определение и вычисление с примерами решения

Следовательно, полная вероятность поражения танка при одном выстреле равна

Р(А) = 0,39 = 39%.

Вывод:    Полученный результат означает, что при проведении

достаточно большого числа стрельб в аналогичных условиях в среднем в 39 случаях из 100 танк окажется поражённым.

Формула Байеса, вероятность появления хотя бы одного события

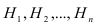
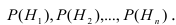
Пусть имеется полная группа несовместных гипотез    Теоремы теории вероятностей - определение и вычисление с примерами решения с известными вероятностями их наступления Теоремы теории вероятностей - определение и вычисление с примерами решения Пусть в результате опыта наступило событие А, условные вероятности которого по каждой из    гипотез    известны, т.е. известны    вероятности

Теоремы теории вероятностей - определение и вычисление с примерами решения

Требуется определить какие вероятности имеют гипотезы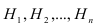Теоремы теории вероятностей - определение и вычисление с примерами решения относительно события А, т.е. условные вероятностиТеоремы теории вероятностей - определение и вычисление с примерами решения

Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, делённому на полную вероятность этого события.

Теоремы теории вероятностей - определение и вычисление с примерами решения

Эта формула называется формулой Байеса.

Доказательство.

По Теореме умножения вероятностей получаем:

Теоремы теории вероятностей - определение и вычисление с примерами решения

Тогда еслиТеоремы теории вероятностей - определение и вычисление с примерами решенияТеоремы теории вероятностей - определение и вычисление с примерами решения

Для нахождения вероятности Р(А) используем формулу полной вероятности.

Теоремы теории вероятностей - определение и вычисление с примерами решения

Если до испытания все гипотезы равновероятны с вероятностью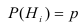Теоремы теории вероятностей - определение и вычисление с примерами решения, то формула Байеса примет вид:
Теоремы теории вероятностей - определение и вычисление с примерами решения
 

Пример №8

Известно, что 30% приборов собирает специалист высшей квалификации, 70% приборов — специалист средней квалификации. Вероятность того, что прибор, собранный специалистом высшей квалификации, надёжен, равна 0,9. Для специалиста средней квалификации эта вероятность равна 0,8. Взятый наудачу прибор оказался надёжным. Найти вероятность того, что этот прибор собран специалистом высшей квалификации.

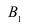
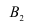
Решение:    пусть событиеТеоремы теории вероятностей - определение и вычисление с примерами решения   — появление прибора, собранного специалистом высшей квалификации; событие Теоремы теории вероятностей - определение и вычисление с примерами решения — появление прибора, собранного специалистом средней квалификации. Вероятности этих событий равны соответственно Теоремы теории вероятностей - определение и вычисление с примерами решения

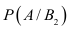
Пусть событие А означает появление надёжного прибора. По условию примера вероятность события А при условии, что появится прибор, собранный специалистом высшей квалификации,Теоремы теории вероятностей - определение и вычисление с примерами решения = 0,9. Аналогично вероятность появления надёжного прибора при условии, что появится прибор, собранный специалистом средней квалификации,Теоремы теории вероятностей - определение и вычисление с примерами решения = 0,8.

Искомая вероятность появления прибора, собранного специалистом высшей квалификации, т.е. события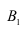Теоремы теории вероятностей - определение и вычисление с примерами решения при условии, что появилось событие А, определяется по формуле

Теоремы теории вероятностей - определение и вычисление с примерами решения

  • Основные законы распределения дискретных случайных величин
  • Непрерывные случайные величины
  • Закон больших чисел
  • Генеральная и выборочная совокупности
  • Ковариация в теории вероятности
  • Функциональные преобразования двухмерных случайных величин
  • Правило «трех сигм» в теории вероятности
  • Производящие функции
Источник

События, которые происходят реально или в нашем воображении, можно разделить на 3 группы. Это достоверные события, которые обязательно произойдут, невозможные события и случайные события. Теория вероятностей изучает случайные события, т.е. события, которые могут произойти или не произойти. В данной статье будет представлена в кратком виде теория вероятности формулы и примеры решения задач по теории вероятности, которые будут в 4 задании ЕГЭ по математике (профильный уровень).

Зачем нужна теория вероятности

Исторически потребность исследования этих проблем возникла в XVII веке в связи с развитием и профессионализацией азартных игр и появлением казино. Это было реальное явление, которое требовало своего изучения и исследования.

Игра в карты, кости, рулетку создавала ситуации, когда могло произойти любое из конечного числа равновозможных событий. Возникла необходимость дать числовые оценки возможности наступления того или иного события.

В XX веке выяснилось, что эта, казалось бы, легкомысленная наука играет важную роль в познании фундаментальных процессов, протекающих в микромире. Была создана современная теория вероятностей.

Основные понятия теории вероятности

Объектом изучения теории вероятностей являются события и их вероятности. Если событие является сложным, то его можно разбить на простые составляющие, вероятности которых найти несложно.

теория вероятности возникла как помощь в игре в кости, в казино и т.п.

Суммой событий А и В называется событие С, заключающееся в том, что произошло либо событие А, либо событие В, либо события А и В одновременно.

Произведением событий А и В называется событие С, заключающееся в том, что произошло и событие А и событие В.

События А и В называется несовместными, если они не могут произойти одновременно.

Событие А называется невозможным, если оно не может произойти. Такое событие обозначается символом oslash.

Событие А называется достоверным, если оно обязательно произойдет. Такое событие обозначается символом Omega.

Пусть каждому событию А поставлено в соответствие число P{А). Это число P(А) называется вероятностью события А, если при таком соответствии выполнены следующие условия.

  1. Вероятность принимает значения на отрезке от 0 до 1, т.е. 0<P(A)<1.
  2. Вероятность невозможного события равна 0, т.е. P(oslash) = 0 .
  3. Вероятность достоверного события равна 1, т.e. P(Omega) = 1.
  4. Если события A и В несовместные, то вероятность их суммы равна сумме их вероятностей, т.е. P(A+B) =P(A)+P(B).

Важным частным случаем является ситуация, когда имеется n равновероятных элементарных исходов, и произвольные k из этих исходов образуют события А. В этом случае вероятность можно ввести по формуле P(A) = frac{k}{n}. Вероятность, введенная таким образом, называется классической вероятностью. Можно доказать, что в этом случае свойства 1-4 выполнены.

Задачи по теории вероятностей, которые встречаются на ЕГЭ по математике, в основном связаны с классической вероятностью. Такие задачи могут быть очень простыми. Особенно простыми являются задачи по теории вероятностей в демонстрационных вариантах. Легко вычислить число благоприятных исходов k, прямо в условии написано число всех исходов n.

Самый простой способ определения вероятности

Ответ получаем по формуле P(A) = frac{k}{n}.

Пример задачи из ЕГЭ по математике по определению вероятности

На столе лежат 20 пирожков – 5 с капустой, 7 с яблоками и 8 с рисом. Марина хочет взять пирожок. Какова вероятность, что она возьмет пирожок с рисом?

Решение.

Всего равновероятных элементарных исходов 20, то есть Марина может взять любой из 20 пирожков. Но нам нужно оценить вероятность того, что Марина возьмет пирожок с рисом, то есть P(A), где А – это выбор пирожка с рисом. Значит у нас количество благоприятных исходов (выборов пирожков с рисом) всего 8. Тогда вероятность будет определяться по формуле:

    [ P(A)=frac{k}{n}=frac{8}{20}=0,4 ]

Ответ: 0,4

Независимые, противоположные и произвольные события

Однако в открытом банке заданий стали встречаться и более сложные задания. Поэтому обратим внимание читателя и на другие вопросы, изучаемые в теории вероятностей.

События А и В называется независимыми, если вероятность каждого из них не зависит от того, произошло ли другое событие.

Событие B состоит в том, что событие А не произошло, т.е. событие B является противоположным к событию А. Вероятность противоположного события равна единице минус вероятность прямого события,т.е. P(B)=1-P(A).

Теоремы сложения и умножения вероятностей, формулы

Для произвольных событий А и В вероятность суммы этих событий равна сумме их вероятностей без вероятности их совместного события, т.е. P(A+B) = P(A)+P(B)-P(AB).

Для независимых событий А и В вероятность произведения этих событий равна произведению их вероятностей, т.е. в этом случае P{AB)= P(A)cdot P(B).

Последние 2 утверждения называются теоремами сложения и умножения вероятностей.

Не всегда подсчет числа исходов является столь простым. В ряде случаев необходимо использовать формулы комбинаторики. При этом наиболее важным является подсчет числа событий, удовлетворяющих определенным условиям. Иногда такого рода подсчеты могут становиться самостоятельными заданиями.

Сколькими способами можно усадить 6 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Для третьего ученика остается 4 свободных места, для четвертого — 3, для пятого — 2, шестой займет единственное оставшееся место. Чтобы найти число всех вариантов, надо найти произведение 1cdot 2 cdot 3 cdot 4 cdot 5 cdot 6, которое обозначается символом 6! и читается “шесть факториал”.

В общем случае ответ на этот вопрос дает формула для числа перестановок из п элементов P_n=1 cdot 2 cdot 3 cdot 4 cdot 5 cdot 6 В нашем случае n= 6.

Рассмотрим теперь другой случай с нашими учениками. Сколькими способами можно усадить 2 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Чтобы найти число всех вариантов, надо найти произведение 6 cdot 5.

В общем случае ответ на этот вопрос дает формула для числа размещений из n элементов по k элементам

    [ A^{k}_{n}=n cdot (n-1) cdot (n-2) dots cdot(n-k+1)= frac{n!}{(n-k)!} ]

В нашем случае n = 6, k = 2.

И последний случай из этой серии. Сколькими способами можно выбрать трех учеников из 6? Первого ученика можно выбрать 6 способами, второго — 5 способами, третьего — четырьмя. Но среди этих вариантов 6 раз встречается одна и та же тройка учеников. Чтобы найти число всех вариантов, надо вычислить величину: frac {6 cdot 5 cdot 4}{1cdot 2 cdot 3} = 20. В общем случае ответ на этот вопрос дает формула для числа сочетаний из n элементов по k элементам:

    [ C^{k}_{n}=frac{n cdot (n-1) cdot (n-2) dots (n-k+1)}{1cdot 2 cdot 3 dots cdot k}=frac{n!}{k! cdot (n-k)!}. ]

В нашем случае n=6, k=3.

Примеры решения задач из ЕГЭ по математике на определение вероятности

Задача 1. Из сборника под ред. Ященко.

На тарелке 30 пирожков: 3 с мясом, 18 с капустой и 9 с вишней. Саша наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.

Решение:

P=frac {9}{30}=0,3.

Ответ: 0,3.

Задача 2. Из сборника под ред. Ященко.

В каждой партии из 1000 лампочек в среднем 20 бракованных. Найдите вероятность того, что наугад взятая лампочка из партии будет исправной.

Решение: Количество исправных лампочек 1000-20=980. Тогда вероятность того, что взятая наугад лампочка из партии будет исправной:

P=frac{980}{1000}=0,98

Ответ: 0,98.

Задача 3.

Вероятность того, что на тестировании по математике учащийся У. верно решит больше 9 задач, равна 0,67. Вероятность того, что У. верно решит больше 8 задач, равна 0,73. Найдите вероятность того, что У. верно решит ровно 9 задач.

Решение:

Если мы вообразим числовую прямую и на ней отметим точки 8 и 9, то мы увидим, что условие “У. верно решит ровно 9 задач” входит в условие “У. верно решит больше 8 задач”, но не относится к условию “У. верно решит больше 9 задач”.

Однако, условие “У. верно решит больше 9 задач” содержится в условии “У. верно решит больше 8 задач”. Таким образом, если мы обозначим события: “У. верно решит ровно 9 задач” – через А, “У. верно решит больше 8 задач” – через B, “У. верно решит больше 9 задач” через С. То решение будет выглядеть следующим образом:

P(A)=P(B)-P(C)=0,73-0,67=0,06.

Ответ: 0,06.

Задача 4.

На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,2. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение.

Давайте подумаем какие у нас даны события. Нам даны два несовместных события. То есть либо вопрос будет относиться к теме “Тригонометрия”, либо к теме “Внешние углы”. По теореме вероятности вероятность несовместных событий равна сумме вероятностей каждого события, мы должны найти сумму вероятностей этих событий, то есть:

P(AB)=P(A)+ P(B)=0,2 +0,15 = 0,35

Ответ: 0,35.

Задача 5.

Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,29. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.

Решение:

Рассмотрим возможные события. У нас есть три лампочки, каждая из которых может перегореть или не перегореть независимо от любой другой лампочки. Это независимые события.

Тогда укажем варианты таких событий. Примем обозначения: bigcirc– лампочка горит, otimes – лампочка перегорела. И сразу рядом подсчитаем вероятность события. Например, вероятность события, в котором произошли три независимых события “лампочка перегорела”, “лампочка горит”, “лампочка горит”: P=0,29 cdot 0,71 cdot 0,71=0,146189, где вероятность события “лампочка горит” подсчитывается как вероятность события, противоположного событию “лампочка не горит”, а именно: P=1-0,29=0,71.

otimes otimes otimes P=0,29 cdot 0,29 cdot 0,29 = 0,024389

otimes bigcirc bigcirc P_1=0,29 cdot 0,71 cdot 0,71 = 0,146189

otimes otimes bigcirc  P_2=0,29 cdot 0,29 cdot 0,71 = 0,05971

bigcirc otimes bigcirc  P_3=0,71 cdot 0,29 cdot 0,71 = 0,05971

bigcirc otimes otimes  P_4=0,71 cdot 0,29 cdot 0,29 = 0,146189

bigcirc bigcirc otimes  P_5=0,71 cdot 0,71 cdot 0,29 = 0,05971

otimes bigcirc otimes  P_6=0,29 cdot 0,71 cdot 0,29 = 0,146189

bigcirc bigcirc bigcirc P_7=0,71 cdot 0,71 cdot 0,71=0,357911

Заметим, что благоприятных нам несовместных событий всего 7. Вероятность таких событий равна сумме вероятностей каждого из событий: P=P_1+P_2+P_3+P_4+P_5+P_6+P_7=0,146189 +0,05971+0,05971+0,146189+0,05971+0,146189+0,357911=0,975608.

Ответ: 0,975608.

Еще одну задачку вы можете посмотреть на рисунке:

решения задачи о монетах

Таким образом, мы с вами поняли, что такое теория вероятности формулы и примеры решения задач по которой вам могут встретиться в варианте ЕГЭ.

Источник

2.1 Теорема умножения вероятностей

Произведением
двух событий
иназывается
событие
,
состоящее в совместном появлении событий
и
.

Произведением
нескольких событий
,,…называется
событие
,
состоящее в совместном появлении всех
этих событий.

Пример:

  1. Если
    событие
    — появление туза при вынимании карты
    из колоды, событие— появление карты бубновой масти, то
    событиеесть появление туза бубновой масти.

  2. Если
    по мишени производится три выстрела и
    рассматриваются события
    — промах при первом выстреле,—
    промах при втором выстреле,— промах при третьем выстреле, то событиесостоит в том, что в мишень не будет ни
    одного попадания.

Теорема
умножения 1

Вероятность
произведения двух событий
иравна произведению вероятности одного
из них на условную вероятность другого,
вычисленную в предположении, что первое
событие уже наступило

, (2.1)

если
в качестве первого события взять

,
(2.2)

если
в качестве первого события взять
.

,
— условные вероятности событийисоответственно.

Условной
вероятностью
называется
вероятность события
,
вычисленную в предположении, что событиеуже наступило.

Пример.
Студент знает 20 билетов из 30. Он тянет
билет шестым. Найти вероятность того,
что он сдаст экзамен (событие
),
если первых 5 человек вытащили 5 известных
ему билетов (событие).

Решение.

Из
формулы (2.1) можно получить формулу для
вычисления условной вероятности

(2.3)

Формула
(2.3) может быть использована при условии
.

Пример.
Проверить формулу (2.3) для предыдущего
примера.

находим
по (1.7) при
,,,.

определяем
по (1.7) при
,,,.

Два
события
иназываютсянезависимыми,
если появление одного из них не меняет
вероятности появления другого, т.е.
условная вероятность события
равна его безусловной вероятности или,
условная вероятность событияравна его безусловной вероятности

(2.4)

.

Если
событие
не зависит от события,
то и событиене зависит от события.

Два
события
иявляютсязависимыми,
если

или
(2.5)

Если
событие
зависит от события,
то и событиезависит от события.

Пример.
Из
полной колоды карт (52 листа) вынимается
одна карта. Рассматриваются события

—
появление туза;

—
появление карты красной масти;

—
появление бубнового туза;

—
появление десятки.

Зависимы
или независимы пары событий
и,и,и?

Решение.

Для
пары
и

справедливо
условие (2.4). Значит
и— независимые.

Для
пары
и

справедливо
(2.5). События
изависимы.

Для
пары
и,
без проверки условий (2.4), (2.5) можно
сказать, что события зависимы, т.к. они
несовместны. Для несовместных событий
(по определению) появление одного
исключает появление другого, т.е. обращает
в нуль его вероятность.

Несколько
событий
называютсяпопарно
независимыми, если
каждые два из них независимы.

Несколько
событий
называютсянезависимыми
в совокупности, если
каждые 2 из них независимы и независимы
каждое событие и все возможные произведения
остальных.

Следствие
из теоремы умножения 1

Для
независимых событий
и(2.1) имеет вид

(2.6)

Пример:

  1. В
    урне 2 белых и 3 черных шара. Из урны
    вынимают подряд два шара (события
    и).
    Найти вероятность того, что оба шара
    белые.

Решение.

.
По (2.1)

  1. Те
    же условия, но после первого вынимания
    шар возвращается в урну, и шары в урне
    перемешиваются.

Решение.

По
(2.6)

Теорема
умножения 2

Вероятность
произведения нескольких событий
,,
…,равна произведению вероятности одного
из них на условные вероятности всех
остальных, причем вероятность каждого
последующего события вычисляется в
предположении, что все предыдущие уже
появились

(2.7)

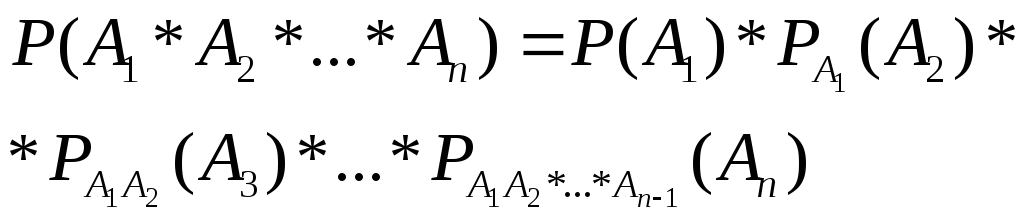
Следствие
из теоремы умножения 2.

Вероятность
произведения нескольких событий
,,
…,,
независимых в совокупности, равна
произведению вероятностей этих событий

(2.8)

Пример:

  1. В
    урне 5 белых, 4 черных и 3 синих шара. Из
    урны вынимают подряд 3 шара. Найти
    вероятность того, что все 3 шара будут
    разноцветными.

Решение.

—
вытащить первым белый шар;

—
вытащить вторым черный шар;

—
вытащить третьим синий шар.

По
(2.7)

  1. Те
    же условия, но после каждого

вынимания
шар возвращается в урну, и шары в урне
перемешиваются.

Решение.

По
(2.8)

    1. Теорема
      сложения вероятностей

Суммой
двух событий

и
называется
событие
,
состоящее в появлении события,
события,
или обоих вместе. Для несовместных
событий— появление либо,
либо,
т.е. только одного из двух событий.

Суммой
нескольких событий
называется
событие
,состоящее
в появлении хотя бы одного из
(для несовместных событий – только
одного).

Пример:

1.
Если
— попадание в цель при первом выстреле,
событие— попадание в цель при втором выстреле,
то событиеесть попадание в цель вообще, безразлично
при каком выстреле – при первом, при
втором или при обоих вместе.

2.
Если опыт состоит в пяти выстрелах

по
мишени и рассматриваются события

— ни одного попадания;

— ровно одно попадание;

— ровно два попадания;

— ровно три попадания;

— ровно четыре попадания;

— ровно пять попаданий;

то
есть событие «не более двух попаданий»;

а
— событие «не менее трех попаданий»

Теорема
сложения 1

Вероятность
суммы двух совместных событий
иравна сумме вероятностей этих событий
без вероятности их совместного появления.

(2.10)

Если
и— зависимые события, то (2.10) принимает
вид

(2.11)

Если
и— независимые события, то (2.10) имеет вид.

(2.12)

Вероятность
суммы двух несовместных событий
иравна сумме вероятностей

этих
событий

(2.13)

Формулу
(2.13) можно рассматривать как частный
случай (2.10), т.к. для несовместных событий
.

Пример.
Вероятность
попадания в цель при стрельбе первого
и второго стрелка соответственно равны.

,.
Найти вероятность попадания хотя бы
одним стрелком при одновременном
выстреле.

Решение.

— попадание первого стрелка;

— попадание второго стрелка.

По
(2.12)

,
т.к.

и
являются совместными и независимыми

Теорема
сложения 2

В
виду громоздкости общей формулы расчета
вероятности суммы совместных событий,
рассмотрим частный случай теоремы
сложения для трех событий
,,(2.14)

Для
нескольких несовместных событий
вероятность их суммы равна

(2.15)

Пример.
В
партии из
изделийизделий бракованных. Для контроля из
партии наугад берутизделий. Какова вероятность того, что
среди них будет не большебракованных (событие)?

Решение.

—
среди взятых на проверку изделий ни
одного бракованного;

—
среди взятых на проверку изделий одно
бракованное;

…

—
среди взятых на проверку изделий
бракованных изделий.

Тогда
.
Т.к.,
,
…,

— несовместные события, то
по (2.15).

Вероятность
события
вычисляем по (1.7):

,

,

Т.о.

Следствие
из теоремы сложения 2

Если
события
образуют полную группу попарно
несовместных событий, то сумма их
вероятностей равна 1.

(2.16)

Пример

Для
АТС вероятность появления вызова с
квартирного телефона
,
с таксофона —.
Остальные вызовы дают учрежденческие
телефоны. Найти вероятность появления
учрежденческого вызова.

Частный
случай следствия из теоремы сложения
2

Сумма
вероятностей противоположных событий
равна 1

(2.17)

Обычно
обозначают
,,
тогда (2.17) примет вид

    1. Применение
      теорем умножения и сложения

На
практике сравнительно редко встречаются
задачи, в которых нужно применять только
теорему умножения или только теорему
сложения вероятностей. Обычно эти
теоремы приходится применять совместно.
При этом, как правило, событие, вероятность
которого требуется определить,
представляется в виде суммы и (или)
произведений нескольких несовместных
(совместных) событий.

Пример.
По
мишени стреляют 3 стрелка. Вероятность
попадания для них
,,.
Найти вероятность следующих событий:

B
– ни одного попадания;

C
– только 1 попадание;

D
– только 2 попадания;

E
– только 3 попадания;

F
– хотя бы одно попадание.

Решение.

по
(2.8), т.к. события
— независимы в совокупности.

по
(2.17)

Аналогично

События
В, С, D, Е образуют полную группу попарно
несовместных событий. Проверим (2.16)

Однако
такой путь решения задачи слишком
сложен. Здесь проще от прямого события
F перейти к противоположному событию –
ни одного попадания – что соответствует
событию B.

Поэтому

На
примере вычисления
проиллюстрирован
принцип
целесообразности применения противоположных
событий в
теории вероятностей – если противоположное
событие распадается на меньшее число
вариантов, чем прямое событие, то имеет
смысл при вычислении вероятностей
переходить к противоположному событию.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Понравилась статья? Поделить с друзьями:
  • Как найти днс сервер в сети
  • Как составить уравнение реакции по химии 8 класс в задаче
  • Как исправить материал на основные средства
  • Как найти дома сеть для телефона
  • Как найти архивы в инстаграме