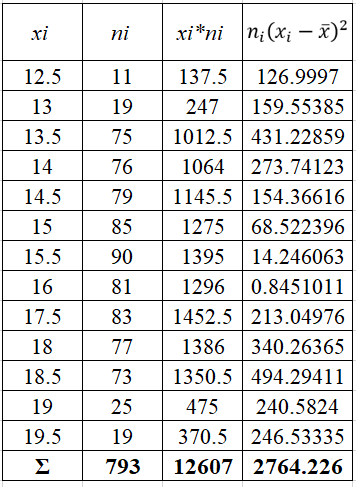
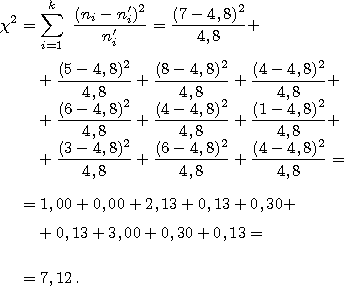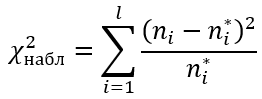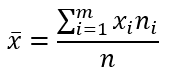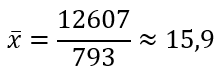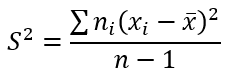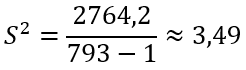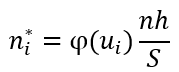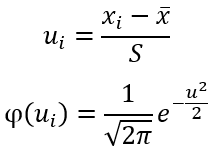Как найти теоретические частот - Исправление недочетов и поиск решений вместе с Examum.ru

Методика вычисления теоретических частот равномерного распределения

Если проверяется
гипотеза о равномерном распределении
выборочной совокупности, теоретические
частоты определяются очень легко.
Действительно, в этом случае на каждый
разряд наблюдаемых значений должно
приходиться одинаковое число наблюдений.
Поэтому для равномерного распределения

где
—
общее число наблюдений, то есть, объем
выборки, а—
число разрядов наблюдаемых значений.

Методика вычисления теоретических частот нормального распределения

Значительно сложнее
обстоит дело в случае нормального
распределения. Один из способов нахождения
теоретических частот нормального
распределения состоит в следующем.

Весь интервал
наблюдаемых значений величины
делят начастичных
интерваловодинаковой длины. Затем — находят
середины этих интервалов

и строят статистическое
распределение равноотстоящих значений

из получившегося набора значений.

Вычисляют выборочное
среднее значение
и выборочное
среднее квадратичное отклонение
.
Нормируют случайную
величину
,
то есть — переходят к случайной величине,
следующим образом:

после чего —
вычисляют границы частичных интервалов,
в пределах которых изменяются значения
:

Вычисляют
теоретические вероятности
попадания величиныв интервалыпо следующим формулам:

где
—
функция Лапласа, значения которой
табулированы.

Наконец, теоретические
частоты
находят, исходя из найденных теоретических
вероятностей:Заметим, что теоретические частоты, в
отличие от эмпирических, могут быть
дробными. Однако их сумма должна, как
и в случае эмпирических частот, давать,
то есть, объем выборки. Этот факт можно
использовать для проверки собственных
вычислений.

Пример применения статистического критерия согласия распределений (Пирсона)

Рассмотрим пример
с распределением выборов испытуемых
из акцентированного и контрольного
списков.

В информатике
важна проблема поиска или выбора
информации. Идея примера состоит в том,
что заголовки HTML-документов можно
акцентировать, исходя из предполагаемой
поисковой фразы, таким образом, что при
прочих равных акцентированный заголовок
будет выбираться пользователями чаще,
чем неакцентированный.

Здесь мы рассмотрим
частоты выборов в двух списках:
контрольном, который состоял из десяти
неакцентированных заголовков, и
экспериментальном, содержащем десять
заголовков, акцентированных пятью
способами. После этого мы установим,
что распределение в акцентированном
случае отличается от равномерного
(тогда как в контрольном случае оно
равномерно).

Частота выборов
в контрольном списке (статистическое
распределение выборов) представлена в
следующей таблице:

Позиция	1	2	3	4	5	6	7	8	9	10
Частота	7	5	8	4	6	4	1	3	6	4

Распределение
данного ряда выборов мы подвергаем
анализу при помощи
-критерия,
для чего выдвигаем следующие статистические
гипотезы:

распределение
выборов в контрольном списке подчинено
равномерному закону;
распределение
выборов в контрольном списке отличается
от равномерного.

В целом пользователи
совершили 48 выборов (число, равное сумме
всех наблюдаемых частот). Следовательно,
если бы предпочтения пользователей
были распределены равномерно, то каждая
позиция получила бы 4,8 выбора. Это и есть
теоретическая частота
.

Вычислим эмпирическое
значение
-критерия
Пирсона:

Равномерное
распределение характеризуется двумя
параметрами — границами возможных
значений — следовательно, вычисляя
число степеней свободы, имеем:

Зададимся уровнем
значимости
и по таблице критических значений
определим.
Итак:

следовательно, на
уровне значимости
,
мы принимаем основную гипотезу:
распределение выборов в контрольном
списке подчинено равномерному закону.

Поступим так же
со второй выборкой, где испытуемые
совершали выбор из акцентированных
заголовков. Частоты этих выборов
представлены в следующей таблице:

Акцент	A	B	C	D	E
Частота	4	4	7	11	22

Данный ряд
распределения выборов мы также подвергаем
анализу при помощи
-критерия,
для этого — выдвигаем статистические
гипотезы:

распределение
выборов в акцентированном списке
подчинено равномерному закону;

распределение
выборов в акцентированном списке
отличается от равномерного.

В данном случае
речь идет о выборе не между позициями
списка, а между различными степенями
акцентированности заголовков: от вообще
не акцентированных (акцент A)
до наиболее акцентированных (акцент
E).
В целом пользователи совершили те же
48 выборов, что и в контрольном случае.
Но на этот раз их предпочтения
распределялись не между десятью позициями
списка, а между пятью способами
акцентированности. Поэтому, если бы
предпочтения распределялись равномерно,
то каждый способ акцента получил бы 9,6
выборов. Это число — теоретическая
частота распределения выборов:
.

Снова вычисляем
эмпирическое значение критерия:

Так же как и в
предыдущем случае, учитывая, что
равномерное распределение характеризуется
двумя параметрами, вычисляем число
степеней свободы:

На уровне значимости
найдем то таблице критических значений-критерия
Пирсона критическое значение:.
Получаем следующее неравенство:

следовательно,
основная гипотеза отвергается и
принимается альтернативная: распределение
выборов в акцентированном списке
отличается от равномерного.

Основной целью
анализа вариационных рядов является
выявление закономерности распределения,
исключая при этом влияние случайных
для данного распределения факторов.
Этого можно достичь, если увеличивать
объем исследуемой совокупности и
одновременно уменьшать интервал ряда.
При попытке изображения этих данных
графически мы получим некоторую плавную
кривую линию, которая для полигона
частот будет являться некоторым пределом.
Эту линию называют кривой распределения.

Иными словами,
кривая
распределения
есть графическое изображение в виде
непрерывной линии изменения частот в
вариационном ряду, которое функционально
связано с изменением вариант. Кривая
распределения отражает закономерность
изменения частот при отсутствии случайных
факторов. Графическое изображение
облегчает анализ рядов распределения.

Известно достаточно
много форм кривых распределения, по
которым может выравниваться вариационный
ряд, но в практике статистических
исследований наиболее часто используются
такие формы, как нормальное распределение
и распределение Пуассона.

Нормальное
распределение зависит от двух параметров:
средней арифметической
и
среднего квадратического отклонения.
Его кривая выражается уравнением

(7.6)

где у — ордината
кривой нормального распределения;
—
стандартизованные отклонения; е и π —
математические постоянные; x — варианты
вариационного ряда;—
их средняя величина;—
cреднее квадратическое отклонение.

Если нужно получить
теоретические частоты f’ при выравнивании
вариационного ряда по кривой нормального
распределения, то можно воспользоваться
формулой

(7.7)

где
—
сумма всех эмпирических частот
вариационного ряда; h — величина интервала
в группах;—
cреднее квадратическое отклонение;—
нормированное отклонение вариантов от
средней арифметической; все остальные
величины легко вычисляются по специальным
таблицам.

При помощи этой
формулы мы получаем теоретическое
(вероятностное)
распределение,
заменяя им эмпирическое
(фактическое)
распределение,
по характеру они не должны отличаться
друг от друга.

Тем не менее в ряде
случаев, если вариационный ряд представляет
собой распределение по дискретному
признаку, где при увеличении значений
признака х частоты начинают резко
уменьшаться, а средняя арифметическая,
в свою очередь, равна или близка по
значению к дисперсии (),
такой ряд выравнивается по кривой
Пуассона.

Кривую
Пуассона можно
выразить отношением

(7.8)

где P_x
— вероятность наступления отдельных
значений х;
—
средняя арифметическая ряда.

При выравнивании
эмпирических данных теоретические
частоты можно определить по формуле

(7.9)

где f’ — теоретические
частоты; N — общее число единиц ряда.

Сравнивая полученные
величины теоретических частот f’ c
эмпирическими (фактическими) частотами
f, убеждаемся, что их расхождения могут
быть весьма невелики.

Объективная
характеристика соответствия теоретических
и эмпирических частот может быть получена
при помощи специальных статистических
показателей, которые называют критериями
согласия.

Для оценки близости
эмпирических и теоретических частот
применяются критерий согласия Пирсона,
критерий согласия Романовского, критерий
согласия Колмогорова.

Закон равномерного
распределения случайной величины

Закон
распределения непрерывной случайной
величины называется равномерным,
если на интервале, которому принадлежат
все возможные значения случайной
величины, плотность распределения
сохраняет постоянное значение (
f(x)
= const
при a
≤ x
≤ b,
f(x)
= 0 при x
< a,
x
> b.

Найдем
значение, которое принимает f(x)
при
Из
условия нормировки следует, что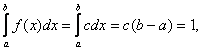откуда.

Вероятность
попадания равномерно распределенной
случайной величины на интервал
равна
при этом

Вид
функции распределения для нормального
закона:

Пример.
Автобусы некоторого маршрута идут с
интервалом 5 минут. Найти вероятность
того, что пришедшему на остановку
пассажиру придется ожидать автобуса
не более 2 минут.

Решение.
Время ожидания является случайной
величиной, равномерно распределенной
в интервале [0, 5]. Тогда

Соседние файлы в папке Лекции

Источник

Проверка гипотезы о нормальном распределении генеральной совокупности

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Краткая теория

Проверка дискретного распределения на нормальность

Пусть
эмпирическое распределение задано в виде последовательности равноотстоящих
вариант и соответствующих им частот:

			…
			…

Требуется, используя критерий Пирсона, проверить
гипотезу о том, что генеральная совокупность

распределена нормально.

Для того,
чтобы при заданном уровне значимости

проверить гипотезу о нормальном распределении
генеральной совокупности, надо:

1. Вычислить
выборочную среднюю

и выборочное среднее квадратическое отклонение

2.
Вычислить теоретические частоты

где

– объем выборки,

— шаг (разность между двумя соседними
вариантами)

3. Сравнить эмпирические и теоретические частоты
с помощью критерия Пирсона. Для этого:

а)
составляют расчетную таблицу (см. пример), по которой находят наблюдаемое
значение критерия

б) по
таблице критических точек распределения

, по заданному уровню
значимости

и числу степеней свободы

(

– число групп выборки) находят критическую
точку

правосторонней критической области.

Если

– нет оснований отвергнуть гипотезу о
нормальном распределении генеральной совокупности. Если

— гипотезу отвергают.

Проверка интервального распределения на нормальность

Пусть
эмпирическое распределение задано в виде последовательности интервалов

и соответствующих им частот

Требуется,
используя критерий Пирсона, проверить гипотезу о том, что генеральная
совокупность

распределена нормально.

Для того,
чтобы при уровне значимости

проверить гипотезу о нормальном распределении
генеральной совокупности, надо:

1.
Вычислить выборочную среднюю

и выборочное среднее квадратическое отклонение

, причем в качестве вариант

принимают среднее арифметическое концов
интервала:

2.
Пронормировать

, то есть перейти к
случайной величине

и
вычислить концы интервалов:

причем
наименьшее значение

, то есть

полагают равным

, а наибольшее, то есть

полагают равным

3. Вычислить теоретические
частоты:

где

– объем выборки

– вероятности попадания

в интервалы

– функция Лапласа.

4. Сравнить эмпирические и
теоретические частоты с помощью критерия Пирсона. Для этого:

а)
составляют расчетную таблицу (см. пример), по которой находят наблюдаемое
значение критерия

б) по
таблице критических точек распределения

, по заданному уровню
значимости

и числу степеней свободы

(

– число групп выборки) находят критическую
точку

правосторонней критической области.

Если

– нет оснований отвергнуть гипотезу о
нормальном распределении генеральной совокупности. Если

— гипотезу отвергают.

Замечание.

Малочисленные частоты

следует объединить, в этом случае и
соответствующие им теоретические частоты также надо сложить. Если производилось
объединение частот, то при определении числа степеней свободы по формуле

следует в качестве

принять число групп выборки, оставшихся после
объединения частот.

Примеры решения задач

Пример 1

Используя
критерий Пирсона при уровне значимости 0,05, проверить, согласуется ли гипотеза
с нормальным распределением генеральной совокупности X с заданным эмпирическим
распределением:

x_i	-4.5	-3.5	-2.5	-1.5	-0.5	0.5	1.5	2.5	3.5	4.5
n_i	1	4	21	30	63	59	34	18	5	2

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Вычислим
характеристики распределения. Для этого составим расчетную таблицу.

Выборочная средняя:

Средняя
квадратов:

Выборочная
дисперсия:

Среднее квадратическое
отклонение:

Вычислим
теоретические частоты.

Вероятность
попадания в соответствующий интервал:

Теоретические
частоты:

где

-объем выборки

Составим
расчетную таблицу:

Проверим
степень согласия эмпирического и теоретического распределения по критерию
Пирсона. Объединяем малочисленные частоты (

Из
расчетной таблицы

Уровень
значимости

Число
степеней свободы

По
таблице критических точек распределения:

Нет
оснований отвергнуть гипотезу о нормальном распределении генеральной
совокупности.

Пример 2

Из большой партии по схеме случайной
повторной выборки было проверено 150 изделий с целью определения процента
влажности древесины, из которой изготовлены эти изделия. Получены следующие
результаты:

Процент влажности, x_i	11-13	13-15	15-17	17-19	19-21
Число изделий, n_i	8	42	51	37	12

На уровне значимости 0,05 проверить
гипотезу о нормальном законе распределения признака (случайной величины) X, используя критерий χ² — Пирсона.

Решение

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Составим расчетную таблицу

Средняя:

Средняя квадратов:

Дисперсия:

Исправленная дисперсия:

Исправленное среднее квадратическое
отклонение:

Вычислим теоретические частоты.

Составим расчетную таблицу:

Вероятность попадания в
соответствующий интервал:

, где

— функция Лапласа

Теоретические частоты:

, где

-объем выборки

Составим расчетную таблицу:

Проверим степень согласия
эмпирического и теоретического распределения по критерию Пирсона:

Из расчетной таблицы

Уровень значимости

Число степеней свободы

По таблице критических точек
распределения:

Нет оснований отвергать гипотезу о
распределении случайной величины по нормальному закону.

Задачи контрольных и самостоятельных работ

Задача 1

Выборка X
объемом n=100 задана таблицей:

	0.8	1.1	1.4	1.7	2	2.3	2.6
	5	13	25	25	19	10	3

1) Построить
полигон относительных частот

2) Вычислить
среднее выборочное

, выборочную дисперсию

и среднее квадратическое отклонение

3) Вычислить
теоретические частоты

. Построить график

на одном рисунке с полигоном.

4) С помощью
критерия χ² проверить гипотезу о нормальном распределении
генеральной совокупности при уровне значимости α=0.05.

Задача 2

Построить
нормальную кривую по опытным данным. Рассчитать теоретические (выравнивающие) частоты
и сравнить с опытным распределением.

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 3

Выборка X
объемом N=100 измерений задана таблицей:

	0.6	1.5	2.4	3.3	4.2	5.1	6
	5	13	26	24	19	10	3

а)
Построить полигон относительных частот

б)
вычислить среднее выборочное

, выборочную дисперсию

и среднее квадратическое отклонение

;

в) по
критерию χ² проверить гипотезу о
нормальном распределении генеральной совокупности при уровне значимости α=0.05.

Задача 4

Для
изучения количественного признака

из генеральной совокупности извлечена выборка

объема n, имеющая данное
статистическое распределение.

а)
Построить полигон частот по данному распределению выборки.

б) Найти
выборочное среднее

, выборочное среднее
квадратическое отклонение

и исправленное среднее квадратическое
отклонение

в) При
данном уровне значимости

проверить по критерию Пирсона гипотезу о
нормальном распределении генеральной совокупности.

г) В
случае принятия гипотезы о нормальном распределении генеральной совокупности
найти доверительные интервалы для математического ожидания

и среднего квадратического отклонения σ при
данном уровне надежности γ=1-α; α=0.05

	4	8	12	16	20	24	28	32
	5	9	15	19	20	16	10	6

Задача 5

Для выборки
объема N=100, представленной вариационным рядом

	-1	0	1	2	3	4	5
	3	8	11	19	37	17	5

построить
полигон относительных частот и гистограмму накопленных частот. Найти выборочное
среднее

и выборочное среднее квадратичное отклонение

. Определить доверительный интервал с
доверительной вероятностью β=0,95 для оценки математического ожидания
генеральной совокупности в предположении, что среднее квадратическое отклонение
генеральной совокупности σ равно исправленному выборочному среднему s. Проверить
гипотезу о нормальности закона распределения генеральной совокупности,
используя критерий Пирсона с уровнем значимости α=0,05.

Задача 6

Для случайной величины X составить интервальный
вариационный ряд, вычислить выборочные средние характеристики, подобрать
теоретический закон распределения, проверить его согласование с теоретическим
критерием Пирсона при α=0,05.

7	4	4	15	1	1	7	15	19	4
0	4	8	14	10	0	1	11	8	2
6	2	5	3	12	2	9	6	2	5
13	5	7	3	3	10	0	11	17	11
9	6	11	7	20	1	14	6	7	4

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 7

Данные о
продолжительности телефонных разговоров, отобранные по схеме
собственно-случайной бесповторной выборки, приведены в таблице:

Время, мин	1.5-2.5	2.5-3.5	3.5-4.5	4.5-5.5	5.5-6.5	6.5-7.5	7.5-8.5	8.5-9.5	9.5-10.5	Итого
Число разговоров	3	4	9	14	37	12	8	8	5	100

Используя χ²-критерий Пирсона при уровне
значимости α=0.05 проверить гипотезу о том, что случайная величина X —
продолжительность телефонных разговоров — распределена по нормальному закону.
Построить на одном чертеже гистограмму и соответствующую нормальную кривую.

Задача 8

Распределение
случайной величины X – заработной платы сотрудников на фирме (в у.е.) –
задано в виде интервального ряда:

Найти:

. Построить теоретическое
нормальное распределение и сравнить его с эмпирическим с помощью критерия
согласия Пирсона χ² при α=0,05.

Задача 9

Записать для выборки интервальное
распределение, построить гистограмму относительных частот. По критерию Пирсона
проверить гипотезу нормальном распределении.

7.81	3.15	2.27	32.64	4.72	5.33	8.51	7.72	30.23	20.12
9.83	8.33	9.61	31.83	8.52	27.22	27.22	8.43	15.91	25.46
24.82	26.54	46.73	17.31	13.05	53.24	5.23	18.28	40.93	17.44
32.34	28.26	9.75	3.72	8.16	22.91	0.74	12.97	12.05	1.53
43.15	45.57	2.02	32.23	8.67	4.83	9.12	6.77	6.48	19.22
36.42	47.81	40.64	5.45	0.21	26.51	17.36	3.62	15.57	23.21
58.73	62.52	10.15	38.36	35.55	6.10	3.04	4.54	1.95	5.24
64.71	67.63	1.21	0.81	2.03	10.17	5.51	8.35	43.76	8.74
4.72	17.54	17.32	29.43	5.91	6.92	4.72	16.04	57.54	15.46
13.31	36.45	3.45	16.15	15.77	2.43	14.24	2.25	15.63	23.72

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 10

Результаты наблюдений над случайной
величиной

оказались
лежащими на отрезке

и были
сгруппированы в 10 равновеликих интервалов. Значения

и частоты
попадания в интервалы приведены в таблице. Построить: гистограмму частот,
эмпирическую функцию распределения, найти медиану. Найти выборочное среднее

и исправленное
среднеквадратическое отклонение

. Указать 95-процентные доверительные интервалы для

. С помощью критерия Пирсона проверить гипотезу о
нормальном (с параметрами

) законе распределения (уровень значимости α=0.02

Задача 11

В таблице приведены результаты
измерения роста (см.) случайно отобранных 100 студентов:

Интервалы
роста

154-158

158-162

162-166

166-170

170-174

174-178

178-182

Число
студентов,

С помощью критерия Пирсона при
уровне значимости α=0.05 проверить правдоподобие гипотезы о нормальном
распределении роста студентов.

Задача 12

При массовых стрельбах из пушек для
одинаковых общих условий были зафиксированы продольные ошибки (м) попадания
снарядов в цель:

На уровне значимости 0,05 проверить
гипотезу о нормальном законе распределения признака (случайной величины) L, используя критерий χ²— Пирсона.

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Источник

Критерии согласия. Теоретические и эмпирические частоты

Эмпирические частоты получают в результате опыта (наблюдения). Теоретические частоты рассчитывают по формулам. Для нормального закона распределения их можно найти следующим образом:

$n_i=frac{varphi(t_i),h}{sigma_text{v}}sumlimits_{j=1}^{n}m_j$

где $sumlimits_{j=1}^{n}m_j$ — сумма эмпирических частот; — разность между двумя соседними вариантами; $sigma_text{v}$ — выборочное среднеквадратическое отклонение; $t_i=frac{x_i-overline{x}_text{v}}{sigma_text{v}}$ ; $overline{x}_text{v}$ — выборочная средняя арифметическая; varphi(t) — см. прил. 1.

Обычно эмпирические и теоретические частоты различаются. Возможно, что расхождение случайно и связано с ограниченным количеством наблюдений; возможно, что расхождение неслучайно и объясняется тем, что для вычисления теоретических частот выдвинута статистическая гипотеза о том, что генеральная совокупность распределена нормально, а в действительности это не так. Распределение генеральной совокупности, которое она имеет в силу выдвинутой гипотезы, называют теоретическим.

Возникает необходимость установить правило (критерий), которое позволяло бы судить, является ли расхождение между эмпирическим и теоретическим распределениями случайным или значимым. Если расхождение окажется случайным, то считают, что данные наблюдений (выборки) согласуются с выдвинутой гипотезой о законе распределения генеральной совокупности и, следовательно, гипотезу принимают; если же расхождение окажется значимым, то данные наблюдений не согласуются с гипотезой, и ее отвергают.

Критерием согласия называют критерий, который позволяет установить, является ли расхождение эмпирического и теоретического распределений случайным или значимым, т. е. согласуются ли данные наблюдений с выдвинутой статистической гипотезой или не согласуются.

Имеется несколько критериев согласия: критерий хи-квадрат chi^2 (Пирсона), критерий Колмогорова, критерий Романовского и др. Ограничимся описанием того, как критерий chi^2 применяется к проверке гипотезы о нормальном распределении генеральной совокупности (критерий применяется аналогично и для других распределений).

Допустим, что в результате наблюдений получена выборка:

значение признака x_1~~~x_2~~~cdots~~~x_s ;

эмпирическая частота m_1~~~m_2~~~cdots~~~m_s .

Выдвинем статистическую гипотезу: генеральная совокупность, из которой извлечена данная выборка, имеет нормальное распределение. Требуется установить, согласуется ли эмпирическое распределение с этой гипотезой. Предположим, что по формуле (11.3) вычислены теоретические частоты n_1,n_2,ldots,n_s .Обозначим chi_q^2 среднее арифметическое квадратов разностей между эмпирическими и теоретическими частотами, взвешенное по обратным величинам теоретических частот:

$chi_q^2=sumlimits_{i=1}^{s}frac{(m_i-n_i)^2}{n_i}.$

Чем больше согласуются эмпирическое и теоретическое распределения, тем меньше различаются эмпирические и теоретические частоты и тем меньше значение chi_q^2 . Отсюда следует, что chi_q^2 характеризует близость эмпирического и теоретического распределений. В разных опытах chi_q^2 принимает различные, наперед неизвестные значения, т. е. является случайной величиной. Плотность вероятности этого распределения (для выборки достаточно большого объема) не зависит от проверяемого закона распределения, а зависит от параметра , называемого числом степеней свободы. При проверке гипотезы о нормальном распределении генеральной совокупности k=s-3 , где — число групп, на которые разбиты данные наблюдений. Существуют таблицы (прил. 6), в которых указана вероятность того, что в результате влияния случайных факторов величина chi^2 примет значение не меньше вычисленного по данным выборки chi_q^2 .

Для определенности примем уровень значимости 0,01. Если вероятность, найденная по таблицам, окажется меньше 0,01, то это означает, что в результате влияния случайных причин наступило событие, которое практически невозможно. Таким образом, тот факт, что chi^2 приняло значение chi_q^2 нельзя объяснить случайными причинами; его можно объяснить тем, что генеральная совокупность не распределена нормально и, значит, выдвинутая гипотеза о нормальном распределении генеральной совокупности должна быть отвергнута. Если вероятность, найденная по таблицам, превышает 0,01, то гипотеза о нормальном распределении генеральной совокупности согласуется с данными наблюдений и поэтому может быть принята. Полученные выводы распространяются и на другие уровни значимости.

На практике надо, чтобы объем выборки был достаточно большим (ngeqslant50) и чтобы каждая группа содержала не менее 5-8 значений признака.

Для проверки гипотезы о нормальном распределении генеральной совокупности нужно:

1) вычислить теоретические частоты по формуле (11.3);

2) вычислить $chi_q^2=sumlimits_{i=1}^{s}frac{(m_i-n_i)^2}{n_i}$ , где m_i,n_i — соответственно частоты эмпирические и теоретические;

3) вычислить число степеней свободы k=s-3 , где — число групп, на которые разбита выборка;

4) выбрать уровень значимости;

5) найти по таблице прил. 6 по найденным и chi_q^2 вероятность $P{chi^2geqslantchi_q^2}$ причем если эта вероятность меньше принятого уровня значимости, то гипотезу о нормальном распределении генеральной совокупности отвергают; если вероятность больше уровня значимости, то гипотезу принимают.

Пример 5. Проверить, согласуются ли данные выборки со статистической гипотезой о нормальном распределении генеральной совокупности, из которой извлечена эта выборка:

$begin{array}{|c|c|c|c|c|c|c|c|c|c|} hline{x_i}&15&20&25&30&35&40&45&50&55\ hline{m_i}&6&13&38&74&106&85&30&10&4\ hlineend{array}$

Решение. Вычислим выборочное среднее и выборочную дисперсию по формулам из первой главы этой части: $overline{x}_text{v}=34,!7;~D_text{v}=7,!38$ . Вычислим теоретические частоты по формулам (11.3)

$begin{array}{|c|c|c|c|c|c|} hline{x_i}&{m_i}&overline{x}_i-overline{x}_text{v}&t_i&varphi(t_i)&n_i\hline 15&6&hfill-19,!7&hfill-2,!67&0,!0113&3\ 20&13&hfill-14,!7&hfill-1,!99&0,!0551&14\ 25&38&hfill-9,!7&hfill-1,!31&0,!1691&42\ 30&74&hfill-4,!7&hfill-0,!63&0,!3271&82\ 35&106&hfill0,!3&hfill0,!05&0,!3984&99\ 40&85&hfill5,!3&hfill0,!73&0,!3056&76\ 45&30&hfill10,!3&hfill1,!41&0,!1476&37\ 50&10&hfill15,!3&hfill2,!09&0,!0449&11\ 55&4&hfill20,!3&hfill2,!77&0,!0086&2\ hline{}&sum{m_i=366}&{}&{}&{}&sum{n_i=366}\hline end{array}$

Найдём chi_q^2 . Вычислим число степеней свободы, учитывая, что число групп выборки s=9;~k=s-3=6. Уровень значимости alpha примем равным 0,01. По таблице прил. 6 при k=6 и chi_q^2=9 находим вероятность P=0,!1736 ; при chi_q^2=10 вероятность P=0,!1247 . Используя линейную интерполяцию, получаем приближённое значение искомой вероятности 0,!16>0,!01 .

Следовательно, данные наблюдения согласуются с гипотезой о нормальном распределении генеральной совокупности.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Критерий согласия Пирсона (или хи-квадрат) вычисляется по формуле:

n_i – эмпирические частоты;

n_i^* – теоретические частоты;

l – количество интервалов (вариант)

Объем выборки по критерию Пирсона:

n>30

Теоретические частоты должны быть больше 5.

Распределение Пирсона с k степенями свободы рассчитывается по формуле:

k=l−r−1

r – число параметров предполагаемого распределения

Если предполагаемое распределение имеет нормальный закон распределения, то число степеней свободы оценивают по двум параметрам (математическое ожидание и СКО) и формула имеет вид:

k=l−3

Пример

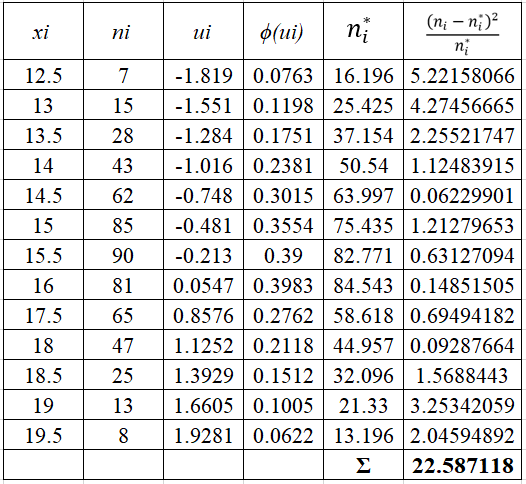
Проверить гипотезу о нормальном распределении по критерию Пирсона при уровне значимости 0,01. Дана выборка данных измерений в виде таблицы

Найдем выборочное среднее по формуле:

Отсюда

Формула выборочной исправленной дисперсии:

Тогда

Откуда получаем выборочную исправленную СКО:

Получаем параметры нормального распределения m_x=15,9, σ=1,87.

Найдем теоретические частоты по формуле:

h – шаг между вариантами, h=0,5

При уровне значимости α=0,01 и число степеней свободы k=13−3=10 по таблице Пирсона найдем критическое значение:

Наблюдаемое значение критерия равно:

Ввиду того, что

следовательно, нулевую гипотезу о нормальном распределении принимаем.

14847

Источник

Нормальное распределение

Время на прочтение
7 мин

Количество просмотров 36K

Автор статьи: Виктория Ляликова

Нормальный закон распределения или закон Гаусса играет важную роль в статистике и занимает особое положение среди других законов. Вспомним как выглядит нормальное распределение

$frac{1}{sigmasqrt{2pi}}e^left(-frac{(x-a)^2)}{2sigma^2}right)$

где a -математическое ожидание, — среднее квадратическое отклонение.

Тестирование данных на нормальность является достаточно частым этапом первичного анализа данных, так как большое количество статистических методов использует тот факт, что данные распределены нормально. Если выборка не подчиняется нормальному закону, тогда предположении о параметрических статистических тестах нарушаются, и должны использоваться непараметрические методы статистики

Нормальное распределение естественным образом возникает практически везде, где речь идет об измерении с ошибками. Например, координаты точки попадания снаряда, рост, вес человека имеют нормальный закон распределения. Более того, центральная предельная теорема вообще утверждает, что сумма большого числа слагаемых сходится к нормальной случайной величине, не зависимо от того, какое было исходное распределение у выборки. Таким образом, данная теорема устанавливает условия, при которых возникает нормальное распределение и нарушение которых ведет к распределению, отличному от нормального.

Можно выделить следующие этапы проверки выборочных значений на нормальность

Подсчет основных характеристик выборки. Выборочное среднее, медиана, коэффициенты асимметрии и эксцесса.
Графический. К этому методу относится построение гистограммы и график квантиль-квантиль или кратко QQ
Статистические методы. Данные методы вычисляют статистику по данным и определяют, какая вероятность того, что данные получены из нормального распределения

При нормальном распределении, которое симметрично, значения медианы и выборочного среднего будут одинаковы, значения эксцесса равно 3, а асимметрии равно нулю. Однако ситуация, когда все указанные выборочные характеристики равны именно таким значениям, практически не встречается. Поэтому после этапа подсчета выборочных характеристик можно переходить к графическому представлению выборочных данных.

Гистограмма позволяет представить выборочные данные в графическом виде – в виде столбчатой диаграммы, где данные делятся на заранее определенное количество групп. Вид гистограммы дает наглядное представление функции плотности вероятности некоторой случайной величины, построенной по выборке.

График QQ (квантиль-квантиль) является графиком вероятностей, который представляет собой графический метод сравнения двух распределений путем построения их квантилей. QQ график сравнивает наборы данных теоретических и выборочных (эмпирических) распределений. Если два сравниваемых распределения подобны, тогда точки на графике QQ будут приблизительно лежать на линии y=x. Основным шагом в построении графика QQ является расчет или оценка квантилей.

Существует множество статистических тестов, которые можно использовать для проверки выборочных значений на нормальность. Каждый тест использует разные предположения и рассматривает разные аспекты данных.

Чтобы применять статистические критерии сформулируем задачу. Выдвигаются две гипотезы H0 и H1, которые утверждают

H0 — Выборка подчиняется нормальному закону распределения

H1 — Выборка не подчиняется нормальному распределению

Установи уровень значимости alpha=0,05.

Теперь задача состоит в том, чтобы на основании какого-то критерия отвергнуть или принять основную нулевую гипотезу при уровне значимости

Критерий Шапиро-Уилка

Критерий Шапиро-Уилка основан на отношении оптимальной линейной несмещенной оценки дисперсии к ее обычной оценке методом максимального правдоподобия. Статистика критерия имеет вид

$W=frac{1}{s^2}{sumlimits_{i=1}^n{a_{n-i+1}(x_{n-i+1}-x_{i})}} s^2=sumlimits_{i=1}^n(x_i-overline x^2) overline x=frac{1}{n}sumlimits_{i=1}^n{x}$

Числитель является квадратом оценки среднеквадратического отклонения Ллойда. Коэффициенты ${a_{n-i+1}}$ и критические значения статистики являются табулированными значениями. Если , то нулевая гипотеза нормальности распределения отклоняется на уровне значимости .

В Python функция содержится в библиотеке scipy.stats и возвращает как статистику, рассчитанную тестом, так и значение p. В Python можно использовать выборку до 5000 элементов. Интерпретация вывода осуществляется следующим образом

Если значение , тогда принимается гипотеза H0, в противном случае, т.е. если, , тогда принимается гипотеза H1, т.е. что выборка не подчиняется нормальному закону.

Критерий Д’Агостино

В данном критерии в качестве статистики для проверки нормальности распределения используется отношение оценки Даутона для стандартного отклонения к выборочному стандартному отклонению, оцененному методом максимального правдоподобия

$D=frac{T}{n^2s} T=sumlimits_{i=1}^nbigg(i-frac{n+1}{2}bigg)x_i s^2=sumlimits_{i=1}^n(x_i-overline x^2), {x_1}leq...leq{x_n}$

В качестве статистики критерия Д’Агостино используется величина

$Y=sqrt{n}frac{(D-0,28209479)}{0,02998598}$

значение которой рассчитывается на основе центральной предельной теоремы, которая утверждает, что при

$limlimits_{x to infty}Pbigg(frac{D-M[D]}{sqrt{D[D]}}{<x}bigg)=Phi(x)$

гдестандартная нормальная случайная величина.

Критические значения являются табулированными значениями. Гипотеза нормальности принимается, если значение статистики лежит в интервале критических значений. Данный критерий показывает хорошую мощность против большого спектра альтернатив, по мощности немного уступая критерию Шапиро-Уилка.

В Python функция normaltest() также содержится в библиотеке scipy.stats и возвращает статистику теста и значение p. Интерпретация результата аналогична результатам в критерии Шапиро-Уилка.

Критерий согласия— Пирсона

Данный критерий является одним из наиболее распространенных критериев проверки гипотез о виде закона распределения и позволяет проверить значимость расхождения эмпирических (наблюдаемых) и теоретических (ожидаемых) частот. Таким образом, данный критерий позволяет проверить гипотезу о принадлежности наблюдаемой выборки некоторому теоретическому закону. Можно сказать, что критерий является универсальным, так как позволяет проверить принадлежность выборочных значений практическому любому закону распределения.

Для решения задачи используется статистика — Пирсона

$G=sumlimits_{k=1}^mfrac{(v_k-np_k)^2}{np_k}$

где — эмпирические частоты (подсчитывается число элементов выборки, попавших в интервал), ${np_k}$ — теоретические частоты. Подсчитывается критическое значение $chi^2_{кр}$ . Если $Ggeq chi^2_{кр}$ , отклоняется гипотеза о принадлежности выборки нормальному распределению и принимается, если $G< chi^2_{кр}$ .

Теперь перейдем к практической части. Для демонстрации функций будем использовать Dataset, взятый с сайта kaggle.com по прогнозированию инсульта по 11 клиническим характеристикам.

Загружаем необходимые библиотеки

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

Загружаем датасет

data_healthcares = pd.read_csv('E:/vika/healthcare-dataset-stroke-data.csv')

Набор состоит из 5110 строк и 12 столбцов.

Посмотрим на основные характеристики, каждого признака.
data_healthcares.describe()

Из данных характеристик можно увидеть, что есть пропущенные значения в показателях индекс массы тела. Посчитаем количество пропущенных значений.

Если бы нам необходимо было делать модель для прогноза, то пропущенные значения bmi являются достаточно большой проблемой, в которой возникает вопрос как их восстановить. Поэтому будем предполагать, что значения столбца bmi (индекс массы тела) подчиняются нормальному закону распределения (предварительно был построен график распределения, поэтому сделано такое предположение). Но так как, на данный момент, у нас нет необходимости в построении модели для прогноза, то удалим все пропущенные значения

new_data=data_healthcares.dropna()

Теперь можем приступать к проверке выборочных значений показателя bmi на нормальность. Вычислим основные выборочные характеристики

Выборочная характеристика	Код в python	Значение характеристики
Выборочное среднее	new_data.bmi.mean()	28,89
Выборочная медиана	new_data.bmi.median()	28,1
Выборочная мода	new_data.bmi.mode()	28,7
Выборочное среднеквадратическое отклонение	new_data.bmi.std()	7.854066729680458
Выборочный коэффициент асиметрии	new_data.bmi.skew()	1.0553402052962928
Выборочный эксцесс	new_data.bmi.kurtosis()	3.362659165623678

После вычислений основных характеристик мы видим, что выборочное среднее и медиана можно сказать принимают одинаковые значения и коэффициент эксцесса равен 3. Но, к сожалению коэффициент асимметрии равен 1, что вводить нас в некоторое замешательство, т.е. мы уже можем предположить, что значения bmi не подчиняются нормальному закону. Продолжим исследования, перейдем к построению графиков.

Строим гистограмму

fig = plt.figure
fig,ax= plt.subplots(figsize=(7,7))
sns.distplot(new_data.bmi,color='red',label='bmi',ax=ax)
plt.show()

Гистограмма достаточно хорошо напоминает нормальное распределение, кроме конечно, небольшого выброса справа, но смотрим дальше. Тут скорее, можно предположить, что значения bmi подчиняются распределению .

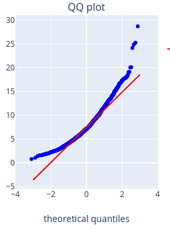
Строим QQ график. В python есть отличная функция qqplot(), содержащаяся в библиотеке statsmodel, которая позволяет строить как раз такие графики.

from statsmodels.graphics.gofplots import qqplot
from matplotlib import pyplot
qqplot(new_data.bmi, line=’s’)
Pyplot.show

Что имеем из графика QQ? Наши выборочные значений имеют хвосты слева и справа, и также в правом верхнем углу значения становятся разреженными.

На основе данных графика можно сделать вывод, что значения bmi не подчиняются нормальному закону распределения. Рядом приведен пример QQ графика распределения хи-квадрат с 8 степенями свободы из выборки в 1000 значений.

Для примера построим график QQ для выборки из нормального распределения с такими же показателями стандартного отклонения и среднего, как у bmi.

std=new_data.bmi.std() # вычисляем отклонение
mean=new_data.bmi.mean() #вычисляем среднее
Z=np.random.randn(4909)*std+mean # моделируем нормальное распределение
qqplot(Z,line='s') # строим график
pyplot.show()

Продолжим исследования. Перейдем к статистическим критериям. Будем использовать критерий Шапиро-Уилка и Д’Агостино, чтобы окончательно принять или опровергнуть предположение о нормальном распределении. Для использования критериев подключим библиотеки

from scipy.stats import shapiro
from scipy.stats import normaltest
shapiro(new_data.bmi)
ShapiroResult(statistic=0.9535483717918396, pvalue=6.623218133972133e-37)
Normaltest(new_data.bmi)
NormaltestResult(statistic=1021.1795052962864, pvalue=1.793444363882936e-222)

После применения двух тестов мы имеем, что значение p-value намного меньше заданного критического значения alpha , значит выборочные значения не принадлежат нормальному закону.

Конечно, мы рассмотрели не все тесты на нормальности, которые существуют. Какие можно дать рекомендации по проверке выборочных значений на нормальность. Лучше использовать все возможные варианты, если они уместны.

На этом все. Еще хочу порекомендовать бесплатный вебинар, который 15 июня пройдет на платформе OTUS в рамках запуска курса Математика для Data Science. На вебинаре расскажут про несколько часто используемых подходов в анализе данных, а также разберут, какие математические идеи работают у них под капотом и почему эти подходы вообще работают так, как нам нужно. Регистрация на вебинар доступна по этой ссылке.

Источник

7	4	4	15	1	1	7	15	19	4
0	4	8	14	10	0	1	11	8	2
6	2	5	3	12	2	9	6	2	5
13	5	7	3	3	10	0	11	17	11
9	6	11	7	20	1	14	6	7	4

7	4	4	15	1	1	7	15	19	4
0	4	8	14	10	0	1	11	8	2
6	2	5	3	12	2	9	6	2	5
13	5	7	3	3	10	0	11	17	11
9	6	11	7	20	1	14	6	7	4

7	4	4	15	1	1	7	15	19	4
0	4	8	14	10	0	1	11	8	2
6	2	5	3	12	2	9	6	2	5
13	5	7	3	3	10	0	11	17	11
9	6	11	7	20	1	14	6	7	4