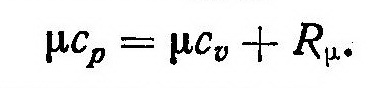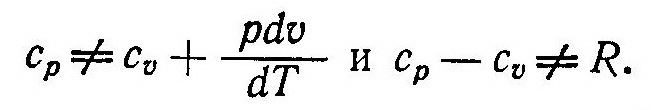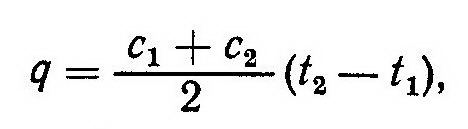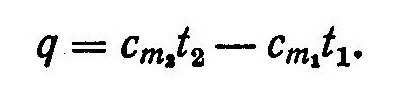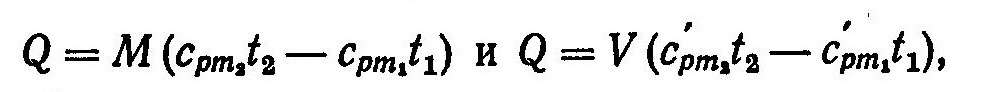Теплоёмкость идеального газа
Если
в результате теплообмена телу передается
некоторое количество теплоты, то
внутренняя энергия тела и его температура
изменяются. Количество теплоты Q,
необходимое для нагревания 1 кг вещества
на 1 К называют удельной
теплоемкостью вещества c.
|
Во
многих случаях удобно использовать молярную
теплоемкость C:
|
где M –
молярная масса вещества.
Определенная
таким образом теплоемкость не
является однозначной
характеристикой вещества. Согласно
первому закону термодинамики изменение
внутренней энергии тела зависит не
только от полученного количества
теплоты, но и от работы, совершенной
телом. В зависимости от условий, при
которых осуществлялся процесс
теплопередачи, тело могло совершать
различную работу. Поэтому одинаковое
количество теплоты, переданное телу,
могло вызвать различные изменения его
внутренней энергии и, следовательно,
температуры.
Такая
неоднозначность определения теплоемкости
характерна только для газообразного
вещества. При нагревании жидких и твердых
тел их объем практически не изменяется,
и работа расширения оказывается равной
нулю. Поэтому все количество теплоты,
полученное телом, идет на изменение его
внутренней энергии. В отличие от жидкостей
и твердых тел, газ в процессе теплопередачи
может сильно изменять свой объем и
совершать работу. Поэтому теплоемкость
газообразного вещества зависит от
характера термодинамического процесса.
Обычно рассматриваются два значения
теплоемкости газов: CV – молярная
теплоемкость в изохорном процессе (V = const)
и Cp – молярная
теплоемкость в изобарном процессе (p = const).
В
процессе при постоянном объеме газ
работы не совершает: A = 0.
Из первого закона термодинамики
для 1 моля газа
следует
|
Изменение ΔU внутренней
энергии газа прямо пропорционально
изменению ΔT его
температуры.
Для
процесса при постоянном давлении первый
закон термодинамики дает:
|
где ΔV –
изменение объема 1 моля идеального газа
при изменении его температуры на ΔT.
Отсюда следует:
|
|
Отношение ΔV / ΔT может
быть найдено из уравнения состояния
идеального газа, записанного для 1 моля:
|
pV = RT, |
где R –
универсальная газовая постоянная.
При p = const
|
|
Таким
образом, соотношение, выражающее связь
между молярными теплоемкостями Cp и CV,
имеет вид (формула
Майера):
|
Cp = CV + R. |
Молярная
теплоемкость Cp газа
в процессе с постоянным давлением всегда
больше молярной теплоемкости CV в
процессе с постоянным объемом
(рис. 3.10.1).
|
|
|
Рисунок Два |
Отношение
теплоемкостей в процессах с постоянным
давлением и постоянным объемом играет
важную роль в термодинамике. Оно
обозначается греческой буквой γ.
|
В
частности, это отношение входит в формулу
для адиабатического процесса (см. §3.9).
Между
двумя изотермами с температурами T1 и T2 на
диаграмме (p, V)
возможны различные пути перехода.
Поскольку для всех таких переходов
изменение температуры ΔT = T2 – T1 одинаково,
следовательно, одинаково
изменение ΔU внутренней
энергии. Однако, совершенные при этом
работы A и
полученные в результате теплообмена
количества теплоты Q окажутся
различными для разных путей перехода.
Отсюда следует, что у газа имеется
бесчисленное количество теплоемкостей. Cp и CV–
это лишь частные (и очень важные для
теории газов) значения теплоемкостей.
|
|
|
Модель. |
Термодинамические
процессы, в которых теплоемкость газа
остается неизменной, называются политропическими.
Все изопроцессы являются политропическими.
В случае изотермического процесса ΔT = 0,
поэтому CT = ∞.
В адиабатическом процессе ΔQ = 0,
следовательно, Cад = 0.
Следует
отметить, что «теплоемкость», как и
«количество теплоты» – крайне неудачные
термины. Они достались современной
науке в наследство от теории теплорода,
господствовавшей в XVIII веке. Эта
теория рассматривала теплоту как особое
невесомое вещество, содержащееся в
телах. Считалось, что оно не может быть
ни создано, ни уничтожено. Нагревание
тел объяснялось увеличением, а охлаждение
– уменьшением содержащегося внутри
них теплорода. Теория теплорода
несостоятельна. Она не может объяснить,
почему одно и то же изменение внутренней
энергии тела можно получить, передавая
ему разное количество теплоты в
зависимости от работы, которую совершает
тело. Поэтому лишено физического смысла
утверждение, что «в данном теле содержится
такой-то запас теплоты».
В
молекулярно-кинетической теории
устанавливается следующее соотношение
между средней кинетической
энергией
поступательного
движения молекул
и абсолютной температурой T:
|
|
Внутренняя
энергия 1 моля идеального газа равна
произведению
на
число Авогадро NА:
|
|
При
изменении температуры на ΔT внутренняя
энергия изменяется на величину
|
Коэффициент
пропорциональности между ΔU и ΔT равен
теплоемкости CV при
постоянном давлении:
|
Это
соотношение хорошо подтверждается в
экспериментах с газами, состоящими из
одноатомных молекул (гелий, неон, аргон).
Однако, для двухатомных (водород, азот)
и многоатомных (углекислый газ) газов
это соотношение не согласуется с
экспериментальными данными. Причина
такого расхождения состоит в том, что
для двух- и многоатомных молекул средняя
кинетическая энергия должна включать
энергию не только поступательного, но
и вращательного движения молекул.
|
|
|
Рисунок Модель |
На
рис. 3.10.2 изображена модель двухатомной
молекулы. Молекула может совершать пять
независимых движений: три поступательных
движения вдоль осей X, Y, Z и
два вращения относительно осей X и Y.
Опыт показывает, что вращение относительно
оси Z,
на которой лежат центры обоих атомов,
может быть возбуждено только при очень
высоких температурах. При обычных
температурах вращение около оси Z не
происходит, так же как не вращается
одноатомная молекула. Каждое независимое
движение называется степенью
свободы.
Таким образом, одноатомная молекула
имеет 3 поступательные степени свободы,
«жесткая» двухатомная молекула имеет
5 степеней (3 поступательные и 2
вращательные), а многоатомная молекула
– 6 степеней свободы (3 поступательные
и 3 вращательные).
В
классической статистической физике
доказывается так называемая теорема
о равномерном распределении энергии
по степеням свободы:
Если
система молекул находится в тепловом
равновесии при температуре T,
то средняя кинетическая энергия
равномерно распределена между всеми
степенями свободы и для каждой степени
свободы молекулы она равна
Из
этой теоремы следует, что молярные
теплоемкости газа Cp и CV и
их отношение γ могут
быть записаны в виде
|
где i –
число степеней свободы газа.
Для
газа, состоящего из одноатомных
молекул (i = 3)
|
Для
газа, состоящего из двухатомных
молекул (i = 5)
|
Для
газа, состоящего из многоатомных
молекул (i = 6)
|
Экспериментально
измеренные теплоемкости многих газов
при обычных условиях достаточно хорошо
согласуются с приведенными выражениями.
Однако, в целом классическая теория
теплоемкости газов не может считаться
вполне удовлетворительной. Существует
много примеров значительных расхождений
между теорией и экспериментом. Это
объясняется тем, что классическая теория
не в состоянии полностью учесть энергию,
связанную с внутренними движениями в
молекуле.
Теорему
о равномерном распределении энергии
по степеням свободы можно применить и
к тепловому движению частиц в твердом
теле. Атомы, входящие в состав
кристаллической решетки, совершают
колебания около положений равновесия.
Энергия этих колебаний и представляет
собой внутреннюю энергию твердого тела.
Каждый атом в кристаллической решетке
может колебаться в трех взаимно
перпендикулярных направлениях.
Следовательно, каждый атом имеет 3
колебательные степени свободы. При
гармонических колебаниях средняя
кинетическая энергия равна средней
потенциальной энергии. Поэтому в
соответствии с теоремой о равномерном
распределении на каждую колебательную
степень свободы приходится средняя
энергия kT,
а на один атом – 3kT. Внутренняя
энергия 1 моля твердого
вещества равна:
|
U = 3NАkT = 3RT. |
Поэтому
молярная теплоемкость вещества в твердом
состоянии равна:
|
Это
соотношение называется законом
Дюлонга–Пти.
Для твердых тел практически не существует
различия между Cp и CV из-за
ничтожно малой работы при расширении
или сжатии.
Опыт
показывает, что у многих твердых тел
(химических элементов) молярная
теплоемкость при обычных температурах
действительно близка к 3R.
Однако, при низких температурах
наблюдаются значительные расхождения
между теорией и экспериментом. Это
показывает, что гипотеза о равномерном
распределении энергии по степеням
свободы является приближением. Наблюдаемая
на опыте зависимость теплоемкости от
температуры может быть объяснена только
на основе квантовых представлений.
Вопрос
№26
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Если в результате теплообмена телу передается некоторое количество теплоты, то внутренняя энергия тела и его температура изменяются. Количество теплоты Q, необходимое для нагревания 1 кг вещества на 1 К называют удельной теплоемкостью вещества c.
Во многих случаях удобно использовать молярную теплоемкость C:
где M – молярная масса вещества.
Определенная таким образом теплоемкость не является однозначной характеристикой вещества. Согласно первому закону термодинамики изменение внутренней энергии тела зависит не только от полученного количества теплоты, но и от работы, совершенной телом. В зависимости от условий, при которых осуществлялся процесс теплопередачи, тело могло совершать различную работу. Поэтому одинаковое количество теплоты, переданное телу, могло вызвать различные изменения его внутренней энергии и, следовательно, температуры.
Такая неоднозначность определения теплоемкости характерна только для газообразного вещества. При нагревании жидких и твердых тел их объем практически не изменяется, и работа расширения оказывается равной нулю. Поэтому все количество теплоты, полученное телом, идет на изменение его внутренней энергии. В отличие от жидкостей и твердых тел, газ в процессе теплопередачи может сильно изменять свой объем и совершать работу. Поэтому теплоемкость газообразного вещества зависит от характера термодинамического процесса. Обычно рассматриваются два значения теплоемкости газов: CV – молярная теплоемкость в изохорном процессе (V = const) и Cp – молярная теплоемкость в изобарном процессе (p = const).
В процессе при постоянном объеме газ работы не совершает: A = 0. Из первого закона термодинамики для 1 моля газа следует
Изменение ΔU внутренней энергии газа прямо пропорционально изменению ΔT его температуры.
Для процесса при постоянном давлении первый закон термодинамики дает:
Qp = ΔU + p (V2 – V1) = CV ΔT + pΔV,
где ΔV – изменение объема 1 моля идеального газа при изменении его температуры на ΔT. Отсюда следует:
Отношение ΔV / ΔT может быть найдено из уравнения состояния идеального газа, записанного для 1 моля:
где R – универсальная газовая постоянная. При p = const
Таким образом, соотношение, выражающее связь между молярными теплоемкостями Cp и CV, имеет вид (формула Майера):
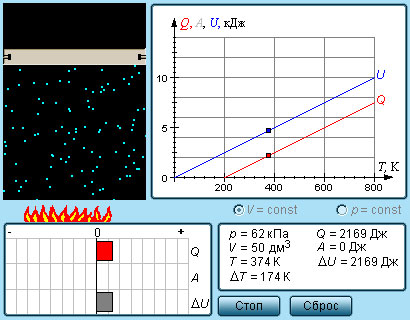
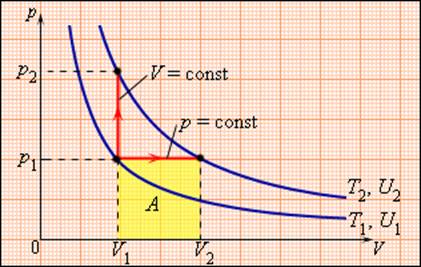
Молярная теплоемкость Cp газа в процессе с постоянным давлением всегда больше молярной теплоемкости CV в процессе с постоянным объемом (рис. 3.10.1).
|
|
|
Рисунок 3.10.1. Два возможных процесса нагревания газа на ΔT = T2 – T1. При p = const газ совершает работу A = p1(V2 – V1). Поэтому Cp > CV |
Отношение теплоемкостей в процессах с постоянным давлением и постоянным объемом играет важную роль в термодинамике. Оно обозначается греческой буквой γ.
В частности, это отношение входит в формулу для адиабатического процесса.
Между двумя изотермами с температурами T1 и T2 на диаграмме (p, V) возможны различные пути перехода. Поскольку для всех таких переходов изменение температуры ΔT = T2 – T1 одинаково, следовательно, одинаково изменение ΔU внутренней энергии. Однако, совершенные при этом работы A и полученные в результате теплообмена количества теплоты Q окажутся различными для разных путей перехода. Отсюда следует, что у газа имеется бесчисленное количество теплоемкостей. Cp и CV – это лишь частные (и очень важные для теории газов) значения теплоемкостей.
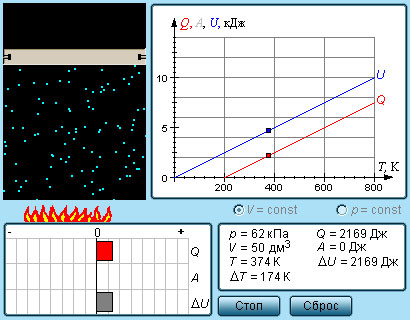 |
|
Модель. Теплоемкости идеального газа. |
Термодинамические процессы, в которых теплоемкость газа остается неизменной, называются политропическими. Все изопроцессы являются политропическими. В случае изотермического процесса ΔT = 0, поэтому CT = ∞. В адиабатическом процессе ΔQ = 0, следовательно, Cад = 0.
Следует отметить, что «теплоемкость», как и «количество теплоты» – крайне неудачные термины. Они достались современной науке в наследство от теории теплорода, господствовавшей в XVIII веке. Эта теория рассматривала теплоту как особое невесомое вещество, содержащееся в телах. Считалось, что оно не может быть ни создано, ни уничтожено. Нагревание тел объяснялось увеличением, а охлаждение – уменьшением содержащегося внутри них теплорода. Теория теплорода несостоятельна. Она не может объяснить, почему одно и то же изменение внутренней энергии тела можно получить, передавая ему разное количество теплоты в зависимости от работы, которую совершает тело. Поэтому лишено физического смысла утверждение, что «в данном теле содержится такой-то запас теплоты».
В молекулярно-кинетической теории устанавливается следующее соотношение между средней кинетической энергией поступательного движения молекул и абсолютной температурой T:
Внутренняя энергия 1 моля идеального газа равна произведению на число Авогадро NА:
При изменении температуры на ΔT внутренняя энергия изменяется на величину
Коэффициент пропорциональности между ΔU и ΔT равен теплоемкости CV при постоянном давлении:
Это соотношение хорошо подтверждается в экспериментах с газами, состоящими из одноатомных молекул (гелий, неон, аргон). Однако, для двухатомных (водород, азот) и многоатомных (углекислый газ) газов это соотношение не согласуется с экспериментальными данными. Причина такого расхождения состоит в том, что для двух- и многоатомных молекул средняя кинетическая энергия должна включать энергию не только поступательного, но и вращательного движения молекул.
|
|
|
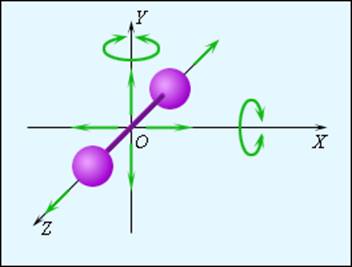
Рисунок 3.10.2. Модель двухатомной молекулы. Точка O совпадает с центром масс молекулы |
На рис. 3.10.2 изображена модель двухатомной молекулы. Молекула может совершать пять независимых движений: три поступательных движения вдоль осей X, Y, Z и два вращения относительно осей X и Y. Опыт показывает, что вращение относительно оси Z, на которой лежат центры обоих атомов, может быть возбуждено только при очень высоких температурах. При обычных температурах вращение около оси Z не происходит, так же как не вращается одноатомная молекула. Каждое независимое движение называется степенью свободы. Таким образом, одноатомная молекула имеет 3 поступательные степени свободы, «жесткая» двухатомная молекула имеет 5 степеней (3 поступательные и 2 вращательные), а многоатомная молекула – 6 степеней свободы (3 поступательные и 3 вращательные).
В классической статистической физике доказывается так называемая теорема о равномерном распределении энергии по степеням свободы:
Если система молекул находится в тепловом равновесии при температуре T, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна
Из этой теоремы следует, что молярные теплоемкости газа Cp и CV и их отношение γ могут быть записаны в виде
где i – число степеней свободы газа.
Для газа, состоящего из одноатомных молекул (i = 3)
Для газа, состоящего из двухатомных молекул (i = 5)
Для газа, состоящего из многоатомных молекул (i = 6)
Экспериментально измеренные теплоемкости многих газов при обычных условиях достаточно хорошо согласуются с приведенными выражениями. Однако, в целом классическая теория теплоемкости газов не может считаться вполне удовлетворительной. Существует много примеров значительных расхождений между теорией и экспериментом. Это объясняется тем, что классическая теория не в состоянии полностью учесть энергию, связанную с внутренними движениями в молекуле.
Теорему о равномерном распределении энергии по степеням свободы можно применить и к тепловому движению частиц в твердом теле. Атомы, входящие в состав кристаллической решетки, совершают колебания около положений равновесия. Энергия этих колебаний и представляет собой внутреннюю энергию твердого тела. Каждый атом в кристаллической решетке может колебаться в трех взаимно перпендикулярных направлениях. Следовательно, каждый атом имеет 3 колебательные степени свободы. При гармонических колебаниях средняя кинетическая энергия равна средней потенциальной энергии. Поэтому в соответствии с теоремой о равномерном распределении на каждую колебательную степень свободы приходится средняя энергия kT, а на один атом – 3kT. Внутренняя энергия 1 моля твердого вещества равна:
Поэтому молярная теплоемкость вещества в твердом состоянии равна:
C = 3R = 25,12 Дж/моль·К.
Это соотношение называется законом Дюлонга–Пти. Для твердых тел практически не существует различия между Cp и CV из-за ничтожно малой работы при расширении или сжатии.
Опыт показывает, что у многих твердых тел (химических элементов) молярная теплоемкость при обычных температурах действительно близка к 3R. Однако, при низких температурах наблюдаются значительные расхождения между теорией и экспериментом. Это показывает, что гипотеза о равномерном распределении энергии по степеням свободы является приближением. Наблюдаемая на опыте зависимость теплоемкости от температуры может быть объяснена только на основе квантовых представлений.
Теплоемкость идеального газа
Определение теплоемкости
Теплоемкость – это количество тепла, которое затрачивается для того, чтобы повысить температуру тела на один кельвин. Теплоемкость зависит от массы вещества, условий при которых системе сообщают теплоту. Уравнение (1) – это определение теплоемкости через интегральные параметры. Иногда удобнее использовать следующее определение теплоемкости:
где – бесконечно мало количество плоты, которое получает тело; dT – приращение температуры тела.
При единичной массе тела теплоемкость называют удельной. Обозначают ее обычно маленькой буквой c. Еще используют молярную теплоемкость () – это теплоемкость одного моля вещества.
Теплоемкость и первое начало термодинамики
Используя первое начало термодинамики в интегральной записи, теплоёмкость можно найти как:
где – изменение внутренней энергии термодинамической системы; A – работа системы над внешними силами. Для идеального газа имеем:
где m – масса газа; – молярная масса газа; R – универсальная газовая постоянная.
В дифференциальном виде:
Для идеального газа теплоемкость равна:
Теплоемкость для процессов, проводимых в идеальном газе
Теплоемкость связана с характером процесса. Она может изменяться от бесконечных отрицательных величин до бесконечных положительных.
Рассмотрим изохорный процесс . При проведении изохорного процесса газ работы не совершает, поэтому теплоемкость газа в изохорном процессе (
) равна:
Или:
При изобарном процессе () теплоемкость обозначают как
. Она равна:
Или:
Теплоемкости, при постоянных давлении и объеме, являются функциями состояний. Надо отметить, что независимость теплоемкости от температуры не подтвердили эксперименты.
В изотермическом процессе теплоемкость идеального газа считают бесконечной:
В адиабатном процессе теплоемкость равна нулю.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |
Здравствуйте! Измерение температуры тела при одном и том же количестве сообщаемой теплоты зависит от характера происходящего при этом процесса, поэтому теплоемкость является функцией процесса. Количество теплоты dq, которая подводится к газу при нагревании или отводится при охлаждении, можно определить, зная изменение температуры dT и удельную теплоемкость с:
dq = cdT. (1)
Удельная теплоемкость с соответствует количеству теплоты, которое необходимо сообщить единице количества вещества для повышения его температуры на один градус:
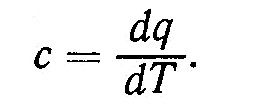
В зависимости от того, к какому количеству вещества отнесена теплоемкость, различают массовую с, объемную с’ и мольную рс теплоемкости. Массовую теплоемкость относят к 1 кг газа и измеряют в Дж/(кг*°С). Ввиду того что эта единица теплоемкости мала, чаще пользуются кратной единицей измерения кДж/(кг*°С). Кроме того, применяется и внесистемная единица ккал/(кг*град).
Объемная теплоемкость с’ характеризует количество теплоты, необходимой для нагревания 1 м3 газа на 1°С . В 1 м3 в зависимости от температуры и давления может содержаться различное по массе количество газа, поэтому объемную теплоемкость принято относить к 1 м3 газа при нормальных условиях. Объемная теплоемкость измеряется в кДж/(нм3*° С). Между массовой и объемной теплоемкостью существует следующая зависимость: c = υнc’.
Мольная теплоемкость газа характеризует теплоаккумулирующую способность 1 киломоля газа и находится как произведение молекулярной массы газа р на массовую теплоемкость с. Мольная теплоемкость μс измеряется в Дж/(кмоль*° С) и кДж/(кмоль*°С). Величину мольной теплоемкости также можно определить, если известна объемная теплоемкость μс = 22,4 с’.
Анализ выражения (2) показывает, что теплоемкость может изменяться в очень широких пределах. В адиабатном процессе, когда работа совершается за счет изменения внутренней энергии (dq = 0), теплоемкость равна нулю.
В изотермическом процессе при подводе и отводе теплоты температура остается постоянной (dT = 0) и, следовательно, теплоемкость с = ∞. Таким образом, теплоемкость газов в отличие от твердых тел и жидкостей изменяется в широких пределах и зависит от характера процесса изменения состояния.
Подведенная к газу теплота, как следует из уравнения первого закона термодинамики,
dq = du+dl,
затрачивается как на изменение внутренней энергии du, так и на работу dl против внешних сил, что учитывается теплоемкостью. Чем больше величина работы dl по отношению к изменению внутренней энергии du, тем больше величина теплоемкости газа в данном процессе. Подставив значение dq из уравнения dq = du+pdυ в выражение (2), получим
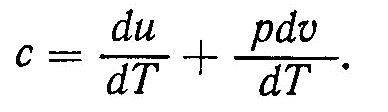
Это равенство определяет величину теплоемкости газа в процессе изменения его состояния. Величина du/dT есть изменение внутренней энергии, соответствующее изменению температуры газа на один градус. Слагаемое pdυ/dT равно работе при изменении температуры на один градус и может принимать различные значения в зависимости от процесса изменения состояния. Следовательно, теплоемкость с газа не определяется только теплоаккумулирующей способностью вещества (величиной du/dT) а, как и работа газа, является функцией процесса. Чем большую работу совершает газ в процессе, тем больше теплоты необходимо подвести для изменения температуры на один градус. Поэтому теплоемкость для газов необходимо определять в зависимости от процесса изменения состояния.
В изохорном процессе (dυ = 0) работа расширения равна нулю, и вся подведенная теплота идет на изменение внутренней энергии:
dq = du. (4)
Из выражений (1) и (4) находим изменение внутренней энергии газа в процессе при постоянном удельном объеме:
du = cυdT, (5)
где сυ — теплоемкость при постоянном объеме (изохорная теплоемкость) .
Можно доказать, что выражение (5) справедливо для любого процесса изменения состояния, если газ идеальный. Так как идеальный газ представляет собой систему материальных точек, лишенных сил взаимодействия, то внутренняя энергия его не зависит от среднего расстояния между молекулами, то есть от удельного объема, а зависит, согласно молекулярно-кинетической теории, только от температуры.
Этот вывод был подтвержден экспериментами Гей-Люссака и Джоуля. В опытах использовались два сосуда, сообщающихся между собой с помощью крана. Из одного сосуда выкачивали воздух, а затем открывали кран. Воздух, находящийся в другом сосуде, расширялся, заполняя объем первого сосуда. Опыты показали, что температура системы в целом при этом не изменяется.
Поскольку теплообмен между системой и средой в этих условиях отсутствовал (dq = 0) и работа газа против внешних сил была равна нулю (dl = 0), из уравнения dq = du+dl следует, что внутренняя энергия газа в опыте оставалась постоянной (du = 0). Так как удельный объем газа и его давление в процессе расширения изменялись, можно сделать вывод, что внутренняя энергия идеального газа не зависит от объема υ и давления р и является функцией абсолютной температуры Т. Поэтому выражение (5) можно применять для идеального газа в любом процессе.
Более точные опыты показывают, что внутренняя энергия реальных газов зависит от удельного объема и давления, и, следовательно, соотношение (5) применимо к реальным газам только для изохорного процесса. В других процессах, связанных с изменением удельного объема и давления, du ≠ cυdT.
Подставив значение du из равенства (5) в уравнение (3), получим выражение, определяющее величину теплоемкости идеального газа:
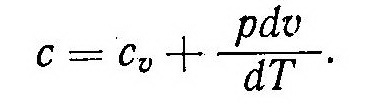
В изобарном процессе величина pdυ/dT, учитывающая работу газа при изменении температуры на один градус, согласно выражению R = pdυ/dT, равна газовой постоянной R. Тогда для теплоемкости cp из соотношения (6) получим уравнение
cр = cυ+R, (7)
которое называется уравнением Майера.
Это выражение показывает, что теплоемкость ср газа в изобарном процессе (изобарная теплоемкость) превышает изохорную теплоемкость сυ на величину газовой постоянной, то есть на величину работы 1 кг газа в изобарном процессе при изменении температуры на 1°С. Умножив левую и правую части уравнения (7) на молекулярную массу μ газа, получим уравнение Майера для одного киломоля газа:
Теплоемкость реального газа нельзя определить из соотношений (6) и (7), так как
Это объясняется наличием сил взаимодействия между молекулами реального газа. Для совершения работы против этих сил к газу в процессе расширения необходимо подводить дополнительное количество теплоты.
Опыты показывают, что теплоемкость газов зависит также от температуры и с ее увеличением обычно возрастает. Экспериментальную зависимость теплоемкости от температуры можно представить в виде степенных рядов типа
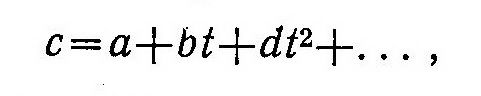
где a, b, d, … — определяемые из опыта коэффициенты.
Число членов ряда выбирается в зависимости от требуемой точности расчета, а также интервала изменения температур. Для небольших температурных интервалов можно пользоваться постоянными теплоемкостями или применять линейную зависимость между теплоемкостью и температурой:
с = а+bt. (9)
Теплоемкость, соответствующая данной температуре, называется истинной. Величина истинной теплоемкости определяется выражениями (2) и (8). В технических расчетах чаще пользуются средними значениями теплоемкости для определенного интервала температур.
Количество подводимой к системе теплоты q можно определить путем интегрирования выражения (2):
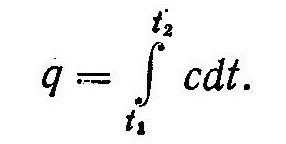
В это выражение вместо теплоемкости с можно подставить экспериментальные зависимости (8), которые приводятся в справочной литературе, и после интегрирования с любой степенью точности вычислить количество теплоты q.
Если пользоваться линейной зависимостью (9), то, согласно выражению (10),
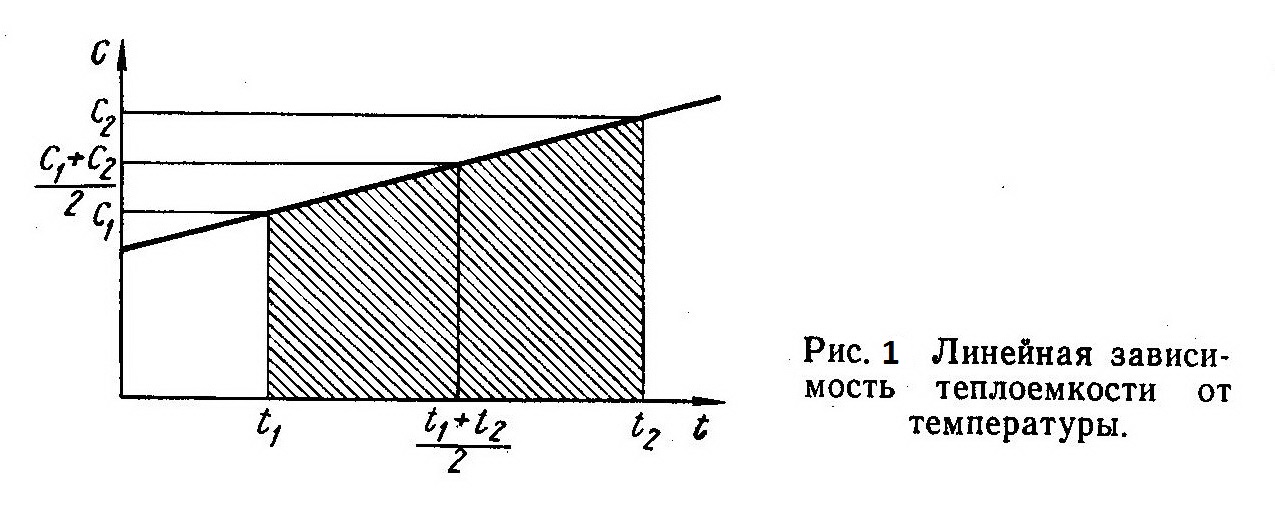
на рис. 1. количеству теплоты соответствует заштрихованная площадь, величина которой может быть определена как площадь трапеции (высота ее равна разности температур t1-t2):
где c1 и с2 — истинные теплоемкости при температурах t1 и t2.
Следовательно, при линейной зависимости теплоемкости от температуры количество теплоты можно определять как произведение средней арифметической теплоемкости на разность температур. Вычисление и составление таблиц средних теплоемкостей между двумя температурами t1 и t2 при нелинейной зависимости типа степенных рядов практически нецелесообразно, так как при этом значительно увеличиваются число табличных величин и размеры таблиц. В справочной литературе обычно приводят таблицы средних значений теплоемкостей для интервала температур от 0°С до t °С (обозначаются индексом m). Например, при определении количества теплоты, подводимой к 1 нм3 газа, в изобарном процессе необходимо пользоваться средней изобарной объемной теплоемкостью с’рm.
Зная средние значения массовых теплоемкостей, легко опре-делить количество теплоты, подводимой к 1 кг газа в интервалах температур от 0° С до t1:
q1 = cm1t1
и от 0° С до t2:
q1 = cm2t2,
где сm1, и сm2 — соответственно средние значения теплоемкостей для интервалов температур от 0°С до t1 и от 0 °С до t2.
Количество теплоты, подводимой в интервале температур от t1 до t2, равно разности количества теплоты q2 для интервала от 0° С до t1 и количества теплоты q1 для интервала от 0° С до t1:
Эта формула наиболее часто применяется в практических расчетах, основанных на использовании средних табличных значений теплоемкости, которые отсчитываются от 0° С. Например, полное количество теплоты Q, подведенной к М кг или V нм3 газа при постоянном давлении, определяется из соотношений
где cpm и c’pm — соответственно удельные массовая и объемная средние изобарные теплоемкости. Исп.литература: 1) Теплотехника, под ред. А.П.Баскакова, Москва, Энергоиздат, 1982. 2)Теплотехника, Бондарев В.А., Процкий А.Е., Гринкевич Р.Н. Минск, изд. 2-е,»Вышейшая школа», 1976.

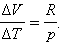


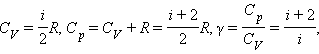
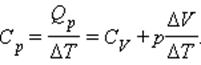
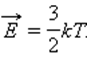
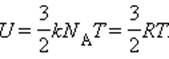
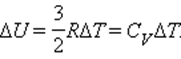
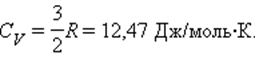
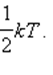
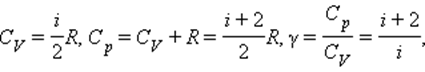
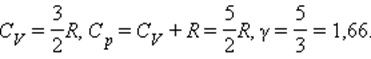
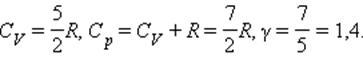
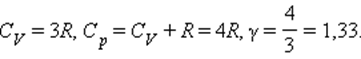
![Rendered by QuickLaTeX.com [C=frac{frac{i}{2}frac{m}{mu}RdT+pdV}{dT}=frac{i}{2}frac{m}{mu}R+pfrac{dV}{dT} qquad (6) ]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-bc49437affd37c7a2b86038ef2b410a7_l3.png)