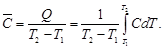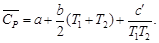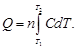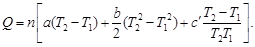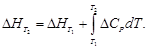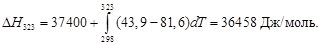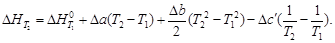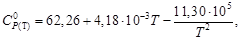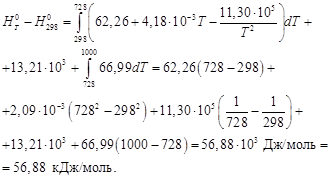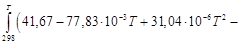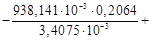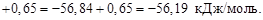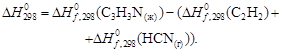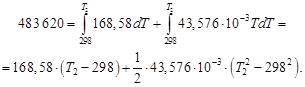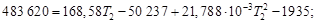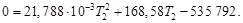Теплоемкость
является одним из важнейших свойств
вещества, она используется при расчетах
многих термодинамических функций. При
р=const
используется изобарная теплоемкость
– Ср,k.
Теплоемкость зависит от температуры,
и эта зависимость Ср,k
для любого вещества выражается степенным
рядом:
Cp
= a
+ bT+
cT²
для органических веществ.
Если в расчетах
используется широкий диапазон температур,
то необходимо учитывать зависимость
теплоемкости от температуры.
Изменение
теплоемкости в ходе химической реакции
рассчитывается по обычной формуле: ΔrCp
= ΣνiCpi
– ΣνjCpj.
Чаще всего в справочной литературе
приводятся трехчленные ряды, выражающие
зависимость теплоемкости от температуры.
Для
того, чтобы получить выражение для ΔrСр,
рассчитаем сначала изменение каждого
коэффициента степенного ряда теплоемкости,
например, Δra
= Σνiai
– Σνjaj.
Таким же образом рассчитаем все остальные
коэффициенты при температуре.
Δra
= -51,71-(21,09+27,28*3) = -112,46
Δrb
=(598,77-(400,12+3*3,26)) ×10-3
= 188,87×10-3
Δrc
=( -230,00+169,87) ×10-6=
-60,13×10-6
Δrc’=1,5×105
В результате
получим выражение:
ΔrCp
= -112,46+188,87*10-3*Т–60,13*10-6*Т2+1,5*105*T-2
1.
(изохорная
теплоемкость, равная
отношению удельного количества теплоты
в изохорном процессе к изменению
температуры рабочего тела dT)
2.
Для идеальных газов связь между изобарной
и изохорной теплоёмкостями
и
устанавливается
известным уравнением Майера
.
Из
уравнения Майера следует, что изобарная
теплоемкость больше изохорной на
значение удельной характеристической
постоянной идеального газа. Это
объясняется тем, что в изохорном
процессе (
)
внешняя работа не выполняется и
теплота расходуется только на изменение
внутренней энергии рабочего тела,
тогда как в изобарном процессе (
)
теплота расходуется не только на
изменение внутренней энергии рабочего
тела, зависящей от его температуры, но
и на совершение им внешней работы.
4. Расчет и построение графической зависимости стандартного теплового эффекта реакции от температуры
Чтобы
получить уравнение зависимости теплоты
реакции от температуры в виде степенного
ряда, воспользуемся уравнением Кирхгоффа:
dΔH°/dT
= ΔCp
, где
ΔrCp
– изменение теплоемкости в ходе
химической реакции.
Для
того, чтобы получить уравнение зависимости
теплоты реакции от температуры
проинтегрируем уравнение Кирхгоффа с
использованием выражения ΔСр в виде
полученного степенного ряда. Получим
уравнение:
ΔrH°
= ΔHj
+ ΔraT
+ ΔrbT²/2
+ ΔrcT³/3
— Δrc’/T,
где
ΔНj
– константа интегрирования, которую
необходимо предварительно рассчитать.
Для этого воспользуемся значением
стандартного теплового эффекта при
температуре 298.15 К и, соответственно, Т
= 298.15 К.
-206070
= ΔHj
+-112,46*Т-0,18887*Т2+0,00006013*Т3
– 150000/T
ΔHj
= -180906,584 Дж/моль;
Теперь
мы имеем уравнение для расчета теплового
эффекта реакции при любой температуре
в пределах, определенных интервалами
температур для Ср,k:
Рассчитаем
тепловой эффект в интервале температур
(Т-200) ÷ (Т+200) с шагом в 50 градусов. Полученные
значения внесем в таблицу 2 и построим
график ΔrH°т
= f(T).
|
Т, К |
rHТ |
|
325 |
-207707,899 |
|
375 |
-210456,135 |
|
425 |
-212830,460 |
|
475 |
-214850,479 |
|
525 |
-216534,056 |
|
575 |
-217898,068 |
|
625 |
-218958,804 |
|
675 |
-219732,179 |
|
725 |
-220233,866 |

1.В данном случае
константа интегрирования не нужна, так
как Ср=Δа
2.Если Ср=0, мы можем
сделать вывод, что процесс в данной
системе адиабатический.
3.
5.
Расчет стандартной энтропии реакции
при Т=298 К.
По
данным об абсолютных значениях энтропии
участников реакции найдем изменение
энтропии реакции: ΔrS°298
= ΣνiS°i,298
– ΣνjS°j,298
ΔrS°298
= 298,24-(269,20+3*130,52) = -362,52 Дж/моль·К
Энтропия
– это функция, которая характеризует
«порядок» в системе – чем больше значение
энтропии, тем больше в системе «беспорядок».
В данном случае при протекании реакции
энтропия значительно уменьшилась.
1.
6.
Расчет изменения стандартной энергии
Гиббса при Т=298 К
Рассчитаем
изменение стандартной энергии Гиббса
при Т=298 К в Дж/моль по уравнению и сделаем
вывод о направлении протекания реакции
при исходных условиях: ΔrG°298
= ΔrH°298
— TΔrS°298
ΔrG°298
= -206070 + 298.15×362,52 = -97984,662 Дж/моль
Энергия Гиббса
является критерием самопроизвольного
протекания процесса. Полученное изменение
энергии Гиббса больше нуля, при Т=298.15К
реакция не может идти в сторону образования
продуктов.
1.
7.
Расчет констант равновесия при р=1 атм.
и Т=298 К
Рассчитаем
lnKp,298
, Kp,298
, Kc
при Т=298,15 К:
Из
уравнения ΔG°т
= -RTlnKp
найдем значение lnKp
= — ΔrG°298/RT
,
lnKp
= 97984,662 / 8.314×298.15 = 39,52634, Kp
= 1,4658×1017
,
а,
используя соотношение между Кр и Кс,
найдем значение Кс: Кр = Кс(RT)Δν
, где Δν = Σνi
– Σνj.
Kc
= 1,4658×1017
/(8.314×298.15)
Δν = 2,14×1021
1.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
ЭЛЕМЕНТЫ ТЕРМОХИМИИ
Термохимия – раздел химии, в котором рассматриваются тепловые явления, происходящие в процессе химических реакций.
Нужен репетитор по химии? Записывайтесь на занятия в каталоге TutorOnline!
Все химические реакции можно разделить на два типа: реакции, идущие с выделением теплоты, их называют экзотермические, и реакции, идущие с поглощением теплоты эндотермические. Критерием таких процессов является тепловой эффект реакции.
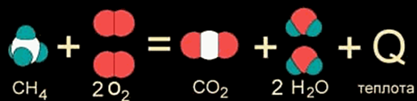
Как правило, к экзотермическим реакциям относятся реакции окисления, т.е. взаимодействия с кислородом, например сгорание метана
СН4 + 2O2 = СО2 + 2Н2О + Q (1)
а к эндотермическим реакциям – реакции разложения. Знак Q в конце уравнения указывает на то, выделяется ли теплота в процессе реакции (+ Q) или поглощается (- Q):
СаCO3 = СаO + CO2 -Q (2)
При химических процессах может выделяться или поглощаться не только тепловая, но и другие виды энергии: электрическая, световая, механическая и др.
Тепловые эффекты прямой и обратной реакций одинаковы по числу, но противоположны по знаку, например, оксид кальция (СаО) при взаимодействии с водой образует гидроксид кальция (Са(ОН)2). Процесс сопровождается выделением большого количества теплоты:
СаО + Н2О = Са(ОН) + 108 кДж (3)
А реакция разложения гидроксида кальция (Са(ОН)2) осуществляется с поглощением такого же количества теплоты извне
Са(ОН)2 = СаО + Н2О — 108 кДж (4)
Если тепловой эффект реакции определяется при постоянном давлении, температуре, то он будет соответствовать стандартной энтальпии реакции, обозначаемой ∆Н, которая противоположна по знаку величине теплового эффекта реакции. Например, если в процессе экзотермической реакции во взаимодействие вступают алюминий (Аl) и оксид железа (Fe2O3), то в конце уравнения это обозначится следующим образом:
2Аl + Fe2O3 = 2Fe + Al2O3 (+Q) или (-∆Н) (5)
А в случае эндотермической реакции значения этих тепловых величин будут иметь противоположные знаки:
С + СО2 = 2СО (-Q) или (+∆Н) (6)
Это объясняется тем, что выделяющаяся в процессе экзотермической реакции теплота как энергия, теряется системой (-∆Н), а при эндотермических процессах, наоборот – приобретается (+∆Н). Величина (Н) называется энтальпией системы. Часто её называют так же теплосодержанием или теплотой образования ∆Н данного вещества. В расчётах применяют справочные значения тепловых эффектов образования (или сгорания) одного моля вещества, отнесённые к 298К (250С) и Р = 101,325 кПа (1 атм). Эти условия считаются стандартными и поэтому используемые значения тепловых эффектов называют стандартными теплотами образования(или сгорания) вещества и обозначают как ∆Н0298. Например, тепловой эффект реакции взаимодействия графита с кислородом, выраженный через изменение энтальпии, следует записать как ∆Н0298 = — 393,6 кДж, а так как при этом из простых веществ образуется 1 моль СО2, то данный тепловой эффект является теплотой образования СО2, выраженной в кДж/моль. Главной характеристикой топлив являются их теплоты сгорания. Тепловой эффект реакции горения одного моля вещества называется теплотой сгорания данного вещества. Следовательно, исходя из вышеприведённых положений, теплота сгорания одного моля графита (12 г) составляет 393,6 кДж/моль.
Уравнение химической реакции, в котором указан тепловой эффект, называется термохимическим уравнением.
На практике это имеет большое значение. При строительстве тепловых трасс, доменных печей, котельных и т.п. теплотопотребляющих промышленных объектов, необходимо предусмотреть или приток энергии для поддержания процессов, или наоборот, отвод избытка теплоты, чтобы не было перегрева вплоть до взрыв
Расчёт теплового эффекта реакции между простыми веществами не предоставляется затруднительным. Например, для реакции образования хлористого водорода:
Н2 + Cl2 = 2НCl (7)
Энергия затрачивается на разрыв двух химических связей Н–Н и Cl — Cl. При этом энергия выделяется при образовании двух химических связей Н- Cl. Значения энергий этих связей можно найти в справочных таблицах и по разности между ними определить тепловой эффект (Q) реакции (7):
ЕН–Н = 436 кДж/моль, ЕCl–Cl = 240 кДж/моль,
ЕН–Cl = 240 кДж/моль,
Q = 2 х 430 — ( 1 х 436 — 1 х 240 ) = 184 кДж.
Приведённая в качестве примера термохимическая реакция (7) является экзотермической. Теплоты образования простых веществ при стандартных условиях приняты равными нулю.
Термохимические уравнения имеют особую форму записи. Они отличаются от обычных уравнений тем, что:
1). В термохимических уравнениях обязательно указывают агрегатные состояния веществ (жидкое, твёрдое, газообразное) Это связано с тем, что одна и та же реакция может иметь различный тепловой эффект в зависимости от фазового состояния вещества
2). Коэффициенты в термохимическом уравнении равны количеству веществ ( в молях), вступивших в реакцию. Например, дана реакция сгорания ацетилена:
2С2Н2(г) + 5О2(г) = 4СО2(г) + 2Н2О (+Q) (8)
При сгорании одного моль ацетилена С2Н2 выделяется 1257кДж теплоты. Поэтому, относительно одного моль С2Н2 необходимо все коэффициенты перед реагентами поделить на 2, тогда получим следующую запись термохимического уравнения:
С2Н2 + 5/2О2 = 2СО2 + Н2О + 1257 кДж (9)
Или другая тождественная запись:
С2Н2 + 2,5О2 = 2СО2 + Н2О + 1257 кДж (10)
Например, дано термохимическое уравнение сгорания метана:
СН4 + 2О2 = СО2 + 2Н2О + 802 кДж (11)
Необходимо вычислить, какое количество теплоты выделится при сгорании 20 г метана?
Поскольку 1 моль метана имеет массу 16 г, а 20 г метана соответственно составляют
n = m/Mr = 20:12 = 1,25 моль,
то, составив пропорцию: при сгорании
1 моль СН4 выделяется 802 кДж теплоты
1,25 СН4 ———«——-Х кДж теплоты
Определим, что на сгорание 20г метана потребуется
Х = 1,25 х 802 / 1 = 1002,5 кДж
Приведём другой пример . Дано уравнение реакции сгорания оксида азота(+4):
4NО2(г) + O2(г) + 2H2O(г) = 4НNО3(ж) + 448 кДж (12)
Необходимо составить термохимическое уравнение относительно сгорания одного моль оксида азота. Определить: какой объём оксида азота потребуется на образование 4258 кДж теплоты в процессе данной реакции?
Для составления термохимического уравнения относительно одного моль оксида азота(+4) необходимо все коэффициенты, стоящие перед реагентами, разделить на коэффициент, стоящий перед NО2, т.е. на «4», тогда уравнение примет вид:
NО2(г) + 1/4O2(г) + 1/2H2O(г) = НNО3(ж) +112 кДж (13)
В уравнении изменится количество выделяющейся теплоты, оно станет равным 112, т.е. в четыре раза меньше, чем в приведённом уравнении. В соответствии с уравнением (13) 1 моль оксида азота(NО2) или 22,4 л в данной реакции образует 112 кДж теплоты, а Х л соответственно 4258 кДж:
22,4 моль NО2 при сгорании образуют 112 кДж теплоты.
Х л —————-«————-4258 кДж теплоты.
Хг = 22,4 х 4258 / 112 = 851,6 кДж
Важнейшим законом термохимии является закон Г.И.Гесса (1840): тепловой эффект реакции зависит только от начального и конечного состояния веществ и не зависит от промежуточных стадий процесса. При помощи закона Гесса можно рассчитывать такие тепловые эффекты реакции, которые измерить трудно или невозможно. Например, теплоту образования угарного газа(СО) можно вычислить, если полное сгорание углерода
С (графит) + О2 = СО2 (∆Н1) (14)
разбить на стадии:
С (графит) + 0,5О2 = СО (∆Н2) (15)
СО + 0,5О2 = СО2 (∆Н3) (16)
Зная, что ∆Н1 = -393,6 кДж/моль и ∆Н3 = — 283,1 кДж/моль, из равенства ∆Н1 = ∆Н2 + ∆Н3
находим, что ∆Н2 = — 110,5 кДж/моль.
В качестве другого примера можно привести образование сульфата алюминия при сгорании алюминия и серы ромбической согласно реакции:
2Al(к) + 3S(ромб) + 6О2(г) = Al2(SO4)3(к) (17)
∆Н может быть найдена по тепловым эффектам отдельных стадий:
2Al + 1,5О2 = Al2O3 ∆Н1= -1670,2 кДж/моль (18)
3S + 1,5О2 = SO3 ∆Н2= -395,3 кДж/моль (19)
Al2O3 + 3SO3 = Al2(SO4)3 ∆Н3= -579,7 кДж/моль (20)
Тогда ∆Н = ∆Н1 + 3∆Н2 + ∆Н3 = (- 1670,2) – 3х (-395,3) – (579,7) = — 3435,8 кДж/моль.
На основании закона Гесса термохимические уравнения можно разбивать на отдельные стадии независимо от того, осуществимы они на практике или нет. Из закона Гесса вытекает важное следствие: тепловой эффект химической реакции равен сумме теплот образования получающихся веществ за вычетом суммы теплот образования исходный веществ:
∆Н = ∑ (𝘮 ∆Н) продукты — ∑ (𝘯 ∆Н) реагенты,
где 𝘮 и 𝘯 – число молей каждого вещества в уравнении реакции. Например, теплоту сгорания ацетилена (10) можно рассчитать, зная теплоты образования С2Н2 , СО2 и Н2О (∆Н002 = 0), как ∆Н0 = 2 ∆Н СО2 + ∆НН2О — ∆НС2Н2 = -2 х 393,6 — 281 — (+226,8) = -1295 кДж/моль.
НАЧАЛА ТЕРМОДИНАМИКИ
Среди многообразия химических реакций, термохимические занимают особое положение. Если рассуждать с точки зрения эволюции жизни на Земле, то в конечном итоге, действительно, от этих процессов зависит жизнь на нашей планете. А что касается человеческой цивилизации в целом, то здесь мы имеем прямую зависимость её развития от термохимических явлений. Ведь благодаря именно данным процессам произошёл отрыв человечества в развитии от всех других видов живых организмов, населяющих нашу планету. С древнейших времён, начиная от пассивного использования огня в качестве средства для согревания и приготовления примитивной пищи, человечество пришло к активному использованию этого явления (изготовление гончарных изделий – плавка меди, железа и других металлов – паровые двигатели – двигатели внутреннего сгорания – управление ядерными реакциями)
Если можно было бы предложить создать проект монумента человеческому прогрессу, то на его фронтоне надо было бы начертать уравнение химической реакции
С + О2 = СО2
Именно со сгорания дров, угля, торфа начался отсчёт человеческой цивилизации. В настоящее время наше с вами существование просто немыслимо без тепловых процесов. Но кроме приведённой выше реакции существует великое множество других термодинамических процессов. Почему именно углероду дано такое предпочтение? Может быть его собрату по IV-й группе – кремнию более выгоден данный процесс?
Si + О2 = SiО2
Тем более, что кремний по массе составляет 27,6% земной коры. Это несравненно больше, чем запасы древесины и её ископаемых на нашей планете. Чего же проще? Кидай в топку кремнезём! Его ведь целая планета! Правда надо оговорить тот факт, что чистого кремния в природе не существует. В наличии только его оксид — SiО2. Но на то и химики, чтобы придумать что-нибудь? А может быть для более сильного окислителя, чем кислород – фтору окисление углерода более выгодно термодинамически?
C + 2F2 = СF4
Как во всём этом разобраться? И возможно ли вообще предсказать осуществления того или иного процесса, ведь на бумаге можно написать уравнение любой химической реакции, а возможна ли она практически? Придётся начинать всё по порядку.
Одним из самых важных и очевидных законов природы является закон сохранения энергии: энергия не возникает из ничего и не исчезает бесследно, она только переходит из одной формы в другую. Аналогичным является закон сохранения массы вещества: массы веществ вступивших в реакцию равны массам веществ, образовавшихся в процессе данной реакции.
Поэтому и при экзотермической и при эндотермической обратимых реакциях одного и того же процесса как количество затрачиваемой и расходуемой энергии равны, но противоположны по знаку, так и массы веществ распадающихся и вновь образующихся равны:
СаО + Н2О = Са(ОН)2 + 108 кДж
Mr=56 Mr=18 Mr=74
Са(ОН)2 = СаО + Н2О — 108 кДж
Mr=74 Mr=56 Mr=18
Но всё дело в том, что в приведённых выше двух реакциях уже указано, какая из них экзотермическая, а какая эндотермическая. А можно ли так, как говорится «на вскидку» по одному только уравнению реакции определить: какая это реакция? В принципе, в большинстве случаев, возможно. К экзотермическим реакциям, в основном, относятся реакции соединения и как их разновидность – реакции окисления.(8,11,12,14). А к реакциям эндотермическим, соответственно – реакции разложения (2,4). Ещё раз уточним: в большинстве случаев. Поскольку реакция окисления:
0,5N2 + 0,5O2 = NО — 90 кДж
требует расхода энергии и является эндотермической, а реакция разложения нитрата натрия
2NaNO3 = 2NaNO2 + O2 (+Q)
осуществляется с выделением большого количества теплоты и является экзотермической.
Значит, принцип «на вскидку» не годится. Но каким же принципом тогда следует руководствоваться в определении реакций данного типа? В приводимых выше примерах (10), (14-20) указывалось, что стандартные теплоты образования веществ (∆Н) являются справочными данными. Такие данные скрупулёзно составлялись на протяжении десятилетий для многочисленных термодинамических реакций. С этой целью использовался прибор калориметр. Именно по этим данным в настоящее время мы можем установить, какой является та или иная реакция: экзотермической или эндотермической.
Теперь попробуем заглянуть как бы внутрь термохимической реакции. Как она начинается? Что способствует её осуществлению? В качестве примера приведём ещё раз две реакции (14) и (2):
С(графит) + О2 = СО2 + 393,3 кДж
СаСО3 = СаО + СО2 (-Q)
Представим себе, что химическими символами (С) и (О2) будут обозначаться не элемент «углерод» и простое вещество «кислород», а дрова (или уголь, торф) и воздух (атмосфера). А в качестве соединения СаСО3 — не карбонат кальция, а известное всем вещество: мел (или известняк). Первую реакцию будем проводить для того, чтобы нагреть печь и вскипятить чайник, а вторую – чтобы получить негашёную известь (СаО) в дальнейшем используемую для побелки садовых деревьев. Для разжигания печи приготовим щепки и, поместив сверху них дрова, зажжём огонь спичками.
Во втором случае, поместим в металлическое ведро мелко накрошенный мел, поставим на плиту и такими же действиями, как в случае разжигания огня в печи, разведём костёр под ведром.
Стоп! Тут что-то не так! Ведь мы установили, что первая реакция экзотермическая, протекает с выделением теплоты, а вторая реакция – эндотермическая, протекает с поглощением теплоты. А мы в обоих случаях разводим огонь, т.е. передаём этим процессам извне тепловую энергию. Значит, обе реакции эндотермические – идут с поглощением теплоты! Да, идут с поглощением теплоты, но это только на первом этапе. Некоторым экзотермическим реакциям требуется небольшой «толчок» — первоначальная подача энергии, а спустя некоторое время, когда загорятся дрова, процесс будет сопровождаться с выделением энергии в окружающую среду и во многие сотни, тысячи раз превзойдёт по величине первоначальное значение этой энергии. А второй процесс ка был так и останется эндотермическим. Ведь с прекращением подачи тепловой энергии мел перестанет разлагаться: реакция остановится. И всё-таки, почему в одних случаях процесс окисления (горения) является экзотермическим, а в других – эндотермическим процессом? И что является движущей силой эндотермических реакций, в ходе которых тепловая энергия поступает из окружающей среды? Ни у кого не вызывает удивление такое явление, как остывание со временем горячего чайника. Это нормально. А почему бы этому же чайнику, уже остывшему, холодному, взять, да и нагреться самому по себе? Вот это уже вызовет удивление.
Так вот, эта самая сила связана со стремлением любой системы к наиболее вероятному состоянию, характеризующимся максимальным беспорядком, называемым энтропией. Это одно из важнейших понятий в термодинамике. Энтропия обозначается символом «S». К примеру, при экзотермических реакциях, при проведении процессов плавления, кипения, переходов из жидкостей к газообразному состоянию, энтропия приобретает максимальное значение, поскольку при тепловых явлениях кинетическая энергия атомов, молекул, ионов возрастает, усиливаются беспорядочные колебания этих частиц. И наоборот, самый большой порядок в химических системах – в идеальном кристалле при температуре абсолютного нуля. Энтропия в данном случае равна нулю
Энтропия имеет численные значения, единицей её измерения является Дж/(моль . К); К примеру энтропия алмаза равна 2,4 Дж/(моль . К), пропана – 269,9 Дж/(моль . К). Энтропия газов значительно превышает энтропию жидких и тем более твёрдых тел. Поскольку в газообразных веществах постоянно происходит беспорядочное распределение молекул по всему объёму.
Существуют экспериментальные и теоретические методы определения энтропий различных химических соединений. Используя их, можно количественно рассчитать изменения энтропии при протекании конкретной реакции аналогично тому, как это делается для теплового эффекта реакции. Составлены специальные справочные данные, которые включают сравнительную характеристику этих величин с учётом температуры.
Подтянуть знания по химии можно записавшись на урок к онлайн-репетиторам TutorOnline
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Зависимость теплового эффекта от температуры. Уравнение Кирхгофа
Поскольку по закону Гесса тепловой эффект процесса (реакции) определяется начальным и конечным состоянием системы, очевидно, что для каждого из участников реакции (как исходных веществ, так и продуктов реакции) будут справедливы выражения (1.32) и (1.33). Тогда уравнение зависимости теплового эффекта реакции от температуры можно записать в виде
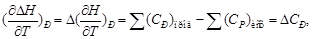
где DCP – разность молярных изобарных теплоемкостей реагентов, взятая с учетом стехиометрических коэффициентов.
Уравнение (1.36) называют уравнением Кирхгофа; оно выражает зависимость теплового эффекта реакции от температуры в дифференциальной форме. Это уравнение строго справедливо лишь при условии, что давление над каждым компонентом при искомой температуре будет таким же, как и при начальной температуре.
Из (1.36) следует, что чувствительность DH к изменению температуры определяется абсолютным значением DCP, а знак температурного коэффициента определяется знаком DCP. При DCP > 0 тепловой эффект реакции растет с повышением температуры; при DCP 2 + Dc′T – 2 + … (1.37)
Подставляя (1.37) в (1.36) и разделяя переменные, в общем виде получим
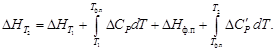
Предполагается, что в рассматриваемом интервале температур T2 ¸ T1 в системе происходит фазовое превращение (плавление, парообразование или сублимация), тепловой эффект которого DHф.п.
Интегрирование уравнения Кирхгофа можно проводить только в том случае, если известна величина 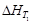
Наличие данных о стандартных тепловых эффектах образования или сгорания различных веществ значительно упрощает расчеты. Так, пользуясь величинами 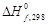
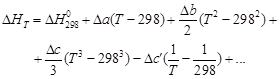
Для газов в сравнительно узком температурном интервале, а для твердых и жидких веществ в достаточно широком, можно считать DCP = const, что дает право пользоваться линейным уравнением
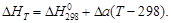
Принимая, что a » DCP,298, можно также записать
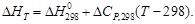
Если значение 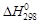
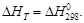
Пример 1.34.
Истинная молярная теплоемкость серебра в интервале температур от 273 до 1234 К выражается уравнением
СP = 23,97 + 5,28×10 –3 Т – 0,25×10 5 Т –2 Дж/(моль∙К).
Вычислить среднюю молярную теплоемкость 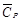
Среднюю теплоемкость в данном интервале температур рассчитывают по уравнению (1.30)
С учетом зависимости истинной теплоемкости от температуры СP = а + bT + c′ . T –2 получим выражение
Подставляя коэффициенты a, b, c′ и температуру из условия задачи, получаем
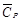
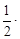
Средняя удельная теплоемкость рутила (TiO2) в интервале от 0 до t °С выражается уравнением
СP = 0,782 + 1,41∙10 –4 t – 0,557∙10 3 t –2 Дж/(г∙°С).
Рассчитать истинную удельную теплоемкость рутила при 500 °С.
Среднюю удельную теплоемкость вычисляем по уравнению (1.30) с учетом (1.34):
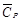
= 0,883 Дж/(г∙°С).
Определить количество теплоты, поглощенной при нагревании 1 кг корунда Al2O3 от 298 до 1000 К, если его молярная теплоемкость в интервале температур 298–1800 К выражается уравнением
СP =114,56 + 12,89·10 ─3 Т-34,31·10 5 Т ─2 Дж(моль·К).
Количество теплоты, затраченное на нагревание n моль вещества от Т1 до Т2,определяется из соотношения
Учитывая, что теплоемкость является функцией температуры, для расчета количества теплоты используем уравнение
Q = 1000/102 [114,56(1000 – 298) + ½ 12,89·10 –3 (1000 2 –
– 298 2 ) – 34,31 . 10 5 (1/298 –1/1000)] = 766 768 Дж = 766,8 кДж.
Молярная теплота испарения метилового спирта при 25 о C составляет 37,4 кДж/моль. Определить теплоту испарения метилового спирта при 50 о C, если молярная теплоемкость жидкого и газообразного метилового спирта соответственно равны 81,6 и 43,9 Дж/(моль∙К). Считать теплоемкость в интервале температур 25-50 о C практически постоянной.
Решение.
Воспользуемся уравнением Кирхгофа в интегральной форме:
T1 = 25 + 273 = 298 К, T2 = 50 + 273 = 323 К
Вычислить тепловой эффект реакции C(т)+CO2(г)=2CO(г) при 500 К, если при стандартных условиях он равен 172,5 кДж, а значения молярных теплоемкостей С, СО, СО2 соответственно следующие:
Воспользуемся уравнением Кирхгофа в интегральной форме:
Зависимость CP реагирующих веществ от температуры представлена уравнениями вида CP = a + bT + c′T –2 (для неорганических веществ), поэтому величину DСP рассчитывают по уравнению
DCP = Da + DbT +Dc′T –2 .
После подстановки в уравнение Кирхгофа и интегрирования получим
Da = 2·28,41 – 44,14 – 17,15 = -4,47,
Db = (2·4,10 – 9,04 – 4,27)10 -3 = -5,1110 –3 ,
Dc′ = [–2·0,46 – (-8,53) – (-8,79)]10 5 = 16,410 5 .
DH500 = 172,5×10 3 – 4,47×(500–298)– 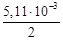
– 298 2 ) + 16,4×10 5 ( 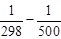
Вычислить изменение энтальпии при нагревании хлорида серебра от 298 до 1000 К при стандартном давлении и полную энтальпию хлорида серебра при 1000 К. При температуре 728 К происходит плавление хлорида серебра, ∆Нпл при температуре плавления 13,21 кДж/моль. Зависимость теплоемкости твердого хлорида серебра от температуры взять в Приложении. Теплоемкость жидкого хлорида серебра в интервале температур от 728 до 1000 К остается практически постоянной и равной 66,99 Дж/(моль·К).
По уравнению (1.38) определим теплоту нагревания хлорида серебра с учетом единственного фазового превращения в заданном интервале температур:
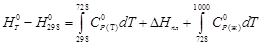
Вычисляем изменение энтальпии, справочные данные берем в приложении 12.
DН 0 = –126,8 + 56,88 = –69,92 кДж/моль.
Выразить уравнением зависимость теплового эффекта химической реакции
СН3ОН(г)+ 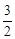
от температуры, которая справедлива в интервале 298–1000 К.
Тепловой эффект реакции в стандартных условиях 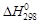
Для получения уравнения зависимости 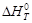
| Вещество | 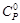 = f(T), Дж/(моль∙К) = f(T), Дж/(моль∙К) |
Температурный интервал, К | |||
| а | b∙10 3 | c′∙10 ─5 | c∙10 6 | ||
| СО2(г) | 44,14 | 9,04 | –8,54 | 298–2500 | |
| Н2О(г) | 30,00 | 10,71 | 0,33 | 273–2500 | |
| СН3ОН(г) | 15,28 | 105,2 | –31,04 | 298–1000 | |
| О2(г) | 31,46 | 3,39 | –3.77 | 273–2000 | |
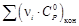 |
104,14 | 32,46 | –7,88 | 298–2500 | |
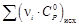 |
62,47 | 110,29 | –5,66 | –31,04 | 298–1000 |
Для данной реакции в интервале температур от 298 до 1000 К уравнение зависимости изменения теплоемкости от температуры будет иметь вид
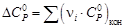
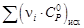
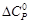
Подставляем под знак интеграла зависимость 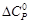
Т ≤ 1000; 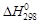
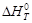
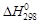
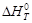
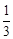

– 9,44 + 3,46 – 0,27 – 0,74)10 3 + 41,67 T – 38,91 ─3 T 2 +
+ 10,35∙10 ─6 T 3 + 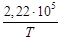
+ 41,67T – 38,91∙10 ─3 T 2 + 10,35∙10 ─6 T 3 + 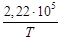
Таким образом, получено уравнение зависимости теплового эффекта реакции от температуры, справедливое в интервале температур от 298 до 1000 К:
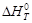
+ 10,36∙10 ─6 Т 3 + 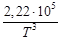
Обжиг известняка проводится при 1100 °С. Определить расход теплоты на обогрев 1 кг сырья до температуры процесса, если оно состоит в основном из карбоната кальция и поступает в печь обжига при 20 °С.
Теплоемкость известняка примем равной теплоемкости СаСО3. Значение средней молярной теплоемкости
СаСО3 рассчитаем по формуле (1.30) с учетом (1.34), значения коэффициентов а, b, c′ возьмем из приложения 12:
а = 104,52; b = 21,92∙10 ─3 ; c′ = –25,94∙10 5 .
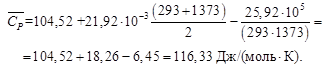
Удельная теплоемкость известняка
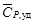
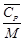
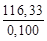
где М = 0,100 кг/моль – молярная масса СаСО3.
Тогда расход теплоты
Q = 1000∙1163,3(1373–293) = 1,259∙10 9 Дж = 1,259 ГДж.
Температура газов пиролиза на выходе из зоны реакции (плазмотрона) равна 1600 °С. Определить необходимый расход воды на закалку (быстрое охлаждение) этих газов в расчете на 1 кг, если их теплоемкость равна 4,15 кДж/(кг∙К), температура на выходе из зоны закалки 150 °С, а температура воды на входе в аппарат 20 °С и на выходе 100 °С. Теплоемкость воды 4,18 кДж/(кг∙К).
Используем уравнение теплового баланса.
Приход теплоты с реакционными газами
Qприх = 4,15(1600 – 150) = 6,02∙10 3 кДж/кг.
Расход теплоты с закалочной водой составляет
где Х – расход воды на закалку, кг.
Отсюда, согласно уравнению теплового баланса, имеем
Х = 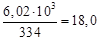
1. При экспериментальном определении энтальпии нейтрализации соляной кислоты гидроксидом натрия смешивали растворы HCl и NaOH в прецизионном калориметре, причем температура содержимого калориметра поднялась на 0,2064 °С. Количество воды, выделившееся в результате реакции, равно 3,4075 ммоль. Кроме того, электрические измерения показали, что удельная теплоемкость калориметра и его содержимого равна 938,141 Дж∙°С ─1 . Вычислить энтальпию нейтрализации на 1 моль соляной кислоты. Необходимо ввести поправку (+649,45 Дж) на 1 моль образовавшейся в конце процесса Н2О к энтальпии смешения растворов HCl и NaOH до того, как прошла реакция.
2. В другом опыте те же исследователи установили, что энтальпия нейтрализации HClO4 в пределах ошибки эксперимента та же, что и для HCl. Однако энтальпия нейтрализации уксусной кислоты гидроксидом натрия равна
–55,727 кДж/моль. Как объяснить тот факт, что энтальпии нейтрализации HCl и HClO4 одинаковы, но отличаются от энтальпии нейтрализации уксусной кислоты?
1. ∆Н = (СР∆Т/ число молей образовавшейся Н2О) + + поправка =
2. HCl и HClO4 – сильные кислоты, они полностью диссоциируют. Разница между наблюдаемыми энтальпиями равна энтальпии диссоциации уксусной кислоты.
Определить тепловой режим реактора синтеза акрилонитрила, если процесс в нем описывается уравнением
а производительность реактора равна 800 кг акрилонитрила в час. Рассчитать расход воды на охлаждение этого реактора, если она подается в аппарат при 18 °С и отводится из него при 82 °С. Теплоемкость воды 4180 Дж/(кг·К).
Температура процесса (82 °С) в данном случае достаточно близка к стандартной (25 °С), поэтому тепловой эффект рассматриваемой реакции можно принять равным стандартному тепловому эффекту и рассчитывать по стандартным теплотам образования реагирующих веществ:
| Вещество, агрегатное состояние | 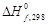 , кДж/моль , кДж/моль |
| С3Н3N(ж), акрилонитрил | 184,93 |
| С2Н2(г), ацетилен | 226,75 |
| НСN(г), циановодород | 132,00 |
Подставив значения в уравнение, получим
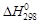
За один пробег реакции образуется 1 моль (0,053 кг) продукта; следовательно, значение теплоты Qуд в расчете на 1кг продукта будет состпвлять
Qуд = 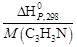
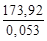
Следовательно, для обеспечения нормальной работы рассматриваемого реактора от него необходимо отводить теплоту:
Необходимый для этого расход охлаждающей воды в реактор
mв = 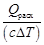
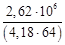
здесь с – удельная теплоемкость воды; ∆Т – повышение температуры воды при прохождении через аппарат,
∆Т = 82 – 18 = 64 °С.
В теплообменнике, питаемом водой, при нормальном давлении конденсируются пары этанола. Определить расход воды, если производительность аппарата 350 кг/ч этанола, температура воды на входе в аппарат 15 °С, на выходе из него 35 °С, а температура выходящего из аппарата этанола 53 °С. Теплоемкость воды равна 4,184 кДж/(кг∙К). Нормальная теплота испарения этанола Qисп = 42,18 кДж/моль.
Воспользуемся уравнением теплового баланса. Приход теплоты в аппарат происходит:
1) за счет конденсации паров этанола:
Qконд = 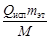
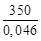
2) за счет остывания сконденсированного этанола от Ткип до 53 °С:
Qост = Сm (Ткип – 53) 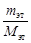
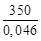
где Сm – молярная теплоемкость этанола, Сm = 111,96 Дж/(моль·К); Мэт – молярная масса этанола, кг/моль.
Расход теплоты из аппарата происходит за счет нагревания воды:
где mв – расход воды в аппарате, кг/ч.
Согласно уравнению теплового баланса имеем
= 3,209∙10 5 + 2,130∙10 4 = 3,422∙10 5 = mв∙83,68 кДж/ч.
mв= 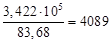
Определить максимально возможную температуру продуктов сгорания 2 объемных частей газообразного водорода и 5 объемных частей воздуха (20 об. % кислорода и 80 об. % азота), если температура зажигания равна 25 °С. Какое заключение можно сделать о полученном выражении для теплоемкости 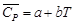
Воспользуемся справочными данными (см. приложение 12):
| Вещество | 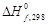 Дж/(моль∙К) Дж/(моль∙К) |
a | b∙10 ─3 |
| H2(г) | – | 29,108 | –0,838 |
| O2(г) | – | 25,538 | 13,630 |
| N2(г) | – | 27,021 | 5,920 |
| H2O(г) | –241,81 | 30,247 | 9,834 |
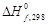
Таким образом, 483,62 кДж нагревают 2 моль Н2О(г) и 4 моль N2(г) от температуры 298 Кдо конечной температуры Т2.
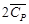
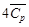
Решая квадратное уравнение и пренебрегая отрицательным корнем, получим Т2 = 2425 К. Этот результат справедлив, только если уравнение для средней теплоемкости применимо в интервале температур от 298 до 2425 К. При более высоких температурах результаты будут ошибочными.
При получении синтез-газа из гексана основная реакция идет по уравнению
Пренебрегая побочными явлениями, определить тепловой эффект процесса, если он протекает при 1350 °С в реакторе производительностью 2,50 т/ч синтез-газа состава СО : Н2 = 6 : 7 (по объему).
По закону Кирхгофа рассчитываем тепловой эффект реакции. Так как средние теплоемкости компонентов системы в заданном интервале температур (до 1623 К) не приводятся, то задачу решаем, пользуясь уравнением (1.39). Для этого воспользуемся справочными данными из приложения 12:
| Компонент i | νi | 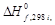 кДж/моль кДж/моль |
ai | bi ∙10 3 | ci ∙10 6 | 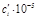 |
| С6Н14(г) | –176,19 | 8,66 | 505,85 | –184,43 | – | |
| О2(г) | 0,00 | 31,46 | 3,39 | – | 3,77 | |
| СО(г) | –110,53 | 29,41 | 4,10 | – | –0,46 | |
| Н2(г) | 0,00 | 27,28 | 3,26 | – | 0,50 | |
| Δ | –495,99 | 258,38 | –468,60 | 184,43 | –10,57 |
Проведем расчет стандартного теплового эффекта реакции ( 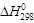
ΔН 0 Т = –495,99∙10 3 + 258,38(1623 – 298) +
+ 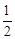
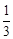
–298 3 ) + (–10,53∙10 5 )( 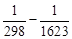
= –4,9170∙10 5 Дж/пробег = –491,70 кДж/пробег.
В результате одного пробега реакции образуется 6 моль СО и 7 моль Н2. Это составляет: m = 6∙0,028 + 7∙0,002 = = 0,182 кг синтез-газа указанного в условиях задачи состава. При образовании 1 кг такого газа в реакторе выделяется теплота Qуд:
Qуд = 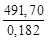
Следовательно, для нормальной работы рассматриваемой установки необходимо предусмотреть отведение тепла от реактора в количестве
Q = 2,702∙10 3 ∙2,50∙10 3 = 6,755∙10 6 кДж/ч = 1876 кВт.
Не нашли, что искали? Воспользуйтесь поиском:
Расчет изменения энтальпии химической реакции при заданной температуре (1500 К)
Образец.
Краткие теоретические сведения
Закон Гессадля стандартных условий (температура 298 К и давление 101325 Па):
(1)
Для расчетов теплового эффекта реакции при любой температуре ( ) применяют интегральную форму закона Кирхгофа:
(2)
Где — разность сумм теплоемкостей конечных и начальных веществ с их стехиометрическими коэффициентами:
(3)
Для проведения точных расчетов надо учитывать зависимости теплоемкости веществ от температуры, например:
(4)
Где – коэффициенты, имеющие определенное численное значение для каждого вещества. В результате осуществления реакции изменение теплоемкости системы:
(5)
А уравнение закон Кирхгофа приобретает вид:
(6)
Изменение энтропии системы, в которой протекает реакция, находя по следующей формуле (для стандартных условий):
(7)
При температуре, отличающейся от стандартной, изменение энтропии рассчитывают по уравнению:
(8)
При любой температуре и стандартных давлениях газообразных веществ изменение энергии Гиббса реакции рассчитывают с учетом температурных зависимостей теплового эффекта и энтропии по уравнению Гиббса-Гельмгольца:
(9)
А для равновесной температуры находят изменение энергии Гиббса по уравнению:
(10)
Константу равновесия для данной температуры вычисляют по величине изменения энергии Гиббса, используя следующее уравнение термодинамики:
(11)
Исходные данные
Таблица 1. Химические реакции для термодинамических расчетов
| Номер задания | Уравнение реакции | T, К |
| 3Fe(тв) + 4H2О(пар) = 4H2(газ) +Fe3O4(тв) |
Таблица 2. Термодинамические свойства веществ (из приложения)
| № п/п | Вещество | , кДж/моль | , Дж/моль·К | ||
| β | γ | ||||
| Fe | 27,15 | 19,25 | 21,0·10 -3 | ||
| H2O(пар) | -241,84 | 188,74 | 30,0 | 10,71·10 -3 | 0,33·10 5 |
| H2 | 130,6 | 27,28 | 3,26·10 -3 | 0,5·10 5 | |
| Fe3O4 | -1117,71 | 151,46 | 167,03 | 78,91·10 -3 | -41,82·10 5 |
Расчетная часть
Расчет изменения энтальпии химической реакции при стандартных условиях (298К)
В основе термохимических расчетов лежит закон Гесса: «Тепловой эффект реакции зависит только от конечного и начального состояния веществ и не зависит от промежуточных стадий процесса». Часто в термохимических расчетах используется следствие из закона Гесса: «Тепловой эффект реакции равен сумме теплот образования продуктов реакции за вычетом суммы теплот образования исходных веществ с учетом коэффициентов реакции»:
DH 0 х.р. = n ´ DH 0 продуктов — n ´ DH 0 исходных веществ
Распишем тепловой эффект реакции, используя следствие из закона Гесса:
= (4 ´ DH 0 (H2) + DH 0 (Fe3O4) — (3 ´ DH 0 (Fe) + 4 ´ DH 0 (H2O)
Подставим справочные данные из таблицы 2 получаем:
= (0+(-1117,71)) – (0+4*(-241,84)) = -150,35 кДж/моль
Вывод: так как полученное значение изменения энтальпии процесса – отрицательная величина, то в результате протекания этой реакции в прямом направлении выделяется теплота и прямая реакция является экзотермической.
Расчет изменения энтальпии химической реакции при заданной температуре (1500 К)
Расчет проводится по формуле Кирхгофа
, так как теплоемкость выражается уравнением (4), после подстановки получаем:
В интегральной форме формула Кирхгофа выглядит следующим образом:
где Δα ,Δβ, Δγ – изменение величин степенных коэффициентов физико-химической системы в уравнении теплоемкости (4) при протекании химической реакции.
Рассчитываем Δα ,Δβ, Δγ, например, для Δα:
=(4*27,28+167,03)-(3*19,25+4*30) = 98,4
Результаты заносим в таблицу:
| Коэффициент | Значение |
| Δα | 98,4 |
| Δβ | -0,01389 |
| Δγ | -4114000 |
Подставляем полученные значения в уравнение для расчета:
-58145 Дж/моль
Вывод: изменение энтальпии при 1500 К относительно теплового эффекта при стандартных условиях имеет меньшее значение, следовательно при температуре 1500 К протекание процесса в прямом направлении сопровождается поглощением теплоты.
Зависимость теплового эффекта химической реакции от температуры. Закон Кирхгофа
Зависимость теплового эффекта химической реакции от температуры. Закон Кирхгофа.
Тепловой эффект химической реакции или изменение энтальпии системы вследствие протекания химической реакции. 3
Стандартная энтальпия образования(ΔHfO). 4
Стандартная энтальпия сгорания(ΔHгоро). 4
Уравнение Кирхгофа. 4
Тепловой эффект химической реакции или изменение энтальпии системы вследствие протекания химической реакции.
Чтобы тепловой эффект являлся величиной, зависящей только от характера протекающей химической реакции, необходимо соблюдение следующих условий:
· Реакция должна протекать либо при постоянном объёме Qv(изохорный процесс), либо при постоянном давлении Qp(изобарный процесс).
· В системе не совершается никакой работы, кроме возможной (при изобарном процессе) работы расширения.
Если реакцию проводят в стандартных условиях при Т = 298 К и Р = 101.3 кПа, тепловой эффект называют стандартным тепловым эффектом реакции или стандартной энтальпией реакции ΔHrO.
Для правильного понимания понятия необходимо знать следующие понятия.
Теплоёмкость тела (обозначается с) — физическая величина, определяющая отношение бесконечно малого количества теплоты ΔQ, полученного телом, к соответствующему приращению его температуры ΔT. Единица измерения теплоёмкости в системе СИ — Дж/К.
Если же говорить про теплоёмкость произвольной системы, то ее уместно формулировать в терминах термодинамически — теплоёмкость есть отношение малого приращения количества теплоты Q к малому изменению температуры T:
Удельная теплоемкость вещества определяется как количество тепловой энергии, необходимой для повышения температуры одного килограмма вещества на один градус по Цельсию.
Формула расчёта удельной теплоёмкости [Дж/(кг• К)]:
Молярная теплоёмкость — это теплоёмкость одного моля вещества(количество теплоты, необходимое для нагревания тела массой 1 кг на 1 К) Часто употребляется обозначение C. Однако буквой C часто обозначается и простая теплоёмкость.
Связь с удельной теплоёмкостью:
где с — удельная теплоёмкость, М — молярная масса [Дж/(К•моль)].
Средняя молярная теплоемкость — количество теплоты, необходимое для нагревания 1 моль вещества на ΔТ.
Для расчета энтальпий и энтропии вещества используют интегралы от теплоемкости:
Стандартная энтальпия образования(ΔHfO).
Стандартная теплота образования – это тепловой эффект реакции образования одного моля вещества из простых веществ, его составляющих, находящихся в устойчивых стандартных состояниях. Обозначается ΔHfO.
Термохимические эффекты можно включать в химические реакции. Химические уравнения в которых указано количество выделившейся или поглощенной теплоты, называются термохимическими уравнениями. Реакции, сопровождающиеcя выделением тепла в окружащию среду имеют отрицательный тепловой эффект и называются экзотермическими. Реакции, сопровождающиеся поглощением тепла имеют положительный тепловой эффект и называются эндотермическими. Тепловой эффект обычно относится к одному молю прореагировавшего исходного вещества, стехиометрический коэффициент которого максимален.
Стандартная энтальпия сгорания(ΔHгоро).
Тепловой эффект реакции сгорания одного моля вещества в кислороде до образования оксидов в высшей степени окисления. Теплота сгорания негорючих веществ принимается равной нулю.
Уравнение Кирхгофа — соотношение, устанавливающее зависимость теплового эффекта химической реакции от температуры.
«Равенство, выражающее температурную зависимость теплового эффекта химических реакций через разность теплоемкостей конечных продуктов и исходных веществ. В частности, для реакций, происходящих при постоянном объеме, уравнение Кирхгофа связывает температурную зависимость изменения внутренней энергии ΔU при реакции с разностью изохорных теплоёмкостей cv в форме
Теплоемкость при постоянном давлении (Р):
Изменение энтальпии равно изменению теплоты:
Теплоемкость при постоянном объеме (V):
Cv1 и Cv2 — суммы теплоёмкостей исходных веществ и продуктов реакции с учётом их стехиометрических коэффициентов в уравнении реакции. Интегрируя это уравнение, можно определить изменение внутренней энергии ΔUT при интересующей температуре Т, если известны ΔUT1 при какой-нибудь другой температуре T1 и теплоёмкости исходных веществ и продуктов реакции в рассматриваемом температурном интервале. Уравнение было выведено в 1858.»
1. , , «Физическая химия», Москва, Высшая школа, 1990.
2. «Физическая химия», Москва, Мир, 1980.
3. Киреев физической химии. 1975 год, с 264-272.
http://poisk-ru.ru/s24119t14.html
http://pandia.ru/text/80/229/3464.php