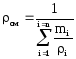Как найти теплоемкость смеси веществ

На практике чаще всего приходится сталкиваться не с отдельными газами, а с их смесями, поэтому необходимо знать определение теплоемкости смеси. При нагревании газовой смеси подведенная теплота расходуется на нагревание отдельных ее компонентов, и теплоемкость смеси определяется по ее составу.

При задании смеси массовыми долями подведенную теплоту можно определить следующим образом:

или

,

где , — удельная теплоемкость и масса i-го компонента соответственно,

следовательно,

.

Деля левую и правую части последнего уравнения на , получим:

.

Но поскольку  – массовая доля i –того компонента, то можно записать

.

Таким образом, массовая теплоемкость смеси равна сумме произведений массовых теплоемкостей газов, входящих в смесь, на их массовые доли.

При задании смеси объемными долями, учитывая, что  и , получим:

,

т.е. объемная теплоемкость газовой смеси равна сумме произведений объемных теплоемкостей газов, входящих в состав смеси, на их объемные доли.

При задании смеси молярными долями, исходя из того, что объемные и мольные доли равны, запишем:

,

т.е. молярная теплоемкость газовой смеси равна сумме произведений молярных теплоемкостей газов, входящих в состав смеси, на их молярные доли.

В
инженерной практике часто приходится
иметь дело не с однородными газами, а
со смесями химически не связанных между
собой газов. Примерами газовых смесей
могут служить: атмосферный воздух,
природный газ, газообразные продукты
сгорания топлив и т.д.

Для
газовых смесей справедливы следующие
положения.

1.
Каждый газ, входящий в смесь, имеет
температуру, равную температуре смеси.

2.
Любой из газов, входящих в смесь,
распространяется по всему объему смеси
и поэтому объем каждого газа равен
объему всей смеси.

3.
Каждый из газов, входящих в смесь,
подчиняется своему уравнению состояния.

4.
Смесь в целом является как бы новым
газом и подчиняется своему уравнению
состояния.

В
основе изучения газовых смесей лежит
закон Дальтона, согласно которому при
постоянной температуре давление смеси
равно сумме парциальных давлений газов,
входящих в смесь:

(1.8)

где
p_см
— давление смеси;

p_i

— парциальное давление i-го газа, входящего
в смесь;

n
— число газов, входящих в смесь.

Парциальным
называют давление, которое окажет газ,
входящий в смесь, если он один будет
занимать весь объем смеси при той же
температуре.

Способы
задания газовых смесей

Состав
газовой смеси может быть задан массовыми,
объемными и мольными долями.

Массовые
доли.
Массовой долей любого газа, входящего
в смесь, называется отношение массы
этого газа к массе смеси.

m₁
= M₁
/
M_см;
m₂
= M₂
/
M_см;
……….; m_n
= M_n
/
M_см,

где
m₁,
m₂,
…, m_n
— массовые доли газов;

М₁,
М₂,
…, М_n
— массы отдельных газов;

М_см
— масса смеси.

Нетрудно
видеть, что
и(100%).

Объемные
доли.
Объемной долей любого газа, входящего
в смесь, называется отношение приведенного
(парциального) объема этого газа к объему
смеси.

r₁
= V₁
/
V_см;
r₂
= V₂
/
V_см;
………, r_n
= V_n
/
V_см;

где
V₁,
V₂,
…, V_n
— приведенные объемы газов;

V_см
—
объем смеси;

r₁,
r₂,
…, r_n
— объемные доли газов.

Приведенный
объем — это объем газа при условиях смеси
(при температуре и давлении смеси).

Приведенный
объем можно представить следующим
образом: если из сосуда, где находится
смесь, удалить все газы, кроме одного,
и оставшийся газ сжать до давления
смеси, сохранив температуру, то его
объем и будет приведенным или парциальным.

Можно
доказать, что объем смеси будет равен
сумме приведенных объемов газов.

Тогда

(100%).

Мольные
доли. Мольной
долей любого газа, входящего в смесь,
называется отношение числа киломолей
этого газа к числу киломолей смеси.

r₁
= n₁
/
n_см;
r₂
= n₂
/
n_см;
………, r_n
= n_n
/
n_см,

где
r₁,
r₂,
…, r_n
— мольные доли газов;

n_см
—
число киломолей смеси;

n₁,
n₂,
…, n_n
— число киломолей газов.

Задание
смеси мольными долями тождественно
заданию смеси объемными долями, т.е.
мольные и объемные доли имеют для каждого
газа, входящего в смесь, одинаковые
численные значения.

Газовая
постоянная и кажущаяся (средняя)
молекулярная масса смеси.
Для вычисления газовой постоянной
смеси, заданной массовыми долями, запишем
уравнения состояния:

для
смеси

p_см
×
V_см
= М_смR_смТ;

(1.9)

для
газов

.

(1.10)

Суммируем
левые и правые части уравнений (1.10)

(p₁
+ p₂
+ …. + p_n)
V_см
= (M₁R₁
+ M₂R₂
+
….. + M_nR_n)
T.

Так
как
,

то
p_смV_см
= (M₁R₁
+ M₂R₂
+
….. + M_nR_n)
T.

(1.11)

Из
уравнений (1.9) и ( 1.11) следует, что

М_смR_смТ
= (M₁R₁
+ M₂R₂
+
….. + M_nR_n)
T.

Отсюда

R_см
=
М₁
/ М_см
R₁
+ М₂
/ М_см
R₂
+ …… + М_n
/ М_см
R_n
=

=
m₁R₁
+ m₂R₂
+ …… + m_nR_n

или

,

(1.12)

где
R_см
— газовая постоянная смеси.

Так
как газовая постоянная i-го газа

R_i
= 8314 / m_i,

то
уравнение (1.12) перепишется следующим
образом:

.

(1.13)

Определяя
параметры газовой смеси, удобно
пользоваться некоторой условной
величиной, называемой кажущейся (средней)
молекулярной массой газовой смеси.
Понятие кажущейся молекулярной массы
смеси позволяет условно рассматривать
смесь как однородный газ, что существенно
упрощает расчеты.

Для
отдельного газа справедливо выражение

m_i
R_i
= 8314.

По
аналогии для смеси можно записать

m_см
R_см
= 8314,
(1.14)

где
m_см

— кажущаяся молекулярная масса смеси.

Из
уравнения (1.14), используя выражения
(1.12) и (1.13), получим

,

(1.15)

.

(1.16)

Рассуждая
подобным образом, можно получить формулы
для расчета R_см
и m_см
через объемные доли , формулы для
пересчета массовых долей в объемные
доли и, наоборот, объемных долей в
массовые, формулы для расчета удельного
объема смеси u_см
и плотности смеси r_см
через массовые и объемные доли и, наконец,
формулы для расчета парциальных давлений
газов, входящих в смесь, через объемные
и массовые доли. Приведем эти формулы
без вывода в таблице.

Формулы
для расчета газовых смесей

Задание состава смеси	Перевод из одного состава в другой	Плотность и удельный объем смеси	Кажущаяся молекуляр-ная масса смеси	Газовая постоянная смеси	Парциаль-ное давление
1	2	3	4	5	6
Массо-выми долями
Объем-ными долями

Теплоемкость
газов

Теплоемкостью
тела называют количество теплоты,
необходимое для нагревания или охлаждения
тела на 1 К. Теплоемкость единицы
количества вещества называют удельной
теплоемкостью.

Итак,
удельной теплоемкостью вещества называют
количество теплоты, которое необходимо
сообщить или отнять от единицы вещества,
чтобы изменить его температуру на 1 К в
данном процессе.

Поскольку
в дальнейшем будут рассматриваться
только удельные теплоемкости, то будем
называть удельную теплоемкость просто
теплоемкостью.

Количество
газа может быть задано массой, объемом
и числом киломолей. Следует оговориться,
что при задании газа объемом этот объем
приводят к нормальным условиям и измеряют
нормальными метрами кубическими (нм³).

В
зависимости от способа задания количества
газа различают следующие теплоемкости:

с
— массовую теплоемкость, Дж/ (кг×К);

с¢
— объемную теплоемкость, Дж/ (нм³
×К);

с_m

— мольную теплоемкость, Дж/(кмоль ×К).

Между
названными теплоемкостями существуют
следующие зависимости:

с
= с_m
/
m;
с_m
= с ×
m;

с¢
= с_m
/
22,4; с_m

= с¢
×
22,4,

отсюда

;
с¢
= с ×
r_н,

где
u_н
и r_н
— удельный объем и плотность при нормальных
условиях.

Изохорная
и изобарная теплоемкости

Количество
теплоты, сообщаемое рабочему телу
зависит от особенностей термодинамического
процесса. Практическое значение имеют
два вида теплоемкости в зависимости от
термодинамического процесса: изохорная
и изобарная.

Теплоемкость
при u
= const — изохорная.

c_u

— массовая изохорная теплоемкость,

c¢_u
— объемная изохорная теплоемкость,

c_mu
— мольная изохорная теплоемкость.

Теплоемкость
при p = const — изобарная.

c_р

— массовая изобарная теплоемкость,

c¢_р
— объемная изобарная теплоемкость,

c_mр
— мольная изобарная теплоемкость.

При
одинаковом изменении температуры в
процессе, осуществляемом при
p
= const, расходуется теплоты больше, чем в
процессе при u
= const. Это объясняется тем, что при u
= const теплота, сообщаемая телу, расходуется
лишь на

изменение
его внутренней энергии, тогда как при
p = const теплота расходуется и на увеличение
внутренней энергии, и на совершение
работы расширения. Разность между
массовой изобарной и массовой изохорной
теплоемкостями по уравнению Майера

c_р
— c_u
=R.

(1.17)

Если
левую и правую части уравнения (1.17)
умножить на массу киломоля m,
то получим

c_mр
— c_mu
=
8314 Дж/(кмоль×К)

(1.18)

В
термодинамике и ее приложениях большое
значение имеет отношение изобарных и
изохорных теплоемкостей:

,

(1.19)

где
к — показатель адиабаты.

Расчеты
показывают, что приближенно можно
принять для одноатомных газов к »
1,67, двухатомных к »
1,4, трехатомных к »
1,29.

Нетрудно
видеть, что значение к
зависит от температуры. Действительно,
из уравнений (1.17) и (1.19) следует, что

,

(1.20)

а
из уравнений (1.18) и (1.19)

.

(1.21)

Так
как с увеличением температуры газа
теплоемкости увеличиваются, то значение
к уменьшается, приближаясь к единице,
но всегда остается больше нее.

Зная
величину к, можно определить значение
соответствующей теплоемкости. Так,
например, из уравнения (1.20) имеем

,

(1.22)

а
т.к. с_р
= к ×
с_u,
то получим

.

(1.23)

Аналогично
для мольных теплоемкостей из уравнения
(1.21) получим

.

(1.24)

.

(1.25)

Средняя
и истинная теплоемкость

Теплоемкость
газов зависит от температуры и в некоторой
степени от давления. Зависимость
теплоемкости от давления невелика и ею
в большинстве расчетов пренебрегают.
Зависимость же теплоемкости от температуры
значительна и ее необходимо учитывать.
Эта зависимость достаточно точно
выражается уравнением

с
= а + вt
+ еt²,
(1.26)

где
а, в
и е — величины, постоянные для данного
газа.

Часто
в теплотехнических расчетах нелинейную
зависимость (1.26) заменяют линейной:

с
= а + вt.
(1.27)

Если построить графически зависимость теплоемкости от температуры по уравнению (1.26), то это будет криволинейная зависимость (рис.1.4). Как показано на рисунке каждому значению температуры соответствует свое значение теплоемкости, которое принято называть истинной теплоемкостью. Математически выражение для истинной теплоемкости запишется так: . (1.28)

Следовательно, истинная теплоемкость есть отношение бесконечно малого количества теплоты dq к бесконечно малому изменению температуры dt. Другими словами, истинная теплоемкость — это теплоемкость газа при данной температуре. На рис. 1.4 истинная теплоемкость при температуре t1 обозначена сt1 и изображается отрезком 1-4, при температуре t2 — сt2 и изображается отрезком 2-3. Из уравнения (1.28) получим dq = cdt. (1.29) В практических расчетах всегда определяют количество теплоты при конечном изменении

температуры.
Очевидно, что количество теплоты q,
которое сообщают единице количества
вещества при нагревании его от t₁
до t₂,
можно найти, проинтегрировав (1.29) от t₁
до t₂.

.
(1.30)

Графически
интеграл (1.30) выражается площадью
4-1-2-3. Если в выражение (1.30) подставить
значение истинной теплоемкости по
линейной зависимости (1.27), то получим

(1.31)

где
—
средняя теплоемкость в интервале
температур от t₁
до t₂.

,
(1.32)

Следовательно,
средняя теплоемкость представляет
собой отношение конечного количества
теплоты q к конечному изменению температуры
t₂
— t₁:

.
(1.33)

Если
на основании 4-3 (рис.1.4) построить
прямоугольник 4-1¢-2¢-3,
равновеликий фигуре 4-1-2-3, то высота
этого прямоугольника будет равна средней
теплоемкости, где
находится в интервале температур t₁
— t₂.

Обычно
значения средних теплоемкостей приводятся
в таблицах термодинамических свойств
веществ. Однако для сокращения объема
этих таблиц в них приводятся значения
средних теплоемкостей, определенных в
диапазоне изменения температуры от 0
^оС
до t ^оС.

Если
необходимо вычислить значение средней
теплоемкости в заданном интервале
температур t₁
— t₂,
то это можно сделать следующим образом.

Площадь
0а14 под кривой с = f(t) (рис.1.4) соответствует
количеству теплоты q₁,
необходимому для повышения температуры
газа от 0 ^оС
до t₁
^оС.

Аналогично
площадь 0а23 соответствует q₂
при повышении температуры от 0 ^оС
до t₂
^оС:

Таким
образом, q = q₂
— q₁
(площадь 4123) может быть представлено в
виде

(1.34)

Подставляя
значение q по (1.34) в выражение (1.33), получим
формулу для средней теплоемкости в
любом диапазоне температур:

.
(1.35)

Таким
образом, среднюю теплоемкость можно
вычислить по табличным средним
теплоемкостям по уравнению (1.35). Причем
получим нелинейную зависимость с = f(t).
Можно также найти среднюю теплоемкость
по уравнению (1.32) по линейной зависимости.
Значения а и в
в уравнении (1.32) для различных газов
приводятся в литературе.

Количество
теплоты, подведенной или отведенной от
рабочего тела, можно рассчитать по
какому-либо из уравнений:

(1.36)

(1.37)

,
(1.38)

где
— соответственно средняя массовая,
объемная и мольная теплоемкости; М —
масса газа; n — число киломолей газа; V_н
— объем газа при нормальных условиях.

Объем
газа V_н
может
быть найден следующим образом. Записав
уравнение состояния для заданных
условий: pV = MRT и для нормальных условий:

p_нV_н
= MRT_н,
отнесем второе уравнение к первому:

,

отсюда

.
(1.39)

Теплоемкость
газовых смесей

Теплоемкость
газовой смеси может быть вычислена,
если задан состав смеси и известны
теплоемкости компонентов, входящих в
смесь.

Для
нагревания смеси массой М_см
на 1К необходимо температуру каждого
из компонентов также повысить на 1К. При
этом на нагревание i-го компонента смеси
массой М_i
затрачивается количество теплоты,
равное c_iM_i.
Для всей смеси количество теплоты

,

где
c_i
и c_см
— массовые теплоемкости i-го компонента
и смеси.

Поделив
последнее выражение на М_см,
получим
расчетную формулу для массовой
теплоемкости смеси:

,
(1.40)

где
m_i
— массовая доля i-го компонента.

Рассуждая
аналогично, найдем объемную c¢_см
и мольную c_mсм
теплоемкости смеси:

(1.41)

где
c¢_i
— объемная теплоемкость i-го компонента,
r_i
— объемная доля i-го компонента,

,
(1.42)

где
c_mi
— мольная теплоемкость i-го компонента,

r_i
— мольная (объемная) доля i-го компонента.

17

    Зная состав смеси, массовые теплоемкости и концентрации ее компонентов, можно определить массовую теплоемкость смеси нефтепродуктов по формуле [c.66]

    Теплоемкость смесей. Теплоемкость смесей, если между их составными частями не происходит химического взаимодействия, подчиняется свойствам аддитивности, т. е. ее можно подсчитывать, пользуясь правилами смешения, на чем мы уже останавливались при рассмотрении закона Дальтона (стр. 52)  [c.95]

    Теплоемкость смесей газов и паров рассчитывается по правилу аддитивности  [c.46]

    В таблице теплосодержаний газов при Р 1 ата (табл. 16), а в приложении — энтропийные и тепловые (4, 5 и 14) диаграммы, с которыми чаще всего приходится сталкиваться ири расчетах. Для определения теплосодержания / газовых смесей необходимо пользоваться правилом смешения, которое применяется для подсчета парциальных давлений, теплоемкостей смесей и т. п.  [c.104]

    Мольная теплоемкость смеси газов вычисляется по формуле [c.112]

    Ср — теплоемкость смеси веществ, отнесенная к 1 моль основного компонента смеси (обычно вещества А), ккал- кмоль » — град . [c.14]

    Теплоемкость смесей идеальных газов вычисляется по закону аддитивности. Если, например, теплоемкости водорода и окиси углерода выражаются уравнениями [c.32]

    Пример 25. Подсчитать тепловой баланс контактного аппарата для частичного окисления SOa производительностью 25000 м /ч. Газовая смесь содержит [% (об.)] SO2 — 9 О2— 11 N2 — 80. Степень окисления 88%. Температура входящего газа 460°С выходящего— 580°С. Средняя теплоемкость смеси (условно считаем 6 неизменной) 2,052 кДж/(м -°С). Потери теплоты в окружающую среду 5% от прихода теплоты. [c.61]

    E. Удельная теплоемкость газовых смесей. Теплоемкость смесей идеальных газов может быть рассчитана как значение, усредненное по мольным либо массовым долям, в зависимости от того, какие именно теплоемкости компонентов известны. Для расчета теплоемкостей чистых компонентов можно использовать методы, приведенные в 4.1,3, Для смесей реальных газов необходимо учитывать отклонение их свойств от свойств идеальных смесей. На рис. 2 показано отклонение теплоемкости реальных газов от теплоемкости идеального газа в зависимости от приведенных температуры и давления 53]. [c.176]

    С р, Ср — удельные теплоемкости смеси исходных веществ на входе в реактор и выходящего потока, содержащего полностью превращенный продукт, отнесенные к 1 моль вещества А, поступающего в реактор  [c.224]

    Для определения теплоемкости смеси при заданных давлении и температуре можно воспользоваться рис. 7, где дается поправка к теплоемкости при атмосферном давлении в зависимости от приведенных параметров (Рпр = Рраб/Ркр, пр— Ураб/Гкр).  [c.47]

    Теплоемкость смеси в конце сжатия [c.175]

    Средняя объемная теплоемкость смеси газов, кДж/(мЗ.°С) [c.19]

    Примем, что теплота реакции и теплоемкость смеси остаются практически постоянными при адиабатическом режиме. Тогда изменение температуры Т для данной степени превращения х может быть выражено уравнением [c.111]

    Аналогично для изобарной удельной теплоемкости смеси Сем справедливо выражение [c.7]

    Ср— средняя теплоемкость смеси при постоянном давлении. [c.17]

    В случае жидких систем, а также при многих превращениях в газовой фазе удельная теплоемкость смеси реагентов изменяется незначительно во время протекания реакции и может считаться постоянной. Тогда уравнение баланса приводится к наиболее часто используемому виду  [c.298]

    Из всех слагаемых выражения (У1.31) наибольшее влияние на условную теплоемкость смеси оказывает [c.141]

    Ср — удельная теплоемкость смеси, Дж/кг К  [c.299]

    Теплоемкость смесей нефтепродуктов [c.66]

    Теплоемкость смеси можно представить как [c.401]

    В расчетах процессов нефтепереработки используют теплоемкости углеводородных смесей. Обработка экспериментальных данных показывает, что при стандартном давлении теплоемкость углеводородной смеси определяется ее температурой Т и плотностью относительно воды при 15°С — р1б , т. е. С°р = = Ср (Г, р15 ). Номограмма для определения С°р жидких и газообразных углеводородных смесей приведена на рис. 4. Если нужно пересчитать теплоемкость смеси для давления р, ощутимо отличающегося от стандартного, можно использовать прием, описанный для индивидуальных веществ (см. рис. 3), выбрав для смеси Гк и рк по представляющему ее индивидуальному веществу. Можно, что менее удобно, использовать и соотношения, приведенные в табл. 3. [c.52]

    Ср — теплоемкость смеси инертных веществ, отнесенная к 1 кмоль основного инертного компонента, ккал кмоль град  [c.14]

    Дополнительные сведения плотность раствора аммиака равна 910 кг/.и плотность формальдегида (42 масс. %)при 25° С равна 1100 кг м теплоемкость смеси реагентов можно считать постоянной С = = 0,556 ккал. (кг-град) скорость обратной реакции ничтожно мала. [c.121]

    Чаще всего приходится иметь дело со смесями веществ. Поэтому в формулу (П1. 4) подставляют теплоемкость смеси Ссм, которая может быть найдена по закону аддитивности. Так, для смеси трех веществ в количестве G, и G3, имеющих теплоемкости Си С2 и Сз [c.45]

    Теплоемкость смесей нефтепродуктов может быть выражена формулой [c.32]

    Определить теплоемкость смеси, состоящей из 600 кг нефтепродукта теплоемкостью 2,42 кДж/(кг-К) и 400 кг нефтепродукта теплоемкостью 2,48 кДж/(кг-К). [c.36]

    Состав производственных газов, используемых для получения аммиака, не изменяется существенно от установки к установке. Теплоемкость смеси при небольших изменениях в составе изменяется незначительно. Следовательно, данные табл. 10 для определенных газовых составов, целесообразно применять в тех случаях, когда требуются приблизительные значения теплоемкостей. [c.230]

    Здесь Т — температура в заданной точке пограничной пленки в данный момент времени (Гер Г Гц) С — концентрация летучих в той же точке в данный момент времени — теплотворная способность смеси летучих в данный момент времени с — теплоемкость смеси летучих. [c.196]

    Как правило, на практике приходится иметь дело со смесями веществ, поэтому в формулу (4,14) подставляют значение теплоемкости смеси (Сс ), которую вычисляют по закону аддитивности. Для смеси трех материалов, имеющих тенлоемкости С], Сг, С , при массе в ней материала, равной Оз, теплоемкость находят по формуле [c.64]

    Су = 0,75 ккал1кгград—теплоемкость смеси углеводородов N = 3,5 — весовая кратность циркуляции катализатора  [c.250]

    Для расчета калорических параметров необходимо рйсполать данными по теплоемкости смеси в состоянии идеального газа. Если известны теплоемкости или с /ил Для каждого компонента, то теплоемкости смеси определяются в соответствии с законом Дальтона—Гиббса [251  [c.41]

    Здесь уравнения (4.62)—(4.66) описывают средние скорости изменения концентраций инициатора, радикалов, мономеров и суммарной степени превращения в частицах дисперсной фазы. Уравнение (4.67) описывает нестационарный перенос тепла от единичного включения к сплошной фазе. Уравнения теплового баланса (4.68)—(4.69) для реактора и рубашки составлены при допущении полного перемепшвания сплошной фазы в реакторе и теплоносителя в рубашке. Уравнение БСА (4.70) характеризует изменение в течение процесса функции распределения частиц дисперсной фазы по массам р (М, 1). В уравнениях (4.62)—(4.70) введены следующие обозначения / ( г) — эффективность инициирования X — суммарная степень превращения мономеров АЯ — теплота полимеризации — эффективная энергия активации полимеризации 2 — коэффициент теплопроводности гранул р . — плотность смеси — теплоемкость смеси — коэффициент теплоотдачи от поверхности гранулы к сплошной среде Оои сво — начальные концентрации мономеров кр (х) — эффективный коэффициент теплопередачи — поверхность теплообмена между реагирующей средой и теплоносителем, Ут — объем теплоносителя в рубашке Гу, и Тт — температура теплоносителя на входе в рубашку и в рубашке соответственно Qт— объемный расход теплоносителя V — объем смеси в реакторе — объем смеси [c.275]

    D. Теплоемкость. В настоящее время нет методов, позволяющих рассчитывать теплоемкость смеси без знания теплоемкостей чистых компонентов. Если имеются значения для чистых компонентов, теплоемкость смеси рассчитывается как невзвешенпое среднее значений для чистых компонентов. При этом имеется в виду, что требования размерности соблюдаются. В таком подходе не учитываются возникновение теплош смешения и другие подобные эффекты. По этой причине в тех случаях, когда теплота смешения НС равна нулю, могут возникнуть большие погрешности. Для углеводородов и близких гомологов применение такого подхода целесообразно, и разброс значений теплоемкости находится в пределах 10%, хотя имеется мало данных для сравнения. При псевдонриведенной температуре ниже 0,85 изобарическую теплоемкость смесн с неопределенным составом, Дж/(кг-К), можно рассчитать по выражению [c.176]

    Пример 4. Для той же смеси и тех же температур, что в примере 3, определить основные характеристики воспламенения в сосуде цилиндрической формы с диаметром d = 100 мм, высотой h == 100 мм, учитывая, что коэффициент теплоотдачи к стенкеа = 10 ккал (м -ч-град)-, удел1)Ная теплоемкость смеси с — = 0,39 ккал (кг X X град) и плотность смеси р = 0,78 нл1 кг. [c.122]

---