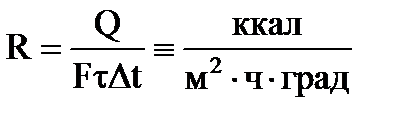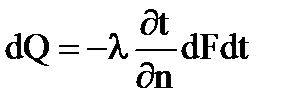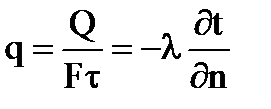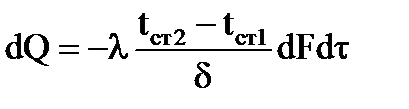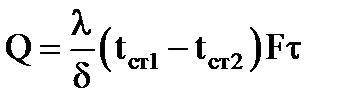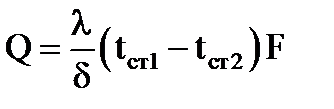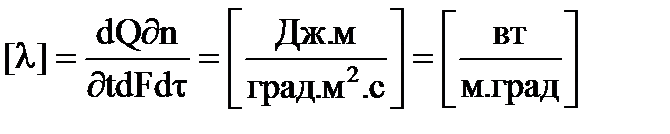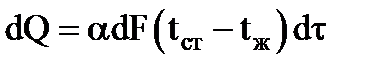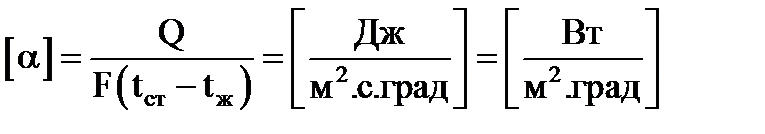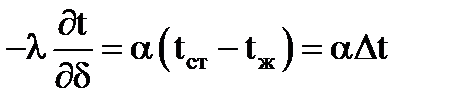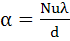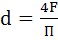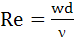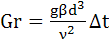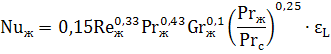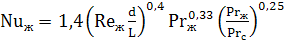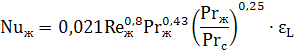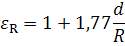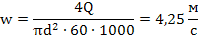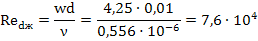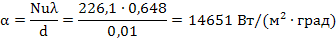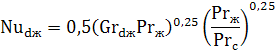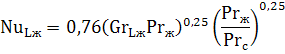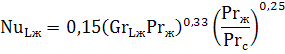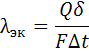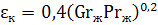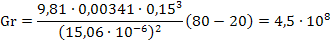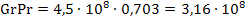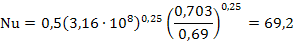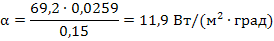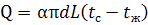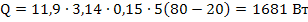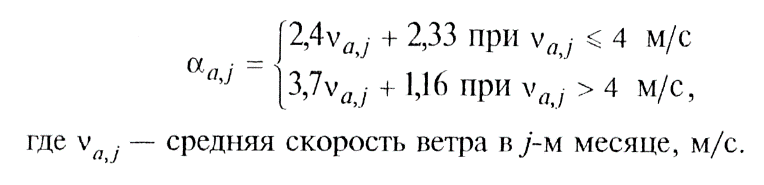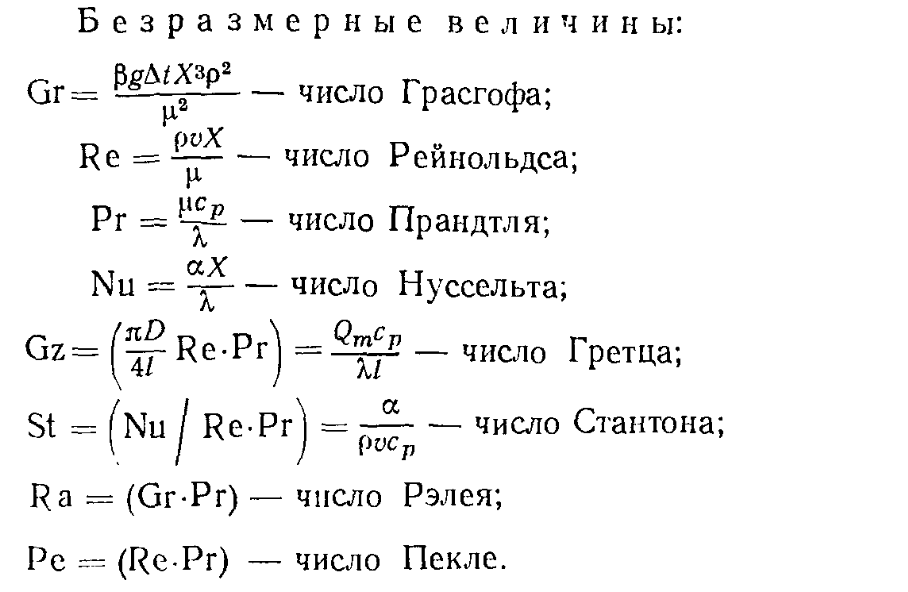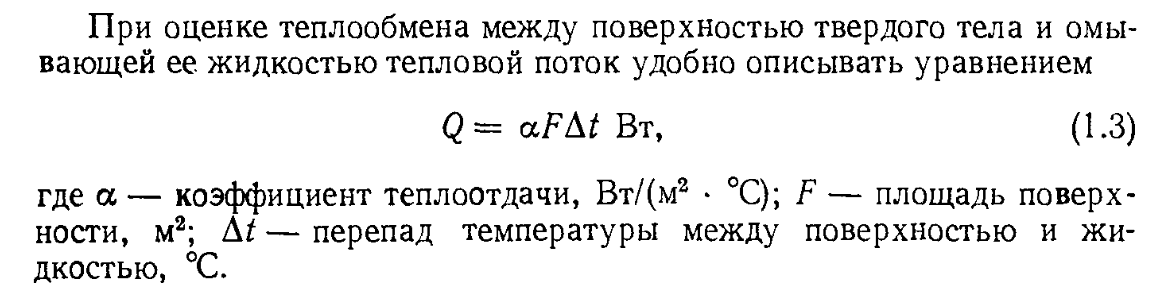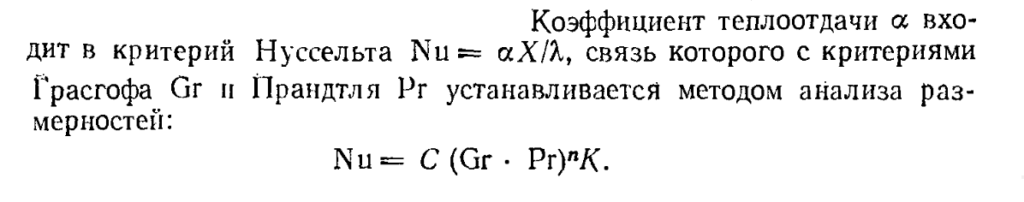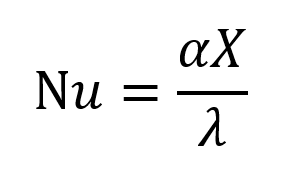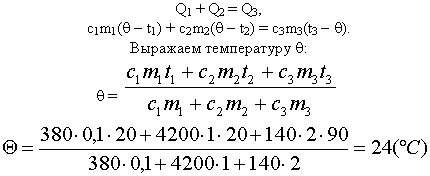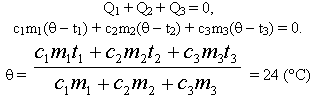Как найти теплообмен с окружающей средой - Исправление недочетов и поиск решений вместе с Examum.ru

Тела, температура которых отличается, могут обмениваться тепловой энергией. То есть, между телами будет происходить теплообмен. Самостоятельно тепловая энергия переходит от более нагретых тел к менее нагретым.

Что такое теплообмен и при каких условиях он происходит

Тела, имеющие различные температуры, будут обмениваться тепловой энергией. Этот процесс называется теплообменом.

Теплообмен – процесс обмена тепловой энергией между телами, имеющими различные температуры.

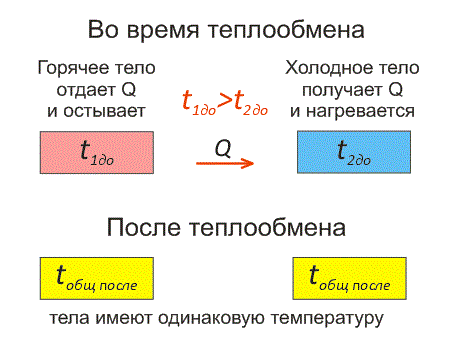
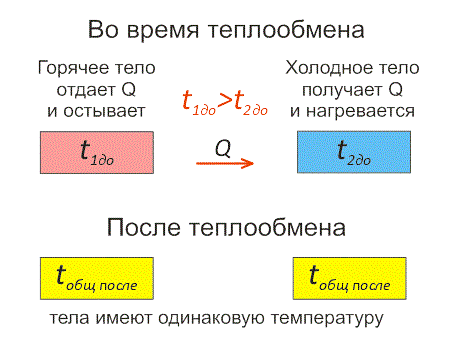
Рассмотрим два тела, имеющие различные температуры (рис. 1).

Тело, имеющее более высокую температуру, будет остывать и отдавать тепловую энергию телу, имеющему низкую температуру. А тело с низкой температурой будет получать количество теплоты и нагреваться.

Рис.1. Два тела во время теплообмена и после

На рисунке, горячее тело имеет розовый оттенок, а холодное изображено голубым цветом.

Когда температуры тел выравниваются, теплообмен прекращается.

Чтобы теплообмен происходил, нужно, чтобы тела имели различные температуры.

Когда температура тел выравняется, теплообмен прекратится.

Тепловое равновесие — это состояние, при котором тела имеют одинаковую температуру.

Уравнение теплового баланса и сохранение тепловой энергии

Когда тело остывает, оно отдает тепловую энергию (теплоту). Утерянное количество теплоты Q имеет знак «минус».

А когда тело нагревается – оно получает тепловую энергию. Приобретенное количество теплоты Q имеет знак «плюс».

Эти факты отражены на рисунке 2.

Рис. 2. Полученное количество теплоты имеет знак «+», а отданное Q – знак «-»

Закон сохранения тепловой энергии: Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом.

Примечание: Существует и другая формулировка закона сохранения энергии: Энергия не появляется сама собой и не исчезает бесследно. Она переходит из одного вида в другой.

Уравнение теплового баланса

Тот факт, что тепловая энергия сохраняется, можно записать с помощью математики в виде уравнения. Такую запись называют уравнением теплового баланса.

Запишем уравнение теплового баланса для двух тел, обменивающихся тепловой энергией:

[large boxed{ Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 }]

(large Q_{text{остывания горяч}} left( text{Дж} right) ) – это количество теплоты горячее тело теряет.

(large Q_{text{нагревания холод}} left( text{Дж} right) ) – это количество теплоты холодное тело получает.

В левой части уравнения складываем количество теплоты каждого из тел, участвующих в теплообмене.

Записываем ноль в правой части уравнения, когда теплообмен с окружающей средой отсутствует. То есть, теплообмен происходит только между рассматриваемыми телами.

В некоторых учебниках применяют сокращения:

[large Q_{1} + Q_{2} = 0 ]

Примечание: Складывая два числа мы получим ноль, когда эти числа будут:

равными по модулю и
имеют различные знаки (одно число — знак «плюс», а второе – знак «минус»).

Если несколько тел участвуют в процессе теплообмена

Иногда в процессе теплообмена участвуют несколько тел. Тогда, для каждого тела нужно записать формулу количества теплоты Q. А потом все количества теплоты подставить в уравнение для теплового баланса:

[large boxed{ Q_{1} + Q_{2} + Q_{3} + ldots + Q_{n} = 0 } ]

При этом:

Q для каждого нагреваемого тела будет обладать знаком «+»,
Q для каждого охлаждаемого тела — знаком «-».

Пример расчетов для теплообмена между холодным и горячим телом

К горячей воде, массой 200 грамм, имеющей температуру +80 градусов Цельсия, добавили холодную воду, в количестве 100 грамм при температуре +15 градусов Цельсия. Какую температуру будет иметь смесь после установления теплового равновесия? Считать, что окружающая среда в теплообмене не участвует.

Примечание: Здесь мы рассматриваем упрощенную задачу, для того, чтобы облегчить понимание закона сохранения энергии. Мы не учитываем в этой задаче, что вода содержится в емкости. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.

При решении других задач обязательно учитывайте, что емкость, в которой будет содержаться вещество, имеет массу. И часть тепловой энергии будет затрачиваться на то, чтобы изменить температуру емкости.

Решение:

В условии сказано, что окружающая среда в теплообмене не участвует. Поэтому, будем считать рассматриваемую систему замкнутой. А в замкнутых системах выполняются законы сохранения. Например, закон сохранения энергии.

Иными словами, с сосудом и окружающим воздухом теплообмен не происходит и, все тепловая энергия, отданная горячей водой, будет получена холодной водой.

1). Запишем уравнение теплового баланса, в правой части которого можно записать ноль:

[large Q_{text{остывания горяч}} + Q_{text{нагревания холод}} = 0 ]

2). Теперь запишем формулу для каждого количества теплоты:

[large Q_{text{остывания горяч}} = c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) ]

[large Q_{text{нагревания холодн}} = c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) ]

Примечания:

(large c_{text{воды}} ) – удельную теплоемкость воды находим в справочнике;
Массу воды переводим в килограммы;
Горячая вода остывает и отдает тепловую энергию. Поэтому, разность (large (t_{text{общ}} — t_{text{горяч}} ) ) будет иметь знак «минус», потому, что конечная температура горячей воды меньше ее начальной температуры;
Холодная вода получает тепловую энергию и нагревается. Из-за этого, разность (large (t_{text{общ}} — t_{text{холодн}} ) ) будет иметь знак «плюс», потому, что конечная температура холодной воды больше ее начальной температуры;

3). Подставим выражения для каждого Q в уравнение баланса:

[large c_{text{воды}} cdot m_{text{горяч}} cdot (t_{text{общ}} — t_{text{горяч}} ) + c_{text{воды}} cdot m_{text{холодн}} cdot (t_{text{общ}} — t_{text{холодн}} ) = 0 ]

4). Для удобства, заменим символы числами:

[large 4200 cdot 0,2 cdot (t_{text{общ}} — 80 ) + 4200 cdot 0,1 cdot (t_{text{общ}} — 15 ) = 0 ]

Проведем упрощение:

[large 840 cdot (t_{text{общ}} — 80 ) + 420 cdot (t_{text{общ}} — 15 ) = 0 ]

Раскрыв скобки и решив это уравнение, получим ответ:

[large t_{text{общ}} = 58,33 ]

Ответ: Температура смеси после прекращения теплообмена будет равна 58,33 градуса Цельсия.

Задача для самостоятельного решения:

В алюминиевом калориметре массой 100 грамм находится керосин массой 250 грамм при температуре +80 градусов Цельсия. В керосин поместили свинцовый шарик, массой 300 грамм. Начальная температура шарика +20 градусов Цельсия. Найдите температуру тел после установления теплового равновесия. Внешняя среда в теплообмене не участвует.

Примечание к решению: В левой части уравнения теплового баланса теперь будут находиться три слагаемых. Потому, что мы учитываем три количества теплоты:

(large Q_{1} ) – охлаждение алюминия от температуры +80 градусов до конечной температуры;
(large Q_{2} ) – охлаждение керосина от температуры +80 градусов до конечной температуры;
(large Q_{3} ) – нагревание свинца от температуры +20 градусов до конечной температуры;

А справа в уравнение теплового баланса запишем ноль. Так как внешняя среда в теплообмене не участвует.

Выводы

Если тела имеют различную температуру, то между ними возможен обмен тепловой энергией, т. е. теплообмен;
Когда тела будут иметь равную температуру, теплообмен прекратится;
Тело с высокой температурой, отдает тепловую энергию (теплоту) и остывает. Отданное количество теплоты Q имеет знак «минус»;
А тело с низкой температурой получает тепловую энергию и нагревается. Полученное количество теплоты Q имеет знак «плюс»;
Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом. Это – закон сохранения тепловой энергии;
Сохранение тепловой энергии можно записать в виде уравнения теплового баланса;
В левой части уравнения складываем количества теплоты (всех тел, участвующих в теплообмене);
В правой части уравнения записываем ноль, когда теплообмен с окружающей средой отсутствует.

Источник

Основные уравнение теплообмена

Основы теории передачи тепла. Классификация теплообменных аппаратов. Конструкции.

Основные понятия

Перенос энергии в форме тепла, происходящий между телами, имеющими различную температуру, называется теплообменом. Движущая сила любого процесса теплообмена — разность температур более и менее нагретого тел. При наличии такой разности тепло самопроизвольно, в соответствии со вторым законом термодинамики, переходит от более нагретого к менее нагретому телу. Теплообмен представляет собой обмен энергией между молекулами, атомами и свободными электронами.

Тела, участвующие в тпелообмене, называются теплоносителями.

Теплопередача — наука о процессах распространения тепла. Различают три элементарных способа передачи тепла.

1) Теплопроводность — перенос тепла вследствие теплового движения микрочастиц, непосредственно соприкасающихся друг с другом. В твердых телах теплопроводность — основной способ распространения тепла.

2) Конвекция — перенос тепла вследствие движения и перемешивания макроскопических объемов газа или жидкости. Различают свободную (естественную) конвекцию, обусловленную разностью плотностей в различных точках объема жидкости или газа за счет разности температур, и вынужденную конвекцию, происходящую при принудительном движении всего объема.

3) Тепловое излучение — распространение электромагнитных колебаний с различной длиной волн, обусловленный тепловым движением атомов или молекул излучающего тела. Все тела способны излучать и поглощать энергию, таким образом осуществляется лучистый теплообмен.

В реальных условиях тепло передается комбинированным путем.

Перенос тепла от стенки к газообразной или жидкой среде или в обратном направлении называется теплоотдачей. Процесс передачи тепла от более нагретой к менее нагретой жидкости или газу через разделяющую их поверхность или твердую стенку называется теплопередачей.

Расчет теплообменной аппаратуры включает:

1) Определение теплового потока — количества тепла Q, которое должно быть передано за определенное время от одного теплоносителя к другому. Тепловой поток вычисляется путем составления и решения тепловых балансов.

2) Определение поверхности теплообмена F аппарата, обеспечивающей передачу требуемого количества тепла в заданное время. Величина поверхности теплообмена определяется скоростью теплопередачи, зависящей от механизмов передачи тепла и их сочетанием друг с другом. Поверхность теплообмена находят из основного уравнения теплопередачи.

Основные уравнение теплообмена

Основное уравнение теплопередачи выражает общую зависимость для процессов теплопередачи, выражающее связь между тепловым потоком Q’ и поверхностью теплообмена F:

K — коэффициент теплопередачи, определяющий среднюю скорость передачи тепла вдоль всей поверхности теплообмена; Dt_ср — средняя разность температур между теплоносителями, определяющая среднюю движущую силу процесса теплопередчи, или температурный напор; t — время.

Физический смысл уравнения: количество тепла, передаваемое от более нагретого к менее нагретому теплоносителю, пропорционально поверхности теплообмена F, среднему температурному напору Dt_ср и времени t.

Для непрерывных процессов теплообмена:

Отсюда коэффициент теплопередачи:

Коэффициент теплопередачи показывает, какое количество тепла (в Дж) переходит за 1 секунду от более нагретого к менее нагретому теплоносителю через поверхность теплообмена 1 м 3 при средней разности температур между теплоносителями 1 градус.

В основе расчета теплопроводности лежит закон Фурье:

То есть, количество тепла dQ, передаваемое посредством теплопроводности через элемент поверхности dF, перпендикулярный тепловому потоку, за время dt прямо порпорционально температурному градиенту ∂t/∂n поверхности dF и времени dt.

Количество тепла, передаваемое через единицу поверхности в единицу времени:

Здесь q — плотность теплового потока. Знак минус указывает на то, что тепло перемещается в сторону падения температуры.

Количество переданного тепла:

Здесь d — толщина стенки, м; t_ст1 – t_ст2 — разность температур поверхностей стенки, град; F — площадь поверхности стенки, м 2 ;  — время, с.

Для непрерывного процесса передачи тепла теплопроводностью при =1:

Коэффициент пропорциональности l называется коэффициентом теплопроводности.

Коэффициент теплопроводности l показывает, какое количество тепла проходит вследствие теплопроводности в единицу времени через единицу поверхности теплообмена при падении температуры на 1 градус на единицу длины нормали к изотермической поверхности. Его величина зависит от природы вещества, его структуры, температуры и некоторых других факторов.

При обычных температурах и давлениях лучшими проводниками тепла являются металлы, худшими — газы.

В основе расчета теплоотдачи лежит закон охлаждения Ньютона:

То есть: количество тепла dQ, отдаваемое за время dt поверхностью стенки dF, имеющей температуур t_ст, к жидкости с температурой t_ж, прямо пропорционально dF и разности температур t_ст – t_ж.

Применительно к поверхности теплообмена всего аппарата F для непрерывного процесса теплоотдачи это уравнение принимает вид:

Коэффициент пропорциональности a называется коэффициентом теплоотдачи. Величина его характеризует интенсивность переноса тепла между поверхностью тела и окружающей средой. Он выражается следующим образом:

То есть, коэффициент теплоотдачи a показывает, какое количество тепла передается от 1 м 2 поверхности стенки к жидкости (или наоборот) в течение 1 секунды при разности температур между стенкой и жидкостью 1 градус.

Вследствие сложной структуры потоков, особенно в условиях турбулентного движения, величина a является сложной функцией многих переменных. Коэффициент теплоотдачи зависит от: — скорости жидкости, ее плотности и вязкости, — тепловых свойств жидкости (удельная теплоемкость, теплопроводность) и коэффициента объемного расширения, — геометрических параметров — формы и определяющих размеров стенки (для труб – от размера и диаметра) и шероховатости стенки.

При сопоставлении уравнений теплопроводности и теплоотдачи получаем следующее выражение для установившегося процесса теплообмена:

После преобразований получим:

Nu — критерий Нуссельта. Равенство критериев Нуссельта характеризует подобие процессов теплопереноса на границе между стенкой и потоком жидкости. Он является мерой соотношения толщины пограничного слоя d и определяющего геометрического размера.

Тепловое равновесие и уравнение теплового баланса

Что такое теплообмен и при каких условиях он происходит

Теплообмен – процесс обмена тепловой энергией между телами, имеющими различные температуры.

Рассмотрим два тела, имеющие различные температуры (рис. 1).

На рисунке, горячее тело имеет розовый оттенок, а холодное изображено голубым цветом.

Когда температуры тел выравниваются, теплообмен прекращается.

Чтобы теплообмен происходил, нужно, чтобы тела имели различные температуры.

Когда температура тел выравняется, теплообмен прекратится.

Тепловое равновесие — это состояние, при котором тела имеют одинаковую температуру.

Уравнение теплового баланса и сохранение тепловой энергии

Эти факты отражены на рисунке 2.

Закон сохранения тепловой энергии: Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом.

Уравнение теплового баланса

Запишем уравнение теплового баланса для двух тел, обменивающихся тепловой энергией:

(large Q_<text<остывания горяч>> left( text <Дж>right) ) – это количество теплоты горячее тело теряет.

(large Q_<text<нагревания холод>> left( text <Дж>right) ) – это количество теплоты холодное тело получает.

В левой части уравнения складываем количество теплоты каждого из тел, участвующих в теплообмене.

В некоторых учебниках применяют сокращения:

[large Q_ <1>+ Q_ <2>= 0 ]

Примечание: Складывая два числа мы получим ноль, когда эти числа будут:

равными по модулю и
имеют различные знаки (одно число — знак «плюс», а второе – знак «минус»).

Если несколько тел участвуют в процессе теплообмена

[large boxed < Q_<1>+ Q_ <2>+ Q_ <3>+ ldots + Q_ = 0 > ]

Q для каждого нагреваемого тела будет обладать знаком «+»,
Q для каждого охлаждаемого тела — знаком «-».

Пример расчетов для теплообмена между холодным и горячим телом

Решение:

1). Запишем уравнение теплового баланса, в правой части которого можно записать ноль:

2). Теперь запишем формулу для каждого количества теплоты:

Примечания:

(large c_<text<воды>> ) – удельную теплоемкость воды находим в справочнике;
Массу воды переводим в килограммы;
Горячая вода остывает и отдает тепловую энергию. Поэтому, разность (large (t_<text<общ>> — t_<text<горяч>> ) ) будет иметь знак «минус», потому, что конечная температура горячей воды меньше ее начальной температуры;
Холодная вода получает тепловую энергию и нагревается. Из-за этого, разность (large (t_<text<общ>> — t_<text<холодн>> ) ) будет иметь знак «плюс», потому, что конечная температура холодной воды больше ее начальной температуры;

3). Подставим выражения для каждого Q в уравнение баланса:

4). Для удобства, заменим символы числами:

[large 4200 cdot 0,2 cdot (t_<text<общ>> — 80 ) + 4200 cdot 0,1 cdot (t_<text<общ>> — 15 ) = 0 ]

[large 840 cdot (t_<text<общ>> — 80 ) + 420 cdot (t_<text<общ>> — 15 ) = 0 ]

Раскрыв скобки и решив это уравнение, получим ответ:

Ответ: Температура смеси после прекращения теплообмена будет равна 58,33 градуса Цельсия.

Задача для самостоятельного решения:

(large Q_ <1>) – охлаждение алюминия от температуры +80 градусов до конечной температуры;
(large Q_ <2>) – охлаждение керосина от температуры +80 градусов до конечной температуры;
(large Q_ <3>) – нагревание свинца от температуры +20 градусов до конечной температуры;

А справа в уравнение теплового баланса запишем ноль. Так как внешняя среда в теплообмене не участвует.

Критериальные уравнения теплообмена: расчет теплоотдачи в трубах и каналах

Теплоотдача при вынужденном течении жидкости в трубах и каналах

Теплоотдача в трубах и каналах может происходить при вынужденном или свободном характере конвекционных потоков (возможны также их сочетания в случае существенного влияния гравитационных сил).

При вынужденном течении (вынужденная конвекция) жидкость нагнетается или отводится под действием сил внешнего давления, например, ветра, насоса или вентилятора.

Свободное течение жидкости происходит под действием подъемных (гравитационных) сил за счет изменения ее плотности из-за разницы температуры – слой жидкости с меньшей плотностью стремиться занять верхнее положение относительно холодного слоя (свободная или естественная конвекция).

Интенсивность теплоотдачи, как при вынужденной, так и при свободной конвекции характеризуется коэффициентом теплоотдачи α, имеющим размерность Вт/(м 2 ·град), который определяется по формуле:

Nu – число Нуссельта; λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);

d – эквивалентный диаметр, равный

F – площадь сечения канала, м 2 ; П – периметр канала, м.

Для трубы круглого сечения, эквивалентный диаметр равен внутреннему диаметру трубы.

В целом, расчет коэффициента теплоотдачи сводится к определению числа Нуссельта, значение которого задается соответствующими критериальными уравнениями конвективного теплообмена, зависящими от режима течения жидкости и формы канала.

Течение жидкости в трубах определяется значением числа Рейнольдса Re и в зависимости от его величины может быть ламинарным, переходным или турбулентным.

Ламинарный режим течения жидкости характеризуется величиной числа Re до 2300.
При значении числа Re от 2300 до 10000 режим течения в трубах является переходным.
Турбулентный режим течения в трубах наблюдается при числах Re более 10000.

Число (критерий) Рейнольдса представляет собой безразмерный комплекс, связывающий скоростные и вязкостные характеристики жидкости с определяющим размером канала (для трубы – это ее диаметр).

Число Re определяется по формуле:

w – скорость течения жидкости, м/с; d – эквивалентный диаметр канала, м; ν — кинематическая вязкость жидкости при средней температуре, м 2 /с.

Теплоотдача в трубах и каналах существенно зависит от режима течения жидкости. При ламинарном режиме интенсивность теплоотдачи значительно меньше, чем при развитом турбулентном.

Теплоотдача при ламинарном течении в трубах и каналах

Ламинарный режим течения жидкости обычно характеризуется низкой скоростью потока. При этом в некоторых случаях влиянием конвекции, обусловленной действием гравитационных сил, пренебрегать нельзя.

Для выбора правильного критериального уравнения теплообмена и оценки влияния естественной конвекции на интенсивность теплопередачи при ламинарном режиме служит критерий Грасгофа Gr.

g – ускорение свободного падения, м/с 2 ;

β – температурный коэффициент объемного расширения, град -1 ;

d – эквивалентный диаметр канала, м;

ν — кинематическая вязкость жидкости при средней температуре, м 2 /с;

Δt – средняя разность температур жидкости и стенки, °С.

Теплоотдача при ламинарном течении в трубах и каналах с учетом естественной конвекции. Если величина комплекса GrPr превышает 8·10 5 , то расчет коэффициента теплоотдачи необходимо проводить с учетом влияния естественной конвекции в потоке жидкости по следующему критериальному уравнению:

Индекс «ж» означает, что свойства среды, входящие в критерии подобия Re, Pr и Gr берутся при средней температуре жидкости.

Число Прандтля с индексом «с» Pr_с берется для жидкости при температуре стенки.

ε_L – коэффициент, учитывающий изменение теплоотдачи по длине трубы или канала. Его можно определить с помощью таблицы:

L/d	1	2	5	10	15	20	30	40	50
ε_L	1,9	1,7	1,44	1,28	1,18	1,13	1,05	1,02	1

Значения коэффициента ε при ламинарном режиме

Теплоотдача при ламинарном течении в трубах и каналах без учета естественной конвекции. При значении GrPr 5 , влияние естественной конвекции на теплоотдачу жидкости пренебрежительно мало, и расчет коэффициента теплоотдачи можно проводить по следующему критериальному уравнению:

d – эквивалентный диаметр канала, м;

L – длина трубы (канала), м.

Представленные критериальные уравнения теплообмена при ламинарном режиме позволяют определить среднее значение числа Нуссельта, по величине которого можно рассчитать средний коэффициент теплоотдачи:

λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);

d – эквивалентный диаметр, м.

Теплоотдача в трубах и каналах при турбулентном режиме

Теплоотдача в трубах и каналах при турбулентном режиме осуществляется путем передачи тепла при интенсивном перемешивании слоев жидкости. Критериальное уравнение теплообмена для расчета средней теплоотдачи в трубах и каналах в этом случае имеет вид:

Критерии подобия Re и Pr берутся при средней температуре жидкости. Число Прандтля с индексом «с» Pr_с берется при температуре стенки.

Представленное критериальное уравнение применяется в диапазоне чисел Re от 1·10 4 до 5·10 6 и Pr от 0,6 до 2500.

ε_L – коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы или канала при турбулентном режиме течения. Значения ε_L приведены в следующей таблице при различных числах Рейнольдса и отношениях длины канала к его эквивалентному диаметру:

Re_ж	L/d
1	2	5	10	15	20	30	40	50
1·10 4	1,65	1,5	1,34	1,23	1,17	1,13	1,07	1,03	1
2·10 4	1,51	1,4	1,27	1,18	1,13	1,1	1,05	1,02	1
5·10 4	1,34	1,27	1,18	1,13	1,1	1,08	1,04	1,02	1
1·10 5	1,28	1,22	1,15	1,1	1,08	1,06	1,03	1,02	1
1·10 6	1,14	1,11	1,08	1,05	1,04	1,03	1,02	1,01	1

Значения коэффициента ε при турбулентном режиме

Расчет теплоотдачи в изогнутых трубах и каналах проводится по тому же критериальному уравнению с добавлением множителя — поправки на действие центробежных сил, которая определяется по формуле:

R — радиус изгиба трубы или канала, м; d – эквивалентный диаметр трубы или канала, м.

Теплоотдача в изогнутых трубах проходит более интенсивно, чем в прямых, за счет большего вихреобразования и лучшего перемешивания жидкости.

Расчет теплоотдачи при вынужденной конвекции

Пример расчета. Рассчитаем средний коэффициент теплоотдачи воды, текущей по трубопроводу длиной 1 м, диаметром d=0,01 м с расходом Q=20 л/мин. Средняя температура воды t_ж=50°С, температура стенки трубы t_с=10°С.

1. Определим физические свойства воды при температуре 50°С:

Теплопроводность воды λ_ж= 0,648 Вт/(м·град);
Плотность воды ρ_ж=988 кг/м 3 ;
Кинематическая вязкость воды ν_ж=0,556·10 -6 , м 2 /с;
Число Прандтля при температуре жидкости Pr_ж=3,54;
Число Прандтля при температуре стенки Pr_с=9,52.

2. Рассчитаем среднюю скорость течения воды w по трубе:

3. Определим число Рейнольдса Re:

4. Поскольку число Рейнольдса имеет значение больше 1·10 4 , то режим течения является турбулентным и расчет теплоотдачи необходимо проводить по следующему критериальному уравнению:

Определим коэффициент ε_L по соотношению L/d=1/0,01=100. Поскольку L/d>50, то коэффициент ε_L=1_.

Выполним расчет числа Нуссельта по приведенному критериальному уравнению:

5. Рассчитаем средний коэффициент теплоотдачи от воды к стенке трубы по формуле:

Таким образом, средний коэффициент теплоотдачи от воды к стенке трубы составляет 14,65 кВт/(м 2 ·град).

Теплоотдача при свободной конвекции в трубах и каналах

Теплообмен при свободном движении жидкости (или газа) происходит вследствие разности плотностей нагретых и холодных ее слоев. Интенсивность теплоотдачи жидкости в трубах и каналах при свободной конвекции существенно зависит от их положения в пространстве относительно силы тяжести.

Теплоотдача при свободной конвекции имеет различный характер в случаях свободного течения в неограниченном пространстве и теплообмена в ограниченном объеме (в узкой трубе или канале).

Свободная конвекция в неограниченном пространстве

Конвекция в неограниченном пространстве протекает, например при охлаждении трубопровода центрального отопления, расположенного на улице в безветренную погоду, вблизи от которого отсутствуют препятствия для движения воздушных потоков.

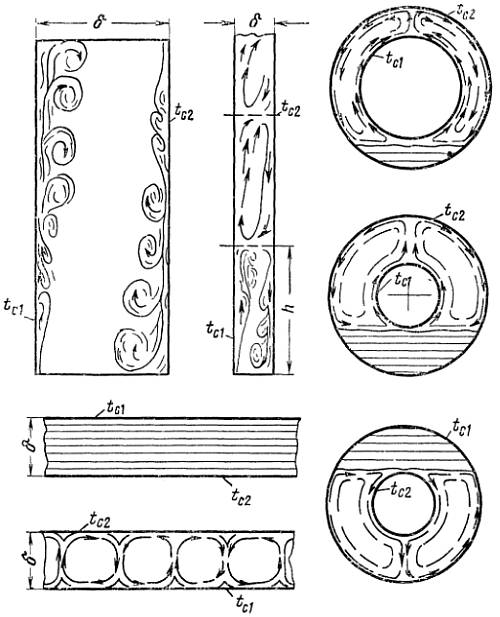
Горизонтальный канал или труба. Интенсивность теплоотдачи при свободной конвекции зависит от величины комплекса GrPr. При значении GrPr от 10 3 до 10 9 критериальное уравнение, описывающее среднюю теплоотдачу от поверхности горизонтальных труб и каналов, имеет вид:

В качестве определяющего размера принимается наружный диаметр d канала или трубы.

Вертикальный канал (труба, пластина). Для вертикальных труб и каналов при значении GrPr от 10 3 до 10 9 критериальное уравнение, описывающее среднюю теплоотдачу, имеет вид:

При GrPr>10 9 :

Примечание: В приведенных критериальных уравнениях теплообмена свойства жидкости, входящие в числа Gr и Pr, определяются при температуре окружающей среды. Число Прандтля с индексом «с» Pr_с берется для жидкости при температуре стенки. В качестве определяющего размера принимается длина L (высота) вертикально стоящей трубы или канала.

Свободная конвекция в ограниченном объеме

Теплообмен жидкости в ограниченном объеме при свободной конвекции характеризуется совместным протеканием процессов нагрева и охлаждения соседних слоев жидкости (или газа). Эти процессы сопровождаются сложным течением нисходящих и восходящих потоков, зависящих от рода жидкости, разницы температуры, формы канала и его геометрических размеров.

Для упрощения расчета таких сложных процессов конвективного теплообмена принято рассматривать их, как явление теплопроводности в щели толщиной δ с учетом понятия эквивалентного коэффициента теплопроводности λ_эк.

Эквивалентный коэффициент теплопроводности определяется по формуле:

Q — количество переданного тепла, Вт; δ — толщина слоя жидкости (или газа), м; F — площадь теплоотдающей поверхности, м 2 ; Δt=t_c1-t_c2 — температурный напор между нагретой и холодной стенками, °С.

Отношение эквивалентного коэффициента теплопроводности λ_эк к величине теплопроводности окружающей жидкости при средней температуре называется коэффициентом конвекции ε_к, который определяется значением комплекса GrPr.

При малых значениях комплекса GrPr 3 6 :

При 10 6 10 :

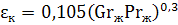
Примечание: Числа подобия Gr и Pr рассчитываются при средней температуре жидкости (или газа), равной t_ж=0,5(t_c1+t_c2). В качестве определяющего размера принимается δ — толщина слоя жидкости.

Расчет теплоотдачи при свободной конвекции

Пример расчета. Рассчитаем потери тепла естественной конвекцией от горизонтального трубопровода центрального отопления, находящегося на открытом воздухе. Диаметр трубопровода d=0,15 м, длина L=5 м, средняя температура наружной стенки t_с=80°С. Температура окружающего воздуха t_ж=20°С.

1. Определим физические свойства воздуха при температуре 20°С:

Теплопроводность воздуха λ_ж= 0,0259 Вт/(м·град);
Кинематическая вязкость воздуха ν_ж=15,06·10 -6 , м 2 /с;
Число Прандтля при температуре жидкости Pr_ж=0,703;
Число Прандтля при температуре стенки Pr_с=0,69;
Коэффициент объемного расширения β_ж=1/(273+20)=0,00341 град -1 .

2. Вычислим число Грасгофа Gr по формуле:

3. Определим значение комплекса GrPr:

Этому значению комплекса соответствует следующее критериальное уравнение теплообмена при свободной конвекции в случае горизонтальной трубы:

4. Вычислим значение числа Нуссельта Nu:

5. Рассчитаем коэффициент теплоотдачи от трубы α по формуле:

6. Определим потери тепла с боковой поверхности трубопровода по формуле:

Подставляя численные значения, окончательно получаем потерю тепла:

Таким образом, только путем естественной (свободной) конвекции рассмотренный трубопровод отопления отдает воздуху 1681 Вт тепла.

источники:

http://formulki.ru/molekulyarka/teplovoe-ravnovesie-i-uravnenie-teplovogo-balansa

http://thermalinfo.ru/eto-interesno/kriterialnye-uravneniya-teploobmena-raschet-teplootdachi-v-trubah-i-kanalah

Источник

Определение

Термодинамика — это одна из основных частей физики. Она применяется в таких отраслях как: гидродинамика, аэродинамика, оптика, физическая химия и другие прикладные разработки.

Возникновение термодинамики относят к 19 веку, ведь именно в этот момент начала развиваться теплотехника. А термодинамика является ее теоретической основой.

Содержание современное термодинамики:

Изучение законов тепловой формы движения материи и все связанные с этим явления.

Цель термодинамики — это изучение общих закономерностей преобразования энергии.

При этом обязательно учитывается внутренняя энергия тел (Q ) , а именно ее изменение.

При этом меняться она может двумя способами:

Совершение работы над системой. То есть преобразования механической энергии во внутреннюю энергию.
Передача тепла — теплообмен.

Количество теплоты, которая была получена телом

В процессе теплообмена изменение внутренней энергии тела, это ни что иное как результат работы внешних сил. Однако это не та работа, которая связана со сменой внешних параметров системы, а работа производится благодаря молекулярным силам.

Пример 1

Соприкосновение тела и горячего газа. При таком взаимодействии через столкновение молекул тела с молекулами газа происходит передача энергии газа.

Мера измерения, которая применяется в процессе теплообмена при изменении внутренней энергии тела выступает количество тепла (Q).

Виды теплообмена:

теплопроводность;
конвекция (конвективный теплообмен);
излучение (теплообмен при помощи излучения).

Рассмотрим пример с помощью рисунка теплообмена ниже.

Пример 2

Есть два тела:

Одно имеет более высокую температуру и второе — низкую температуру.

Первое будет остывать и отдавать тепловую энергию до тех пор, когда температура двух тел не станет идентичной. Это будет называться тепловым равновесием взаимодействующих тел.

Когда работ в системе не совершается, но при этом к ней проводится тепло. При таком раскладе в соответствии с законом сохранения энергии (первым началом термодинамики) все тепло, которое будет передано системе, идет на увеличение внутренней энергии системы:

[Delta Q=Delta U text { (№1) }]

В этом случае, [triangle U] каждого тела при нагревании будет равняться массе тела (m) умноженной на удельную теплоемкость вещества (c) и умноженное на изменение температуры тела [(triangle T)].

[Delta U=m c Delta T(text { №2) }]

При плавлении и кристаллизации для расчета [triangle U] будет использована следующая формула:

[Delta U=pm lambda m text { (№3) }]

[lambda-] удельная теплота плавления или кристаллизации вещества.
m — масса тела.
Для определения при конденсации или парообразования применяем:

[Delta U=pm r m text { (№4) }]

r — удельная теплота конденсации или парообразования.
m — масса тела.

При этом не следует забывать, что все вышеупомянутые процессы: плавление, кристаллизация, конденсация, парообразование происходят без изменения температуры, то есть при постоянной температуре.

По изложению формул под номерами три и четыре, мы можем ясно увидеть, что изменение внутренней энергии системы не зависит от температуры.
Когда топливо полностью подлежит сгоранию выделяется теплота, которую можно определить с помощью следующей формуле:

[Delta Q=Delta U=q m text { (№5) }]

q — удельная теплота сгорания топлива.
m — масса тела.

Сохранение тепловой энергии и уравнение теплового баланса

При остывании одного тела, происходит отдача тепловой энергии, то есть теплообмен с окружающей средой. Утерянная теплота Q будет иметь знак “минус”.

При нагревании тела — оно получает тепловую энергию. И та приобретенная теплота Q будет иметь знак “плюс”.

Формулы

В изолированной системе может происходить только теплообмен. Один из главных законов в физике, а именно в термодинамике, является закон сохранения и превращения энергии.

В том случае, когда в системе, которая изолирована, не происходит никаких процессов превращений кроме теплообмена, количество теплоты, которая будет отдана телами (их внутренняя энергия будет уменьшаться) будет равна количеству тепла полученного телами (их внутренняя энергия будет увеличиваться). Но не смотря на процесс теплообмена, общая -суммарная энергия системы будет неизменна и мы сможем записать первое начало термодинамики с помощью формулы:

[Delta U=sum_{i=1}^{n} Delta U_{i}=0(mathrm{№} 6)]

Это и является уравнением теплового баланса.
Также можно его выразить иначе. Общее количество тепла, которое выделилось в изолированной системе будет равное суммарному количеству тепла, которое было поглощено в системе. Записать это можно в следующем виде:

[Q_{1}+Q_{2}+Q_{2}+ldots+Q_{n}=Q_{1}^{prime}+Q_{2}^{prime}+Q_{2}^{prime}+ldots Q_{k}^{prime} text { (№7). }]

Если брать смысл теплового баланса, он заключается в сохранении энергии для процессов, связанных с теплообменом в термоизолированных системах.

Нет времени решать самому?

Наши эксперты помогут!

Пример теплообмена между холодным и горячим телом

Пример 3

В горячую воду с температурой +80 градусов Цельсия, которая имеет массу двести грамм, добавили охлажденную воду, имеющею температуру +15 градусов Цельсия с массой сто грамм.

Вопрос:

Какая температура будет у смешанной воды после того, как произойдет тепловое равновесия?

Примечание: не учитывать теплообмен с окружающей средой.

В данном случае, мы с вами рассмотрим упрощенную задачу, для лучшего понимания закона сохранения энергии. В данной задаче, мы не будем учитывать осуществляемый теплообмен с емкостью, которая наполнена водой.

Решение:

Считаем систему изолированной, так как в условии было сказано, что окружающая среда не будет участвовать в теплообмене.

Из-за того, что теплообмен с окружающей средой и воздухом происходить не будет, вся тепловая энергия, которую получит холодная вода, будет отдана горячей водой

Записываем уравнение теплового баланса:
[Q_{text {остывания горячей воды }}+Q_{text {нагревания холодной воды }}]
Записываем формулу для каждого количества теплоты:
[Q_{text {остывания горячей воды }}=mathrm{C}_{text {воды }}^{*} m_{text {горячей воды }} *left(t_{text {общ }}-t_{text {горячей воды }}right)]
[Q_{text {нагревания холодной воды }}=mathrm{C}_{text {воды }}^{*} m_{text {холодной воды }}^{*}left(t_{text {общ }}-t_{text {холодной воды }}right)]

Примечания:

[c_{воды}] — берем из справочника
Массу воды обязательно переводим в килограммы
Разность [left(t_{text {общ }}-t_{text {горячей воды }}right)] будет с отрицательным знаком, потому что ее окончательная температура будет меньше ее изначальной.

Подставляем выражения и выводим окончательную формулу:
[c_{text {воды }} * m_{text {горячей воды }} *left(t_{text {общ }}-t_{text {горячей воды }}right)+c_{text {воды }} * m_{text {холодной воды }} * left(t_{о б щ}-t_{text {холодной воды }}right)]
Заменяем символы числами:
[begin{aligned}
&4200 * 0,2 *left(t_{text {общ }}-80right)+4200 * 0,1 *left(t_{text {общ }}-15right)=0 \
&840 *left(t_{text {общ }}-80right)+420 *left(t_{text {общ }}-15right)=0
end{aligned}]
Раскрываем скобки и получаем ответ [t_{text {общ }}=58,33]

Ответ: Температура смешанной воды будет равна 58,33 градуса Цельсия.

Пример на определение массы пара

Пример 4

В латунный калориметр, который имеет массу [m_{k}=0.1] килограмм со льдом, который имеет массу [m_{i}=1] килограмм , которые имеют общую температуру [T_{k i}=200 mathrm{~K}], начали пускать пар, который имеет температуру [T_{p}=400 mathrm{~K}]. После этого, в калориметре изменилась температура и стала постоянной [Theta=300 K].

Вопрос:

Какую массу имел пар?

Примечание:

Считать, что система, состоящая из льда, колориметра и пара — изолирована. Следовательно, теплообмена с окружающей средой нет.

Решение:

Исходя из условия задачи, мы можем сделать вывод, что все процессы теплообмена, которые будут происходить в системе, можно описать с помощью уравнения теплового баланса, учитывая агрегатные превращения.

В результате того, что лед плавится при помощи пара, калориметр наполняется водой ( если делать выводы по температуре, которая установилась в калориметре [Theta=300 K=27] градусов Цельсия). Происходит теплообмен сред: пар отдает свою теплоту, а калориметр со льдом её получают.

К исходным данным добавляем справочные:

Удельная теплоемкость пара [c_{p}=1,7 * 10^{3} frac{text { Дж }}{кгК}]
Удельная теплоемкость воды [c_{v}=4,2 * 10^{3}frac{text{ Дж }}{кгК}]
Удельная теплоемкость льда [c_{i}=2,1 * 10^{3} frac{text { Дж }}{кгK}]
Удельная теплоемкость латуни [c_{k}=0,386 * 10^{3} frac{ text { Дж }}{кгК}]
Удельная теплотапарообразования воды [r=2,1 * 10^{6} frac{text { Дж }}{кг}]
Удельная теплотапри плавлении льда [lambda=3,3 * 10^{5} frac{text { Дж }}{кг}]

Чтобы решить данную задачу, мы должны описывать каждую стадию изменения внутренней энергии.

Пар, когда отдает теплоту, начинает остывать от своей температуры [T_{p}] до конденсированной [T_{k o n d}], которая равняется 373 К.
Пар будет конденсироваться при постоянной температуре
Вода, которая была получена из пара будет остывать до температуры [Theta].
Как результат внутренняя энергия пара становится меньше [Delta U_{1}=Q_{o t d}=m_{p} c_{p}left(T_{p}-T_{c o n d}right)+m_{p} r+m_{p} c_{v}left(T_{k o n d}-Thetaright)].
Происходит нагревания льда благодаря тому, что он получает теплоту от пара и он от [T_{k i}] доходит до [T_{text {plav }}] и равняется 273 K.
Плавление льда
Нагревание воды до температуры [Theta].
Как результат, внутренняя энергия льда будет увеличена.
[Delta U_{1}=Q_{text {poluch }}=m_{i} c_{i}left(T_{text {plav }}-T_{k i}right)+m_{i} lambda+m_{i} c_{v}(Theta-T_{text {plav }})]
Происходит теплообмен с калориметром и он нагревается до [Theta].

Составляем уравнение теплового баланса:

[Delta U_{1}=Delta U_{2}+Delta U_{3}]

Для описания всего процесса составим уравнение теплового баланса:

[begin{aligned}
&m_{p} c_{p}left(T_{p}-T_{text {cond }}right)+m_{p} r+m_{p} c_{v}left(T_{text {kond }}-Thetaright)= \
&m_{i} c_{i}left(T_{text {plav }}-T_{k i}right)+m_{i} lambda+m_{i} c_{v}left(Theta-T_{text {plav }}right)+ \
&m_{k} c_{k}left(Theta-T_{k i}right)
end{aligned}]

[m_{p}=frac{m_{i} c_{i}left(T_{p l a v}-T_{k i}right)+m_{i} lambda+m_{i} c_{V}left(Theta-T_{text {plav }}right) m_{k} c_{k}left(Theta-T_{k i}right)}{c_{p}left(T_{p}-T_{text {cond }}right)+r+c_{V}left(T_{text {kond }}-Thetaright)}]

Заменяем символы на цифры:

[begin{aligned}
&m_{p}= \
&frac{1 * 2,1 * 10^{3} *(273-200)+1 * 3,3 * 10^{5}+1 * 4,2 * 10^{3} *(300-273)+0.1 * 3,9 * 10^{3} *}{1.7 * 10^{3} *(400-373)+2,1 * 10^{6}+4,2 * 10^{3} *(373-300)} \
&=frac{9,8 * 10^{5}}{2.5 * 10^{6}}=0.392(кг)
end{aligned}]

Ответ: Масса пара будет равна примерно 392 грамма.

Источник

Расчет и оценка коэффициента теплоотдачи

Теплоотдача при теплообмене между атмосферным воздухом и дневной поверхностью может быть определена несколькими формулами. Наиболее распространённая из них следующая [1].

Несмотря на то, что расчёт по данным формулам показывает отличающиеся друг от друга значения, выбор конкретных формулы для моделирования не всегда важен. Дело в том, что если проводить адаптацию параметров теплообмена с окружающей средой, то данной процедурой несколько нивелируются погрешности определения других составляющих теплообмена, в том числе и теплоотдачи.

При моделировании инженерных сооружений, часто бывает необходимым определение коэффициента теплоотдачи от инженерного сооружения к поверхности.

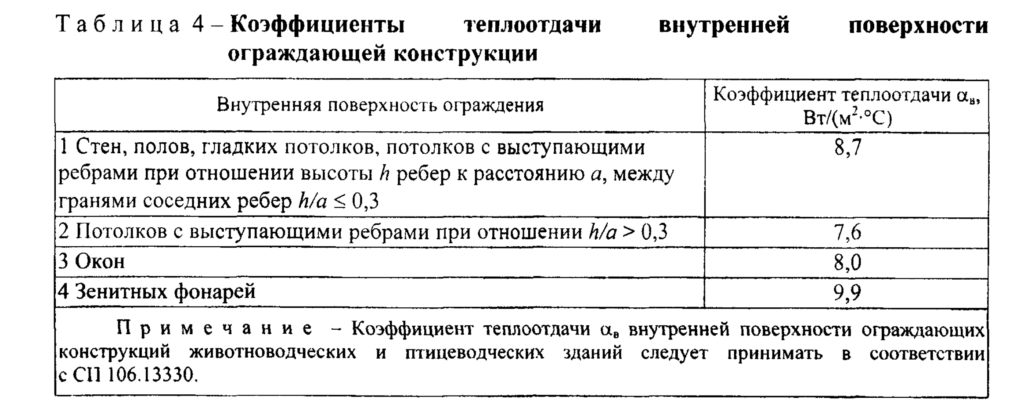
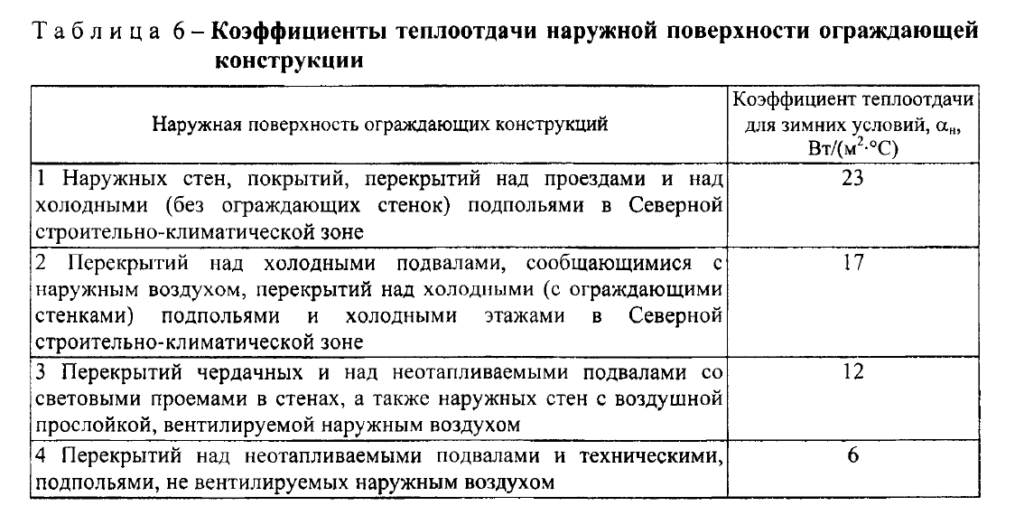
При наличии воздуха, осуществляющего теплоотдачу, расчёт может быть затруднён, так как зачастую достаточно сложно рассчитать или оценить скорость его движения (например, конвекция воздуха в замкнутых полостях). Для проектирования, можно рекомендовать использовать коэффициенты рекомендуемые СП 50.13330.2012 «Тепловая защита зданий. (Актуализированная редакция СНиП 23-02.2003)».

Данные коэффициенты представляются нам несколько завышенными, но для использования при проектировании, они будут обеспечивать некоторый запас надёжности, закладываемый вами в расчёт. Как правило, это то, что нужно.

В случае, когда мы имеем подвижную среду (жидкую или газообразную), т.е. имеющую конвективную составляющую теплообмена, отличного от воздуха вещества или если нам нужно будет более точно определить коэффициент теплоотдачи от воздуха, то следует воспользоваться формулами из теории теплообмена. Теория теплообмена обычно имеет эмпирический закономерности основанные на критериях подобия.

Критерии подобия — это числа, имеющие безразмерную величину и характеризующие различные аспекты подобия моделей и процессов (например, критерий Эйлера характеризует геометрическое подобие, а критерий Рейнольдса гидродинамическое). Таким образом, получив зависимость от критерия подобия на экспериментальных данных с лабораторного стенда, мы можем перенести эту зависимость на другие объекты имеющих имеющие те же значения критериев подобия. Более подробную информацию о критериях подобия и теории теплообмена можно получить различной литературе по теплообмену.

Зависимости для расчёта коэффициента теплоотдачи часто будут иметь следующий вид:

Где C, n и К – значения, которые принимаются по методике или справочнику для конкретного процесса;

Gr — число Графгофа;

Pr — число Прандтля;

Nu — число Нуссельта.

Обычно значение числа Нуссельта Nu находят по критериальной зависимости из теории теплообмена, а теплоотдачу α получают, выражая ее из определения критерия Нуссельта.

Эмпирические зависимости из теории теплообмена могут иметь достаточно сложную форму. Для строительного проектирования можно рекомендовать справочники по теплообмену [2-6], в которых различные зависимости будут представлены в несколько упрощённом виде.

Часто бывают такие ситуации, что воспользоваться формулами из теории теплообмена не представляется возможным в виду отсутствия исходных данных (например, связанных со скоростями движения воздуха или теплоносителя). В ряде случаев, при проектировании объектов, нужны величины обеспечивающие некоторые запас поступления теплоты в модель. Т.е. в этих случаях определение точных значений теплоотдачи не является необходимым, а достаточно оценки величины теплоотдачи с некоторым запасом.

В заметке для многослойной стенки мы уже рассматривали следующую особенность. Наибольший вклад в значение коэффициента теплопередачи вносит наибольшее термическое сопротивление. Например, учёт термического сопротивления металла при расчёте суммарного коэффициента теплопередачи теплоизолированного трубопровода приводит к изменению коэффициента теплопередачи менее чем на 0,1% (ссылка).

Схожая ситуация имеет место быть с другими инженерными сооружениями. Часто бывает так, что термическое сопротивление грунта (а теплопроводность грунта достаточно небольшая величина), оказывается наибольшим и теплоотдача от многих инженерных сооружений вносит незначительный вклад в суммарной коэффициент теплопередачи.

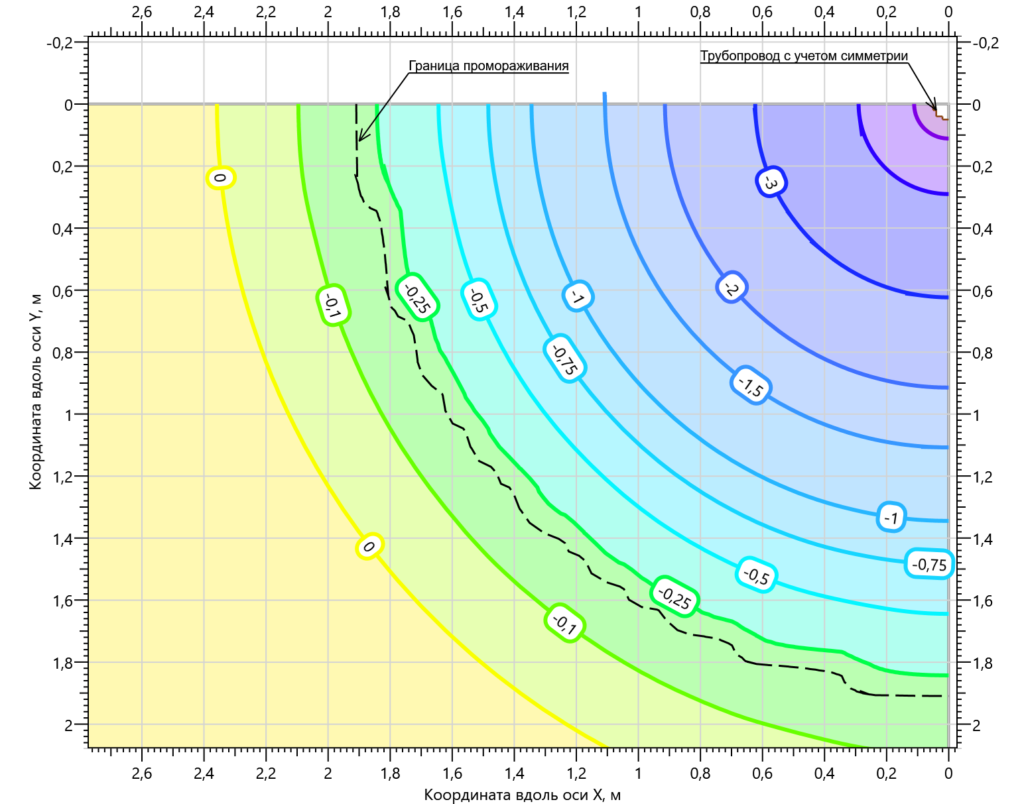
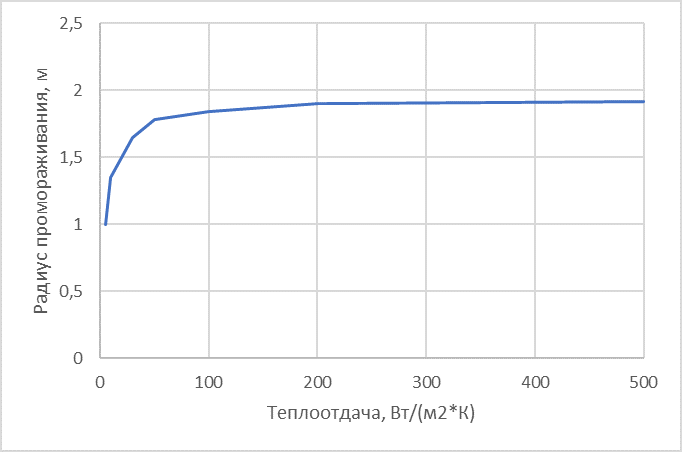
Для иллюстрации этого факта рассмотрим изменение радиуса промораживания грунта вокруг трубопровода 100 мм за 1 год, при изменении коэффициента теплоотдачи от трубопровода.

Из представленных результатов мы видим, что начиная с некоторых величин теплоотдачи радиус промораживания грунта перестаёт расти. Дело в том, что в процессе промораживания увеличивается слой мерзлого грунта и с некоторого момента времени данный слой начинает оказывать наибольшее термическое сопротивление. Что в свою очередь приводит к тому, что коэффициент теплоотдачи начинает вносить всё меньший и меньший вклад в теплообмен.

Т.е. для ряда сооружений достаточно оценить коэффициент теплоотдачи с некоторым запасом, а не пользоваться сложными соотношениями и методиками из теории теплообмена. Например, коэффициенты теплоотдачи при транспортировке нефти, газа или воды по трубопроводу, зачастую настолько велики, что их учёт в задачах теплообмена с грунтами не имеет практического смысла. В таком случае температуру на внутренней стенке трубы или на внутренней поверхности теплоизоляции можно принять равной температуре транспортируемой среды.

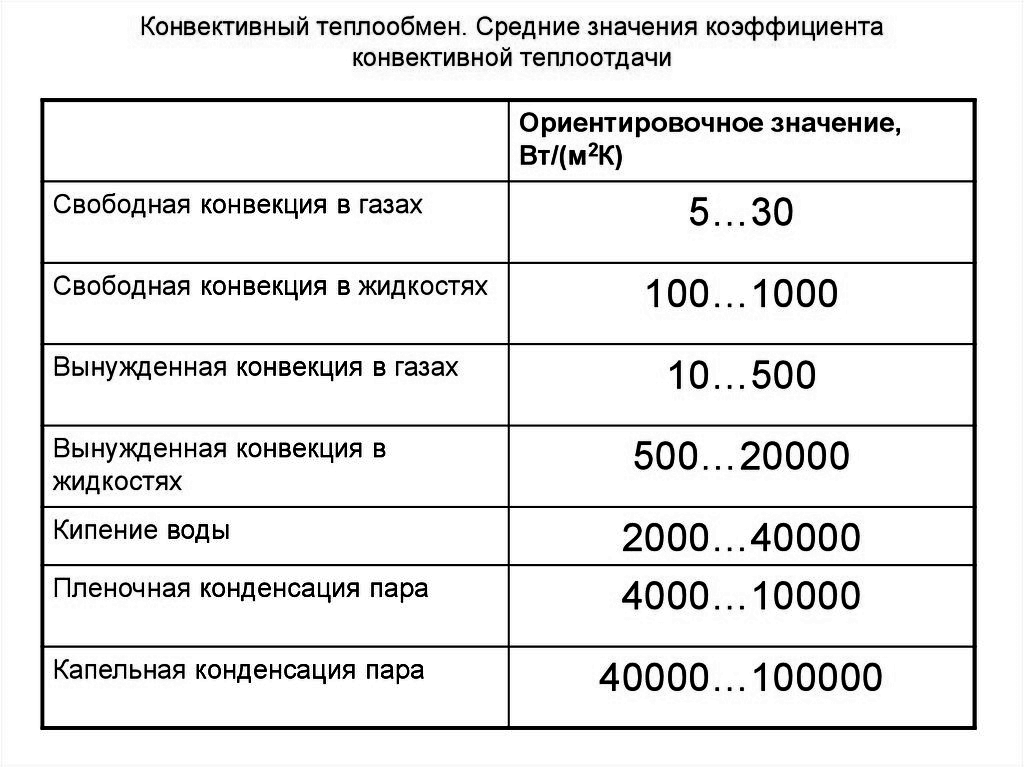
Для выполнения оценки коэффициента теплоотдачи можно воспользоваться таблицами ориентировочных значений теплоотдачи в различных процессах.

Несмотря на то, что во многих случаях коэффициент теплоотдачи достаточно просто оценить, при проектировании ряда инженерных сооружений простой экспресс оценки коэффициента теплоотдачи недостаточно и нужно прибегать к использованию сложных зависимостей теории теплообмена для точного расчета теплоотдачи.

Список литературы

Хрусталев Л.Н. Основы геотехники в криолитозоне: Учебник. – М.: Изд-во МГУ, 2005.
Уонг Х., Основные формулы и данные по теплообмену для инженеров. М.:Атомиздат, 1979г.
Цветков Ф.Ф., Керимов Р.В., Величко В.И. Задачник по тепломассообмену. Второе издание, исправленное и дополненное. М.: Издательский дом МЭИ, 2008г. — 195с.
Бажан П.И. и др. Справочник по теплообменным аппаратам. М.:Машиностроение, 1989.-369с.
Справочник по теплообменникам: В 2-х т. Т. 1 / Пер. с англ. под ред. О. Г. Мартыненко и др.— М.: Энергоатомиздат, 1987.— 560 с: ил.
Справочник по теплообменникам: В 2-х т. Т. 2 / Пер. с англ. под ред. О. Г. Мартыненко и др.— М.: Энергоатомиздат, 1987.— 352 с: ил.

Источник

Пособие рекомендовано учащимся, желающим
получить практические навыки в решении задач на
теплообмен, и может быть полезным для учителей и
абитуриентов.

При соприкосновении тел, имеющих разные
температуры, между этими телами происходит
теплообмен. С точки зрения
молекулярно-кинетической теории, это
объясняется так: молекулы более нагретого тела
имеют большую кинетическую энергию, чем молекулы
тела, менее нагретого. При “столкновениях”
молекул соприкасающихся тел происходит процесс
выравнивания их средних кинетических энергий.
Молекулы более нагретого тела теряют часть своей
кинетической энергии, при этом нагретое тело
будет остывать. Кинетическая энергия молекул
холодного тела возрастает, поэтому температура
этого тела будет увеличиваться. В конечном итоге
кинетические энергии молекул обоих тел
сравняются, и температуры тел станут
одинаковыми. На этом теплообмен прекращается.

Энергию, которую тело получает или отдаёт в
процессе теплообмена, называют количеством
теплоты (Q).

Количество теплоты, как и все другие виды
энергии, измеряется в системе СИ в Джоулях: [Q] = Дж.
(Здесь и в дальнейшем единицы измеряются в
системе СИ.)

Нагревание или охлаждение

При нагревании или охлаждении тела количество
теплоты, поглощаемое или выделяемое им,
рассчитывается по формуле:

Q = сm(t₂– t₁), (1)

где m – масса тела, кг;

(t₂– t₁) – разность температур
тела,° С (или К);

с – удельная теплоёмкость вещества, из
которого состоит тело,

Удельная теплоёмкость вещества – это
количество теплоты, которое нужно сообщить
одному килограмму данного вещества, чтобы
увеличить его температуру на 1° С (или это
количество теплоты, которое выделяет один
килограмм данного вещества, остывая на 1° С).

Значения удельных теплоемкостей других
веществ можно найти в справочниках, а также в
школьном учебнике или задачнике.

При нагревании тела его внутренняя энергия
увеличивается. Это требует притока энергии к
телу от других тел. Значит, оно поглощает
некоторое количество теплоты, принимая его от
других тел, участвующих в теплообмене.

При охлаждении тела его внутренняя энергия
уменьшается. Поэтому остывающее тело отдаёт
кому-либо некоторое количество теплоты.

Обычно конечную температуру, установившуюся в
результате теплообмена, обозначают греческой
буквой (тэта).

В формуле (1) произведение cm для каждого
конкретного тела есть величина постоянная. Её
называют теплоёмкостью тела и обозначают С:

C = c m.(2)

Размерность теплоемкости: Теплоемкость тела показывает,
сколько энергии нужно подвести к данному телу,
чтобы нагреть его на 1° С (или сколько энергии
выделяет это тело, остывая на 1° С).

Теплообмен между телами, имеющими одинаковые
температуры, не происходит, даже если
контактируют вещества, находящиеся в разных
агрегатных состояниях. Например, при температуре
плавления (0° С) лёд и вода могут находиться
бесконечно долго, при этом количество льда и
количество воды останутся неизменными.
Аналогично ведут себя пар и жидкость,
находящиеся при температуре кипения. Теплообмен
между ними не происходит.

Плавление или кристаллизация

Если при нагревании тела его температура
достигнет температуры плавления, то начинает
происходить процесс перехода этого вещества из
твердого состояния в жидкое. При этом идут
изменения в расположении и характере
взаимодействия молекул. Температура при
плавлении не изменяется. Это означает, что
средние кинетические энергии молекул жидкости и
твердого тела при температуре плавления
одинаковы. Однако внутренняя энергия тела при
плавлении возрастает за счет увеличения энергии
взаимодействия молекул. Количество теплоты,
поглощаемое телом при плавлении, рассчитывается
по формуле

(3)

где m – масса тела, кг;

–
удельная теплота плавления,

При кристаллизации, наоборот, внутренняя
энергия тела уменьшается на величину и эта теплота данным
телом выделяется. Она поглощается другими
телами, участвующими в теплообмене.

Удельная теплота плавления показывает,
сколько энергии нужно сообщить одному
килограмму данного вещества, взятого при
температуре плавления, чтобы полностью
превратить его при этой температуре в жидкость
(или сколько энергии выделяет 1 кг жидкости,
взятой при температуре кристаллизации, если вся
она при этой температуре полностью превратится в
твёрдое тело).

Удельную теплоту плавления любого вещества
можно найти в справочниках. Для льда же

Температура плавления у каждого вещества своя.
Её также можно найти в справочниках. Важно
подчеркнуть, что температура плавления вещества
равна температуре кристаллизации этого же
вещества. У льда t_пл = 0° С.

Кипение или конденсация

При достижении жидкостью температуры кипения
начинает происходить другой фазовый переход –
кипение, при котором расстояния между молекулами
значительно увеличиваются, а силы
взаимодействия молекул уменьшаются. Вся
подводимая к жидкости теплота идет на разрыв
связей между молекулами. При конденсации пара в
жидкость, наоборот, расстояния между молекулами
значительно сокращаются, а силы взаимодействия
молекул увеличиваются. Для кипения жидкости
энергию к жидкости нужно подводить, при
конденсации пара энергия выделяется. Количество
теплоты, поглощаемое при кипении или выделяемое
при конденсации, рассчитывается по формуле:

где m – масса тела, кг; L – удельная
теплота парообразования,

Удельная теплота парообразования
показывает, сколько энергии нужно сообщить
одному килограмму жидкости, взятой при
температуре кипения, чтобы при этой температуре
полностью превратить её в пар (для конденсации:
сколько энергии выделяет один килограмм пара,
взятого при температуре конденсации, полностью
превращаясь в жидкость).

При одинаковом давлении температура кипения и
температура конденсации одного и того же
вещества одинаковы.

Температуры кипения и удельные теплоты
парообразования также можно найти в
справочниках. Для воды же они соответственно
равны: рис. 9 (при нормальном атмосферном
давлении).

Уравнение теплового баланса

Тела, участвующие в теплообмене, представляют
собой термодинамическую систему.
Термодинамическая система называется теплоизолированной,
если она не получает энергию извне и не отдаёт её;
теплообмен происходит только между телами,
входящими в эту систему. Для любой
теплоизолированной системы тел справедливо
следующее утверждение: количество теплоты,
отданное одними телами, равно количеству
теплоты, принимаемому другими телами.

Q_отд.= Q_получ. (5)

Это утверждение описывает частный случай
закона сохранения и превращения энергии в
применении к процессу теплообмена. А формула (5)
является одним из видов уравнения теплового
баланса.

При решении задач с помощью данного вида
уравнения теплового баланса в формуле (1) в
качестве t₂ следует брать большую
температуру, а в качестве t₁ – меньшую.
Тогда разность (t₂– t₁) будет
положительна и всё произведение cm(t₂–t₁)
также будет положительным. Все теплоты, отданные
и полученные, будут положительными.

Уравнение теплового баланса можно записать и в
таком виде:

Q₁+ Q₂+…+ Q_n= 0, (6)

где n – количество тел системы.

Алгебраическая сумма всех количеств теплоты
(поглощенных и выделенных) в теплоизолированной
системе равна нулю.

Q₁, Q₂, …, Q_n – это теплоты,
поглощаемые или выделяемые участниками
теплообмена. Очевидно, что в этом случае какие-то
теплоты должны быть положительны, а какие-то –
отрицательны. При записи уравнения теплового
баланса в виде (6) всегда t₂ – конечная
температура, а t₁ – начальная.

Если тело нагревается, то разность (t₂ – t₁)положительна и все произведение cm(t₂– t₁)
положительно. То есть Q > 0 тогда, когда теплота к
данному телу подводится.

А если t₂< t₁ (тело остывает), то
разность (t₂ – t₁) отрицательна, то есть
Q < 0. В этом случае тело энергию выделяет.

Если при фазовом переходе энергия к телу
подводится (плавление, кипение), то Q > 0; если
тело выделяет энергию (кристаллизация,
конденсация), то Q < 0.

В принципе уравнения (5) и (6) равносильны.
Результат решения задачи не зависит от того,
каким видом уравнения пользуемся. Выбор способа
решения – за читателем.

Применим уравнение теплового баланса для
решения ряда задач (здесь приводим лишь одну
задачу, остальные материалы можно найти по
адресу http:// kirov-festival.nm.ru).

Задача 1

В медном калориметре массой 100 г находится 1 кг
воды при температуре 20° С. В воду опускают
свинцовую деталь массой 2 кг, имеющую температуру
90° С. До какой температуры нагреется вода? (В этой
и последующих задачах потерями теплоты в
калориметре пренебречь.)

Решение

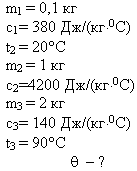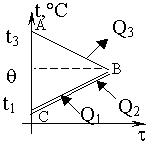	Проведём анализ: Вода и калориметр находились в тепловом равновесии, поэтому они имели одинаковую температуру: t₁= t₂= 20° С. При опускании в воду с температурой 20° С свинцового тела с температурой 90° С между водой и свинцом будет происходить теплообмен. Свинец будет остывать, а вода — нагреваться. В этом же процессе участвует и калориметр, который, как и вода, будет тоже нагреваться.
	Изменение температур тел с течением времени удобно изображать на графике зависимости t(t ). Отрезок АВ соответствует графику изменения температуры свинцового тела. Стрелка, идущая от него, показывает, что, остывая, свинец выделяет энергию Q₃.
	Два параллельных отрезка СВ соответствуют графикам изменения температур калориметра и воды. Стрелки, идущие к ним, показывают, что для нагревания калориметра и воды требуется энергия Q₁ и Q₂, которую они поглощают.
Решим задачу с использованием уравнения теплового баланса в виде (5):

Решим задачу с использованием уравнения
теплового баланса в виде (6):

Ответ: Вода нагреется до 24° С.

Предлагаю читателю самостоятельно сделать
проверку размерности.

Напомним, остальной материал (полноценную
версию пособия) можно найти по адресу http:// kirov-festival.nm.ru.

Источник