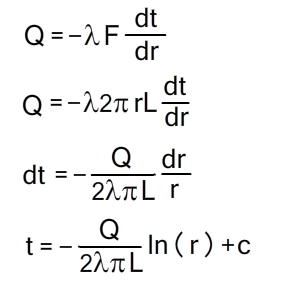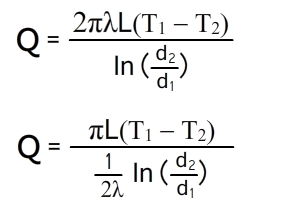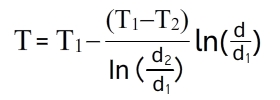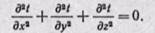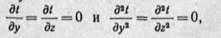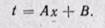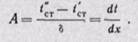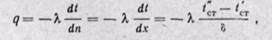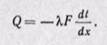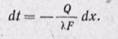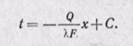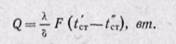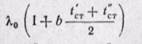Р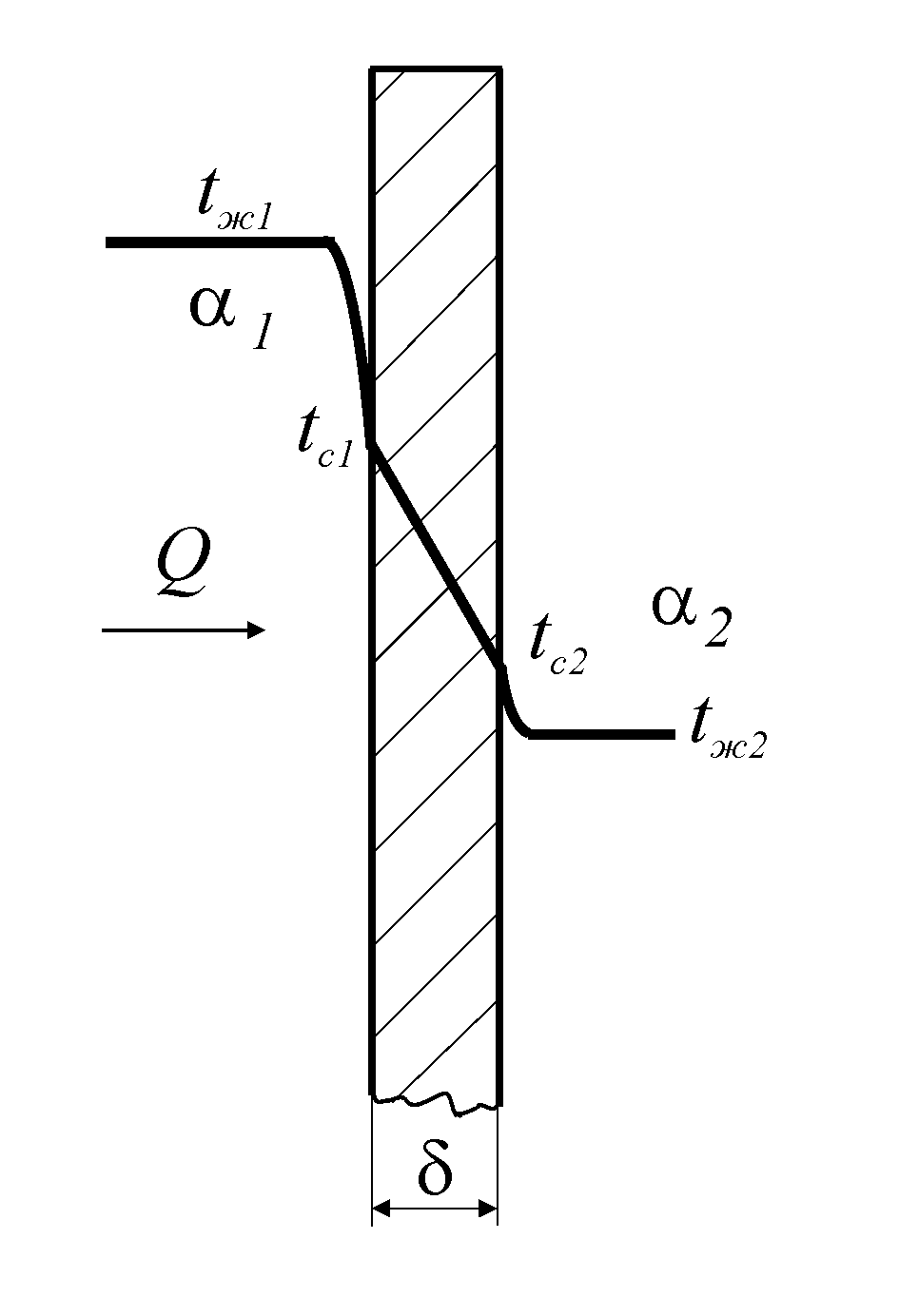
процесс передачи теплоты через плоскую
стенку поверхностьюF,
толщиной
и
коэффициентом теплопроводности.
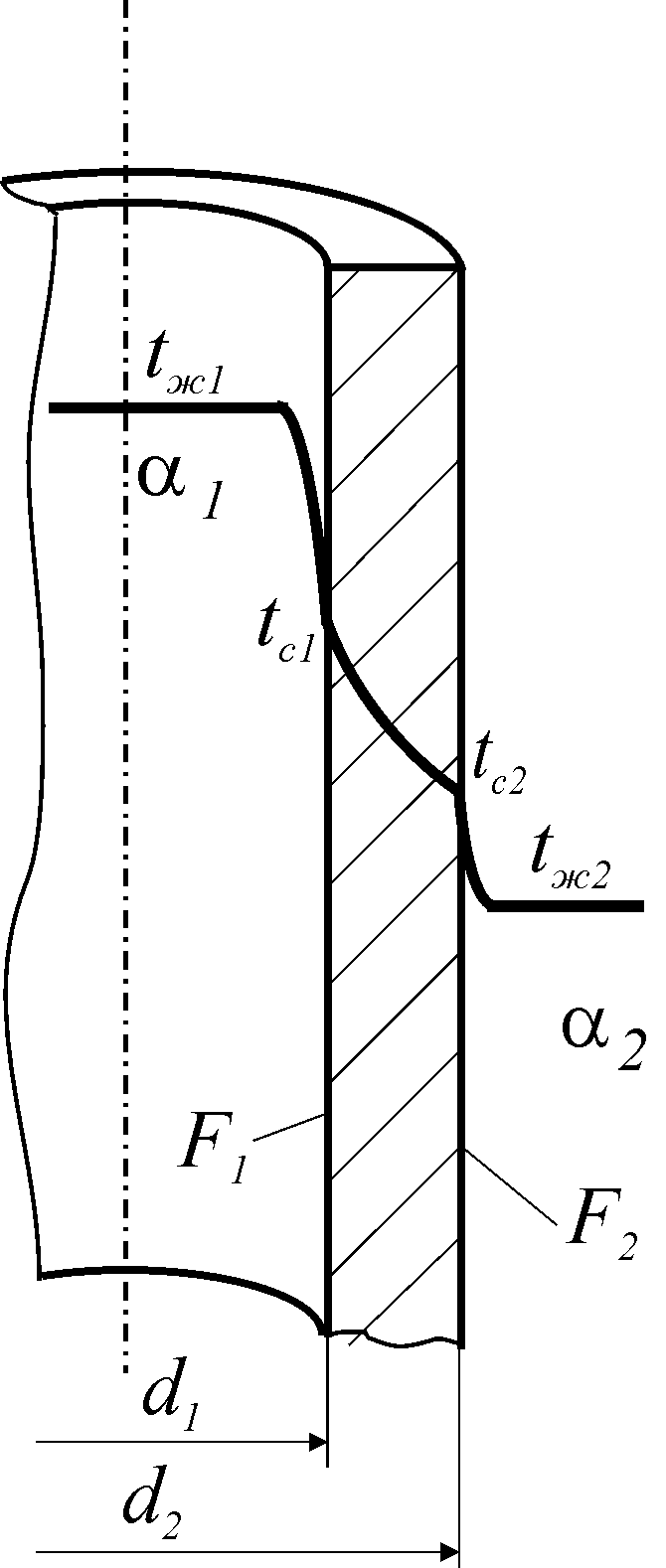
При известных температурах горячегои холодного теплоносителя
,
а также коэффициентов теплоотдачи от
горячегои холодного
теплоносителей решение сводится к
определению теплового потока, плотности
теплового и температур внутренней и
наружной поверхности стенки (граничные
условия третьего рода). Принимая во
внимание условие постоянства теплового
потока можно записать ряд равенств
;
;
(1.204)
В этом ряду равенств
первое уравнение определяет количество
теплоты, передаваемой конвекцией (и
излучением) от горячего теплоносителя
к стенке; второе уравнение – то же
количество теплоты, передаваемой
теплопроводностью через стенку; третье
уравнение – передачу того же самого
количества теплоты, передаваемого
конвекцией (и излучением) от стенки к
холодному теплоносителю.
Выделим из этого
ряда равенств разности температур
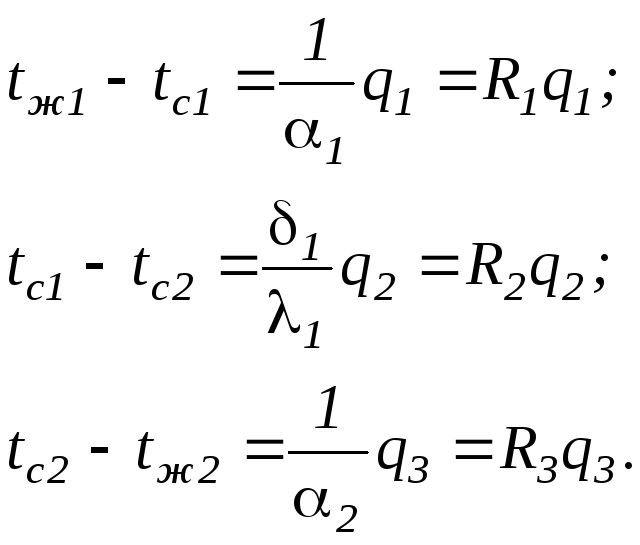
Складывая левые
и правые части уравнений характеризующих
разности температур и учитывая, что
получим выражение для итоговой разности
температур
(1.206)
где
–термическое
сопротивление плоской стенки
(м2
0СBm)
Отсюда, следует
выражение для плотности теплового
потока и теплового потока (уравнение
теплопередачи плоской стенки)
,
(1.207)
где q
– плотность теплового потока (Вт/м2
);
Q
– тепловой поток (Вт);
k=1/R
– коэффициентом теплопередачи плоской
стенки (Вт/м2
ºС)
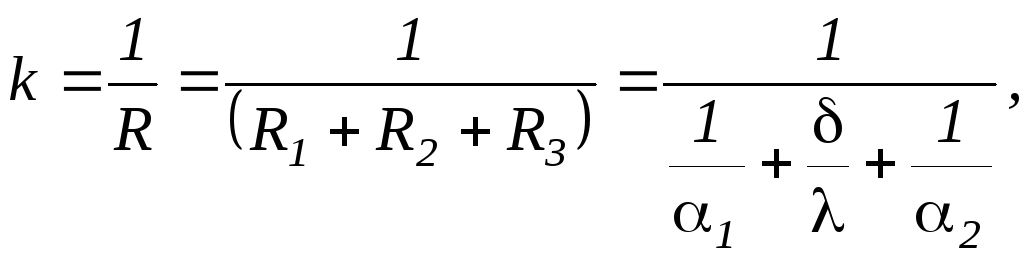
)
где
—термическое сопротивление теплопередачи
плоской стенки (м2
ºС/Вт);
;
— термические сопротивления теплоотдачи
со стороны горячего теплоносителя,
теплопроводности плоской стенки и
термические сопротивления теплоотдачи
со стороны холодного теплоносителя
соответственно.
Температура
внутренней и наружной поверхности
стенки определяется из следующих
соображений:
,
(1.209)
отсюда имеем
,
(1.210)
В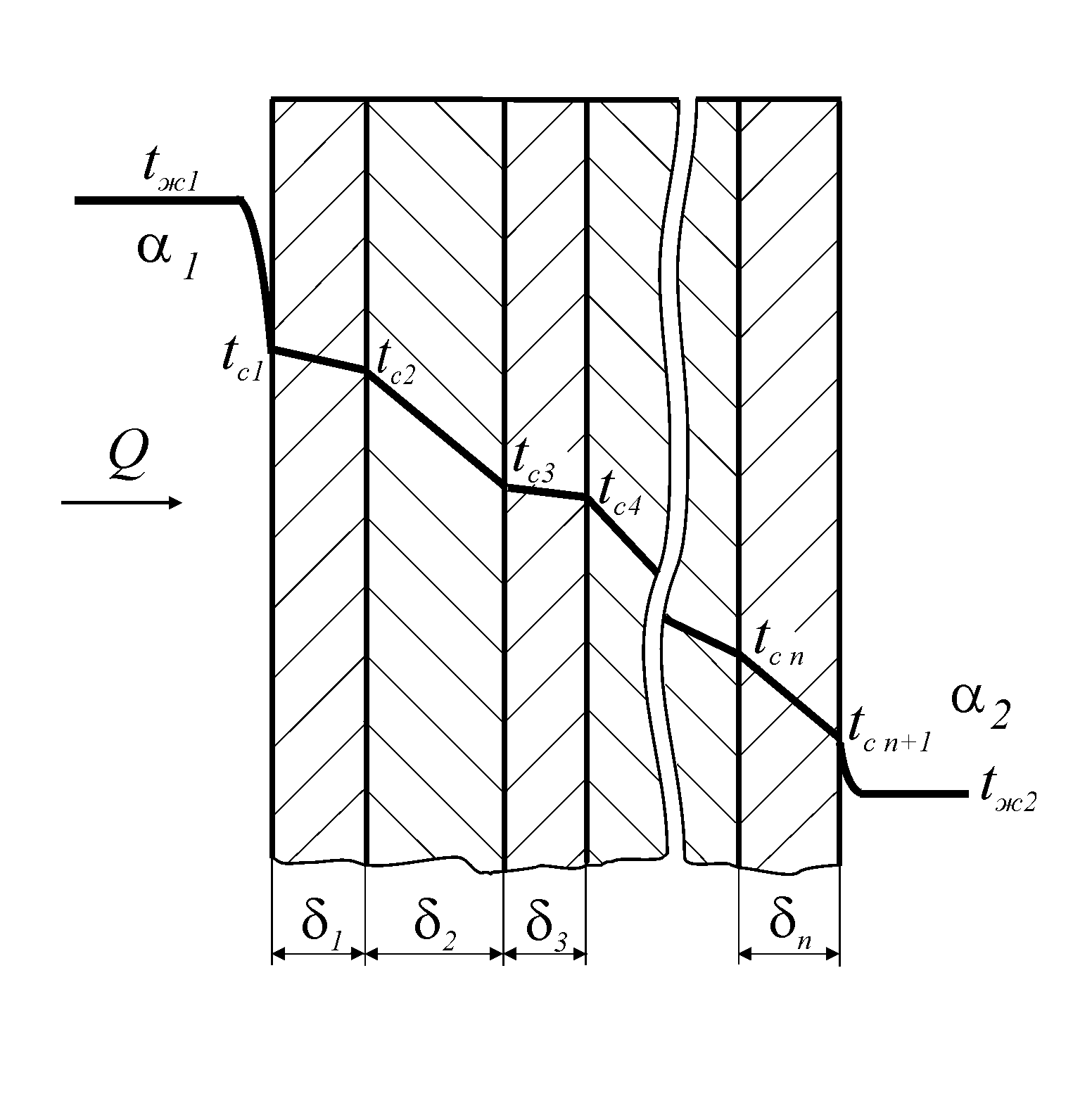
из п слоев тепловой поток и плотность
теплового потока определяются по
уравнениям аналогичным однослойной
(1.207) за исключением того, что термическое
сопротивление и следовательно коэффициент
теплопередачи определяются с учетом
термических сопротивлений каждого
слоя.
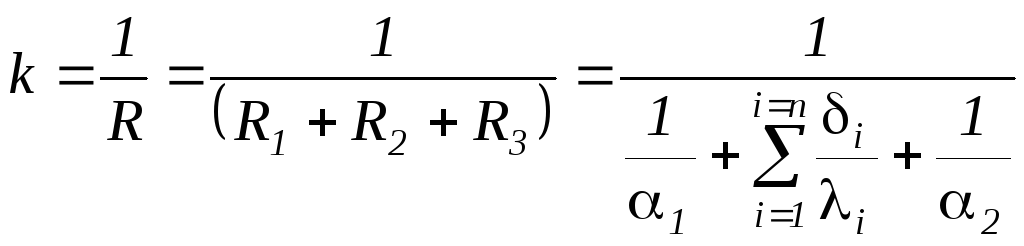
Температура
поверхности и на стыке слоев определяется
из тех же соображений, что и для однослойной
стенки
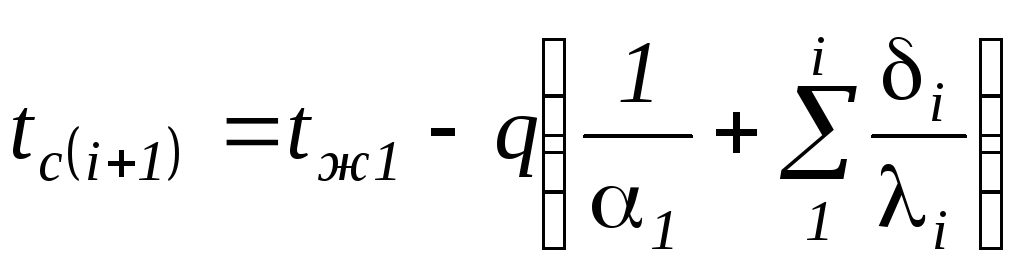
38. Теплопередача через криволинейные однослойные и многослойные стенки.
Для криволинейных
стенок произведение kF
неразделимо
и только для плоской стенки вследствие
равенства F1
= Fm,i
= F2
= F
это
произведение распадается на k
и F. Тогда
для плоской стенки выражение коэффициента
теплопередачи запишется следующим
образом;
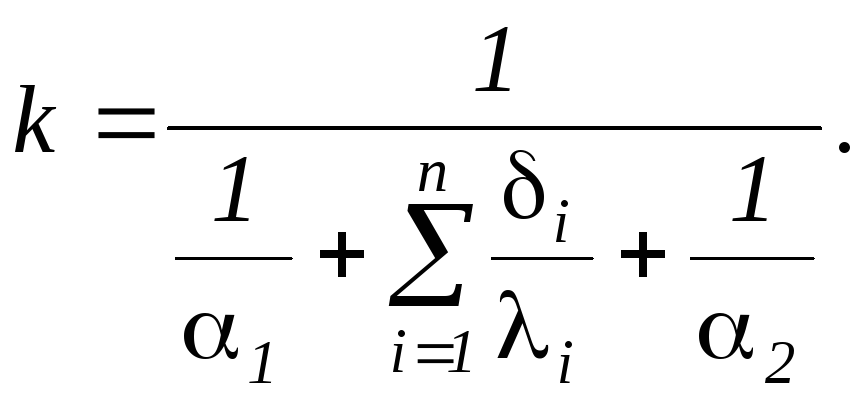
Для криволинейных
стенок коэффициент теплопередачи
принято определять по тому же уравнению,
что и для плоской стенки. В этом случае
для криволинейных стенок расчетная
поверхность теплопередачи определяется
из выражения
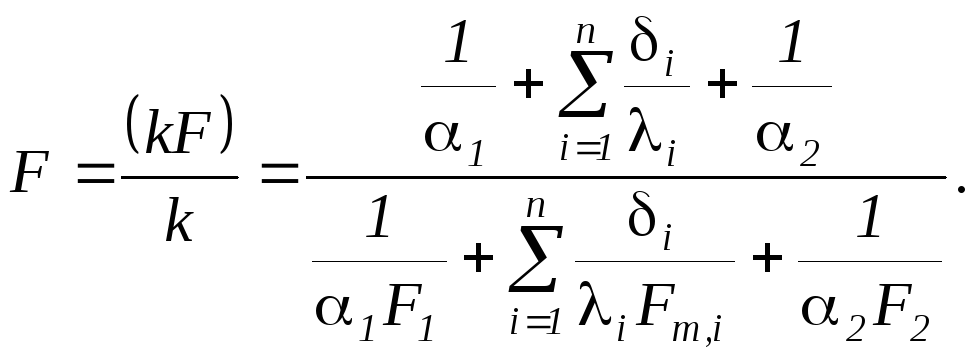
Удельная линейная
плотность теплового потока ql
для цилиндрической стенки в условиях
теплопередачи является частным выражением
основного уравнения
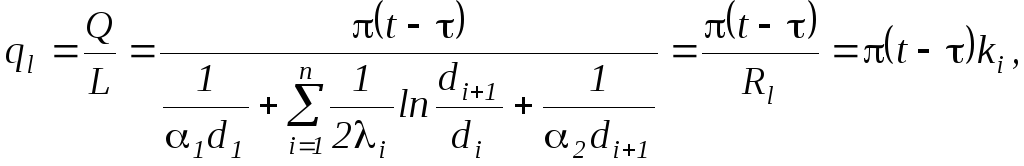
где
—
линейное термическое сопротивление;
В технических
расчетах чаще всего приходится решать
проблему двух видов: уменьшение тепловых
потерь (изоляция поверхности теплообмена)
и увеличение количества передаваемого
тепла (интенсификация теплопередачи).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Тема 12.Теплопередача
12.1. Теплопередача через плоскую стенку
Теплопередачей
называется передача теплоты от горячего теплоносителя к холодному теплоносителю
через стенку, разделяющую эти теплоносители.
Примерами теплопередачи являются: передача теплоты от греющей воды
нагревательных элементов (отопительных систем) к воздуху помещения; передача
теплоты от дымовых газов к воде через стенки кипятильных труб в паровых котлах;
передача теплоты от раскаленных газов к охлаждающей воде (жидкости) через
стенку цилиндра двигателя внутреннего сгорания; передача теплоты от внутреннего
воздуха помещения к наружному воздуху и т. д. При этом ограждающая стенка
является проводником теплоты, через которую теплота передается
теплопроводностью, а от стенки к окружающей среде конвекцией и излучением.
Поэтому процесс теплопередачи является сложным процессом теплообмена.
При передаче теплоты от стенки к окружающей среде в основном преобладает
конвективный теплообмен, поэтому будут рассматриваться такие задачи.
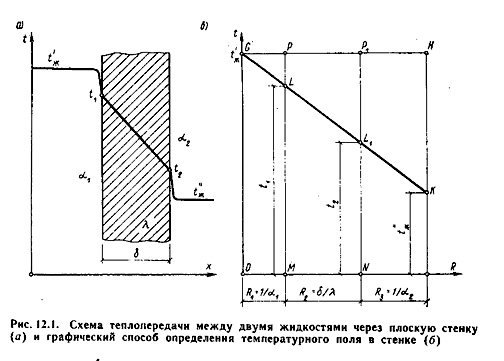
1). Теплопередача через плоскую стенку.
Рассмотрим однослойную плоскую стенку толщиной
d и
теплопроводностью l (рис12.1).
Q = a1 · (t‘ж – t1) · F, (12.1)
где a1
– коэффициент теплоотдачи от горячей среды с температурой t‘ж
к поверхности стенки• с температурой t1;
F – расчетная поверхность плоской стенки.
Тепловой поток, переданный через стенку определяется по уравнению:
Q = l/d · (t1 – t2) · F. (12.2)
Тепловой поток от второй поверхности стенки к холодной среде
определяется по формуле:
Q = б2 · (t2 — t»ж) · F, (12.3)
где a2
– коэффициент теплоотдачи от второй поверхности стенки к холодной среде с
температурой t»ж.
Решая эти три уравнения получаем:
Q
= (t‘ж – t»ж) • F • К, (12.4)
где К = 1 / (1/a1 + / l + 1/a2) – коэффициент теплопередачи, (12.5)
или
R0
= 1/К = (1/a1
+ d/l + 1/a2) – полное термическое сопротивление теплопередачи через
однослойную плоскую стенку. (12.6)
1/a1,
1/a2
– термические сопротивления теплоотдачи поверхностей стенки;
d/l — термическое
сопротивление стенки.
Для многослойной плоской стенки полное термическое сопротивление будет
определяться по следующей формуле:
R0
= (1/a1
+ d1/l1 + d2/l2 + … + dn/ln +1/a2),
(12.7)
а коэффициент теплопередачи:
К
= 1 / (1/a1
+ d1/l1 + d2/l2 + … + dn/ln +1/a2),
(12.8)
Теплопроводность через стенку
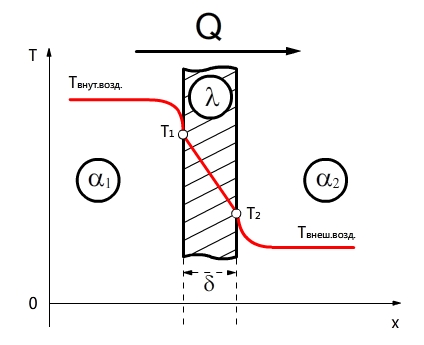
Под теплопередачей через стенку понимают процесс передачи теплоты между двумя средами через непроницаемую стенку любой геометрической формы в стационарном и нестационарном режимах теплообмена. Стенка может быть многослойной.
Рассмотрим стационарный режим теплопередачи через плоскую, цилиндрическую и сферическую стенки при котором теплопередача — величина постоянная и температурное поле не изменяется во времени и зависит только от координаты. В этом случае при условии постоянства теплофизических свойств тела температура в плоской стенке изменяется линейно, а в цилиндрической — по логарифмическому закону, т.е.
Q = const и T = f(x) — линейная (при плоской стенке) или логарифмическая функция (при круглой стенке).
Согласно второму закону термодинамики процесс теплопередачи идет от среды с большей температурой к среде с меньшей температурой.
Теплопередача через непроницаемую стенку включает в себя следующие процессы:
- теплоотдачу от горячей среды к стенке;
- теплопроводность внутри стенки;
- теплоотдачу от стенки к холодной среде.
Теплопередача через плоскую стенку (граничные условия первого рода)
Теплопроводность — первое элементарное тепловое явление переноса теплоты посредством теплового движения микрочастиц в сплошной среде, обусловленное неоднородным распределением температуры.
Совокупность значений температуры для всех точек пространства в данный момент времени называется температурным полем.
Если температурное поле не изменяется во времени, то мы имеем дело со стационарным тепловым режимом.
Тепловой поток Q [Вт] — это количество теплоты, передаваемой в единицу времени (1 Дж/с=1 Вт).
Поверхностная плотность теплового потока рассчитывается по формуле:
где Q — тепловой поток [Вт]; F — площадь стенки [м 2 ].
На основании закона Фурье q=-λdT/dx, значение плотности теплового потока для однослойной стенки будет определяться по формуле:
где δ = dx — толщина стенки, λ
λ/δ; [Вт/м 2 *К] — коэфициент тепловой проводности стенки.
а обратная величина —
R = δ/λ; [м 2. К/Вт] — термическое сопротивление стенки.
Для теплового потока формулу так же можно представить в виде:
Общее количество теплоты проходящее через площадь стены S за время t можно представить как:
Распределение температуры в плоской стенке
Рассмотрим изменение температуры в нашей стене. Так как у нас тепловой поток постоянный, то dT/dx = const=C1; T=C1х+С2 (1). Определим С1 и С2 через граничные условия.
При х=0 T=T1, подставим в уравнение (1) и получим T1=С2.
При х=δ T=T2, подставим в уравнение (1) и получим T2=С1*δ+С2, T2=С1*δ+T1, получим: С1=(Т2-T1)/δ. Теперь подставим в уравнение (1) найденные С1 и С2, получим следующее распределение температуры в нашей стене:
Если нам нужно узнать на какой глубине стены Т=То, то формула преобразуется в следующий вид:
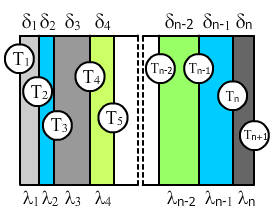
Теплопроводность через многослойную стенку
Если у нас есть стенка из нескольких (n) слоев с разными коэффициентами теплопроводности λi и разной толщиной δi.
Термическое сопротивление стенки считается так:
Для теплового потока формула будет иметь вид:
Температура на границе слоя вычисляется по следующей формуле:
Например, если нужно вычислить температуру между 3-м и 4-м слоем, формула будет такая:
Эквивалентная теплопроводность многослойной стенки:
Теплопередача через плоскую стенку в граничащую среду (граничные условия третьего рода)
Теплопередача — это более сложный процесс теплообмена между жидкими и газообразными средами, разделенными твердой стенкой. Теплопередача включает в себя и процесс теплопроводности, и процесс теплоотдачи.
Коэффициент теплоотдачи α, Вт/(м 2 ·К) — это количество теплоты, отдаваемое в единицу времени единицей поверхности при разности температур между поверхностью и окружающей средой, равной одному градусу.
Коэффициент теплопередачи k, Вт/(м 2 ·К), характеризует тепловой поток, проходящий через единицу площади поверхности стенки при разности температуры сред, равной одному градусу:
q = k * (Tвозд.внутри — Tвозд.снаружи); Вт/м 2
Коэффициент теплопередачи для n слойной стенки:
Термические сопротивления теплоотдаче на внешних поверхностях стенки будут равны:
Тогда общее термическое сопротивление теплопередаче будет равно:
Температуры на поверхности стенки можно определить по формулам:
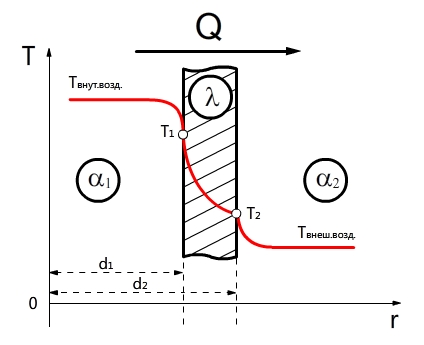
Теплопроводность через цилиндрическую стенку (граничные условия первого рода)
Теплообменные аппараты в большинстве случаев имеют не плоские, а цилиндрические поверхности, например рекуператоры типа «труба в трубе», кожухотрубные водонагреватели и т.д. Поэтому возникает необходимость рассмотрения основных принципов расчета цилиндрических поверхностей.
Согласно закону Фурье, количество теплоты, проходящее в единицу времени через этот слой, равно:
Подставим значения граничные значение и вспомним, что разность логарифмов равна логарифму отношению аргументов, получим:
Распределение температур внутри однородной цилиндрической стенки подчиняется логарифмическому закону, и уравнение температурной кривой имеет вид:
Количество теплоты, проходящее через стенку трубы, может быть отнесено либо к единице длины трубы L, либо к единице внутренней F1 или внешней F2 поверхности трубы. При этом расчетные формулы принимают следующий вид:
Все материалы, представленные на сайте, носят исключительно справочный и ознакомительный характер и не могут считаться прямой инструкцией к применению. Каждая ситуация является индивидуальной и требует своих расчетов, после которых нужно выбирать нужные технологии.
Не принимайте необдуманных решений. Имейте ввиду, что то что сработало у других, в ваших условиях может не сработать.
Администрация сайта и авторы статей не несут ответственности за любые убытки и последствия, которые могут возникнуть при использовании материалов сайта.
Сайт может содержать контент, запрещенный для просмотра лицам до 18 лет.
Теплопроводность через однослойную плоскую стенку
Дифференциальное уравнение теплопроводности позволяет определить температуру в зависимости от времени и координат в любой точке поля.
Для любого конкретного случая к нему надо присоединить необходимые краевые условия.
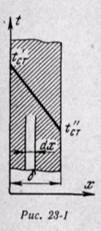
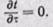
Но при принятых условиях первые и вторые производные от ( по y иz также равны нулю:
поэтому уравнение теплопроводности можно написать в следующем виде:
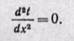
Интегрируя уравнение (23-1), находим
После вторичного интегрирования получаем
При постоянном коэффициенте теплопроводности это уравнение прямой линии. Следовательно, закон изменения температуры при прохождении теплоты через плоскую стенку будет линейным.
Найдем постоянные интегрирования А и В.
При х = 0 температура t = t’cr — B; при х = δ температура t = t»cr — Аδ +tст, откуда
Плотность теплового потока найдем из уравнения Фурье (22-7)
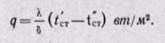
Зная удельный тепловой поток, можно вычислить общее количество теплоты, которое передается через поверхность стенки F за время τ:
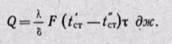
Количество теплоты, которое передается теплопроводностью через плоскую стенку, прямо пропорционально коэффициенту теплопроводности стенки К, ее площади F, промежутку времени т, разности температур на наружных поверхностях стенки (t’ст — t»ст) и обратно пропорционально толщине стенки δ. Тепловой поток зависит не от абсолютного значения температур, а от их разности
t’ст — t»ст = Δt наtзываемой температурным напором.
Полученное уравнение (23-2) является справедливым для случая, когда коэффициент теплопроводности является постоянной величиной. В действительности коэффициент теплопроводности реальных тел зависит от температуры и закон изменения температур будет выражаться кривой линией. Если коэффициент теплопроводности зависит от температуры в незначительной степени, то на практике закон изменения температур считают линейным.
Уравнение (23-2) можно получить непосредственно из закона Фурье (22-6), считая, что температура изменяется только в направлении оси х:
Разделив переменные, получаем
Интегрируя последнее уравнение при условии Q = const, находим
Постоянную интегрирования С найдем из граничных условий:
при х = 0 температура
при х = δ температура 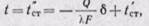
Введем в уравнение (23-2) поправки па зависимость λ от t, считая эту зависимость линейной:

В этом случае, подставив в уравнение Фурье вместо К его значение из формулы (а), получаем

Разделив переменные и интегрируя в пределах от х = 0 до x = δ и в интервале температур от t’ст до t»ст, получаем
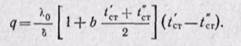
Полученное уравнение (23-4) позволяет определить плотность теплового потока при переменном коэффициенте теплопроводности. В этом уравнении множитель
является среднеинтегралыюй величиной коэффициента теплопроводности.
В уравнении (23-2) было принято λ,=const и равным среднему значению λср. Поэтому, сравнивая уравнения (23-2) и (23-4), получаем

Следовательно, если λср определяется при среднеинтегральной температуре то формулы (23-2) и (23-4) равнозначны.
При этом плотность теплового потока может определяться из уравнения
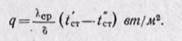
Интегрируя уравнение (б) в пределах от х — О до любой текущей координаты х и в интервале температур от t’ст ДО tx, получим уравнение температурного поля
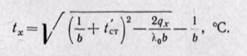
Из этого уравнения следует, что температура внутри стенки изменяется по кривой. Если коэффициент b отрицателен, то кривая будет направлена выпуклостью вниз; если b положителен, то выпуклостью вверх.
Передача теплоты через плоскую однослойную и многослойную стенки (теплопередача)


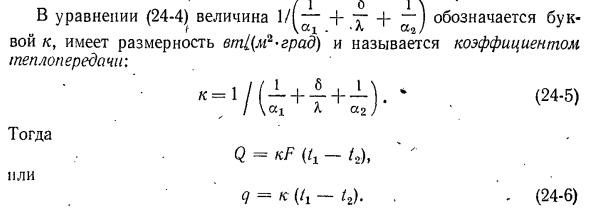


Передача теплоты через плоскую однослойную и многослойную стенки (теплопередача)
- Теплопередача через плоские однослойные и многослойные стены (теплообмен) Передача тепла от одной движущейся среды (тепла) к другой движущейся среде (холоду) через однослойную или многослойную сплошную стенку любой формы называется теплопередачей. ••. , Примеры теплопередачи: теплопередача от
отопительной воды через стенку радиатора центрального отопления к комнатному воздуху, теплопередача от дымовых газов через стенку котла к воде, теплопередача от нагретого газа к воде, проходящей через стенки цилиндров двигателей внутреннего
сгорания и т. Д. — Во всех рассмотренных случаях стенка действует как проводник тепла и проводимость. • В других случаях стены необходимы для уменьшения потерь тепла, если это необходимо. Это изолятор и изготовлен из материала с хорошими теплоизоляционными свойствами. Стены встречаются в самых
конденсированный пар через стенку конденсатора Теплопередача от воды к воде, Людмила Фирмаль
разных формах: в форме плоского листа или ребристого листа, в форме цилиндрического, ребристого или игольчатого пучка труб, в сферической форме и т. Д. Теплообмен — это очень сложный процесс, при котором тепло передается всеми способами, включая теплопроводность, конвекцию и излучение. , Фактически, если есть
стена, процесс теплопередачи состоит из трех звеньев (Рисунок 24-1). Первое звено — это теплопередача путем конвекции от теплоносителя к стене. Конвекция всегда включает теплопроводность, часто излучение. Вторым звеном является теплопередача через стенку за счет теплопроводности. Во время распространения тепла в пористом
теле теплопроводность связана с конвекцией и излучением внутри пор. Третье звено — это передача тепла за счет конвекции от второй поверхности стенки к теплоносителю. В этой передаче тепла конвекция также включает теплопроводность и излучение. Количество тепла, передаваемого стене высокотемпературным теплоносителем! Из-за конвективного теплообмена он определяется
- уравнением Ньютона-Ричмана. i ■ Q = * iF ((, -с’т), (24-1). * Рис. 244 Где коэффициент теплопередачи от постоянной температуры высокотемпературного теплоносителя к стене с учетом всех типов теплопередачи? F — расчетная поверхность плоской стенки, м2 Людмила Фирмаль
или ? =. , (24-6) «Значение коэффициента теплопередачи представляет количество тепла, которое проходит через настенный блок в единицу времени. Разница температур от горячей воды до холодной воды в единицу времени составляет 1 °. v Полученное уравнение (24-6) называется уравнением теплопередачи. Для определения k требуется
предварительное определение ax и a2. Это чаще всего сложное число. Он учитывает теплообмен конвекцией и излучением. И 5 = 5 аконов aisl «- Значение k всегда меньше минимума a. «Взаимный коэффициент теплопередачи, Я tf = — = — + -f + — (24-7) K Ctj A ss2 Это называется общим термическим сопротивлением через единственную плоскую стенку. Это значение имеет размерность (м2> град) / Вт. Где 11 б-а —
внешнее тепловое сопротивление. J- это тепловое сопротивление стены. Для теплопередачи через многослойную плоскую стенку в знаменателе уравнения (24-4) должна быть включена сумма тепловых сопротивлений всех слоев. Q = -G (/> — / 2) -, ‘(24-8) JL + 2> + -L 0 Ux-h) ■ • F 1 ^ «i l ‘ce, ^ at a2 Коэффициент теплопередачи через многослойную плоскую стенку составляет k = -! -. (24-9) ^ ч «2 Общее
тепловое сопротивление через многослойные плоские стены Температура поверхности плоской стенки определяется из следующего уравнения: Ul
tl aiF9 г = т + л ‘(24-10)’ tcr a2p ‘ Используя известные a и k, температуру поверхности плоской стенки можно рассчитать по «Я (тф» — «» «Пи — В. (24’у> , a2




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
источники:
http://helpiks.org/3-16578.html
http://lfirmal.com/peredacha-teploty-cherez-ploskuyu-odnoslojnuyu-i-mnogoslojnuyu-stenki-teploperedacha/