Как найти точки через дискриминант - Исправление недочетов и поиск решений вместе с Examum.ru

В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.

Функция вида , где называется квадратичной функцией.

В уравнении квадратичной функции:

a — старший коэффициент

b — второй коэффициент

с — свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции y=x^2 имеет вид:

Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции y=x^2 , составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент a=1 , то график квадратичной функции имеет ровно такую же форму, как график функции y=x^2 при любых значениях остальных коэффициентов.

График функции y=-x^2 имеет вид:

Для нахождения координат базовых точек составим таблицу:

Обратите внимание, что график функции y=-x^2 симметричен графику функции y=x^2 относительно оси ОХ.

Итак, мы заметили:

Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.

Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.

Второй параметр для построения графика функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции f(x) — это точки пересечения графика функции y=f(x) с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .

В случае квадратичной функции нужно решить квадратное уравнение .

Теперь внимание!

В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.

И здесь возможны три случая:

1. Если D<0 ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если a>0 ,то график функции выглядит как-то так:

2. Если D=0 ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. Если a>0 ,то график функции выглядит примерно так:

3. Если D>0 ,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:

$x_1={-b+sqrt{D}}/{2a}$ , $x_2={-b-sqrt{D}}/{2a}$

Если a>0 ,то график функции выглядит примерно так:

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный параметр графика квадратичной функции — координаты вершины параболы:

$x_0=-{b/{2a}}$

$y_0=-{D/{4a}}=y(x_0)$

Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.

И еще один параметр, полезный при построении графика функции — точка пересечения параболы с осью OY.

Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: y(0)=c .

То есть точка пересечения параболы с осью OY имеет координаты (0;c).

Итак, основные параметры графика квадратичной функции показаны на рисунке:

Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.

1. Функция задана формулой .

Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции

1. Направление ветвей параболы.

Так как a=2>0 ,ветви параболы направлены вверх.

2. Найдем дискриминант квадратного трехчлена

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.

Для того, чтобы найти их координаты, решим уравнение:

$x_1={-3+7}/4=1$ , $x_1={-3-7}/4=-2,5$

3. Координаты вершины параболы:

$x_0=-{b/{2a}}=-3/4 =-0,75$

$y_0=-{D/{4a}}=-49/8=-6,125$

4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.

Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:

Этот способ можно несколько упростить.

1. Найдем координаты вершины параболы.

2. Найдем координаты точек, стоящих справа и слева от вершины.

Воспользуемся результатами построения графика функции

Кррдинаты вершины параболы

$x_0=-{b/{2a}}=-3/4 =-0,75$

$y_0=-{D/{4a}}=-49/8=-6,125$

Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3

Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2

Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:

Нанесем эти точки на координатную плоскость и соединим плавной линией:

2. Уравнение квадратичной функции имеет вид — в этом уравнении x_0;y_0 — координаты вершины параболы

или в уравнении квадратичной функции a=1 , и второй коэффициент — четное число.

Построим для примера график функции .

Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно

сначала построить график функции ,
затем одинаты всех точек графика умножить на 2,
затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
а затем вдоль оси OY на 4 единицы вверх:

Теперь рассмотрим построение графика функции . В уравнении этой функции a=1 , и второй коэффициент — четное число.

Выделим в уравнении функции полный квадрат:

Следовательно, координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):

3. Уравнение квадратичной функции имеет вид y=(x+a)(x+b)

Построим для примера график функции y=(x-2)(x+1)

1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:

(х-2)(х+1)=0, отсюда

2. Координаты вершины параболы: $x_0={x_1+x_2}/2={2-1}/2=1/2$

$y_0=y(-1)=({1/2}-2)({1/2}+1)=-9/4=-2,25$

3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.

Нанесем эти точки на координатную плоскость и построим график:

График квадратичной функции.

Перед вами график квадратичной функции вида .

Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции от значения коэффициента ,
— сдвига графика функции вдоль оси от значения ,

— сдвига графика функции вдоль оси от значения
— направления ветвей параболы от знака коэффициента
— координат вершины параболы от значений и :

Скачать таблицу квадратичная функция

И.В. Фельдман, репетитор по математике.

Источник

Определение

Функция вида y=ax²+bx+c, где а, b, с – некоторые числа, причем, а≠0 число, х – переменная, называется квадратичной функцией.

Графиком квадратичной функции является парабола, она имеет вершину и две ветви, которые могут быть направлены либо вверх, либо вниз (рис.1). Красной точкой обозначена вершина параболы, из которой выходят ветви. Её координаты по графику – (3; –4). Направление ветвей зависит от значения коэффициента «а», то есть, если «а» – положительное число, то ветви направлены вверх; если число «а» – отрицательное, то ветви направлены вверх. На данном рисунке ветви направлены вверх, значит коэффициент «а» у формулы, которая задает эту функцию – положительное число. Коэффициент «с» показывает ординату (у) точки пересечения ветви параболы с осью у. Так, на рисунке №1 парабола пересекает ось у в точке (5;0), значит коэффициент с=5.

Рисунок №1.

Вершина параболы. Формула.

Чтобы найти координаты вершины параболы (х₀; у₀), надо воспользоваться формулой:

х₀=−b2a

для нахождения у₀ можно просто подставить значение х₀ в формулу данной функции y₀=ax²+bx+c вместо х.

Рассмотрим это на примере конкретно заданной функции.

Пример №1

Найти вершину параболы, заданной формулой у=2х² – 8х + 5.

Найдем, чему равны коэффициенты: а=2; b= – 8

Подставим их в формулу и вычислим значение х₀:

х₀=−b2a=82∙2=84=2

Теперь в заданную по условию формулу вместо х подставим найденное значение у₀=2∙2² – 8∙2 + 5=8 – 16 + 5= –3

Итак, мы нашли координаты вершины параболы: (2; –3).

Ответ: (2; –3).

Нули параболы

Значения х, при которых функция принимает значения, равные нулю, называются нулями функции. Другими словами, Значения абсцисс (х) точек пересечения ветвей параболы с осью х, называются нулями функции. На рисунке №1 точки координаты точек пересечения ветвей параболы с осью х следующие: (1;0) и (5;0). Значит, нули функции – это значения х, равные 1 и 5.

Рассмотрим, как найти нули функции не по рисунку, а по заданной формуле.

Пример №2

Найти нули функции у=х² +4х – 5

Так как нули функции это абсциссы точек пересечения ветвей параболы с осью х, то их координаты будут (х;0), то есть у=0. Значит, вместо у подставляем нуль в нашу формулу 0=х² +4х – 5 и получаем квадратное уравнение, решив которое, мы и найдем значения нулей функции:

х² +4х – 5=0

а=1, b=4, с= –5

D=b² – 4ac=4² – 4∙1∙(−5)=36

x=−b±√D2a

x=−4±√362; х₁=–5; х₂=1

Значит, нули функции равны –5 и 1

Ответ: –5 и 1

Примечание к заданию по нахождению нулей функции без графика

Если дискриминант уравнения отрицательный, значит, нулей функции нет, то есть парабола не пересекает ось х (вершина находится выше неё, если ветви направлены вверх и ниже, если ветви направлены вниз).

Рассмотрим нахождение соответствия рисунков парабол, расположенных в системе координат значениям а и с.

Пример №3

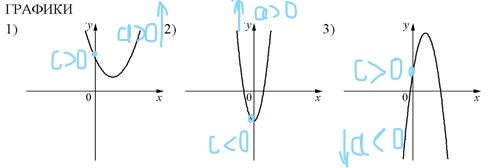
Для выполнения данного задания на соответствие необходимо сначала поработать с графиками, подписав на них, какими – отрицательными или положительными являются коэффициенты а и с.

Теперь можно выполнить соответствие:

Ответ: 231

Пример №4

Рассмотрим еще пример на соответствие

В данном задании рассмотрим коэффициенты в формулах и подчеркнем их: так, в формуле под буквой А коэффициент а=-2, т.е. отрицательный, значит, ветви направлены вниз, а это график под номером 2. В формулах под буквами Б и В первые и третьи коэффициенты одинаковые, значит, сравнить по рисунку их невозможно, следовательно, будем сравнивать по расположению вершины (справа или слева от оси у), а именно х₀.

Итак, найдем х₀ для формулы «Б»:

х₀=−b2a=−42∙2=−44=−1

Видим, что х₀ отрицательное, значит, вершина расположена слева от оси у, а это рисунок 3. Ну и осталось привести в соответствие В и 1.

Запишем в таблицу

Ответ: 231

Задание 11OM21R

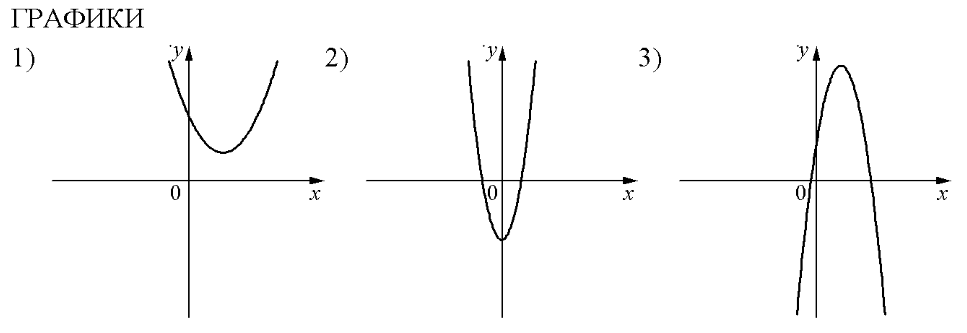
На рисунках изображены графики функций вида . Установите соответствие между знаками коэффициентов а и с и графиками функций.

КОЭФФИЦИЕНТЫ

А) a>0, с >0 Б) а<0; с>0 В) а>0, с<0

В таблице под каждой буквой укажите соответствующий номер.

Ответ:

Решение

На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a<0 – ветви вниз; а>0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с<0 – пересечение в отрицательном направлении).

Теперь поработаем с графиками и подпишем на каждом из них соответствующие коэффициенты.

Теперь расставим в соответствии с указанными коэффициентами:

А) a>0, с >0 – это график №1

Б) а<0; с>0 – это график №3

В) а>0, с<0 – это график №2

Ответ: 132

pазбирался: Даниил Романович | обсудить разбор

Задание OM1105o

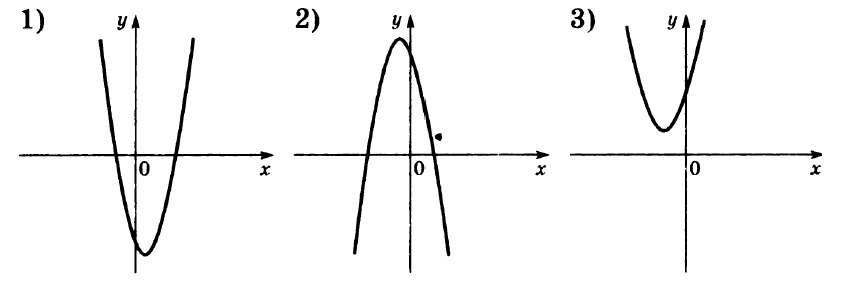
Установите соответствие между функциями и их графиками.

ФУНКЦИИ

А) у=–х²–4х–3 Б) у=–х²+4х–3 В) у=х²+4х+3

Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х² (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.

Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3<0 в обоих случаях.

Далее надежнее всего вычислить вершины оставшихся двух парабол из уравнений А и Б по формуле -b/2a. Видим, что случае А (- (-4)) / (2 • -1) = -2, следовательно, вершина левее оси Y, так как x₀ отрицателен, значит, А-1, а Б-2.

Ответ: 123

pазбирался: Даниил Романович | обсудить разбор

Задание OM1101o

На рисунках изображены графики функций вида

y = ax² + bx + c

Установите соответствие между знаками коэффициентов a и c и графиками функций.

Коэффициенты:

А) a > 0, c > 0

Б) a < 0, c > 0

В) a > 0, c < 0

Графики:

Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида

y = ax² + bx + c

Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a < 0, то ветви направлены вниз.

Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a < 0.

У первой и третьей ветви направлены вверх, то есть a > 0.

Далее мы смотрим, на что влияет коэффициент c.

Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:

если c > 0, то вершина параболы расположена выше оси х

если c < 0, то вершина параболы расположена ниже оси x

Так, у первой параболы c < 0, у второй и третьей c > 0.

Из всего вышеперечисленного можно найти ответ:

А) 3

Б) 2

В) 1

Ответ: 321

pазбирался: Даниил Романович | обсудить разбор

Даниил Романович | Просмотров: 10.7k

Источник

Home » 8 класс » Как построить параболу? Что такое парабола? Как решаются квадратные уравнения?

Урок: как построить параболу или квадратичную функцию?

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Парабола — это график функции описанный формулой ax²+bx+c=0.
Чтобы построить параболу нужно следовать простому алгоритму действий:

1 ) Формула параболы y=ax²+bx+c,
если а>0 то ветви параболы направленны вверх,
а<0 то ветви параболы направлены вниз.
Свободный член c эта точке пересекается параболы с осью OY;

2 ) Вершина параболы, ее находят по формуле x=(-b)/2a, найденный x подставляем в уравнение параболы и находим y;

3) Нули функции или по другому точки пересечения параболы с осью OX они еще называются корнями уравнения. Чтобы найти корни мы уравнение приравниваем к 0 ax²+bx+c=0;

Виды уравнений:

a) Полное квадратное уравнение имеет вид ax²+bx+c=0 и решается по дискриминанту;
b) Неполное квадратное уравнение вида ax²+bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0:
ax²+bx=0,
х(ax+b)=0,
х=0 и ax+b=0;
c)Неполное квадратное уравнение вида ax²+c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a);

Как решать квадратные уравнения посмотреть тут.

4) Найти несколько дополнительных точек для построения функции.

ПРАКТИЧЕСКАЯ ЧАСТЬ

И так теперь на примере разберем все по действиям:
Пример №1:
y=x²+4x+3
c=3 значит парабола пересекает OY в точке х=0 у=3. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2)²+4*(-2)+3=4-8+3=-1 вершина находится в точке (-2;-1)
Найдем корни уравнения x²+4x+3=0
По дискриминанту находим корни
a=1 b=4 c=3
D=b²-4ac=16-12=4
x=(-b±√(D))/2a
x₁=(-4+2)/2=-1
x₂=(-4-2)/2=-3

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=-2

х -4 -3 -1 0
у 3 0 0 3

Подставляем вместо х в уравнение y=x²+4x+3 значения
y=(-4)²+4*(-4)+3=16-16+3=3
y=(-3)²+4*(-3)+3=9-12+3=0
y=(-1)²+4*(-1)+3=1-4+3=0
y=(0)²+4*(0)+3=0-0+3=3
Видно по значениям функции,что парабола симметрична относительно прямой х=-2

Пример №2:
y=-x²+4x
c=0 значит парабола пересекает OY в точке х=0 у=0. Ветви параболы смотрят вниз так как а=-1 -1<0.
a=-1 b=4 c=0 x=(-b)/2a=(-4)/(2*(-1))=2 y=-(2)²+4*2=-4+8=4 вершина находится в точке (2;4)
Найдем корни уравнения -x²+4x=0
Неполное квадратное уравнение вида ax²+bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0.
х(-x+4)=0, х=0 и x=4.

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=2
х 0 1 3 4
у 0 3 3 0
Подставляем вместо х в уравнение y=-x²+4x значения
y=0²+4*0=0
y=-(1)²+4*1=-1+4=3
y=-(3)²+4*3=-9+13=3
y=-(4)²+4*4=-16+16=0
Видно по значениям функции,что парабола симметрична относительно прямой х=2

Пример №3
y=x²-4
c=4 значит парабола пересекает OY в точке х=0 у=4. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0)²-4=-4 вершина находится в точке (0;-4)
Найдем корни уравнения x²-4=0
Неполное квадратное уравнение вида ax² +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
x²=4
x₁=2
x₂=-2

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=0
х -2 -1 1 2
у 0 -3 -3 0
Подставляем вместо х в уравнение y= x²-4 значения
y=(-2)²-4=4-4=0
y=(-1)²-4=1-4=-3
y=1²-4=1-4=-3
y=2²-4=4-4=0
Видно по значениям функции,что парабола симметрична относительно прямой х=0

Подписывайтесь на канал на YOUTUBE, чтобы быть в курсе всех новинок и готовится с нами к экзаменам.

Источник

Функция вида , где называется квадратичной функцией.

График квадратичной функции – парабола.

Рассмотрим случаи:

I СЛУЧАЙ, КЛАССИЧЕСКАЯ ПАРАБОЛА

, то есть , ,

Для построения заполняем таблицу, подставляя значения x в формулу:

Отмечаем точки (0;0); (1;1); (-1;1) и т.д. на координатной плоскости (чем с меньшим шагом мы берем значения х ( в данном случае шаг 1 ), и чем больше берем значений х, тем плавнее будет кривая), получаем параболу:

Нетрудно заметить, что если мы возьмем случай , , , то есть , то мы получим параболу, симметричную относительно оси (ох). Убедиться в этом несложно, заполнив аналогичную таблицу:

II СЛУЧАЙ, «a» ОТЛИЧНО ОТ ЕДИНИЦЫ

Что же будет, если мы будем брать , , ? Как изменится поведение параболы? При парабола изменит форму, она “похудеет” по сравнению с параболой (не верите – заполните соответствующую таблицу – и убедитесь сами):

На первой картинке (см. выше) хорошо видно, что точки из таблицы для параболы (1;1), (-1;1) трансформировались в точки (1;4), (1;-4), то есть при тех же значениях ордината каждой точки умножилась на 4. Это произойдет со всеми ключевыми точками исходной таблицы. Аналогично рассуждаем в случаях картинок 2 и 3.

А при парабола «станет шире» параболы :

Давайте подитожим:

III СЛУЧАЙ, ПОЯВЛЯЕТСЯ «С»

Теперь давайте введем в игру (то есть рассматриваем случай, когда ), будем рассматривать параболы вида . Нетрудно догадаться (вы всегда можете обратиться к таблице), что будет происходить смещение параболы вдоль оси вверх или вниз в зависимости от знака :

IV СЛУЧАЙ, ПОЯВЛЯЕТСЯ «b»

Когда же парабола “оторвется” от оси и будет, наконец, “гулять” по всей координатной плоскости? Когда перестанет быть равным .

Здесь для построения параболы нам понадобится формула для вычисления вершины: $x_o=frac{-b}{2a}$ , .

Так вот в этой точке (как в точке (0;0) новой системы координат) мы будем строить параболу , что уже нам по силам. Если имеем дело со случаем , то от вершины откладываем один единичный отрезок вправо, один вверх, – полученная точка – наша (аналогично шаг влево, шаг вверх – наша точка); если имеем дело с , например, то от вершины откладываем один единичный отрезок вправо, два – вверх и т.д.

Например, вершина параболы :

$x_o=frac{4}{2}=2$ , . Теперь главное уяснить, что в этой вершине мы будем строить параболу по шаблону параболы , ведь в нашем случае.

При построении параболы после нахождения координат вершины очень удобно учитывать следующие моменты:

1) парабола обязательно пройдет через точку . Действительно, подставив в формулу x=0, получим, что . То есть ордината точки пересечения параболы с осью (оу), это . В нашем примере (выше), парабола пересекает ось ординат в точке , так как .

2) осью симметрии параболы является прямая $x=frac{-b}{2a}$ , поэтому все точки параболы будут симметричны относительно нее. В нашем примере, мы сразу берем точку (0; -2) и строим ей симметричную относительно оси симметрии параболы, получим точку (4; -2), через которую будет проходить парабола.

3) Приравнивая к , мы узнаем точки пересечения параболы с осью (ох). Для этого решаем уравнение . В зависимости от дискриминанта, будем получать одну (, $x=-frac{b}{2a}$ ), две (, $x_{1,2}=frac{-bpmsqrt{b^2-4ac}}{2a}$ ) или нИсколько () точек пересечения с осью (ох). В предыдущем примере у нас корень из дискриминанта – не целое число, при построении нам особо нет смысла находить корни, но мы видим четко, что две точки пересечения с осью (ох) у нас будут (так как ), хотя, в общем, это видно и без дискриминанта.

Итак, давайте выработаем

Алгоритм для построения параболы, если она задана в виде

1) определяем направление ветвей ( а>0 – вверх, a<0 – вниз)

2) находим координаты вершины параболы по формуле $x_o=frac{-b}{2a}$ , .

3) находим точку пересечения параболы с осью (оу) по свободному члену , строим точку, симметричную данной относительно оси симметрии параболы (надо заметить, бывает, что эту точку невыгодно отмечать, например, потому, что значение велико… пропускаем этот пункт…)

4) В найденной точке – вершине параболы (как в точке (0;0) новой системы координат) строим параболу . Если , то парабола становится у’же по сравнению с , если , то парабола расширяется по сравнению с

5) Находим точки пересечения параболы с осью (оу) (если они еще сами “не всплыли”), решая уравнение

Пример 1

Пример 2

Замечание 1. Если же парабола изначально нам задана в виде , где – некоторые числа (например, ), то построить ее будет еще легче, потому что нам уже заданы координаты вершины . Почему?

Возьмем квадратный трехчлен и выделим в нем полный квадрат: $ax^2+bx+c=a(x^2+frac{b}{a}x+frac{c}{a})=a((x^2+2frac{b}{2a}x+frac{b^2}{4a^2})-frac{b^2}{4a^2}+frac{c}{a})=a(x+frac{b}{2a})^2-frac{b^2}{4a}+c.$ Посмотрите, вот мы и получили, что $m=frac{-b}{2a}$ , $n=-frac{b^2}{4a}+c=y(frac{-b}{2a})$ . Мы с вами ранее называли вершину параболы , то есть теперь , .

Например, $y=-frac{1}{3}{(x+2)}^2+6$ . Отмечаем на плоскости вершину параболы , понимаем, что ветви направлены вниз, парабола расширена (относительно ). То есть выполняем пункты 1; 3; 4; 5 из алгоритма построения параболы (см. выше).

Замечание 2. Если парабола задана в виде, подобном этому (то есть представлен в виде произведения двух линейных множителей), то нам сразу видны точки пересечения параболы с осью (ох). В данном случае – (0;0) и (4;0). В остальном же действуем согласно алгоритму, раскрыв скобки.

Источник

С квадратными уравнениями мы уже встречались в курсе алгебры (7)-го класса.

Квадратное уравнение — это уравнение второй степени. Общий вид квадратного уравнения

ax2+bx+c=0

, где (а, b, с) могут быть любыми числами и

a≠0

Применяя знания о функциях и их графиках, которые нам известны, мы можем решать некоторые квадратные уравнения. Рассмотрим (5) графических способов решения квадратного уравнения

x2−2x−8=0

Первый способ

Построим график функции

x2−2x−8=0

1. Имеем: (a = 1), (b = -2),

x0=−b2a=1,y0=f(1)=12−2−8=−9

. Значит, вершиной параболы служит точка ((1; -9)), а осью параболы является прямая (x = 1).

2. Возьмём на оси (x) две точки, симметричные относительно оси параболы, например, точки (x = -2) и (x = 4). Имеем (f(-2) = f(4) = 0). Построим на координатной плоскости точки ((-2; 0)) и ((4; 0)).

3. Построим параболу по точкам ((-2; 0)), ((1; -9)), ((4; 0)).

Корни уравнения

x2−2x−8=0

— это первые координаты точек, в которых функция равна нулю (то есть в которых график пересекает ось (х)); поэтому имеем решение:

x1=−2;x2=4

Второй способ

Запишем уравнение в другом виде

x2=2x+8

. Рассмотрим функции в левой и правой частях уравнения

y=x2;y=2x+8

. В одной системе координат построим их графики и найдём точки пересечения графиков:

Получили две точки:: (C(- 2; 4)) и (D(4; 16)). Решением уравнения будут первые координаты точек (C) и (D), имеем:

x1=−2;x2=4

Преобразуем уравнение к виду

x2−8=2x

. Построим в одной системе координат графики функций:

y=x2−8;y=2x

и определим точки их пересечения:

Получили две точки: (C(-2; — 4)) и (D(4; 8)). Решением уравнения будут первые координаты точек (C) и (D), то есть

x1=−2;x2=4

Четвёртый способ

Преобразуем уравнение к виду

x2−2x+1−9=0

и далее

x2−2x+1=9→x−12=9

.
Построим в одной системе координат параболу

y=x−12

, прямую (y = 9) и определим точки их пересечения:

Получили две точки: (C(-2; 9)) и (D(4; 9)). Решением уравнения будут первые координаты точек (C) и (D), поэтому

x1=−2;x2=4

Пятый способ

Так как (x=0) не является корнем уравнения, то разделим левую и правую части на (x):

x−2−8x=0;x−2=8x.

Рассмотрим функции в левой и правой частях уравнения

y=8x

, (y = x — 2) и определим точки их пересечения:

Получили две точки: (A (-2; -4)) и (B(4; 2)). Решением уравнения будут первые координаты точек (A) и (B), следовательно,

x1=−2;x2=4

Источник