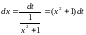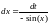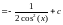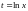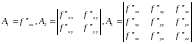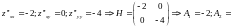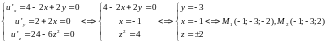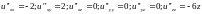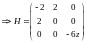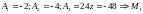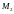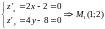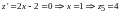Как найти точки экстремума функции интеграл

НАЙТИ ТОЧКИ ЭКСТРЕМУМА И ТОЧКИ ПЕРЕГИБА ФУНКЦИИ
Представим исходный интеграл, как сумму табличных интегралов и найдем функцию:
EQ i(;;f(t3;3)+t2)dt=i(;;f(t3;3))dx+i(;;t2)dt = EQ f(t4;12)+f(t3;3)+C

Подставим значения интеграла 0 и X, получим функцию
F(x) = EQ f(x4+4 x3;12)
Найдем точки экстремума
Необходимое условие экстремума функции одной переменной.
Уравнение f’0(x*) = 0 – это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки xс, в которых функция не возрастает и не убывает.
Достаточное условие экстремума функции одной переменной.
Пусть f0(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие:
f’0(x*) = 0
f”0(x*) > 0
то точка x* является точкой локального (глобального) минимума функции.
Если в точке x* выполняется условие:
f’0(x*) = 0
f”0(x*) < 0
то точка x* – локальный (глобальный) максимум.
Решение.
Находим первую производную функции:
EQ yʹ = f(x3;3)+x2
или
EQ yʹ = f(x2·(x+3);3)
Приравниваем ее к нулю:
EQ f(x3;3)+x2 = 0
x1 = 0
x2 = -3
Вычисляем значения функции
f(0) = 0
EQ f(-3) = -f(9;4)

Решение:

EQ fmin = -f(9;4), fmax = 0
Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную:
yʺ = x2+2·x
или
yʺ = x·(x+2)
Вычисляем:
yʺ(0) = 0=0 – значит точка x = 0 точка перегиба функции.
yʺ(-3) = 3>0 – значит точка x = -3 точка минимума функции.

Найдем точки перегиба
1. Находим интервалы возрастания и убывания. Первая производная.
EQ fʹ(x) = f(x3;3)+x2 или EQ fʹ(x)=f(x2·(x+3);3)
Находим нули функции. Для этого приравниваем производную к нулю
x2·(x+3) = 0
Откуда:
x1 = 0
x2 = -3

EQ (-∞ ;-3) EQ (-3; 0) EQ (0; +∞)
f ‘(x) < 0 f ‘(x) > 0 f ‘(x) > 0
функция убывает
функция возрастает
функция возрастает

В окрестности точки x = -3 производная функции меняет знак с (-) на (+). Следовательно, точка x = -3 – точка минимума.

2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная.
EQ fʺ(x) = f(x2;3)+f(2·x·(x+3);3) или fʺ(x) = x·(x+2)
Находим корни уравнения. Для этого полученную функцию приравняем к нулю.
x·(x+2) = 0
Откуда точки перегиба:
x1 = 0
x2 = -2

EQ (-∞ ;-2) EQ (-2; 0) EQ (0; +∞)
f ”(x) > 0 f ”(x) < 0 f ”(x) > 0
функция вогнута
функция выпукла
функция вогнута

математический-анализ — Найти точки экстремума функции

Алгоритм
решения:

1. Берем
   некоторое выражение за новую переменную
   t.

2. Заменяем
   dx
   по формуле:
   
   .

3. Подставляем
   в изначальное выражение.

4. Делаем
   обратную замену.

Советы:

1. Берите
   «средние» функции – не простые и не
   сложные (Пример: (kx+m)
   – простая функция,
   

   — сложная,
   

   — средняя).

2. Старайтесь
   брать за t
   так, чтобы в итоге все оставшиеся после
   замены выражения с х сократились с
   
   .

3. Ничего
   страшного если взяли за t
   не то выражение, возьмите другое.

Примеры:

11.9

.

Решение:

1. t=arctg(x)

2. 

3. 
   .

11.15

Решение:

1. 

2. 

3. 
   
   .

11.27

Решение:

1. 

2. 

3. 
   .

5.4 Определенный интеграл.

Определенный
интеграл высчитывается точно также как
и неопределенный, но в конце мы подставляем
значения пределов интегрирования по
четвертому свойству интегралов.

Пример:

11.54


=
.

5.5 Двойные интегралы.

Двойной
интеграл имеет вид:

,
где D
– пределы интегрирования по х и по у.

Чтобы
решить данный интеграл необходимо взять
поочередно определенный интеграл по
одной переменной, а затем по другой. При
этом стоит учитывать, что если пределы
интегрирования заданы константами, то
нет разницы, какой интеграл сначала
брать: по х или по у, но если один из
пределов задан через переменную, то
необходимо сначала взять интеграл с
переменной в пределах интегрирования.

Примеры:

18.1

Решение:

Запишем
в виде:

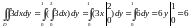
Т.е.
мы взяли сначала интеграл по х с пределами
интегрирования по х, а затем по у с
пределами интегрирования у.

18.2

Этот
пример осложнен тем, что один из пределов
интегрирования выражается через
переменную. Возьмем сначала интеграл
по у (т.к. его предел интегрирования
выражается через х), а затем по х:

18.12

Решение:

=

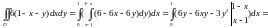
P.S.
Заметьте, что когда мы берем интеграл
от -6х по у, мы получаем -6ху, т.к. считаем,
что в этом случае х – константа (что
аналогично взятию производной от функции
нескольких переменных)

Глава VI. Точки экстремума функции нескольких переменных.

6.1 Локальный экстремум функции.

Для
того чтобы найти точки минимума/максимума
функции необходимо выполнить два
условия:

1. Необходимое
   условие. Находим все возможные критические
   точки.

Для
этого необходимо приравнять каждую
производную функции по всем переменным
к нулю, а затем решить систему.

1. Достаточное
   условие. Находим точки минимума и
   максимума.

Теперь
необходимо работать с матрицой Гессе: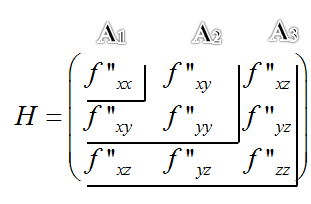

Во-первых,
необходимо найти все вторые производные
матрицы и заполнить таблицу.

Во-вторых,
если у нас

>0
либо

<0
в некой критической точке, то перед нами
точка минимума, а если знаки чередуются
(например,
),
то максимума. В ином случае – точки
экстремума нет.

.

P.S.
соответственно, если у нас функция не
от 3х переменных, а от двух, то матрица
Гессе будет 2х2 и


не будет вообще.

Пример:

16.1.

1)

.
Как видно у нас всего одна критическая
точка.

2)

8
max.

Ответ:
(1;2) – точка максимума.

16.17.

1. 

2. 
   
   .

Определим
сначала точку

:

—
max.

Теперь
точку

:
—
не является экстремумом.

Ответ:
(-1;-3;-2) – max.

6.2 Локальный условный экстремум.

Отличается
локальный условный экстремум, лишь
некоторыми нововведениями:

Примеры:

Решение:

1. Выразим
   х через у и подставим в z:

Теперь найдем критические точки, взяв
производную и приравняв ее к 0.

.

1. Можно
   решать через матрицу Гессе, а можно
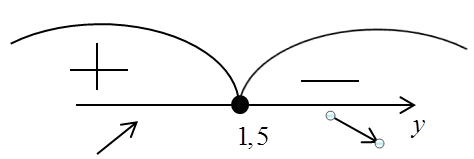
   вспомнить школьный курс:

Отсюда
видно, что в точке у=1,5 – максимум.

Ответ:

— max.

17.24.
Найдите
наибольшее и наименьшее значения функции

в области, ограниченной осями координат
и прямой

.

Решение:

Эта
задача отличается тем, что мы ищем
максимальное и минимальное значение
z,
а не только точки максимума минимума,
это значит, что нужно смотреть чему z
равняется на границах.

1. Найдем
   точки экстремума:
   

   и найдем значение z
   в этой точке:
   

2. Сделаем
   чертеж области:

И
найдем значения z
в указанных точках:

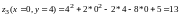
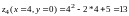
1. Найдем
   критические точки на прямых, ограничивающих
   область:

Ось
ОХ:
на оси х

,
значит на этой прямой

,
а значит:
.

Ось
ОУ:
на оси у х=0, значит на этой прямой

,
а значит:

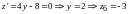
Прямая

:

.

1. Выбираем
   минимальное и максимальное значение
   z.

Ответ:

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #