Как найти точки касательной к двум окружностям

Поиск общих касательных к двум окружностям

Даны две окружности. Требуется найти все их общие касательные, т.е. все такие прямые, которые касаются обеих окружностей одновременно.

Описанный алгоритм будет работать также в случае, когда одна (или обе) окружности вырождаются в точки. Таким образом, этот алгоритм можно использовать также для нахождения касательных к окружности, проходящих через заданную точку.

Количество общих касательных

Сразу отметим, что мы не рассматриваем вырожденные случаи: когда окружности совпадают (в этом случае у них бесконечно много общих касательных), или одна окружность лежит внутри другой (в этом случае у них нет общих касательных, или, если окружности касаются, есть одна общая касательная).

В большинстве случаев, две окружности имеют четыре общих касательных.

Если окружности касаются, то у них будет три обших касательных, но это можно понимать как вырожденный случай: так, как будто две касательные совпали.

Более того, описанный ниже алгоритм будет работать и в случае, когда одна или обе окружности имеют нулевой радиус: в этом случае будет, соответственно, две или одна общая касательная.

Подводя итог, мы, за исключением описанных в начале случаев, всегда будем искать четыре касательные. В вырожденных случаях некоторые из них будут совпадать, однако тем не менее эти случаи также будут вписываться в общую картину.

Алгоритм

В целях простоты алгоритма, будем считать, не теряя общности, что центр первой окружности имеет координаты . (Если это не так, то этого можно добиться простым сдвигом всей картины, а после нахождения решения — сдвигом полученных прямых обратно.)

Обозначим через и радиусы первой и второй окружностей, а через — координаты центра второй окружности (точка отлична от начала координат, т.к. мы не рассматриваем случае, когда окружности совпадают, или одна окружность находится внутри другой).

Для решения задачи подойдём к ней чисто алгебраически. Нам требуется найти все прямые вида , которые лежат на расстоянии от начала координат, и на расстоянии от точки . Кроме того, наложим условие нормированности прямой: сумма квадратов коэффициентов и должна быть равна единице (это необходимо, иначе одной и той же прямой будет соответствовать бесконечно много представлений вида ). Итого получаем такую систему уравнений на искомые :

Чтобы избавиться от модулей, заметим, что всего есть четыре способа раскрыть модули в этой системе. Все эти способы можно рассмотреть общим случаем, если понимать раскрытие модуля как то, что коэффициент в правой части, возможно, умножается на .

Иными словами, мы переходим к такой системе:

Введя обозначения и , мы приходим к тому, что четыре раза должны решать систему:

Решение этой системы сводится к решению квадратного уравнения. Мы опустим все громоздкие выкладки, и сразу приведём готовый ответ:

Итого у нас получилось решений вместо . Однако легко понять, в каком месте возникают лишние решения: на самом деле, в последней системе достаточно брать только одно решение (например, первое). В самом деле, геометрический смысл того, что мы берём и , понятен: мы фактически перебираем, по какую сторону от каждой из окружностей будет прямая. Поэтому два способа, возникающие при решении последней системы, избыточны: достаточно выбрать одно из двух решений (только, конечно, во всех четырёх случаях надо выбрать одно и то же семейство решений).

Последнее, что мы ещё не рассмотрели — это как сдвигать прямые в том случае, когда первая окружность не находилась изначально в начале координат. Однако здесь всё просто: из линейности уравнения прямой следует, что от коэффициента надо отнять величину (где и — координаты первоначального центра первой окружности).

Реализация

Опишем сначала все необходимые структуры данных и другие вспомогательные определения:

Тогда само решение можно записать таким образом (где основная функция для вызова — вторая; а первая функция — вспомогательная):

Две окружности на плоскости.
Общие касательные к двум окружностям

Взаимное расположение двух окружностей

Взаимное расположение на плоскости двух окружностей радиусов r₁ и r₂ с центрами O₁ и O₂ определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов

r₁ – r₂ лежит внутри другой

Расстояние между центрами окружностей меньше разности их радиусов

d r₁ и r₂ с центрами O₁ и O₂ определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов

r₁ – r₂ лежит внутри другой

Расстояние между центрами окружностей меньше разности их радиусов

d r₁ и r₂ с центрами O₁ и O₂ определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей меньше разности их радиусов

d внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также
две общих внешних касательных. Других общих касательных нет.

Каждая из окружностей лежит вне другой

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

Фигура	Рисунок	Свойства
Две окружности на плоскости
Каждая из окружностей лежит вне другой
Внешнее касание двух окружностей
Внутреннее касание двух окружностей
Окружности пересекаются в двух точках
Каждая из окружностей лежит вне другой
Внешнее касание двух окружностей
Внутреннее касание двух окружностей
Окружности пересекаются в двух точках
Каждая из окружностей лежит вне другой
Расстояние между центрами окружностей больше суммы их радиусов
Внешнее касание двух окружностей
Расстояние между центрами окружностей равно сумме их радиусов
Внутреннее касание двух окружностей
Окружности пересекаются в двух точках
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой
Внутренняя касательная к двум окружностям
Внутреннее касание двух окружностей
Окружности пересекаются в двух точках
Внешнее касание двух окружностей

Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

Внешняя касательная к двум окружностям

Внутренняя касательная к двум окружностям

Внутреннее касание двух окружностей

Окружности пересекаются в двух точках

Внешнее касание двух окружностей

Каждая из окружностей лежит вне другой

Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

Формулы для длин общих касательных и общей хорды двух окружностей

Внешняя касательная к двум окружностям

Внутренняя касательная к двум окружностям

Внутреннее касание двух окружностей

Окружности пересекаются в двух точках

Внешнее касание двух окружностей

Каждая из окружностей лежит вне другой

Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле

Фигура	Рисунок	Формула
Внешняя касательная к двум окружностям
Внутренняя касательная к двум окружностям
Общая хорда двух пересекающихся окружностей

Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле

Внешняя касательная к двум окружностям

Внутренняя касательная к двум окружностям

Общая хорда двух пересекающихся окружностей

Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Внешняя касательная к двум окружностям

Внутренняя касательная к двум окружностям

Общая хорда двух пересекающихся окружностей

Длина общей хорды двух окружностей вычисляется по формуле Доказательства формул для длин общих касательных и общей хорды двух окружностей Утверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Общие касательные Выясним сколько общих касательных имеют две окружности и как эти общие касательные могут быть расположены. Если две окружности не пересекаются и окружность меньшего радиуса лежит внутри окружности большего радиуса, то они не имеют общих касательных. В другом случае не пересекающиеся окружности имеют четыре общие касательные. внешние общие касательные При этом, если обе окружности лежат по одну сторону от касательной (в одной полуплоскости), то такая касательная называется внешней. внутренние общие касательные Если окружности лежат по разные стороны от общей касательной (в разных полуплоскостях), то такая касательная называется внутренней. Если две окружности имеют внутреннее касание, то у них есть одна общая касательная. При внешнем касании две окружности имеют три общие касательные. Две пересекающиеся окружности имеют две общие касательные. источники: http://www.resolventa.ru/demo/him/demohim.htm Общие касательные

mat:geom:circle-angles

При
вычерчивании контуров предметов
сравнительно часто приходится строить
общие касательные к двум дугам окружностей.
Общая касательная к двум окружностям
может быть внешней, если обе окружности
расположены с одной стороны от нее, и
внутренней, если окружности расположены
с разных сторон касательной.

Построение
общей внешней касательной к двум
окружностям радиусами R и r (рисунок
47). Из центра окружности большего радиуса
– точкиO₁
описывают окружность радиусомR
– r(рисунок
47, а). Находят середину отрезкаO₂O₁
– точкуO₃и из нее проводят вспомогательную
окружность радиусомO₃O₂
илиO₃O_1.Обе проведенные окружности пересекаются
в точкахA иВ. ТочкиO₁
иB соединяют
прямой и в пересечении ее с окружностью
радиусомR
определяют точку касанияD
(рисунок 47, б). Из точкиO₂параллельно прямойO₁D
проводят линию до пересечения с
окружностью радиусомrи получают
вторую точку касанияC.
ПрямаяCDявляется
искомой касательной. Так же строится
вторая общая внешняя касательная к этим
окружностям (прямаяEF).

а
б

Рисунок
47

Построение
общей внутренней касательной к двум
окружностями радиусов R и r (рисунок
48). Из центра любой окружности, например:
точкиO₁,
описывают окружность радиусомR
+r (рисунок
48, а). Разделив отрезокO₂O₁
пополам, получают точкуO₃.
Из точкиO₃как из центра описывают вторую
вспомогательную окружность радиусомO₃O₂
= O₃О₁
и отмечают точки A
и
В
пересечения вспомогательных окружностей.
Соединив прямой точки A
и
O₁
(рисунок
48, б), в пересечении ее с окружностью
радиуса R
получают
точку касания D.
Через центр окружности радиуса r
проводят
прямую, параллельную прямой O₁D,
и
в пересечении ее с заданной окружностью
определяют вторую точку касания С.
Прямая CD
– внутренняя
касательная к заданным окружностям.
Аналогично строится и вторая касательная
EF.

а
б

Рисунок
48

3.3 Сопряжения с помощью дуги окружности

3.3.1 Сопряжение двух прямых дугой окружности

Все
задачи на сопряжение дугой могут быть
сведены к двум видам. Сопряжение
осуществляется либо заданным радиусом
сопрягающей дуги, либо через точку,
заданную на одной из сопрягаемых линий.
В том и другом случаях необходимо
построить центр сопрягающей дуги.

Сопряжение
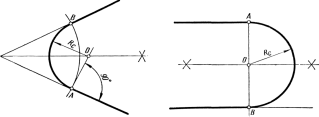
двух пересекающихся прямых дугой
заданным радиусом R_c
(рисунок 49, а). Так как сопрягающая
дуга должна касаться заданных прямых,
то центр ее должен быть удален от каждой
прямой на величину равную радиусуR_c.
Сопряжение строят так. Проводят две
прямые, параллельные заданным и удаленные
от них на величину радиусаR_cи в пересечении этих прямых отмечают
точкуO – центр
сопрягающей дуги. Из точкиОопускают перпендикуляр на каждую из
заданных прямых. Основания перпендикуляров
– точкиA иB – являются
точками касания сопрягающей дуги. Такое
построение сопряжения справедливо для
двух пересекающихся прямых, составляющих
любой угол. Для сопряжения сторон прямого
угла можно воспользоваться также
способом, указанным на рисунке 49, б.

а
б

Рисунок
49

Сопряжение
двух пересекающихся прямых, на одной
из которых задана точка касания А
сопрягающей дуги (рисунок 50).
Известно, что геометрическим местом
центров дуг, сопрягающих две пересекающиеся
прямые, является биссектриса угла,
образованного этими прямыми. Поэтому,
построив биссектрису угла, из точки
касанияA
восстанавливают
перпендикуляр к прямой до пересечения
его с биссектрисой и отмечают точку O
– центр
сопрягающей дуги. Опустив из точки О
перпендикуляр на другую прямую, получают
вторую точку касания В и радиусом R_c=
OA = OB
осуществляют сопряжение двух прямых,
на одной из которых была задана точка
касания.

Сопряжение
двух параллельных прямых дугой, проходящей
через заданную точку касания А (рисунок
51). Из точкиA
восставляют перпендикуляр к заданным
прямым и на пересечении его со второй
прямой отмечают точкуB.
ОтрезокAB делят
пополам и получают точкуО–
центр сопрягающей дуги радиусом.

Рисунок
50 Рисунок 51

Угол между касательной и хордой

Угол между касательной и хордой равен половине градусной меры дуги, которая находится внутри угла.

Прежде всего: как это понимать? Подробнее о том, что такое «градусная мера дуги», написано в теме «Окружность. Вписанный угол».

Здесь напомним только, что в дуге столько же градусов, сколько в центральном угле, заключающем эту дугу. 

То есть «градусная мера дуги» – это «сколько градусов в центральном угле» – и всё!

Ну вот, как говорит Карлсон, продолжаем разговор. Рисуем ещё раз теорему об угле между касательной и хордой.

Смотри, хорда ( displaystyle AB) разбила окружность на две дуги. Одна дуга находится ВНУТРИ угла ( displaystyle BAC), а другая дуга – внутри угла ( displaystyle BAD).

И теорема об угле между касательной и хордой говорит, что ( displaystyle angle CAB) равен ПОЛОВИНЕ угла ( displaystyle AOB), ( displaystyle angle DAB) равен ПОЛОВИНЕ большего (на рисунке — зеленого) угла ( displaystyle AOB).

При чем же тут тот факт, что радиус, проведенный в точку касания, перпендикулярен касательной?

Сейчас и увидим. ( displaystyle OA) – радиус, ( displaystyle AC) – касательная.

Значит, ( displaystyle angle OAC=90{}^circ ).

Поэтому:( displaystyle angle 1=90{}^circ -angle 4).

Но ( displaystyle angle 2=angle 1) (( displaystyle OA) и ( displaystyle OB) – радиусы)( displaystyle angle 2=90{}^circ -angle 4).

И осталось вспомнить, что сумма углов треугольника ( displaystyle AOB) равна ( displaystyle 180{}^circ ).

Пишем:

Короче:

Здорово, правда? И самым главным оказалось то, что ( displaystyle angle OAC=90{}^circ ).

Равенство отрезков касательных

Задумывался ли ты над вопросом «а сколько касательных можно провести из одной точки к одной окружности»? Вот, представь себе, ровно две! Вот так:

А ещё более удивительный факт состоит в том, что:

Отрезки касательных, проведённых из одной точки к одной окружности, равны.

То есть, на нашем рисунке, ( displaystyle AB=AC).

И для этого факта тоже самым главным является то, что радиус, проведённый в точку касания, перпендикулярен касательной.

Вот, убедись.

Проведём радиусы ( displaystyle OB) и ( displaystyle OC) и соединим ( displaystyle O) и ( displaystyle A).

( displaystyle OB) – радиус.

( displaystyle AB) – касательная, значит, ( displaystyle OBbot AB).
Ну, и так же ( displaystyle OCbot AC).

Получилось два прямоугольных треугольника ( displaystyle AOB) и ( displaystyle AOC), у которых:

( displaystyle Rightarrow Delta AOB = Delta AOC)

(заглядываем в тему «Прямоугольный треугольник«, если не помним, когда бывают равны прямоугольные треугольники).

Но раз ( displaystyle Delta AOB=Delta AOC,) то( displaystyle AB=AC). УРА!

И ещё раз повторим – этот факт тоже очень важный:

Отрезки касательных, проведённых из одной точки, – равны.

И есть ещё один факт, который мы здесь не будем доказывать, но он может оказаться тебе полезен при решении задач.

Для любой прямой ( displaystyle AD), пересекающей окружность,( displaystyle ADcdot AC=A{{B}^{2}}), где ( displaystyle AB) – отрезок касательной.

Хитроумными словами об этом говорят так:

«Квадрат длины отрезка касательной равен произведению секущей на её внешнюю часть».

Страшно? Не бойся, помни только, что в буквах это:

План урока:

Понятие окружности и круга

Касательная к окружности

Взаимное расположение двух окружностей

Понятие окружности и круга

Тарелки, шины, колеса и монеты – все эти предметы имеют одинаковую форму, их называют круглыми. Этот термин понятен каждому, однако в геометрии каждое понятие надо строго определять. Дадим строгое определение понятию окружности:

Та точка, от которой равноудалены все точки, образующие окруж-ть, именуется центром окружности. Обратите внимание, что сам центр частью окружности НЕ считается. Расстояние, отделяющее точки окруж-ти от ее центра, именуют радиусом окружности. Получается, что для построения окруж-ти достаточно знать только ее радиус и центр. Выглядит она так:

Для построения окруж-ти используется специальный инструмент – циркуль. Он представляет собой два длинных стрежня, которые соединены шарниром. На конце одного стержня находится иголка, на конце другого – грифель карандаша или иной пишущий предмет. Сначала необходимо выставить расстояние между концами стержней – оно будет равно радиусу окруж-ти. Потом иголку ставят в центр будущей окруж-ти, после чего поворачивают циркуль так, что его пишущий конец оставил на бумаге след:

Отрезок, соединяющий две точки окруж-ти, именуется хордой. Хорда, проходящая через центр окруж-ти, именуется диаметром окружности.

Особо отметим, что сам диаметр также считается хордой.

Непосредственно из определения окруж-ти вытекает первое важное её свойство – все радиусы, построенные в одной окруж-ти, равны друг другу.

Так как центр окруж-ти делит ее диаметр на два отрезка, каждый из которых – это радиус, то диаметр окружности равен двум ее радиусам:

Традиционно диаметр обозначается буквой D, а радиус – буквой R. Получается, что справедлива формула:

D = 2R

Очевидно, что диаметр длиннее, чем любая другая хорда окружности, не являющаяся диаметром. Докажем это. Пусть хорда AВ не проходит через О, центр окруж-ти (он почти всегда обозначается именно этой буквой). Тогда можно построить ∆AВО:

Мы знаем про неравенство треугольника, согласно которому любая сторона треугольника меньше суммы двух других. В данном случае можно записать, что

AB < OA + OB

ОА и ОВ – радиусы. Обозначив их буквой R, получим, что

AB < R + R

AB < 2R

Величина 2R как раз равна диаметру, то есть

AB < D

ч. т. д.

Ещё раз сформулируем простейшие свойства окруж-ти:

Задание. AВ и СD – диаметры окружности. Верно ли, что BD = АС?

Решение. Выполним построение по условию задачи:

Заметим, что отрезки ОА, ОВ, ОС и ОD одинаковы, ведь они являются радиусами одной окруж-ти:

В итоге получается, что у ∆АОС и ∆ВОD одинаковы две стороны образованный ими угол. Тогда по первому признаку равенства треуг-ков они равны:

Отсюда вытекает, что одинаковы и отрезки АС и BD.

Ответ: верно.

Задание. AВ и CD – диаметры, проходящие через точку О. Длина ВС составляет 13, а АВ – 16. Вычислите периметр ∆АОD.

Решение.

Чтобы вычислить периметр, нужно узнать длины всех сторон треугольника, то есть AD, OD и ОА. Как и в предыдущей задаче, хорды ВС и AD оказываются одинаковыми, так как ∆ОВС и ∆ОАD равны:

AB = DC = 13

Нам известен отрезок AВ, который является диаметром. Поделив его на два, узнаем и радиус:

Задание. Точки А и В на окруж-ти выбраны так, что радиусы АО и ВО пересекаются под углом 40°. Найдите ∠ОВА.

Решение.

Заметим, что в ∆ОAВ есть две одинаковые стороны. Это ОА и ОВ, которые являются радиусами и потому одинаковы. Значит, ∆ОAВ равнобедренный, причем AВ – это его основание. Но тогда углы при основании должны быть одинаковы:

Задание. Угол между радиусом ОА и хордой AВ составляет 60°. AВ имеет длину 29. Каков радиус окруж-ти?

Решение. Исследуем ∆ОAВ. ОВ и ОА являются радиусами одной длины, поэтому он равнобедренный. Тогда ∠ОAВ и ∠ОВА одинаковы:

В итоге получили, что у ∆ОAВ все углы составляют по 60°. Из этого вытекает, что он равносторонний, то есть все его стороны, в частности AВ и ОВ, одинаковы:

OB = AB = 29

Ответ: 29.

Выделяют ещё несколько элементов окруж-ти. Всякие две точки окруж-ти разбивают ее на две кривые линии, которые именуются дугами окружности. Для обозначения дуг используется символ ⋃, после которого пишутся три буквы. Первая и третья буквы указывают на концы дуги, а вторая буква – на какую-либо точку между ними:

Но иногда дугу обозначают только двумя буквами, указывая только ее концы: ⋃AВ. Так поступают, когда ясно, о какой именно из двух дуг идет речь.

Часть плоскости, ограниченная окруж-тью, именуется кругом. То есть окруж-ть – это лишь линия, граница круга, имеющая длину, не имеющая площади. Круг же, наоборот, обладает какой-то площадью, но не имеет длины. На рисунке точка А принадлежит кругу, но НЕ принадлежит окруж-ти:

Очевидно, что любая точка внутри окруж-ти ближе к ее центру, чем точки на самой окруж-ти. Действительно, через центр O и точку A внутри окруж-ти можно построить прямую, которая пересечет окруж-ть в некоторой точке B:

Ясно, что

OB = OA + AB

Значит, отрезок ОВ длиннее ОА. Точки на самой окруж-ти обычно также считают частью круга. Таким образом, круг представляет собой множество точек, удаленных от некоторого центра не более чем на величину заданного радиуса.

Круг можно разделить на две части, либо проведя хорду, либо построив два радиуса. В первом случае образуется фигура, которую называют сегментом. Во втором случае образуется сектор окружности:

Касательная к окружности

Возможно три варианта расположения прямой и окруж-ти относительно друг друга. Если расстояние между центром окруж-тии прямой меньше радиуса, то у них обязательно будут две общие точки. В таком ситуации прямую именуют секущей:

Если же расстояние между прямой и центром окруж-ти больше радиуса, то тогда никаких точек пересечения не будет:

Наконец, возможен особый случай, когда расстояние между прямой и центром окруж-ти в точности равно радиусу. Тогда окруж-ть и прямая будут иметь только одну общую точку. Прямую же в такой ситуации называют касательной к окружности:

Общая точка касательной и окруж-ти именуется точкой касания. Сформулируем одну важную теорему, которая представляет собой основное свойство касательной:

Действительно, предположим, что это утверждение ошибочно, и радиус может образовать с касательной угол, отличный от 90°. Тогда из центра окруж-ти опустим перпендикуляр на прямую, и он упадет на нее в точке B, не совпадающую с точкой касания A. Далее от В на прямой AВ отложим отрезок ВA₁, который будет равен AВ.

Получается, что в ∆АОА₁ ОВ одновременно высота (ведь ОВ – это перпендикуляр) и медиана (ведь AВ = ВА₁). Но это возможно лишь в том случае, если ∆АОА₁ – равнобедренный, то есть АО = А₁О. Отсюда вытекает, что точка А₁ находится на том же расстоянии от О, что и точка А, поэтому она также должна принадлежать окруж-ти. Но тогда прямая имеет уже 2 общие точки с окруж-тью, А и А₁, а потому по определению она уже не касательная, ч. т. д.

Оказывается, верна и обратная теорема, которая представляет собой признак касательной.

Действительно, пусть прямая, описанная в теореме, не является касательной. Тогда она имеет не одну, а 2 общие точки с окруж-тью, которые можно обозначить буквами А и А₁:

Заметим, что ∆АОА₁ равнобедренный, так как две его стороны, ОА и ОА₁, представляют собой одинаковые радиусы. Тогда и углы при его основании одинаковы. Если один из них составляет 90°, то и другой также будет составлять 90°. Однако треугольник с двумя прямыми углами не может существовать. Полученное противоречие показывает, что прямая должна быть не секущей, а касательной, ч. т. д.

Из каждой точки плоскости, не принадлежащей кругу, можно провести не одну, а сразу 2 касательных к окруж-ти:

Докажем, что образовавшиеся отрезки AВ и АС (их называют отрезками касательных) одинаковы. Посмотрим на ∆АОС и ∆АОВ. Они прямоугольные, ведь

по свойству касательной. Также у них общая гипотенуза АО и одинаковые катеты ОС и ОВ, которые одинаковы как радиусы одной окруж-ти. Получается, что ∆АOС и ∆АOВ равны, AВ = АС. Также можно запомнить, что и ∠OАС = ∠OAВ, то есть OА оказывается биссектрисой ∠СAВ.

Задание. Угол между двумя касательными к одной окруж-ти составляет 39°.Каков угол между радиусами, построенными к точкам касания?

Решение. Обозначим точки касания буквами С и B, а точку их пересечения буквой А:

Теперь посмотрим на четырехугольник AВОС. Сумма углов в нем, как и во всяком выпуклом четырехугольнике, составляет 360°. По условию известен ∠A, а ∠B и ∠C составляют по 90°. Зная три угла, легко найдем и четвертый:

Задание. Радиус окруж-ти ОМ делит хорду AB пополам. Докажите, что эта хорда будет параллельна касательной к окружности в точке С.

Решение: Обозначим точку касания как С, а середину хорды буквой Н:

Проведем из центра радиусы к точкам А и В. В результате мы получим ∆ОAВ, который оказывается равнобедренным, ведь радиусы ОА и ОВ одинаковы. Так как радиус ОС делит AВ пополам, то он является медианой. Но в равнобедренном треуг-ке медиана, проведенная к основанию, ещё и высота, поэтому прямые ОС и AВ перпендикулярны. В свою очередь касательная также перпендикулярна радиусу. Получается, что хорда и касательная одновременно перпендикулярны третьей прямой, значит, они параллельны, ч. т. д.

Задание. Касательная проходит через точку А окруж-ти. Хорда AВ равна радиусу окруж-ти. Какой угол образуют хорда и касательная?

Решение. Соединим точки А и В с центром окруж-ти:

Хорда по условию имеет такую же длину, как и радиусы, поэтому в ∆ОAВ оказывается три одинаковых стороны. Следовательно, он равносторонний, а у него все углы составляют по 60°. В частности,

∠BAO = 60°

Нам надо найти ∠СAВ. ∠САО должен быть прямым как угол между радиусом и касательной, но ∠САО также является суммой ∠СAВ и ∠ВАО, что позволяет найти ∠СAВ:

Задание. В окруж-ти проведены радиус ОВ длиной 5 и перпендикулярная ему хорда АС, которая отсекает от радиуса отрезок BD длиной 1. Какова длина этой хорды?

Решение:

Сначала можно найти длину OD:

OD = OB — BD = 5 -1 = 4

Теперь исследуем ∆АОD. Он прямоугольный, при этом мы знаем длину его гипотенузы ОА и катет OD. Значит, по теореме Пифагора можно найти и второй катет:

Так как ∆ОАС – равнобедренный, то высота OD– это также и медиана, поэтому DC = AВ = 3. (Примечание: вообще всегда хорда, перпендикулярная диаметру, делится им на одинаковых отрезка). Тогда

AC = DC + AB = 3 + 3 = 6

Ответ: 6.

Задание. Через центр окруж-ти О проходит секущая ОА, а AВ – касательная. Найдите величину радиуса ОВ, если AВ = 12, АО = 13.

Решение. Выполним построение:

Ясно, что угол между отрезками AВ и ОВ должен быть прямым по свойству касательной. Тогда ∆АОВ оказывается прямоугольным, и для него справедлива теорема Пифагора. С ее помощью легко найдем неизвестный нам катет ОВ:

Задание. Длина хорды окружности составляет 72, и находится эта хорда на расстоянии 27 от центра окруж-ти. Каков диаметр этой окруж-ти?

Решение. Ещё раз напомним, что расстояние между точкой и некоторым отрезком – это длина перпендикуляра, опущенного из этой точки на отрезок. С учетом этого построим рисунок:

Здесь отрезок ОН – это как раз перпендикуляр к хорде AВ. Так как ОА и ОВ – радиусы, то ∆ОAВ – равнобедренный, и ОН в нем – это высота, проведенная к основанию. Значит, она является и медианой тоже, то есть делит AВ пополам. Это позволяет найти АН:

AH = AB/2 = 72/2 = 36

∆АОН – прямоугольный, и в нем нам известны оба катета. По теореме Пифагора можно найти и гипотенузу ОА:

Отрезок АО является радиусом. Нам надо в ответе указать диаметр. Диаметр вдвое длиннее радиуса, то есть он равен 45•2 = 90.

Ответ:90.

Задание. Хорда МК образует с касательной КH угол 83°. Найдите угол между этой хордой и радиусом ОМ.

Решение. 

Заметим, что ∠ОКН составляет 90°, так как он образован касательной НК и радиусом ОК. Но он состоит из двух углов, ∠МКН и ∠МКО. Так как ∠МКН известен, то можно найти и ∠МКО:

Задание. Точка А находится на расстоянии 8 от центра окруж-ти. Если из точки А провести касательные к окруж-ти, то они образуют угол в 60°. Каков радиус окруж-ти?

Решение:

По условию ∠ВАС = 60°. ОА разбивает этот угол пополам, то есть

∠OAB = ∠OАС = 30°

Посмотрим на ∆AВО. Он прямоугольный, и ∠ОAВ = 30°. Известно, что в прямоугольном треугольнике с углом 30° напротив этого угла находится катет, который вдвое короче гипотенузы. Но гипотенуза в ∆AВО – это ОА, значит, катет ОВ в 2 раза меньше:

OB = OA/2 = 8/2 = 4

ОВ – это и есть искомый нами радиус окруж-ти.

Ответ: 4.

Взаимное расположение двух окружностей

Касаться друг друга могут не только прямая и окруж-ть, но и две окруж-ти. Это значит, что у них есть ровно одна общая точка. Докажем важное утверждение:

Действительно, предположим обратное, что окруж-ти с центрами в точках О₁ и О₂ касаются в точке К, но точки О₁, О₂ и К НЕ лежат на одной прямой. Тогда можно построить ∆О₁КО₂, причем отрезки О₁К и О₂К будут радиусами соответствующих окруж-тей:

Отложим от точки О₁ луч так, чтобы он образовывал с О₁О₂ угол, равный ∠О₂О₁K, но не совпадал с лучом ОК. Аналогично отложим луч и от О₂ так, чтобы он образовал с О₂О₁ угол, равный ∠О₁О₂К. Эти лучи пересекутся в некоторой точке M:

У ∆О₁О₂К и ∆О₁О₂М есть общая сторона О₁О₂, а прилегающие к ней углы одинаковы. По 2-ому признаку равенства треугольников они оказываются равными. То есть

O₁K = O₁M = R₁

O₂K = O₂M = R₂

Выходит, что точка М лежит на том же расстоянии от О₁, что и K. Значит, по определению окруж-ти, она принадлежит окруж-ти с центром в О₁ и радиусом R₁. Аналогично М лежит на том же расстоянии от О₂, что и К. Значит, она также принадлежит и второй окруж-ти, с центром в О₂. То есть М принадлежит обеим окруж-тям, а значит, является их общей точкой. Но тогда оказывается, что у окруж-тей уже есть сразу две общие точки, М и К, а изначально мы предположили, что они только касаются, то есть имеют 1 общую точку. Противоречие означает, что точки О₁, О₂ и K обязательно должны лежать на одной прямой, ч. т. д.

Очевидно, что когда три точки лежат на прямой, то каждая из низ либо лежит между двумя другими, либо находится «с краю», то есть по одну сторону от двух других точек. В связи с этим возможны два принципиально различных случая касания окружностей. В первом случае точка касания находится между центрами окруж-тей. Тогда говорят, что окруж-ти касаются внешним образом:

Важно заметить, что при внешнем касании двух окружностей расстояние между их центрами равно сумме их радиусов:

O₁O₂ = O₁K + O₂K

Во втором случае одна из окруж-тей находится внутри другой, в таком случае говорят, что окруж-ти касаются внутренним образом. Такое расположение окруж-тей означает, что точка касания находится «с краю»:

При внутреннем касании двух окружностей расстояние между их центрами – это уже разность их радиусов:

O₁O₂ = O₁K — O₂K

Заметим, что если в точке касания двух окружностей провести ещё и касательную прямую, то она, во-первых, окажется общей касательной для обоих окруж-тей, а во-вторых, будет перпендикулярна линии, соединяющей их центра:

Однако окруж-ти (не обязательно касающиеся друг друга) могут иметь и другие общие касательные, которые соприкасаются с ними в различных точках. Важно отличать внешние и внутренние касательные. Если обе окруж-ти лежат по одну сторону от касающейся их прямой, то эту прямую именуют внешней касательной. Обычно можно построить сразу две таких внешних касательных:

Однако касательную можно провести и так, что окруж-ти окажутся по разные стороны от нее. В этом случае ее называют уже внутренней касательной:

Задание. Две окруж-ти соприкасаются в точке К. Построена общая касательная к этим окруж-тям, которая касается первой окруж-ти в точке А, а второй – в точке В. Длины хорд АК и ВК равны 15 и 8. Найдите длину отрезка AВ.

Решение:

Решение. Выполним дополнительное построение – проведем общую касательную к окруж-тям через точку К:

Получается, что АМ и КМ – это отрезки касательных, проведенные из одной точки. Мы знаем, что они должны быть одинаковыми:

AM = KM

По той же логике одинаковую длину имеют и отрезки ВМ и КВ, ведь это также касательные к одной окруж-ти, проведенные из одной точки:

BM = KM

В итоге получается, что на рисунке есть два равнобедренных треугольника, ∆АМК и ∆КМВ. Значит, углы при их основании одинаковы. Вместе же они образуют ∆AВК. Попытаемся найти в нем ∠АКВ. Пусть ∠МАК = α, а ∠AВК = β. Тогда можно записать, что

Заметим, что сумма углов в ∆AВК должна составлять 180°, то есть можно записать уравнение:

Задание. Центры окруж-тей, радиусы которых составляют 3 и 10, находятся на расстоянии 25 друг от друга. К ним построена внешняя касательная, касающаяся их в точках А и В. Какова длина отрезка AВ?

Решение. Построим к точкам касания окружностей радиусы, а также проведем через центр меньшей окруж-ти прямую О₂Н, параллельную касательной:

Радиусы перпендикулярны касательным. Так как О₂Н параллельна AВ, то она также должна быть перпендикулярна радиусам. Получается, что в четырехугольнике AВО₂Н все углы прямые, то есть это прямоугольник. Его противоположные стороны одинаковы, поэтому нам достаточно найти длину НО₂. Также заметим, что одинаковы и стороны АН и ВО₂:

AH = BO₂ = 3

Тогда можно найти и длину НО₁:

HO₁ = AO₁ — AH = 10 — 3 = 7

Заметим, что ∆НО₁О₂ прямоугольный, поэтому длину его катета НО₂ можно найти по теореме Пифагора:

Ответ: 24.

Задание. В окруж-ти на радиусе О₁А (его длина составляет 10) отмечена точка К на расстоянии 4 от центра окруж-ти О₁. Построена ещё одна окруж-ть, которая касается как исходной окруж-ти, так и отрезка О₁А в точке К. Какой у неё радиус?

Решение: Соединим центры обоих окруж-тей прямой, которая также пройдет через их точку касания. Также построим радиус О₂К:

Обозначим искомый нами радиус буквой R. Теперь посмотрим на отрезок О₁О₂. С одной стороны, его можно найти как разность радиусов окруж-тей:

Задание на построение. Постройте три окруж-ти, которые касаются друг друга внешним образом. Известны радиусы окруж-тей, они составляют 2, 3 и 4 см.

Решение. Для построения окруж-тей надо лишь знать их центры и величины их радиусов. Радиусы уже известны. Если окруж-ти касаются внешним образом, то расстояние между их центрами равно сумме их радиусов. Значит, в данном случае эти расстояния составят:

2 + 3 = 5 см

2 + 4 = 6 см

3 + 4 = 7 см

Но если расстояния между центрами составляют 5, 6 и 7 см, то это значит, что они образуют треугольник, стороны которого имеют такую же длину. Значит, нам надо просто построить треугольник со сторонами 5, 6 и 7 см, а строить треугольник по известным сторонам мы уже научились в 7 классе:

Сегодня мы узнали многие свойства окруж-ти, а также касательных к ней. Однако это только малая часть геометрических знаний об окруж-ти. В будущих уроках мы узнаем об соотношениях между углами, которые можно в ней провести, вписанных и описанных многоугольниках, вычислениях площадей окруж-ти и способах ее построения.