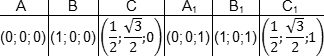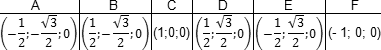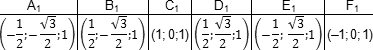Проекции точек на поверхностях геометрических тел
Вы уже знаете, как построить проекции предмета или объекта. Часто при изготовлении изделий необходимо по заданным проекциям определить геометрическую форму предметов и их частей. Предмет можно рассматривать как комбинацию различных геометрических элементов: вершин, ребер, граней и т. д.
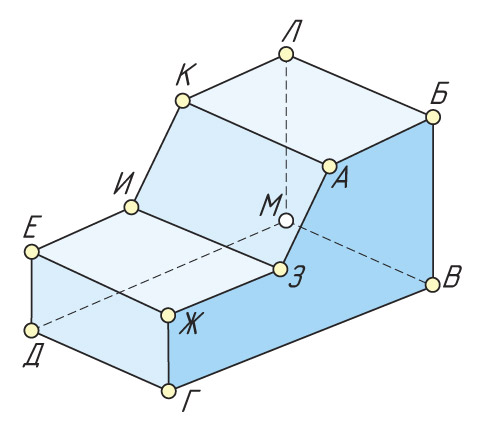
Укажите количество вершин, ребер и граней изображенного предмета.
|
Для точного построения изображений ряда деталей необходимо уметь находить проекции отдельных точек. Чтобы построить проекции точки, принадлежащей поверхности геометрического тела, необходимо понять, на какой поверхности или на каком элементе поверхности (ребре, вершине, грани) находится эта точка. Представив любую деталь как совокупность геометрических тел, можно легко найти проекцию точки. |
 |
|
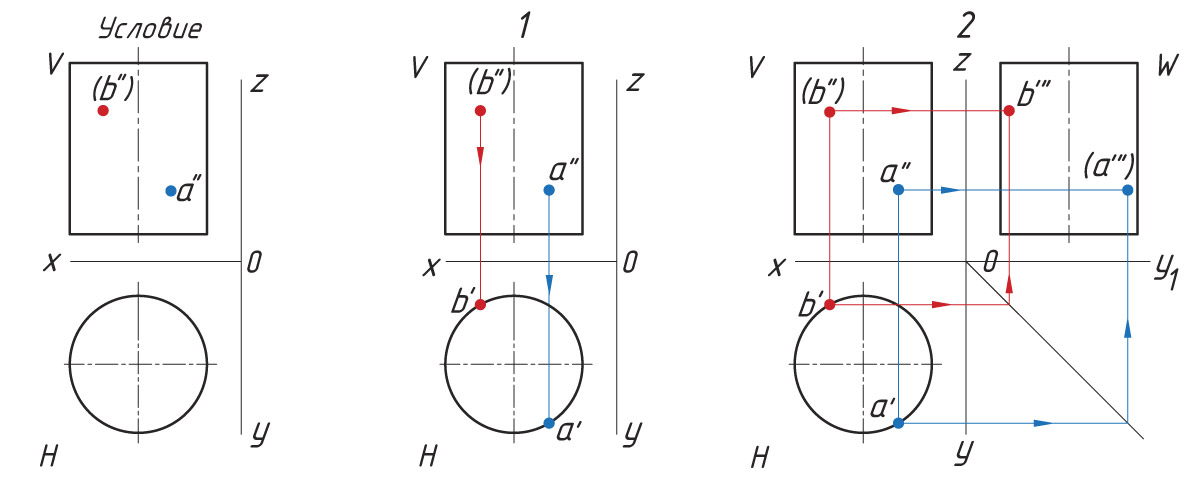
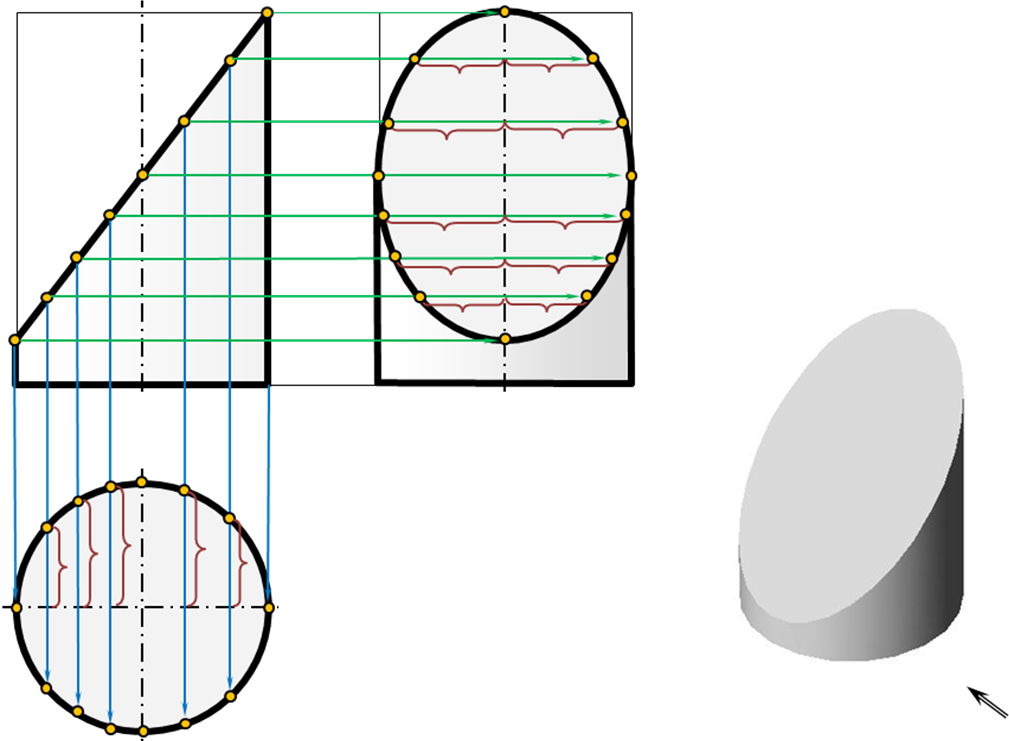
Рассмотрим проекции точки на геометрических телах. Проецирование точек на поверхности цилиндра Последовательность проецирования точек 1. Находят горизонтальные проекции точек а′ и b′. Так как горизонтальная проекция боковой проекции цилиндра отображается в виде круга, то проекции точек а′ и b′ будут находиться на нем. Для их нахождения проводят вертикальные линии связи из проекций точек а″ и b″ до пересечения с окружностью. 2. Проекции точек а′″ и b′″ находят на пересечении линий проекционной связи. |
 |
Направление взгляда на плоскости проекций H, W помогает определить видимость проекций точек на горизонтальной и профильной плоскости проекций. Например, проекции а′ и b′ на плоскости H видны. Проекция а′″ на плоскости W не видна (показана в скобках), проекция b′″ видна (показана без скобок).
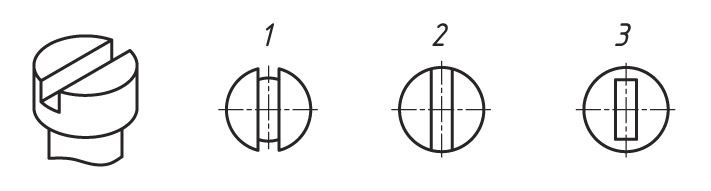
Определите, какая из горизонтальных проекций на рисунке является проекцией наглядного изображения головки винта.
|
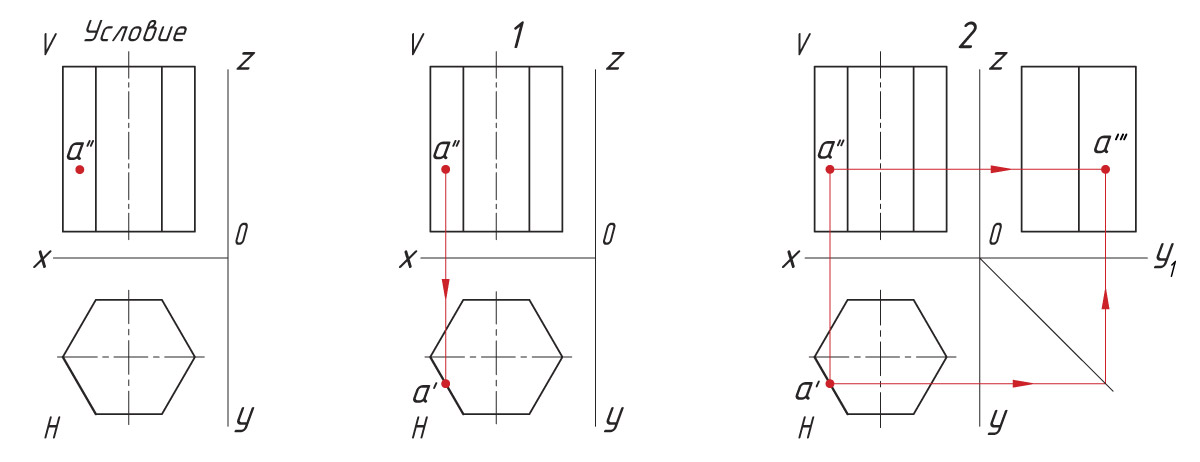
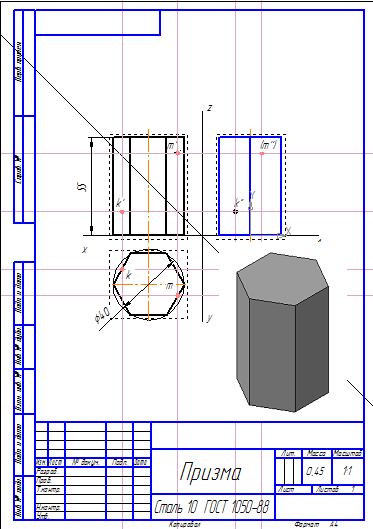
Проецирование точек на поверхности призмы Последовательность проецирования точек 1. Находят горизонтальную проекцию точки а′. Для ее нахождения проводят вертикальную линию связи из проекции точки а″ до пересечения с шестиугольником (горизонтальная проекция призмы). 2. Проекцию точки а′″ находят на пересечении линий проекционной связи. |
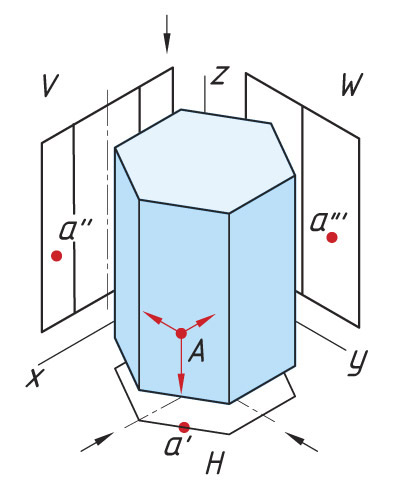 |
Опишите последовательность проецирования точки, находящейся на ребре призмы. Выполните это построение.
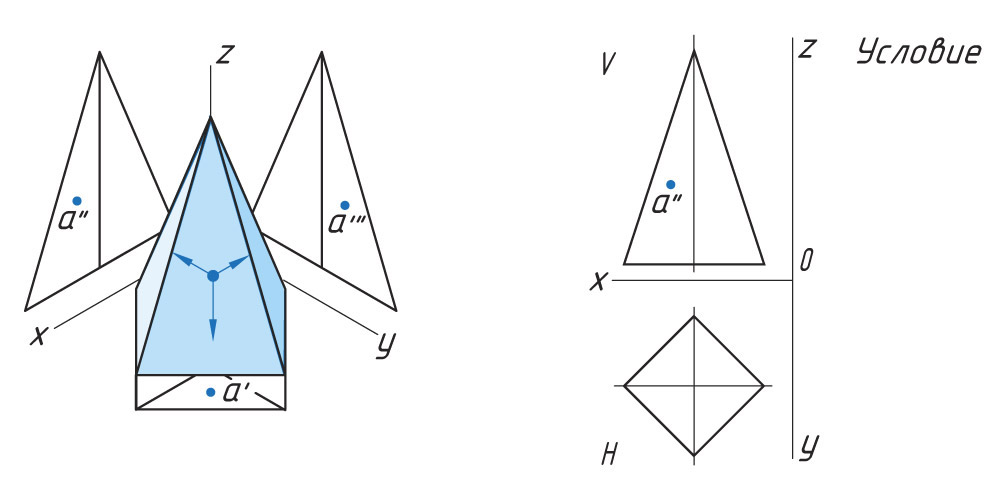
Проецирование точек на поверхности пирамиды
Построение проекции точки, лежащей на ребре
Если точка находится на ребре предмета, то сначала необходимо выполнить проекцию ребра, а затем при помощи линий проекционной связи найти проекции точки, лежащей на ребре.
Как вы считаете, можно ли таким способом спроецировать точку, находящуюся не на ребре, а на грани четырехгранной пирамиды? Свои предположения проверьте на практике.
Общий метод определения точки, лежащей на поверхности геометрического тела, заключается в следующем: через точку на поверхности проводят вспомогательную прямую, проекции которой легко определяются на данной поверхности.
Построение проекции точки, лежащей на грани
Задана фронтальная проекция а″ точки А, лежащая на боковой поверхности четырехгранной пирамиды.
Проекции точек можно определить несколькими способами. Рассмотрим каждый из них.
|
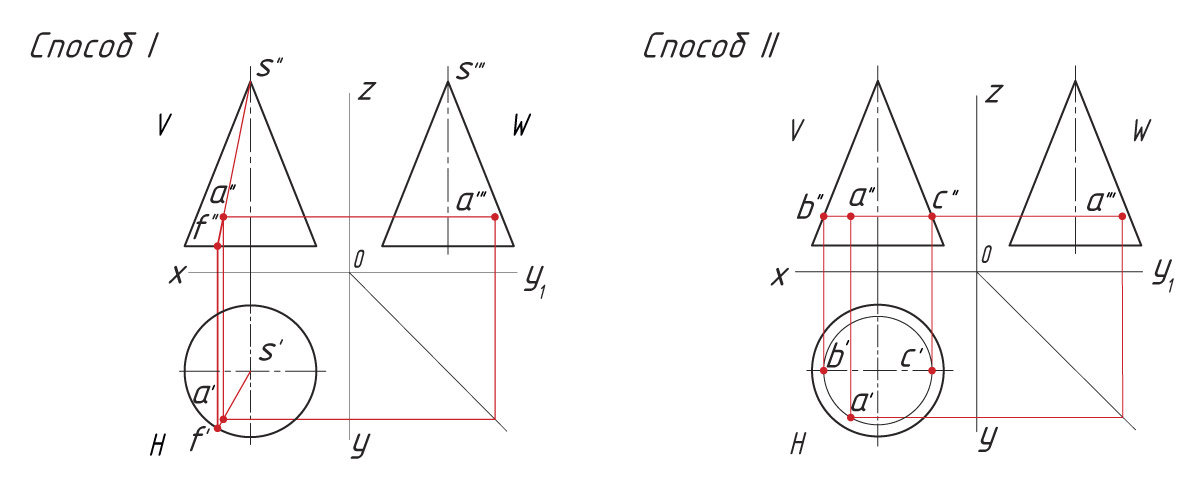
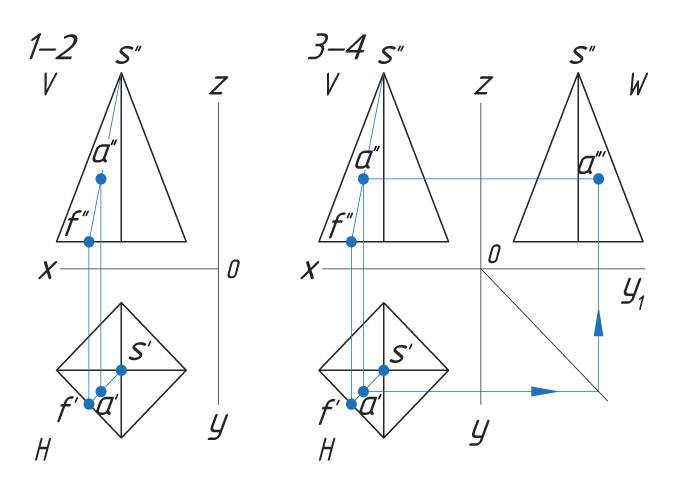
Способ I. 1. Находят горизонтальную проекцию точки а′: вспомогательной прямой соединяют заданную проекцию точки а″ с проекцией вершины пирамиды s″ и продлевают ее до пересечения с основанием в точке f″. |
 |
|
Способ II. 1. Через проекцию а″ точки А проводят вспомогательную прямую и получают точки пересечения с ребрами пирамиды 1″ и 2″. |
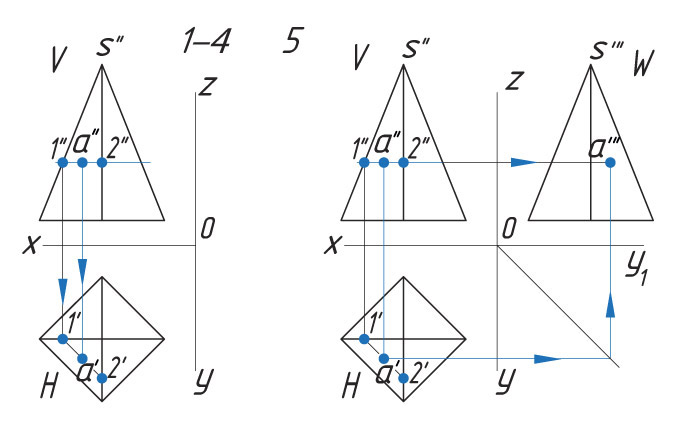 |
На ваш взгляд, изменится ли положение проекции точки, если вспомогательную прямую провести не параллельно, а наклонно к горизонтальной плоскости?
|
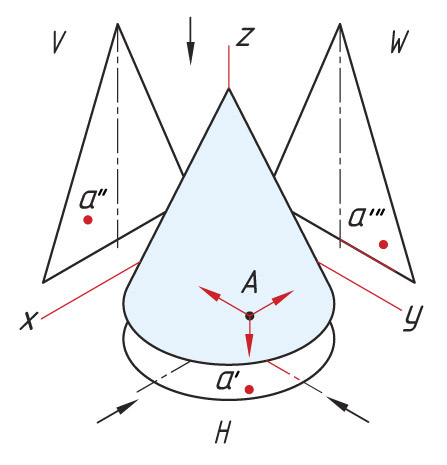
Проецирование точек на поверхности конуса. На поверхности конуса проекции точек можно также определить двумя способами. Способ I заключается в определении проекций точки с помощью вспомогательной линии — образующей, расположенной на поверхности конуса и проведенной через точку А. |
 |



Здравствуйте! Сегодня мы научимся создавать ассоциативный чертеж по готовой 3d модели призмы и пирамиды. Их мы построили на уроке по 3d моделированию
Урок 2. Создаем 3d модели призмы, пирамиды, цилиндра и конуса. Или как создать четыре 3d модели за 10 минут.
Также на этом уроке вы узнаете, как находить проекции точек на чертежах призмы и пирамиды.
Создаем ассоциативный чертеж по 3d модели
Для того, чтобы создать ассоциативный чертеж выполним следующее: создаем чертеж→на компактной панели выбираем кнопку
панель стандартные виды
«Вид»→ ниже выбираем «Стандартные виды»→в открывшемся окне выбираем файл с 3d моделью (расширение .m3d)
выбираем 3d модель призмы
→ на панели свойств, вкладка «схема» подбираем количество видов и расстояние между ними→жмем на поле чертежа и все, три проекции призмы или пирамиды готовы.
схема видов чертежа
Остается только вставить изометрию и оформить чертеж по ГОСТу.
Чтобы вставить изометрию открываем файл с 3d моделью призмы (пирамиды) и пересохраняем ее как рисунок в формате .png.
сохраняем модель в формате рисунка
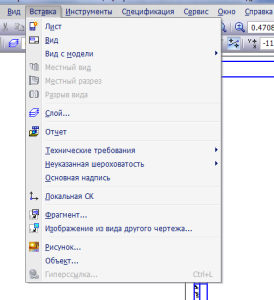
Возвращаемся к созданию ассоциативного чертежа. В строке главного меню жмем на вкладку «Вставка»→ «Рисунок»→ в открывшемся окне выбираем рисунок с призмой (пирамидой)→ вставляем рисунок в чертеж.
вставляем рисунок в чертеж
Как найти проекции точек на пирамиде и призме?
Как найти проекции точек на призме?
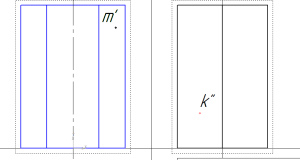
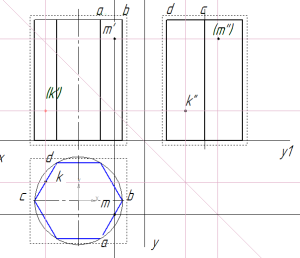
В задании на построение геометрических тел требуется найти недостающие проекции точек К и М (задачник Мироновой Р.С., стр. 65).
проекции точек на призме
Найдем проекции точек на призме.
Задана фронтальная проекция точки М – m’ и профильная проекция точки К – k’’.
Найдем горизонтальную проекцию точки m. Для этого построим вспомогательную прямую через точку m’ до пересечения с горизонтальной проекцией призмы.
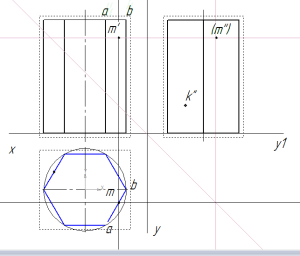
находим проекции точек на призме
Как видно из рисунка, точка m’ принадлежит грани ab. Поэтому горизонтальная проекция m будет находиться в месте пересечения вспомогательной прямой с гранью ab на горизонтальной проекции призмы.
Профильную проекцию находят с по линиям связи, построенным из m’ и m. Так как на профильной проекции призмы точку m’’ не видно, она взята в скобки.
Для того, чтобы найти недостающие проекции точки К поступаем аналогично.
строим горизонтальную и фронтальную проекции точек
По линиям связи находим горизонтальную проекцию k, принадлежащую грани cd. Фронтальную проекцию (k’) также строим по линиям связи.
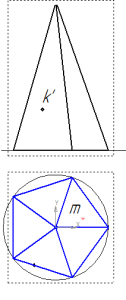
Как найти проекции точек на пирамиде?
Точка М на пирамиде задана горизонтальной проекцией m, точка К – фронтальной проекцией k’.
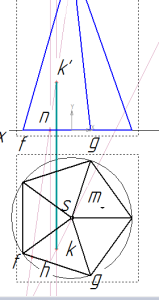
точки на пирамиде
строим горизонтальную проекцию точки
Начнем с нахождения горизонтальной проекции k. Для этого через вершину пирамиды и k’ проводим вспомогательную прямую. Затем через полученную точку n проводим линию связи до пересечения с гранью fg. Через полученную точку h и вершину s проводим еще одну вспомогательную прямую.
И по линии связи опускаемся из точки k’ до пересечения с этой прямой hs. Горизонтальная проекция k найдена.
Профильную проекцию k’’ находим по линиям связи без дополнительных построений.
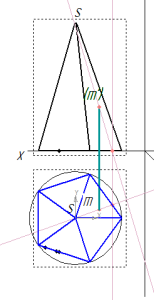
Фронтальную проекцию m’ находим аналогично построению горизонтальной проекции k. Описывать процесс не буду. Вот вам рисунок.
строим фронтальную проекцию точки М
Профильную проекцию m’’ найти особого труда не составит, все по тем же линиям связи.
Таким образом находят проекции точек на пирамиде и призме.
Чтобы лучше все уяснить посмотрите видеоурок.
Скачать чертежи бесплатно можно здесь
Теперь-то вы точно сможете быстро создать ассоциативный чертеж и найти по указанию преподавателя проекции точек на пирамиде или призме.

The following two tabs change content below.
- Bio
- Latest Posts
Рада приветствовать Вас в своем блоге! Я создала его с целью помочь всем желающим освоить программу Компас 3d. Мы пройдем весь путь от азов черчения до создания серьезных сборок. Присоединяйтесь!
Понравился материал? Подпишись на обновления!
Вы можете пропустить чтение записи и оставить комментарий. Размещение ссылок запрещено.
Введение системы координат
30 мая 2011
Метод координат — это, конечно, очень хорошо, но в настоящих задачах C2 никаких координат и векторов нет. Поэтому их придется вводить. Да-да, вот так взять и ввести: указать начало отсчета, единичный отрезок и направление осей x, y и z.
Самое замечательное свойство этого метода заключается в том, что не имеет никакого значения, как именно вводить систему координат. Если все вычисления будут правильными, то и ответ будет правильным.
Тем не менее, приведу некоторые рекомендации, как лучше ввести систему координат для самых часто встречающихся в задаче C2 многогранников. С указанием конкретных точек. Во всех случаях упор делается на минимизацию объема вычислений.
Координаты куба
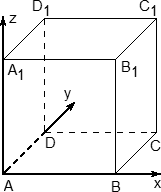
Если в задаче C2 будет куб — считайте, что вам повезло. Это самый простой многогранник, все двугранные углы которого равны 90°.
Система координат также вводится очень просто:
- Начало координат — в точке A;
- Чаще всего ребро куба не указано, поэтому принимаем его за единичный отрезок;
- Ось x направляем по ребру AB, y — по ребру AD, а ось z — по ребру AA1.
Обратите внимание: ось z направляется вверх! После двумерной системы координат это несколько непривычно, но на самом деле очень логично.
Итак, теперь у каждой вершины куба есть координаты. Соберем их в таблицу — отдельно для нижней плоскости куба:
| Точка | A | B | C | D |
| Координаты | (0; 0; 0) | (1; 0; 0) | (1; 1; 0) | (0; 1; 0) |
И для верхней:
| Точка | A1 | B1 | C1 | D1 |
| Координаты | (0; 0; 1) | (1; 0; 1) | (1; 1; 1) | (0; 1; 1) |
Несложно заметить, что точки верхней плоскости отличаются соответствующих точек нижней только координатой z. Например, B = (1; 0; 0), B1 = (1; 0; 1). Главное — не запутаться!
Координаты трехгранной призмы
Призма — это уже намного веселее. При правильном подходе достаточно знать координаты только нижнего основания — верхнее будет считаться автоматически.
В задачах C2 встречаются исключительно правильные трехгранные призмы (прямые призмы, в основании которых лежит правильный треугольник). Для них система координат вводится почти так же, как и для куба. Кстати, если кто не в курсе, куб — это тоже призма, только четырехгранная.
Итак, поехали! Вводим систему координат:
- Начало координат — в точке A;
- Сторону призмы принимаем за единичный отрезок, если иное не указано в условии задачи;
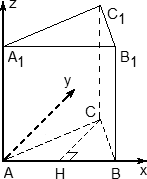
- Ось x направляем по ребру AB, z — по ребру AA1, а ось y расположим так, чтобы плоскость OXY совпадала с плоскостью основания ABC.
Здесь требуются некоторые пояснения. Дело в том, что ось y НЕ совпадает с ребром AC, как многие считают. А почему не совпадает? Подумайте сами: треугольник ABC — равносторонний, в нем все углы по 60°. А углы между осями координат должны быть по 90°, поэтому сверху картинка будет выглядеть так:
Надеюсь, теперь понятно, почему ось y не пойдет вдоль AC. Проведем в этом треугольнике высоту CH. Треугольник ACH — прямоугольный, причем AC = 1, поэтому AH = 1 · cos A = cos 60°; CH = 1 · sin A = sin 60°. Эти факты нужны для вычисления координат точки C.
Теперь взглянем на всю призму вместе с построенной системой координат:
Получаем следующие координаты точек:
Как видим, точки верхнего основания призмы снова отличаются от соответствующих точек нижнего лишь координатой z. Основная проблема — это точки C и C1. У них есть иррациональные координаты, которые надо просто запомнить. Ну, или понять, откуда они возникают.
Координаты шестигранной призмы
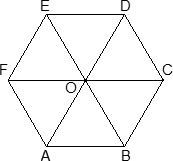
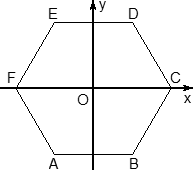
Шестигранная призма — это «клонированная» трехгранная. Можно понять, как это происходит, если взглянуть на нижнее основание — обозначим его ABCDEF. Проведем дополнительные построения: отрезки AD, BE и CF. Получилось шесть треугольников, каждый из которых (например, треугольник ABO) является основанием для трехгранной призмы.
Теперь введем собственно систему координат. Начало координат — точку O — поместим в центр симметрии шестиугольника ABCDEF. Ось x пойдет вдоль FC, а ось y — через середины отрезков AB и DE. Получим такую картинку:
Обратите внимание: начало координат НЕ совпадает с вершиной многогранника! На самом деле, при решении настоящих задач вы обнаружите, что это очень удобно, поскольку позволяет значительно уменьшить объем вычислений.
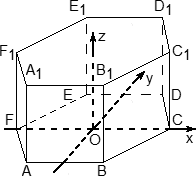
Осталось добавить ось z. По традиции, проводим ее перпендикулярно плоскости OXY и направляем вертикально вверх. Получим итоговую картинку:
Запишем теперь координаты точек. Предположим, что все ребра нашей правильной шестигранной призмы равны 1. Итак, координаты нижнего основания:
Координаты верхнего основания сдвинуты на единицу по оси z:
Координаты четырехугольной пирамиды
Пирамида — это вообще очень сурово. Мы разберем только самый простой случай — правильную четырехугольную пирамиду, все ребра которой равны единице. Однако в настоящих задачах C2 длины ребер могут отличаться, поэтому ниже приведена и общая схема вычисления координат.
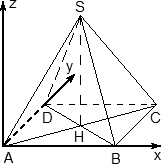
Итак, правильная четырехугольная пирамида. Это такая же, как у Хеопса, только чуть поменьше. Обозначим ее SABCD, где S — вершина. Введем систему координат: начало в точке A, единичный отрезок AB = 1, ось x направим вдоль AB, ось y — вдоль AD, а ось z — вверх, перпендикулярно плоскости OXY. Для дальнейших вычислений нам потребуется высота SH — вот и построим ее. Получим следующую картинку:
Теперь найдем координаты точек. Для начала рассмотрим плоскость OXY. Здесь все просто: в основании лежит квадрат, его координаты известны. Проблемы возникают с точкой S. Поскольку SH — высота к плоскости OXY, точки S и H отличаются лишь координатой z. Собственно, длина отрезка SH — это и есть координата z для точки S, поскольку H = (0,5; 0,5; 0).
Заметим, что треугольники ABC и ASC равны по трем сторонам (AS = CS = AB = CB = 1, а сторона AC — общая). Следовательно, SH = BH. Но BH — половина диагонали квадрата ABCD, т.е. BH = AB · sin 45°. Получаем координаты всех точек:
Вот и все с координатами пирамиды. Но не с координатами вообще. Мы рассмотрели лишь самые распространенные многогранники, однако этих примеров достаточно, чтобы самостоятельно вычислить координаты любых других фигур. Поэтому можно приступать, собственно, к методам решения конкретных задач C2.
Смотрите также:
- Четырехугольная пирамида в задаче C2
- Метод координат в пространстве
- Сложение и вычитание дробей
- Не пишите единицы измерения в задаче B12
- Как решать простейшие логарифмические уравнения
- Задача B4: транзит нефти
Пошаговое построение сечения шестиугольной призмы
В этой статье приведено несколько примеров пошагового построения сечения правильной шестиугольной призмы методом следов. Иногда к методу следов был взят в помощь аксиоматический метод. Я старалась избегать пользоваться методом внутреннего проецирования намеренно, чтобы показать построение именно методом следов.
Задача 1.
Построить методом следов сечение шестиугольной призмы плоскостью, проходящей через точки
.
Задача 1. Дано.
Шаг 1. Проведем прямую , принадлежащую плоскости сечения. Благодаря тому, что точки
и
лежат в основании призмы, прямая
также принадлежит плоскости основания, а значит, будет пересекаться с другими прямыми, также лежащими в этой плоскости. Тогда можно провести прямую
, и определить точку пересечения
и
—
. Точка
принадлежит плоскости грани
, поскольку прямая
принадлежит ей.
Задача 1. Шаг 1.
Шаг 2. Точки и
можно соединить прямой. Прямая
пересечет ребро
в точке
. Проводим прямую
в плоскости основания и находим ее пересечение с прямой
— точку
.
Задача 1. Шаг 2.
Шаг 3. Через точки и
проводим прямую. Она принадлежит плоскости грани
, поэтому обязательно пересечется с прямой
этой плоскости — в точке
. Точка
лежит «под» призмой, ниже ее основания. Точка
, благодаря принадлежности прямой
, также принадлежит и плоскости грани
, а в этой плоскости у нас имеется точка — точка
.
Задача 1. Шаг 3.
Шаг 4. Следовательно, можно соединить точки и
прямой. Эта прямая пересечет ребро
в точке
.
Задача 1. Шаг 4.
Шаг 5. Точка принадлежит прямой
, а следовательно, лежит в плоскости грани
, таким образом, ее можно соединить с точкой
этой же плоскости прямой
. Эта прямая пересечет ребро
в точке
. Для дальнейшего построения нам нужны точки в плоскости верхней грани призмы. Добудем их. Продлим прямую
до пересечения с прямой
. Отметим точку
.
Задача 1. Шаг 5.
Шаг 6. Проведем прямую , принадлежащую грани
, и найдем точку ее пересечения с прямой
— точку
. Тогда точки
и
принадлежат плоскости верхней грани (за счет принадлежности прямым этой плоскости) и их можно соединять прямой.
Задача 1. Шаг 6.
Шаг 7. Находим точки пересечения прямой с ребрами
и
— точки
и
.
Задача 1. Шаг 7.
Шаг 8. Соединяем все полученные точки отрезками.
Задача 1. Шаг 8.
Окончательный вид сечения:
Окончание построения
Задача 2.
Построить методом следов сечение шестиугольной призмы плоскостью, проходящей через точки
.
Задача 2. Дано
Шаг 1. Проведем прямую . Она принадлежит секущей плоскости. Также проведем проекцию этой прямой на плоскость нижнего основания призмы — прямую
. Точка их пересечения одновременно принадлежит секущей плоскости и плоскости нижнего основания призмы. Обозначим ее
.
Задача 2. Шаг 1.
Шаг 2. Аналогично поступим с точками и
: проводим прямую
и ее проекцию в плоскости нижнего основания. Их пересечение — точка секущей плоскости
, одновременно лежащая в нижнем основании.
Задача 2. Шаг 2.
Шаг 3. Имея две точки в плоскости нижнего основания, проведем через них прямую , точки которой принадлежат секущей плоскости.
Проведем прямую . Она лежит в плоскости основания, но одновременно — в плоскости боковой грани, поэтому ее точки принадлежат этой боковой грани. Точка пересечения прямых
и
, таким образом, принадлежит плоскости боковой грани призмы и плоскости сечения.
Задача 2. Шаг 3.
Шаг 4. Проводим прямую в плоскости боковой грани
и отыскиваем точку пересечения ею ребра
— точку
.
Осталось немного: найти точку плоскости сечения на ребре , и пару точек в плоскости основания.
Задача 2. Шаг 4.
Шаг 5. Проведем прямые и
в плоскости основания. Они пересекут прямую
секущей плоскости в точках
и
.
Задача 2. Шаг 5.
Шаг 6. Точки и
принадлежат плоскости грани
, проведем через них прямую. Найдем точку, где эта прямая пересечет ребро
— точку
. Точки
и
лежат в плоскости грани
. Проводим через них прямую и находим точку пересечения этой прямой с ребром
—
.
Задача 2. Шаг 6.
Шаг 7. Соединяем точки отрезками.
Задача 2. Шаг 7.
Окончательный вид построенного сечения:
Окончательный вид построенного сечения
Задача 3.
Построить методом следов сечение шестиугольной призмы плоскостью, проходящей через точки
.
Задача 3. Дано
Шаг 1. Проводим прямую секущей плоскости, а также ее проекцию в плоскости основания
. Прямая
принадлежит плоскости основания и пересечет прямую
в точке
. Заметим, что точка
не является точкой секущей плоскости.
Задача 3. Шаг 1.
Шаг 2. Из точки проводим перпендикуляр к плоскости основания (к прямой
), его пересечение с прямой
— точка
— принадлежит секущей плоскости, а также плоскости грани
.
Задача 3. Шаг 2.
Шаг 3. Соединим точки и
. Прямая
пересечет ребро призмы
в точке
.
Задача 3. Шаг 3.
Шаг 4. Заполучив точку , можем провести отрезок
. Вот тут-то нам и понадобится аксиоматический метод. Так как грань
параллельна грани
, то плоскость рассечет ее по прямой, которая будет параллельна
. Вот и проведем через
такую параллельную прямой
прямую. Она пересечет ребро
в точке
.
Задача 3. Шаг 4.
Шаг 5. Проведем также через точку прямую, параллельную прямой
. Это можно сделать, так как грань
параллельна грани
. Прямая эта пересечет ребро
в точке
.
Задача 3. Шаг 5.
Шаг 6. Соединяем точки отрезками.
Задача 3. Шаг 6.
Окончательный вид:
Задача 3. Окончательный вид
Задача 4.
Построить методом следов сечение шестиугольной призмы плоскостью, проходящей через точки
.
Задача 4. Дано
Шаг 1. Через точки и
проводим прямую секущей плоскости. Также проведем проекции этой прямой на верхнее и нижнее основание —
на верхнее, и
— на нижнее. Точки пересечения прямой
с проекциями — это точки прокола данной прямой оснований призмы. Верхнее основание прямая
прошьет в точке
, а нижнее — в точке
. Таким образом, мы заполучили точки секущей плоскости в плоскостях верхнего и нижнего оснований.
Задача 4. Шаг 1.
Шаг 2. Точки и
принадлежат одной плоскости, проводим через них прямую. Эта прямая даст нам две точки: точку
, в которой она пересечет ребро
, и точку
, в которой она пересечет ребро
.
Шаг 3. Приобретя точку в грани
, проведем прямую
. Она пересечет ребро
в точке
.
Задача 4. Шаги 2-3.
Шаг 4. Проведем через точку в плоскости основания призмы прямую, параллельную прямой
(или можно провести через точки
и
). Эта прямая пересечет ребро
в точке
.
Задача 4. Шаг 4.
Шаг 5. Соединяем точки отрезками.
Задача 4. Шаг 5.
Окончательный вид:
Окончательный вид сечения
Точка принадлежит
поверхности, если она находится на линии
этой поверхности. План решения задачи
на принадлежность точки поверхности
включает:
-
определение
вида заданной поверхности; -
выбор
графически простой для построения на
чертеже линии поверхности, проходящей
через заданную точку (прямая или
окружность); -
построение
проекций этой линии на чертеже; -
построение
искомых проекций точки.
Для лучшего
представления и понимания эпюр каждой
поверхности сопровождается наглядным
изображением, а стрелкой указывается
направление взгляда (фронтальная
проекция – вид спереди).
Точки и линии на поверхности призмы
Рассмотрим
построение точки и линии на поверхности
прямой призмы.
Т
?
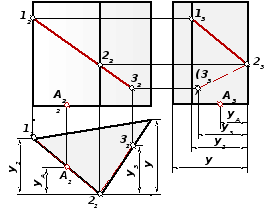
очки и линии на поверхности пирамиды
П
S2
остроить профильную проекцию
пирамиды и недостающие проекции точки
и прямой.
m2
В2
E2
C2(G2)
D2(F2)
А1
В1
С1
D1
E1
G1
F1
S1
m1
Т
?
очки и линии на поверхности цилиндра
Построить профильную
проекцию цилиндра и недостающие проекции
точки и прямой.
Т
?
очки и линии на поверхности конуса
Построить профильную
проекцию конуса и недостающие проекции
точки и прямой.
Точки и линии
на поверхности сферы
П
?
остроение проекций точек на сфере
понятно из построения точкиF,
заданной на фронтальной проекции сферы.
Горизонтальная проекцияF1точкиFнайдена с
помощью параллели, проходящей через
точку F
(F2).
На горизонтальной проекции радиус
параллелиRF,
проведенный из центра сферы, пересекается
с линией связи от фронтальной проекцииF2точки
F. Для построения
профильной проекцииF3точки F
необходимо замерить координатуyточкиF (уF).
П
недостающие проекции точек и обозначить
их на наглядном изображении.
Точки и линии на поверхности тора
П
?
остроение проекций точек на торе
понятно из построения точкиА
(через параллель с
радиусом RА),
заданной на фронтальной проекции тора
Построить недостающие
проекции точек и обозначить их на
наглядном изображении.
Лекция
№ 5
СЕЧЕНИЕ
ПОВЕРХНОСТЕЙ ПРОЕЦИРУЮЩИМИ
ПЛОСКОСТЯМИ
1. Сечение
многогранников проецирующими плоскостями
(призма, пирамида). 2. Сечение поверхностей
вращения проецирующими плоскостями
(цилиндр, конус, сфера).
1
СЕЧЕНИЕ МНОГОГРАННИКОВ ПРОЕЦИРУЮЩИМИ
ПЛОСКОСТЯМИ
П
?
лоскость пересекает многогранник
по плоским многоугольникам. Для построения
многоугольника необходимо найти его
вершины (точки пересечения плоскости
с ребрами и гранями).
Призма
Пирамида
2
СЕЧЕНИЕ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ
ПРОЕЦИРУЮЩИМИ ПЛОСКОСТЯМИ
При построении
точек сечения применяется способ
построения точек по принадлежности.
Сечение
цилиндра
Любая плоскость
может пересекать поверхность прямого
кругового цилиндра:
по
окружности,
если плоскость
сечения перпендикулярна его образующим
(рис. 63), такоесечение называется
нормальным;
по двум
образующим,
если секущая
плоскость
параллельна оси цилиндра (рис. 64);по эллипсу, если секущая
плоскостьнаклонена
к оси цилиндра и пересекает все
его образующие (построить три проекции
цилиндра).
Сечение конуса
Конус
является геометрическим
телом, которое может
иметь в сечении пять различных фигур:
треугольник,
если
секущая плоскость
пересекает конус через вершину по
двум образующим (рис. 65, а, б);
окружность,
если секущая
плоскость
параллельна основанию или перпендикулярна
оси, а конус прямой круговой
(рис. 66);
эллипс,
если
секущая плоскость пересекает
все образующие конуса под
некоторым углом к основанию конуса
(рис. 67);
параболу,
если
секущая плоскость параллельна
одной из образующих конуса
(рис. 68);
гиперболу,
если секущая
плоскость параллельна
оси конуса или параллельна
двум его образующим (рис. 69).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #