Скачать материал

Скачать материал


- Сейчас обучается 387 человек из 62 регионов


- Сейчас обучается 267 человек из 65 регионов




Описание презентации по отдельным слайдам:
-
1 слайд
ИНЖЕНЕРНАЯ ГРАФИКА
«Проецирование геометрических тел на три плоскости проекции.
Проекции точек, лежащих на поверхности геометрических тел» -
2 слайд
ГЕОМЕТРИЧЕСКИЕ ТЕЛА
Геометрическим телом называют часть пространства, ограниченной геометрическими поверхностями.
Все геометрические тела можно разделить на две группы:
Многогранники
Тела вращения -
3 слайд
Многогранники
Многогранники-тела, ограниченные со всех сторон плоскостями.
Многогранники различают в зависимости от формы и количества граней. -
4 слайд
Призма
Призма — многогранник, у которого боковые грани – прямоугольники или параллелограммы, а основаниями служат два равных многоугольника.
Если у призмы основания — правильные многоугольники, а высота перпендикулярна основанию, то призма – правильная и прямая.
В зависимости от количества сторон основания призмы бывают треугольные, четырехугольные и т. д. -
5 слайд
Прямая четырехугольная призма (параллелепипед)
Верхнее основание
Нижнее основание
Ребра основания
Боковые ребра
Высота
Боковая грань -
6 слайд
Плоские фигуры, ограничивающие многогранник, называются гранями.
Грани пересекаются между собой по прямым линиям, которые называются ребрами многогранника.
Ребра пересекаются в точках-вершинах многогранника. -
7 слайд
Пирамида
Пирамида-многогранник, у которого боковые грани представляют собой треугольники, имеющие общую вершину.
В основании у пирамиды – многоугольник. В зависимости от количества сторон основания пирамида называется трех-, четырех-, пятиугольной и т. д.
Если у пирамиды основание правильный многоугольник, а высота перпендикулярна основанию, то пирамида правильная и прямая -
8 слайд
Прямая правильная шестиугольная пирамида
Боковые
ребра
Вершина
Боковая грань
Основание
Ребра основания
Высота -
9 слайд
Тела вращения
Тела вращения – тела, ограниченные поверхностью вращения
-
10 слайд
Прямой круговой цилиндр
Основания цилиндра – круги. Цилиндрическая поверхность образуется от вращения образующей вокруг оси цилиндра.
Цилиндр, ось которого перпендикулярна к горизонтальной плоскости проекций называется прямым. -
11 слайд
Прямой круговой цилиндр
Х’
Y’
Z’
Высота
Ось
Верхнее основание
Боковая цилиндрическая
поверхность
Образующая
Нижнее основание -
12 слайд
Прямой круговой конус
Прямой круговой конус – тело вращения, ограниченное конической поверхностью и плоскостью, перпендикулярной к оси вращения.
У прямого кругового конуса коническая поверхность образована вращением прямой линии (образующей), пересекающей ось вращения в точке (вершине), вокруг этой оси вращения.
Конус, ось которого перпендикулярна к горизонтальной плоскости проекций, называется прямым. -
13 слайд
Прямой круговой конус
X’
Y’
Z’
Вершина
Высота
ось
Боковая коническая
поверхность
Образующая
Основание конуса -
14 слайд
х
у
у’
z
S’
S
S”Построение проекций прямого кругового конуса
-
15 слайд
Построение проекций прямого кругового цилиндра
Z
y
Y’
х -
16 слайд
Построение проекций правильной прямой шестиугольной призмы
x
y
Y’
z -
17 слайд
Построение проекций прямой правильной шестиугольной пирамиды
s
S’
S”
х
у’
у
z -
18 слайд
Определение недостающих проекций точки «а», расположенной на поверхности пирамиды, по заданной фронтальной проекции (1-й способ)
1
2
3
4
s
1’
2’(6’)
3’(5’)
4’
S’
5
6
S”
6”(5”)
1”(4”)
2”(3”)
а´
n´
n
а″
а -
19 слайд
Определение недостающих проекций точки «а», расположенной на поверхности пирамиды, по заданной фронтальной проекции (2-й способ)
1
2
3
4
s
1’
2’(6’)
3’(5’)
4’
S’
5
6
S”
6”(5”)
1”(4”)
2”(3”)
а´
n´
m´
n
m
а
а″ -
20 слайд
Определение недостающих проекций точки «а», расположенной на поверхности конуса, по заданной фронтальной проекции (1-й способ)
х
z
y
Y’
b’
b
c’c
a’
a
s
s’
s’’
a’’ -
21 слайд
х
у
у’
z
S’
S
S”
Нахождение недостающих проекций точки «а», расположенной на поверхности конуса, по заданной фронтальной проекции
(2-й способ)
а´
n´
n
а
а» -
22 слайд
Определение недостающих проекций точек «а» и «в», расположенных на поверхности цилиндра, по заданным фронтальным проекциям
Z
y
Y’
х
а´
а
а»
в´
в
в» -
23 слайд
Определение недостающих проекций точек «а» и «в»,
расположенным на поверхности призмы, по заданным
фронтальным проекциям
x
y
Y’
z
1´
2´
3´
4´
а´
а
4(1)
3(2)
4″
3″(6″)
1″
2″(5″)
а″
в´
в
5´
6´
6(5)
в
в» -
24 слайд
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Боголюбов С. К. Инженерная графика – М.: Машиностроение, 2002.
Куликов В.П. Стандарты инженерной графики. – М.: И Д «Форум», 2008.
Миронов Р. С. Индивидуальные задания по курсу черчения. –
М.: Высшая школа, 2002.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 266 312 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 11.05.2016
- 894
- 5
- 11.05.2016
- 591
- 0
- 11.05.2016
- 2340
- 13
- 11.05.2016
- 1967
- 4
- 11.05.2016
- 1213
- 1
- 11.05.2016
- 368
- 0
- 11.05.2016
- 1570
- 16
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Методика написания учебной и научно-исследовательской работы в школе (доклад, реферат, эссе, статья) в процессе реализации метапредметных задач ФГОС ОО»
-
Курс повышения квалификации «Организация научно-исследовательской работы студентов в соответствии с требованиями ФГОС»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС юридических направлений подготовки»
-
Курс повышения квалификации «Финансы: управление структурой капитала»
-
Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»
-
Курс повышения квалификации «Организация маркетинга в туризме»
-
Курс профессиональной переподготовки «Разработка эффективной стратегии развития современного вуза»
-
Курс профессиональной переподготовки «Метрология, стандартизация и сертификация»
-
Курс профессиональной переподготовки «Организация маркетинговой деятельности»
-
Курс повышения квалификации «Информационная этика и право»
-
Курс профессиональной переподготовки «Управление качеством»
-
Курс профессиональной переподготовки «Стратегическое управление деятельностью по дистанционному информационно-справочному обслуживанию»
I. Основные формулы:
1. Расстояние между точками А (,
), В
,
) равно
=
.
2. Угол между плоскостями. Если β – угол между плоскостями, заданными уравнениями х+
z+
=0 и
х+
z+
=0, то
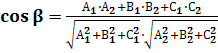
3. Расстояние от точки до плоскости. Если ρ – расстояние от точки (
,
), до плоскости
х+
z+D =0, то
ρ=.
4. Уравнение плоскости, проходящей через три заданные точки (
,
),
(
,
),
(
,
), в координатной форме:
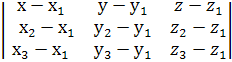
5. Если отрезок, концами которого служат точки А (,
), В
,
) разделен точкой С (х, у,
) в отношении λ, то координаты точки С определяются по формулам
Х = ; у=
; z=
.
II. Координаты вершин многогранников.
Определите координаты вершин многогранников:
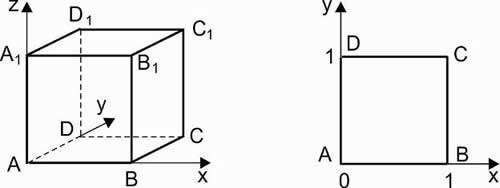
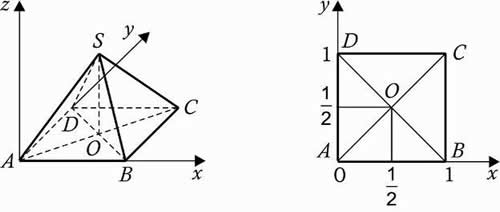
1. Единичный куб A…D1
Решение: координаты вершин А (0, 0, 0), А1 (0, 0, 1), В (1, 0, 0), В1 (1, 0, 1), D (0, 1, 0), D1 (0, 1, 1), С (1, 1, 0), С1 (1, 1, 1).
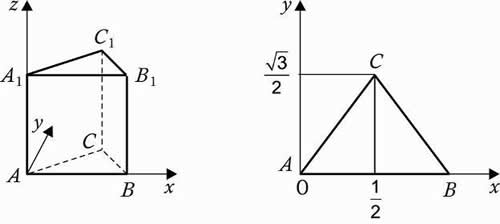
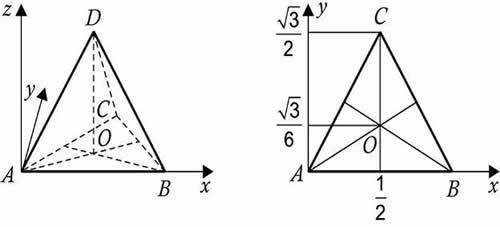
2. Правильная треугольная призма A…C1 , все ребра, которой равны 1.
Решение: координаты вершин: А (0, 0, 0), А1 (0, 0, 1), В (1, 0, 0), В1 (1, 0, 1), С (0,5; , 0), С1 (0,5;
, 1).
3. Правильная шестиугольная призма A…F1, все ребра которой равны 1.
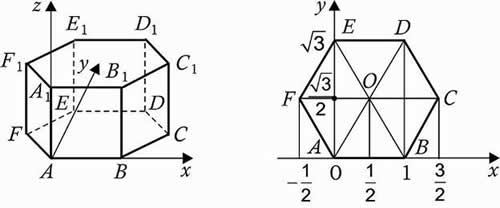
Решение: координаты вершин: А (0, 0, 0), А1 (0, 0, 1), В (1, 0, 0), В1 (1, 0, 1), С (1,5; , 0), С1 (1,5;
, 1), D (1,
(1,
Е (0,
,
(0,
,
F(-0,5 , 0),
(-0,5,
1).
4. Правильная треугольная пирамида (тетраэдр) ABCD все ребра которой равны 1.
Решение: координаты вершин: А (0, 0, 0), В (1, 0, 0), С (0,5; , 0), D (0,5,
5. Правильная четырехугольная пирамида SABCD, все ребра которой равны 1.
Решение: координаты вершин: А (0, 0, 0), В (1, 0, 0), С (1, 1, 0), D (0, 1, 0 S (0,5; 0,5;
).
6. Правильная шестиугольная пирамида SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2.
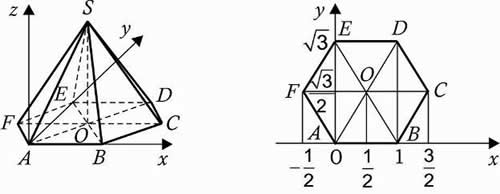
III. Решение задач.
Решение: координаты вершин: А (0, 0, 0), В (1, 0, 0), С (1,5; , 0), D (1,
Е (0,
, F (-05,
0), S (0,5;
).
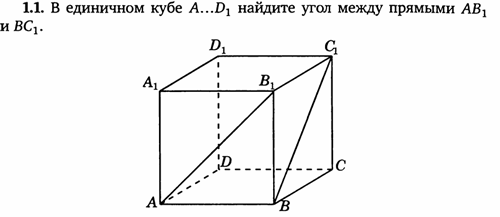
Решение:
- А (0, 0, 0), А1 (0, 0, 1), В (1, 0, 0), В1 (1, 0, 1), D (0, 1, 0), D1 (0, 1, 1), С (1, 1, 0), С1 (1, 1, 1).
- Найдем координаты векторов
(1, 0, 1) и
= (0, 1, 1)
- Найдем косинус угла между векторами
=
=
; α=60.
Ответ: 60.
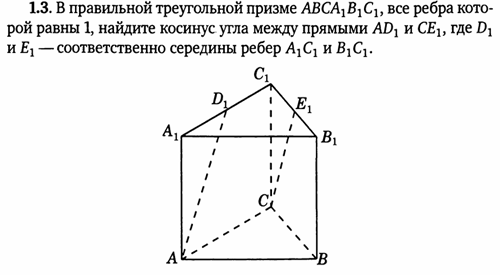
Решение:
- координаты вершин А (0, 0, 0), D1 (
,
, 1), С (0,5;
, 0), Е1 (
;
, 1).
- Найдем координаты векторов:
и
(
,
, 1)
- Найдем косинус угла между векторами
=
=0,7;
Ответ: 0,7.
Полностью текст работы приведен в Приложении.

Обозначения
- $SABCDEF$ — правильная шестиугольная пирамида
- $O$ — центр основания пирамиды
- $a$ — длина стороны основания пирамиды
- $h$ — длина бокового ребра пирамиды
- $S_{text{осн.}}$ — площадь основания пирамиды
- $V_{text{пирамиды}}$ — объем пирамиды
Площадь основания пирамиды
В основаниях пирамиды находится правильный шестиугольник со стороной $a$. По свойствам правильного шестиугольника, площадь основания пирамиды равна $$ S_{text{осн.}}=frac{3sqrt{3}}{2}cdot a^2 $$
Правильный шестиугольник в основании пирамиды

Находим $SO$
Прямая $SO$ является высотой пирамиды, поэтому $angle SOF=90^{circ}$. Треугольник $SOF$ прямоугольный, в нем $FO=a, FS=h$. По свойствам прямоугольного треугольника $$ SO=sqrt{FS^2-FO^2}=sqrt{h^2-a^2} $$
Объем пирамиды
Объем пирамиды вычисляется как треть произведения площади ее основания на ее высоту. Высотой правильной пирамиды является отрезок $SO$. В основании правильной шестиугольной призмы находится правильный шестиугольник, площадь которого нам известна. Получаем $$ V_{text{пирамиды}}=frac{1}{3}cdot S_{text{осн.}}cdot SO=frac{sqrt{3}}{2}cdot a^2 cdot sqrt{h^2-a^2} $$
Находим $ST$ и $TO$

Построение сечения шестиугольной пирамиды
Здравствуйте, друзья! В этой статье предложено рассмотреть два случая построения сечения шестиугольной пирамиды. Пирамида всегда «рассекается» сложнее, чем призма, а чем больше у нее углов в основании, тем труднее. В первой задаче я постаралась пользоваться методом следов, а во второй — преимущественно использован метод внутреннего проецирования. Так как чертежи насыщены построениями, я использовала разные цвета, и не всегда соблюдала правило «невидимое — пунктиром». Постараюсь сопроводить картинки подробным описанием.
Задача 1. Построить сечение правильной шестиугольной пирамиды плоскостью, проходящей через заданные точки.
Задача 1. Дано
Шаг 1. Точки и
лежат в плоскости основания пирамиды, что для нас очень удобно. Проведем прямую
, она пересечется с лучом
плоскости основания. За счет принадлежности обеим прямым —
и
точка
принадлежит как плоскости грани
, так и секущей плоскости.
Задача 1. Шаг 1.
Шаг 2. Через точки и
можем проводить прямую, она пересечет ребро
в точке
.
Задача 1. Шаг 2.
Шаг 3. Так как прямая , также принадлежащая плоскости основания, не параллельна
, то она пересечет эту прямую, и таким образом, можно было бы получить точку плоскости грани
. Но пересечение этих прямых — за границами чертежа. Где невозможно применение метода следов, на помощь приходит метод внутреннего проецирования. Проведем прямую
и ее проекцию в плоскости основания —
.
Задача 1. Шаг 3.
Шаг 4. Проведем проекцию будущей прямой секущей плоскости — (просто соединим вершины).
пересечет
в точке
,
— в точке
. Из точки
поднимемся вверх до секущей плоскости — построим перпендикуляр к плоскости основания
.
— точка прокола перпендикуляром секущей плоскости.
Задача 1. Шаг 4.
Шаг 5. Точка принадлежит секущей плоскости, точка
— также. Проводим прямую
. Прямая
пересечет ребро
в точке
(поздно было переделывать картинку, пусть уж будет вторая точка
). Она принадлежит обеим плоскостям — и
, и
.
Задача 1. Шаг 5.
Шаг 6. Вернемся к методу следов. Проводим прямую , и ищем ее пересечение с
. Это точка
. Она лежит в плоскости грани
.
Задача 1. Шаг 6.
Шаг 7. Проводим , эта прямая пересечет ребро
в точке
.
Задача 1. Шаг 7.
Шаг 8. Соединим полученные точки отрезками.
Задача 1. Шаг 8.
Окончательный вид сечения с противоположной стороны.
Окончательный вид сечения.
Задача 2. Построить сечение правильной шестиугольной пирамиды плоскостью, проходящей через заданные точки.
Задача 2. Дано
Задача 2. Шаг 1. Проводим диагонали основания пирамиды ,
,
. Из точек
и
секущей плоскости опускаем перпендикуляры к основанию, определяем точки
и
, в которых эти перпендикуляры достигнут основания пирамиды.
Задача 2. Шаг 1.
Шаг 2. Проводим прямые и
секущей плоскости и их проекции
и
. Проекцией прямой
будет прямая
. Определяем точку пересечения
и
, и из этой точки поднимаем перпендикуляр до пересечения с
— получили точку
.
Задача 2. Шаг 2.
Шаг 3. Из точки , которая является пересечением диагонали
и проекции
, поднимаем перпендикуляр до пересечения с
— получаем точку
. Из точки
, которая является пересечением диагонали
и проекции
, поднимаем перпендикуляр до пересечения с
— получаем точку
. Через точки
и
проведем прямую, которая пересечет ребро пирамиды
в точке
.
Задача 2. Шаг 3.
Шаг 4. Через точки и
также проведем прямую. Определим место пересечения ею ребра
— точку
. Осталось найти две точки — на ребре
и на ребре
.
Задача 2. Шаг 4.
Шаг 5. Проведем прямую — продолжение ребра основания. Также через точки
и
проведем прямую, принадлежащую грани
. Найдем место пересечения прямых
и
— точку
.
Задача 2. Шаг 5.
Шаг 6. Через точки и
секущей плоскости, лежащие в основании, проводим прямую, которая пересечет ребро
в точке
.
Задача 2. Шаг 6.
Шаг 7. Прямая пересечет продолжение диагональ
в точке
. Проведем прямую через точки
и
, чтобы определить точку пересечения этой прямой с ребром
— точку
.
Задача 2. Шаг 7.
Шаг 8. Соединяем все точки отрезками.
Задача 2. Шаг 8.
Окончательный вид сечения:
Окончательный вид
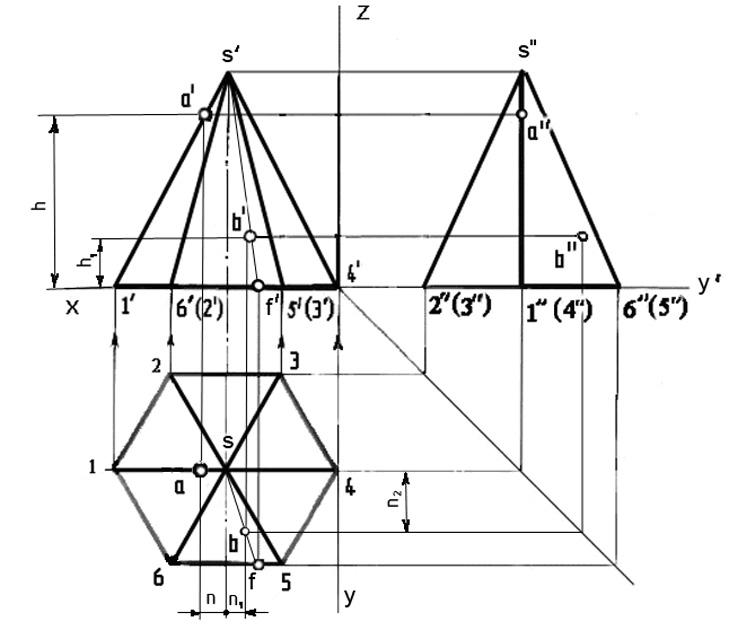
Построение
фронтальной проекции пирамиды:
1)
Из вершин шестиугольника – точек 1,
2, 3, 4,
5 и
6 (рис. 4.4,
а) –
проводим вверх вертикальные линии связи
и чертим фронтальную проекцию основания
пирамиды –
отрезок 1′–
4′.
2)
Из горизонтальной проекции вершины
пирамиды –
точки s
–
проводим вертикальную линию связи и
от отрезка
1′–
4′
откладываем высоту пирамиды, получаем
точку s‘
–
фронтальную проекцию вершины.
3)
Строим фронтальные проекции ребер
пирамиды –
соединяем
точку s‘
с точками 1′,
6′(2′), 5(3‘),
4′.
Построение
профильной проекции пирамиды;
1)
Координаты
y
точек 1, 2,
3, 4,
5, 6 (рис.
4.4, а) и вершины – точки
s
– переносим с помощью линий связи с
горизонтальной проекции на профильную
проекцию.
2)
Координаты z
основания и вершины пирамиды —
точки s’
— переносим
с помощью линии связи с фронтальной
проекции на профильную проекцию.
3)
Чертим профильные проекции основания
пирамиды отрезок 2»—
6»
и вершины – точку s».
4)
Строим профильные
проекции ребер пирамиды –
соединяем
точку s»
с точками
2»(3»),
1′‘(4»),
6»(5»).
а)
б)
Рисунок
4.4 Комплексный чертеж и изометрия
шестигранной пирамиды
Построение
проекций точек на поверхности пирамиды:
На
рисунке 4.4, а фронтальная проекция
точки А
– точка
а‘–
находится на ребре
s’-1‘, поэтому
для построения горизонтальной проекции
– точки а
– надо опустить линию связи из точки
а‘
на
горизонтальную проекцию этого ребра –
отрезок s-1.
Чтобы
построить профильную проекцию – точку
а»
– надо из точки
а‘
провести
линию связи на профильную проекцию
ребра – отрезок
s‘‘-1‘‘.
Точка
В расположена
не на ребре, поэтому для построения ее
проекций надо сначала провести через
точку в‘
(она задана) отрезок, соединяющий вершину
с основанием (s’-f
‘).
Затем найти горизонтальную проекцию
этого отрезка (s-f
) и, опустив на него из точки а‘
линию
связи, построить точку а..
Профильная
проекция — точка
а»
– строится на пересечении линий связи,
проведенных из точек а
и
а‘.
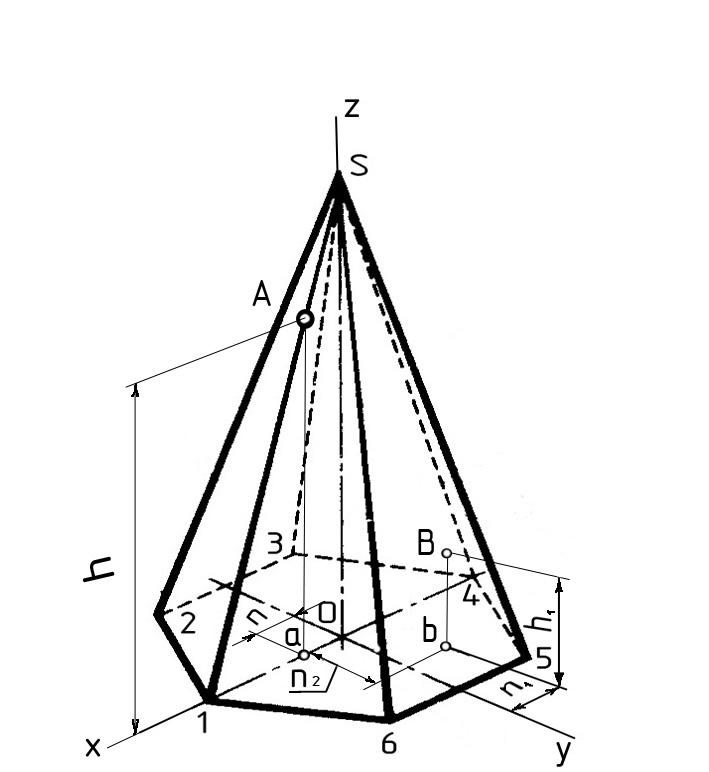
Построение
изометрии
В
А
пирамиды:
1)
На горизонтальной плоскости строим
изометрию многоугольника основания
пирамиды. На рисунке 4.4, б это шестиугольник.
2)
Из точки О
откладываем вверх высоту пирамиды и
получаем точку s
–
вершину
пирамиды.
3)
Соединяем точку s
с точками 1,
2, 3, 4, 5, 6 и
получаем изометрическую проекцию
пирамиды.
Построение
изометрии точек на поверхности пирамиды:
Изометрию
точек А
и В
строим по их координатам, взятым из
комплексного
чертежа (рис. 4.4, б).
1)
От точки О
отложим на оси х
расстояние n
(координата
y
точки А,
взятая с комплексного чертежа, рис.
3.5), получим точку
а.
2)
От точки
а
отложим
вверх высоту h
(координата z
точки А,
взятая также с комплексного чертежа,
рис. 3.5) и получим
точку А.
3)
От точки О
отложим на оси х
расстояние n1,
а на оси у
расстояние n2,
взятые с комплексного чертежа, рис. 3.5,
получим точку
в.
4)
От точки
в
отложим вверх высоту h1
и получим
точку В.
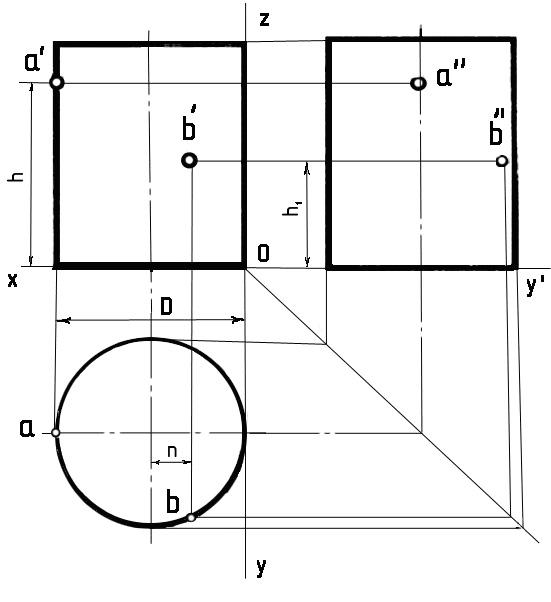
4.3 Цилиндр
Построение
фронтальной проекции цилиндра:
От
горизонтальной проекции проводим вверх
вертикальные линии связи и чертим
фронтальную проекцию нижнего основания
цилиндра –
горизонтальный отрезок, равный диаметру
D
(рис. 4.5).
От концов этого отрезка откладываем
вверх два вертикальных отрезка, равных
высоте цилиндра и чертим фронтальную
проекцию верхнего основания цилиндра
– еще один отрезок, равный диаметру
D.
Рис.
4.5 Проекции цилиндра Рис. 4.6 Изометрия
окружности Рис. 4.7 Изометрия цилиндра
Построение
профильной проекции цилиндра:
1)
Координаты
y
переносим на профильную проекцию с
помощью линий связи с горизонтальной
проекции.
2)
Координаты z
нижнего и верхнего оснований переносим
с помощью линий связи с фронтальной
проекции. Профильная проекция цилиндра
является повторением его фронтальной
проекции
Построение
проекций точек на поверхности цилиндра:
Горизонтальные
проекции точек А
и В
можно найти, проводя из данных точек
а’
и b‘
вертикальные
линии связи до их пересечения с окружностью
в точках а
и b.
Профильная
проекция точки А
— точка
а»
– строится на пересечении линий связи,
проведенных из точек а.
и
а‘.
Профильная проекция точки В
— точка
b»
– строится на пересечении линий связи,
проведенных из точек.
b
и
b‘.
Построение
изометрии
А
окружности:
Изометрическая
проекция окружности заменяется овалом.
У овала две оси – большая и малая. В
плоскости хОz
малой осью овала является ось Оу,
в плоскости
хОу
малой осью овала является ось Оz,
в плоскости
zОу
малой осью
овала является ось Ох.
Большие оси
овалов перпендикулярны малым осям.
-
Проводим
малую ось овала (рис. 4.6). -
Проводим
перпендикулярно малой оси большую ось
и обозначаем точку пересечения малой
и большой оси – О1
— центр овала. -
Через
центр овала О1
проводим две осевые штрих-пунктирные
линии, параллельные осям — Ох
и Oz
для плоскости хОz;
Оz
и Оу
для плоскости
zОу;
Ох
и Оу
для плоскости хОу. -
Из
центра О1
проводим
вспомогательную окружность радиусом,
равным радиусу изображаемой окружности. -
Из
точек 1
и 2 –
проводим
большие дуги овала радиусом 1А
= 1В = 2С = 2D.
-
Из
точек 1
или 2
проводим отрезки 1А
и 1В
или 2С
и 2D
и получаем на большой оси овала точки
3 и 4. (рис. 4.4, плоскость z
О у). -
Из
точек 3
и 4
проводим
малые дуги радиусом 3А
= 3C
= 4В = 4D.
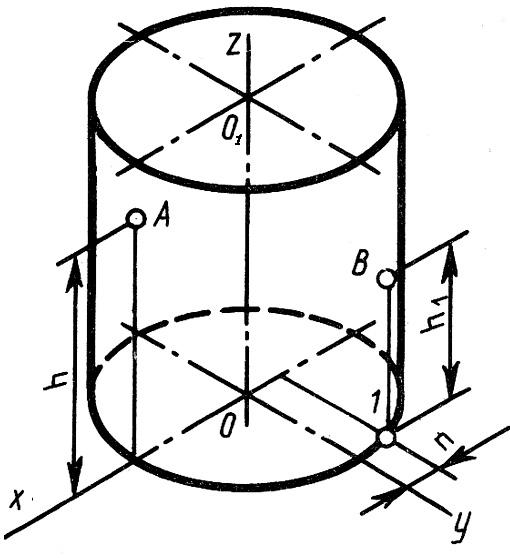
Построение
изометрии цилиндра:
1)
Строим овал — изометрию нижнего основания
в горизонтальной плоскости (рис 4.7).
2)
Из точки О
поднимаем высоту цилиндра и получаем
точку О1,
относительно которой строим второй
такой же овал – изометрию верхнего
основания.
3)
Соединяем два основания образующими
вертикальными линиями.
Построение
изометрии точек на поверхности цилиндра:
Изометрию
точек А
и В
строим по их координатам, взятым из
комплексного
чертежа (рис. 4.7).
1)
От точки пересечения оси х
с овалом нижнего основания откладываем
вверх расстояние h
(координата z
точки А),
получаем точку А.
2)
Проводим прямую, параллельную оси у
на расстоянии n
от нее, получаем точку 1.
3)
От точки 1 откладываем вверх расстояние
h1
(координата z
точки В)
получаем точку В.
(Расстояния
n,
h,
h1
взяты
с комплексного чертежа).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
























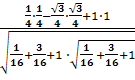 =0,7;
=0,7;