Как найти точки перегиба функции онлайн - Исправление недочетов и поиск решений вместе с Examum.ru

Интервалы выпуклости и вогнутости графика функции

С помощью онлайн-калькулятора можно найти точки перегиба и промежутки выпуклости графика функции с оформлением решения в Word. Является ли функция двух переменных f(x1,x2) выпуклой решается с помощью матрицы Гессе.

Решение онлайн
Видеоинструкция

Направление выпуклости графика функции. Точки перегиба

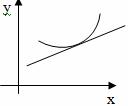
Определение: Кривая y=f(x) называется выпуклой вниз в промежутке (a; b), если она лежит выше касательной в любой точке этого промежутка.

Определение: Кривая y=f(x) называется выпуклой вверх в промежутке (a; b), если она лежит ниже касательной в любой точке этого промежутка.

Определение: Промежутки, в которых график функции обращен выпуклостью вверх или вниз, называются промежутками выпуклости графика функции.

Выпуклость вниз или вверх кривой, являющейся графиком функции y=f(x), характеризуется знаком ее второй производной: если в некотором промежутке f’’(x) > 0, то кривая выпукла вниз на этом промежутке; если же f’’(x) < 0, то кривая выпукла вверх на этом промежутке.

Определение: Точка графика функции y=f(x), разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба.

Точками перегиба могут служить только критические точки II рода, т.е. точки, принадлежащие области определения функции y = f(x), в которых вторая производная f’’(x) обращается в нуль или терпит разрыв.

Правило нахождения точек перегиба графика функции y = f(x)

Найти вторую производную f’’(x).
Найти критические точки II рода функции y=f(x), т.е. точки, в которой f’’(x) обращается в нуль или терпит разрыв.
Исследовать знак второй производной f’’(x) в промежутка, на которые найденные критические точки делят область определения функции f(x). Если при этом критическая точка x₀ разделяет промежутки выпуклости противоположных направлений, то x₀ является абсциссой точки перегиба графика функции.
Вычислить значения функции в точках перегиба.

Пример 1. Найти промежутки выпуклости и точки перегиба следующей кривой: f(x) = 6x²–x³.

Решение: Находим f ‘(x) = 12x – 3x², f ‘’(x) = 12 – 6x.

Найдем критические точки по второй производной, решив уравнение 12-6x=0. x=2.

f(2) = 6*2² – 2³ = 16

Ответ: Функция выпукла вверх при x∈(2; +∞); функция выпукла вниз при x∈(-∞; 2); точка перегиба (2;16).

Пример 2. Имеет ли точки перегиба функция: f(x)=x³-6x²+2x-1

Пример 3. Найти промежутки, на которых график функции является выпуклым и выгнутым: f(x)=x³-6x²+12x+4

Источник

Точкой перегиба
функции называется такая точка

в которой выпуклость меняется на вогнутость.

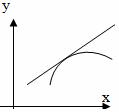
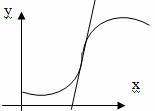
Поясним вышесказанное на примере. Рассмотрим функцию, изображенную на рисунке.

Из графика следует, что на интервале

график функции является выпуклым вверх (или вогнутым вниз). На интервале

— выпуклым вниз (или вогнутым вверх). При этом точка

является точкой перегиба функции.

Интервалы выпуклости (вогнутости) функции легко найти, используя следующую теорему:

Если на некотором промежутке вторая производная функции положительна, тогда график функции является выпуклым вниз на этом промежутке. Если отрицательна — выпуклым вверх. Т.е.:

Стоит также отметить, что в точках перегиба функции вторая производная равна нулю и при переходе через такие точки меняет свой знак.

Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha позволяет найти точки перегиба функции с описанием подробного хода решения.

Источник

Найти точки перегиба графика функции и интервалы его выпуклости и вогнутости онлайн.

Основные функции

$x^{a}$ : x^a

модуль x: abs(x)

: Sqrt[x]
: x^(1/n)
$a^{x}$ : a^x
$log_{a}x$ : Log[a, x]
: Log[x]
: cos[x] или Cos[x]

: sin[x] или Sin[x]

: tan[x] или Tan[x]

: cot[x] или Cot[x]

: sec[x] или Sec[x]

: csc[x] или Csc[x]

: ArcCos[x]

: ArcSin[x]

: ArcTan[x]

: ArcCot[x]

: ArcSec[x]

: ArcCsc[x]

: cosh[x] или Cosh[x]

: sinh[x] или Sinh[x]

: tanh[x] или Tanh[x]

: coth[x] или Coth[x]

: sech[x] или Sech[x]

: csch[x] или Csch[е]

: ArcCosh[x]

: ArcSinh[x]

: ArcTanh[x]

: ArcCoth[x]

: ArcSech[x]

: ArcCsch[x]

[19.67] =19: integral part of (19.67) — выделяет целую часть числа (integerPart)

Источник

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	— twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{»}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	—
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Показать Этапы

Номер Строки

Примеры

точки:перегиба:y=x^{3}-x
точки:перегиба:f(x)=x^4-x^2
точки:перегиба:f(x)=sqrt[3]{x}
точки:перегиба:f(x)=xe^{x^{2}}
точки:перегиба:f(x)=sin(x)
Показать больше

Описание

Пошаговый поиск точек перегиба функций

function-inflection-points-calculator

Блог-сообщения, имеющие отношение к Symbolab

Functions

A function basically relates an input to an output, there’s an input, a relationship and an output. For every input…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

22:12

Калькулятор для исследования функций

Полное исследование функции и построение графика.

С помощью данных калькуляторов можно пошагово провести полное исследование функции, и построить график функции с асимптотами.

Для этого вставляем исследуемую функцию в каждый калькулятор, как показано в примере, и получаем ответ.

1. Находим область определения функции.

2. Выясняем, не является ли функция:

а) четной, нечетной • Функции, не являющиеся ни четными, ни нечетными (neither even nor odd), называются функциями общего вида.

б) периодической

3. Находим точки пересечения графика функции с осями координат и интервалы знакопостоянства функции.

Для того, чтобы найти точки пересечения с осью Ох выбираем знак «=», для нахождения интервалов на которых функция положительна — зак «>», для интервалов на которых функция отрицательна — знак «<«.

4. Находим вертикальные, наклонные, горизонтальные асимптоты графика функции.
5. Находим точки экстремума

6. Найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.

7. Построить график функции, используя все полученные результаты исследования.

Смотри также решенные примеры в авторском исполнении. В примере подробно изложена методика исследования функций.

Категория: Исследовать функцию,построить график | Просмотров: 470199 | | Теги: построить график, найти асимптоты, исследовать функцию, найти экстремумы функции | Рейтинг: 3.2/50

Источник