Как найти точки перегиба примеры решения - Исправление недочетов и поиск решений вместе с Examum.ru

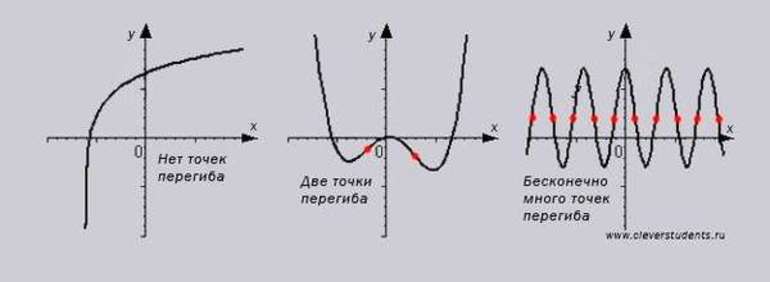
Точки перегиба графика функции

В задачах на исследование функции в одном из пунктов предлагается найти точки перегиба графика функции. Как это решить? Необходимо понимать, что такое точка перегиба по определению и её признаки.

Точка перегиба функции — это точка, в которой график функции изменяет свою выпуклость или вогнутость

Как найти?

Найти вторую производную функции $ y»(x) $
Найти точки $ x_0 $, в которых вторая производная равна нулю, имеет разрыв, или не существует
Исследовать каждую найденную точку $ x_0 $ на перегиб, с помощью третьей производной $ y»'(x) $

Как проверить является ли найденная точка $ x_0 $ перегибом? Необходимо найти третью производную $ y»'(x)$. Если $ y»'(x_0) $ ≠ $ 0 $, то исследуемая точка — это точка перегиба.

Примеры решений

Пример 1

Найти точки перегиба графика функции: $ y = 2x^4-6x^2+1 $

Решение

Найдем первую производную, заданной функции:

$$ y’ = (2x^4 — 6x^2 + 1)’ = 8x^3 — 12x $$

Теперь получим вторую производную:

$$ y» = (y’)’ = (8x^3 — 12x)’ = 24x^2 — 12 $$

Приравниваем к нулю $ y» = 0 $ и решаем уравнение:

$$ 24x^2 — 12 = 0 $$

$$ x^2 = frac{1}{2} $$

$$ x_1 = -frac{1}{sqrt{2}}, x_2 = frac{1}{sqrt{2}} $$

Найдем третью производную и вычислим её значения в точках $ x_1 $ и $ x_2 $:

$$ y»'(x) = (y»(x))’ = 48x $$

$$ y»'(x_1) = y»'(-frac{1}{sqrt{2}}) = -frac{48}{sqrt{2}} $$

$$ y»'(x_2) = y»'(frac{1}{sqrt{2}}) = frac{48}{sqrt{2}} $$

Так как $ y»'(x_1) $ и $ y»'(x_2) $ не равны нулю, то точки $ x_1 $ и $ x_2 $ соответственно точки перегиба функции.

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ x_1 = — frac{1}{sqrt{2}}, x_2 = frac{1}{sqrt{2}} $$

Пример 2

Узнать, является ли для графика функции $ y = cos x $ точка $ x_0 = frac{pi}{2} $ точкой перегиба

Решение

Найдем производные до третьего порядка фунции, указанной в условии к задаче:

$$ y'(x) = (cos x)’ = — sin x $$ $$ y»(x) = (-sin x)’ = -cos x $$ $$ y»'(x) = (-cos x)’ = sin x $$

Вычислим значения $ y»(x_0) text{ и } y»'(x_0) $:

$$ y»(x_0) = y»(frac{pi}{2}) = — cos frac{pi}{2} = 0 $$

$$ y»'(x_0) = y»'(frac{pi}{2}) = sin frac{pi}{2} = 1 $$

Так как $ y»(frac{pi}{2}) = 0 $, а $ y»'(frac{pi}{2}) neq 0 $, то делаем вывод, что точка $ x_0 = frac{pi}{2} $ является точкой перегиба для функции $ y = cos x $

Ответ

Точка $ x_0 = frac{pi}{2} $ точка перегиба

Источник

Содержание:

Теоремы о выпуклости функции и точках перегиба
Схема исследования функции на выпуклость, вогнутость

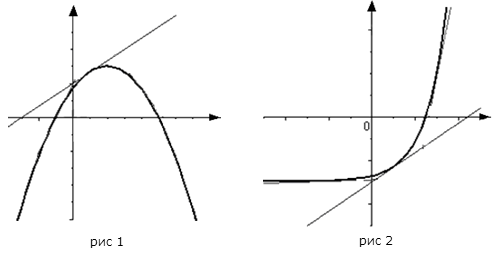
График функции $y=f(x)$, дифференцируемой на интервале
$(a ; b)$, является на этом интервале выпуклым, если график
этой функции в пределах интервала $(a ; b)$ лежит не выше любой
своей касательной (рис. 1).

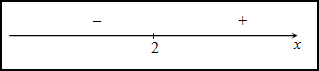
График функции $y=f(x)$, дифференцируемой на интервале
$(a ; b)$, является на этом интервале вогнутым, если график
этой функции в пределах интервала $(a ; b)$ лежит не ниже любой
своей касательной (рис. 2).

Теоремы о выпуклости функции и точках перегиба

Теорема

(Об условиях выпуклости или вогнутости графика функции)

Пусть функция $y=f(x)$ определена на интервале
$(a ; b)$ и имеет непрерывную, не равную нулю в точке
$x_{0} in(a ; b)$ вторую производную. Тогда, если
$f^{prime prime}(x)>0$ всюду на интервале
$(a ; b)$, то функция имеет вогнутость на этом интервале,
если $f^{prime prime}(x) lt 0$, то функция имеет выпуклость.

Определение

Точкой перегиба графика функции $y=f(x)$
называется точка $Mleft(x_{1} ; fleft(x_{1}right)right)$, разделяющая промежутки выпуклости и вогнутости.

Теорема

(О необходимом условии существования точки перегиба)

Если функция $y=f(x)$ имеет перегиб в точке
$Mleft(x_{1} ; fleft(x_{1}right)right)$, то
$f^{prime prime}left(x_{1}right)=0$ или не существует.

Теорема

(О достаточном условии существования точки перегиба)

Если:

первая производная $f^{prime}(x)$
непрерывна в окрестности точки $x_{1}$;
вторая производная $f^{prime prime}(x)=0$ или не существует в точке $x_{1}$;
$f^{prime prime}(x)$ при переходе через точку $x_{1}$ меняет свой знак,

тогда в точке $Mleft(x_{1} ; fleft(x_{1}right)right)$ функция $y=f(x)$ имеет перегиб.

Схема исследования функции на выпуклость, вогнутость

Найти вторую производную функции.
Найти точки, в которых вторая производная равна нулю или не существует.
Исследовать знак производной слева и справа от каждой найденной точки и сделать вывод об интервалах выпуклости и точках перегиба.

Пример

Задание. Найти интервалы выпуклости/вогнутости функции
$y=frac{x^{3}}{6}-x^{2}+3 x+1$

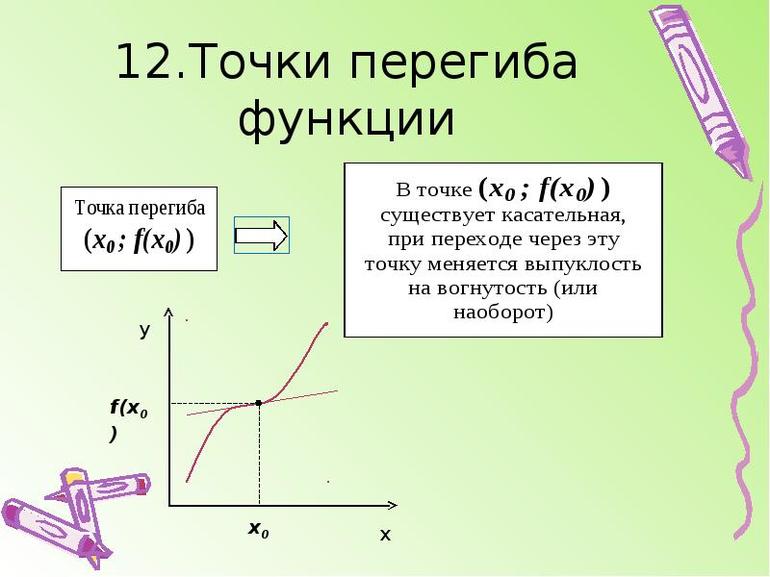
Решение. Найдем вторую производную заданной функции:

$y^{prime prime}=left(frac{x^{3}}{6}-x^{2}+3 x+1right)^{prime prime}=left(frac{x^{2}}{2}-2 x+3right)^{prime}=x-2$

Находим точки, в которых вторая производная равна нулю, для этого решаем уравнение
$y^{prime prime}(x)=0$:

$y^{prime prime}(x)=x-2=0 Rightarrow x=2$

Исследуем знак второй производной слева и справа от полученной точки:

Так как на промежутке $(-infty ; 2)$ вторая производная
$y^{prime prime}(x) lt 0$, то на этом промежутке функция
$y(x)$ выпукла; в силу того, что на промежутке
$(2 ;+infty)$ вторая производная
$y^{prime prime}(x)>0$ — функция вогнута. Так как при переходе через
точку $x=2$ вторая производная сменила знак, то
эта точка является точкой перегиба графика функции.

Ответ. Точка $x=2$ — точка перегиба графика функции.

На промежутке $(-infty ; 2)$ функция выпукла, на промежутке
$(2 ;+infty)$ функция вогнута.

Читать дальше: асимптоты графика функции.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

Общие сведения

Для определения точек перегиба функции необходимо разобрать основные определения и базовые компоненты, необходимые для их нахождения. Функция — математическая запись зависимости одной переменной от другой. Последняя называется аргументом, а на графике в декартовой системе координат ее определяет абсцисса.

Графиком или графическим представлением называется геометрическое тело, находящееся в системе координат и состоящее из определенного количества точек с заданными координатами. Перегиб — совокупность координат по ординате и абсциссе, в которой наблюдается изменение поведения функции, образующих выпуклость или вогнутость.

Для нахождения последних следует иметь определенные базовые навыки определения производных первого, второго и третьего порядков.

Понятие производной

Производная — операция, используемая не только при исследовании функции, но и при описании какого-либо процесса, определения площади геометрических тел и т. д. Она позволяет существенно сократить время, необходимое для вычислений. Главным условием ее определения является постоянный рост функции. Если последняя не растет (остается постоянной — константой), ее дифференциал равен нулю. В этом случае говорят, что она не существует.

Однако производная применяется не только в алгебре, но и в других сферах деятельности человека. С ее помощью можно вычислить силу, мощность, величину тока и другие физические величины, зависящие от определенных параметров.

В медицине производная применяется при исследовании лекарственных препаратов, обладающих побочными действиями. Последние отрицательно влияют на жизнедеятельность организма человека. Следовательно, ученые в области фармацевтики добиваются лучшего лечебного эффекта с минимальной вероятностью пагубного воздействия на организм.

Производная применяется при проектировании компьютерных игр, в которых персонажи осуществляют сложные движения.

Траектории последних нужно рассчитать скоростными методами, а их и предоставляют дифференциалы функций движения различных компонентов системы, т. е. прыжки героя и противников, движение элементов внешней среды (деревьев, травы и т. д. ).

Смысловые интерпретации

Для понимания физического и математического смысла производной нужно разобрать ее определение в математической интерпретации: производная представляет границу предела отношения приращения некоторой функциональной зависимости двух или более переменных к приращению независимой переменной (аргумента), который стремится к нулевой величине.

Из определения можно сделать вывод, что обязательное условие существование дифференциала — постоянный рост или убывание функции в заданной точке. Обратной операцией дифференцирования является интегрирование или поиск первообразной.

Геометрическим смыслом является величина тангенса угла наклона прямой-касательной к графическому отображению. Для построения необходимо провести прямую, которая должна пересекать график функции минимум в двух точках, а затем рассмотреть место пересечения. Это будет ось вращения прямой. Если и далее вращать секущую, она в некотором положении будет касаться графика функции в одной точке, т. е. преобразуется в касательную.

Физический смысл основан на характеристике изменения скорости роста физической величины. Например, при рассмотрении закона движения тела в пространстве S= s (t). Путь, пройденный им, зависит от времени и скорости. Для нахождения последней V (tм) в текущий момент времени tм необходимо вычислить производную, т. е. V (tм)=[s (tм)]’.

При вычислении производной второго порядка величина будет называться ускорением, т. е. a (tм)=[[s (tм)]’]’=[V (tм)]’. Для выполнения операции дифференцирования необходимо знать основные правила.

Правила дифференцирования

Для нахождения производных простых и сложных функций существуют определенные правила. К ним относятся:

Постоянную величину (const) можно вынести за знак производной, т. е. (const*p (t))’=const*(p (t))’
Дифференциал суммы (разности) двух и более тождеств эквивалентен производной каждой из компонентов, т. е. (p (t)+r (t)+s (t))’=p'(t)+r'(t)+s'(t) или (p (t)-r (t)-s (t))’=p'(t)-r'(t)-s'(t).
Производная произведения двух простых выражений соответствует сумме дифференциала первой функции, умноженной на вторую, и l компонента, который умножается на дифференциал второго тождества. Математическая запись: (p (t)*r (t))’=p'(t)*r (t)+p (t)*r'(t).
Если взять производную тождества частного двух функций, в числителе обыкновенной дроби следует записать разность произведений, состоящих из дифференциала I компонента и II, и дифференциала второго и первого, а затем результат разделить на квадрат второго выражения. Короткая математическая формулировка имеет вид: (p (t)/r (t))’=[p'(t)*r (t)-p (t)*r'(t)]/[r (t)]^2.
Дифференциал сложного тождества состоит из произведения производных элементов, которые входят в его состав, т. е. [р (r (t))]’=[r (t)]’ * [p (r (t))]’.

Для понимания последнего пункта необходимо разобрать пример p=(3/2)*sin (4t²−5). Для вычисления производной следует воспользоваться специальным алгоритмом, первым и последним правилами:

Записать выражение с учетом знака дифференциала: p’=[(3/2)*sin (4t²−5)]’.
Постоянную величину вынести за знак дифференциала (1 правило): p’=(3/2)*[sin (4t²−5)]’.
Взять производную I элемента: [4t²−5]’=8t-0=8t.
II: [sin (4t²−5)]’=cos (4t²−5).
Записать результат: p’=8tcos (4t²−5).

Очень важно правильно «разбивать» исходное выражение на компоненты, поскольку от этого зависит результат и достоверность вычислений. После рассмотрения правил дифференцирования следует перейти к методике нахождения производной.

Методика нахождения

Нахождение производной заданной функции строится на правилах. Методика имеет следующий вид:

Написать выражение.
Произвести математические операции по упрощению тождества, чтобы удобно было находить дифференциал.
Выполнить операцию нахождения производной.
Записать ответ.

Однако при нахождении точек перегиба необходимо уметь вычислять дифференциалы второго и третьего порядка. Это делать несложно, поскольку достаточно взять один раз производную (l порядка), а затем — второй (II), а также III.

Все правила действуют для дифференциалов любого порядка. Кроме того, очень важно после операции дифференцирования приводить подобные компоненты, т. к. это действие позволит осуществить вычисления за короткий промежуток времени, а также избежать множества ошибок.

Для реализации алгоритма необходимо разобрать решение примера «s (t, v)=4t*8v+2t²+3v³», в котором требуется определить дифференциал II порядка. Нахождение производной выполняется по методике:

Написать выражение, учитывая знак производной: s'(t, v)=[4t*8v+2t²+3v³]’.
Найти производную произведения: [4t*8v]’=32v+32t.
Дифференциал суммы: [2t²+3v³]’=t+v.
Привести подобные слагаемые: 32v+32t+t+v=33t+33v.
Вынести 33 за скобки и взять вторую производную: 33[t+v]’=66.
Результат: s'(t, v)=66.

Cледует обратить внимание на четвертый пункт алгоритма, в котором нужно приводить подобные элементы, поскольку в пятом пункте дифференциал найти довольно просто.

Для проверки результата можно воспользоваться специальным приложением, которое называется онлайн-калькулятором. Однако на начальных стадиях обучения специалисты не рекомендуют пользоваться им для решения задач.

Выпуклости и вогнутости

Для нахождения точек перегиба на заданном интервале необходимо знать основное условие их существования.

Оно гласит: функция s (t) имеет выпуклость или вогнутость в некоторой точке P (to, s (t)), когда производная II порядка обращается в нулевую величину, отсутствует или является разрывом. Кроме того, существуют 2 достаточных условия существования искомых точек:

ll производная меняет знак и направление, но по модулю эквивалентна искомой функции.
В заданной точке дифференциал ll порядка эквивалентен нулю, а третьего — нет.

Первое условие записывается в математической форме следующим образом: |s (t)|=|-[s (t)]»|. Во втором случае формула имеет вид: [s (t)]»=0 и [s (t)]»’ ≠0. Знак в последнем выражении «≠» называется «неравенством». Кроме того, последнюю формулу можно записать следующим образом: [s (t)]»’ <> 0.

Пример решения

Следует найти точки перегиба для тождества вида s (t)=(¼)t⁴−(1/12)4t³+2t+7.

Задача решается по следующему алгоритму:

s'(t)=[(¼)t⁴−(1/12)4t³+2t+7]’=t³-t²+2.
s»(t)=3t²−2t.
Приравнять s»(t) к 0: 3t²−2t=0.
Найти корни уравнения в третьем пункте: t1=0 и t2=2/3.
Третья производная: s»'(t)=6t-2.
Подставить корни тождества, полученные в четвертом пункте, в s»'(t): s»'(0)=6*0−2=-2<0 и s»'(2/3)=6*(2/3)-2=2>0.
Координаты искомых точек: (0;-2) и (2/3;2).

Следует обратить внимание на 6 пункт алгоритма. В нем значения не равны нулю. Из этого следует, что у этого графика функции всего 2 точки перегиба, координаты которых эквивалентны (0;-2) и (2/3;2).

Таким образом, для нахождения точек перегиба функции для начала следует ознакомиться с производной и правилами ее нахождения, а затем переходить к условиям поиска вогнутостей и выпуклостей.

Источник

Загрузить PDF

В дифференциальном исчислении точка перегиба — эта точка кривой, в которой ее кривизна меняет знак (с плюса на минус или с минуса на плюс). Это понятие используется в машиностроении, экономике и статистике для определения существенных изменений в данных.

1

Определение вогнутой функции. Середина любой хорды (отрезок, соединяющий две точки) графика вогнутой функции лежит либо под графиком, либо на нем.
2

Определение выпуклой функции. Середина любой хорды (отрезок, соединяющий две точки) графика выпуклой функции лежит либо над графиком, либо на нем.
3
Определение корней функции. Корень функции – это такое значение переменной «х», при котором у = 0.
- При построении графика функции корни – это точки, в которых график пересекает ось Х.
Реклама

1
Найдите первую производную функции. Посмотрите правила дифференцирования в учебнике; вы должны научиться брать первые производные, и только потом переходить к более сложным вычислениям. Первые производные обозначаются как f ‘(х). Для выражений вида ax^p + bx^(p−1) + cx + d первая производная имеет вид: apx^(p−1) + b(p − 1)x^(p−2) + c.
- Например, найдите точки перегиба функции f(х) = х^3 +2х -1. Первая производная этой функции имеет вид:
  f ′(x) = (x^3 + 2x − 1)′ = (x^3)′ + (2x)′ − (1)′ = 3x^2 + 2 + 0 = 3×2 + 2
2
Найдите вторую производную функции. Вторая производная – это производная от первой производной исходной функции. Вторая производная обозначается как f ′′(x).
- В приведенном выше примере вторая производная имеет вид:
  f ′′(x) = (3×2 + 2)′ = 2 × 3 × x + 0 = 6x
3
Приравняйте вторую производную к нулю и решите полученное уравнение. Полученный результат будет предполагаемой точкой перегиба.
- В приведенном выше примере ваш расчет выглядит следующим образом:
  f ′′(x) = 0
  6x = 0
  x=0
4
Найдите третью производную функции. Чтобы убедиться, что полученный результат на самом деле является точкой перегиба, найдите третью производную, которая является производной от второй производной исходной функции. Третья производная обозначается как f ′′′(x).
- В приведенном выше примере третья производная имеет вид:
  f ′′′(x) = (6x)′ = 6
Реклама

1
Проверьте третью производную. Стандартное правило оценки предполагаемой точки перегиба: если третья производная не равна нулю (то есть f ′′′(x) ≠ 0), то предполагаемая точка перегиба является настоящей точкой перегиба. Проверьте третью производную; если она не равна нулю, то вы нашли настоящую точку перегиба.
- В приведенном выше примере третья производная равна 6, а не 0. Поэтому вы нашли настоящую точку перегиба.
2
Найдите координаты точки перегиба. Координаты точки перегиба обозначаются как (x,f(x)), где х — значение независимой переменной «х» в точке перегиба, f(х) — значение зависимой переменной «у» в точке перегиба.
- В приведенном выше примере при приравнивании второй производной к нулю вы нашли, что х = 0. Таким образом, чтобы определить координаты точки перегиба, найдите f(0). Ваш расчет выглядит следующим образом:
  f(0) = 0^3 +2×0−1 = −1.
3
Запишите координаты точки перегиба. Координаты точки перегиба – это найденные значения «х» и f(x).
- В приведенном выше примере точка перегиба — это точка с координатами (0, -1).
Реклама

Советы

Первая производная от свободного члена (простого числа) всегда равна нулю.

Об этой статье

Эту страницу просматривали 21 999 раз.

Была ли эта статья полезной?

Источник

1. Исследование выпуклости графика функции

График функции (f(x)) имеет на ((a,b)) выпуклость, направленную вниз (вверх), если он расположен не ниже (не выше) любой касательной к графику функции на ((a,b)).

Если функция (f(x)) имеет на интервале ((a,b)) вторую производную и

f′′(x)≥0

(

f′′(x)≤0

) во всех точках ((a,b)), то график функции (f(x)) имеет на ((a,b)) выпуклость, направленную вниз (вверх).

Пример:

определить выпуклости функции

f(x)=x3+x

Вторая производная этой функции — это

f′′(x)=6x

. Она отрицательна, если (x<0), положительна, если (x>0).

Значит, график (f(x)) в интервале

−∞;0

имеет выпуклость, направленную вверх, и в интервале

0;+∞

имеет выпуклость, направленную вниз.

2. Нахождение точек перегиба функции

Чтобы определить точки перегиба функции (f(x)), нужно найти точки, в которых вторая производная этой функции является нулём или не существует (и которые принадлежат области определения функции). Тогда можно определить знак второй производной функции в соответствующих интервалах — вычислив значения второй производной в какой-либо точке интервала.

Если вторая производная функции в точке меняет знак, эта точка является точкой перегиба, если не меняет, не является точкой перегиба.

Пример:

рассмотрим функцию

f(x)=x3+x

Вторая производная этой функции — это

f′′(x)=6x

. Она отрицательна, если (x<0), и положительна, если (x>0). Значит, в точке (x=0) вторая производная меняет знак, и эта точка — точка перегиба функции.

Источник