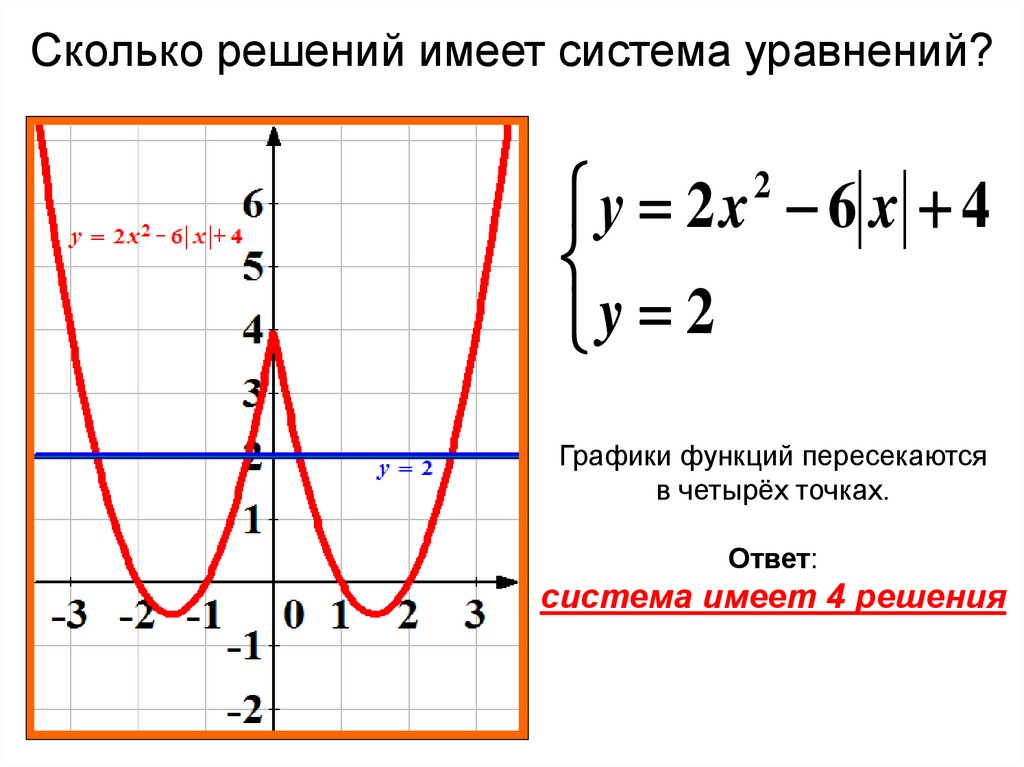
Как найти точки перемены знака - Исправление недочетов и поиск решений вместе с Examum.ru

Область определения функции

Сегодня потренируемся в отыскании области определения выражения и функции.

Когда отыскивают область определения функции, то часто она совпадает с областью определения выражения, задающего функцию: такая область определения называется естественной. Но бывает и так, что условия задачи накладывают особые ограничения: например, естественная область определения функции от (-8) до 8, но аргумент этой функции — время (или вес). Понятно тогда, что время (как и вес) не может быть отрицательной величиной и тогда естественная область определения такой функции сужается до промежутка (0; 8).
При отыскании области определения функции надо помнить о следующих ограничениях:
1. При извлечении корня четной степени подкоренное выражение обязано быть неотрицательным (что не запрещает ему быть равным нулю). 2. Знаменатель дроби не может быть равным нулю. 3. Выражение, стоящее под знаком логарифма, не может быть отрицательным или равняться нулю. 4. Выражение, стоящее под знаком арксинуса или арккосинуса, не может превышать 1 по модулю
Также надо помнить, что область определения всегда нужно искать для исходной функции, до каких-либо преобразований.
Например, функции y=-1 и y=-x/x имеют разные области определения: для первой это — вся числовая ось, а вторая не определена в точке 0. То же относится к функциям $y=sqrt{x^2}$ и $y=(sqrt{x})^2$ — у первой область определения — также вся числовая ось, а у второй — x{in} [)

1. Найдите область определения выражения:
$sqrt{(x^2-11x+24)^{-1}}$
Перепишем выражение:
$sqrt{1/{x^2-11x+24}}$
Так как выражение стоит под корнем четной степени, значение его не должно быть отрицательным:
${1/{x^2-11x+24}}>=0$
Дробь положительна, если числитель и знаменатель ее одновременно положительны или отрицательны. У нас в числителе положительное число, поэтому знаменатель неотрицателен. Кроме того, знаменатель не может быть равен нулю, поэтому неравенство становится таким:
${x^2-11x+24}>0$
Получили квадратное неравенство. Находим корни квадратного уравнения, чтобы выяснить точки перемены знака:
${x^2-11x+24}=0$
$D={b^2-4ac}=121-4*24=25$
$x_1={11-5}/2=3$
$x_2={11+5}/2=8$
Наносим полученные точки на координатную прямую и расставляем знаки. Так как x^2 (старший член) — со знаком «плюс», то ветви параболы направлены вверх, на самом правом отрезке ставим знак «плюс», а далее знаки меняются. Точки выкалываем, поскольку неравенство строгое:

Ответ: — круглые скобки показывают, что концы интервалов не входят в ответ.

2. Найдите область определения выражения:

$sqrt{-2x^2+5x+2}$
Так как выражение стоит под корнем четной степени, значение его не должно быть отрицательным:
${-2x^2+5x+2}>=0$
Получили квадратное неравенство. Находим корни квадратного уравнения, чтобы выяснить точки перемены знака:
${2x^2-5x-2}=0$
$D={b^2-4ac}=25-4*(-2)2=41$
$x_1={5+sqrt{41}}/4$
$x_2={5-sqrt{41}}/4$

Наносим полученные точки на координатную прямую и расставляем знаки. Так как x^2 (старший член) в исходном неравенстве — со знаком «минус», то ветви параболы направлены вниз, на самом правом отрезке ставим знак «минус», а далее знаки меняются. Точки закрашиваем, поскольку неравенство нестрогое.
Ответ: – квадратные скобки показывают, что концы отрезка входят в ответ.

3. Найдите область определения функции:

Очевидно, что область определения функции будет совпадать с областью определения выражения – ищем естественную область определения функции. Данное выражение имеет смысл только при — задача сводится к решению этого неравенства. Определяем точки перемены знака:

Изображаем полученные точки на числовой оси, ставим знаки:

Точки закрашены, концы интервалов входят в решение. Тогда область определения функции: {D(f)}= (] union [)
4. Найдите область определения функции:
Очевидно, что область определения функции будет совпадать с областью определения выражения – ищем естественную область определения функции. Данное выражение имеет смысл только при ; – задача сводится к решению системы неравенств. Определяем точки перемены знака:

Изображаем полученные точки на числовой оси:

Решение системы неравенств: {x>=1}
Область определения функции: D(f)= [ )
5. Найдите область определения функции:
Очевидно, что область определения функции будет совпадать с областью определения выражения
– ищем естественную область определения функции. Данное выражение имеет смысл только при – задача сводится к решению неравенства.
Рассмотрим два случая:

Решение:
Или

Решение: x<{-2}
Область определения функции: [)
6. Найти область определения функции:
$y=log_3{delim{|}{x+3}{|}}+2log_3{1-x^3)$
Решение:
$delim{lbrace}{matrix{2}{1}{{{1-x^3}>0}{delim{|}{x+3}{|}>0}}}{}$

Ответ:

7. Найти область определения функции: $y=log_{0,3}(4^{2x-1}-2^{3x})$
Решение:
$4^{2x-1}-2^{3x}>0$
${1/4}*8^{x}*2^{x}-8^{x}>0$
$8^{x}*({1/4}*2^{x}-1)>0$
$2^{x}-4>0$
$2^{x}>2^2$
x>2
Ответ:
8. Найти область определения функции:
$y={{lg(x+3)-sqrt{x^2-x-6}}/{25-x^2}}*arccos{{1/7}(x-1)}$
Решение:
$delim{lbrace}{matrix{5}{1}{{{x+3}>0}{x^2-x-6>=0}{25-x^2<>0}{{1/7}(x-1)>=-1}{{1/7}(x-1)<=1}}}{}$

Ответ:

Источник

Download Article

Learn how to take the derivative of a function to get its inflection points

Download Article

Understanding Concavity and Inflection

Finding the Derivatives of a Function

Checking the Candidate Inflection Points

Troubleshooting

Using a Scientific Calculator

Video

Tips

You just learned about inflection points in calculus and now you’ve got a bunch of math problems asking you to find them. You’ve got a function and a graph, so where do you go from there? With our help and a bit of derivative magic, finding a function’s inflection points is actually pretty easy! In this article, we’ll provide you with all the steps you need to find and check points of inflection. As a bonus, we’ll show you how to use your scientific calculator to calculate points of inflection for you. If you’re ready to solve your math problems, read on!

Things You Should Know

An inflection point is where a function changes concavity and where the second derivative of the function changes signs.
Take the first and second derivative of the function using the power rule.
Set the second derivative equal to 0 to find the candidate, or possible, inflection points.
Plug in a value greater than and less than the candidate point to see if the second derivative changes signs at the point.

1
Learn the difference between concave up and concave down. To understand inflection points, you need to understand when a function is concave up or down on a graph. Many functions have both concave up and concave down intervals, with an inflection point existing where a function changes concavity. Luckily, concave up and down are easy to distinguish based on their names and what they look like.^[1]
- A concave down function is shaped like a hill or an upside-down U. It’s a function where the slope is decreasing. When it’s graphed, no line segment that joins 2 points on its graph ever goes above the curve.
- A concave up function, on the other hand, is shaped like a U. It’s a function where the slope is increasing. No line segment that joins 2 points on its graph ever goes below the curve.
- In the graph above, the red curve is concave up, while the green curve is concave down.
2
Identify the roots of a function. A root of a function is the point where the function equals zero, or where the function intersects the x-axis. In the graph above, the roots of the green parabola are at and ^[2]
- A function can also have more than 1 root.
Advertisement
3
Find an inflection point where a function changes concavity. Remember how there’s a difference between concave up and concave down? An inflection point is a point on a function where its concavity changes, either from upwards to downwards or downwards to upwards. It is also the point where the second derivative of the function changes signs from positive to negative or negative to positive. For the point to be a point of inflection, it has to both switch concavity and change signs on the second derivative.^[3]
- To find the inflection point on a graph, look for the point where the function switches concavity. On the graph above, it’s the middle point where the function changes from concave down to concave up.

1
Take the first derivative of the given function. You’ll need your function’s second derivative to find your inflection points. Before you get the second derivative, you have to find the first derivative of the function. First derivatives are denoted as $f^{{prime }}(x)$ or ${frac {{mathrm {d}}f}{{mathrm {d}}x}}$ . To solve your function’s first derivative, use the power rule. Multiply x by its exponent and then reduce the exponent by 1.^[4]
- For example, find the inflection point of the function below.
- The derivatives of basic functions are usually found in most calculus textbooks; you need to learn how to find basic derivatives before moving on to more complex functions.
2

Differentiate the function again to get the second derivative. The second derivative is the derivative of the first derivative. It is denoted as $f^{{prime prime }}(x)$ or ${frac {{mathrm {d}}^{{2}}f}{{mathrm {d}}x^{{2}}}}.$ Simply use the power rule again to get the second derivative.
3

Set f’’(x) equal to 0 to find the candidate inflection points. Solving f’’(x) = 0 only gives you the candidate inflection points. These are the x-values of the possible inflection points for the function. You still need to test the points on the second derivative to make sure it changes concavity, or switches its sign from positive to negative or negative to positive.^[5]

1

Plug a value higher and lower than the inflection point into f’’(x). To check if the second derivative changes signs, select 1 value that is greater than the candidate point and 1 value that is less than it. Then, plug each value into the second derivative. If the sign of the second derivative is different for both values, the candidate inflection point is an inflection point. If the sign doesn’t change, the candidate point is not an inflection point.^[6]
2

Substitute the inflection point into the original function to get its y-value. While you now know the x-value of the inflection point, you don’t know where it is on the y-axis. Simply go back to the original function and plug in the inflection point to get its y-value.^[7]
3

Evaluate the function to find the inflection point’s coordinates. The coordinate of the inflection point is denoted as In our example, the coordinates of the inflection point are ^[8]

1

Check the concavity of every candidate inflection point. Oftentimes, people assume there’s no inflection point when the candidate point is . However, this isn’t true. Remember, 0 can be graphed, so if you get 0 as your candidate point, it might be an inflection point.^[9]
2

Include candidate points where the derivative is undefined. When you find possible inflection points, you have to look for instances where the second derivative equals 0 and where the second derivative is undefined. If you only look for points where the second derivative is 0, you might miss inflection points where the function is undefined.^[10]
3

Analyze the second derivative, not the first one. When you’re finding inflection points, you only consider the second derivative. If you set the first derivative equal to 0, your answer will give you extremum points instead.^[11]

1
Head to your “Plots” function on your calculator. It’s easy to use a scientific calculator to find inflection points. On most scientific calculators, just press the “diamond” or the “second” button, then click F1. This takes you to your Y plots where you can enter up to 7 functions.^[12]
- This is true on both the TI-84 and the TI-89, but it may not be the exact same on older models.
2
Enter the function into y1. Clear out any remaining functions you had in your y plots. Then, type in the function after the equal sign. Remember to keep any parentheses involved in the function so your answer is correct.^[13]
- For example, the function might be ${displaystyle y1=x^{3}-9/2x^{2}-12x+3}$
3
Click “graph.” On most calculators, you press the “diamond” or “second” button then click F3. If you have to adjust your window on the calculator, hit “diamond” or “second” and press F2. Then, select “standard zoom.”^[14]
- Don’t worry if your screen doesn’t show the whole graph just yet—you will adjust the zoom later.
4
Adjust the window until you see the whole graph. When you open up the graphing window, you might not see the entire curve of your graph. If that’s the case, click the “diamond” or “second” button, then open up F2 for zoom again. Simply increase or decrease your minimum and maximum axis to get the graph to fit inside the window.^[15]
- It might take a little adjustment and back-and-forth to find your graph.
5
Click “Math,” then “Inflection.” Hit the “diamond” or “second” button, then select F5 to open up “Math.” In the dropdown menu, select the option that says “Inflection.”^[16]
- This is—you guessed it—how to tell your calculator to calculate inflection points.
6
Place the cursor on the lower and upper bound of the inflection. Your calculator will give you a message saying “Lower?” Move the arrows on your calculator until the cursor is to the left of the inflection point. Then, your calculator will ask “Upper?” Move your cursor so it’s to the right of the inflection point. To get your inflection point, hit “Enter.”^[17]
- This is how you get your calculator to guess where the inflection point is. Now you have your answer!

Add New Question

Question

What if the second derivative intersects with the x-axis, but does not dip below it?

This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.

wikiHow Staff Editor

Staff Answer

The second derivative has to cross the x-axis for there to be an inflection point. If the second derivative only touches the x-axis but doesn’t cross it, there’s no inflection point.
Question

What if the second derivative is a constant? How do I find the inflection point?

Inflection points are where the second derivative changes sign. If it is constant, it never changes sign, so there exists no inflection point for the function.
Question

Can the first derivative become zero at an inflection point?

Orangejews

Community Answer

Yes, for example x^3. It changes concavity at x=0, and the first derivative is 0 there.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

Alternatively, take the third derivative of a function to find the inflection points. If the third derivative does not equal 0, there is an inflection point. If the third derivative is positive, the inflection point is increasing; if it’s negative, the point is decreasing.^[18] However, taking such derivatives with more complicated expressions is often not desirable.
All linear functions have no inflection points. This is because linear functions do not change slope (the entire graph has the same slope), so there is no point at which the slope changes.
When you’re testing the candidate points, you are only looking for a sign change. You are not actually evaluating the value.

Show More Tips

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

To find inflection points, start by differentiating your function to find the derivatives. Then, find the second derivative, or the derivative of the derivative, by differentiating again. To locate a possible inflection point, set the second derivative equal to zero, and solve the equation. Finally, find the inflection point by checking if the second derivative changes sign at the candidate point, and substitute back into the original function. For more tips on finding inflection points, like understanding concave up and down functions, read on!

Did this summary help you?

Thanks to all authors for creating a page that has been read 337,303 times.

Reader Success Stories

«Here is what helped me: If the sign of the second derivative changes as you pass through the candidate inflection…» more

Did this article help you?

Источник

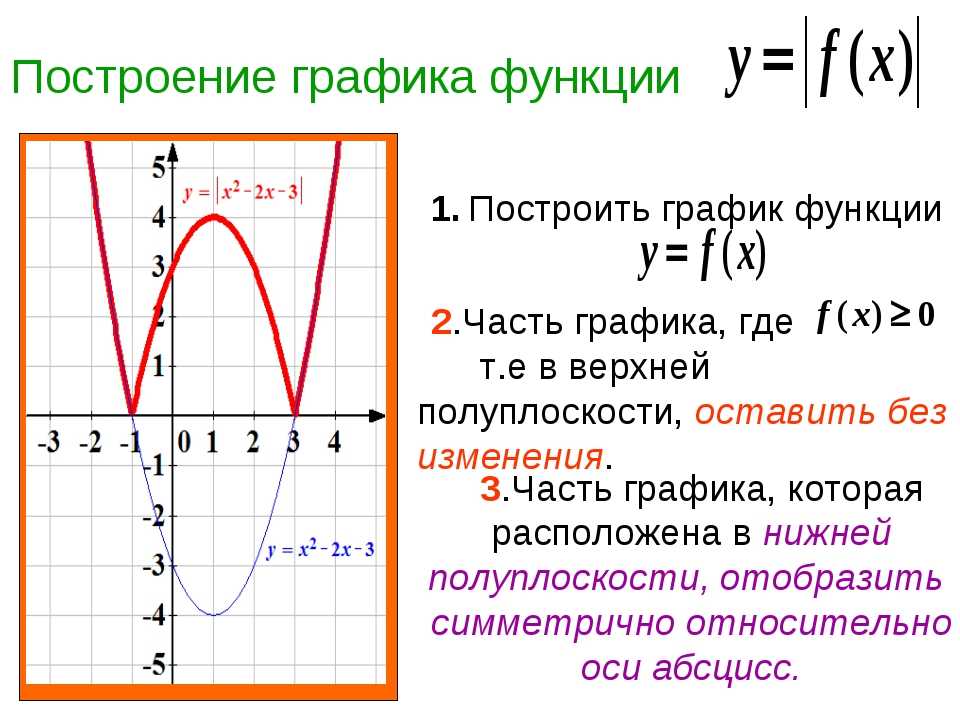
Обучение
учащихся построению графиков функций с модулем

Построение графиков,
содержащих модуль, осуществляется двумя способами:

1. На
основании определения модуля

Построение графика функции

Приведем пример построения графика функции

Построение графика функции

Приведем пример построения графика функции

2. На
основании правил геометрического преобразования графиков функций.

Какие геометрические преобразования, можно
использовать при построении графиков функций? (параллельный перенос вдоль
осей ОХ и ОУ, симметричное отображение относительно осей или точки)

Построение
графика .

Чтобы построить график функции , если известен график функции , нужно оставить на месте ту его часть, где , и симметрично отобразить относительно оси Х другую его часть,
где .

Алгоритм построения графика:

1. Построить график функции ,

2. Часть графика , лежащая над осью ОХ, сохраняется, а часть его, лежащая под
осью ОХ, отображается симметрично относительно оси ОХ.

Построение
графика .

Чтобы построить график функции , если известен график функции , нужно оставить на месте ту его часть, где , а при отобразить построенную часть симметрично относительно оси ОУ.

Алгоритм построения графика:

Построить график функции ,

При график сохраняется, а при отображается построенная часть симметрично относительно оси ОУ.

o Приведем пример
построения графика функции

В “основе” его лежит
график функции, он выглядит
так :

Теперь построим график

Чтобы получить этот
график, достаточно всего лишь сдвинуть полученный ранее график на три единицы
вправо. Заметим, что, если бы в знаменателе дроби стояло бы выражение х+3, то
мы сдвинули бы график влево:

Теперь необходимо
умножить на два все ординаты, чтобы получить график функции

Наконец, сдвигаем график вверх на две
единицы:

Последнее, что нам осталось сделать, это
построить график данной функции, если она заключена под знак модуля. Для этого
отражаем симметрично вверх всю часть графика, ординаты которой отрицательны (ту
часть, что лежит ниже оси х):

o Теперь
построим график функции

Выражение, стоящее под
знаком модуля, меняет знак в точке х=2/3. При х<2/3 функция запишется так:

При х>2/3 функция запишется так:

То есть точка х=2/3 делит нашу координатную
плоскость на две области, в одной из которых (правее) мы строим функцию ,

а в другой (левее) – график функции

o Следующий график –
также ломаная, но имеет две точки излома, так как содержит два выражения под
знаками модуля:

Посмотрим, в каких точках подмодульные
выражения меняют знак:

Расставим знаки для подмодульных выражений
на координатной прямой:

Раскрываем модули на первом интервале:

На втором интервале:

На третьем интервале:

Таким образом, на интервале (-∞; 1.5] имеем
график, записанный первым уравнением, на интервале [1.5; 2] – график,
записанный вторым уравнением, и на интервале [2;∞) — график по третьему
уравнению:

Строим:

4. Теперь можем построить график,
похожий на один из предыдущих, и все же отличающийся:

В основе опять знакомый нам график функции

но, если в знаменателе x стоит под знаком
модуля,

то график имеет вид:

Теперь произведем сдвиг на три единицы,

при этом сдвинутся обе части: правая
— вправо, левая — влево (своеобразное зеркало : отходишь дальше — видно больше)

График этой функции, умноженной на два,

выглядит так:

Теперь можно поднять график по оси у:

и тогда он будет таким:

Наконец, строим окончательный вид графика,
отражая все, что ниже оси абсцисс, вверх:

5.Очень интересно выглядит график функции

В точках 2 и (-2) знак подмодульного
выражения меняет знак, поэтому функция состоит из трех кусков (точки 2 и (-2)
выколоты). На участках (-∞; -2) и (2; ∞) справедливо первое
уравнение, а на участке (-2;2) — второе:

6. Две следующие функции отличаются знаком,
и графики их выглядят по разному:

7. Еще два похожих графика, вид которых
меняется в зависимости от х в показателе степени:

Первый:

Второй:

8.Теперь построим график такой функции:

Здесь точкой перемены знака подмодульного
выражения является х=4. Тогда на интервале (-∞; 4] функция выглядит так:

А на интервале [4; ∞) так:

Точка вершины первой параболы (2;-12), она
обращена вниз ветвями, точка вершины второй параболы (6, -20), ветви ее
обращены вверх. В итоге имеем:

9. Построим график функции, которая, на
первый взгляд, выглядит устрашающе:

Однако многочлен в числителе раскладывается
на множители:

Точки перемен знака подмодульных выражений
– 4 и (-2). Точки эти (они выколоты) разбивают числовую прямую на три
интервала, на которых данная функция будет выглядеть:

На первом интервале (-∞; -2):

На втором интервале (-2;4):

На третьем интервале (4;∞):

Строим:

Внесем небольшие изменения, добавив двойку
в знаменатель исходной функции:

Тогда точки перемены знака остаются те же,
но функция выглядит иначе на разных интервалах:

На первом интервале (-∞; -2):

На втором интервале (-2;4):

На третьем интервале (4;∞):

График изменится:

10. Наконец, последний график мы построим
для функции

Начнем построение с “базовой” для этого
графика функции

она выглядит так:

Далее добавим знак модуля под корень:

Теперь опустим этот график вниз на 4
единице по оси у:

“Опрокинем” все, что ниже оси х, вверх,

и не забудем поделить все ординаты на 2:

Источник

Выпуклость, вогнутость кривой. Точки перегиба.

Исследование
функции на экстремум и определение его
типа (максимум или минимум) во многих
случаях проще выполняется не путем
анализа перемены знака производной при
ее прохождении через критическую
точку, а с помощью второй производной.

Определение
1.
Непрерывная линия называется
выпуклой или обращенной выпуклостью
вверх на отрезке [а, b],
если все точки этой линии лежат выше
(не ниже) хорды, соединяющей любые две
ее точки (рис. 4. а).

Аналогично,
вогнутой (обращенной
выпуклостью вниз)
называется линия, проходящая ниже
(не выше) своих хорд (рис.
4, б).

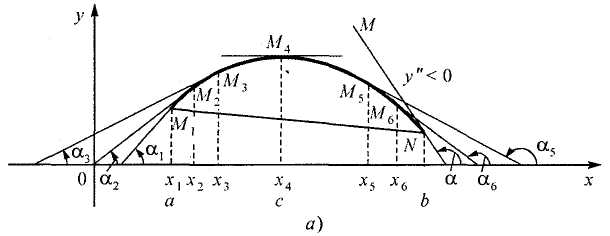
Рис.
4.

Замечание.
В некоторых руководствах
выпуклость и вогнутость иногда
определяются противоположным образом.

Определение
2. Точки,
отделяющие выпуклые участки линии от
вогнутых (и наоборот), называются точками
перегиба.

Теорема.
Если вторая производная функции
у = f(х) в
данном промежутке значений х
положительна, то кривая вогнута в этом
промежутке, а если отрицательна —
выпукла.

Точками
перегиба являются те точки, при переходе
через которые вторая производная меняет
знак.

Линия
называется выпуклой (или
вогнутой) в точке, если
значение ее второй производной в
данной точке меньше (или больше) нуля.

Пример
1. Выяснить, выпуклая или вогнутая
линия у = 3x³
+ 8 в точке с абсциссой х = 3.

Решение.
Находим производные у’ = 6х²
и у» = 12х. В точке х
= 3 имеем:

у»(3) = 12 • 6
= 36 > 0. Значит, в точке х = 3 данная
линия вогнута.

Нахождение точки перегиба

Чтобы
исследовать функцию на вогнутость,
необходимо определить знак второй
производной. Если на данном промежутке
f «(х) < 0 для
всех х, то линия вогнута, если f
«(х) > 0 для всех х, то линия
выпукла. Выпуклую часть кривой от
вогнутой отделяет точка перегиба.

Правило
нахождения точек перегиба

Чтобы
найти точку перегиба линии у
= f(х),
нужно:

1. Найти
вторую производную функции у =
f(х).

2.
Приравняв ее к нулю, решить полученное
уравнение.

3.
Расположив корни второй производной
х₁, х₂, х₃,
… в порядке их возрастания, подставить
в выражение для второй производной
сначала любое число, меньшее х₁
затем — любое число

х

(х_1, х₂); если в обоих
случаях получатся разные знаки, то
при х = х₁ имеется точка перегиба;
если же одинаковые, то точки перегиба
нет; аналогично определяется знак второй
производной и далее аналогично поступить
с числами х₂, х₃ и т.
д.

4. Найти
ординаты точек перегиба, т. е. найти
значения функции в соответствующих
точках.

Пример
1. Найти точки перегиба линии
f(х) = х³.

Решение.
Находим: f ‘(х) =
Зх²; f «(х)
= 6х; 6х = 0 => х = 0;
f(0) = 0.

Следовательно,
A (0;0) – точка
перегиба.

Пример
2. Найти точки перегиба линии
у = х ⁴ — 2х² —
3.

Решение.
1) у’ = 4х³ — 4х;
у» = 12х²— 4.

2)
у» = 0 => 12х² = 4; х
= ±
.

3)
При |х| >

имеем у» > 0 — линия вогнута; при
|х| <

имеем у» < 0 — линия выпукла.
Точки ±

являются точками перегиба (рис. 7).

Асимптоты
графика функции.

Определение
1. Асимптотой
графика функции y
= f (x)
называется прямая, обладающая тем
свойством, что расстояние от точки
M(x,
f(x))
до этой прямой стремится к нулю при
неограниченном удалении точки графика
от начала координат.

Определение
2. Прямая
x = x_o
называется вертикальной асимптотой
графика функции

y
= f(x),
если хотя бы один из односторонних
пределов f(x_о–
0) =

(предел слева) или f(x_о
+ 0) =
(предел
справа) равен +

или —

(см. рис. 8).

Определение
3. Прямая
у = kx + b
называется наклонной асимптотой
графика функции y
= f(x)
при x
+
если
функцию y = f(x)
можно представить в виде

f(x)
= kx + b + a(x),

где
a(x)

при x

При x

наклонная асимптота называется правой,
а при x

— левой. При k
= 0

асимптота
называется горизонтальной.

Теорема.
Для того чтобы график функции у =
f(x)
имел при

наклонную асимптоту y
= kx + b,
необходимо и достаточно, чтобы существовали
пределы

и

.

Пример
2. Рассмотрим функцию y
=

Так
как y = f(x)
= x + 2 +

,
где a (x)
=

при x
,
то прямая у = x +
2 является левой и правой наклонной
асимптотой графика функции.

Замечание.
Для рациональной функции (отношение
двух многочленов) левая и правая асимптоты
совпадают.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Простая физика — EASY-PHYSIC
Графики уравнений, содержащих знак модуля
функций абсолютного значения | Колледж Алгебра
- - Результаты обучения
- Понимание абсолютного значения
  - A Общее примечание: Функция абсолютного значения
  - Пример: определение числа в пределах заданного расстояния
  - Попробуйте
  - Пример: Сопротивление резистора
  - Попробуйте
  - Пример: Написание уравнения для функции абсолютного значения
  - Попробуйте
- Поиск точек пересечения функции абсолютного значения
  - Как: Имея формулу для функции абсолютного значения, найдите точки пересечения ее графика по горизонтали.
  - Пример: поиск нулей функции абсолютного значения
  - Попробуйте
- Поддержите!
График функции абсолютного значения | МАТЕМАТИКА 1314: Колледж Алгебра |
- - Пример 3. Написание уравнения для функции абсолютного значения
  - Решение
  - Попробуйте 3
  - Лицензии и атрибуты
    - Лицензионный контент CC, ранее опубликованный

Простая физика — EASY-PHYSIC

Здравствуйте, уважаемые посетители! В этой статье мы попробуем подробно разобраться, как построить график функции, если эта функция содержит модуль. В статье разобраны различные примеры с пошаговым построением и подробным объяснением, как получен тот или иной график.

1. Начнем с построения графика

В «основе» его лежит график функции

и все мы знаем, как он выглядит:

Теперь построим график

Чтобы получить этот график, достаточно всего лишь сдвинуть полученный ранее график на три единицы вправо. Заметим, что, если бы в знаменателе дроби стояло бы выражение х+3, то мы сдвинули бы график влево:

Теперь необходимо умножить на два все ординаты, чтобы получить график функции

Наконец, сдвигаем график вверх на две единицы:

Последнее, что нам осталось сделать, это построить график данной функции, если она заключена под знак модуля. Для этого отражаем симметрично вверх всю часть графика, ординаты которой отрицательны (ту часть, что лежит ниже оси х):

2. Теперь построим график функции

Выражение, стоящее под знаком модуля, меняет знак в точке х=2/3. При х<2/3 функция запишется так:

При х>2/3 функция запишется так:

То есть точка х=2/3 делит нашу координатную плоскость на две области, в одной из которых (левее) мы строим функцию

а в другой (правее) — график функции

Строим:

3. Следующий график — также ломаная, но имеет две точки излома, так как содержит два выражения под знаками модуля:

Посмотрим, в каких точках подмодульные выражения меняют знак:

Расставим знаки для подмодульных выражений на координатной прямой:

Раскрываем модули на первом интервале:

На втором интервале:

На третьем интервале:

Таким образом, на интервале (-∞; 1.5] имеем график, записанный первым уравнением, на интервале [1.5; 2] — график, записанный вторым уравнением, и на интервале [2;∞) — график по третьему уравнению:

Строим:

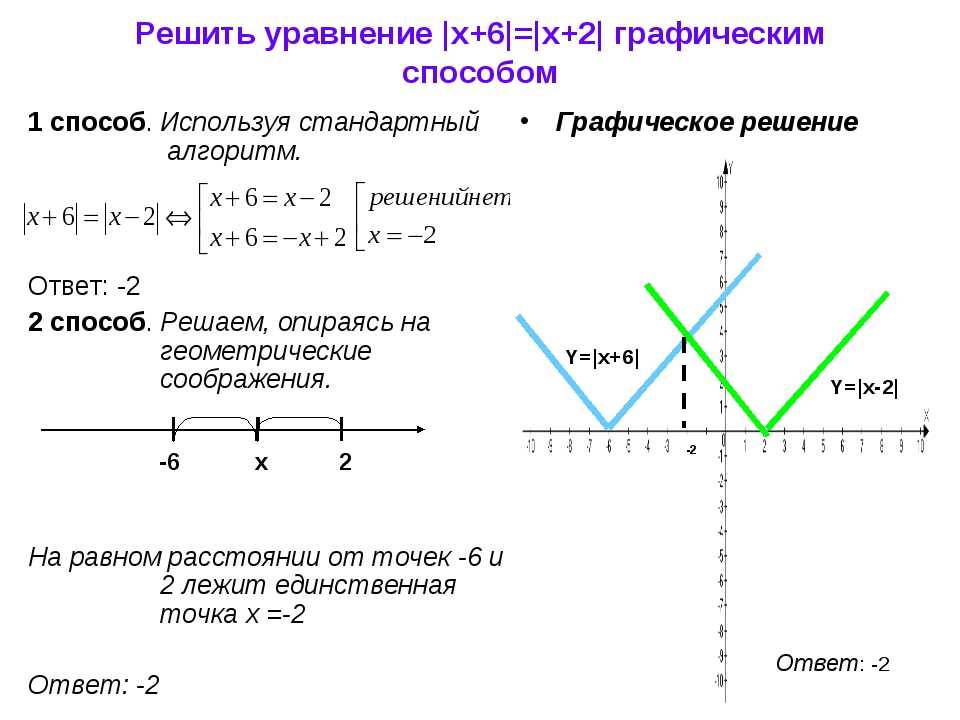
4. Теперь можем построить график, похожий на один из предыдущих, и все же отличающийся:

В основе опять знакомый нам график функции

но, если в знаменателе x стоит под знаком модуля,

то график имеет вид:

Теперь произведем сдвиг на три единицы,

при этом сдвинутся обе части: правая — вправо, левая — влево (своеобразное зеркало : отходишь дальше — видно больше)

График этой функции, умноженной на два,

выглядит так:

Теперь можно поднять график по оси у:

и тогда он будет таким:

Наконец, строим окончательный вид графика, отражая все, что ниже оси абсцисс, вверх:

5.Очень интересно выглядит график функции

В точках 2 и (-2) знак подмодульного выражения меняет знак, поэтому функция состоит из трех кусков (точки 2 и (-2) выколоты). На участках (-∞; -2) и (2; ∞) справедливо первое уравнение, а на участке (-2;2) — второе:

6. Две следующие функции отличаются знаком, и графики их выглядят по-разному:

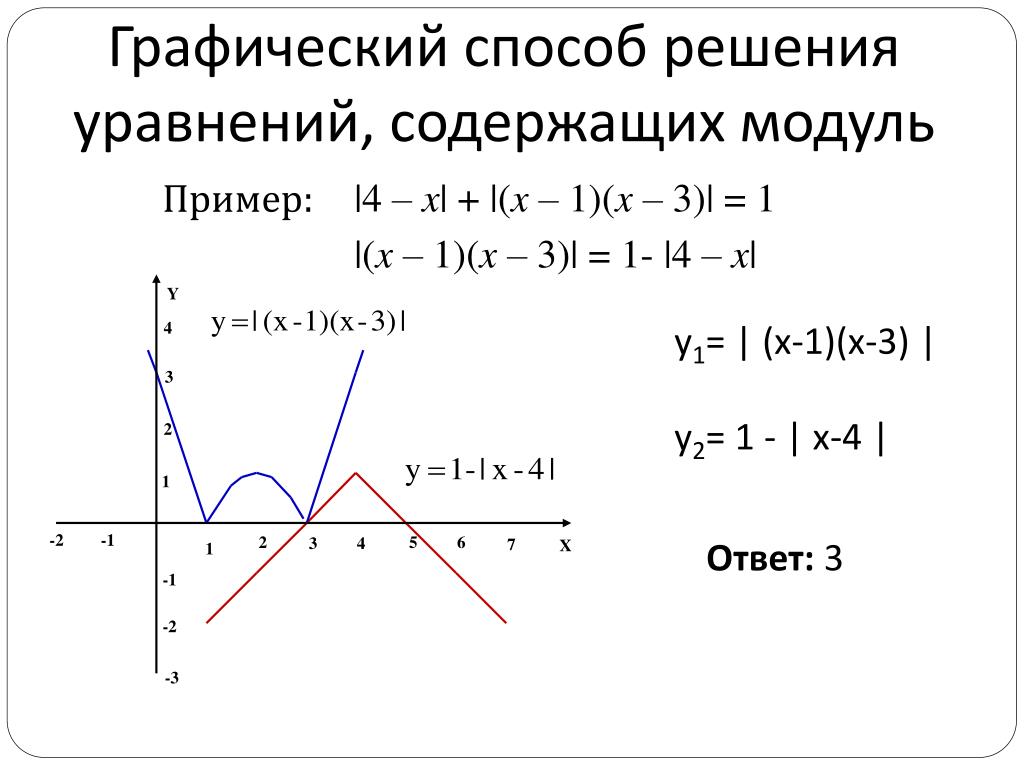
7. Еще два похожих графика, вид которых меняется в зависимости от х в показателе степени:

Первый:

Второй:

8.Теперь построим график такой функции:

Здесь точкой перемены знака подмодульного выражения является х=4. Тогда на интервале (-∞; 4] функция выглядит так:

А на интервале [4; ∞) так:

Точка вершины первой параболы (2;-12), она обращена вниз ветвями, точка вершины второй параболы (6, -20), ветви ее обращены вверх. В итоге имеем:

9. Построим график функции, которая, на первый взгляд, выглядит устрашающе:

Однако многочлен в числителе раскладывается на множители:

Точки перемен знака подмодульных выражений — 4 и (-2). Точки эти (они выколоты) разбивают числовую прямую на три интервала, на которых данная функция будет выглядеть:

На первом интервале (-∞; -2):

На втором интервале (-2;4):

На третьем интервале (4;∞):

Строим:

Внесем небольшие изменения, добавив двойку в знаменатель исходной функции:

Тогда точки перемены знака остаются те же, но функция выглядит иначе на разных интервалах:

На первом интервале (-∞; -2):

На втором интервале (-2;4):

На третьем интервале (4;∞):

График изменится:

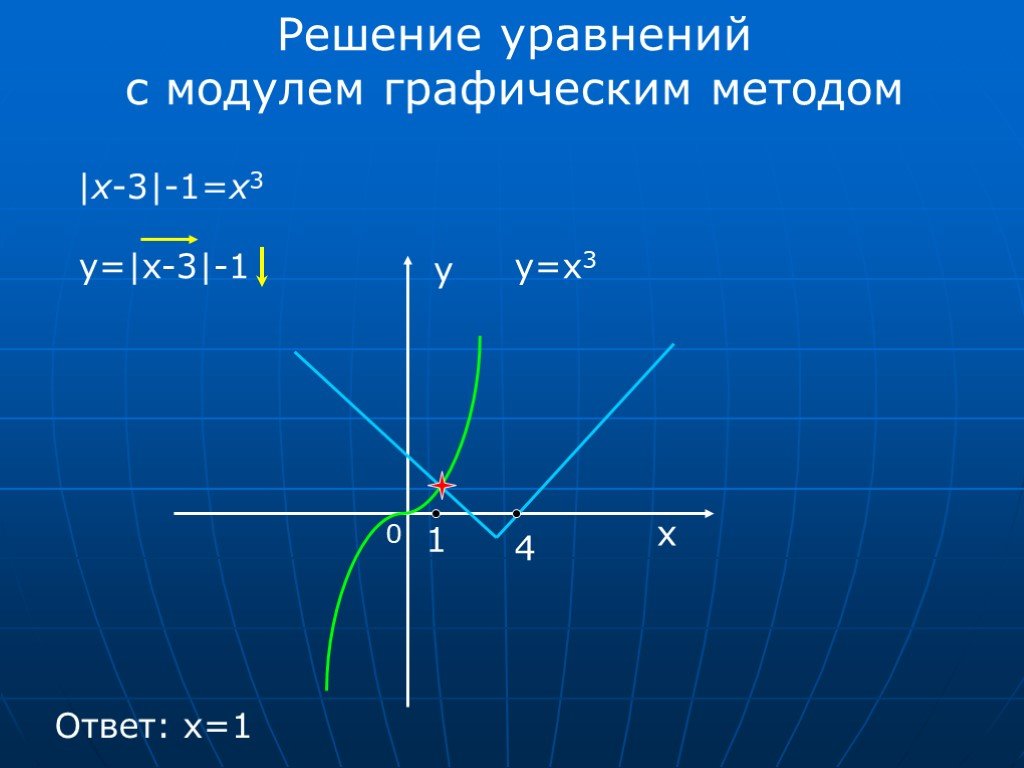
10. Наконец, последний график мы построим для функции

Начнем построение с «базовой» для этого графика функции

она выглядит так:

Далее добавим знак модуля под корень:

Теперь опустим этот график вниз на 4 единицы по оси у:

«Опрокинем» все, что ниже оси х, вверх,

и не забудем поделить все ординаты на 2:

Графики уравнений, содержащих знак модуля

Категория: Математика.

Цель:

закрепить методы построения графика линейной
функции,
закрепить умение учащихся задавать уравнением
функцию, заданную при помощи графика,
познакомить учащихся с тем, каким образом
влияет знак модуля на отображение графика
линейной функции

Оборудование: презентация (приложение
1)

Ход урока №1

При решении многих математических задач
необходимо быстро и точно строить графики любых
функций, изучаемых в школьном курсе алгебры.
Т.к. на уроке предстоит много построений,
начинаем, вспоминая, как строить график линейной
функции y = kx + b на основе анализа
углового коэффициента и коэффициента смещения
(слайд 2)

Сопоставляем уравнения и графики (слайд 3):

Построим в тетрадях в одной системе координат
графики функций (y = —x; y = —x -4; y =
-1/3 x – 2; y = 2x + 5; y = x + 1), проверяя
себя при помощи слайда 4

Вспомним определение модуля числа x (слайд 5)

Рассматриваем, как можно построить график
функции y = |x| на основании определения
модуля, отбрасывая части прямых, не лежащих в
полуплоскостях x < 0 и x> 0 (слайд
6)

Аналогично рассматриваем способ построения
графика функции y = |x + 1| (слайд
7)

Сравнивая графики и уравнения функций (слайд 8-9),

делаем вывод о том, как можно построить график
функции y = |x + a| — b смещением
графика функции y = |x| (слайд
10-11)

Строим в тетрадях графики функций y = |x-3|
+ 3, y = |x – 3| — 2, y = |

x+2| — 5, y = |x +
3| + 2 и проверяем себя при помощи слайда 12

Далее учащиеся должны на основе рисунка,
представленного на слайде 13, задать функцию
уравнением:

При построении графиков очень важно научить
ребят анализировать область определения и
множество значений функции и “переносить”
указанные множества на координатную плоскость.

Заполняем таблицу (слайд 12):

D(y) E (y)

y = |x|

y = |x – 3|

y = |x – 3| +2

y = — |x|

y = |x + 2| -5

y = — |x +2| -5

И рассматриваем, как множества значений можно
определить на основе графиков (слайд
15)

Учащимся предлагается определить D (y) и E(y)
по рисунку (слайд 16):

Ученики самостоятельно придумывают уравнение
функции по заданным D(y) и E(y) (слайд
17):

Анализируя графики и уравнения (слайд
18), ученики делают вывод о том, как влияет знак
минуса перед модульными скобками на график.

И
самостоятельно задают уравнение по графикам,
представленным на слайде 19.

Ход урока № 2

Устно проговариваем уравнения функций по
графикам (слайд 20):

Аналогично схеме предыдущего урока (слайд
21-27) ученики знакомятся с тем, каким образом
влияет коэффициент перед аргументом функции на
график. В результате они должны научиться
описывать уравнением следующие графики:

Для закрепления полученных знаний, в тетрадях в
одной системе координат ребята строят следующие
графики:

y = |0,5x| при -3 < x< 3;

y = 3 при -1 < x< 1;

y = -|x + 3| + 6 при -4 < x < -2;

y = -|x — 3| + 6 при 2 < x < 4;

y = |x + 3| + 4 при -4 < x < -2;

y = |x — 3| + 4 при 2

x ? 4;

y = -|0,5x – 1,5| + 7 при -5 < x < -1;

y = -|0,5x + 1,5| + 7 при 1 < x < 5.

Проверяют себя по слайду 29:

Домашнее задание: придумать картину,
состоящую из отрезков прямых, и описать ее при
помощи уравнений функций.

Ход урока № 3

Построим графики функций y = |3x| — 3 и y =
|3x – 3|. Как в каждом случае связаны y(x)
и y(-x)?

Наличие условия y(x) = y(-x) означает
симметрию относительно …?

Приведите примеры уравнений функции, графики
которых будут симметричны относительно оси
ординат

Если в модульные скобки заключается переменная
y, то мы получаем условие |y| = |-y|. Какую
симметрию задает это условие?

На слайде 34 последовательно рассматриваем
цепочку построения графиков:

y = 3x – 3, |y| = 3x – 3, |y| = |3x| — 3, |y|
= |3x – 3| путем преобразований симметрии.

Выводим и запоминаем три правила:

Распределите, к какому типу из трех (y = f(|x|,
|y| = f(x), y = |f(x)|), можно
отнести каждое уравнение:

|y| = 2 – x, y = |3x — 4|, |x| + |y| = 2, |y|
= 3x – 4, y = |3|x| — 4|, y = |3x| — 4, |y| =
|3|x| — 4|, |y| = |3x – 4|.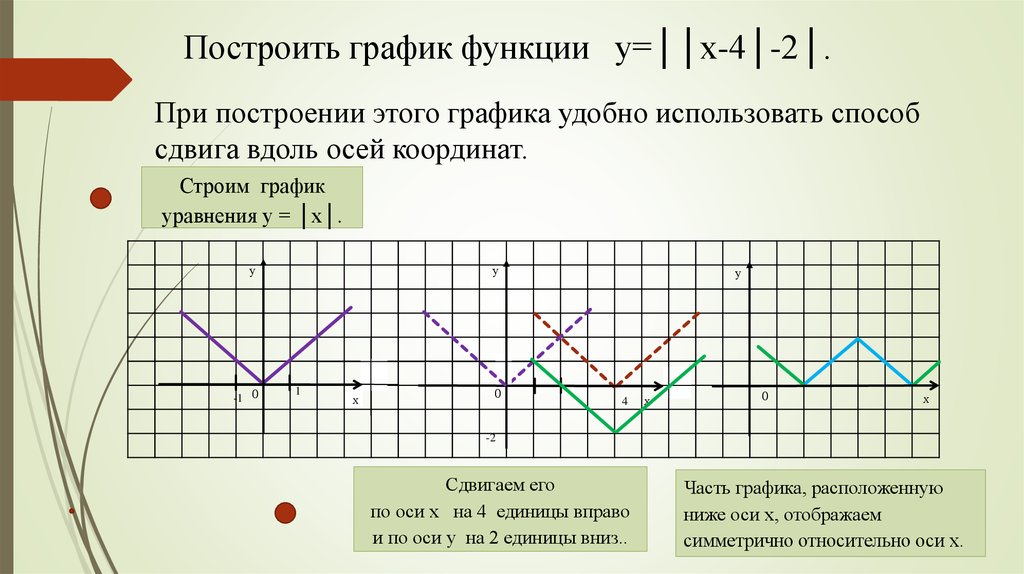

Проверяем себя (слайд 35)

Строим последовательную цепочку графиков
(тонкими линиями в тетрадях):

1) y = 3x – 4,

y = |3x – 4|, y = |3|x| —
4|, |y| = |3|x| — 4|

2) y = 3x – 4, y = 3|x| — 4, y = |3|x| — 4|

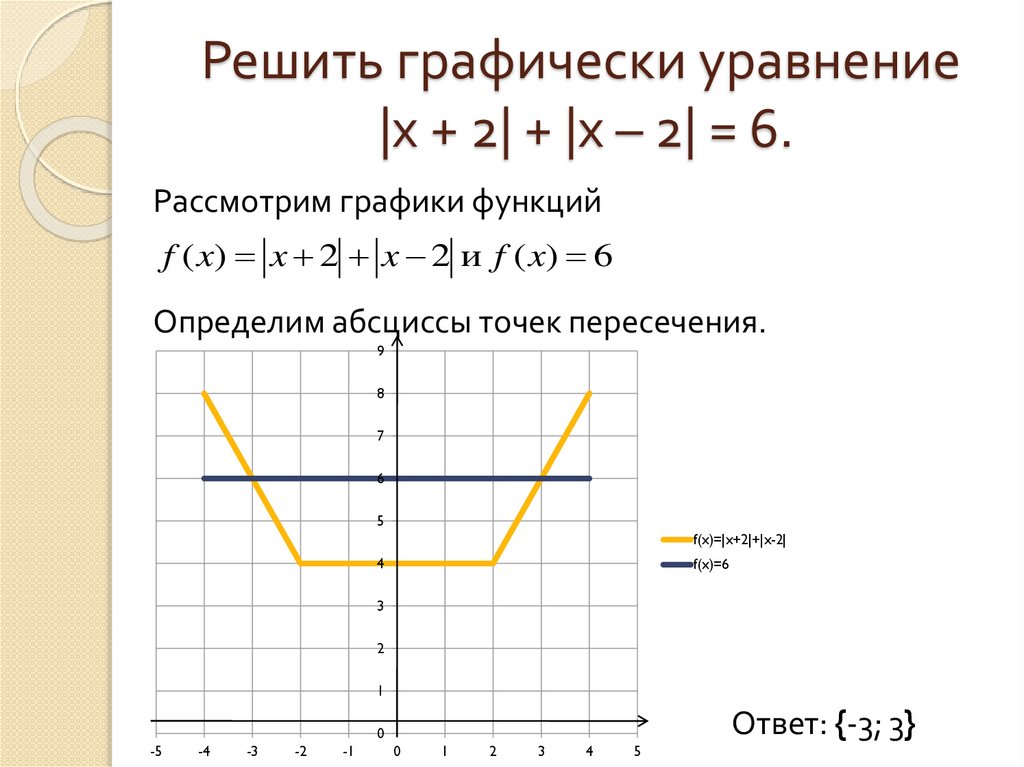
Рассматриваем способ построения графика
соответствия |x| + |y| = 2.

Самостоятельно строим график |x| — |y| = 2 и
проверяем себя по слайду 39.

Домашнее задание: придумать пять уравнений
соответствий с модулем, в которых встречаются
все случаи, рассмотренные на уроке, и построить
графики.

17.03.2008

функций абсолютного значения | Колледж Алгебра

Результаты обучения

График функции абсолютного значения.
Найти точки пересечения функции абсолютного значения.

Расстояния в глубоком космосе можно измерять во всех направлениях. Таким образом, полезно рассматривать расстояние с точки зрения абсолютных значений. (Источник: «s58y»/Flickr)

До 1920-х годов считалось, что так называемые спиральные туманности представляют собой облака пыли и газа в нашей собственной галактике, находящейся в нескольких десятках тысяч световых лет от нас. Затем астроном Эдвин Хаббл доказал, что эти объекты сами по себе являются галактиками на расстоянии в миллионы световых лет. Сегодня астрономы могут обнаруживать галактики, удаленные от нас на миллиарды световых лет. Расстояния во Вселенной можно измерить во всех направлениях. Таким образом, полезно рассматривать расстояние как функцию абсолютного значения. В этом разделе мы рассмотрим Функции абсолютного значения .

Понимание абсолютного значения

Напомним, что в своей основной форме [латекс]displaystyle{f}left({x}right)={|x|}[/латекс] функция абсолютного значения является одной из наших инструментальные функции. Функция абсолютного значения обычно рассматривается как определение расстояния числа от нуля на числовой прямой.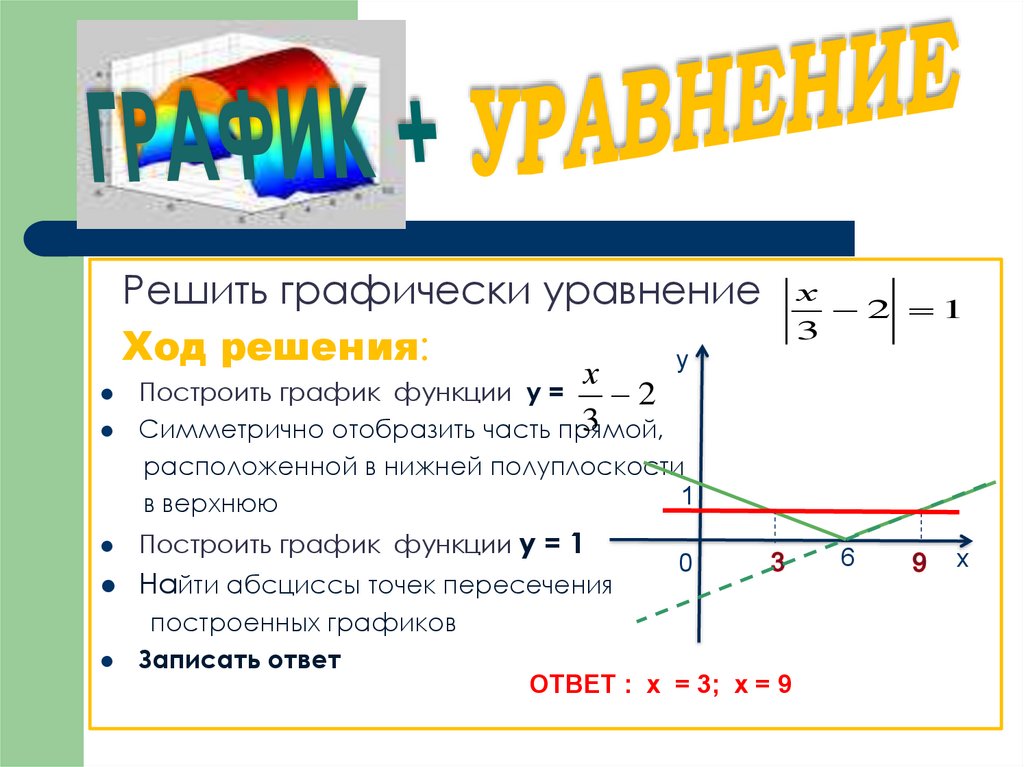 Алгебраически, независимо от входного значения, выходным является значение без учета знака.

A Общее примечание: Функция абсолютного значения

Функция абсолютного значения может быть определена как кусочная функция

[latex]f(x) =begin{cases}x , x geq 0 \ -x , x < 0\ end{cases} [/latex]

Пример: определение числа в пределах заданного расстояния

Опишите все значения [latex]x[/latex] в пределах или включая расстояние 4 от числа 5.

Показать решение

Попробуйте

Опишите все значения [latex]x[/latex] на расстоянии 3 от числа 2.

Показать решение

Пример: Сопротивление резистора

Электрические детали, такие как резисторы и конденсаторы, поставляются с заданными значениями рабочих параметров: сопротивления, емкости и т. д. Однако из-за неточности изготовления фактические значения этих параметров несколько отличаются от куска к кусочку, даже если они должны быть одинаковыми.

Лучшее, что могут сделать производители, — это попытаться гарантировать, что вариации останутся в пределах указанного диапазона, часто [латекс]pm 1%,pm5%,[/латекс] или [латекс]displaystylepm10% [/латекс].

Предположим, у нас есть резистор номиналом 680 Ом, [латекс]pm 5%[/латекс]. Используйте функцию абсолютного значения, чтобы выразить диапазон возможных значений фактического сопротивления.

Показать раствор

Попробуйте

Учащиеся, набравшие не более 20 баллов из 80, проходят тест. Запишите это как расстояние от 80, используя обозначение абсолютного значения.

Показать решение

Наиболее важной особенностью графика абсолютных значений является угловая точка, в которой график меняет направление. Эта точка показана на происхождение .

На приведенном ниже графике [латекс]у=2влево|х — 3вправо|+4[/латекс]. График [latex]y=|x|[/latex] был сдвинут вправо на 3 единицы, растянут по вертикали в 2 раза и сдвинут вверх на 4 единицы.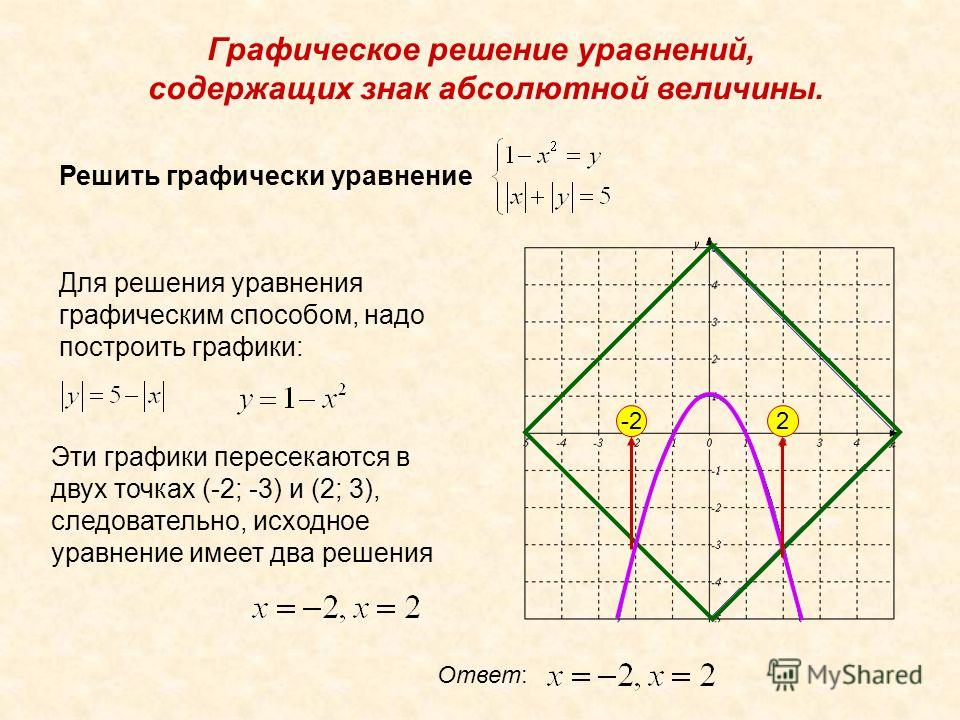 Это означает, что угловая точка для этой преобразованной функции расположена в [латекс]влево(3,4вправо)[/латекс].

Пример: Написание уравнения для функции абсолютного значения

Напишите уравнение для функции, показанной ниже.

Показать решение

Вопросы и ответы

Если бы мы не могли наблюдать растяжение функции по графикам, могли бы мы определить его алгебраически?

Да. Если мы не можем определить растяжение на основе ширины графика, мы можем определить коэффициент растяжения, введя известную пару значений для [латекс]x[/латекс] и [латекс]fleft(x справа)[/латекс].

[латекс]fleft(xright)=a|x — 3|-2[/latex]

Теперь подставим в точке (1, 2)

[латекс]begin{array}{l}2=a|1 — 3|-2hfill \ 4=2ahfill \ a=2hfill end{array} [/latex]

Попробуйте

Напишите уравнение для функции абсолютного значения, которая сдвигается по горизонтали влево на 2 единицы, переворачивается по вертикали и сдвигается по вертикали вверх на 3 единицы.

Показать решение

Вопросы и ответы

Всегда ли графики функций абсолютного значения пересекают вертикальную ось? Горизонтальная ось?

Да, они всегда пересекают вертикальную ось. График функции абсолютного значения будет пересекать вертикальную ось, когда вход равен нулю.

Нет, они не всегда пересекают горизонтальную ось. График может пересекать или не пересекать горизонтальную ось в зависимости от того, как график был сдвинут и отражен. Функция абсолютного значения может пересекать горизонтальную ось в нуле, одной или двух точках.

(a) Функция абсолютного значения не пересекает горизонтальную ось. (b) Функция абсолютного значения пересекает горизонтальную ось в одной точке. (c) Функция абсолютного значения пересекает горизонтальную ось в двух точках.

Поиск точек пересечения функции абсолютного значения

Полезно знать, как решать задачи, связанные с функциями абсолютного значения . Например, нам может понадобиться идентифицировать числа или точки на линии, которые находятся на заданном расстоянии от заданной контрольной точки.

Как: Имея формулу для функции абсолютного значения, найдите точки пересечения ее графика по горизонтали.

Изолировать термин абсолютного значения.
Используйте [latex]|A|=B[/latex] для записи [latex]A=B[/latex] или [latex]mathrm{-A}=B[/latex], предполагая, что [latex]B>0 [/латекс].
Найдите [латекс]х[/латекс].

Пример: поиск нулей функции абсолютного значения

Для функции [latex]fleft(xright)=|4x+1|-7[/latex] найдите значения [latex]x[ /latex] такой, что [latex]text{ }fleft(xright)=0[/latex] .

Показать решение

Попробуйте

Для функции [латекс]fвлево(хвправо)=|2x — 1|-3[/латекс] найдите значения [латекс]х[/латекс] такие, что [латекс] fвлево(хвправо)=0[/латекс].

Показать решение

Поддержите!

У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.

Улучшить эту страницуПодробнее

График функции абсолютного значения | МАТЕМАТИКА 1314: Колледж Алгебра |

Наиболее важной особенностью графика абсолютных значений является угловая точка, в которой график меняет направление. Эта точка показана в начале координат .

Рисунок 3

Рисунок 4 — график

y=2∣x−3∣+4y=2left|x — 3right|+4\y=2∣x−3∣+4

. График

y=∣x∣y=|x|\y=∣x∣

был сдвинут вправо на 3 единицы, растянут по вертикали в 2 раза и сдвинут вверх на 4 единицы. Это означает, что угловая точка для этой преобразованной функции расположена в точке

(3,4)влево(3,4вправо)\(3,4)

Рис. 4

Пример 3. Написание уравнения для функции абсолютного значения

Напишите уравнение для функции, изображенной на рисунке 5.

Рисунок 5

Решение

Основная функция абсолютного значения изменяет направление в начале координат, поэтому этот график был сдвинут на 3 единицы вправо и на 2 единицы вниз по сравнению с базовой функцией набора инструментов.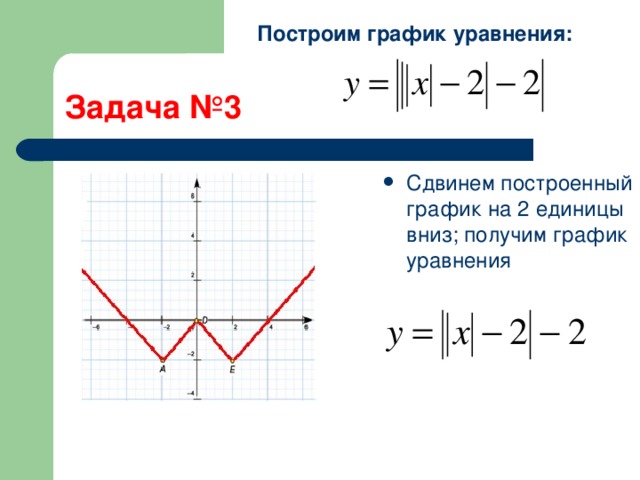

Рисунок 6

Мы также замечаем, что график кажется вытянутым по вертикали, потому что ширина окончательного графика на горизонтальной линии не равна удвоенному расстоянию по вертикали от угла до этой линии, как это было бы для нерастянутая функция абсолютного значения. Вместо этого ширина равна 1-кратному вертикальному расстоянию. 9Рис. 7 −3)∣−2, рассматривая растяжение как горизонтальное сжатие.begin{cases}fleft(xright)=2left|x — 3right|-2,qquad & text{обработка растягивание как вертикальное растяжение, или}qquad \ fleft(xright)=left|2left(x — 3right)right|-2,qquad & text{обработка растяжения как горизонтальное сжатие}.qquad end{cases}\{f(x)=2∣x−3∣−2,f(x)=∣2(x−3)∣−2,обрабатывая растяжение как вертикальное растяжение или рассмотрение растяжения как горизонтального сжатия.

Вопросы и ответы

Если бы мы не могли наблюдать растяжение функции по графикам, могли бы мы определить его алгебраически?

Да. Если мы не можем определить растяжение на основе ширины графика, мы можем найти коэффициент растяжения, подставив известную пару значений для

xx\x

f(x)fleft(x справа)\f(x)

f(x)=a∣x−3∣−2fleft(xright)=a|x — 3|-2\f(x)=a∣x−3∣−2

Теперь подставляем в точку (1, 2)

{2=a∣1−3∣−24=2aa=2begin{cases}2=a|1 — 3|-2qquad \ 4= 2aqquad \ a=2qquad end{cases}\⎩

⎨

⎧2=a∣1−3∣−24=2aa=2

Попробуйте 3

Решение

Вопросы и ответы

Всегда ли графики функций абсолютного значения пересекают вертикальную ось? Горизонтальная ось?

Нет, они не всегда пересекают горизонтальную ось. График может пересекать или не пересекать горизонтальную ось, в зависимости от того, как график был сдвинут и отражен. Функция абсолютного значения может пересекать горизонтальную ось в нуле, одной или двух точках.

Рис. 8. (a) Функция абсолютного значения не пересекает горизонтальную ось. (b) Функция абсолютного значения пересекает горизонтальную ось в одной точке. (c) Функция абсолютного значения пересекает горизонтальную ось в двух точках.

Лицензии и атрибуты

Лицензионный контент CC, ранее опубликованный

Precalculus. Автор : Джей Абрамсон и др. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/precalculus/pages/1-introduction-to-functions.

Источник

	D(y)	E (y)
y = \|x\|
y = \|x – 3\|
y = \|x – 3\| +2
y = — \|x\|
y = \|x + 2\| -5
y = — \|x +2\| -5