Как найти точки пересечения ломаных

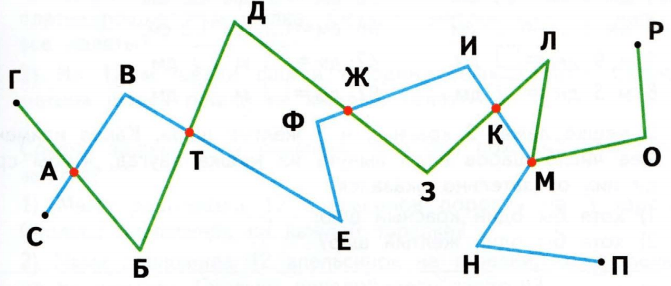
На чертеже изображены две ломаные.

1) Назови точки пересечения ломаных.
2) Укажи еще несколько точек, принадлежащих:
а) только синей ломаной;
б) только зеленой ломаной.
3) Запиши названия и обозначения многоугольников, которые получились при пересечении ломаных.

Ломаная линия — определение

Одним из наиболее простых и понятных геометрических терминов считают прямую линию. Есть в математике похожая фигура, но с некоторыми характерными чертами. Давайте попробуем разобраться, что такое ломаная линия и каковы её особенности.

Ломаная линия — математическая фигура, включающая в себя несколько отрезков, которые меняют направление.

Если выражаться более чётко, то это черта, которая не является прямой по всей длине, но может не иметь изгибов на отдельном отрезке.

Таким образом, фигура в обязательном порядке отвечает нескольким признакам:

• состоит из отрезков, которые являются её звеньями;
• конец каждого звена является началом следующего (кроме последнего);
• находящиеся рядом отрезки не могут располагаться на прямой, то есть угол между ними не равен 180 градусам.

Обозначение ломаной линии

Чтобы отметить ломаную линию на чертеже вам необходимо указать наименования точек стыка, в которых она меняет направление, латинскими буквами.

Из чего состоит ломаная линия

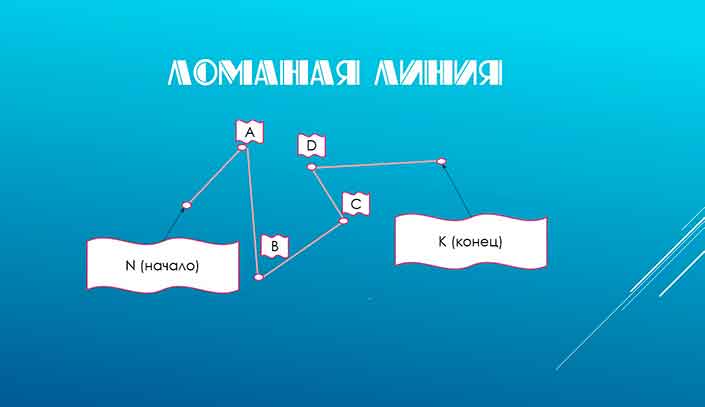
Как вы уже успели заметить, на рисунках присутствуют звенья — отрезки, составляющие ломаную линию. А вот начальные и конечные точки этих составных частей — вершины. На картинке вершины ломаной ABCD — позиции A, B, C, D.

Признак замкнутости ломаной линии

Классификация ломаных линий прежде всего осуществляется по свойству замыкания.

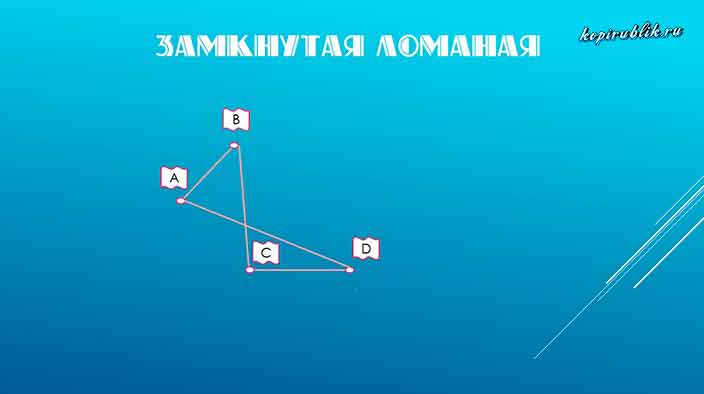
Замкнутая ломаная линия — фигура, у которой конечная позиция совпадает с начальной. Иначе говоря, когда она заканчивается в том же месте, где начиналась.

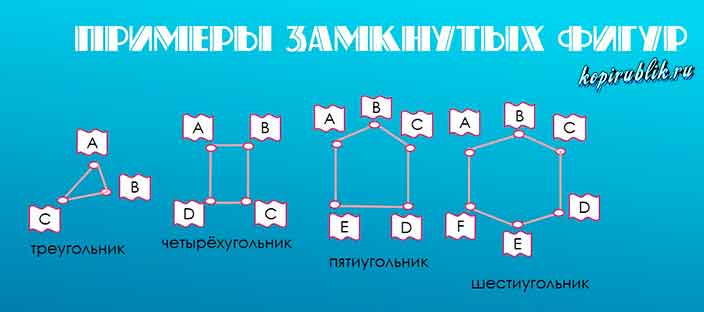
Яркие представители — треугольник и квадрат, а также остальные виды многоугольников:

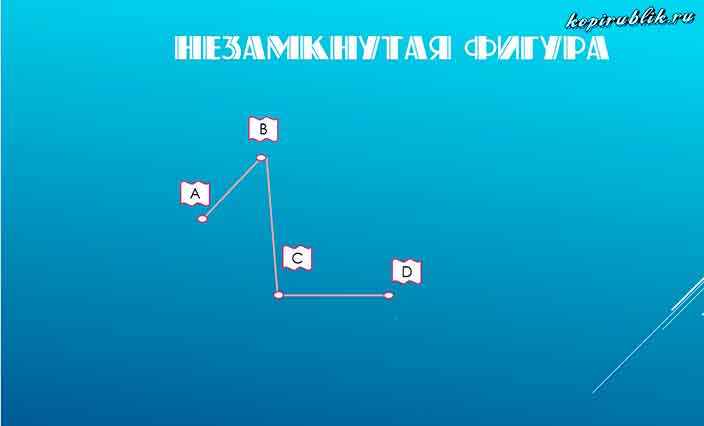
Незамкнутая ломаная линия — фигура, которая приходит в позицию, отличающуюся от начальной.

Время от времени, у учащихся возникает вопрос: «Как определить, замкнутая фигура или нет?». Ответ будет весьма прост:»Когда число отрезков равно количеству вершин — она замкнутая, а при наблюдающемся неравенстве — незамкнутая».

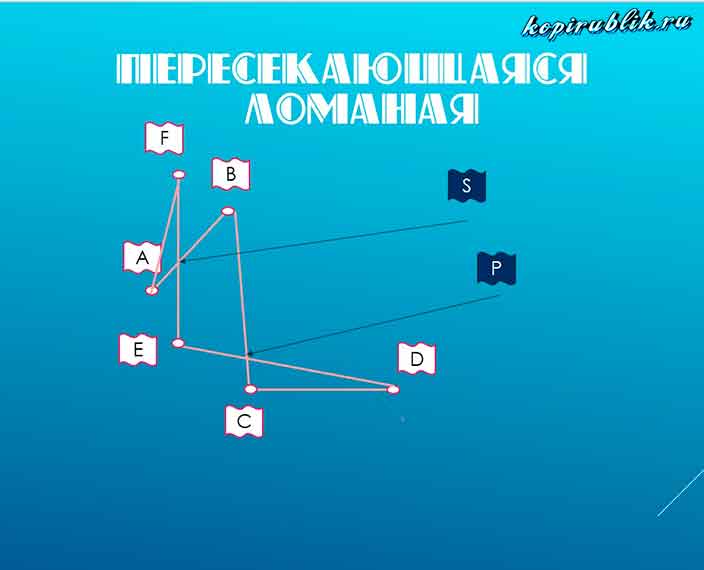
В качестве дополнительного вида рассматривают понятие самопересекающаяся ломаная линия — та, которая скрещивается на пути своего следования. Для данного термина не имеет значения сколько раз произошло пересечение.

На рисунке отмечены точки пересечения — S, P, а также вершины — A,B,C,D,E,F.

Иногда люди спрашивают — «Могут ли вершины являться точками пересечения?». Чтобы найти ответ, обратите внимание на рисунок с пересекающейся и одновременно замыкающейся — ломаной линией:

Изображение отличается от предыдущего: отрезок EB перемещён, поэтому вершина A приобрела статус точки пересечения.

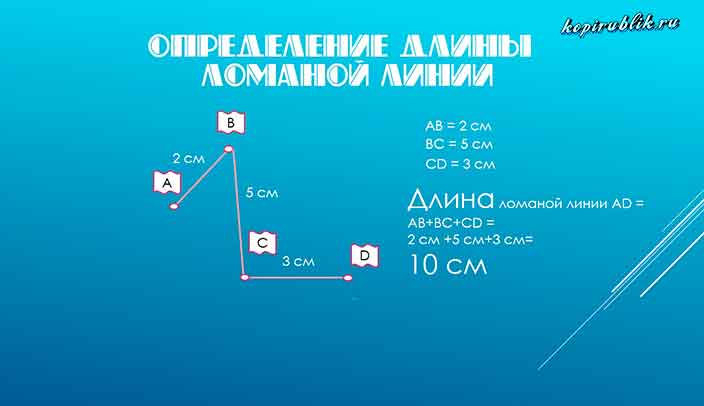
Как измерить длину ломаной линии

Ломаная линия, имеющая начало и конец, имеет распространённую стандартную характеристику — длину. Имея цель сделать замер её длины, необходимо суммировать длины всех её составных частей — отрезков.

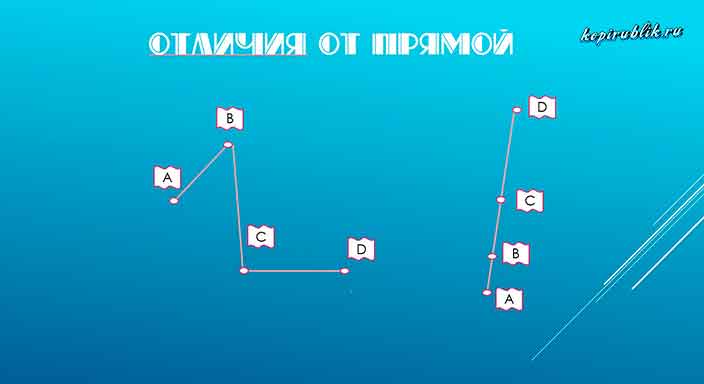
Чем ломаная линия отличается от прямой

При взгляде на рисунок очевидно: уникальный признак ломаной линии — отсутствие углов, равных 180 градусам. В остальном, фигуры одинаковые и обладают схожими свойствами, например, длиной.

Примеры ломаных линий в быту

В целях наилучшего усвоения теории, разумно на практике ознакомиться с примерами ломаных линий из жизни.

Ломаная линия— график фондового рынка. Так как отрезки графика очень маленькие, поэтому может показаться, что это кривая, но при ближайшем рассмотрении оказывается, что это не так.

Фасад дома при переводе на «язык геометрии» выглядит как замкнутая ломаная линия.

Пирамиды древнего Египта обладали формой треугольника — одной из самых популярных ломаных линий.

Ломаная линия

• Замкнутая и незамкнутая ломаная
• Самопересекающаяся ломаная
• Длина ломаной

Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.

Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.

Построим ломаную из четырёх отрезков:

Отрезки  AB,  BC,  CD  и  DE  — это звенья ломаной. Точки  A,  B,  C,  D  и  E  — вершины ломаной. Обозначение ломаной линии составляют из букв, стоящих при её вершинах, называя их по порядку. Например, говорят или пишут: ломаная  ABCDE  или ломаная  EDCBA.

Замкнутая и незамкнутая ломаная

Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:

незамкнутая ломаная  ABCD.

Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:

замкнутая ломаная  ABC.

Самопересекающаяся ломаная

Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:

точки  F,  T,  K  — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.

Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником:

многоугольник  ABCDE.

Длина ломаной

Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.