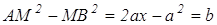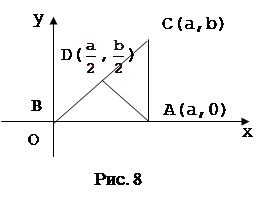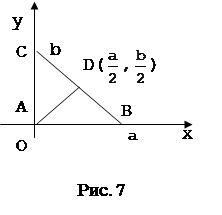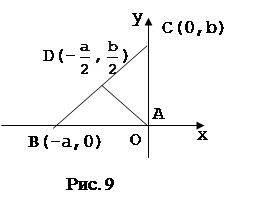Как найти точки пересечения параболы с окружностью

Уравнение траектории космического аппарата: $y = ax^2+bx+c$.

Аппарат запускается из начала координат, т.е. его траектория пересекается с осью OY в точке (0;0). Значит, в уравнении параболы c = 0.

Пропорции для параметров (см. пример 3) с учетом c = 0:

Уравнение траектории космического аппарата с «перехватом» кометы в вершине:

Этап: построение окружности и параболы; нахождение точек их пересечения

2 этап: построение окружности и параболы; нахождение точек их пересечения.

3 этап: количество точек пересечения окружности и параболы является ответом на поставленный вопрос.

№2. Найдите множество точек, для каждой из которых расстояния от двух данных точек равны.

Обозначим данные точки через А и В. Выберем систему координат так, чтобы ось Ох совпадала с прямой АВ, а началом координат служила точка А Предположим далее, что АВ=а, тогда в выбранной системе координат А(0,0) и В(а,0). Точка М(х,у) принадлежит искомому множеству тогда и только тогда, когда АМ=МВ, или, что то же самое, АМ 2= МВ 2 . Используя формулу расстояния от одной точки координатной плоскости до другой, получаем АМ 2 =x 2 +y 2 , MB 2 =(x-a) 2 +y 2 . Тогда х 2 +у 2 =(х-а) 2 + у 2

Равенство х 2 +у 2 =(х-а) 2 +у 2 и является алгебраической моделью ситуации, данной в задаче. На этом заканчивается первый этап ее решения (перевод задачи на координатный язык).

На втором этапе осуществляется преобразование полученного выражения, в результате которого получаем соотношение .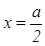

На третьем этапе осуществляется перевод языка уравнения на геометрический язык. Полученное уравнение является уравнением прямой, параллельной оси Оу и отстоящей от точки А на расстояние 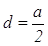, т.е. серединного перпендикуляра к отрезку АВ.

2.2 Задачи, обучающие координатному методу

Для разработки методики формирования умения применять координатный метод важно выявить требования, которые предъявляет логическая структура решения задач мышлению решающего. Координатный метод предусматривает наличие у обучающихся умений и навыков, способствующих применению данного метода на практике. Проанализируем решение нескольких задач. В процессе этого анализа выделим умения, являющиеся компонентами умения использовать координатный метод при решении задач. Знание компонентов этого умения позволит осуществить его поэлементное формирование.

Задача №1 . В треугольнике ABC: AC=b, AB=c, ВС=а, BD — медиана. Докажите, что .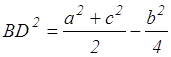

Выберем систему координат так, чтобы точка А служила началом координат, а осью Ох — прямая АС (рис. 2).

(умение оптимально выбирать систему координат, т. е. так, чтобы наиболее просто находить координаты данных точек).

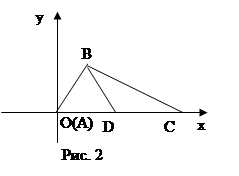
В выбранной системе координат точки А, С и D имеют следующие координаты: А(0,0), D(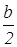,0) и С(b,0)

(умение вычислять координаты заданных точек). Обозначим координаты точки В через х и у. Тогда используя формулу для нахождения расстояний между двумя точками, заданными своими координатами, получаем:

х 2 +у 2 =с 2 , (x-b) 2 +y 2 =a 2 (1)

(умение находить расстояние между двумя точками, заданными координатами)

По той же формуле 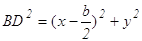. (2)

Используя формулы (1) находим х и у.

; .

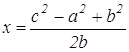
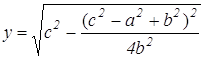
Далее, подставляя х и у в формулу (2), находим .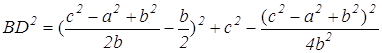

.

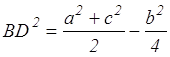
(умение выполнять преобразования алгебраических выражений)

Задача №2. Найти множество точек, для каждой из которых разность квадратов расстояний от двух данных точек есть величина постоянная.

Обозначим данные точки через А и В. Выберем систему координат так, чтобы ось Ох совпадала с прямой АВ, а началом координат служила точка А.

(умение оптимально выбирать систему координат).

Предположим АВ=а, тогда в выбранной системе координат А(0,0), В(а,0).

(умение находить координаты заданных точек)

Точка М(х,у) принадлежит искомому множеству тогда только тогда, когда AM 2 -MB 2 =b 2 где b — постоянная величина

(умение переводить геометрический язык на аналитический, составлять уравнения фигур).

Используя формулу расстояний между двумя точками, получаем:

, ,

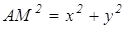
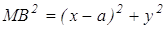
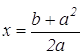
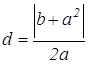
(умение вычислять расстояние между точками, заданными координатами), или . Данное уравнение является уравнением прямой, параллельной оси Оу и отстоящей от точки А на расстояние .

(умение видеть за уравнением конкретный геометрический образ)

Нетрудно видеть, что и для решения этой задачи необходимо овладение перечисленными выше умениями. Кроме того, для решения приведенной задачи, а также и других задач важно умение «видеть за уравнением» конкретный геометрический образ, которое является обратным к умению составлять уравнения конкретных фигур.

Выделенные умения являются основой при решении и более сложных задач.

Задача №3. В трапеции меньшая диагональ перпендикулярна основаниям. Найти большую диагональ, если сумма противоположных углов равна 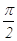, а основания равны а и b.

Направим оси координат по меньшей диагонали и одному из оснований (рис. 3).

(умение оптимально выбирать систему координат).

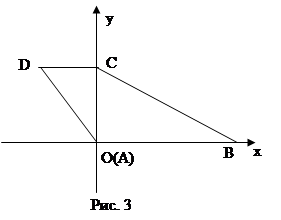
Тогда точка А имеет координаты (0,0), точка В — (а,0), точка С — (0,c), точка D — (b,c).

(умение находить координаты заданных точек)

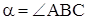
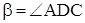
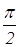
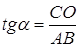
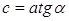
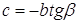
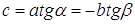
Пусть и острые углы в трапеции АВСD, тогда их сумма равна . Для вычисления длины большей диагонали BD надо найти значение с. Его можно вычислить 2 способами. Первый — из прямоугольного треугольника АВС по формуле находим . Второй способ из прямоугольного треугольника ACD: . Отсюда получили, что

(1)

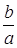
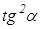
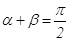
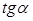
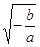
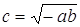
Из равенства (1) находим отношение : оно равно —, так как . Выразим . Он равен , исходя из этого, пользуясь зависимостью (1), получаем .

(умение выразить недостающие координаты через уже известные величины)

Далее воспользовавшись координатной формулой расстояния между двумя точками, найдем длину BD.

(умение вычислять расстояние между точками, заданными координатами)

Она равна .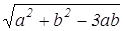

Итак, компонентами умения применять координатный метод в конкретных ситуациях являются следующие умения:

1. переводить геометрический язык на аналитический для одного типа задач и с аналитического на геометрический для другого;

2. стоить точку по заданным координатам;

3. находить координаты заданных точек;

4. вычислять расстояние между точками, заданными координатами;

5. оптимально выбирать систему координат;

6. составлять уравнения заданных фигур;

7. видеть за уравнением конкретный геометрический образ;

8. выполнять преобразование алгебраических соотношений.

Данные умения можно отработать на примере следующих задач, формирующих координатный метод:

1) задачи на построение точки по ее координатам;

2) задачи на нахождение координат заданных точек;

3) задачи на вычисление расстояния между точками, заданными координатами;

4) задачи на оптимальный выбор системы координат;

5) задачи на составление уравнения фигуры по ее характеристическому свойству;

6) задачи на определение фигуры по ее уравнению;

7) задачи на преобразование алгебраических равенств;

Приведем примеры таких задач.

I. Построение точек на плоскости.

С координатной прямой, а затем и с координатной плоскостью учащиеся знакомятся в 5-6 классах при изучении математического материала. При этом удобно использовать мультимедийные презентации, которые позволяют в динамике излагать необходимый материал, использовать всевозможные иллюстрации и звуковые эффекты, тем самым, заинтересовывая учащихся и являясь хорошим наглядным средством. Одним из примеров является презентация «Метод координат», опирающаяся на учебник [7]. (см. приложение 1). Приведем несколько примеров задач, которые можно использовать при изучении координатной плоскости. Эти задачи могут быть использованы:

— для оттачивания навыков построения точек по их координатам со всем классом;

— для дополнительных заданий отстающим ученикам;

— для развития интереса к изучаемой теме.

1) На координатной плоскости постройте точки А(7,2), B(-2,1), C(0,2).

2) Отметьте на плоскости несколько точек. Начертите произвольную систему координат и найдите в ней координаты заданных точек.

3) Постройте фигуры по координатам их узловых точек. Указание: узловыми будем называть точки, служащие концами отрезков, образующих фигуры. Точки, координаты которых записаны подряд через запятую, соединяйте последовательно друг с другом. Если же координаты разделяются знаком «;», то соответствующие точки не следует соединять. Они нужны для изображения вспомогательных элементов.

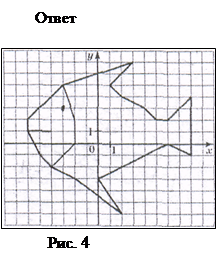
А) Камбала (Рис. 4)

Б)Найдите координаты выделенных на рисунке точек, двигаясь по часовой стрелке от самой жирной точки. (Рис. 5 и 6)

II.Задачи на выбор системы координат

Выбор системы координат имеет очень важное значение при применении метода координат.

Для примера возьмем задачу, которая рассмотрена в учебнике [2] «Середина гипотенузы прямоугольного треугольника равноудалена от его вершин».

Первым шагом при применении метода координат является такой выбор осей и системы координат, при котором алгебраические выкладки становятся более простыми. Для данной задачи удачный выбор системы координат показан на рисунке 7. Таким образом, начало координат помещаем в точку А, а оси проводим через точки В и С так, чтобы эти точки лежали на положительных лучах осей. Следовательно, В(а,0) и С(0,b). Поэтому по формуле середины отрезка D(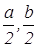). 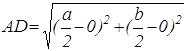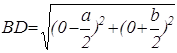Теперь , .

Поэтому AD=BD. А так как по определению середины отрезка BC=CD, то теорема доказана.

Можно выбрать систему координат и по-другому (рис.8, рис.9). Если выбрать оси совсем случайно, то легкую задачу можно превратить в очень трудную. Чтобы начать доказательство исходя из рисунка 10, нужно найти способ, позволяющий выразить алгебраически, что треугольник ABC имеет при вершине А прямой угол. Сделать это можно, но будет это не очень просто.

Поэтому необходимо вырабатывать у учащихся, начиная с 6 класса, представления о возможности произвольного выбора системы координат. Эту работу целесообразно вести в процессе решения задач. В целях пропедевтической работы можно рекомендовать в 6 классе задачи из учебника на нахождение координат точек по рисунку, разнообразя их с помощью изменения направления осей и начала координат. (см. приложение1)

1. Длина отрезка АВ равна 5см. а)Выберите систему координат, в которой можно было бы наиболее просто определить координаты концов отрезка. б)Выберите систему координат так, чтобы координаты концов отрезка были бы: А (-2.5,0), В(2.5,0).

2. Постройте квадрат ABCD со стороной 2 см; отметьте точку М- центр квадрата. Поместите начало координат последовательно в точки A, B, C, D и выберите направление осей координат так, чтобы точка М в каждой системе координат имела координаты (1;1). За единичный примите отрезок длиной 1 см.

3. Треугольник ABC равносторонний (длина стороны равна 6 см.). Выберите систему координат так, чтобы можно проще было бы определить координаты его вершин.

III. Расстояние между точками

1) Точка М(а,с) находится от начала координат и точки А(4,0) соответственно на расстояниях 3 и 4 см. Определите координаты точки М.

2) Дан прямоугольник ABCD (АВ=2 см., ВС=4 см.). Как выбрать систему координат, чтобы его вершины имели координаты А(-1,-2), В(-1,2), С(1,2), D(l,-2)?

3) Длины сторон треугольника ABC равны 3, 4 и 5 см. Выберете систему координат и определите в ней координаты вершин треугольника ABC.

4) Вершины четырехугольника ABCD имеют следующие координаты: А(-3,1), В(3,6), С(2,2) и D(-4,3). Установите вид четырехугольника.

IV. Составление уравнения фигур

Это умение является одним из основных умений, которые необходимы при применении метода координат к решению задач.

1) Изобразите систему координат. Отметьте на оси Ох точки А и В. Запишите соотношения, которым удовлетворяют координаты точек, принадлежащих: а)отрезку АВ; б)лучу АВ; в)лучу ВА;

2) Запишите уравнение прямой, содержащей начало координат и точку А(2,5).

3) Запишите уравнение прямой, содержащей точки А(2,7)и В(1,3).

4) Изобразите на координатной плоскости произвольную прямую и найдите ее уравнение.

5) Запишите соотношения, которым удовлетворяю координаты точек прямоугольника с вершинами А(2,3), В(2,5), С(4,5), D(4,3).

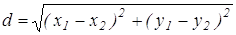
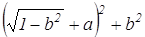
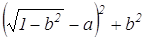
6) Что представляют собой множества точек плоскости, координаты которых удовлетворяют неравенствам: а)х≤3; b)-5≤х≤0; c)x>1; d)x 2 +АР 2 не зависит от переменной b. Найдем АМ 2 и АР 2 используя формулу нахождения расстояния между двумя точками по их координатам: . Они соответственно равны и , а их сумма после приведения подобных равна 2а 2 +2. Это число не зависит от переменной b, что и требовалось доказать.

Пример 2. Доказать, что сумма квадратов длин сторон четырехугольника равна сумме квадратов длин его диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналей. (Теорема Эйлера)

Решение: Введем прямоугольную систему координат как показано на рисунке 12.

Пусть точки А, В, С и D имеют координаты (0,0), (d,0), (c,d) и (0,d) соответственно. Следовательно, координаты точек L и P есть () и (). Найдем квадраты длин отрезков, с помощью формулы нахождения расстояния между точками по их координатам.

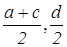
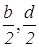
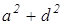
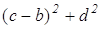
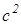
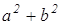
AD 2 =; BC 2 =; DC 2 =; AB 2 =;

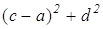
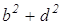
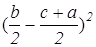
AC 2 =; BD 2 =; LP 2 =.

Запишем выражение, которое необходимо доказать, используя найденные нами значения.

AD 2 +BC 2 +DC 2 +AB 2 =AC 2 +BD 2 +4LP 2

+++=++4

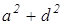
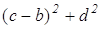
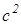
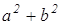
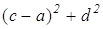
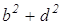
Раскроем скобки, приведем подобные и получим верное равенство 0=0. Значит, сумма квадратов длин сторон четырехугольника равна сумме квадратов длин его диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналей.

Пример 3. Диаметры AB и CD окружности перпендикулярны. Хорда ЕА пересекает диаметр СD в точке К, хорда ЕС пересекает диаметр АВ в точке L. Докажите, что если СК:KD так же как 2:1, то AL:LB так же как 3:1.

Решение: Введем прямоугольную систему координат, направив оси по данным диаметрам AB и CD (рис. 13).

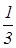
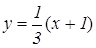
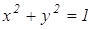
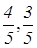
Радиус окружности будем считать равным 1. Тогда точки А, В, С, D будут иметь координаты (-1,0), (1,0), (0,-1), (0,1) соответственно. Так как СК:KD=2:1, то точка К имеет координаты (0,). Найдем координаты точки Е как точки пересечения прямой АК, имеющей уравнение и окружности, заданной уравнением . Получаем, что точка Е имеет координаты (). Точка L – это точка пересечения прямых СЕ и оси абсцисс, значит ординаты точки L равна 0.

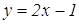
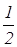
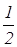
Найдем абсциссу точки L. Прямая СЕ задана уравнением . Она пересекает ось Ох в точке (,0). Отсюда координаты точки L(,0). Найдем отношение AL:LB. Оно равно трем, что и требовалось доказать.

1. Доказать, что если в треугольнике две медианы конгруэнтны, то треугольник равнобедренный.

2. Найти множество таких точек Р, что отношение расстояний от каждой из них до двух данных точек равно а.

3. Докажите, что уравнение окружности с центром в точке С (а,с) и радиусом r имеет вид: (х-а) 2 +(у-с) 2 =r 2

4. Найти угол между прямыми Зх-4у+6=0 и 12х+5у+8=0

5. Определите расстояние от точки А(-3,4) до прямой у=х+2.

6. Вычислите площадь треугольника, вершины которого имеют следующие координаты: А (0,-2), В(6,2) и С(2,4) .

7. На прямой с даны три точки А, В, С так, что точка В лежит между точками А и С. В одной полуплоскости с границей а построены равносторонние треугольники АМВ и ВРС. Доказать, что середина отрезка РА, середина отрезка МС и точка В являются вершинами равностороннего треугольника.

8. Доказать, что для любой точки Р лежащей между вершинами В и треугольника ABC, справедливо равенство :

АВ 2 *РС+АС*ВР-АР 2 *ВС=ВС*ВР*РС.

9. Дан прямоугольник. Докажите, что сумма квадратов расстояний от произвольной точки, принадлежащей плоскости этого прямоугольника до его вершин, в два раза больше суммы квадратов расстояний от этой точки до сторон прямоугольника.

10. Доказать, что если через некоторую точку М провести прямую, пересекающую окружность в точках А и В, то произведение МА*МВ постоянно и не зависит от положения прямой.

11. Дан прямоугольник ABCD. Найти множество точек М, для которых MA 2 +MC 2 =MB 2 +MD 2 . (ответ: множество точек М есть плоскость)

Как найти пересечение окружности и параболы

Найдите все значения параметра а, при каждом из которых система имеет ровно 4 решения.

Первое уравнение задает части двух парабол (см. рисунок):

Второе уравнение задает окружность радиусом с центром

На рисунке видно, что четыре решения системы получаются в двух случаях.

1. Окружность касается каждой из ветвей обеих парабол.

2. Окружность пересекает каждую из ветвей обеих парабол в двух точках, лежащих по разные стороны от оси абсцисс.

Составим уравнение для ординат общих точек окружности и параболы Получим: откуда

Чтобы окружность касалась парабол, уравнение должно иметь нулевой дискриминант: откуда

Во втором случае радиус окружности заключен между числами 3 и 9.

Ответ:

Аналоги к заданию № 484646: 484647 484648 511316 Все

Exzellenz писал(а):

Построить точки пересечения «в лоб» мне не удалось

Мне тоже не удалось найти чисто геометрическое решение (поэтому я и опубликовал эту задачу, надеясь, что Glotov1 решит геометрически). И я тоже решал аналитически. Правда, как мне кажется, я делал проще: просто приравнял Х^2 из уравнения окружности и х^2 из уравнения параболы, и решил квадратное уравнение. Я не возился с касательной. Ответ у меня получился такой же, но визуально несколько другой: под корнем у меня получилось

[math]sqrt{(2f-a)^{2} + R^{2} -a^{2} }[/math]

В вашем ответе скобки раскрыты, а я не стал раскрывать скобки, ибо с точки зрения построения отрезка это не даёт преимущества.

Exzellenz писал(а):

Построить по этой формуле отрезок с длиной, равной y0, в принципе несложно, но канительно.

Что там канительного? Ваш отрезок под корнем строится «в три линии» (не считая вспомогательных линий, которые мы здесь никогда не рисуем).

Мне кажется, что, после аналитических расчетов, такое построение будет легковеснее, чем построение в чисто геометрическом решении.

Кстати, если уж возиться с касательными, то, кроме касательной к параболе, можно найти и касательную к окружности, и найти точку пересечения этих двух касательных.

В п.3.1.3 изучено
уравнение вида
– уравнение первой степени (прямая на
плоскости).

Здесь рассмотрим
линии, которым соответствуют уравнения
второй степени

.
(3.21)

В (3.21) хотя бы один из коэффициентов
A, B
илиCотличен от
нуля.

Определение. Любая линия
на плоскости, уравнение которой есть
уравнение (3.21) – уравнение второй степени
относительно координатx,
y, называется кривой
второго порядка.

В подробных курсах аналитической
геометрии доказывается, что основными
кривыми второго порядка являются
окружность, эллипс, гипербола и парабола.

Рассмотрим эти
кривые, получим канонические уравнения
и исследуем их геометрическую форму.

1⁰. Окружность.
В п.3.1.2,2⁰была получена формула
(3.6) – уравнение окружности радиусаR
с центром в точке.
Раскрывая здесь скобки, придем к уравнению
(3.21) – окружность есть кривая второго
порядка (3.21), в котором.

Обратно, можно показать, что
если в уравнении (3.21) коэффициенты при
иодинаковы (A=B),
нет слагаемого с произведением(то есть коэффициентB=0),
то уравнение (3.21) есть уравнение окружности
(точнее, всякому уравнению (3.21), в которомсоответствует или действительная
окружность радиуса,
или мнимая окружность).

Пример. Составить уравнение
окружности, проходящей через три точки,и.

Решение. Запишем искомое
уравнение в виде.
Подставляя в него координаты точекA,B иC,
получим три уравнения для определения
трех неизвестныхиc:;и.

Решение этой
системы:
и уравнение окружности запишется в виде.
Преобразуя, придем к (каноническому)
уравнению окружности:– окружность с центром в точкерадиуса.

2⁰. Эллипс.
Получим каноническое уравнение эллипса,
исследуем его форму.

1) Определение, каноническое
уравнение эллипса.

Определение. Эллипсом
называется геометрическое место точек
(на плоско-

сти), сумма расстояний от которых
до двух фиксированных точек, называемых

фокусами, есть величина
постоянная, равная 2a.

Получим, исходя из определения,
уравнение эллипса.

Обозначим
ифокусы эллипса, через 2c– (заданное) расстояние между ними:=2c.
По определению,

.
(3.22’)

Выберем на плоскости прямоугольную
декартову систему координат, проведя
ось
через фокусы эллипсаии осьпосредине между фокусами (рис.3.13 хх ).
Имеем тогда:– текущая точка эллипса,,,
расстояния,и уравнение (3.22’) принимает вид:

.
(3.22”)

Приведем уравнение эллипса
(3.22”) к каноническому виду.

Перенесем второй
корень в (3.22”) направо; полученное
равенство возведем в квадрат. После
алгебраических преобразований придем
к равенству

.

Возводя это соотношение в
квадрат, вводя обозначение (так как
)

,
(3.22”’)

придем к уравнению

.

Деля обе части этого уравнения
на
,
получим каноническое уравнение эллипса:

.
(3.22)

В уравнении (3.22) aназывается большой полуосью, аb
– малой полуосью.

Эллипс есть кривая второго
порядка (можно показать, что в любой
другой прямоугольной декартовой системе
координат уравнение эллипса остается
уравнением второго порядка).

2) Исследование формы эллипса.
Исследуем форму эллипса.

Так как в уравнение (3.22)
координаты xиyвходят в четной степени, то если точкалежит на эллипсе, то точкии,
симметричные с точкойMотносительно осейи,
и точка,
симметричная с точкойMотносительно начала координат, также
лежат на нем (рис.3.14 хх ).

Таким образом, оси координат
идля эллипса, заданного уравнением
(3.22), являются осями симметрии, начало
координат – центром симметрии.

Определение. Кривая, имеющая
центр симметрии, называется центральной
кривой.

Эллипс – центральная кривая.

Замечание. Можно показать,
что всякий эллипс имеет единственный
центр симметрии и две оси симметрии
(если он не является окружностью).

Из уравнения (3.22) следует оценка
для координат точек эллипса:
,– эллипс расположен внутри прямоугольника
со сторонами,,,.

Точки пересечения эллипса с
его осями симметрии называются вершинами
эллипса; таким образом, эллипс имеет
четыре вершины:
,,,.

Из предыдущих результатов
исследования формы эллипса следует,
что достаточно определить вид кривой
в одном из координатных углов, например,
в том, где
.
Из соображений симметрии легко представить
характер кривой в остальных трех
координатных углах.

Разрешая уравнение эллипса
относительно ординаты y,
беря дляyлишь
неотрицательные значения:,
считая, что,
получим точки эллипса, лежащие в первом
квадранте. Из этого уравнения следует,
что а) ординатаyпринимает наибольшее значение (именно,)
приx=0; б) с
возрастаниемxот 0 доaордината точки
эллипса убывает; в) приx=aордината становится наименьшей,y=0
(рис.3.15 хх ).

Из равенства (3.22”’) можно
проследить за изменением формы эллипса
в зависимости от изменения междуфокусного
расстояния
=2c:
а) при сближении фокусов величинас
уменьшается, приближаясь к нулю. При
этом малая полуосьb
все меньше отличается от большой
полуосиa, а эллипс –
от окружности радиусаa.
Приc=0 эллипс (3.22)
совпадает с окружностью– окружность есть частный случай
эллипса. б) пусть фокусы удаляются друг
от друга, приближаясь к вершинами;
тогдаи из (3.22) следует, что:
эллипс, сжимаясь по вертикали, все меньше
отличается от отрезка.

За меру отклонения
эллипса от окружности принимают отношение

(3.23)

– эксцентриситет эллипса.
Очевидно,
.
Приимеем окружность; прималая ось эллипса уменьшается, а сам
эллипс, «сплющиваясь» по вертикали, все
меньше отличается от отрезка.

Замечание. Приведем (один)
признак того, что кривая второго порядка
(3.21) есть эллипс: коэффициентыA
иCимеют одинаковые
знаки, отсутствует член с произведениемxy– коэффициентB=0.

Пример. В эллипсвписан правильный треугольник, одна из
вершин которого совпадает с концом
большой оси. Найти координаты вершин
треугольника.

Решение. Приведем уравнение
эллипса к видуи,(рис.3.16 хх ). Поместим одну из вершин
треугольника в точку;
тогда угол,
откуда следует, что угловой коэффициент
прямой.
Запишем уравнение прямойAB:.

Из системы
,находим точку пересечения прямойABи эллипса – точкуB:.
Из соображений симметрии эллипса и
треугольникаABCотносительно осинаходим координаты вершиныC:.

3⁰. Гипербола.
Получим каноническое уравнение гиперболы,
исследуем ее форму.

1) Определение, каноническое
уравнение гиперболы.

Определение. Гиперболой
называется геометрическое место точек
(на плоскости), разность расстояний от
которых до двух фиксированных точек,
называемых фокусами, есть величина
постоянная, равная 2a.

Получим, исходя из определения,
уравнение гиперболы. Обозначим
ифокусы гиперболы, через 2c– (заданное) расстояние между ними:=2c.
По определению,

.
(3.24’)

Выбирая на плоскости прямоугольную
декартову систему координат, как это
было проделано для эллипса (см. рис.3.13),
сведем уравнение (3.24’) к виду:

.
(3.24”)

Проведя вычисления, аналогичные
приведенным в п.2⁰, вводя обозначение
(так как)

,
(3.24”’)

придем к уравнению

.

Деля обе части этого уравнения
на
,
получим каноническое уравнение гиперболы:

.
(3.24)

2) Исследование формы
гиперболы. Исследуем форму гиперболы.

Гипербола пересекается с осью
в точкахии не пересекается с осью.
Так же, как и для эллипса, можно показать,
что оси координат являются осями
симметрии гиперболы (3.24), а начало
координат – центром симметрии.

Таким образом, гипербола –
центральная кривая.

Замечание. Можно показать,
что всякая гипербола имеет единственный
центр симметрии и две оси симметрии.

Очевидно, что достаточно
исследовать вид гиперболы в одном из
координатных углов, например, в том, где
.
Из соображений симметрии легко представить
характер кривой в остальных трех
координатных углах.

Разрешая уравнение гиперболы
относительно ординаты y,
беря дляyлишь
неотрицательные значения, найдем:

.
(3.25)

Из (3.25) следует,
что абсциссы точек гиперболы, расположенных
в первой четверти, удовлетворяют условию:
или.

Преобразуя
уравнение (3.25) к виду

,
(3.25’)

замечаем, что для больших
значений xвеличина
корняблизка к единице:;
поэтому для такихxзначение

.
(3.25”)

Можно показать (опустим это),
что с возрастанием xразность между ординатами гиперболы
(3.25’) и прямой (3.25”) стремится к нулю,
принимая отрицательные значения –
точки гиперболы располагаются ниже
точек прямой.

Объединяя результаты
исследования, строим гиперболу (рис.3.17
хх ).

Замечание 1. Прямые,
к которым неограниченно приближаются
точки гиперболы при,
называются асимптотами гиперболы.

Замечание 2. Напомним, что
отрезокназывается действительной или фокальной
осью гиперболы,– мнимой осью, расстояниеназывается междуфокусным расстоянием.

Замечание 3. Если в уравнении
(3.24)полуосиa=b,
уравнение принимает вид

;
(3.26)

подобная гипербола называется
равнобочной гиперболой.

Замечание 4. Уравнение

(3.27)

также определяет гиперболу
(так называемую сопряженную (3.24)
гиперболу), для которой отрезок
является действительной осью гиперболы,
а отрезок– мнимой осью. Фокусы гиперболы (3.27)
находятся в точкахи,
где.
Асимптоты гипербол (3.24) и (3.27) совпадают
(рис.3.18 хх ).

Замечание 5. Здесь также
вводят понятие «эксцентриситет гиперболы»

.
(3.28)

Для гиперболы
,
так как.
Ограничимся здесь этим замечанием.

Пример. Составить каноническое
уравнение гиперболы, зная, что расстояние
одной из ее вершин до фокусов равны 9 и
1.

Решение. По условию,(рис.3.19 хх ). Так как фокусимеет координаты,,
вершина,
то,.

Имеем систему
уравнений:
,,
откуда,.
Мнимая полуось=3
и уравнение гиперболы есть.

4⁰. Парабола.
Получим каноническое уравнение параболы,
исследуем ее форму.

1) Определение, каноническое
уравнение параболы.

Определение. Параболой
называется геометрическое место точек
(на плоскости), равноудаленных от
фиксированной точки (называемую фокусом)
и от данной прямой (называемую директрисой).

Предполагается, что данная
прямая не проходит через фокус. Расстояние
pот фокуса параболы
до ее директрисы называется параметром
параболы. Эксцентриситет параболы
принимается равным единице:.

Выберем систему координат.
Опустим перпендикуляр из фокуса F
на директрису параболы:FA=p.
Направим осьпо прямойAF, а ось– через середину отрезкаAF(рис.3.20). Тогда уравнение

(3.29)

определяет уравнение директрисы;
координаты фокуса
.

Пусть
– текущая точка параболы. Из определения
параболы имеем равенство,
или

.
(3.30’)

Возводя (3.30’) в квадрат и
выполнив приведение подобных, придем
к уравнению

(3.30)

каноническое уравнение параболы.

2) Исследование формы
параболы. Исследуем форму параболы.

Парабола пересекает оси
координат в точке (0,0). Из представления
(3.30) заключаем, что все точки параболы
лежат справа от оси
.

Парабола симметрична относительно
оси
,
ибо если уравнению (3.30) удовлетворяют
координаты точки,
то ему удовлетворяют и координаты точки.
Точка (0, 0)называется вершиной параболы.

Для точек параболы, расположенных
в первом квадранте
,,
– с возрастаниемxординататакже возрастает. С учетом симметрии,
достраиваем параболу в четвертом
квадранте (рис.3.21 хх ).

Заметим, что у параболы нет
центра – парабола нецентральная кривая.

Пример. Написать уравнение
параболы и ее директрисы, если парабола
проходит через точку пересечения прямойи окружностии симметрична относительно оси.

Решение. Решая совместно
уравнения прямой и окружности:,,
найдем их точки пересечения –и.
Из условия симметрии параболы относительно
оси,
заключаем, что парабола проходит также
и через точку(рис.3.22 хх ).

Точка Oлежит
на оси симметрии параболы, она – вершина
параболы. Тогда уравнение параболы
должно иметь вид:.
Точкалежит на параболе, то есть выполняется
равенствоиp=1.

Таким образом,
уравнение
есть уравнение искомой параболы. Так
как расстояние от вершины параболы до
ее директрисы равно,
то точкаA– точка
пересечения директрисы с осью симметрии
имеет координаты.
Уравнениеи есть уравнение директрисы искомой
параболы.

Всякая кривая второго порядка относительно декартовых координат задается уравнением:

, (18)

Где – константы.

Это уравнение задает окружность, эллипс, параболу или гиперболу в зависимости от соотношений между его коэффициентами. Например, если в уравнении и , то оно является уравнением окружности.

Если уравнение (18) разлагается на два линейных множителя, то в этом случае оно определяет пару прямых, которые могут пересекаться, быть параллельными или совпадать.

Определение. Окружностью называется геометрическое место точек плоскости, равноудаленных от некоторой фиксированной точки плоскости, называемой ее центром.

Каноническое уравнение окружности имеет вид:

, (19)

Где – координаты центра, а – радиус окружности.

Пример 1. Найти центр и радиус окружности .

Решение. Выделяя полные квадраты по и по , приведем уравнение к виду , откуда, сравнивая с (19), находим и .

Пример 2. Составить уравнение окружности, проходящей через три точки , , .

Решение. Центр окружности находится в точке пересечения перпендикуляров, проведенных через середины хорд. Точка – середина хорды , а – середина и , . Уравнения перпендикуляров к хордам и , проходящих через их середины, имеют вид: и или и . Точка пересечения этих прямых .

Для нахождения радиуса найдем расстояние между точками и : . Запишем уравнение окружности: .

Определение. Эллипсом называется геометрическое место всех точек плоскости, сумма расстояний которых до двух данных точек плоскости, называемых фокусами, есть величина постоянная.

Каноническое уравнение эллипса:

, (20)

Где – большая полуось, – малая полуось, – эксцентриситет эллипса.

Прямую, на которой расположены фокусы эллипса , называют фокальной осью, а и – фокальными радиусами.

Прямые называют директрисами эллипса.

Пример 3. Убедитесь, что уравнение определяет эллипс. Найдите полуоси, координаты фокусов, эксцентриситет, уравнения директрис.

Решение. Приведем уравнение к каноническому виду , откуда , . Из условия найдем , то есть . Тогда , а уравнение директрис .

Пример 4. Доказать, что уравнение определяет эллипс. Найти координаты его центра симметрии.

Решение. Преобразуем данное уравнение, выделив полные квадраты по и по :

.

Обозначим , где – новые переменные. Тогда уравнение примет вид или, приводя к каноническому виду, . Сравнивая полученное уравнение с уравнением (20) убеждаемся, что кривая – эллипс. Центр его симметрии находится в точке .

Определение. Гиперболой называется геометрическое место точек плоскости, разность расстояний которых до двух данных точек и плоскости, называемых фокусами, есть величина постоянная.

Каноническое уравнение гиперболы:

, (21)

Где .

Точки , называются вершинами гиперболы, прямые являются асимптотами гиперболы, – действительная полуось, – мнимая полуось, – эксцентриситет гиперболы, прямые – ее директрисы.

Пример 5. Написать уравнение гиперболы и ее асимптот, если фокусы гиперболы находятся в точках и длина вещественной оси равна 6.

Решение. По условию , тогда из формулы найдем . Каноническое уравнение гиперболы: уравнения асимптот: .

Пример 6. Написать уравнение гиперболы, проходящей через точку , асимптоты которой .

Решение. Из уравнения асимптот следует, что . Уравнение гиперболы будем искать в виде . Так как точка лежит на гиперболе, то . Решая систему найдем , . Получаем или .

Пример 7. Доказать, что уравнение определяет гиперболу. Написать уравнения ее асимптот.

Решение. Выделим полные квадраты по и по :

или

. Обозначая и деля обе части уравнения на 9, получим каноническое уравнение , откуда следует, что , центр находится в точке то есть . Учитывая, что асимптоты проходят через точку и , запишем их уравнения: или .

Определение. Параболой называется геометрическое место точек плоскости, равноудаленных от данной точки плоскости, называемой фокусом, и данной прямой, называемой директрисой.

Каноническое уравнение параболы

, (22)

Где (параметр параболы) – расстояние между фокусом и директрисой, а уравнение ее директрисы .

Так как уравнение параболы содержит , то она симметрична относительно оси . Ось симметрии параболы называется осью параболы.

Вершиной параболы называется точка пересечения параболы с ее осью симметрии.

Пример 8. Парабола с вершиной в начале координат проходит через точку и симметрична относительно оси . Написать ее каноническое уравнение.

Решение. Подставляя координаты точки в уравнение (22), найдем, что . Значит, уравнение параболы .

Пример 9. Доказать, что уравнение определяет параболу. Найти значение ее параметра и координаты вершины.

Решение. Выделяя полный квадрат, получим . Если положить то уравнение примет вид . Сравнивая его с каноническим уравнением (22), находим , откуда . Вершина параболы находится в точке , , то есть .

Для самостоятельного решения.

1. Найти координаты центра и радиус окружности .

Ответ: , .

2. Составить уравнение окружности, если она проходит через точки и , а центр ее лежит на прямой .

Ответ: .

3. Найти площадь четырехугольника, две вершины которого лежат в фокусах эллипса , а две другие совпадают с концами его малой оси.

Ответ: 16.

4. Составить уравнение хорды параболы , которая проходит через ее вершину перпендикулярно прямой .

Ответ: .

5. На параболе найти точку , ближайшую к прямой , и вычислить расстояние от точки до прямой.

Ответ: .

6. Найти площадь треугольника, образованного асимптотами гиперболы и прямой .

Ответ: 12.

7. Дана окружность . Найти уравнение радиусов, проведенных из центра в точки пересечения окружности с осью ординат, а также угол между этими радиусами.

Ответ: .

< Предыдущая		Следующая >