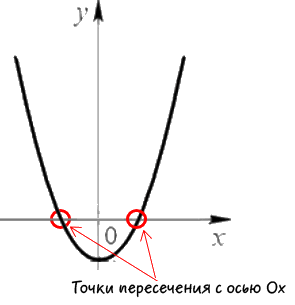
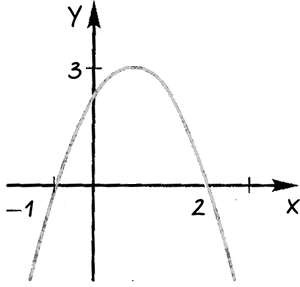Расположение графика квадратного трёхчлена относительно осей координат
В §28 данного справочника мы показали, что квадратный трёхчлен можно представить в виде:
$$ ax^2+bx+c = a(x+ frac{b}{2a})^2-frac{D}{4a}, D = b^2-4ac $$
Мы получаем:
- ось симметрии $x = -frac{b}{2a}$
- вершину параболы на оси симметрии $(–frac{b}{2a}; -frac{D}{4a})$
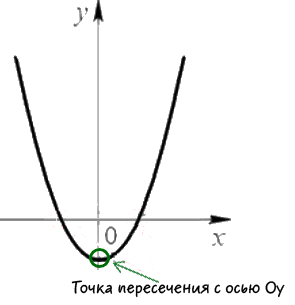
- точку пересечения (0;c) с осью OY
Любая парабола $y = ax^2+bx+c, a ≠ 0$ пересекается с осью OY в единственной точке (0;c).
Количество точек пересечения параболы $y = ax^2+bx+c$ с осью OX зависит от знака дискриминанта.
Если $D gt 0$, парабола имеет две точки пересечения с $x_1,2 = frac{-b pm sqrt{D}}{2a}$ на оси OX.
Если D = 0, парабола имеет одну точку пересечения $x_0 = -frac{b}{2a}$, которая лежит на оси OX и является вершиной параболы.
Если $D lt 0$ у параболы нет ни одной точки пересечения с осью OX.
Точки пересечения параболы с осью OX
|
$a gt 0$ |
$a lt 0$ |
|
|
$D gt 0$ |
 |
 |
|
$x_(1,2) = frac{-b pm sqrt{D}}{2a}$ |
||
|
D = 0 |
 |
 |
|
$x_0 = -frac{b}{2a}$ |
||
|
$ D lt 0 $ |
 |
 |
|
${ varnothing }$-нет пересечений |
Точки пересечения двух парабол
На практике часто возникает задача «перехвата» одного тела другим, т.е. поиска точек пересечения двух траекторий; а тела в поле тяготения Земли нередко движутся по параболе.
Поэтому исследовать возможные точки пересечения двух парабол – важная прикладная задача. Пусть уравнения парабол:
$$ y = a_1 x^2+b_1 x+c_1, quad y = a_2 x^2+b_2 x+c_2 $$
В точках пересечения выполняется равенство:
$$ a_1 x^2+b_1 x+c_1 = a_2 x^2+b_2 x+c_2 $$
$$ (a_1-a_2 ) x^2+(b_1-b_2 )x+(c_1-c_2 ) = 0 $$
Если ввести обозначения $A = a_1-a_2, B = b_1-b_2, C = c_1-c_2$, получаем уравнение:
$$ Ax^2+Bx+C = 0 $$
Количество решений этого уравнения в зависимости от нулевых и ненулевых значений параметров равно 11 и описывается схемой общего алгоритма решений квадратного уравнения (см.§25 данного справочника).
A = B = C = 0
$ a_1 = a_2, b_1 = b_2, $
$ c_1 = c_2 $
Две параболы совпадают
Бесконечное множество общих точек, $x in Bbb R$
$A = B = 0, C neq 0$
$ a_1 = a_2, b_1 = b_2, $
$ c_1 neq c_2 $
Параболы имеют вид
$y = ax^2+bx+c_1$
$ y = ax^2+bx+c_2 $
У них общая ось симметрии
$ x = -frac{b}{2a}$, одна парабола находится над другой.
Ветки сходятся только на бесконечности.
Точек пересечения нет
$A = 0, B neq 0, C = 0$
$ a_1 = a_2, b_1 neq b_2 $
$ c_1 = c_2 $
Параболы имеют вид
$y = ax^2+b_1 x+c$
$ y = ax^2+b_2 x+c $
Обе проходят через точку (0;c).
Это – единственная точка пересечения.
Одна точка пересечения
(0;c)
$A = 0, B neq 0, C neq 0$
$ a_1 = a_2, b_1 neq b_2 $
$ c_1 neq c_2 $
Параболы имеют вид
$y = ax^2+b_1 x+c_1$
$ y = ax^2+b_2 x+c_2 $
Абсцисса точки пересечения
$ x = — frac{C}{B} = -frac{c_1-c_2}{b_1-b_2}$
Одна точка пересечения (касание)
$A neq 0, B = 0, C = 0$
$ a_1 neq a_2, b_1 = b_2 $
$ c_1 = c_2 $
Параболы имеют вид
$ y = a_1 x^2+bx+c$
$ y = a_2 x^2+bx+c $
Пересекаются при x=0 (точка касания)
Одна точка пересечения (касание) (0;c)
$A neq 0, B = 0, C neq 0$
$ a_1 neq a_2, b_1 = b_2 $
$ c_1 neq c_2 $
Параболы имеют вид
$ y = a_1 x^2+bx+c_1$
$ y = a_2 x^2+bx+c_2 $
Не пересекаются, если
$- frac{c_1-c_2}{a_1-a_2} lt 0 $
Две точки пересечения
Если
$- frac{c_1-c_2}{a_1-a_2} gt 0 $
Пересекаются в двух точках
$$ x_{1,2} = pm sqrt{-frac{c_1-c_2}{a_1-a_2}} $$
Две точки пересечения
$A neq 0, B neq 0, C = 0$
$ a_1 neq a_2, b_1 neq b_2 $
$ c_1 = c_2 $
Параболы имеют вид
$$ y = a_1 x^2+b_1 x+c $$
$$ y = a_2 x^2+b_2 x+c $$
Две точки пересечения
$ x_1 = 0 $
$$x_2 = -frac{b_1-b_2}{a_1-a_2}$$
Две точки пересечения,
одна из которых (0;c)
$A neq 0, B neq 0, C neq 0$
$ a_1 neq a_2, b_1 neq b_2 $
$ c_1 neq c_2 $
Все параметры парабол разные
Ищем дискриминант:
$$ D = B^2-4AC $$
Если $D gt 0$
Две точки пересечения
$$ x_1,2 = frac{-B pm sqrt{D}}{2A} $$
Две точки пересечения
Если D = 0
Одна точка пересечения (касание)
$$ x_0 = -frac{B}{2A} $$
Одна точка пересечения
(касание)
Если $D lt 0$
Точек пересечения нет
Точек пересечения нет
Внимание!
Если две параболы не совпадают, то они могут иметь 1) две точки пересечения; 2) одну точку пересечения; 3) ни одной точки пересечения.
Иметь ровно 3, 4, 5 и т.д. точек пересечения две параболы не могут!
Примеры
Пример 1. Найдите точки пересечения параболы с осями координат:
$а) y = 3x^2+2x-1$
Пересечение с осью OY: ${left{ begin{array}{c} x = 0 \ y = -1end{array} right.}$
Пересечение с осью OX:
$$ 3x^2+2x-1 = 0 Rightarrow (3x-1)(x+1) = 0 Rightarrow $$
$ Rightarrow left[ begin{array}{cc} {left{ begin{array}{c} x = frac{1}{3} \ y = 0 end{array} right.} \ {left{ begin{array}{c} x = -1 \ y = 0 end{array} right.} end{array} right.$ — две точки пересечения
$б) y = -4x^2-3x+1$
Пересечение с осью OY: ${left{ begin{array}{c} x = 0 \ y = 1end{array} right.}$
Пересечение с осью OX:
$$ -4x^2-3x+1 = 0 Rightarrow 4x^2+3x-1 = 0 $$
$$ (4x-1)(x+1) = 0 Rightarrow$$
$ Rightarrow left[ begin{array}{cc} {left{ begin{array}{c} x = frac{1}{4} \ y = 0 end{array} right.} \ {left{ begin{array}{c} x = -1 \ y = 0 end{array} right.} end{array} right.$ — две точки пересечения
$в) y = 5x^2-2x+1$
Пересечение с осью OY: ${left{ begin{array}{c} x = 0 \ y = 1end{array} right.}$
Пересечение с осью OX:
$$ 5x^2-2x+1 = 0 $$
$$ D = 2^2-4 cdot 5 cdot 1 = 4-20 = -16 lt 0 $$
Парабола не пересекает ось OX
$ г) y = -x^2+4x-4 $
Пересечение с осью OY: ${left{ begin{array}{c} x = 0 \ y = -4end{array} right.}$
Пересечение с осью OX:
$$ -x^2+4x-4 = 0 Rightarrow x^2-4x+4 = 0 Rightarrow $$
$$ Rightarrow (x-2)^2 = 0 Rightarrow {left{ begin{array}{c} x = 2 \ y = 0 end{array} right.}$$ — одна точка пересечения
Пример 2*. Даны две параболы
$$ y = 2x^2+5x+1 и y = x^2+3x+k $$
Найдите такое значение параметра k, чтобы параболы
1) имели две точки пересечения; 2) имели одну точку пересечения; 3) не пересекались.
По условию
$$ a_1 = 2, b_1 = 5, c_1 = 1, a_2 = 1, b_2 = 3, c_2 = k $$
$$ a_1 neq a_2, b_1 neq b_2 $$
A = 2-1 = 1, B = 5-3 = 2, C = 1-k
Нам необходимо рассмотреть 4 последних случая из представленных выше, в таблице §29.
1) Параболы имеют две точки пересечения в двух случаях:
1 случай: $c_2 = c_1$, k = 1
$$x_1 = 0, x_2 = -frac{B}{A} = -2$$
$${left{ begin{array}{c} y = 2x^2+5x+1 \ y = x^2+3x+1 end{array} right.} Rightarrow left[ begin{array}{cc} {left{ begin{array}{c} x_1 = 0 \ y_1 = 1end{array} right.} \ {left{ begin{array}{c} x_2 = -2 \ y_2 = -1 end{array} right.} end{array} right.$$
2 случай: $c_2 ≠ c_1, D gt 0$
$$ D = B^2-4AC = 2^2-4 cdot 1 cdot (1-k) = 4k gt 0 Rightarrow k gt 0 $$
Например, k = 4
$$ D = 4k = 16 = 4^2 $$
$$ x_1,2 = frac{-B pm sqrt{D}}{2A} = frac{-2 pm 4}{2} = left[ begin{array}{cc} x_1 = -3\ x_2 = 1 end{array} right. $$
Оба случая можем объединить требованием $k gt 0$.
2) Параболы имеют одну точку пересечения, если:
$$ D = 4k = 0 Rightarrow k = 0 $$
$${left{ begin{array}{c} y = 2x^2+5x+1 \ y = x^2+3x end{array} right.} $$
$$ x_0 = frac{-B}{2A} = -1 $$
3) Параболы не имеют общих точек, если:
$$ D = 4k lt 0 Rightarrow k lt 0 $$
Например, k = -1
Ответ: 1) $k gt 0$; 2) k = 0; 3) $k lt 0$
Пример 3. Две параболы с общей вершиной
Найдите соотношение параметров двух парабол, при котором они будут пересекаться в одной точке – вершине парабол.
Пусть уравнения парабол:
$$ y = a_1 x^2+b_1 x+c_1, y = a_2 x^2+b_2 x+c_2 $$
Координаты вершин:
$$ left( -frac{b_1}{2a_1}, — frac{D_1}{4a_1} right), left(- frac{b_2}{2a_2},- frac{D_2}{4a_2} right) $$
По условию:
$$ {left{ begin{array}{c} -frac{b_1}{2a_1} = -frac{b_2}{2a_2} \ -frac{D_1}{4a_1} = -frac{D_2}{4a_2} end{array} right.} Rightarrow {left{ begin{array}{c} frac{b_1}{a_1} = frac{b_2}{2a_2} \ frac{D_1}{a_1} = frac{D_2}{a_2} end{array} right.} $$
Получаем две пропорции, которым параметры уравнений должны удовлетворять одновременно.
Пример 4. Используя результаты примера 3, найдите две параболы, у которых такая же вершина, как у $y = frac{x^2}{2}-3x+1$.
Координаты вершины:
$$ x_0 = — frac{b}{2a} = — frac{-3}{2 cdot frac{1}{2}} = 3, D = b^2-4ac = 3^2-4 cdot frac{1}{2} cdot 1 = 7 $$
$$ y_0 = — frac{D}{4a} = — frac{7}{4 cdot frac{1}{2}} = -3,5 $$
Уравнение искомой параболы: $y = ax^2+bx+c$
Пропорции для параметров (см. пример 3):
$$ {left{ begin{array}{c} frac{b}{a} = frac{-3}{1/2} = -6 \ frac{D}{a} = frac{7}{1/2} = 14 end{array} right.} Rightarrow {left{ begin{array}{c} b = -6a \ D = 14a end{array} right.} $$
Пусть для искомых двух парабол a=1 и a=-0,2 (можно взять любые другие значения). Получаем:
$$ {left{ begin{array}{c} a = 1 \ b = -6a = -6 \ D = 14a = 14 end{array} right.} Rightarrow {left{ begin{array}{c} a = 1 \ b = -6 \ b^2-4ac = 14 end{array} right.} Rightarrow {left{ begin{array}{c} a = 1 \ b = -6 \ 36-4c = 14 end{array} right.} Rightarrow {left{ begin{array}{c} a = 1 \ b = -6 \ c = frac{36-14}{4} = 5,5 end{array} right.}$$
$$ y = x^2-6x+5,5 $$
$$ {left{ begin{array}{c} a = -0,2 \ b = -6a = 1,2 \ D = 14a = -2,8 end{array} right.} Rightarrow {left{ begin{array}{c} a = -0,2 \ b = 1,2 \ 1,2^2-4 cdot (-0,2)c = -2,8 end{array} right.} Rightarrow {left{ begin{array}{c} a = -0,2 \ b = 1,2 \ c = — frac{1,44+2,8}{0,8} = -5,3 end{array} right.} $$
$$ y = -0,2x^2+1,2x-5,3 $$
Параболы
$$ y = frac{x^2}{2}-3x+1, y = x^2-6x+5,5, y = -0,2x^2+1,2x-5,3 $$
имеют общую вершину (3;-3,5)
Пример 5. Комета движется по параболической траектории, которая в выбранной системе координат описывается уравнением $y = frac{x^2}{3}-2x+5$.
Космический аппарат запускается из начала координат и также движется по параболической траектории. Рассчитайте уравнение этой траектории так, чтобы её вершина совпала с вершиной траектории кометы.
Координаты вершины траектории кометы:
$$ x_0 = -frac{b}{2a} = -frac{-2}{2 cdot frac{1}{3}} = 3, D = b^2-4ac = 2^2-4 cdot frac{1}{3} cdot 5 = — frac{8}{3} $$
$$ y_0 = — frac{D}{4a} = — frac{-8/3}{4 cdot 1/3} = 2 $$
Уравнение траектории космического аппарата: $y = ax^2+bx+c$.
Аппарат запускается из начала координат, т.е. его траектория пересекается с осью OY в точке (0;0). Значит, в уравнении параболы c = 0.
Пропорции для параметров (см. пример 3) с учетом c = 0:
$$ {left{ begin{array}{c} frac{b}{a} = frac{-2}{1/3} = -6 \ frac{D}{a} = frac{-frac{8}{3}}{frac{1}{3}} = -8 end{array} right.} Rightarrow {left{ begin{array}{c} b = -6a \ D = b^2-4a underbrace{c}_{text{= 0 }} = b^2 = -8a end{array} right.} Rightarrow {left{ begin{array}{c} b = -6a \ b^2 = -8a end{array} right.} Rightarrow $$
$$ {left{ begin{array}{c} b = frac{-8a}{-6a} = frac{4}{3} \ a = -frac{b}{6} = -frac{2}{9} end{array} right.} $$
Уравнение траектории космического аппарата с «перехватом» кометы в вершине:
$$ y = -frac{2}{9} x^2+ frac{4}{3} x $$
Как вычислять координаты точек пересечения парабол
Параболы на плоскости могут пересекаться в одной или двух точках, либо вообще не иметь точек пересечения. Поиск таковых точек — типичная задача алгебры, входящая в программу школьного курса.
Инструкция
Убедитесь в том, что по условиям задачи вам известны уравнения обеих парабол. Парабола — это кривая на плоскости, задаваемая уравнением следующего вида y = ax² + bx + c (формула 1), где a, b и c — некоторые произвольные коэффициенты, причем коэффициент a ≠ 0. Таким образом, две параболы будут заданы посредством формул y = ax² + bx + c и y = dx² + ex + f. Пример — заданы параболы с формулами y = 2x² — x — 3 и y = x² -x + 1.
Теперь вычтите из одного из уравнений параболы другое. Произведите, таким образом, расчет следующего вида: ax² + bx + c — (dx² + ex + f) = (a-d)x² + (b-e)x + (c-f). Получился полином второй степени, коэффициенты которого вы легко можете вычислить. Чтобы найти координаты точек пересечения парабол, достаточно поставить знак равенства нулю и найти корни получившегося квадратного уравнения (a-d)x² + (b-e)x + (c-f) = 0 (формула 2). Для приведенного выше примера получим y = (2-1)x² -x + x + (-3 — 1) = x² — 4 = 0.
Корни квадратного уравнения (формула 2) ищем по соответствующей формуле, которая есть в любом учебнике алгебры. Для приведенного примера существует два корня x = 2 и x = -2. Кроме того, в формуле 2 значение коэффициента при квадратичном члене (a-d) может быть равным нулю. В этом случае уравнение окажется не квадратным, а линейным и всегда будет иметь один корень. Заметьте, в общем случае квадратное уравнение (формула 2) может иметь два корня, один корень, либо вовсе не иметь ни одного — в последнем случае параболы не пересекаются и задача не имеет решения.
Если, все же, найден один или два корня, их значения нужно подставить в формулу 1. В нашем примере подставляем вначале x = 2, получаем y = 3, затем подставляем x = -2, получаем y = 7. Две получившиеся точки на плоскости (2;3) и (-2;7) и являются координатами пересечения парабол. Других точек пересечения у этих парабол нет.
Обратите внимание
Особым случаем является поиск точек пересечения тождественно равных парабол, то есть двух парабол, задаваемых одинаковыми уравнениями. В этом случае можно сказать, что параболы совпадают, все точки у них общие.
Источники:
- координаты точки параболы
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
В предыдущем уроке мы подробно разобрали,
как построить параболу.
В этом уроке мы разберем, как решать типовые задачи на квадратичную функцию.
Как найти нули квадратичной функции
Запомните!
Чтобы найти координаты точек нулей функции, нужно
в исходную функцию подставить вместо «y» число
ноль.
Рассмотрим задачу.
Найти нули квадратичной
функции «y = x2 − 3».
Подставим в исходную функцию вместо «y» ноль и решим полученное
квадратное уравнение.
0 = x2 − 3
x2 − 3 = 0
x1;2 =
| 0 ± √02 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
x1;2 = ±√3
Ответ: нули функции «y = x2 − 3» :
x1 = √3;
x2 = −√3 .
Как найти при каких значениях
«x» квадратичная функция принимает заданное
числовое значение
Запомните!
Чтобы найти при каких значениях «x» квадратичная функция принимает заданное числовое значение,
нужно:
- вместо «y» подставить в функцию заданное числовое значение;
- решить полученное квадратное уравнение относительно «x».
Рассмотрим задачу.
При каких значениях «x» функция
«y = x2 − x − 3» принимает значение
«−3».
Подставим в исходную функцию
«y = x2 − x − 3» вместо «y = −3» и
найдем «x».
y = x2 − x − 3
−3 = x2 − x − 3
x2 − x − 3 = −3
x2 − x − 3 + 3 = 0
x2 − x = 0
x1;2 =
| 1 ± √12 − 4 · 1 · 0 |
| 2 · 1 |
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 1 | x2 = 0 |
Ответ: при «x = 0» и
«x = 1» функция «y = x2 − x − 3»
принимает значение «y = −3».
Как найти координаты точек пересечения параболы и прямой
Запомните!
Чтобы найти точки пересечения параболы с прямой нужно:
- приравнять правые части функций (те части функций, в которых содержатся «x»);
- решить полученное уравнение относительно «x»;
- подставить полученные числовые значения «x»
в любую из функций и найти координаты точек по оси «Оy».
Рассмотрим задачу.
Найти координаты точек пересечения параболы «y = x2»
и прямой «y = 3 − 2x».
Приравняем правые части функций и решим
полученное уравнение относительно «x».
x2 = 3 − 2x
x2 − 3 + 2x = 0
x2 + 2x − 3 = 0
x1;2 =
| −2 ± √22 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 1 | x2 = −3 |
Теперь подставим в любую из заданных функций (например, в
«y = 3 − 2x») полученные
числовые значения «x», чтобы найти координаты
«y» точек пересечения.
1) x = −3
y = 3 − 2x
y(−3) = 3 − 2 · (−3) = 3 − (−6) = 3 + 6 = 9
(·) A (−3; 9) — первая точка пересечения.
2) x = 1
y = 3 − 2x
y(1) = 3 − 2 · 1 = 3 − 2 = 1
(·) B (1; 1) — вторая точка пересечения.
Запишем полученные точки пересечения с их координатами в ответ.
Ответ: точки пересечения параболы
«y = x2»
и прямой «y = 3 − 2x»:
(·) A (−3; 9) и
(·) B (1; 1).
Как определить, принадлежит ли точка графику функции параболы
Запомните!
Чтобы проверить принадлежность точки параболе нет необходимости строить график функции.
Достаточно подставить координаты точки в формулу функции (координату по оси
«Ox» вместо
«x», а координату по оси
«Oy» вместо «y») и выполнить арифметические расчеты.
- Если получится верное равенство, значит, точка принадлежит графику функции.
- Если получится неверное равенство, значит, точка
не принадлежит графику функции.
Рассмотрим задачу:
Не строя графика функции «y = x2», определить, какие точки принадлежат ему:
(·) А(2; 6),
(·) B(−1; 1).
Подставим в функцию
«y = x2»
координаты точки (·) А(2; 6).
y = x2
6 = 22
6 = 4
(неверно)
Значит, точка (·) А(2; 6)
не принадлежит графику функции
«y = x2».
Подставим в функцию
«y = x2»
координаты точки (·) B(−1; 1).
y = x2
1 = (−)12
1 = 1
(верно)
Значит, точка (·) B(−1; 1)
принадлежит графику функции
«y = x2».
Как найти точки пересечения параболы с осями координат
Рассмотрим задачу
Найти координаты точек пересечения параболы
«y = x2 −3x + 2» с осями координат.
Сначала определим точки пересечения функции с осью «Ox».
На графике функции эти точки выглядят так:
Как видно на рисунке выше, координата «y» точек пересечения с осью «Ox»
равна нулю, поэтому подставим «y = 0» в
исходную функцию «y = x2 −3x + 2»
и найдем их координаты по оси «Ox».
0 = x2 −3x + 2
x2 −3x + 2 = 0
x1;2 =
| 3 ± √32 − 4 · 1 · 2 |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 2 | x2 = 1 |
Запишем координаты точек пересечения графика с осью «Ox»:
(·) A (2; 0) и
(·) B (1; 0).
Теперь найдем координаты точки пересечения с осью «Oy».
Как видно на рисунке выше, координата «x»
точки пересечения с осью «Oy» равна нулю.
Подставим «x = 0»
в исходную функцию
«y = x2 −3x + 2»
и найдем координату точки по оси
«Oy».
y(0) = 02 − 3 · 0 + 2 = 2
Выпишем координаты полученной точки: (·) C (0; 2)
Запишем в ответ все координаты точек пересечения параболы с осями.
Ответ: точки пересечения с осью «Ox»:
(·) A (2; 0) и
(·) B (1; 0).
С осью «Oy»: (·)C (0; 2).
Как определить при каких значениях x функция принимает
положительные или
отрицательные значения
Напоминаем, что когда в задании говорится «функция принимает
значения» — речь идет о
значениях«y».
Другими словами, необходимо ответить на вопрос: при каких значениях
«x», координата
«y» положительна или отрицательна.
Запомните!
Чтобы по графику функции определить, где функция принимает положительные или отрицательные значения нужно:
- провести прямые через точки в местах, где график пересекает ось «Ox»;
- определить положительные или отрицательные значения принимает функция на промежутках между проведенными прямыми;
- записать ответ для каждого промежутка относительно «x».
Рассмотрим задачу.
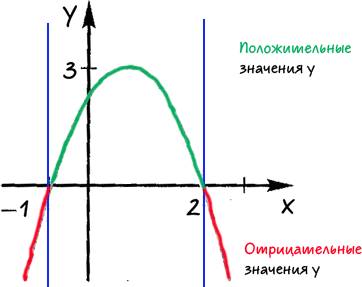
С помощью графика квадратичной функции, изображенного на рисунке, ответить:
При каких значениях «x» функция принимает 1) положительные значения; 2) отрицательные значения.
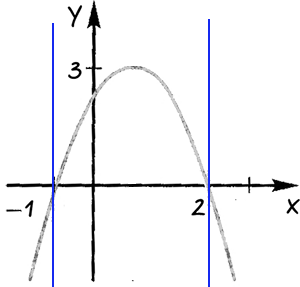
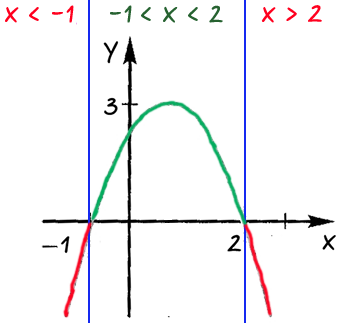
Проведем через точки, где график функции пересекает ось «Ox» прямые.
Определим области, где функция принимает отрицательные или положительные значения.
Подпишем над каждой полученной областью, какие значения принимает
«x» в каждой из выделенных областей.
Ответ: при «x < −1» и
«x > 2» функция принимает отрицательные значения;
при «−1 < x < 2» функция принимает
положительные значения.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Как найти координаты точек пересечения графика функции: примеры решения
Ирина Алексеевна Антоненко
Эксперт по предмету «Математика»
Задать вопрос автору статьи
В практике и в учебниках наиболее распространены нижеперечисленные способы нахождения точки пересечения различных графиков функций.
Первый способ
Первый и самый простой – это воспользоваться тем, что в этой точке координаты будут равны и приравнять графики, а из того что получится можно найти $x$. Затем найденный $x$ подставить в любое из двух уравнений и найти координату игрек.
Пример 1
Найдём точку пересечения двух прямых $y=5x + 3$ и $y=x-2$, приравняв функции:
$5x = x- 2$;
$4x = -2$;
$x=-frac{1}{2}$
Теперь подставим полученный нами икс в любой график, например, выберем тот, что попроще — $y=x-2$:
$y=-frac{1}{2} – 2 = — 2frac12$.
Точка пересечения будет $(-frac{1}{2};- 2frac12)$.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Второй способ
Второй способ заключается в том, что составляется система из имеющихся уравнений, путём преобразований одну из координат делают явной, то есть, выражают через другую. После это выражение в приведённой форме подставляется в другое.
Пример 2
Узнайте, в каких точках пересекаются графики параболы $y=2x^2-2x-1$ и пересекающей её прямой $y=x+1$.
Решение:
Составим систему:
$begin{cases} y=2x^2-2x-1 \ y= x + 1 \ end{cases}$
Второе уравнение проще первого, поэтому подставим его вместо $y$:
$x+1 = 2x^2 – 2x-1$;
$2x^2 – 3x – 2 = 0$.
Вычислим, чему равен x, для этого найдём корни, превращающие равенство в верное, и запишем полученные ответы:
$x_1=2; x_2 = -frac{1}{2}$
Подставим наши результаты по оси абсцисс по очереди во второе уравнение системы:
$y_1= 2 + 1 = 3; y_2=1 — frac{1}{2} = frac{1}{2}$.
Точки пересечения будут $(2;3)$ и $(-frac{1}{2}; frac{1}{2})$.
Третий способ
«Как найти координаты точек пересечения графика функции: примеры решения» 👇
Перейдём к третьему способу — графическому, но имейте в виду, что результат, который он даёт, не является достаточно точным.
Для применения метода оба графика функций строятся в одном масштабе на одном чертеже, и затем выполняется визуальный поиск точки пересечения.
Данный способ хорош лишь в том случае, когда достаточно приблизительного результата, а также если нет каких-либо данных о закономерностях рассматриваемых зависимостей.
Пример 3
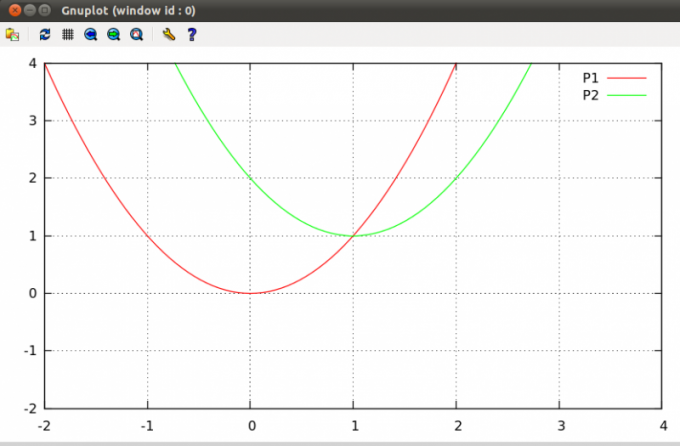
Найдите точку пересечения графиков на общем рисунке.
Рисунок 1. Точка пересечения двух функций. Автор24 — интернет-биржа студенческих работ
Решение:
Тут всё просто: ищем точки пересечения пунктиров, опущенных с графиков с осями абсцисс и ординат и записываем по порядку. Здесь точка пересечения равна $(2;3)$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 07.05.2023
Координаты точки пересечения графиков функций
Как найти?
- Чтобы найти координаты точки пересечения графиков функций нужно приравнять обе функции друг к другу, перенести в левую часть все члена, содержащие $ x $, а в правую остальные и найти корни, полученного уравнения.
- Второй способ заключается в том, что нужно составить систему уравнений и решить её путём подстановки одной функции в другую
- Третий способ подразумевает графическое построение функций и визуальное определение точки пересечения.
Случай двух линейных функций
Рассмотрим две линейные функции $ f(x) = k_1 x+m_1 $ и $ g(x) = k_2 x + m_2 $. Эти функции называются прямыми. Построить их достаточно легко, нужно взять любые два значения $ x_1 $ и $ x_2 $ и найти $ f(x_1) $ и $ (x_2) $. Затем повторить тоже самое и с функцией $ g(x) $. Далее визуально найти координату точки пересечения графиков функций.
Следует знать, что линейные функции имеют только одну точку пересечения и только тогда, когда $ k_1 neq k_2 $. Иначе, в случае $ k_1=k_2 $ функции параллельны друг другу, так как $ k $ — это коэффициент угла наклона. Если $ k_1 neq k_2 $, но $ m_1=m_2 $, тогда точкой пересечения будет $ M(0;m) $. Это правило желательно запомнить для ускоренного решения задач.
| Пример 1 |
| Пусть даны $ f(x) = 2x-5 $ и $ g(x)=x+3 $. Найти координаты точки пересечения графиков функций. |
| Решение |
|
Как это сделать? Так как представлены две линейные функции, то первым делом смотрим на коэффициент угла наклона обеих функций $ k_1 = 2 $ и $ k_2 = 1 $. Замечаем, что $ k_1 neq k_2 $, поэтому существует одна точка пересечения. Найдём её с помощью уравнения $ f(x)=g(x) $: $$ 2x-5 = x+3 $$ Переносим слагаемые с $ x $ в левую часть, а остальные в правую: $$ 2x — x = 3+5 $$ $$ x = 8 $$ Получили $ x=8 $ абциссу точки пересечения графиков, а теперь найдём ординату. Для этого подставим $ x = 8 $ в любое из уравнений хоть в $ f(x) $, либо в $ g(x) $: $$ f(8) = 2cdot 8 — 5 = 16 — 5 = 11 $$ Итак, $ M (8;11) $ — является точкой пересечения графиков двух линейных функций. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ M (8;11) $$ |
| Пример 2 |
| Дано $ f(x)=2x-1 $ и $ g(x) = 2x-4 $. Найти точки пересечения графиков функций. |
| Решение |
| Как найти? Опять же обращаем внимание на то, что угловые коэффициенты равны $ k_1 = k_2 = 2 $. Это означает, что линейные функции параллельны между собой, поэтому у них нет точек пересечения! |
| Ответы |
| Графики функций параллельны, нет точек пересечения. |
Случай двух нелинейных функций
| Пример 3 |
| Найти координаты точки пересечения графиков функций: $ f(x)=x^2-2x+1 $ и $ g(x)=x^2+1 $ |
| Решение |
|
Как быть с двумя нелинейными функциями? Алгоритм простой: приравниваем уравнения друг к другу и находим корни: $$ x^2-2x+1=x^2+1 $$ Разносим по разным сторонам уравнения члены с $ x $ и без него: $$ x^2-2x-x^2=1-1 $$ $$ -2x=0 $$ $$ x=0 $$ Найдена абцисса искомой точки, но её недостаточно. Ещё нехватает ординаты $ y $. Подставляем $ x = 0 $ в любое из двух уравнений условия задачи. Например: $$ f(0)=0^2-2cdot 0 + 1 = 1 $$ $ M (0;1) $ — точка пересечения графиков функций |
| Ответ |
| $$ M (0;1) $$ |