| Исходная система уравнений |
| Фундаментальное решение системы уравнений |
Определяем точку пересечения трех плоскостей, как решение системы из трех уравнений
Уравнения плоскостей заданы в виде
Решая эту систему уравнений, мы получаем однозначный результат
Например,
Мы также можем это решить через ФСР. Фундаментальная система решений
Введя данные мы получим
| Исходная система уравнений |
*x_{1}+(-3)*x_{2}+(1)*x_{3}+(-12)=0\(-2)*x_{1}+(1)*x_{2}+(1)=0\(1)*x_{1}+(2)*x_{2}+(-1)*x_{3}+(3)=0) |
| Фундаментальная система решений (ФСР) данной системы уравнений |
 |
| База системы/знаменатель |
|
|
То есть точка пересечения имеет координаты x=2,y=3, z=11
Линия пересечения плоскостей онлайн
С помощю этого онлайн калькулятора можно найти линию пересечения плоскостей. Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Линия пересечения плоскостей − теория, примеры и решения
Две плоскости в пространстве могут быть параллельными, могут совпадать или пересекаться. В данной статье мы определим взаимное расположение двух плоскостей, и если эти плоскости пересекаются, выведем уравнение линии пересечения плоскостей.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы плоскости α1 и α2:
| α1: A1x+B1y+C1z+D1=0, | (1) |
| α2: A2x+B2y+C2z+D2=0, | (2) |
где n1={A1, B1, C1} и n2={A2, B2, C2} − нормальные векторы плоскостей α1 и α2, соответственно.
Найдем уравнение линии пересеченя плоскостей α1 и α2. Для этого рассмотрим следующие случаи:
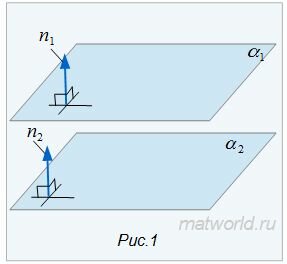
1. Нормальные векторы n1 и n2 плоскостей α1 и α2 коллинеарны (Рис.1).
Поскольку векторы n1 и n2 коллинеарны, то существует такое число λ≠0, что выполнено равенство n1=λn2, т.е. A1=λA2, B1=λB2, C1=λC2.
Умножив уравнение (2) на λ, получим:
| α2: A1x+B1y+C1z+λD2=0, | (3) |
Если выполненио равенство D1=λD2, то плоскости α1 и α2 совпадают, если же D1≠λD2то плоскости α1 и α2 параллельны, то есть не пересекаются.
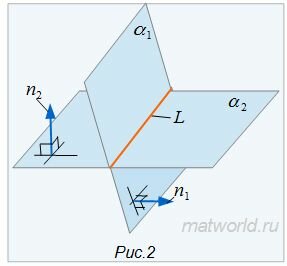
2. Нормальные векторы n1 и n2 плоскостей α1 и α2 не коллинеарны (Рис.2).
Если векторы n1 и n2 не коллинеарны, то решим систему линейных уравнений (1) и (2). Для этого переведем свободные члены на правую сторону уравнений и составим соответствующее матричное уравнение:
Как решить уравнение (4) посмотрите на странице Метод Гаусса онлайн или Метод Жоржана-Гаусса онлайн.
Так как в системе линейных уравнений (4) векторы n1={A1, B1, C1} и n2={A2, B2, C2} не коллинеарны, то решение этой системы линейных уравнений имеет следующий вид:
где x0, y0, z0, m, p, l действительные числа, а t − переменная.
Равенство (5) можно записать в следующем виде:
Мы получили параметрическое уравнение прямой, которое является линией пересечения плоскостей α1 и α2. Полученное уравнение прямой можно записать в каноническом виде:
Пример 1. Найти линию пересечения плоскостей α1 и α2:
Решение. Определим, сначала, взаимное расположение данных плоскостей. Плоскость α1 имеет нормальный вектор n1={A1, B1, C1}={1, 2, 1}. Плоскость α2 имеет нормальный вектор n2={A2, B2, C2}={2, 9, −5}.
Поскольку направляющие векторы n1 и n2 неколлинеарны, то плолскости α1 и α2 пересекаются.
Для нахождения линии пересечения влоскостей α1 и α2 нужно решить систему линейных уравнений (7) и (8). Для этого составим матричное уравнение этой системы:
Решим систему линейных уравнений (9) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 2 со строкой 1, умноженной на −2:
Второй этап. Обратный ход Гаусса.
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на −2/5:
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
Получим решение:
где t− произвольное действительное число.
Запишем (11) в следующем виде:
Получили уравнение линии пересечения плоскостей α1 и α2 в параметрическом виде. Запишем ее в каноническом виде.
Из равентсв выше получим каноническое уравнение прямой:
Ответ. Уравнение линии пересечения плоскостей α1 и α2имеет вид:
Пример 2. Найти линию пересечения плоскостей α1 и α2:
Решение. Определим, сначала, взаимное расположение данных плоскостей. Плоскость α1 имеет нормальный вектор n1={A1, B1, C1}={1, 2, 7}. Плоскость α2 имеет нормальный вектор n2={A2, B2, C2}={2, 4, 14}.
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/2), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/2:
Так как нормальные векторы уравнений (14) и (16) совпадают, а свободные члены разные, то плоскости α1 и α2 не совпадают. Следовательно они параллельны, т.е. не пересекаются.
Пример 3. Найти линию пересечения плоскостей α1 и α2:
Решение. Определим, сначала, взаимное расположение данных плоскостей. Плоскость α1 имеет нормальный вектор n1={A1, B1, C1}={5, −2, 3}. Плоскость α2 имеет нормальный вектор n2={A2, B2, C2}={15, −6, 9}.
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/3), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/3:
Так как нормальные векторы уравнений (17) и (19) совпадают, и свободные члены равны, то плоскости α1 и α2 совпадают.
Нахождение уравнений прямой, заданной пересечением двух плоскостей
Этот онлайн калькулятор находит уравнения прямой, заданной пересечением двух плоскостей в пространстве.
Этот онлайн калькулятор предназначен для проверки решений задач, которые можно сформулировать следующим образом:
Записать канонические уравнения прямой, заданной уравнениями двух плоскостей
Вы задаете коэффициенты уравнений плоскостей, калькулятор выдает уравнения прямой в канонической форме. Немного теории, как обычно, можно почерпнуть под калькулятором
Нахождение уравнений прямой, заданной пересечением двух плоскостей
Канонические уравнения прямой, заданной пересечением двух плоскостей
Если плоскости пересекаются, то система уравнений, приведенная в начале статьи, задает прямую в пространстве. Для записи уравнений этой прямой в каноническом виде, надо найти какую либо точку, принадлежащую этой прямой, и направляющий вектор.
Точка, принадлежащая прямой, также принадлежит и каждой из плоскостей, то есть является одним из решений системы уравнений выше. Для нахождения точки, принадлежащей прямой, переходят от системы из двух уравнений с тремя неизвестными к системе из двух уравнений с двумя неизвестными, произвольно принимая какую-либо координату точки за ноль. Как правило, при решении задач, выбирают ту координату, при занулении которой решение системы из двух уравнений с двумя неизвестными дает в ответе целые числа. Калькулятор учитывает этот факт и также пытается найти целочисленное решение, зануляя все координаты по очереди.
Направляющий вектор прямой ортогонален нормальным векторам плоскостей, которые задаются коэффициентами A, B и С в общем уравнении плоскости . Таким образом его можно найти как результат векторного произведения нормальных векторов плоскостей .
Точка и вектор дают нам канонические уравнения прямой:
Существуют частные случаи, когда одна или две координаты направляющего вектора равны нулю.
В случае, если нулю равны две координаты, направляющий вектор коллинеарен одной из координатных осей. Соответственно, точки прямой могут принимать любое значение по этой оси, при этом значения по двум другим осям будут постоянны. Например, если двумя нулевыми координатами будут y и z, канонические уравнения прямой будут выглядеть так:
В случае. если нулю равна одна координата, направляющий вектор лежит в одной из координатных плоскостей (плоскостей, образованных парами координатных осей), значение координаты по третьей оси, ортогональной этой плоскости (как раз той, для которой координата направляющего вектора равна нулю), опять будет постоянным. Например, если нулевой координатой будет x, то канонические уравнения прямой будут выглядеть так:
Эти случаи также учитываются калькулятором.
Линия пересечения плоскостей онлайн
С помощю этого онлайн калькулятора можно найти линию пересечения плоскостей. Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Линия пересечения плоскостей − теория, примеры и решения
Две плоскости в пространстве могут быть параллельными, могут совпадать или пересекаться. В данной статье мы определим взаимное расположение двух плоскостей, и если эти плоскости пересекаются, выведем уравнение линии пересечения плоскостей.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы плоскости α1 и α2:
| α1: A1x+B1y+C1z+D1=0, | (1) |
| α2: A2x+B2y+C2z+D2=0, | (2) |
Найдем уравнение линии пересеченя плоскостей α1 и α2. Для этого рассмотрим следующие случаи:
Умножив уравнение (2) на λ, получим:
| α2: A1x+B1y+C1z+λD2=0, | (3) |
Если векторы n1 и n2 не коллинеарны, то решим систему линейных уравнений (1) и (2). Для этого переведем свободные члены на правую сторону уравнений и составим соответствующее матричное уравнение:
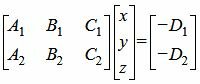 |
(4) |
Как решить уравнение (4) посмотрите на странице Метод Гаусса онлайн или Метод Жоржана-Гаусса онлайн.
Так как в системе линейных уравнений (4) векторы n1=<A1, B1, C1> и n2=<A2, B2, C2> не коллинеарны, то решение этой системы линейных уравнений имеет следующий вид:
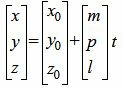 , , |
(5) |
Равенство (5) можно записать в следующем виде:
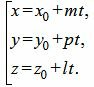 . . |
(6) |
Мы получили параметрическое уравнение прямой, которое является линией пересечения плоскостей α1 и α2. Полученное уравнение прямой можно записать в каноническом виде:
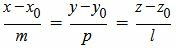
Пример 1. Найти линию пересечения плоскостей α1 и α2:
Поскольку направляющие векторы n1 и n2 неколлинеарны, то плолскости α1 и α2 пересекаются.
Для нахождения линии пересечения влоскостей α1 и α2 нужно решить систему линейных уравнений (7) и (8). Для этого составим матричное уравнение этой системы:
 . . |
(9) |
Решим систему линейных уравнений (9) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
 . . |
(10) |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 2 со строкой 1, умноженной на −2:
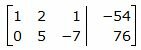
Второй этап. Обратный ход Гаусса.
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на −2/5:
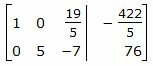
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

 . . |
(11) |
где t− произвольное действительное число.
Запишем (11) в следующем виде:
 . . |
(12) |
Получили уравнение линии пересечения плоскостей α1 и α2 в параметрическом виде. Запишем ее в каноническом виде.
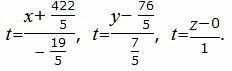 |
(13) |
Из равентсв выше получим каноническое уравнение прямой:
Ответ. Уравнение линии пересечения плоскостей α1 и α2имеет вид:
Пример 2. Найти линию пересечения плоскостей α1 и α2:
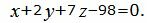 |
(14) |
 |
(15) |
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/2), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/2:
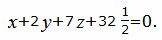 |
(16) |
Так как нормальные векторы уравнений (14) и (16) совпадают, а свободные члены разные, то плоскости α1 и α2 не совпадают. Следовательно они параллельны, т.е. не пересекаются.
Пример 3. Найти линию пересечения плоскостей α1 и α2:
 |
(17) |
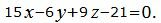 |
(18) |
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/3), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/3:
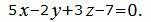 |
(19) |
Так как нормальные векторы уравнений (17) и (19) совпадают, и свободные члены равны, то плоскости α1 и α2 совпадают.
Уравнение прямой как результат пересечения плоскостей
| Коэффициенты первой плоскости | |
| Коэффициенты второй плоскости | |
| Уравнение первой плоскости |
| Уравнение второй плоскости |
| Уравнение прямой как пересечение двух плоскостей |
Определяем уравнение прямой в пространстве если нам известны общие уравнения двух плоскостей.
Обновление от 13 октября 2019 года: Используется алгоритм описанный в статье ФРС. Фундаментальное решение системы уравнений
Если первая плоскость задана уравнением вида
а другая плоскость уравнением вида
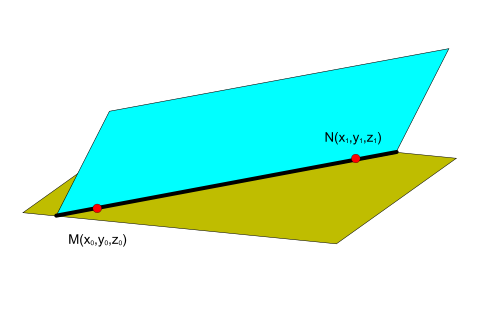
и они перескаются, то уравнение полученной прямой можно найти по двум точкам, принадлежащих одновременно этим плоскостям.
Прямая в пространстве, проходящая через две точки и может быть представлена в виде канонического уравнения
B принципе этого достаточно что бы решить уравнение. Положим что z=0 ( можно брать любое число, но с нулем оно как то удобнее) тогда уравнения плоскости приобретают вид
Получили систему линейных уравнений которая легко решается.
Определили таким образом точку
Теперь пусть z=1 и решаем систему
и получаем вторую точку
Эти две точки принадлежат обеим плоскостям и значит уравнение прямой имеет вид
Есть еще второй способ, использующий вектора. Рассмотрим и его.
Если известна точка в пространстве и направляющий вектор
то уравнение прямой имеет вид
Узнав координаты точки ( например по выше приведенному решению) нам осталось узнать направляющий вектор.
и подставив вычисленные значения в уравнение
мы узнаем уравнение прямой в пространстве, как пресечение двух плоскостей.
Созданный онлайн калькулятор позволяет автоматически находить уравнение прямой по двум заданным общим уравнениям плоскостей.
Условие параллельности плоскостей
Две плоскости заданные уравнениями вида
лишь тогда параллельны, когда верным становится соотношение
http://matworld.ru/analytic-geometry/linija-peresechenija-ploskostej.php
http://abakbot.ru/online-2/413-line3d
Уравнение прямой как результат пересечения плоскостей
| Коэффициенты первой плоскости | |
| Коэффициенты второй плоскости | |
| Уравнение первой плоскости |
| Уравнение второй плоскости |
| Уравнение прямой как пересечение двух плоскостей |
Определяем уравнение прямой в пространстве если нам известны общие уравнения двух плоскостей.
Обновление от 13 октября 2019 года: Используется алгоритм описанный в статье ФРС. Фундаментальное решение системы уравнений
Если первая плоскость задана уравнением вида
а другая плоскость уравнением вида
и они перескаются, то уравнение полученной прямой можно найти по двум точкам, принадлежащих одновременно этим плоскостям.
Прямая в пространстве, проходящая через две точки )
)
(cfrac{x-x_0}{x_1-x_0}=cfrac{y-y_0}{y_1-y_0}=cfrac{z-z_0}{z_1-z_0})
B принципе этого достаточно что бы решить уравнение. Положим что z=0 ( можно брать любое число, но с нулем оно как то удобнее) тогда уравнения плоскости приобретают вид
Получили систему линейных уравнений которая легко решается.
Определили таким образом точку
Теперь пусть z=1 и решаем систему
и получаем вторую точку
Эти две точки принадлежат обеим плоскостям и значит уравнение прямой имеет вид
(cfrac{x-x_0}{x_1-x_0}=cfrac{y-y_0}{y_1-y_0}=cfrac{z}{1})
Есть еще второй способ, использующий вектора. Рассмотрим и его.
Если известна точка в пространстве )
то уравнение прямой имеет вид
(cfrac{x-x_0}{m}=cfrac{y-y_0}{n}=cfrac{z-z_0}{p})
Узнав координаты точки )
Для этого вычислим векторное произведение
(begin{pmatrix}i&j&k\A_1&B_1&C_1\A_2&B_2&C_2end{pmatrix}=im+jn+kp)
и подставив вычисленные значения в уравнение
(cfrac{x-x_0}{m}=cfrac{y-y_0}{n}=cfrac{z-z_0}{p})
мы узнаем уравнение прямой в пространстве, как пресечение двух плоскостей.
Созданный онлайн калькулятор позволяет автоматически находить уравнение прямой по двум заданным общим уравнениям плоскостей.
Условие параллельности плоскостей
Две плоскости заданные уравнениями вида
лишь тогда параллельны, когда верным становится соотношение
(cfrac{A_1}{A_2}=cfrac{B_1}{B_2}=cfrac{C_1}{C_2})
Точка пересечения прямой и плоскости онлайн
С помощю этого онлайн калькулятора можно найти точку пересечения прямой и плоскости. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямой и плоскости задайте вид уравнения прямой («канонический» или «параметрический» ), введите данные в уравнения прямой и плоскости и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Точка пересечения прямой и плоскости − теория, примеры и решения
- Содержание
- 1. Точка пересечения плоскости и прямой, заданной в каноническом виде.
- 2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.
- 3. Примеры нахождения точки пересечения прямой и плоскости.
1. Точка пересечения плоскости и прямой, заданной в каноническом виде
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямая L1:
 , , |
(1) |
и плоскость α:
где M1(x1, y1, z1) − точка, лежащая на прямой L1, q1={m1, p1, l1} − направляющий вектор прямой L1, а n={A,B,C} − нормальный вектор плоскости α.
Найти точку пересечения прямой L1 и плоскости α (Рис.1).
Запишем уравнение (1) в виде системы двух линейных уравнений:
Сделаем перекрестное умножение в уравнениях (3) и (4):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Решим систему линейных уравнений (2), (5), (6) с тремя неизвестными x, y, z. Для этого в уравнении (2) переведем свободный член в правую часть уравнения и запишем эту систему в матричном виде:
Как решить систему линейных уравнений (11)(или (2), (5), (6)) посмотрите на странице Метод Гаусса онлайн или на примерах ниже. Если система линейных уравнениий (7) несовместна, то прямая L1 и плоскость α не пересекаются. Если система (7) имеет множество решений, то прямая L1 лежит на плоскости α. Единственное решение системы линейных уравнений (7) указывает на то, что это решение определяет координаты точки пересечения прямой L1 и плоскости α.
Замечание. Если прямая задана параметрическим уравнением, то уранение прямой нужно приводить к каноническому виду и применить метод, описанный выше, или же
2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L1 в параметрическом виде:
и плоскость α:
где M1(x1, y1, z1) − точка, лежащая на прямой L1, q1={m1, p1, l1} − направляющий вектор прямой L1, а n={A,B,C} − нормальный вектор плоскости α.
Задачу нахождения нахождения точки пересечения прямых L1 и плоскости α можно решить разными методами.
Метод 1. Приведем уравнения прямой L1 к каноническому виду.
Для приведения уравнения (8) к каноническому виду, выразим параметр t через остальные переменные:
Так как левые части уравнений (10) равны, то можем записать:
Далее, для нахождения точки пересечения прямой и плоскости нужно воспользоваться параграфом 1.
Метод 2. Для нахождения точки пересечения прямой L1 и плоскости α решим совместно уравнения (8) и (9). Из уравнений (8) подставим x, y, z в (9):
Откроем скобки и найдем t:
Если числитель и знаменатель в уравнении (14) одновременно равны нулю, то это значит, что прямая L1 лежит на полскости α. Если в уравнении (14) числитель отличен от нуля, а знаменатель равен нулю, то прямая и плоскость параллельны.
Если же числитель и знаменатель в уравнении (14) отличны от нуля, то прямая и плоскость пересекаются в одной точке. Для нахождения координат точки пересечения прямой L1 и плоскости α подставим полученное значение t из (14) в (8).
3. Примеры нахождения точки пересечения прямой и плоскости.
Пример 1. Найти точку пересечения прямой L1:
и плоскости α:
Представим уравнение (15) в виде двух уравнений:
Сделаем перекрестное умножение в уравнениях (17) и (18):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Упростим:
Для нахождения точки пересечения прямой L1 и плосклсти α нужно решить совместно уравнения (2), (19) и (20). Для этого переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (19) и (20):
Решим систему линейных уравнений (21) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −7/3:
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 3 со строкой 2, умноженной на 4/3:
Второй этап. Обратный ход Гаусса.
Исключим элементы 3-го столбца матрицы выше элемента a33. Для этого сложим строку 2 со строкой 3, умноженной на −3/2:
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на 1/2:
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
Запишем решение:
Ответ. Точка пересечения прямой L1 и плоскости α имеет следующие координаты:
Пример 2. Найти точку пересечения прямой L1:
и плоскости α:
Представим уравнение (22) в виде двух уравнений:
Сделаем перекрестное умножение в уравнениях (24) и (25):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Упростим:
Для нахождения точки пересечения прямой L1 и плосклсти α нужно решить совместно уравнения (2), (26) и (27). Переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (26) и (27):
Решим систему линейных уравнений (21) отностительно x, y, z. Для этого построим расширенную матрицу:
Обозначим через aij элементы i-ой строки и j-ого столбца.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 3 со строкой 1, умноженной на 6/5:
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 3 со строкой 2, умноженной на −1/5:
Из расширенной матрицы восстановим систему линейных уравнений:
Легко можно заметить, что последнее уравнение в (29) несовместна, так как несуществуют такие x, y, z чтобы выполнялось это равенство. Следовательно система линейных уравнений (2), (26) и (27) несовместна. Тогда прямая L1 и плоскость α не пересекаются, т.е. они параллельны.
Ответ. Прямая L1 и плоскость α параллельны, т.е. не имеют общую точку.
Пример 3. Найти точку пересечения прямой в параметрическом виде L1:
и плоскости α:
Решение. Для нахождения точки пересечения прямой L1 и плоскости α нужно найти такое значение t, при котором точка M(x, y, z) удовлетворяет уравнению (31). Поэтому подставим значения x, y, z из (30) в (31):
Откроем скобки:
Упростив уравнение, получим:
Как видим, любое значение t удовлетворяет уравнению (33), т.е. любая точка на прямой L1 удовлетворяет уравнению плоскости α. Следовательно прямая L1 лежит на плоскости α.
Ответ. Прямая L1 лежит на плоскости α.

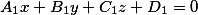
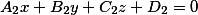


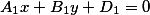
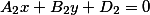
)
=0)
=0)
)
)