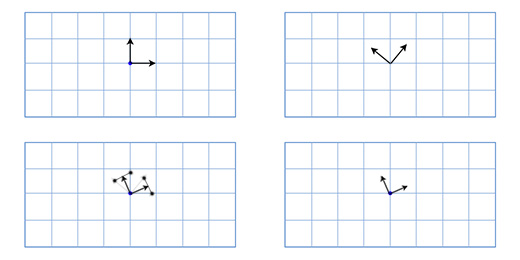
Графики прямолинейного движения
Рассмотрим поступательное движение. Когда тело движется поступательно, его координаты изменяются.
Прямолинейное движение – это когда тело движется по прямой. Прямую, вдоль которой движется тело, назовем осью Ox.
Будем отдельно рассматривать:
- движение без ускорения (равномерное), и
- движение с ускорением (неравномерное).
1). Равномерное движение — скорость тела остается одной и той же (т. е. не изменяется). При таком движении ускорения нет: (vec =0).
2). Неравномерное движение — скорость меняется и появляется ускорение.
Пусть ускорение есть и, оно не изменяется: (vec =const). Такое неравномерное движение называют равнопеременным. Чтобы уточнить, увеличивается ли скорость, или уменьшается, вместо слова «равнопеременное» говорят:
- Равноускоренное движение — скорость тела увеличивается.
- Равнозамедленное движение — скорость уменьшается.
Примечание: Когда изменяется скорость, всегда появляется ускорение!
Движение будем изображать графически, используя две перпендикулярные оси.
На графиках будем откладывать:
- по горизонтали — время в секундах.
- по вертикали — координаты тела, или проекции скорости и ускорения.
Для каждого вида движения получим три графика. Графики будем называть так:
- x(t) – зависимость координаты от времени;
- v(t) – зависимость проекции скорости от времени;
- a(t) – зависимость проекции ускорения от времени.
Прочитайте вначале, что такое проекция вектора на ось, это поможет лучше усвоить материал.
Тело покоится, его координата не меняется, а скорость и ускорение отсутствуют
Пусть тело покоится на оси Ox – (рис 1а).
Точкой (x_<0>) обозначена координата этого тела. Когда тело неподвижно, его координата не меняется. На графике неизменную координату обозначают горизонтальной линией, расположенной параллельно оси времени (рис. 1б).
[x=x_<0>]
Скорость и ускорение неподвижного тела равны нулю:
Из-за этого, графики скорости (рис. 1в) и ускорения (рис. 1г) – это горизонтальные линии, лежащие на оси t времени.
Скорость не меняется — движение равномерное
Разберём равномерное движение в направлении оси (рис. 2а).
Начальная координата тела – это точка (x_<0>), а конечная координата — точка (x) на оси Ox. В точку «x» тело переместится к конечному времени «t».
Красной стрелкой обозначено направление, в котором тело движется.
Примечание: Тело движется туда, куда направлен вектор его скорости.
Координата возрастает со временем, так как тело движется туда же, куда указывает ось. Поэтому график координаты от времени — это возрастающая прямая x(t) – рис. б).
Уравнение, описывающее изменение координаты выглядят так:
[ x = x_ <0>+ v cdot t ]
Скорость на графике рис. в) изображена горизонтальной прямой линией, потому, что скорость остается одной и той же (не изменяется). Уравнение скорости записывается так:
Ускорение рис. г) изображается прямой, лежащей на оси времени, так как ускорения нет. Математики посмотрят на такой график и скажут: «Ускорение равно нулю и не изменяется». Эту фразу они запишут формулой:
Равномерное движение в направлении противоположном оси
Пусть теперь тело движется с одной и той же скоростью в направлении, противоположном оси (рис. 3а).
Так как тело теперь движется против направления оси, то координата тела будет уменьшаться. График (рис 3б) координаты x(t) выглядит, как убывающая прямая линия.
Так как скорость не изменяется, то график v(t) – это горизонтальная прямая.
Тело движется против оси, его вектор скорости направлен противоположно оси Ox. Поэтому проекция скорости будет отрицательной (рис 3в) и на графике v(t) скорость — это горизонтальная прямая, лежащая ниже оси времени.
А график ускорения (рис 3г) лежит на оси времени, так как ускорение нулевое.
Равноускоренное движение в направлении оси, скорость увеличивается
Следующий набор графиков – это случай, когда тело движется вдоль оси Ox с возрастающей скоростью (рис. 4). То есть, мы рассматриваем равноускоренное движение.
Координата «x» теперь изменяется не по линейному, а по квадратичному закону. На графике квадратичное изменение выглядит, как ветвь параболы (рис. 4б). Тело движется по оси и скорость его растет. Такое движение описывается правой ветвью параболы, направленной вверх.
Уравнение, которое описывает квадратичное изменение координаты, выглядит так:
Скорость, так же, растет (рис. 4в). Рост скорости описан наклонной прямой линией – то есть, линейной зависимостью:
[ v = v_ <0>+ a cdot t ]
Ускорение есть (рис. 4г) и оно не меняется:
Скорость и ускорение сонаправлены с осью Ox, поэтому их проекции на ось положительны, а их графики лежат выше оси времени.
Примечания:
1). Координата «x» будет изменяться:
- по линейному закону, когда скорость не меняется — остается одной и той же.
- по квадратичному закону, когда скорость будет изменяться (расти, или убывать).
2). Линейный закон – это уравнение первой степени, на графике – наклонная прямая линия.
3). Квадратичный закон – это уравнение второй степени, на графике — парабола.
4). Когда скорость увеличивается, для графика координаты x(t) выбираем правую ветвь параболы, а когда скорость уменьшается – то левую ветвь.
Равноускоренное движение против оси
Если тело будет увеличивать свою скорость, двигаясь в направлении, противоположном оси (рис. 5а), то ветвь параболы, описывающая изменение координаты тела, будет направлена вниз (рис. 5б).
Скорость направлена против оси и увеличивается в отрицательную область. Такое изменение скорости изображаем прямой, направленной вниз (рис. 5в).
Примечание: Чтобы скорость увеличивалась (по модулю), нужно, чтобы векторы скорости и ускорения были сонаправленными (ссылка).
Так как скорость увеличивается, то векторы скорости и ускорения сонаправлены. Но при этом, они направлены против оси, поэтому проекции векторов (vec) и (vec) на ось Ox будут отрицательными. Значит, графики скорости и ускорения будут лежать ниже горизонтальной оси времени.
Ускорение (рис. 5г) не изменяется, поэтому изображается горизонтальной прямой. Но эта прямая будет лежать ниже горизонтальной оси времени, так как ускорение имеет отрицательную проекцию на ось Ox.
Скорость уменьшается — движение равнозамедленное
Когда скорость тела уменьшается с постоянным ускорением, движение называют равнозамедленным. Координата в этом случае изменяется по квадратичному закону. График координаты – это ветвь параболы. Когда скорость уменьшается, координату описываем с помощью левой ветви параболы, с вершиной вверху (рис. 6б).
Примечание: Чтобы скорость уменьшалась по модулю, нужно, чтобы векторы скорости и ускорения были направлены в противоположные стороны (ссылка).
Скорость уменьшается, при этом, скорость направлена по оси. Поэтому, график скорости – это убывающая прямая линия, лежащая выше оси времени (рис. 6в).
А ускорение есть, оно не изменяется и направлено против оси. Поэтому, ускорение отрицательное, его график – это горизонтальная прямая, лежащая ниже оси времени (рис. 6г).
Равнозамедленное движение против оси
Если тело будет двигаться против оси, замедляясь, то график координаты — это левая ветвь параболы, вершиной вниз (рис. 7б).
Скорость вначале была большой, но так как тело замедляется, она падает до нуля. Но тело двигается против оси Ox, поэтому график скорости лежит ниже оси времени (рис. 7в).
Скорость отрицательная. А чтобы она уменьшалась, нужно, чтобы ускорение было направлено противоположно скорости. Поэтому ускорение будет положительным. Значит, график ускорения будет лежать выше оси времени. Так как ускорение не меняется, то его график изображен горизонтальной прямой линией (рис. 7г).
Примечание: Можно вычислить перемещение тела по графику скорости v(t), не пользуясь для этого графиком функции x(t) для координат тела.
Выводы
1). Все, что лежит:
- выше оси t – положительное;
- ниже оси t – отрицательное;
- на горизонтальной оси t – равно нулю.
2). Когда ускорение, или скорость направлены против оси, они будут отрицательными, т. е. будут лежать ниже горизонтальной оси t. Если график ускорения лежит на горизонтальной оси, то ускорение отсутствует (т. е. равно нулю, нулевое).
3). Если скорость не меняется, ускорения нет.
- График x(t) координаты – это прямая линия.
- График v(t) скорости – горизонтальная прямая.
- График a(t) ускорения лежит на оси t.
4). Если скорость растет, ускорение и скорость направлены в одну и ту же сторону.
- График x(t) координаты – это правая ветвь параболы.
- График v(t) скорости – наклонная прямая.
- График a(t) ускорения – горизонтальная прямая.
5). Если скорость уменьшается, ускорение и скорость направлены в противоположные стороны.
- График x(t) координаты – это левая ветвь параболы.
- График v(t) скорости – наклонная прямая.
- График a(t) ускорения – горизонтальная прямая.
Геометрия для новичков. Часть 1: координаты и векторы — теория
Внимание! Этот документ ещё не опубликован.
О чем данная статья
В данной статье дается теоретическое описание векторов, координат векторов и операций над ними.
На кого рассчитана статья
Прежде чем читать эту статью, нужно знать:
- что такое прямоугольная система координат и координаты точки на плоскости
- что такое теорема Пифагора
Введение
Зачем нужны координаты точек в играх
В любой игре положение игрового объекта задается координатами какой-либо точки, привязанной к этому объекту, т.е. эта точка перемещается вместе с объектом. Например, мы можем задать координаты объектов в «Супер Марио» следующим образом:
На этом рисунке крупные черные точки — это точки, привязанные к игровым объектам. Координаты этих точек мы и будем считать координатами игровых объектов.
Итак, на этом рисунке:
- координаты Марио равны (-0.5, -2)
- координаты улитки равны (3, -2)
- координаты кубика равны (4, 1)
Пример координат вектора
Я намеренно не написал конкретные значения для координат точек – пусть они будут произвольными.
Зададим себе вопрос «Как нужно изменить начальные координаты Марио, что получить конечные?» Чтобы ответить на этот вопрос, нам нужно найти пару чисел (x, y), таких, чтобы:
Ax + x = Bx
Ay + y = By
Решая эти 2 уравнения, получаем:
x = Bx — Ax
y = By — Ay
Пара (x, y) в нашей задаче является координатами вектора перемещения Марио. Но это — лишь конкретный пример координат вектора. Что такое вектор и что такое его координаты в общем случае? Сейчас узнаем.
Векторы
Что такое направленный отрезок
Стрелка показывает, что А – начало отрезка, а B – конец.
Что такое вектор
Что у этих отрезков общего? Хм, пожалуй 2 вещи:
- Направление
- Длина
Так вот, вектор – это как раз и есть совокупность направления и длины.
Направленный отрезок – не вектор, который мы изучаем в геометрии. Направленный отрезок задает, или как еще говорят, представляет вектор. Но это — не вектор.
В нашем примере направленный отрезок 

Примечание: о тонкостях приведенного мной определения — в конце статьи.
Равенство векторов
Если задуматься, все направленные отрезки одинаковой длины, которые лежат на параллельных прямых и указывают в одну сторону, имеют одинаковое направление и длину. Следовательно, все эти направленные отрезки представляют один и тот же вектор. Из этого следует определение равенства 2 векторов:
Два вектора 



Из данного определения следует, что при параллельном переносе произвольный направленный отрезок продолжает представлять тот же вектор, что он представлял до переноса. Это свойство активно используется для операций над векторами.
Длина вектора
Коллинеарные векторы
На рисунке любая пара из векторов 


Если отрезки, представляющие коллинеарные векторы, имеют одинаковое направления, то векторы называют сонаправленными:
Пишут:
Если отрезки, представляющие коллинеарные векторы, имеют противоположное направления, то векторы, представленные данными отрезками, называют противоположно направленными:
Пишут:
Нулевой вектор
Единичные векторы

Обратный вектор
Арифметические операции над векторами
- Вектор можно умножать на число. Вектор
, умноженный на число, записывается как k*
. Вектор будет сонаправлен (противоположно направлен) с вектором
, если k — положительное (отрицательное) число. Вектор k*
будет иметь длину |k|*|
|:
|k*

k* 

k* 

|k * 
Т.е. в результате нормализации мы получаем единичный вектор, сонаправленный с исходным вектором 
Важно: нулевой вектор НЕЛЬЗЯ нормализовать, так как для любого числа k:
|k*

Итак, как же найти это число k?
Распишем |k * 
|k * 


Здесь мы убрали с k знак модуля, так как по определению k > 0.
Итак:
k * |
Из этого следует, что:
k = 1 / |
Т.е. чтобы нормализовать произвольный ненулевой вектор, нам нужно разделить вектор на его длину.
Координаты вектора
Вроде бы из примера, приведенного в начале статьи, все понятно: координаты вектора — разность координат конца и начала направленного отрезка, представляющего вектор.
Но это не так. Действительно, значения координат вектора численно равны этой разности. Но определение координат вектора в корне отличается от определения координат точки.
Разложение вектора по 2 неколлинеарным векторам
В геометрии доказывается следующий факт.
Ecли мы возьмем 2 неколлинеарных вектора 

то для каждого вектора 


Теперь возьмем в качестве таких неколлинеарных векторов 

Векторы 

Определение координат вектора


то пара чисел (x, y) будет называться координатами вектора 
Часто пишут:

Эта запись означает, что вектор 
Арифметические операции над координатами векторов
— 
Координаты вектора, умноженного на число, равны координатам исходного вектора, умноженными на это число:
k* 
Пусть у нас есть 2 произвольных вектора 

- кoординаты суммы 2 векторов равны сумме x- и y-координат векторов:
+
= (ax + bx, ay + by)
- как следствие из предыдущих свойств, координаты разности 2 векторов равны разности координат этих векторов:
—
= (ax — bx, ay — by)
Т.е. арифметика для координат векторов – такая же, как и для обычных чисел, только все считается покоординатно.
Радиус-вектор
Можно доказать, что численные значения координат точки совпадают со значения координат ее радиус-вектора. Здесь примем это как факт: 
где (Ax, Ay) — координаты точки A
Связь между координатами вектора и координатами концов отрезка
если 


(x, y) = (Bx — Ax, By — Ay)
где (Ax, Ay), (Bx, By) — координаты точек А и B соответственно.
Докажем это.
Мы можем записать простое равенство для произвольного вектора 


Заметим, что 

Из равенства значений координат точки и радиус-вектора и предыдущей формулы следует, что:
(x, y) = (Bx — Ax, By — Ay)
Нахождение длины вектора по его координатам
Пусть у нас есть вектор 


Чтобы найти длину вектора 


По теореме Пифагора:
AC = |
СB = |
то в итоге получаем равенство:
Заключение
Применению векторов в реальных задачах игровой разработки будет посвящена следующая моя статья. В ней практически не будет математики и будет много программирования.
Здесь же я описал то, что будет необходимо для понимания практических приемов использования векторов.
Если не иметь представления, как связаны координаты точек и координаты векторов, очень сложно понять, как работают алгоритмы определения расстояний от точки до геометрической фигуры, алгоритмы обнаружения столкновений и т.д.
Так что не жалейте, если вы (о ужас!) кое-что запомнили из «всей этой математики». Все это вам пригодится очень скоро, обещаю.
Литература
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. «Геометрия», 7-9 классы»
Главы: «Векторы», «Метод координат».
PS: корректность определения вектора в статье
Вся хитрость в том, что существует несколько определений вектора даже в рамках геометрии.
Направленный отрезок – тоже вектор, так называемый фиксированный вектор. Но нужно учитывать один важный факт – 2 фиксированных вектора равны тогда и только тогда, когда их концы и начала совпадают. А это не то определение равенства 2 векторов, что дает учебник геометрии.
Определение вектора, данное в этой статье – определение так называемого свободного вектора.
Каждый свободный вектор – это множество фиксированных векторов, которые имеют равную длину и одинаковое направление.
Именно это определение учебник геометрии и пытается дать в неявном виде, когда вводит понятие равенства векторов. Но здесь возникает нестыковка – учебник объясняет, как работать со свободными векторами, изначально дав определение фиксированного вектора.
Надеюсь, вышесказанное объясняет, почему я привел в данной статье «свое» определение вектора.
Линейная алгебра для разработчиков игр
Эта статья является переводом цикла из четырёх статей «Linear algebra for game developers», написанных David Rosen и посвящённых линейной алгебре и её применению в разработке игр. С оригинальными статьями можно ознакомиться тут: часть 1, часть 2, часть 3 и часть 4. Я не стал публиковать переводы отдельными топиками, а объединил все статьи в одну. Думаю, что так будет удобнее воспринимать материал и работать с ним. Итак приступим.
Зачем нам линейная алгебра?
Одним из направлений в линейной алгебре является изучение векторов. Если в вашей игре применяется позиционирование экранных кнопок, работа с камерой и её направлением, скоростями объектов, то вам придётся иметь дело с векторами. Чем лучше вы понимаете линейную алгебру, тем больший контроль вы получаете над поведением векторов и, следовательно, над вашей игрой.
Что такое вектор?
В играх вектора используются для хранения местоположений, направлений и скоростей. Ниже приведён пример двухмерного вектора: 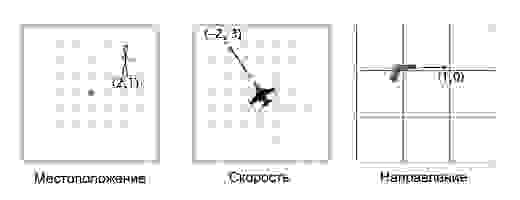
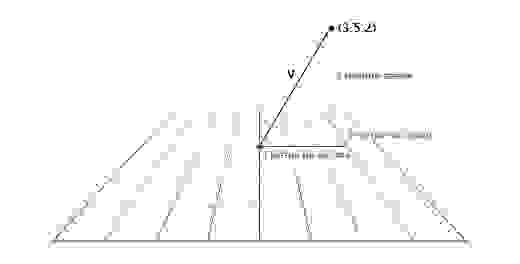
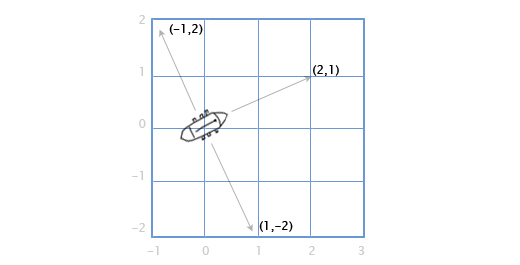
Вектор местоположения (также называемый «радиус-вектором») показывает, что человек стоит в двух метрах восточнее и в одном метре к северу от исходной точки. Вектор скорости показывает, что за единицу времени самолёт перемещается на три километра вверх и на два — влево. Вектор направления говорит нам о том, что пистолет направлен вправо.
Как вы можете заметить, вектор сам по себе всего лишь набор цифр, который обретает тот или иной смысл в зависимости от контекста. К примеру, вектор (1, 0) может быть как направлением для оружия, как показано на картинке, так и координатами строения в одну милю к востоку от вашей текущей позиции. Или скоростью улитки, которая двигается вправо со скоростью в 1 милю в час (прим. переводчика: довольно быстро для улитки, 44 сантиметра в секунду).
Важно отслеживать единицы измерения. Допустим у нас есть вектор V (3,5,2). Это мало что говорит нам. Три чего, пять чего? В нашей игре Overgrowth расстояния указываются в метрах, а скорости в метрах в секунду. Первое число в этом векторе — это направление на восток, второе — направление вверх, третье — направление на север. Отрицательные числа обозначают противоположные направления, на запад, вниз и на юг. Местоположение, определяемое вектором V (3,5,2), находится в трёх метрах к востоку, в пяти метрах вверху и в двух метрах к северу, как показано на картинке ниже.
Итак, мы изучили основы работы с векторами. Теперь узнаем как вектора использовать.
Сложение векторов
Чтобы сложить вектора, нам надо просто сложить каждую их составляющую друг с другом. Например:
(0, 1, 4) + (3, -2, 5) = (0+3, 1-2, 4+5) = (3, -1, 9)
Зачем нам нужно складывать вектора? Наиболее часто сложение векторов в играх применяется для физического интегрирования. Любой физический объект будет иметь вектора для местоположения, скорости и ускорения. Для каждого кадра (обычно это одна шестидесятая часть секунды), мы должны интегрировать два вектора: добавить скорость к местоположению и ускорение к скорости.
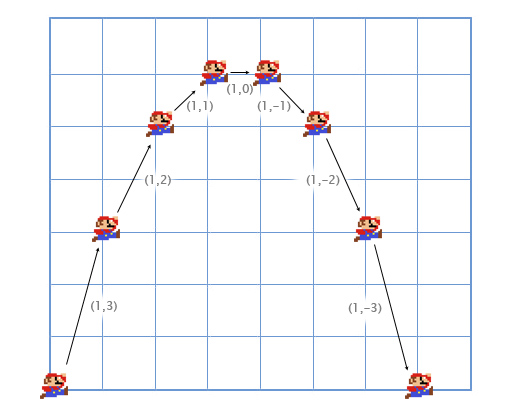
Давайте рассмотрим пример с прыжками Марио. Он начинает с позиции (0, 0). В момент начала прыжка его скорость (1, 3), он быстро двигается вверх и вправо. Его ускорение равно (0, -1), так как гравитация тянет его вниз. На картинке показано, как выглядит его прыжок, разбитый на семь кадров. Чёрным текстом показана его скорость в каждом фрейме.
Давайте рассмотрим первые кадры поподробнее, чтобы понять как всё происходит.
Для первого кадра, мы добавляем скорость Марио (1, 3) к его местоположению (0, 0) и получаем его новые координаты (1, 3). Затем мы складываем ускорение (0, -1) с его скоростью (1, 3) и получаем новое значение скорости Марио (1, 2).
Делаем то-же самое для второго кадра. Добавляем скорость (1, 2) к местоположению (1, 3) и получаем координаты (2, 5). Затем добавляем ускорение (0, -1) к его скорости (1, 2) и получаем новую скорость (1, 1).
Обычно игрок контролирует ускорение игрового персонажа с помощью клавиатуры или геймпада, а игра, в свою очередь, рассчитывает новые значения для скоростей и местоположения, используя физическое сложение (через сложение векторов). Это та-же задача, которая решается в интегральном исчислении, просто мы его сильно упрощаем для нашей игры. Я заметил, что мне намного проще внимательно слушать лекции по интегральному исчислению, думая о практическом его применении, которое мы только что описали.
Вычитание векторов
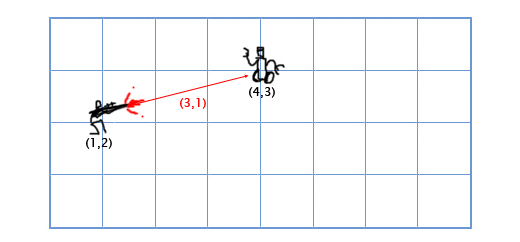
Вычитание рассчитывается по тому-же принципу что и сложение — вычитаем соответствующие компоненты векторов. Вычитание векторов удобно для получения вектора, который показывает из одного местоположения на другое. Например, пусть игрок находится по координатам (1, 2) с лазерным ружьём, а вражеский робот находится по координатам (4, 3). Чтобы определить вектор движения лазерного луча, который поразит робота, нам надо вычесть местоположение игрока из местоположения робота. Получаем:
(4, 3) — (1, 2) = (4-1, 3-2) = (3, 1).
Умножение вектора на скаляр
Когда мы говорим о векторах, мы называем отдельные числа скалярами. Например (3, 4) — вектор, а 5 — это скаляр. В играх, часто бывает нужно умножить вектор на число (скаляр). Например, моделируя простое сопротивление воздуха путём умножения скорости игрока на 0.9 в каждом кадре. Чтобы сделать это, нам надо умножить каждый компонент вектора на скаляр. Если скорость игрока (10, 20), то новая скорость будет:
0.9*(10, 20) = (0.9 * 10, 0.9 * 20) = (9, 18).
Длина вектора
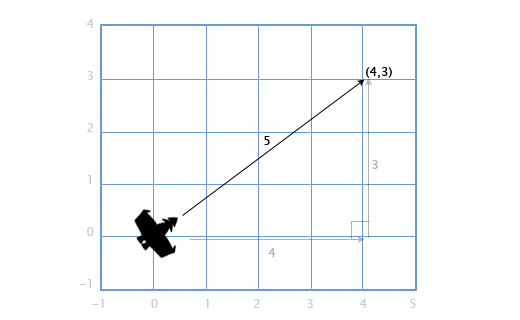
Если у нас есть корабль с вектором скорости V (4, 3), нам также понадобится узнать как быстро он двигается, чтобы посчитать потребность в экранном пространстве или сколько потребуется топлива. Чтобы сделать это, нам понадобится найти длину (модуль) вектора V. Длина вектора обозначается вертикальными линиями, в нашем случае длина вектора V будет обозначаться как |V|.
Мы можем представить V как прямоугольный треугольник со сторонами 4 и 3 и, применяя теорему Пифагора, получить гипотенузу из выражения: x 2 + y 2 = h 2
В нашем случае — длину вектора H с компонентами (x, y) мы получаем из квадратного корня: sqrt(x 2 + y 2 ).
Итак, скорость нашего корабля равна:
|V| = sqrt(4 2 + 3 2 ) = sqrt(25) = 5
Этот подход используется и для трёхмерных векторов. Длина вектора с компонентами (x, y, z) рассчитывается как sqrt(x 2 + y 2 + z 2 )
Расстояние
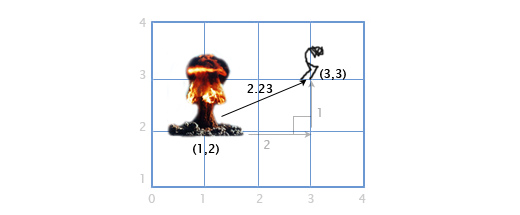
Если игрок P находится в точке (3, 3), а взрыв произошёл в точке E по координатам (1, 2), нам надо определить расстояние между игроком и взрывом, чтобы рассчитать степень ущерба, нанесённого игроку. Это легко сделать, комбинируя две вышеописанных операции: вычитание векторов и их длину.
Мы вычитаем P — E, чтобы получить вектор между ними. А затем определяем длину этого вектора, что и даёт нам искомое расстояние. Порядок следования операндов тут не имеет значения, |E — P| даст тот-же самый результат.
Расстояние = |P — E| = |(3, 3) — (1, 2)| = |(2, 1)| = sqrt(2 2 +1 2 ) = sqrt(5) = 2.23
Нормализация
Когда мы имеем дело с направлениями (в отличие от местоположений и скоростей), важно, чтобы вектор направления имел длину, равную единице. Это сильно упрощает нам жизнь. Например, допустим орудие развёрнуто в направлении (1, 0) и выстреливает снаряд со скоростью 20 метров в секунду. Каков в данном случае вектор скорости для выпущенного снаряда?
Так как вектор направления имеет длину равную единице, мы умножаем направление на скорость снаряда и получаем вектор скорости (20, 0). Если-же вектор направления имеет отличную от единицы длину, мы не сможем сделать этого. Снаряд будет либо слишком быстрым, либо слишком медленным.
Вектор с длиной равной единице называется «нормализованным». Как сделать вектор нормализованным? Довольно просто. Мы делим каждый компонент вектора на его длину. Если, к примеру, мы хотим нормализовать вектор V с компонентами (3, 4), мы просто делим каждый компонент на его длину, то есть на 5, и получаем (3/5, 4/5). Теперь, с помощью теоремы Пифагора, мы убедимся в том, что его длина равна единице:
(3/5) 2 + (4/5) 2 = 9/25 + 16/25 = 25/25 = 1
Скалярное произведение векторов
Что такое скалярное произведение (записывается как •)? Чтобы рассчитать скалярное произведение двух векторов, мы должны умножить их компоненты, а затем сложить полученные результаты вместе
(a1, a2) • (b1, b2) = a1b1 + a2b2
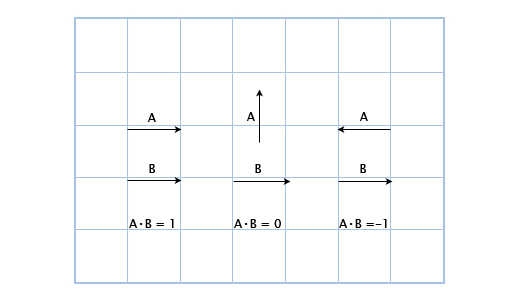
Например: (3, 2) • (1, 4) = 3*1 + 2*4 = 11. На первый взгляд это кажется бесполезным, но посмотрим внимательнее на это:
Здесь мы можем увидеть, что если вектора указывают в одном направлении, то их скалярное произведение больше нуля. Когда они перпендикулярны друг другу, то скалярное произведение равно нулю. И когда они указывают в противоположных направлениях, их скалярное произведение меньше нуля.
В основном, с помощью скалярного произведения векторов можно рассчитать, сколько их указывает в одном направлении. И хоть это лишь малая часть возможностей скалярного произведения, но уже очень для нас полезная.
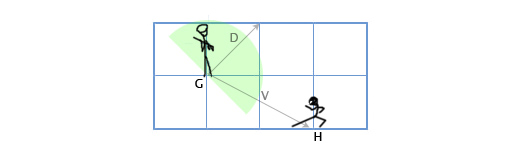
Допустим у нас есть стражник, расположенный в G(1, 3) смотрящий в направлении D(1,1), с углом обзора 180 градусов. Главный герой игры подсматривает за ним с позиции H(3, 2). Как определить, находится-ли главный герой в поле зрения стражника или нет? Сделаем это путём скалярного произведения векторов D и V (вектора, направленного от стражника к главному герою). Мы получим следующее:
V = H — G = (3, 2) — (1, 3) = (3-1, 2-3) = (2, -1)
D•V = (1, 1) • (2, -1) = 1*2 + 1*-1 = 2-1 = 1
Так как единица больше нуля, то главный герой находится в поле зрения стражника.
Мы уже знаем, что скалярное произведение имеет отношение к определению направления векторов. А каково его более точное определение? Математическое выражение скалярного произведения векторов выглядит так:
Где Θ (произносится как «theta») — угол между векторами A и B.
Это позволяет нам найти Θ (угол) с помощью выражения:
Как я говорил ранее, нормализация векторов упрощает нашу жизнь. И если A и B нормализованы, то выражение упрощается следующим образом:
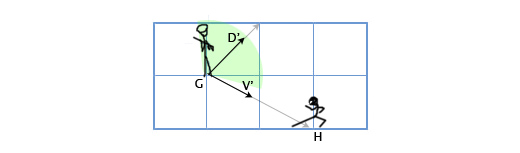
Давайте опять рассмотрим сценарий со стражником. Пусть теперь угол обзора стражника будет равен 120 градусам. Получим нормализованные вектора для направления взгляда стражника (D’) и для направления от стражника к главному герою (V’). Затем определим угол между ними. Если угол более 60 градусов (половина от угла обзора), то главный герой находится вне поля зрения стражника.
D’ = D / |D| = (1, 1) / sqrt(1 2 + 1 2 ) = (1, 1) / sqrt(2) = (0.71, 0.71)
V’ = V / |V| = (2, -1) / sqrt(2 2 + (-1) 2 ) = (2,-1) / sqrt(5) = (0.89, -0.45)
Θ = acos(D’V’) = acos(0.71*0.89 + 0.71*(-0.45)) = acos(0.31) = 72
Угол между центром поля зрения стражника и местоположением главного героя составляет 72 градуса, следовательно стражник его не видит.
Понимаю, что это выглядит довольно сложно, но это потому, что мы всё делаем вручную. В программе это всё довольно просто. Ниже показано как я сделал это в нашей игре Overgrowth с помощью написанных мной С++ библиотек для работы с векторами:
Векторное произведение
Допустим у нас есть корабль с пушками, которые стреляют в правую и в левую стороны по курсу. Допустим, что лодка расположена вдоль вектора направления (2, 1). В каких направлениях теперь стреляют пушки?
Это довольно просто в двухмерной графике. Чтобы повернуть направление на 90 градусов по часовой стрелке, достаточно поменять местами компоненты вектора, а затем поменять знак второму компоненту.
(a, b) превращается в (b, -a). Следовательно у корабля, расположенного вдоль вектора (2, 1), пушки справа по борту будут стрелять в направлении (1, -2), а пушки с левого борта, будут стрелять в противоположном направлении. Меняем знаки у компонент вектора и получаем (-1, 2).
А что если мы хотим рассчитать это всё для трехмерной графики? Рассмотрим пример с кораблём.
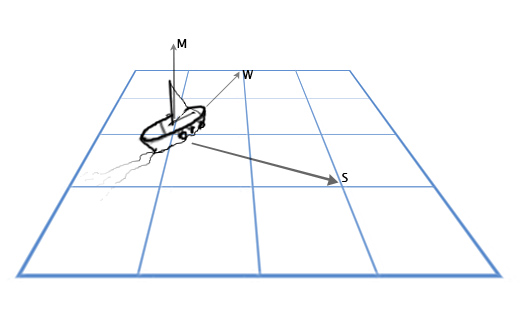
У нас есть вектор мачты M, направленной прямо вверх (0, 1, 0) и направление ветра: север-северо-восток W (1, 0, 2). И мы хотим вычислить вектор направления паруса S, чтобы наилучшим образом «поймать ветер».
Для решения этой задачи мы используем векторное произведение: S = M x W.
Подставим теперь нужные нам значения:
S = MxW = (0, 1, 0) x (1, 0, 2) = ([1*2 — 0*0], [0*1 — 0*2], [0*0 — 1*1]) = (2, 0, -1)
Для расчётов вручную довольно сложно, но для графических и игровых приложений я рекомендую написать функцию, подобную той, что указана ниже и не вдаваться более в детали подобных расчётов.
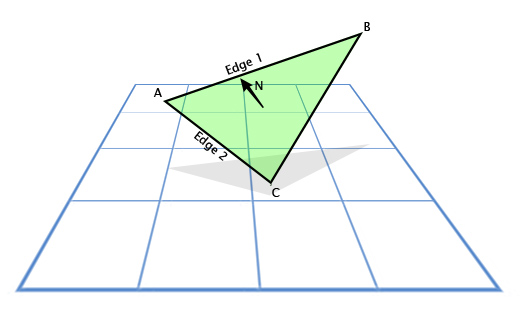
Векторное произведение часто используется в играх, чтобы рассчитать нормали к поверхностям. Направления, в которых «смотрит» та или иная поверхность. Например, рассмотрим треугольник с векторами вершин A, B и С. Как мы найдем направление в котором «смотрит» треугольник, то есть направление перпендикулярное его плоскости? Это кажется сложным, но у нас есть инструмент для решения этой задачи.
Используем вычитание, для определения направления из A в С (C — A), пусть это будет «грань 1» (Edge 1) и направление из A в B (B — A), пусть это будет «грань 2» (Edge 2). А затем применим векторное произведение, чтобы найти вектор, перпендикулярный им обоим, то есть перпендикулярный плоскости треугольника, также называемый «нормалью к плоскости».
Вот так это выглядит в коде:
В играх основное выражение освещённости записывается как N • L, где N — это нормаль к освещаемой поверхности, а L — это нормализованный вектор направления света. В результате поверхность выглядит яркой, когда на неё прямо падает свет, и тёмной, когда этого не происходит.
Теперь перейдем к рассмотрению такого важного для разработчиков игр понятия, как «матрица преобразований» (transformation matrix).
Для начала изучим «строительные блоки» матрицы преобразований.
Базисный вектор
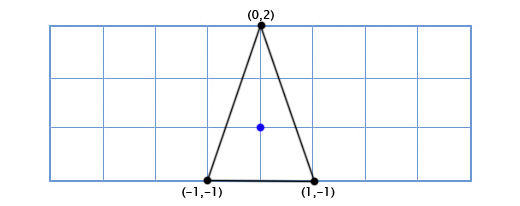
Допустим мы пишем игру Asteroids на очень старом «железе» и нам нужен простой двухмерный космический корабль, который может свободно вращаться в своей плоскости. Модель корабля выглядит так:
Как нам рисовать корабль, когда игрок поворачивает его на произвольный градус, скажем 49 градусов против часовой стрелки. Используя тригонометрию, мы можем написать функцию двухмерного поворота, которая принимает координаты точки и угол поворота, и возвращает координаты смещённой точки:
Применяя эту функцию ко всем трём точкам, мы получим следующую картину:
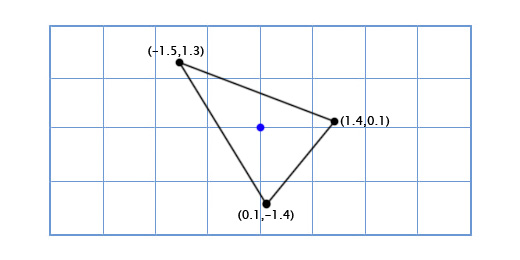
Операции с синусами и косинусами работают довольно медленно, но так как мы делаем расчёты лишь для трёх точек, это будет нормально работать даже на старом «железе» (прим. переводчика: в случаях, когда предполагается интенсивное использование тригонометрических функций, для ускорения вычислений, в памяти организуют таблицы значений для каждой функции и рассчитывают их во время запуска приложения. Затем при вычислении той или иной тригонометрической функции просто производится обращение к таблице).
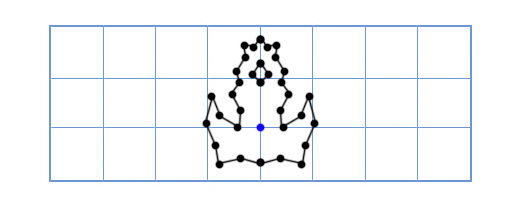
Пусть теперь наш корабль выглядит вот так:
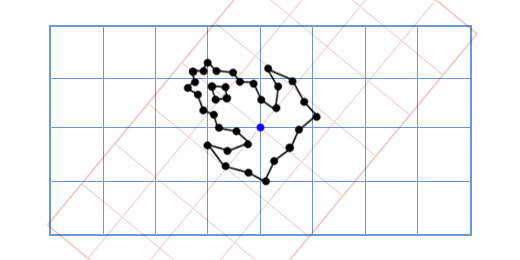
Теперь старый подход будет слишком медленным, так как надо будет поворачивать довольно большое количество точек. Одно из элегантных решений данной проблемы будет звучать так — «Что если вместо поворота каждой точки модели корабля, мы повернём координатную решётку нашей модели?»
Как это работает? Давайте посмотрим внимательнее, что собой представляют координаты.
Когда мы говорим о точке с координатами (3, 2), мы говорим, что её местоположение находится в трех шагах от точки отсчёта по координатной оси X, и двух шагах от точки отсчёта по координатной оси Y.
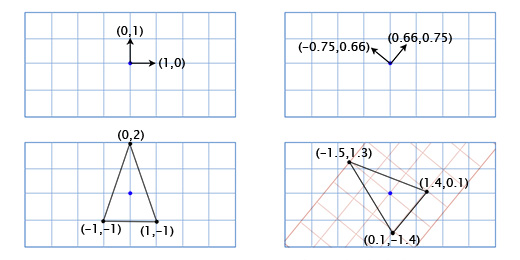
По-умолчанию координатные оси расположены так: вектор координатной оси X (1, 0), вектор координатной оси Y (0, 1). И мы получим расположение: 3(1, 0) + 2(0, 1). Но координатные оси не обязательно должны быть в таком положении. Если мы повернём координатные оси, в это-же время мы повернём все точки в координатной решётке.
Чтобы получить повернутые оси X и Y мы применим тригонометрические функции, о которых говорили выше. Если мы поворачиваем на 49 градусов, то новая координатная ось X будет получена путём поворота вектора (0, 1) на 49 градусов, а новая координатная ось Y будет получена путём поворота вектора (0, 1) на 49 градусов. Итак вектор новой оси X у нас будет равен (0.66, 0.75), а вектор новой оси Y будет (-0.75, 0.66). Сделаем это вручную для нашей простой модели из трёх точек, чтобы убедиться, что это работает так, как нужно:
Координаты верхней точки (0, 2), что означает, что её новое местоположение находится в 0 на новой (повёрнутой) оси X и 2 на новой оси Y:
0*(0.66,0.75) + 2*(-0.75, 0.66) = (-1.5, 1.3)
Нижняя левая точка (-1, -1), что означает, что её новое местоположение находится в -1 на повернутой оси X, и -1 на повернутой оси Y:
-1*(0.66,0.75) + -1*(-0.75, 0.66) = (0.1, -1.4)
Нижняя правая точка (1, -1), что означает её новое местоположение находится в 1 на повернутой оси X, и -1 на повернутой оси Y
1*(0.66,0.75) + -1*(-0.75, 0.66) = (1.4, 0.1)
Мы показали, как координаты корабля отображаются в другой координатной сетке с повернутыми осями (или «базисными векторами»). Это удобно в нашем случае, так как избавляет нас от необходимости применять тригонометрические преобразования к каждой из точек модели корабля.
Каждый раз, когда мы изменяем базисные вектора (1, 0) и (0, 1) на (a, b) и (c, d), то новая координата точки (x, y) может быть найдена с помощью выражения:
Обычно базисные вектора равны (1, 0) и (0, 1) и мы просто получаем x(1, 0) + y(0, 1) = (x, y), и нет необходимости заботиться об этом дальше. Однако, важно помнить, что мы можем использовать и другие базисные вектора, когда нам это нужно.
Матрицы
Матрицы похожи на двухмерные вектора. Например, типичная 2×2 матрица, может выглядеть так:
Когда вы умножаете матрицу на вектор, вы суммируете скалярное произведение каждой строки с вектором, на который происходит умножение. Например, если мы умножаем вышеприведённую матрицу на вектор (x, y), то мы получаем:
Будучи записанным по-другому, это выражение выглядит так:
Выглядит знакомо, не так-ли? Это в точности такое-же выражение, которые мы использовали для смены базисных векторов. Это означает, что умножая 2×2 матрицу на двухмерный вектор, мы тем самым меняем базисные вектора. Например, если мы вставим стандартные базисные вектора в (1, 0) и (0, 1) в колонки матрицы, то мы получим:
Это единичная матрица, которая не даёт эффекта, который мы можем ожидать от нейтральных базисных векторов, которые мы указали. Если-же мы повернём базисные вектора на 49-градусов, то мы получим:
Эта матрица будет поворачивать двухмерный вектор на 49 градусов против часовой стрелки. Мы можем сделать код нашей игры Asteriods более элегантным, используя матрицы вроде этой. Например, функция поворота нашего корабля может выглядеть так:
Однако, наш код будет ещё более элегантным, если мы сможем также включить в эту матрицу перемещение корабля в пространстве. Тогда у нас будет единая структура данных, которая будет заключать в себе и применять информацию об ориентации объекта и его местоположении в пространстве.
К счастью есть способ добиться этого, хоть это и выглядит не очень элегантно. Если мы хотим переместиться с помощью вектора (e, f), мы лишь включаем его в нашу матрицу преобразования:
И добавляем дополнительную единицу в конец каждого вектора, определяющего местоположение объекта, например так:
Теперь, когда мы перемножаем их, мы получаем:
(a, c, e) • (x, y, 1) + (b, d, f) • (x, y, 1) + (0, 0, 1) • (x, y, 1)
Что, в свою очередь, может быть записано как:
x(a, b) + y(c, d) + (e, f)
Теперь у нас есть полный механизм трансформации, заключённый в одной матрице. Это важно, если не принимать в расчёт элегантность кода, так как с ней мы теперь можем использовать все стандартные манипуляции с матрицами. Например перемножить матрицы, чтобы добавить нужный эффект, или мы можем инвертировать матрицу, чтобы получить прямо противоположное положение объекта.
Трехмерные матрицы
Матрицы в трехмерном пространстве работают так-же как и в двухмерном. Я приводил примеры с двухмерными векторами и матрицами, так как их просто отобразить с помощью дисплея, показывающего двухмерную картинку. Нам просто надо определить три колонки для базисных векторов, вместо двух. Если базисные вектора это (a,b,c), (d,e,f) and (g,h,i) то наша матрица будет выглядеть так:
Если нам нужно перемещение (j,k,l), то мы добавляем дополнительную колонку и строку, как говорили раньше:
И добавляем единицу [1] в вектор, как здесь:
Вращение в двухмерном пространстве
Так как в нашем случае у нас только одна ось вращения (расположенная на дисплее), единственное, что нам надо знать, это угол. Я говорил об этом ранее, упоминая, что мы можем применять тригонометрические функции для реализации функции двухмерного вращения наподобие этой:
Более элегантно это можно выразить в матричной форме. Чтобы определить матрицу, мы можем применить эту функцию к осям (1, 0) и (0, 1) для угла Θ, а затем включить полученные оси в колонки нашей матрицы. Итак, начнём с координатной оси X (1, 0). Если мы применим к ней нашу функцию, мы получим:
(1*cos(Θ) — 0*sin(Θ), 1*sin(Θ) + 0*cos(Θ)) = (cos(Θ), sin(Θ))
Затем, мы включаем координатную ось Y (0, 1). Получим:
(0*cos(Θ) — 1*sin(Θ), 0*sin(Θ) + 1*cos(Θ)) = (-sin(Θ), cos(Θ))
Включаем полученные координатные оси в матрицу, и получаем двухмерную матрицу вращения:
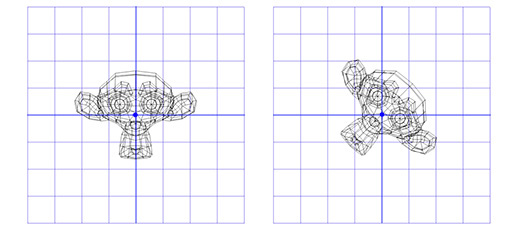
Применим эту матрицу к Сюзанне, мартышке из графического пакета Blender. Угол поворота Θ равен 45 градусов по часовой стрелке.
Как видите — это работает. Но что если нам надо осуществить вращение вокруг точки, отличной от (0, 0)?
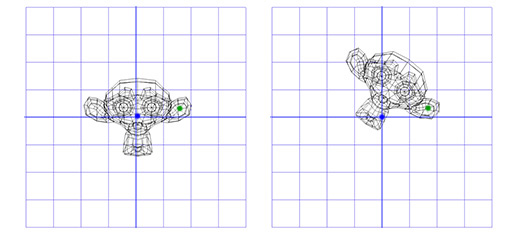
Например, мы хотим вращать голову мартышки вокруг точки, расположенной в её ухе:
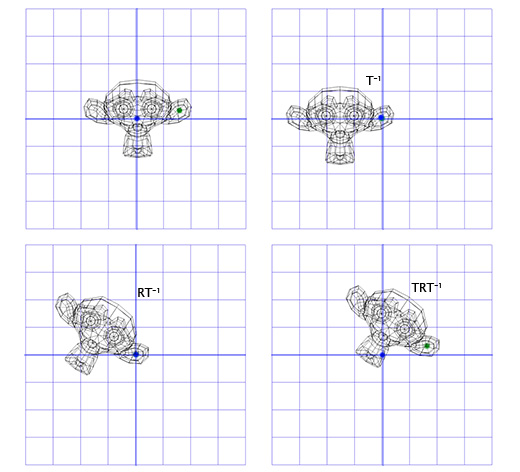
Чтобы сделать это, мы можем начать с создания матрицы перемещения (translation matrix) T, которая перемещает объект из начальной точки в точку вращения в ухе мартышки, и матрицу вращения R, для вращения объекта вокруг начальной точки. Теперь для вращения вокруг точки, расположенной в ухе, мы можем сперва переместить точку в ухе на место начальной точки, с помощью инвертирования матрицы T, записанной как T -1 . Затем, мы вращаем объект вокруг начальной точки, с помощью матрицы R, а затем применяем матрицу T для перемещения точки вращения назад, к своему исходному положению.
Ниже дана иллюстрация к каждому из описанных шагов:
Это важный шаблон, который мы будем применять позднее — применение вращения для двух противоположных трансформаций позволяет нам вращать объект в другом «пространстве». Что очень удобно и полезно.
Теперь рассмотрим трёхмерное вращение.
Трёхмерное вращение
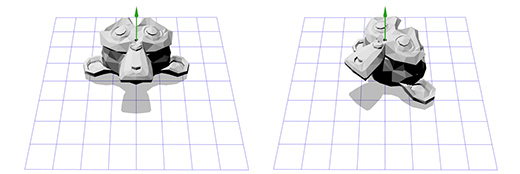
Вращение вокруг оси Z работает по тому-же принципу, что и вращение в двухмерном пространстве. Нам лишь нужно изменить нашу старую матрицу, добавив к ней дополнительную колонку и строку:
Применим эту матрицу к трехмерной версии Сюзанны, мартышки из пакета Blender. Угол поворота Θ пусть будет равен 45 градусов по часовой стрелке.
То-же самое. Вращение только вокруг оси Z ограничивает нас, как насчёт вращения вокруг произвольной оси?
Вращение, определяемое осью и углом (Axis-angle rotation)
Представление вращения, определяемого осью и углом, также известно как вращение в экспоненциальных координатах, параметризованное вращением двух величин. Вектора, определяющего вращение направляющей оси (прямая линия) и угла, описывающего величину поворота вокруг этой оси. Вращение осуществляется согласно правилу правой руки.
Итак, вращение задаётся двумя параметрами (axis, angle), где axis — вектор оси вращения, а angle — угол вращения. Этот приём довольно прост и являет собой отправную точку для множества других операций вращения, с которыми я работаю. Как практически применить вращение, определяемое осью и углом?
Допустим мы имеем дело с осью вращения, показанной на рисунке ниже:
Мы знаем как вращать объект вокруг оси Z, и мы знаем как вращать объект в других пространствах. Итак, нам лишь надо создать пространство, где наша ось вращения будет являться осью Z. И если эта ось будет осью Z, то что будет являться осями X и Y? Займемся вычислениями сейчас.
Чтобы создать новые оси X и Y нам нужно лишь выбрать два вектора, которые перпендикулярны новой оси Z и перпендикулярны друг другу. Мы уже говорили ранее о векторном умножении, которое берёт два вектора и даёт в итоге перпендикулярный им вектор.
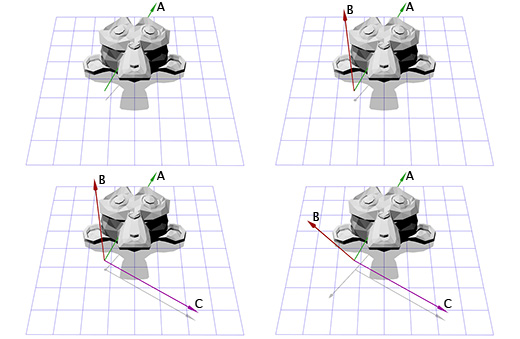
У нас есть один вектор сейчас, это ось вращения, назовём его A. Возьмём теперь случайный другой вектор B, который находится не в том-же направлении, что и вектор A. Пусть это будет (0, 0, 1) к примеру.
Теперь мы имеем ось вращения A и случайный вектор B, мы можем получить нормаль C, через векторное произведение A и B. С перпендикулярен векторам A и B. Теперь мы делаем вектор B перпендикулярным векторам A и C через их векторное произведение. И всё, у нас есть все нужные нам оси координат.
На словах это звучит сложно, но довольно просто выглядит в коде или будучи показанным в картинках.
Ниже показано, как это выглядит в коде:
Тут показана иллюстрация для каждого шага:
Теперь, имея информацию о новых координатных осях, мы можем составить матрицу M, включив каждую ось как колонку в эту матрицу. Нам надо убедиться, что вектор A является третьей колонкой, чтобы он был нашей новой осью координат Z.
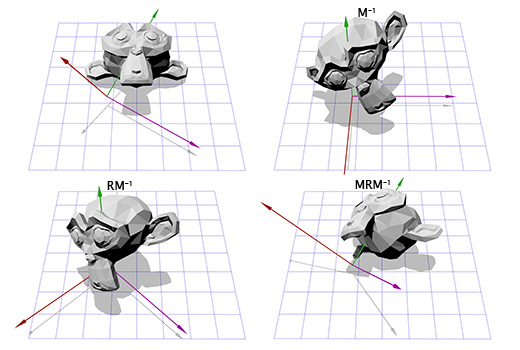
Теперь это похоже на то, что мы делали для поворота в двухмерном пространстве. Мы можем применить инвертированную матрицу M, чтобы переместиться в новую систему координат, затем произвести вращение, согласно матрице R, чтобы повернуть объект вокруг оси Z, затем применить матрицу M, чтобы вернуться в исходное координатное пространство.
Теперь мы можем вращать объект вокруг произвольной оси. В конце концов мы можем просто создать матрицу T = T = M -1 RM и использовать её много раз, без дополнительных усилий с нашей стороны. Есть более эффективные способы конвертирования вращений, определяемых осью и углом во вращения, определяемые матрицами. Просто описанный нами подход показывает многое из того, о чём мы говорили ранее.
Вращение, определяемое осью и углом, возможно, самый интуитивно понятный способ. Применяя его, очень легко инвертировать поворот, поменяв знак у угла, и легко интерполировать, путём интерполяции угла. Однако тут есть серьёзное ограничение, и заключается оно в том, что такое вращение не является суммирующим. То есть вы не можете комбинировать два вращения, определяемых осью и углом в третье.
Вращение, определяемое осью и углом — хороший способ для начала, но оно должно быть преобразовано во что-то другое, чтобы использоваться в более сложных случаях.
Эйлеровские углы
Эйлеровские углы представляют собой другой способ вращения, заключающийся в трёх вложенных вращениях относительно осей X, Y и Z. Вы, возможно, сталкивались с их применением в играх, где камера показывает действие от первого лица, либо от третьего лица.
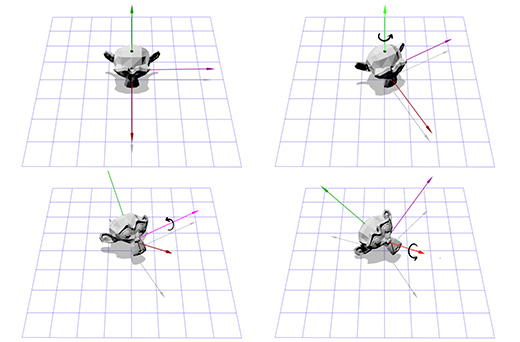
Допустим вы играете в шутер от первого лица и вы повернулись на 30 градусов влево, а затем посмотрели на 40 градусов вверх. В конце-концов в вас стреляют, попадают, и, в результате удара, камера поворачивается вокруг своей оси на 45 градусов. Ниже показано вращение с помощью углов Эйлера (30, 40, 45).
Углы Эйлера — удобное и простое в управлении средство. Но у этого способа есть два недостатка.
Первый, это вероятность возникновения ситуации под названием «блокировка оси» или «шарнирный замок» (gimbal lock). Представьте, что вы играете в шутер от первого лица, где вы можете посмотреть влево, вправо, вверх и вниз или повернуть камеру вокруг зрительной оси. Теперь представьте, что вы смотрите прямо вверх. В этой ситуации попытка взглянуть налево или направо будет аналогична попытке вращения камеры. Всё что мы можем вы этом случае, это вращать камеру вокруг своей оси, либо посмотреть вниз. Как вы можете представить, это ограничение делает непрактичным применение углов Эйлера в лётных симуляторах.
Второе — интерполяция между двумя эйлеровскими углами вращения не даёт кратчайшего пути между ними.
Например, у вас две интерполяции между двумя одинаковыми вращениями. Первая использует интерполяцию эйлеровского угла, вторая использует сферическую линейную интерполяцию (spherical linear interpolation (SLERP)), чтобы найти кратчайший путь.
Итак, что-же больше подойдет для интерполяции вращений? Может быть матрицы?
Вращение с помощью матриц
Как мы уже говорили ранее, матрицы вращения хранят в себе информацию о трёх осях. Это означает, что интерполяция между двумя матрицами лишь линейно интерполирует каждую ось. В результате это даёт нам эффективный путь, то так-же привносит новые проблемы. Например, тут показаны два вращения и одно интерполированное полу-вращение:
Как вы можете заметить, интерполированное вращение значительно меньше, чем любое из исходных вращений, и две оси более не перпендикулярны друг другу. Это логично, если вдуматься — середина отрезка, соединяющего любые две точки на сфере будет расположена ближе к центру сферы.
Это в свою очередь порождает известный «эффект фантика» (candy wrapper effect), при применении скелетной анимации. Ниже показана демонстрация этого эффекта на примере кролика из нашей игры Overgrowth (прим. переводчика: обратите внимание на середину туловища кролика).
Вращение, основанное на матричных операциях, очень полезно, так как они могут аккумулировать вращения без всяких проблем, вроде блокировки оси (gimbal lock), и может очень эффективно применяться к точкам сцены. Вот почему поддержка вращения на матрицах встроена в графические карты. Для любого типа трёхмерной графики матричный формат вращения — это всегда итоговый применяемый способ.
Однако, как мы уже знаем, матрицы не очень хорошо интерполируются, и они не столь интуитивно понятны.
Итак, остался только один главный формат вращения. Последний, но тем не менее, важный.
Кватернионы
Что-же такое кватернионы? Если очень кратко, то это альтернативный вариант вращения, основанный на оси и угле (axis-angle rotation), который существует в пространстве.
Подобно матрицам они могут аккумулировать вращения, то есть вы можете составлять из них цепочку вращений, без опаски получить блокировку оси (gimbal lock). И в то-же время, в отличие от матриц, они могут хорошо интерполироваться из одного положения в другое.
Являются-ли кватернионы лучшим решением, нежели остальные способы вращений (rotation formats)?
На сегодняшний день они комбинируют все сильные стороны других способов вращений. Но у них есть два слабых места, рассмотрев которые, мы придём к выводу, что кватернионы лучше использовать для промежуточных вращений. Итак, каковы недостатки кватернионов.
Во-первых кватернионы непросто отобразить на трёхмерном пространстве. И мы вынуждены всегда реализовывать вращение более простым способом, а затем конвертировать его. Во-вторых, кватернионы не могут эффективно вращать точки, и мы вынуждены конвертировать их в матрицы, чтобы повернуть значительное количество точек.
Это означает, что вы скорее всего не начнете или не закончите серию вращений с помощью кватернионов. Но с их помощью можно реализовать промежуточные вращения более эффективно, нежели при применении любого другого подхода.
«Внутренняя кухня» механизма кватернионов не очень понятна и не интересна мне. И, возможно, не будет интересна и вам, если только вы не математик. И я советую вам найти библиотеки, которые работают с кватернионами, чтобы облегчить вам решение ваших задач с их помощью.
Математические библиотеки «Bullet» или «Blender» будут хорошим вариантом для начала.
http://gamedev.ru/code/articles/geometry_for_beginners_1
http://habr.com/ru/post/131931/
Знакомимся с вектором
Основы линейной алгебры для тех, кого это миновало в универе.
Вы наверняка слышали много историй о программистах, которые учились в технических вузах, изучали высшую математику и теперь пользуются этими знаниями в программировании. И если кого-то это не коснулось, может быть ощущение, что он пропустил в жизни что-то важное.
Будем это исправлять. Попробуем разобрать некоторые базовые понятия из математики за пределами школьной программы. И заодно покажем, как оно связано с программированием и для каких задач полезно.
⚠️ Математики, помогайте. Мы тут многое упростили, поэтому будем рады увидеть ваши уточнения и замечания в комментариях.
Линейная алгебра
Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта. И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства.
Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.
Например, мы знаем, что если a + b = c , то a = c − b . Мы не знаем, что стоит на местах a, b или c, но для нас это такой абстрактный закон, который подтверждается практикой.
Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра.
В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения.
Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать.
Что такое вектор
Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.
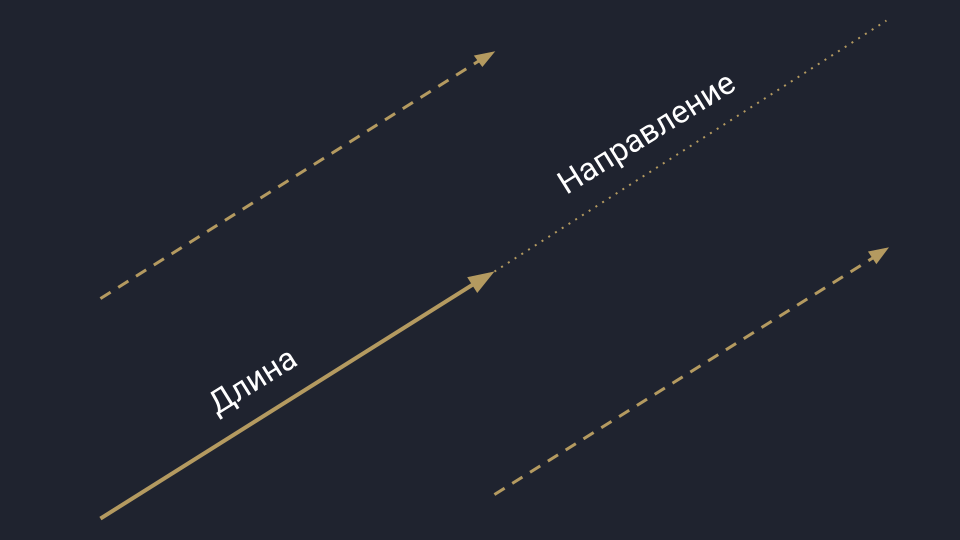
У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.
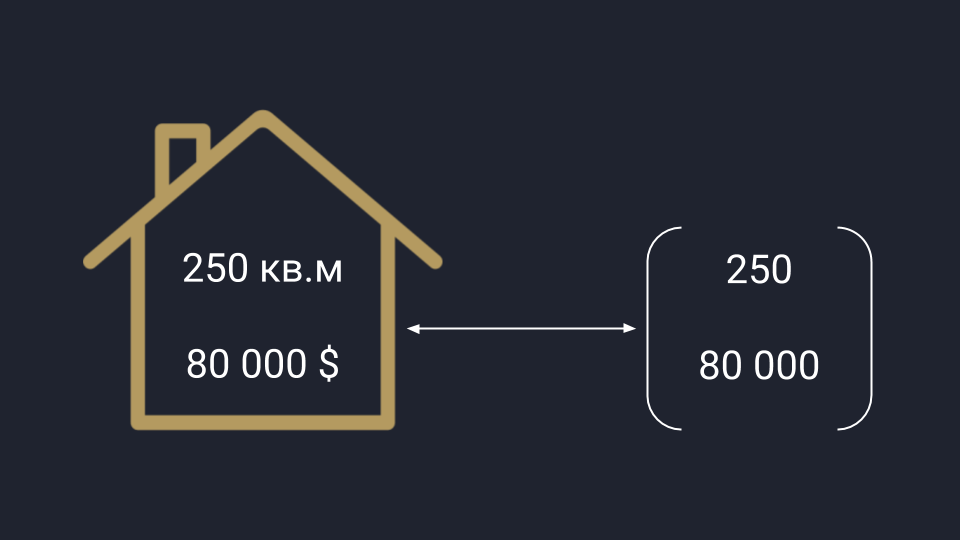
Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.
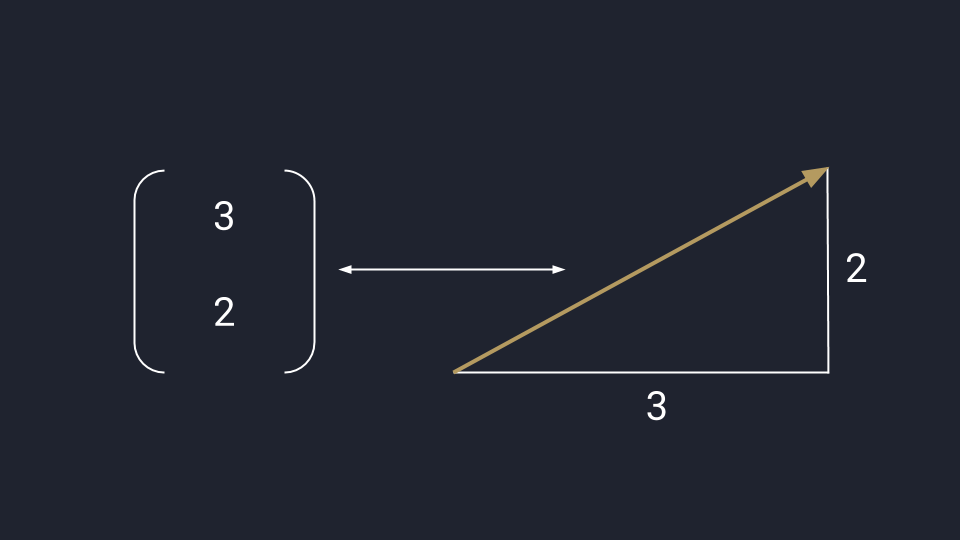
В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.
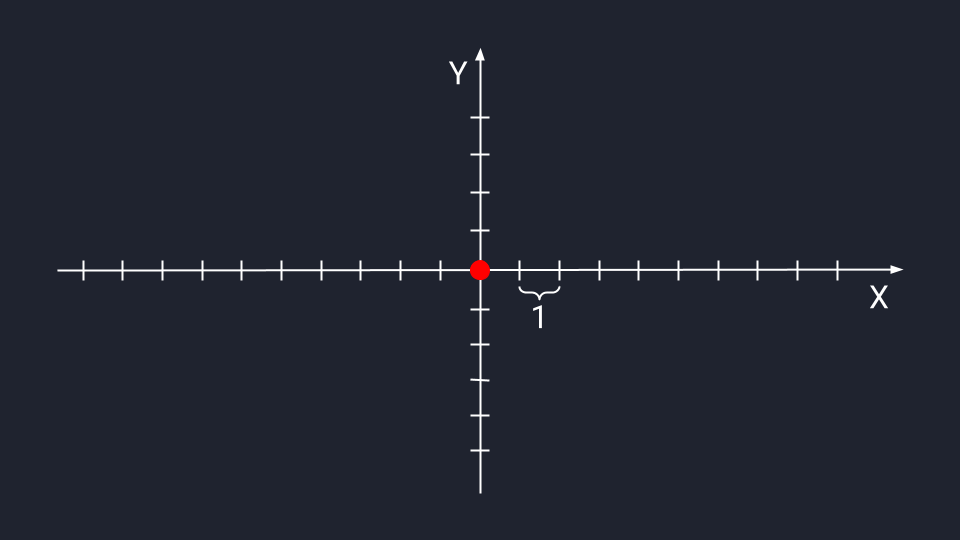
👉 Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.
Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.
Как записывать
Вектор можно записать в строку или в столбец. Для строчной записи вектор обозначают одной буквой, ставят над ней черту, открывают круглые скобки и через запятую записывают координаты вектора. Для записи в столбец координаты вектора нужно взять в круглые или квадратные скобки — допустим любой вариант.
Строгий порядок записи делает так, что каждый набор чисел создаёт только один вектор, а каждый вектор ассоциируется только с одним набором чисел. Это значит, что если у нас есть координаты вектора, то мы их не сможем перепутать.
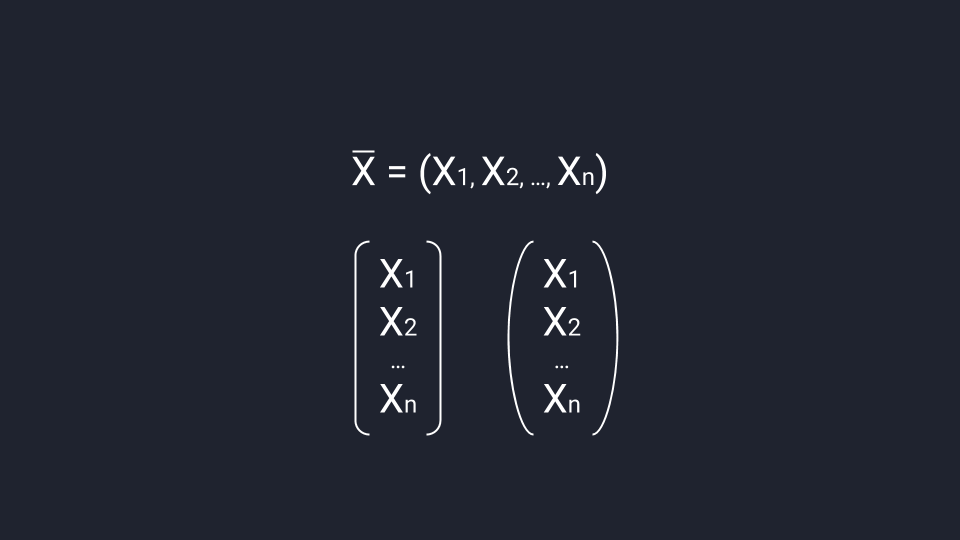
Скаляр
Помимо понятия вектора есть понятие скаляра. Скаляр — это просто одно число. Можно сказать, что скаляр — это вектор, который состоит из одной координаты.
Помните физику? Есть скалярные величины и есть векторные. Скалярные как бы описывают просто состояние, например, температуру. Векторные величины ещё и описывают направление.
Как изображать
Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.
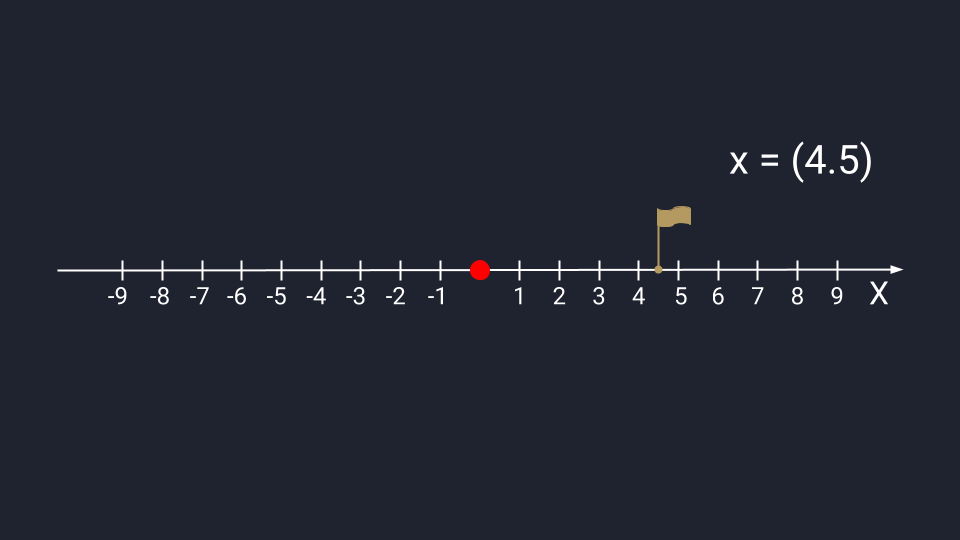
Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.
Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.
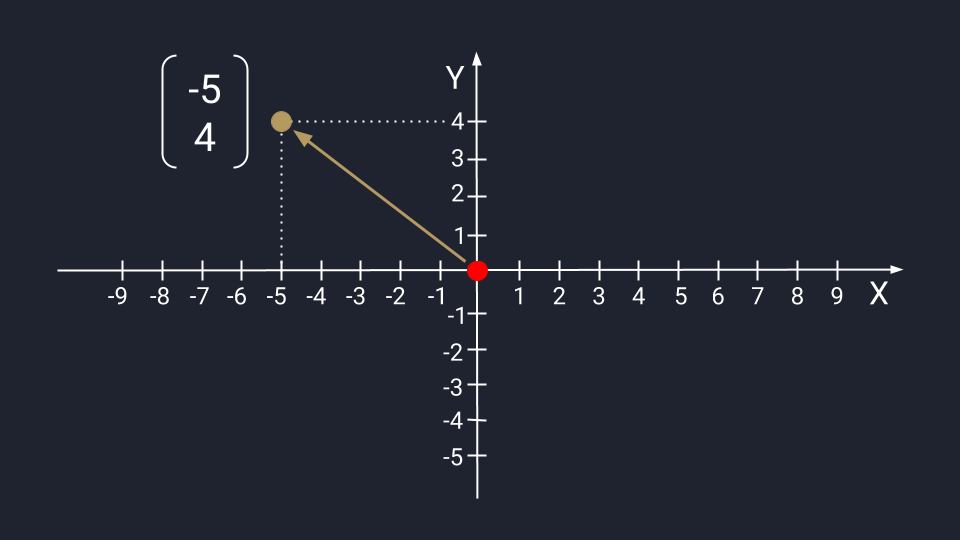
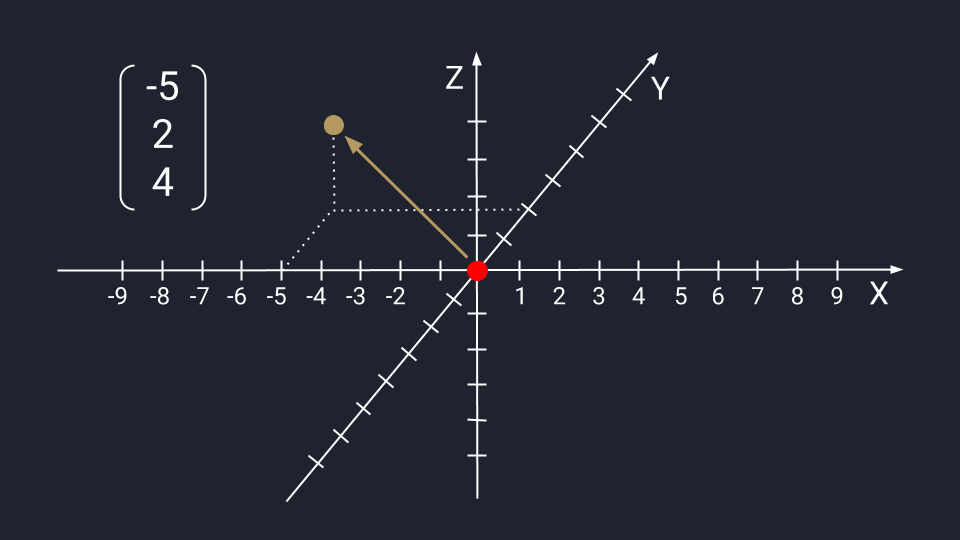
Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.
Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.
Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке. Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства.
Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.
И зачем нам это всё
Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:
- На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
- Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.
Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.
И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.
Что дальше
В следующий раз разберём операции с векторами. Пока мы готовим материал — рекомендуем почитать интервью с Анастасией Никулиной. Анастасия ведёт ютуб-канал по дата-сайнс и работает сеньором дата-сайентистом в Росбанке.
Нахождение координат вектора через координаты точек
Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i → должно совпадать с осью O x , а направление вектора j → с осью O y .
Векторы i → и j → называют координатными векторами.
Координатные векторы неколлинеарны. Поэтому любой вектор p → можно разложить по векторам p → = x i → + y j → . Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p → по координатным векторам называются координатами вектора p → в данной системе координат.
Координаты вектора записываются в фигурных скобках p → x ; y . На рисунке вектор O A → имеет координаты 2 ; 1 , а вектор b → имеет координаты 3 ; — 2 . Нулевой вектор представляется в виде 0 → 0 ; 0 .
Если векторы a → и b → равны, то и y 1 = y 2 . Запишем это так: a → = x 1 i → + y 1 j → = b → = x 2 i → + y 2 j → , значит x 1 = x 2 , y 1 = y 2 .
Таким образом, координаты равных векторов соответственно равны.
Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на O x y заданы координаты точек начала и конца A B → : A x a , y a , B x b , y b . Найти координаты заданного вектора.
Изобразим координатную ось.
Из формулы сложения векторов имеем O A → + A B → = O B → , где O – начало координат. Отсюда следует, что A B → = O B → — O A → .
O A → и O B → – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения O A → = x a , y a , O B → = x b , y b .
По правилу операций над векторами найдем A B → = O B → — O A → = x b — x a , y b — y a .
Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек.
Для нахождения координат вектора, необходимо найти разность его точек конца и начала.
Найти координаты O A → и A B → при значении координат точек A ( 2 , — 3 ) , B ( — 4 , — 1 ) .
Для начала определяется радиус-вектор точки A . O A → = ( 2 , — 3 ) . Чтобы найти A B → , нужно вычесть значение координат точек начала из координат точек конца.
Получаем: A B → = ( — 4 — 2 , — 1 — ( — 3 ) ) = ( — 6 , 2 ) .
Ответ: O A → = ( 2 , — 3 ) , A B → = ( — 6 , — 2 ) .
Задано трехмерное пространство с точкой A = ( 3 , 5 , 7 ) , A B → = ( 2 , 0 , — 2 ) . Найти координаты конца A B → .
Подставляем координаты точки A : A B → = ( x b — 3 , y b — 5 , z b — 7 ) .
По условию известно, что A B → = ( 2 , 0 , — 2 ) .
Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: x b — 3 = 2 y b — 5 = 0 z b — 7 = — 2
Отсюда следует, что координаты точки B A B → равны: x b = 5 y b = 5 z b = 5
Ответ: B ( 5 , 5 , 5 ) .
Геометрия для новичков. Часть 1: координаты и векторы — теория
Внимание! Этот документ ещё не опубликован.
О чем данная статья
В данной статье дается теоретическое описание векторов, координат векторов и операций над ними.
На кого рассчитана статья
Прежде чем читать эту статью, нужно знать:
- что такое прямоугольная система координат и координаты точки на плоскости
- что такое теорема Пифагора
Введение
Зачем нужны координаты точек в играх
В любой игре положение игрового объекта задается координатами какой-либо точки, привязанной к этому объекту, т.е. эта точка перемещается вместе с объектом. Например, мы можем задать координаты объектов в «Супер Марио» следующим образом:
На этом рисунке крупные черные точки — это точки, привязанные к игровым объектам. Координаты этих точек мы и будем считать координатами игровых объектов.
Итак, на этом рисунке:
- координаты Марио равны (-0.5, -2)
- координаты улитки равны (3, -2)
- координаты кубика равны (4, 1)
Пример координат вектора
Я намеренно не написал конкретные значения для координат точек – пусть они будут произвольными.
Зададим себе вопрос «Как нужно изменить начальные координаты Марио, что получить конечные?» Чтобы ответить на этот вопрос, нам нужно найти пару чисел (x, y), таких, чтобы:
Ax + x = Bx
Ay + y = By
Решая эти 2 уравнения, получаем:
x = Bx — Ax
y = By — Ay
Пара (x, y) в нашей задаче является координатами вектора перемещения Марио. Но это — лишь конкретный пример координат вектора. Что такое вектор и что такое его координаты в общем случае? Сейчас узнаем.
Векторы
Что такое направленный отрезок
Стрелка показывает, что А – начало отрезка, а B – конец.
Что такое вектор
Что у этих отрезков общего? Хм, пожалуй 2 вещи:
- Направление
- Длина
Так вот, вектор – это как раз и есть совокупность направления и длины.
Направленный отрезок – не вектор, который мы изучаем в геометрии. Направленный отрезок задает, или как еще говорят, представляет вектор. Но это — не вектор.
В нашем примере направленный отрезок 

Примечание: о тонкостях приведенного мной определения — в конце статьи.
Равенство векторов
Если задуматься, все направленные отрезки одинаковой длины, которые лежат на параллельных прямых и указывают в одну сторону, имеют одинаковое направление и длину. Следовательно, все эти направленные отрезки представляют один и тот же вектор. Из этого следует определение равенства 2 векторов:
Два вектора 



Из данного определения следует, что при параллельном переносе произвольный направленный отрезок продолжает представлять тот же вектор, что он представлял до переноса. Это свойство активно используется для операций над векторами.
Длина вектора
Коллинеарные векторы
На рисунке любая пара из векторов 


Если отрезки, представляющие коллинеарные векторы, имеют одинаковое направления, то векторы называют сонаправленными:
Пишут:
Если отрезки, представляющие коллинеарные векторы, имеют противоположное направления, то векторы, представленные данными отрезками, называют противоположно направленными:
Пишут:
Нулевой вектор
Единичные векторы

Обратный вектор
Арифметические операции над векторами
- Вектор можно умножать на число. Вектор
, умноженный на число, записывается как k*
. Вектор будет сонаправлен (противоположно направлен) с вектором
, если k — положительное (отрицательное) число. Вектор k*
будет иметь длину |k|*|
|:
|k*

k* 

k* 

|k * 
Т.е. в результате нормализации мы получаем единичный вектор, сонаправленный с исходным вектором 
Важно: нулевой вектор НЕЛЬЗЯ нормализовать, так как для любого числа k:
|k*

Итак, как же найти это число k?
Распишем |k * 
|k * 


Здесь мы убрали с k знак модуля, так как по определению k > 0.
Итак:
k * |
Из этого следует, что:
k = 1 / |
Т.е. чтобы нормализовать произвольный ненулевой вектор, нам нужно разделить вектор на его длину.
Координаты вектора
Вроде бы из примера, приведенного в начале статьи, все понятно: координаты вектора — разность координат конца и начала направленного отрезка, представляющего вектор.
Но это не так. Действительно, значения координат вектора численно равны этой разности. Но определение координат вектора в корне отличается от определения координат точки.
Разложение вектора по 2 неколлинеарным векторам
В геометрии доказывается следующий факт.
Ecли мы возьмем 2 неколлинеарных вектора 

то для каждого вектора 


Теперь возьмем в качестве таких неколлинеарных векторов 

Векторы 

Определение координат вектора


то пара чисел (x, y) будет называться координатами вектора 
Часто пишут:

Эта запись означает, что вектор 
Арифметические операции над координатами векторов
— 
Координаты вектора, умноженного на число, равны координатам исходного вектора, умноженными на это число:
k* 
Пусть у нас есть 2 произвольных вектора 

- кoординаты суммы 2 векторов равны сумме x- и y-координат векторов:
+
= (ax + bx, ay + by)
- как следствие из предыдущих свойств, координаты разности 2 векторов равны разности координат этих векторов:
—
= (ax — bx, ay — by)
Т.е. арифметика для координат векторов – такая же, как и для обычных чисел, только все считается покоординатно.
Радиус-вектор
Можно доказать, что численные значения координат точки совпадают со значения координат ее радиус-вектора. Здесь примем это как факт: 
где (Ax, Ay) — координаты точки A
Связь между координатами вектора и координатами концов отрезка
если 


(x, y) = (Bx — Ax, By — Ay)
где (Ax, Ay), (Bx, By) — координаты точек А и B соответственно.
Докажем это.
Мы можем записать простое равенство для произвольного вектора 


Заметим, что 

Из равенства значений координат точки и радиус-вектора и предыдущей формулы следует, что:
(x, y) = (Bx — Ax, By — Ay)
Нахождение длины вектора по его координатам
Пусть у нас есть вектор 


Чтобы найти длину вектора 


По теореме Пифагора:
AC = |
СB = |
то в итоге получаем равенство:
Заключение
Применению векторов в реальных задачах игровой разработки будет посвящена следующая моя статья. В ней практически не будет математики и будет много программирования.
Здесь же я описал то, что будет необходимо для понимания практических приемов использования векторов.
Если не иметь представления, как связаны координаты точек и координаты векторов, очень сложно понять, как работают алгоритмы определения расстояний от точки до геометрической фигуры, алгоритмы обнаружения столкновений и т.д.
Так что не жалейте, если вы (о ужас!) кое-что запомнили из «всей этой математики». Все это вам пригодится очень скоро, обещаю.
Литература
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. «Геометрия», 7-9 классы»
Главы: «Векторы», «Метод координат».
PS: корректность определения вектора в статье
Вся хитрость в том, что существует несколько определений вектора даже в рамках геометрии.
Направленный отрезок – тоже вектор, так называемый фиксированный вектор. Но нужно учитывать один важный факт – 2 фиксированных вектора равны тогда и только тогда, когда их концы и начала совпадают. А это не то определение равенства 2 векторов, что дает учебник геометрии.
Определение вектора, данное в этой статье – определение так называемого свободного вектора.
Каждый свободный вектор – это множество фиксированных векторов, которые имеют равную длину и одинаковое направление.
Именно это определение учебник геометрии и пытается дать в неявном виде, когда вводит понятие равенства векторов. Но здесь возникает нестыковка – учебник объясняет, как работать со свободными векторами, изначально дав определение фиксированного вектора.
Надеюсь, вышесказанное объясняет, почему я привел в данной статье «свое» определение вектора.
http://zaochnik.com/spravochnik/matematika/vektory/nahozhdenie_kordinat_vectora/
http://gamedev.ru/code/articles/geometry_for_beginners_1
Система координат
С чего было бы логично начать обсуждение метода координат? Наверное, с понятия системы координат. Вспомни, когда ты с нею впервые столкнулся.
Мне кажется, что в 7 классе, когда ты узнал про существование линейной функции ( y=ax+b), например, ( y=2{x}-3).
Напомню, ты строил ее по точкам. Помнишь?
Ты выбирал произвольное число ( x), подставлял ее в формулу ( y=2{x}-3) и вычислял таким образом ( y).
Например, если ( x=0), то ( y=2cdot 0-3=-3), если же ( x=1), то ( y=2cdot 1-3=-1)и т. д.
Что же ты получал в итоге?
А получал ты точки с координатами: ( Aleft( 0,-3 right)) и ( Bleft( 1,-1 right)).
Далее ты рисовал «крестик» (систему координат ( X0Y)), выбирал на ней масштаб (сколько клеточек у тебя будет единичным отрезком) и отмечал на ней полученные тобою точки, которые затем соединял прямой линией, полученная линия и есть график функции ( y=2{x}-3).
Тут есть несколько моментов, которые стоит объяснить тебе чуть подробнее:
- Единичный отрезок ты выбираешь из соображений удобства, так, чтобы все красиво и компактно умещалось на рисунке;
- Принято, что ось ( displaystyle X) идет слева направо, а ось ( displaystyle Y) – cнизу вверх;
- Они пересекаются под прямым углом, а точка их пересечения называется началом координат. Она обозначается буквой ( displaystyle O);
- В записи координаты точки, например ( displaystyle Aleft( 0,-3 right)), слева в скобках стоит координата точки по оси ( displaystyle X), а справа, по оси ( displaystyle Y). В частности, ( displaystyle Aleft( 0,-3 right)) просто означает, что у точки ( displaystyle A) ( displaystyle x=0,~y=-3.);
- Для того, чтобы задать любую точку на координатной оси, требуется указать ее координаты (2 числа);
- Для любой точки, лежащей на оси ( displaystyle Ox,), ( displaystyle y=0.);
- Для любой точки, лежащей на оси ( displaystyle Oy), ( displaystyle x=0.);
- Ось ( displaystyle Ox) называется осью абсцисс;
- Ось ( displaystyle Oy) называется осью ординат.
Векторы
Теперь давай с тобой сделаем следующий шаг: отметим две точки ( displaystyle Aleft( {{x}_{1}},{{y}_{1}} right)) ( displaystyle Bleft( {{x}_{2}},{{y}_{2}} right)).
Соединим эти две точки отрезком. И поставим стрелочку так, как будто мы проводим отрезок из точки ( displaystyle A) к точке ( displaystyle B):
То есть мы сделаем наш отрезок направленным!
Вспомни, как еще называется направленный отрезок? Верно, он называется вектором!
Вектором называется направленный отрезок, имеющий начало и конец.
Таким образом, если мы соединим точку ( displaystyle A) c точкой ( displaystyle B), причем началом у нас будет точка A, а концом – точка B, то мы получим вектор ( displaystyle overrightarrow{AB}).
Это построение ты тоже делал в 8 классе, помнишь?
Координаты вектора
Оказывается, векторы, как и точки, можно обозначать двумя цифрами: эти цифры называются координатами вектора.
Вопрос: как ты думаешь, достаточно ли нам знать координаты начала и конца вектора, чтобы найти его координаты?
Оказывается, что да! И делается это очень просто:
Координаты вектора = координаты точки конца – координаты точки начала.
Таким образом, так как в векторе ( displaystyle overrightarrow{AB}) точка ( displaystyle Aleft( {{x}_{1}},{{y}_{1}} right)) – начало, а ( displaystyle Bleft( {{x}_{2}},{{y}_{2}} right)) – конец, то вектор ( displaystyle overrightarrow{AB}) имеет следующие координаты:
( displaystyle overrightarrow{AB}left( {{x}_{2}}-{{x}_{1}},{{y}_{2}}-{{y}_{1}} right))
Например, если ( displaystyle Aleft( 2,0 right))( displaystyle Bleft( 1,2 right)), то координаты вектора ( displaystyle overrightarrow{AB})
( displaystyle overrightarrow{AB}left( 1-2,2-0 right)=overrightarrow{AB}left( -1,2 right))
Теперь давай сделаем наоборот, найдем координаты вектора ( displaystyle overrightarrow{BA}).
Что нам для этого нужно поменять? Да, нужно поменять местами начало и конец: теперь начало вектора будет в точке ( displaystyle B), а конец – в точке ( displaystyle A).
Тогда:
( displaystyle overrightarrow{BA}left( 2-1,text{ }!!~!!text{ }0-2 right)=overrightarrow{BA(}1,-2).)
Посмотри внимательно, чем отличаются векторы ( displaystyle overrightarrow{AB}) и ( displaystyle overrightarrow{BA})?
Единственное их отличие – это знаки в координатах. Они противоположны. Этот факт принято записывать вот так:
( displaystyle overrightarrow{AB}=-overrightarrow{BA})
Иногда, если не оговаривается специально, какая точка является началом вектора, а какая – концом, то векторы обозначают не двумя заглавными буквами, а одной строчной, например: ( displaystyle {vec{a}}), ( displaystyle {vec{p}}) и т. д.
Еще больше о векторах и проекциях (эту тему мы непременно затронем) ты можешь прочитать в статье по физике «Большая теория по векторам» 🙂
Действия с векторами
Что еще можно делать с векторами?
Да почти все то же самое, что и с обычными числами:
- Векторы можно складывать друг с другом;
- Векторы можно вычитать друг из друга;
- Векторы можно умножать (или делить) на произвольное ненулевое число;
- Векторы можно умножать друг на друга.
Что же происходит при выполнении этих действий с координатами векторов?
1. При сложении (вычитании) двух векторов, мы складываем (вычитаем) поэлементно их координаты.
То есть:
( vec{a}left( {{x}_{1}},{{y}_{1}} right)+vec{b}left( {{x}_{2}},{{y}_{2}} right)=vec{c}left( {{x}_{1}}+{{x}_{2}},{{y}_{1}}+{{y}_{2}} right))
( vec{a}left( {{x}_{1}},{{y}_{1}} right)-vec{b}left( {{x}_{2}},{{y}_{2}} right)=vec{c}left( {{x}_{1}}-{{x}_{2}},{{y}_{1}}-{{y}_{2}} right))
2. При умножении (делении) вектора на число, все его координаты умножаются (делятся) на это число:
( kcdot vec{a}left( {{x}_{1}},{{y}_{1}} right)=vec{b}left( k{{x}_{1}},k{{y}_{1}} right))
Например:
Найдите сумму координат вектора ( vec{a}+vec{b}).
Вектор растягивается или сжимается или меняет направление при умножении или делении на число:
Давай вначале найдем координаты каждого из векторов.
Оба они имеют одинаковое начало – точку начала координат. Концы у них разные.
Тогда ( vec{a}left( 2-0,6-0 right)=vec{a}left( 2,6 right)), ( vec{b}left( 8-0,4-0 right)=vec{b}left( 8,4 right)).
Теперь вычислим координаты вектора ( vec{c}=vec{a}+vec{b}=vec{c}left( 2+8,4+6 right)=vec{c}left( 10,10 right))
Тогда сумма координат полученного вектора равна ( 20).
Ответ: ( 20)
Теперь реши сам следующую задачу:
Найти сумму координат вектора ( 3vec{a}-2vec{b})
Проверяем:
- ( vec{a}=vec{a}left( 4-2,10-4 right)=vec{a}left( 2,6 right));
- ( vec{b}=vec{b}left( 10-2,6-2 right)=vec{b}left( 8,4 right));
- ( vec{c}=3vec{a}-2vec{b}=3vec{a}left( 2,6 right)-2vec{b}left( 8,4 right)=left( 6,18 right)-left( 16,8 right)=vec{c}left( -10,10 right));
- ( -10+10=0).
Ответ: ( 0)
Расстояние между двумя точками на координатной плоскости
Давай рассмотрим теперь следующую задачу: у нас есть две точки на координатной плоскости. Как найти расстояние между ними?
Пусть первая точка будет ( {{P}_{1}}({{x}_{1}},{{y}_{1}})), а вторая ( {{P}_{2}}left( {{x}_{2}},{{y}_{2}} right)).
Обозначим расстояние между ними через ( d). Давай сделаем для наглядности следующий чертеж:
Что я сделал?
Я, во-первых, соединил точки ( {{P}_{1}}left( {{x}_{1}},{{y}_{1}} right)) и ( {{P}_{2}}left( {{x}_{2}},{{y}_{2}} right)).
А также из точки ( {{P}_{1}}) провел линию, параллельную оси ( Ox), а из точки ( {{P}_{2}}) провел линию, параллельную оси ( Oy).
Они пересеклись в точке ( R), образовав при этом замечательную фигуру. Чем она замечательна?
Да мы с тобой почти что все знаем про прямоугольный треугольник. Ну уж теорему Пифагора – точно!
Искомый отрезок – это гипотенуза этого треугольника, а отрезки ( {{P}_{1}}R,~{{P}_{2}}R) – катеты.
Чему равны координаты точки ( R)?
Да, их несложно найти по картинке: ( Rleft( {{x}_{2}},{{y}_{1}} right).~)
Так как отрезки ( {{P}_{1}}R,~{{P}_{2}}R) параллельны осям ( Ox) и ( Oy) соответственно, то их длины легко найти: если обозначить длины отрезков ( {{P}_{1}}R,~{{P}_{2}}R) соответственно через ( left| {{P}_{1}}Rleft| ,~ right|{{P}_{2}}R right|), то
( left| {{P}_{1}}R right|={{x}_{2}}-{{x}_{1}})
( left| {{P}_{2}}R right|={{y}_{2}}-{{y}_{1}})
Теперь воспользуемся теоремой Пифагора. Длины катетов нам известны, гипотенузу мы найдем:
( {{d}^{2}}=text{ }!!~!!text{ }left| {{P}_{1}}{{P}_{2}} right|=text{ }!!~!!text{ }{{left| {{P}_{1}}R right|}^{2}}+{{left| {{P}_{2}}R right|}^{2}}=({{x}_{2}}-{{x}_{1}}){{~}^{2}}+({{y}_{2}}-{{y}_{1}}){{~}^{2}}~)
( d=~sqrt{({{x}_{2}}-{{x}_{1}}){{~}^{2}}+({{y}_{2}}-{{y}_{1}}){{~}^{2}}})
Таким образом, расстояние между двумя точками – это корень из суммы квадратов разностей из координат.
Или же – расстояние между двумя точками – это длина отрезка, их соединяющего.
Легко заметить, что расстояние между точками не зависит от направления.
Тогда:
( d=left| overrightarrow{{{P}_{1}}{{P}_{2}}} right|=left| overrightarrow{{{P}_{2}}{{P}_{1}}} right|=sqrt{({{x}_{2}}-{{x}_{1}}){{~}^{2}}+({{y}_{2}}-{{y}_{1}}){{~}^{2}}})
Отсюда делаем три вывода:
- Длина вектора = корень из суммы квадратов его координат;
- Найти расстояние между двумя точками = найти длину вектора, их соединяющего (в любом направлении);
- Длины векторов, соединяющих две точки в разном направлении, равны.
Давай немного поупражняемся в вычислении расстояния между двумя точками:
Например, если ( Aleft( 1,2 right),~Bleft( 3,4 right)), то расстояние между ( A) и ( B) равно
( d=sqrt{{{left( 3-1 right)}^{2}}+{{left( 4-2 right)}^{2}}}=sqrt{4+4}=sqrt{8}=2sqrt{2})
Или пойдем по-другому: найдем координаты вектора ( overrightarrow{AB})
( overrightarrow{AB}left( 3-1,4-2 right)=overrightarrow{AB}left( 2,2 right))
И найдем длину вектора:
( left| overrightarrow{AB} right|=sqrt{{{2}^{2}}+{{2}^{2}}}=sqrt{8}=2sqrt{2})
Как видишь, одно и то же!
Теперь немного потренируйся сам:
Задание. Найти расстояние между указанными точками:
- ( Aleft( 2,sqrt{3} right),~Bleft( 5,2sqrt{3} right));
- ( Cleft( 2,4 right),~Dleft( 1,-5 right));
- ( Fleft( sqrt{12},1 right),~Gleft( sqrt{3},-1 right)).
Проверяем:
- ( d=sqrt{{{left( 5-2 right)}^{2}}+{{left( 2sqrt{3}-sqrt{3} right)}^{2}}}=sqrt{9+3}=sqrt{12}=2sqrt{3});
- ( displaystyle d=sqrt{{{left( 1-2 right)}^{2}}+{{left( -5-4 right)}^{2}}}=sqrt{1+81}=sqrt{82});
- ( displaystyle d=sqrt{{{left( sqrt{3}-sqrt{12} right)}^{2}}+{{left( -1-1 right)}^{2}}}=sqrt{left( 3-2sqrt{3}sqrt{12}+12 right)+4}=); ( displaystyle=sqrt{3-2sqrt{36}+12+4}=sqrt{3-12+12+4}=sqrt{7}).
Вот еще пара задачек на ту же формулу, правда звучат они немного по-другому:
1. Найдите квадрат длины вектора ( vec{a}-vec{b}).
2. Найдите квадрат длины вектора ( overrightarrow{AB})
Я так думаю, ты с ними без труда справился? Проверяем:
1. А это на внимательность) Мы уже нашли координаты векторов ( displaystyle {vec{a}}) и ( displaystyle {vec{b}}) ранее: ( displaystyle vec{a}left( 2,6 right),~vec{b}left( 8,4 right)). Тогда вектор ( displaystyle vec{a}-vec{b}) имеет координаты ( displaystyle left( 2-8,6-4 right)=left( -6,2 right)). Квадрат его длины будет равен:
( displaystyle {{d}^{2}}={{left( -6 right)}^{2}}+{{2}^{2}}=36+4=40.)
2. Найдем координаты вектора ( displaystyle overrightarrow{AB}=overrightarrow{AB}left( 8-2,6-4 right)=overrightarrow{AB}left( 6,2 right))
Тогда квадрат его длины равен
( displaystyle {{d}^{2}}={{6}^{2}}+{{2}^{2}}=36+4=40.)
Ничего сложного, правда? Обычная арифметика, не более того.
Следующие задачки нельзя однозначно классифицировать, они скорее на общую эрудицию и на умение рисовать простенькие картинки.
Задача 1. Найдите синус угла наклона отрезка, соединяющего точки ( displaystyle Oleft( 0;~0 right)),( displaystyle Aleft( 6;~8 right)) с осью абсцисс.
Как мы будем поступать здесь?
Нужно найти синус угла между ( displaystyle OA) и осью ( displaystyle Ox).
А где мы умеем искать синус? Верно, в прямоугольном треугольнике.
Так что нам нужно сделать? Построить этот треугольник!
Поскольку координаты точки ( displaystyle A-6) и ( displaystyle 8), то отрезок ( displaystyle OB) равен ( displaystyle 6), а отрезок ( displaystyle AB-8).
Нам нужно найти синус угла ( displaystyle angle AOB).
Напомню тебе, что синус – это отношение противолежащего катета к гипотенузе, тогда
( displaystyle sinangle AOB=frac{AB}{OA})
Что нам осталось сделать?
Найти гипотенузу.
Ты можешь сделать это двумя способами: по теореме Пифагора (катеты-то известны!) или по формуле расстояния между двумя точками (на самом деле одно и то же, что и первый способ!).
Я пойду вторым путем:
( displaystyle OA=sqrt{{{left( 6-0 right)}^{2}}+{{left( 8-0 right)}^{2}}}=10)
Тогда
( displaystyle sinangle AOB=frac{AB}{OA}=frac{8}{10}=0.8)
Ответ: ( displaystyle 0.8)
Следующая задача покажется тебе еще проще. Она – на координаты точки.
Задача 3. В условиях предыдущей задачи найти сумму расстояний от точки ( displaystyle A) до осей координат.
Задача – вообще элементарная, если знать, что такое расстояние от точки до осей.
Ты знаешь?
Я надеюсь, но все же напомню тебе:
Расстояние от точки до осей координат – это длины перпендикуляров, опущенных из точки к осям.
Итак, на моем рисунке, расположенном чуть выше, я уже изобразил один такой перпендикуляр. К какой он оси?
К оси ( displaystyle Ox).
И чему же равна тогда его длина?
Она равна ( displaystyle 8).
Теперь сам проведи перпендикуляр к оси ( displaystyle Oy) и найди его длину. Она будет равна ( displaystyle 6), ведь так?
Тогда их сумма равна ( displaystyle 14).
Ответ: ( displaystyle 14).
Задача 4. В условиях задачи 2, найдите ординату точки, симметричной точке ( displaystyle A) относительно оси абсцисс.
Решение:
Я думаю, тебе интуитивно ясно, что такое симметрия?
Очень многие объекты ею обладают: многие здания, столы, самолеты, многие геометрические фигуры: шар, цилиндр, квадрат, ромб и т. д.
Грубо говоря, симметрию можно понимать вот как: фигура состоит из двух (или более) одинаковых половинок. Такая симметрия называется осевой.
А что тогда такое ось?
Это как раз та линия, по которой фигуру можно, условно говоря, «разрезать» на одинаковые половинки (на данной картинке ось симметрии – прямая ( displaystyle l)):
Теперь давай вернемся к нашей задаче.
Нам известно, что мы ищем точку, симметричную относительно оси ( displaystyle Ox).
Тогда эта ось – ось симметрии.
Значит, нам нужно отметить такую точку ( displaystyle {{A}_{1}}), чтобы ось ( displaystyle Ox) разрезала отрезок ( displaystyle A{{A}_{1}}) на две равные части.
Попробуй сам отметить такую точку. А теперь сравни с моим решением:
У тебя получилось так же?
Хорошо! У найденной точки нас интересует ордината.
Она равна ( displaystyle -8)
Ответ: ( displaystyle -8)
Теперь задачка на параллелограмм:
Задача 5. Точки ( displaystyle Oleft( 0;~0 right),~Aleft( 6;~8 right),~Cleft( 0;~6 right)~) являются вершинами параллелограмма. Найдите ординату точки ( displaystyle B).
Можно решать эту задачу двумя способами: логикой и методом координат.
Я вначале применю метод координат, а потом расскажу тебе, как можно решить иначе.
Совершенно ясно, что абсцисса точки ( displaystyle B) равна ( displaystyle 6). (она лежит на перпендикуляре, проведенной из точки ( displaystyle A) к оси абсцисс).
Нам нужно найти ординату.
Воспользуемся тем, что наша фигура – параллелограмм, это значит, что ( displaystyle CA=OB).
Найдем длину отрезка ( displaystyle CA), используя формулу расстояния между двумя точками:
( d=sqrt{{{left( 6-0 right)}^{2}}+{{left( 8-6 right)}^{2}}}=sqrt{40})
Тогда ( OB=sqrt{40}.~~)
Опускаем перпендикуляр, соединяющий точку ( B) с осью ( Ox).
Точку пересечения обозначу буквой ( D).
Длина отрезка ( OD) равна ( 6). (найди сам задачу, где мы обсуждали этот момент), тогда найдем длину отрезка ( BD) по теореме Пифагора:
( BD=sqrt{40-36}=2)
Длина отрезка – в точности совпадает с его ординатой.
Ответ: ( 2).
Другое решение (я просто приведу рисунок, который его иллюстрирует)
Ход решения:
- Провести ( CE);
- Найти координаты точки ( E) и длину ( AE);
- Доказать, что ( BD=AE).
Еще одна задачка на длину отрезка:
Точки ( Oleft( 0;~0 right),~Aleft( 6;~8 right),~Bleft( 8;~2 right)) являются вершинами треугольника. Найдите длину его средней линии ( CD), параллельной ( OA).
Ты помнишь, что такое средняя линия треугольника?
Тогда для тебя эта задача элементарна. Если не помнишь, то я напомню: средняя линия треугольника – это линия, которая соединяет середины противоположных сторон.
Она параллельна основанию и равна его половине.
Основание – это отрезок ( OA).
Его длину нам приходилось искать ранее, оно равно ( 10).
Тогда длина средней линии вдвое меньше и равна ( 5).
Ответ: ( 5).
Комментарий: эту задачу можно решить и другим способом, к которому мы обратимся чуть позже.
А пока – вот тебе несколько задачек, потренируйся на них, они совсем простые, но помогают «набивать руку», на использовании метода координат!
1. Точки ( Oleft( 0;~0 right),~Aleft( 10;~0 right),~Bleft( 8;~6 right),~Cleft( 2;~6 right)) являются вершинами трапеции. Найдите длину ее средней линии ( DE).
2. Точки ( Oleft( 0;~0 right),~Bleft( 8;~2 right),~Cleft( 2;~6 right)) и ( A) являются вершинами параллелограмма. Найдите ординату точки ( A).
3. Найдите длину отрезка, соединяющего точки ( Aleft( 6 ;~8 right)) и ( Bleft( -2;~2 right).)
4. Найдите площадь закрашенной фигуры на координатной плоскости.
5. Окружность с центром в начале координат проходит через точку ( displaystyle Pleft( 8;text{ }6 right)). Найдите ее радиус.
6. Найдите радиус окружности, описанной около прямоугольника ( displaystyle ABCD), вершины которого имеют координаты соответственно ( displaystyle left( -2;~-2 right),~left( 6;~-2 right),~left( 6;~4 right),~left( -2;~4 right).)
Решения:
1. Известно, что средняя линия трапеции равна полусумме ее оснований.
Основание ( displaystyle CB) равно ( displaystyle 6), а основание ( displaystyle OA-10).
Тогда ( displaystyle ED=frac{CB+OA}{2}=frac{16}{2}=8)
Ответ: ( displaystyle 
2. Проще всего решить эту задачу так: заметить, что ( displaystyle overrightarrow{OA}=overrightarrow{OC}+overrightarrow{OB}) (правило параллелограмма).
Вычислить координаты векторов ( displaystyle overrightarrow{OC}) и ( displaystyle overrightarrow{OB}) не представляет труда: ( displaystyle overrightarrow{OC}left( 2,6 right),~overrightarrow{OB}left( 8,2 right)).
При сложении векторов координаты складываются.
Тогда ( displaystyle overrightarrow{OA}) имеет координаты ( displaystyle left( 10,8 right)).
Эти же координаты имеет и точка ( displaystyle A), поскольку начало вектора ( displaystyle overrightarrow{OA}) – это точка с координатами ( displaystyle left( 0,0 right)).
Нас интересует ордината. Она равна ( displaystyle 8).
Ответ: ( displaystyle 
3. Действуем сразу по формуле расстояния между двумя точками:
( displaystyle d=sqrt{{{left( 6-left( -2 right) right)}^{2}}+{{left( 8-2 right)}^{2}}}=sqrt{64+36}=10)
Ответ: ( displaystyle 10)
4. Посмотри на картинку и скажи, между какими двумя фигурами «зажата» заштрихованная область?
Она зажата между двумя квадратами. Тогда площадь искомой фигуры равна площади большого квадрата минус площадь маленького.
Сторона маленького квадрата – это отрезок, соединяющий точки ( displaystyle left( 0,2 right)) и ( displaystyle left( 2,0 right).) Его длина равна
( displaystyle {{d}_{1}}=sqrt{{{left( 0-2 right)}^{2}}+{{left( 2-0 right)}^{2}}}=sqrt{8})
Тогда площадь маленького квадрата равна
( displaystyle {{S}_{1}}=d_{1}^{2}={{sqrt{8}}^{2}}=8)
Точно так же поступаем и с большим квадратом: его сторона – это отрезок, соединяющий точки ( displaystyle left( 0,4 right)) и ( displaystyle left( 4,0 right).)
Его длина равна
( displaystyle {{d}_{2}}=sqrt{{{left( 0-4 right)}^{2}}+{{left( 4-0 right)}^{2}}}=sqrt{32}).
Тогда площадь большого квадрата равна
( displaystyle {{S}_{2}}=d_{2}^{2}={{sqrt{32}}^{2}}=32)
Площадь искомой фигуры найдем по формуле:
( displaystyle S={{S}_{2}}-{{S}_{1}}=32-8=24)
Ответ: ( displaystyle 24)
5. Если окружность имеет в качестве центра начало координат и проходит через точку ( displaystyle P), то ее радиус ( displaystyle R) будет в точности равен длине отрезка ( displaystyle OP) (сделай рисунок и ты поймешь, почему это очевидно).
Найдем длину этого отрезка:
( displaystyle R=sqrt{{{6}^{2}}+{{8}^{2}}}=10)
Ответ: ( displaystyle 10)
6. Известно, что радиус описанной около прямоугольника окружности равен половине его диагонали.
Найдем длину любой из двух диагоналей (ведь в прямоугольнике они равны!)
( displaystyle left| AC right|=sqrt{{{left( 6-left( -2 right) right)}^{2}}+{{left( 4-left( -2 right) right)}^{2}}}=10)
Тогда
( displaystyle R=frac{1}{2}left| AC right|=5)
Ответ: ( displaystyle 5)
Ну что, ты со всем справился?
Было не очень сложно разобраться, ведь так? Правило здесь одно – уметь сделать наглядную картинку и просто «считать» с нее все данные.
Нам осталось совсем немного. Есть еще буквально два момента, которые бы мне хотелось обсудить:
- как найти координаты середины отрезка и
Координаты середины отрезка
Давай попробуем решить вот такую нехитрую задачку.
Пусть даны две точки ( displaystyle Aleft( {{x}_{1}},{{x}_{2}} right)~) и ( displaystyle Bleft( {{x}_{2}},{{y}_{2}} right)).
Найти координаты середины отрезка ( displaystyle AB). Решение этой задачки следующее: пусть точка ( displaystyle D) – искомая середина, тогда ( displaystyle D) имеет координаты:
( displaystyle Dleft( frac{{{x}_{1}}+{{x}_{2}}}{2},frac{{{y}_{1}}+{{y}_{2}}}{2} right))
То есть: координаты середины отрезка = среднее арифметическое соответствующих координат концов отрезка.
Это правило очень простое и как правило не вызывает затруднений у учащихся. Давай посмотрим, в каких задачках и как оно употребляется:
1. Найдите ординату середины отрезка, соединяющего точки ( displaystyle Aleft( 6,~8 right)~) и ( displaystyle Bleft( -2,~2 right).)
2. Точки ( displaystyle Oleft( 0;~0 right),~Aleft( 6;~8 right),~Bleft( 6;~2 right),~Cleft( 0;~6 right)) являются вершинами четырехугольника. Найдите ординату точки ( displaystyle P) пересечения его диагоналей.
3. Найдите абсциссу центра окружности, описанной около прямоугольника ( displaystyle ABCD), вершины которого имеют координаты соответственно ( displaystyle left( -2;~-2 right),~left( 6;~-2 right),~left( 6;~4 right),~left( -2;~4 right)).
Решения:
1. Первая задачка – просто классика. Действуем сразу по определению середины отрезка. Она имеет координаты ( displaystyle left( frac{6-2}{2},~frac{8+2}{2} right)=left( 2,5 right)).
Ордината равна ( displaystyle 5).
Ответ: ( displaystyle 5)
2. Легко видеть, что данный четырехугольник является параллелограммом (даже ромбом!). Ты и сам можешь это доказать, вычислив длины сторон и сравнив их между собой.
Что я знаю про параллелограмм?
Его диагонали точкой пересечения делятся пополам! Ага! Значит точка пересечения диагоналей – это что?
Это середина любой из диагоналей!
Выберу, в частности диагональ ( displaystyle OA). Тогда точка ( displaystyle P) имеет координаты ( displaystyle left( frac{6+0}{2},frac{8+0}{2} right)=left( 3,4 right).)
Ордината точки ( displaystyle P) равна ( displaystyle 4).
Ответ: ( displaystyle 4)
3. С чем совпадает центр описанной около прямоугольника окружности?
Он совпадает с точкой пересечения его диагоналей. А что ты знаешь про диагонали прямоугольника?
Они равны и точкой пересечения делятся пополам. Задача свелась к предыдущей.
Возьму, например, диагональ ( displaystyle AC). Тогда если ( displaystyle P) – центр описанной окружности, то ( displaystyle P) – середина ( displaystyle AC).
Ищу координаты: ( displaystyle Pleft( frac{-2+6}{2},frac{-2+4}{2} right)=Pleft( 2,1 right).) Абсцисса равна ( displaystyle 2).
Ответ: ( displaystyle 2)
Теперь потренируйся немного самостоятельно, я лишь приведу ответы к каждой задачи, чтобы ты мог себя проверить.
1. Найдите радиус окружности, описанной около треугольника, вершины которого имеют координаты ( displaystyle left( 8;~0 right),~left( 0;~6 right),~left( 8;~6 right).)
2. Найдите ординату центра окружности, описанной около треугольника, вершины которого имеют координаты ( displaystyle left( 8;~0 right),~left( 0;~6 right),~left( 8;~6 right).)
3. Какого радиуса должна быть окружность с центром в точке ( displaystyle Pleft( 8;~6 right),) чтобы она касалась оси абсцисс?
4. Найдите ординату точки пересечения оси ( displaystyle Oy) и отрезка, соединяющего точки ( displaystyle Aleft( 6;text{ }8 right)) и ( displaystyle Bleft( -6;text{ }0 right).)
Ответы:
- ( displaystyle 5);
- ( displaystyle 3);
- ( displaystyle 6);
- ( displaystyle 4).
Умножение векторов
Все удалось? Очень на это надеюсь! Теперь – последний рывок.
Сейчас будь особенно внимателен. Тот материал, который я сейчас буду объяснять, имеет непосредственное отношение не только к простым задачам на метод координат, но также встречается повсеместно и в задачах повышенной сложности.
Какое из своих обещаний я еще не сдержал?
Вспомни, какие операции над векторами я обещал ввести и какие в конечном счете ввел? Я точно ничего не забыл?
Забыл! Забыл объяснить, что значит умножение векторов.
Есть два способа умножить вектор на вектор. В зависимости от выбранного способа у нас будут получаться объекты разной природы:
- Скалярное произведение (результат – число);
- Векторное произведение (результат – вектор).
Векторное произведение выполняется довольно хитро. Как его делать и для чего оно нужно, мы с тобой обсудим чуть позже. А пока мы остановимся на скалярном произведении.
Есть аж два способа, позволяющих нам его вычислить:
- Через координаты векторов;
- Через длины векторов и угол между ними.
Как ты догадался, результат должен быть один и тот же! Итак, давай вначале рассмотрим первый способ:
Найдите скалярное произведение векторов ( displaystyle {vec{a}}) и ( displaystyle {vec{b}})
Справился? Может, и подвох небольшой заметил? Давай проверим:
( displaystyle vec{a}left( 2,6 right)), ( displaystyle vec{b}left( 8,4 right)) – координаты векторов, как в прошлой задаче! Ответ: ( displaystyle 40).
Скалярное произведение через длины векторов и косинус угла между ними
Помимо координатного, есть и другой способ вычислить скалярное произведение, а именно, через длины векторов и косинус угла между ними:
( displaystyle left( vec{a},~vec{b} right)=left| {vec{a}} right|left| {vec{b}} right|coswidehat{vec{a},~vec{b}})
( displaystyle widehat{vec{a},~vec{b}}) – обозначает угол между векторами ( displaystyle {vec{a}}) и ( displaystyle {vec{b}}).
То есть скалярное произведение равно произведению длин векторов на косинус угла между ними.
Зачем же нам эта вторая формула, если у нас есть первая, которая намного проще, в ней по крайней мере нет никаких косинусов?
А нужна она для того, что из первой и второй формулы мы с тобой сможем вывести, как находить угол между векторами!
Пусть ( displaystyle vec{a}left( {{x}_{1}},{{y}_{1}} right),~vec{b}left( {{x}_{2}},{{y}_{2}} right).) Тогда вспоминай формулу для длины вектора!
( displaystyle left| {vec{a}} right|=sqrt{x_{1}^{2}+y_{1}^{2}})
( displaystyle left| {vec{b}} right|=sqrt{x_{2}^{2}+y_{2}^{2}})
Тогда если я подставлю эти данные в формулу скалярного произведения, то я получу:
( displaystyle left( vec{a},~vec{b} right)=sqrt{x_{1}^{2}+y_{1}^{2}}cdot sqrt{x_{2}^{2}+y_{2}^{2}}coswidehat{vec{a},~vec{b}})
Но с другой стороны:
( displaystyle left( vec{a},~vec{b} right)={{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}})
Тогда
( displaystyle {{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}=sqrt{x_{1}^{2}+y_{1}^{2}}cdot sqrt{x_{2}^{2}+y_{2}^{2}}coswidehat{vec{a},~vec{b}})
Или
( displaystyle coswidehat{vec{a},~vec{b}}=frac{{{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}}{sqrt{x_{1}^{2}+y_{1}^{2}}cdot sqrt{x_{2}^{2}+y_{2}^{2}}})
Таким образом, что же мы с тобой получили?
У нас теперь есть формула, позволяющая вычислять угол между двумя векторами! Иногда ее для краткости записывают еще и так:
( displaystyle coswidehat{vec{a},~vec{b}}=frac{left( vec{a},~vec{b} right)}{left| {vec{a}} right|left| {vec{b}} right|})
Решение:
1. Эти вектора – наши старые знакомые. Их скалярное произведение мы уже считали и оно было равно ( displaystyle 40).
Координаты у них такие: ( displaystyle vec{a}left( 2,6 right)), ( displaystyle vec{b}left( 8,4 right)). Тогда найдем их длины:
( left| {vec{a}} right|=sqrt{{{2}^{2}}+{{6}^{2}}}=sqrt{40})
( left| {vec{b}} right|=sqrt{{{8}^{2}}+{{4}^{2}}}=sqrt{80})
Тогда ищем косинус между векторами:
( coswidehat{vec{a},~vec{b}}=frac{left( vec{a},~vec{b} right)}{left| {vec{a}} right|left| {vec{b}} right|}=frac{40}{sqrt{40}sqrt{80}}=frac{sqrt{40}sqrt{40}}{sqrt{40}sqrt{80}}=frac{1}{sqrt{2}})
Косинус какого угла равен ( frac{1}{sqrt{2}})? Это угол ( 45{}^circ ).
Ответ: ( 45)
Ну а теперь сам реши вторую задачу, а потом сравним! Я приведу лишь очень краткое решение:
2. ( vec{a}+vec{b}) имеет координаты ( left( 10,10 right)), ( vec{a}-vec{b}) имеет координаты ( left( -6,2 right)).
( left( vec{a}+vec{b},vec{a}-vec{b} right)=-60+20=-40)
( left| vec{a}+vec{b} right|=sqrt{{{10}^{2}}+{{10}^{2}}}=10sqrt{2})
( left| vec{a}-vec{b} right|=sqrt{{{left( -6 right)}^{2}}+{{2}^{2}}}=sqrt{40}).
Пусть ( a) – угол между векторами ( vec{a}+vec{b}) и ( vec{a}-vec{b}), тогда
( cosa=frac{-40}{10sqrt{2}sqrt{40}}=-frac{sqrt{40}}{10sqrt{2}}=-frac{sqrt{20}}{10}=-frac{sqrt{5}}{5})
Ответ: ( -frac{sqrt{5}}{5})
Метод координат (продвинутый уровень)
Мы с тобой продолжаем изучать метод координат. В прошлой части мы вывели ряд важных формул, которые позволяют:
- Находить координаты вектора;
- Находить длину вектора (альтернативно: расстояние между двумя точками);
- Складывать, вычитать векторы. Умножать их на вещественное число;
- Находить середину отрезка;
- Вычислять скалярное произведение векторов;
- Находить угол между векторами.
Конечно, в эти 6 пунктов не укладывается весь координатный метод.
Он лежит в основе такой науки, как аналитическая геометрия, с которой тебе предстоит познакомиться в ВУЗе. Я лишь хочу построить фундамент, который позволит тебе решать задачи ЕГЭ любого уровня сложности!
Этот раздел будет посвящен методу решения тех задач, в которых будет разумно перейти к методу координат. Эта разумность определяется тем, что в задаче требуется найти, и какая фигура дана.
Когда стоит применять метод координат
Итак, я бы стал применять метод координат, если ставятся вопросы:
- Найти угол между двумя плоскостями;
- Найти угол между прямой и плоскостью;
- Найти угол между двумя прямыми;
- Найти расстояние от точки до плоскости;
- Найти расстояние от точки до прямой;
- Найти расстояние от прямой до плоскости;
- Найти расстояние между двумя прямыми.
Подходящими фигурами для метода координат являются:
- Куб;
- Прямоугольный параллелепипед;
- Прямая призма (треугольная, шестиугольная…);
- Пирамида (треугольная, четырехугольная, шестиугольная);
- Тетраэдр (одно и то же, что и треугольная пирамида).
Неподходящими фигурами для метода координат являются тела вращения:
- шар;
- цилиндр;
- конус
По моему опыту, нецелесообразно использовать метод координат для:
- Нахождения площадей сечений;
- Вычисления объемов тел.
Однако следует сразу отметить, что три «невыгодные» для метода координат ситуации на практике достаточно редки.
В большинстве же задач он может стать твоим спасителем, особенно если ты не очень силен в трехмерных построениях (которые порою бывают довольно замысловатыми).
Как применять метод координат
Какими являются все перечисленные мною выше фигуры?
Они уже не плоские, как, например, квадрат, треугольник, окружность, а объемные! Соответственно, нам нужно рассматривать уже не двухмерную, а трехмерную систему координат.
Строится она достаточно легко: просто помимо оси абсцисс и ординат, мы введем еще одну ось, ось аппликат. На рисунке схематично изображено их взаимное расположение:
Все они являются взаимно перпендикулярными, пересекаются в одной точке ( displaystyle O), которую мы будем называть началом координат.
Ось абсцисс, как и прежде, будем обозначать ( Ox), ось ординат – ( Oy), а введенную ось аппликат – ( Oz).
Если раньше каждая точка на плоскости характеризовалась двумя числами – абсциссой и ординатой, то каждая точка в пространстве уже описывается тремя числами – абсциссой, ординатой, аппликатой.
Например:
Соответственно абсцисса точки ( displaystyle P) равна ( displaystyle 1), ордината – ( displaystyle 2), а аппликата – ( displaystyle 3).
Иногда абсциссу точки еще называют проекцией точки на ось абсцисс, ординату – проекцией точки на ось ординат, а аппликату – проекцией точки на ось аппликат. Соответственно, если задана точка ( Aleft( x,y,z right)) то, точку с координатами:
( Aleft( x,y,0 right)) называют проекцией точки ( Aleft( x,y,z right)) на плоскость ( Oxy)
( Aleft( x,0,z right)) называют проекцией точки ( Aleft( x,y,z right)) на плоскость ( Oxz)
( Aleft( 0,y,z right)) называют проекцией точки ( Aleft( x,y,z right)) на плоскость ( Oyz)
Встает естественный вопрос: справедливы ли все формулы, выведенные для двухмерного случая, в пространстве?
Ответ утвердительный, они справедливы и имеют тот же самый вид. За маленькой деталью. Я думаю, ты уже сам догадался, за какой именно.
Во все формулы мы должны будем добавить еще один член, отвечающий за ось аппликат.
Формулы метода координат для трехмерных фигур
1. Если заданы две точки: ( Aleft( {{x}_{1}},{{y}_{1}},{{z}_{1}} right)), ( Aleft( {{x}_{2}},{{y}_{2}},{{z}_{2}} right)), то:
- Координаты вектора ( overrightarrow{AB}): ( overrightarrow{AB}left( {{x}_{2}}-{{x}_{1}},{{y}_{2}}-{{y}_{1}},{{z}_{2}}-{{z}_{1}} right));
- Расстояние между двумя точками (или длина вектора ( overrightarrow{AB})) ( d=left| overrightarrow{AB} right|=sqrt{{{left( {{x}_{2}}-{{x}_{1}} right)}^{2}}+{{left( {{y}_{2}}-{{y}_{1}} right)}^{2}}+{{left( {{z}_{2}}-{{z}_{1}} right)}^{2}}});
- Середина ( D) отрезка ( AB) имеет координаты
- ( Dleft( frac{{{x}_{1}}+{{x}_{2}}}{2},frac{{{y}_{1}}+{{y}_{2}}}{2},frac{{{z}_{1}}+{{z}_{2}}}{2} right)).
2. Если дано два вектора: ( vec{a}left( {{x}_{1}},{{y}_{1}},{{z}_{1}} right)) и ( vec{b}left( {{x}_{2}},{{y}_{2}},{{z}_{2}} right)), то:
- Их скалярное произведение равно: ( left( vec{a},~vec{b} right)=left| {vec{a}} right|left| {vec{b}} right|cosoverset{}{widehat{vec{a},~vec{b}}},) или ( left( vec{a},~vec{b} right)={{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}+{{z}_{1}}{{z}_{2}});
- Косинус угла между векторами равен:
- ( cosoverset{}{widehat{vec{a},~vec{b}}},=frac{left( vec{a},~vec{b} right)}{left| {vec{a}} right|left| {vec{b}} right|}=frac{{{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}+{{z}_{1}}{{z}_{2}}}{sqrt{x_{1}^{2}+y_{1}^{2}+z_{1}^{2}}cdot sqrt{x_{2}^{2}+y_{2}^{2}+z_{2}^{2}}}).
Плоскость — как «обобщение» прямой
Однако с пространством не все так просто.
Как ты понимаешь, добавление еще одной координаты вносит существенное разнообразие в спектр фигур, «живущих» в этом пространстве. И для дальнейшего повествования мне потребуется ввести некоторое, грубо говоря, «обобщение» прямой.
Этим «обобщением» будет плоскость. Что ты знаешь про плоскость? Попробуй ответить на вопрос, а что такое плоскость? Очень сложно сказать.
Однако мы все интуитивно представляем, как она выглядит:
Грубо говоря, это некий бесконечный «лист», засунутый в пространство. «Бесконечность» следует понимать, что плоскость распространяется во все стороны, то есть ее площадь равна бесконечности.
Однако, это объяснение «на пальцах» не дает ни малейшего представления о структуре плоскости. А нас будет интересовать именно она.
Давай вспомним одну из основных аксиом геометрии: через две различные точки на плоскости проходит прямая, притом только одна.
Или ее аналог в пространстве: через три точки, не лежащие на одной прямой, проходит плоскость, притом только одна.
Уравнение прямой в плоскости и пространстве
Конечно, ты помнишь, как по двум заданным точкам вывести уравнение прямой, это совсем нетрудно: если первая точка имеет координаты: ( Aleft( {{x}_{0}},{{y}_{0}} right)) а вторая ( Bleft( {{x}_{1}},{{y}_{1}} right)), то уравнение прямой будет следующим:
( frac{x-{{x}_{0}}}{{{x}_{1}}-{{x}_{0}}}=frac{y-{{y}_{0}}}{{{y}_{1}}-{{y}_{0}}})
( left( x-{{x}_{0}} right)left( {{y}_{1}}-{{y}_{0}} right)=left( y-{{y}_{0}} right)left( {{x}_{1}}-{{x}_{0}} right))
Это ты проходил еще в 7 классе.
В пространстве уравнение прямой выглядит вот так: пусть у нас даны две точки с координатами: ( Aleft( {{x}_{0}},{{y}_{0}},{{z}_{0}} right)), ( Bleft( {{x}_{1}},{{y}_{1}},{{z}_{1}} right)), то уравнение прямой, через них проходящей, имеет вид:
( frac{x-{{x}_{0}}}{{{x}_{1}}-{{x}_{0}}}=frac{y-{{y}_{0}}}{{{y}_{1}}-{{y}_{0}}}=frac{z-{{z}_{0}}}{{{z}_{1}}-{{z}_{0}}})
Например, через точки ( Aleft( 1,2,3 right)), ( Bleft( 4,5,6 right)) проходит прямая:
( frac{x-1}{4-1}=frac{y-2}{5-2}=frac{z-3}{6-3})
( frac{x-1}{3}=frac{y-2}{3}=frac{z-3}{3})
( x-1=y-2=z-3)
Как это следует понимать?
Это следует понимать вот как: точка ( Dleft( x,y,z right)) лежит на прямой, если ее координаты удовлетворяют следующей системе:
( displaystyle left{ begin{array}{l}x-1=y-2\x-1=z-3end{array} right.)
Нас не очень будет интересовать уравнение прямой, но нам нужно обратить внимание на очень важное понятие направляющего вектора прямой.
Направляющий вектор прямой
Направляющий вектор прямой – любой ненулевой вектор, лежащий на данной прямой или параллельный ей.
Например, оба вектора ( overrightarrow{{{M}_{0}}{{M}_{1}}}), ( vec{s}) являются направляющими векторами прямой ( l). Пусть ( Mleft( {{x}_{0}},{{y}_{0}},{{z}_{0}} right)) – точка, лежащая на прямой, а ( vec{p}left( m,n,q right)) – ее направляющий вектор.
Тогда уравнение прямой можно записать в следующем виде:
( frac{x-{{x}_{0}}}{m}=frac{y-{{y}_{0}}}{n}=frac{z-{{z}_{0}}}{p})
Еще раз повторюсь, мне не очень будет интересно уравнение прямой, но мне очень нужно, чтобы ты запомнил, что такое направляющий вектор!
Еще раз: это ЛЮБОЙ ненулевой вектор, лежащий на прямой, или параллельный ей.
Уравнение плоскости
Вывести уравнение плоскости по трем заданным точкам уже не так тривиально, и обычно этот вопрос не рассматривается в курсе средней школы.
А зря!
Этот прием жизненно необходим, когда мы прибегаем к методу координат для решения сложных задач. Однако, я предполагаю, что ты полон желания научиться чему-то новому?
Более того, ты сможешь поразить своего преподавателя в ВУЗе, когда выяснится, что ты уже умеешь с методикой, которую обычно изучают в курсе аналитической геометрии. Итак, приступим.
Уравнение плоскости не слишком отличается от уравнения прямой на плоскости, а именно оно имеет вид:
( Ax+By+Cz+D=0)
( A,B,C,D-) некоторые числа (не все равные нулю), а ( x,y,z-~) переменные, например: ( 3x+2y-z+1=0,~0.5x-2z-2=0,~x+y=0) и т.д.
Как видишь, уравнение плоскости не очень отличается от уравнения прямой (линейной функции). Однако, вспомни, что мы с тобой утверждали? Мы говорили, что если у нас есть три точки ( Aleft( {{x}_{0}},{{y}_{0}},{{z}_{0}} right),~Bleft( {{x}_{1}},{{y}_{1}},{{z}_{1}} right),~Cleft( {{x}_{2}},{{y}_{2}},{{z}_{2}} right)), не лежащие на одной прямой, то уравнение плоскости однозначно по ним восстанавливается.
Но как? Попробую тебе объяснить.
Поскольку уравнение плоскости имеет вид:
( Ax+By+Cz+D=0)
А точки ( Aleft( {{x}_{0}},{{y}_{0}},{{z}_{0}} right),~Bleft( {{x}_{1}},{{y}_{1}},{{z}_{1}} right),~Cleft( {{x}_{2}},{{y}_{2}},{{z}_{2}} right)) принадлежат этой плоскости, то при подстановке координат каждой точки в уравнение плоскости мы должны получать верное тождество:
( A{{x}_{0}}+B{{y}_{0}}+C{{z}_{0}}+D=0)
( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D=0)
( A{{x}_{2}}+B{{y}_{2}}+C{{z}_{2}}+D=0)
Таким образом, встает необходимость решать три уравнения аж с ( displaystyle 4) неизвестными!
Дилемма! Однако всегда можно предполагать, что ( D=1) (для этого нужно разделить ( ~Ax+By+Cz+D=0) на ( D)).
Таким образом, мы получим три уравнения с тремя неизвестными ( displaystyle A,B,C):
( A{{x}_{0}}+B{{y}_{0}}+C{{z}_{0}}+1=0)
( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+1=0)
( A{{x}_{2}}+B{{y}_{2}}+C{{z}_{2}}+1=0)
Однако мы не будем решать такую систему, а выпишем загадочное выражение, которое из него следует:
Уравнение плоскости, проходящей через три заданные точки
(left| {begin{array}{*{20}{c}}{x — {x_0}}&{{x_1} — {x_0}}&{{x_2} — {x_0}}\{y — {y_0}}&{{y_1} — {y_0}}&{{y_2} — {y_0}}\{z — {z_0}}&{{z_1} — {z_0}}&{{z_2} — {z_0}}end{array}} right| = 0)
Стоп! Это еще что такое? Какой-то очень необычный модуль!
Однако объект, который ты видишь перед собой не имеет ничего общего с модулем. Этот объект называется определителем третьего порядка.
Определитель третьего порядка
Отныне и впредь, когда ты будешь иметь дело с методом координат на плоскости, тебе очень часто будут встречаться эти самые определители.
Что же такое определитель третьего порядка? Как ни странно, это всего-навсего число. Осталось понять, какое конкретно число мы будем сопоставлять с определителем.
Давай вначале запишем определитель третьего порядка в более общем виде:
( left| {begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}&{{a_{13}}}\{{a_{21}}}&{{a_{22}}}&{{a_{23}}}\{{a_{31}}}&{{a_{32}}}&{{a_{33}}}end{array}} right|),
Где ( {{a}_{ij}}) – некоторые числа.
Причем под первым индеком ( displaystyle i) мы понимаем номер строки, а под индеком ( displaystyle j) – номер столбца.
Например, ( {{a}_{23}}) означает, что данное число стоит на пересечении второй строки и третьего столбца.
Давай поставим следующий вопрос: каким именно образом мы будем вычислять такой определитель?
То есть, какое конкретно число мы будем ему сопоставлять?
Для определителя именно третьего порядка есть эвристическое (наглядное) правило треугольника оно выглядит следующим образом:
Как его читать? А понимать его надо следующим образом: мы составляем два выражения:
- Произведение элементов главной диагонали (с верхнего левого угла до нижнего правого) ( displaystyle +) произведение элементов, образующих первый треугольник «перпендикулярный» главной диагонали ( displaystyle +) произведение элементов, образующих второй треугольник «перпендикулярный» главной диагонали;
- Произведение элементов побочной диагонали (с верхнего правого угла до нижнего левого) ( displaystyle +) произведение элементов, образующих первый треугольник «перпендикулярный» побочной диагонали ( displaystyle +) произведение элементов, образующих второй треугольник «перпендикулярный» побочной диагонали;
- Тогда определитель равен разности значений, полученных на шаге ( displaystyle 1) и ( displaystyle 2).
Если записать все это цифрами, то мы получим следующее выражение:
( left| {begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}&{{a_{13}}}\{{a_{21}}}&{{a_{22}}}&{{a_{23}}}\{{a_{31}}}&{{a_{32}}}&{{a_{33}}}end{array}} right| = )
( = {a_{11}}{a_{22}}{a_{33}} + {a_{12}}{a_{23}}{a_{31}} + {a_{21}}{a_{32}}{a_{13}} — left( {{a_{13}}{a_{22}}{a_{31}} + {a_{23}}{a_{32}}{a_{11}} + {a_{21}}{a_{12}}{a_{33}}} right))
Тем не менее, запоминать способ вычисления в таком виде не нужно, достаточно в голове просто держать треугольники и саму идею, что с чем складывается и что из чего затем вычитается).
Давай проиллюстрируем метод треугольников на примере:
Метод треугольников на примере
1. Вычислить определитель: ( left| {begin{array}{*{20}{c}}2&3&{ — 1}\{11}&{21}&{ — 5}\4&6&9end{array}} right|)
Давай разбираться, что мы складываем, а что – вычитаем.
Слагаемые, которые идут с «плюсом»:
Это главная диагональ: произведение элементов равно
( 2cdot 21cdot 9=378)
Первый треугольник, «перпендикулярный главной диагонали: произведение элементов равно
( 3cdot left( -5 right)cdot 4=-60)
Второй треугольник, «перпендикулярный главной диагонали: произведение элементов равно
( 11cdot 6cdot left( -1 right)=-66)
Складываем три числа: ( 378-60-66=252)
Слагаемые, которые идут с «минусом»:
Это побочная диагональ: произведение элементов равно
( left( -1 right)cdot 21cdot 4=-84)
Первый треугольник, «перпендикулярный побочной диагонали: произведение элементов равно
( 3cdot 11cdot 9=297)
Второй треугольник, «перпендикулярный побочной диагонали: произведение элементов равно
( 6cdot left( -5 right)cdot 2=-60)
Складываем три числа:
( -84+297-60=153)
Все, что осталось сделать – это вычесть из суммы слагаемых «с плюсом» сумму слагаемых «с минусом»:
( 252-153=99)
Таким образом,
( left| {begin{array}{*{20}{c}}2&3&{ — 1}\{11}&{21}&{ — 5}\4&6&9end{array}} right| = 99)
Как видишь, ничего сложного и сверхъестественного в вычислении определителей третьего порядка нет. Просто важно помнить про треугольники и не допускать арифметических ошибок.
Теперь попробуй самостоятельно вычислить:
( left| {begin{array}{*{20}{c}}2&{ — 2}&4\3&2&5\1&2&2end{array}} right|)
Проверяем:
- Главная диагональ: ( 2cdot 2cdot 2=8);
- Первый треугольник, перпендикулярный главной диагонали: ( left( -2 right)cdot 5cdot 1=-10);
- Второй треугольник, перпендикулярный главной диагонали: ( 3cdot 2cdot 4=24);
- Сумма слагаемых с плюсом: ( 8-10+24=22);
- Побочная диагональ: ( 1cdot 2cdot 4=8);
- Первый треугольник, перпендикулярный побочной диагонали: ( 2cdot 5cdot 2=20);
- Второй треугольник, перпендикулярный побочной диагонали: ( left( -2 right)cdot 3cdot 2=-12);
- Сумма слагаемых с минусом: ( 8+20-12=16);
- Сумма слагаемых с плюсом минус сумма слагаемых с минусом: ( 22-16=6).
Вывод:
( left| {begin{array}{*{20}{c}}2&{ — 2}&4\3&2&5\1&2&2end{array}} right| = 6)
Вот тебе еще пара определителей, вычисли их значения самостоятельно и сравни с ответами:
- ( left| {begin{array}{*{20}{c}}1&3&{ — 1}\0&4&2\{ — 3}&2&0end{array}} right|);
- ( left| {begin{array}{*{20}{c}}3&1&7\6&2&{14}\{ — 1}&0&8end{array}} right|).
Ответы:
- ( displaystyle -34);
- ( displaystyle 0).
Ну что, все совпало?
Отлично, тогда можно двигаться дальше! Если же есть затрудения, то совет мой таков: в интернете есть куча программ вычисления определителя онлайн.
Все, что тебе нужно – придумать свой определитель, вычислить его самостоятельно, а потом сравнить с тем, что посчитает программа.
И так до тех пор, пока результаты не начнут совпадать. Уверен, этот момент не заставит себя долго ждать!
Теперь давай вернемся к тому определителю, который я выписал, когда говорил про уравнение плоскости, проходящей через три заданные точки:
( left| {begin{array}{*{20}{c}}{x — {x_0}}&{{x_1} — {x_0}}&{{x_2} — {x_0}}\{y — {y_0}}&{{y_1} — {y_0}}&{{y_2} — {y_0}}\{z — {z_0}}&{{z_1} — {z_0}}&{{z_2} — {z_0}}end{array}} right| = 0)
Все, что тебе нужно – это вычислить его значение непосредственно (методом треугольников) и приравнять результат к нулю.
Естественно, поскольку ( displaystyle x,y,z) – переменные, то ты получишь некоторое выражение, от них зависящее.
Именно это выражение и будет уравнением плоскости, проходящей через три заданные точки, не лежащие на одной прямой!
( Ax+By+Cz+D=0)
Давай проиллюстрируем сказанное на простом примере:
1. Построить уравнение плоскости, проходящей через точки
( displaystyle {{M}_{1}}left( -3,2,-1 right), {{M}_{2}}left( -1,2,4 right), {{M}_{3}}left( 3,3,-1 right))
Cоставляем для этих трех точек определитель:
( left| {begin{array}{*{20}{c}}{x — left( { — 3} right)}&{ — 1 — left( { — 3} right)}&{3 — left( { — 3} right)}\{y — 2}&{2 — 2}&{3 — 2}\{z — left( { — 1} right)}&{4 — left( { — 1} right)}&{ — 1 — left( { — 1} right)}end{array}} right|).
Упрощаем:
( left| {begin{array}{*{20}{c}}{x + 3}&2&6\{y — 2}&0&1\{z + 1}&5&0end{array}} right|)
Теперь вычисляем его непосредственно по правилу треугольников:
[{left| {begin{array}{*{20}{c}}{x + 3}&2&6\{y — 2}&0&1\{z + 1}&5&0end{array}} right| = left( {x + 3} right) cdot 0 cdot 0 + 2 cdot 1 cdot left( {z + 1} right) + left( {y — 2} right) cdot 5 cdot 6 — }]
( displaystyle -left( left( z+1 right)cdot 6cdot 0+left( x+3 right)cdot 5cdot 1+left( y-2 right)cdot 2cdot 0 right)=)
( displaystyle=2left( z-1 right)+30left( y-2 right)-5left( x+3 right)=-5x+30y+2z-73)
Таким образом, уравнение плоскости, проходящей через точки ( displaystyle {{M}_{1}}left( -3,2,-1 right), {{M}_{2}}left( -1,2,4 right), {{M}_{3}}left( 3,3,-1 right)), имеет вид:
( -5x+30y+2z-73=0)
То есть ( A=-5,~B=30,~C=2,~D=-73)
Теперь попробуй решить одну задачку самостоятельно, а потом мы ее обсудим:
2. Найти уравнение плоскости, проходящей через точки
( {{M}_{1}}left( 1,2,-1 right),~{{M}_{2}}left( -1,0,4 right),~{{M}_{3}}left( -2,-1,1 right))
Ну что, давай теперь обсудим решение:
Составляем определитель:
( left| {begin{array}{*{20}{c}}{x — 1}&{ — 2}&{ — 3}\{y — 2}&{ — 2}&{ — 3}\{z + 1}&5&2end{array}} right|)
И вычисляем его значение:
( begin{array}{l}left| {begin{array}{*{20}{c}}{x — 1}&{ — 2}&{ — 3}\{y — 2}&{ — 2}&{ — 3}\{z + 1}&5&2end{array}} right| = \ = — 4left( {x — 1} right) — 15left( {y — 2} right) + 6left( {z + 1} right) + 15left( {x — 1} right) + 4left( {y — 2} right) — 6left( {z + 1} right) = \ = 11x — 11y + 11end{array})
Тогда уравнение плоскости имеет вид:
( 11x-11y+11=0)
Или же, сократив на ( 11), получим:
( x-y+1=0)
То есть, ( A=1,B=-1,C=0,D=1.)
Теперь две задачи для самоконтроля:
- Построить уравнение плоскости, проходящей через три точки: ( Kleft( 2,3,4 right),~Lleft( 6,-3,4 right),~Mleft( -4,6,-4 right).);
- Построить уравнение плоскости, проходящей через три точки:
- ( Aleft( 5,-1,3 right),~Bleft( 2,2,0 right),~Cleft( -1,1,1 right).).
Проверим:
- ( 6x+4y-3z-12=0);
- ( y+z-2=0).
Все совпало?
Опять-таки, если есть определенные затруднения, то мой совет таков: берешь из головы три точки (с большой степенью вероятности они не будут лежать на одной прямой), строишь по ним плоскость.
А потом проверяешь себя онлайн. Например, на сайте:
http://www.webmath.ru/web/prog9_1.php
Однако при помощи определителей мы будем строить не только уравнение плоскости.
Вспомни, я говорил тебе, что для векторов определено не только скалярное произведение. Есть еще векторное, а также смешанное произведение.
Векторное произведение векторов
И если скалярным произведением двух векторов и будет число, то векторным произведением двух векторов ( vec{a}) и ( vec{b}) будет вектор ( ~vec{c}=vec{a}cdot vec{b}), причем данный вектор будет перпендикулярен к заданным:
Причем его модуль будет равен площади параллелограмма, построенного на векторах ( vec{a}) и ( vec{b}).
Данный вектор понадобится нам для вычисления расстояния от точки до прямой. Как же нам считать векторное произведение векторов ( vec{a}) и ( vec{b}), если их координаты заданы?
На помощь к нам опять приходит определитель третьего порядка.
Однако, прежде чем я перейду к алгоритму вычисления векторного произведения, я вынужден сделать небольшое лирическое отступление.
Данное отступление касается базисных векторов.
Базисными векторами в трехмерном пространстве называются три вектора:
( vec{i}left( 1,0,0 right),~vec{j}left( 0,1,0 right),~vec{k}left( 0,0,1 right))
Схематично они изображены на рисунке:
Как ты думаешь, а почему они называется базисными? Дело в том, что любой вектор в трехмерном пространстве можно представить через сумму трех базисных векторов:
( vec aleft( {x,y,z} right) = x cdot vec i + y cdot vec j + z cdot vec k.)
Или на картинке:
Справедливость этой формулы очевидна, ведь:
( begin{array}{l}xcdot vec{i}=left( x,0,0 right)\ycdot vec{j}=left( 0,y,0 right)\zcdot vec{k}=left( 0,0,z right)end{array})
Тогда
( vec{a}left( x,y,z right)=xcdot vec{i}+ycdot vec{j}+zcdot vec{k}=left( x,0,0 right)+left( 0,y,0 right)+left( 0,0,z right)=left( x,y,z right)=vec{a}.)
Смешанное произведение трех векторов
Последняя конструкция, которая мне понадобится – это смешанное произведение трех векторов.
Оно, как и скалярное, является числом. Есть два способа его вычисления. ( displaystyle 1) – через определитель, ( displaystyle 2) – через смешанное произведение.
А именно, пусть у нас даны три вектора:
( vec{a}left( {{x}_{1}},{{y}_{1}},{{z}_{1}} right),~vec{b}left( {{x}_{2}},{{y}_{2}},{{z}_{2}} right),~vec{c}left( {{x}_{3}},{{y}_{3}},{{z}_{3}} right)), тогда смешанное произведение трех векторов, обозначаемое через ( (vec{a},vec{b},vec{c})) можно вычислить как:
1. ( left( vec{a},vec{b},vec{c} right)=left( vec{a},vec{b}cdot vec{c} right)) – то есть смешанное произведение – это скалярное произведения вектора на векторное произведение двух других векторов
2. ( left( {vec a,vec b,vec c} right) = left| {begin{array}{*{20}{c}}{{x_1}}&{{y_1}}&{{z_1}}\{{x_2}}&{{y_2}}&{{z_2}}\{{x_3}}&{{y_3}}&{{z_3}}end{array}} right|)
Например, смешанное произведение трех векторов ( vec{a}left( 2,3,5 right),~vec{b}left( 1,4,4 right),~vec{c}left( 3,5,7 right)) равно:
( left( {vec a,vec b,vec c} right) = left| {begin{array}{*{20}{c}}2&3&5\1&4&4\3&5&7end{array}} right| = — 4)
Самостоятельно попробуй вычислить его через векторное произведение и убедись, что результаты совпадут!
И опять – два примера для самостоятельного решения:
- ( vec{a}left( 1,2,3 right),~vec{b}left( 1,1,1 right),~vec{c}left( 1,2,1 right));
- ( vec{a}left( 1,2,3 right),~vec{b}left( 1,-1,1 right),~vec{c}left( 2,0,-1 right)).
Ответы:
- ( displaystyle 2);
- ( displaystyle 1).
Выбор системы координат
Ну вот, теперь у нас есть весь необходимый фундамент знаний, чтобы решать сложные стереометрические задачи по геометрии.
Однако прежде чем приступать непосредственно к примерам и алгоритмам их решения, я считаю, что будет полезно остановиться еще вот на каком вопросе: как именно выбирать систему координат для той или иной фигуры.
Ведь именно выбор взаимного расположения системы координат и фигуры в пространстве в конечном счете определит, насколько громоздкими будут вычисления.
Я напомню, что в этом разделе мы рассматриваем следующие фигуры:
- куб;
- Прямоугольный параллелепипед;
- Прямая призма (треугольная, шестиугольная…);
- Пирамида (треугольная, четырехугольная);
- Тетраэдр (одно и то же, что и треугольная пирамида).
Для каждой из фигур я дам практические рекомендации, как выбирать систему координат.
Я неслучайно расположил задачи в таком порядке. Пока ты еще не успел начать ориентироваться в методе координат, я сам разберу наиболее «проблемные» фигуры, а тебе предоставлю разобраться с простейшим кубом!
Постепенно тебе предстоит научиться работать со всеми фигурами, сложность задач я буду увеличивать от теме к теме.
Приступаем к решению задач:
1. Рисуем тетраэдр, помещаем его в систему координат так, как я предлагал ранее. Поскольку тетраэд правильный – то все его грани (включая основание) – правильные треугольники.
Поскольку нам не дана длина стороны, то я могу принять ее равной ( 1). Я думаю, ты понимаешь, что угол на самом деле не будет зависеть от того, насколько наш тетраэдр будет «растянут»?
Также проведу в тетраэдре высоту и медиану ( displaystyle BM).
Попутно я нарисую его основание (оно нам тоже пригодится).
Мне нужно найти угол между ( displaystyle DH) и ( displaystyle BM). Что нам известно?
Нам известна только координата точки ( displaystyle B). Значит, надо найти еще координаты точек ( displaystyle D,H,M).
Теперь думаем: точка ( displaystyle H) – это точка пересечения высот (или биссектрисс или медиан) треугольника ( displaystyle ABC).
А точка ( displaystyle D) – это приподнятая точка ( displaystyle H).
Точка же ( displaystyle M) – это середина отрезка ( displaystyle AD).
Тогда окончательно нам надо найти: координаты точек: ( displaystyle A,D,H,M).
Начнем с самого простого: координаты точки ( displaystyle A).
Смотри на рисунок: Ясно, что аппликата точки ( displaystyle A) равна нулю (точка лежит на плоскости ( displaystyle Oxy)).
Её ордината равна ( displaystyle 0,5) (так как ( displaystyle AK) – медиана).
Сложнее найти ее абсциссу. Однако это легко делается на основании теоремы Пифагора: Рассмотрим треугольник ( displaystyle BAS). Его гипотенуза ( displaystyle BA) равна ( displaystyle 1), а один из катетов ( displaystyle AS) равен ( displaystyle 0,5)
Тогда:
( BS=sqrt{B{{A}^{2}}-A{{S}^{2}}}=sqrt{1-frac{1}{4}}=frac{sqrt{3}}{2})
Окончательно имеем: ( Aleft( frac{sqrt{3}}{2},frac{1}{2},0 right)).
Теперь найдем координаты точки ( displaystyle H).
Ясно, что ее аппликата опять равна нулю, а ее ордината такая же, как у точки ( displaystyle A), то есть ( 0,5).
Найдем ее абсциссу. Это делается достаточно тривиально, если помнить, что высоты равностороннего треугольника точкой пересечения делятся в пропорции ( displaystyle mathbf{2}:mathbf{1}), считая от вершины. Так как: ( AK=BS=frac{sqrt{3}}{2}), то искомая абсцисса точки, равная длине отрезка ( displaystyle KH), равна: ( KH=frac{AK}{3}=frac{sqrt{3}}{6}). Т
аким образом, координаты точки ( displaystyle H) равны:
( Hleft( frac{sqrt{3}}{6},frac{1}{2},0 right).)
Найдем координаты точки ( displaystyle D).
Ясно, что ее абсцисса и ордината совпадают с абсциссой и ординатой точки ( displaystyle H). А аппликата равна длине отрезка ( displaystyle DH). ( displaystyle DH) – это один из катетов треугольника ( displaystyle DAH). Гипотенуза треугольника ( displaystyle DAH) – это отрезок ( AD=AB=1.) ( displaystyle AH) – катет.
Он ищется из соображений, которые я выделил жирным шрифтом:
( AH=frac{2}{3}cdot frac{sqrt{3}}{2}=frac{sqrt{3}}{3})
Тогда:
( DH=sqrt{1-{{left( frac{sqrt{3}}{3} right)}^{2}}}=sqrt{frac{2}{3}})
Отсюда:
( Dleft( frac{sqrt{3}}{6},frac{1}{2},sqrt{frac{2}{3}} right).)
Точка ( M) – это середина отрезка ( AD). Тогда нам нужно вспомнить формулу координат середины отрезка:
( Mleft( frac{frac{sqrt{3}}{2}+frac{sqrt{3}}{6}}{2},~frac{frac{1}{2}+frac{1}{2}}{2},frac{0+sqrt{frac{2}{3}}}{2} right)=Mleft( frac{sqrt{3}}{3},frac{1}{2},frac{1}{sqrt{6}} right).~)
Ну все, теперь мы можем искать координаты направляющих векторов:
( overrightarrow{BM}left( frac{sqrt{3}}{3},frac{1}{2},frac{1}{sqrt{6}} right))
( overrightarrow{DH}left( 0,0,-sqrt{frac{2}{3}} right))
Ну что, все готово: подставляем все данные в формулу:
( displaystyle cosvarphi =frac{left| frac{1}{sqrt{6}}cdot left( -sqrt{frac{2}{3}} right) right|}{sqrt{{{left( frac{sqrt{3}}{3} right)}^{2}}+{{left( frac{1}{2} right)}^{2}}+{{left( frac{1}{sqrt{6}} right)}^{2}}}cdot sqrt{{{left( -sqrt{frac{2}{3}} right)}^{2}}}}=frac{frac{1}{3}}{sqrt{frac{19}{36}}cdot sqrt{frac{2}{3}}}=frac{frac{1}{3}}{sqrt{frac{19}{54}}}=frac{sqrt{54}}{3sqrt{19}}=sqrt{frac{6}{19}})
Таким образом, ( varphi =arccossqrt{frac{6}{19}}.)
Ответ: ( varphi =arccossqrt{frac{6}{19}}.)
Тебя не должны пугать такие «страшные» ответы: для задач С2 это обычная практика. Я бы скорее удивился «красивому» ответу в этой части. Также, как ты заметил, я практически не прибегал ни к чему, кроме как к теореме Пифагора и свойству высот равностороннего треугольника. То есть для решения стереометрической задачи я использовал самый минимум стереометрии. Выигрыш в этом частично «гасится» достаточно громоздкими вычислениями. Зато они достаточно алгоритмичны!
2. Изобразим правильную шестиугольную пирамиду вместе с системой координат, а также ее основание:
Нам нужно найти угол между прямыми ( displaystyle SB) и ( displaystyle CD).
Таким образом, наша задача сводится к поиску координат точек: ( displaystyle S,B,C,D).
Координаты последних трех мы найдем по маленькому рисунку, а коодинату вершины ( displaystyle S) найдем через координату точки ( displaystyle O).
Работы навалом, но надо к ней приступать!
a) Координата ( displaystyle D): ясно, что ее аппликата и ордината равны нулю.
Найдем абсциссу. Для этого рассмотрим прямоугольный треугольник ( displaystyle EDP). Увы, в нем нам известна только гипотенуза, которая равна ( displaystyle 1). Катет ( displaystyle DP) мы будем стараться отыскать (ибо ясно, что удвоенная длина катета ( displaystyle DP) даст нам абсциссу точки ( displaystyle D)).
Как же нам ее искать?
Давай вспомним, что за фигура у нас лежит в основании пирамиды? Это правильный шестиугольник.
А что это значит? Это значит, что у него все стороны и все углы равны. Надо бы найти один такой угол. Есть идеи?
Идей масса, но есть формула:
Сумма углов правильного n-угольника равна ( left( n-2 right)cdot 180{}^circ ).
Таким образом, сумма углов правильного шестиугольника равна ( displaystyle 720) градусов. Тогда каждый из углов равен:
( frac{720{}^circ }{6}=120{}^circ )
Вновь смотрим на картинку.
Ясно, что отрезок ( displaystyle EB) – биссектрисса угла ( displaystyle DEF). Тогда угол ( displaystyle DEP) равен ( displaystyle 60) градусам.
Тогда:
( sin60{}^circ =frac{sqrt{3}}{2}=frac{DP}{ED}=frac{DP}{1}=DP)
Тогда ( DP=frac{sqrt{3}}{2}), откуда ( DF=2DP=sqrt{3}).
Таким образом, ( displaystyle D) имеет координаты ( Dleft( sqrt{3},0,0 right))
b) Теперь легко найдем координату точки ( C): ( Cleft( sqrt{3},1,0 right)).
c) Найдем координаты точки ( displaystyle B).
Так как ее абсцисса совпадает с длиной отрезка ( FP) то она равна ( frac{sqrt{3}}{2}).
Найти ординату тоже не очень сложно: если мы соединим точки ( displaystyle C) и ( displaystyle A) а точку пересечения прямой ( displaystyle AC) обозначим, скажем за ( displaystyle M). (сделай сам несложное построение). Тогда ( BM=EP.)
Таким образом, ордината точки B равна сумме длин отрезков ( PM+MB). Вновь обратимся к треугольнику ( displaystyle DEP).
Тогда
( frac{1}{2}=cos60{}^circ =frac{EP}{ED}=EP)
Тогда так как ( PM=DC=1,~mo~PB=1+frac{1}{2}=frac{3}{2}.) Тогда точка ( B) имеет координаты ( Bleft( frac{sqrt{3}}{2},frac{3}{2},0 right).)
d) Теперь найдем координаты точки ( displaystyle O).
Рассмотри прямоугольник ( displaystyle ACDF) и докажи, что ( PO=frac{1}{2}.)
Таким образом, координаты точки ( displaystyle O): ( Oleft( frac{sqrt{3}}{2},frac{1}{2},0 right).)
e) Осталось найти координаты вершины ( S). Ясно, что ее абсцисса и ордината совпадает с абсциссой и ординатой точки ( O).
Найдем аппликату. Так как ( FC=EB=2), то ( OF=1). Рассмотрим прямоугольный треугольник ( displaystyle OFS). По условию задачи боковое ребро ( FS=2). Это гипотенуза моего треугольника.
Тогда высота пирамиды ( displaystyle OS) – катет.
( OS=sqrt{F{{S}^{2}}-O{{F}^{2}}}=sqrt{4-1}=sqrt{3})
Тогда точка ( S) имеет координаты: ( Sleft( frac{sqrt{3}}{2},frac{1}{2},sqrt{3} right).)
Ну все, у меня есть координаты всех интересующих меня точек. Ищу координаты направляющих векторов прямых:
( overrightarrow{SB}left( frac{sqrt{3}}{2}-frac{sqrt{3}}{2},frac{1}{2}-frac{3}{2},sqrt{3}-0 right)=overrightarrow{SB}left( 0,-1,sqrt{3} right).)
( overrightarrow{CD}left( sqrt{3}-sqrt{3},0-1,0 right)=overrightarrow{CD}left( 0,-1,0 right).)
Ищем угол между этими векторами:
( cosvarphi =frac{left| 0+left( -1 right)cdot left( -1 right)+sqrt{3}cdot 0 right|}{sqrt{{{left( -1 right)}^{2}}+{{left( sqrt{3} right)}^{2}}}cdot sqrt{{{left( -1 right)}^{2}}}}=frac{1}{2})
Тогда ( varphi =arccos left( frac{1}{2} right)=60{}^circ )
Ответ: ( 60{}^circ )
Опять-таки, при решении этой задачи я не использовал никаких изошренных приемов, кроме формулы суммы углов правильного n-угольника, а также определения косинуса и синуса прямоугольного треугольника.
3. Поскольку нам опять не даны длины ребер в пирамиде, то я буду считать их равными единице.
Таким образом, поскольку ВСЕ ребра, а не только боковые, равны между собой, то в основании пирамиды и меня лежит квадрат, а боковые грани – правильные треугольники.
Изобразим такую пирамиду, а также ее основание на плоскости, отметив все данные, приведенные в тексте задачи:
Ищем угол между ( displaystyle BM) и ( displaystyle PH).
Я буду делать очень краткие выкладки, когда буду заниматься поиском координат точек. Тебе необходимо будет «расшифровать» их:
a) ( Bleft( 0,1,0 right))
b) ( displaystyle H) – середина отрезка ( displaystyle AC). Её координаты:
( Hleft( frac{1}{2},frac{1}{2},0 right))
c) Длину отрезка ( displaystyle AH) я найду по теореме Пифагора в треугольнике ( displaystyle AHD). ( AH=frac{sqrt{2}}{2}.) Найду ( displaystyle PH) по теореме Пифагора в треугольнике ( displaystyle AHP).
( PH=sqrt{1-frac{1}{2}}=frac{1}{sqrt{2}})
Координаты ( P): ( Pleft( frac{1}{2},frac{1}{2},frac{1}{sqrt{2}} right).)
d) ( M) – середина отрезка ( AP). Ее координаты равны ( Mleft( frac{1}{4},frac{1}{4},frac{1}{2sqrt{2}} right).)
e) Координаты вектора ( overrightarrow{PH}:~overrightarrow{PH}left( 0,0,-frac{1}{sqrt{2}} right).~)
f) Координаты вектора ( overrightarrow{BM}:~overrightarrow{BM}left( frac{1}{4},-frac{3}{4},frac{1}{2sqrt{2}} right).)
g) Ищем угол: ( cosvarphi =frac{frac{1}{4}}{frac{1}{sqrt{2}}cdot frac{sqrt{3}}{2}}=frac{1}{sqrt{6}})
h) Ответ: ( arccosfrac{1}{sqrt{6}})
Куб – простейшая фигура. Я уверен, что с ней ты разберешься самостоятельно. Ответы к задачам 4 и 5 следующие:
4. ( arccosfrac{4}{sqrt{30}})
5. ( arccosfrac{1}{sqrt{15}})
Нахождение угла между прямой и плоскостью
Ну что, время простых задачек окончено!
Теперь примеры будут еще сложнее. Для отыскания угла между прямой и плоскостью мы будем поступать следующим образом:
- По трем точкам строим уравнение плоскости: ( Ax+By+Cz+D=0), используя определитель третьего порядка;
- По двум точкам ищем координаты направляющего вектора прямой: ( vec{s}left( l,m,n right));
- Применяем формулу для вычисления угла между прямой и плоскостью: ( sinvarphi =frac{left| Al+Bm+Cn right|}{sqrt{{{A}^{2}}+{{B}^{2}}+{{C}^{2}}~}cdot sqrt{{{l}^{2}}+{{m}^{2}}+{{n}^{2}}}})
Как видишь, эта формула очень похожа на ту, что мы применяли для поиска углов между двумя прямыми.
Структура правой части просто одинакова, а слева мы теперь ищем синус, а не косинус, как раньше. Ну и добавилось одно противное действие – поиск уравнения плоскости.
Опять я решу первые две задачи подробно, третью – кратко, а последние две оставляю тебе для самостоятельного решения.
К тому же тебе уже приходилось иметь дело с треугольной и четырехугольной пирамидами, а вот с призмами – пока что нет.
Решения:
1. Изобразим призму, а также ее основание. Совместим ее с системой координат и отметим все данные, которые даны в условии задачи:
Извиняюсь за некоторое несоблюдение пропорций, но для решения задачи это, по сути, не так важно. Плоскость ( BC{{C}_{1}}) – это просто «задняя стенка» моей призмы. Достаточно просто догадаться, что уравнение такой плоскости имеет вид:
( x=0)
Однако, это можно показать и непосредственно:
Выберем произвольные три точки на этой плоскости: например, ( Bleft( 0,0,0 right),~Cleft( 0,8,0 right),~{{B}_{1}}left( 0,0,3 right)).
Составим уравнение плоскости:
( left| {begin{array}{*{20}{c}}x&0&0\y&8&0\z&0&3end{array}} right| = 0)
Упражнение тебе: самостоятельно вычислить этот определитель. У тебя получилось ( 24x)? Тогда уравение плоскости имеет вид:
( 24x=0)
Или просто
( x=0)
Таким образом, ( A=1,B=0,C=0,D=0.)
Для решения примера мне нужно найти координаты направляющего вектора прямой ( B{{A}_{1}}).
Так как точка ( B) cовпала с началом координат, то координаты вектора (overrightarrow{B{{A}_{1}}}) просто совпадут с координатами точки ( {{A}_{1}}.)
Для этого найдем вначале координаты точки ( displaystyle A).
Для этого рассмотрим треугольник ( displaystyle ABC).
Проведем высоту (она же – медиана и биссектрисса) из вершины ( displaystyle A).
Так как ( BC=8), то ордината точки ( displaystyle A) равна ( displaystyle 4).
Для того, чтобы найти абсциссу этой точки, нам нужно вычислить длину отрезка ( displaystyle AT).
По теореме Пифагора имеем:
( AT=sqrt{A{{B}^{2}}-B{{T}^{2}}}=sqrt{25-16}=3.)
Тогда точка ( displaystyle A) имеет координаты:
( Aleft( 3,4,0 right))
Точка ( {{A}_{1}})– это «приподнятая» на ( displaystyle 3) точка ( displaystyle A):
( {{A}_{1}}left( 3,4,3 right))
Тогда координаты вектора ( overrightarrow{B{{A}_{1}}}):
( overrightarrow{B{{A}_{1}}}left( 3,4,3 right).)
( sinvarphi =frac{left| 3cdot 1+4cdot 0+3cdot 0 right|}{sqrt{{{1}^{2}}+{{0}^{2}}+{{0}^{2}}}cdot sqrt{{{3}^{2}}+{{4}^{2}}+{{3}^{2}}}}=frac{3}{sqrt{34}}.)
( varphi =arcsinfrac{3}{sqrt{34}}.)
Ответ: ( arcsinfrac{3}{sqrt{34}}.)
Как видишь, ничего принципиально сложного при решении таких задач нет. На самом деле процесс еще немного упрощает «прямота» такой фигуры, как призма.
Теперь давай перейдем к следующему примеру:
2. Рисуем параллелепипед, проводим в нем плоскость и прямую, а также отдельно вычерчиваем его нижнее основание:
Вначале найдем уравнение плоскости: Координаты трех точек, лежащих в ней:
( Aleft( 0,0,0 right),~Bleft( 0,2,0 right),{{C}_{1}}left( 1,2,1 right)) (первые две координаты получены очевидным способом, а последнюю координату ты легко найдешь по картинке из точки ( C)). Тогда составляем уравнение плоскости:
( left| {begin{array}{*{20}{c}}x&0&1\y&2&2\z&0&1end{array}} right| = 0)
Вычисляем:
( 2x-2z=0,~x-z=0)
Тогда ( A=1,B=0,C=-1,D=0.)
Ищем координаты направляющего вектора ( overrightarrow{A{{B}_{1}}}): Ясно, что его координаты совпадают с координатами точки ( {{B}_{1}}), не правда ли?
Как найти координаты ( {{B}_{1}})?
Это же координаты точки ( B), приподнятые по оси аппликат на единицу! ( {{B}_{1}}left( 0,2,1 right)). Тогда ( overrightarrow{A{{B}_{1}}}left( 0,2,1 right).)
Ищем искомый угол:
( sinvarphi =frac{left| 1cdot 0+0cdot 2+left( -1 right)cdot 1 right|}{sqrt{{{1}^{2}}+{{left( -1 right)}^{2}}+{{0}^{2}}~}cdot sqrt{0+{{2}^{2}}+{{1}^{2}}}}=frac{1}{sqrt{10}}.)
( ~varphi =arcsinfrac{1}{sqrt{10}}.)
Ответ: ( arcsinfrac{1}{sqrt{10}}.)
3. Рисуем правильную шестиугольную призму, а затем проводим в ней плоскость и прямую.
Тут даже плоскость нарисовать проблемно, не говоря уже о решении этой задачи, однако методу координат все равно! Именно в его универсальности и заключается его основное преимущество!
Плоскость проходит через три точки: ( A,C,{{D}_{1}}). Ищем их координаты:
1) ( Aleft( 0,0,0 right),~left( frac{sqrt{3}}{2},frac{3}{2},0 right), {{D}_{1}}left( sqrt{3},1,1 right)). Сам выведи координаты для последних двух точек. Тебе пригодится для этого решение задачи с шестиугольной пирамидой!
2) Строим уравнение плоскости:
( left| {begin{array}{*{20}{c}}x&{frac{{sqrt 3 }}{2}}&{sqrt 3 }\y&{frac{3}{2}}&1\z&0&1end{array}} right| = 0)
( -sqrt{3}x+y+2z=0)
( A=-sqrt{3},B=1,C=2,D=0.)
Ищем координаты вектора ( overrightarrow{A{{C}_{1}}}): ( text{ }!!~!!text{ }overrightarrow{A{{C}_{1}}}left( frac{sqrt{3}}{2},frac{3}{2},1 right)). (снова смотри задачу с треугольной пирамидой!)
3) Ищем угол:
( sinvarphi =frac{left| -sqrt{3}cdot frac{sqrt{3}}{2}+frac{3}{2}+2 right|}{sqrt{{{left( frac{sqrt{3}}{2} right)}^{2}}+{{left( frac{3}{2} right)}^{2}}+{{1}^{2}}~}cdot sqrt{{{left( -sqrt{3} right)}^{2}}+{{1}^{2}}+{{2}^{2}}}}=frac{2}{2sqrt{8}}=frac{1}{2sqrt{2}}.)
Ответ: ( arcsinfrac{1}{2sqrt{2}}.)
Как видишь, ничего сверхъестественно сложного в этих задачах нет. Нужно лишь быть очень внимательным с корнями. К последним двум задачам я дам лишь ответы:
4. ( text{arcsin}frac{12}{sqrt{193}}~)
5. ( text{arcsin}frac{1}{sqrt{6}}~)
Как ты мог убедиться, техника решения задач везде одинаковая: основная задача найти координаты вершин и подставить их в некие формулы. Нам осталось рассмотреть еще один класс задач на вычисление углов, а именно: вычисление углов между двумя плоскостями.
Решения задач:
1. Сторона основания правильной треугольной призмы ( ABC{{A}_{1}}{{B}_{1}}{{C}_{1}}) равна ( 2), а диагональ боковой грани равна ( sqrt{5}). Найдите угол между плоскостью ( {{A}_{1}}BC) и плоскостью основания призмы.
Рисую правильную (в основании – равносторонний треугольник) треугольную призму и отмечаю на ней плоскости, которые фигурируют в условии задачи:
Нам нужно найти уравнения двух плоскостей: ( ABC~и~BC{{A}_{1}}.) Уравнение основания получается тривиально: ты можешь составить соответствующий определитель по трем точкам, я же составлю уравнение сразу:
( z=0.)
То есть:
( {{A}_{1}}=0, {{B}_{1}}=0, {{C}_{1}}=1, {{D}_{1}}=0.)
Теперь найдем уравнение ( BC{{A}_{1}}.) Точка ( B) имеет координаты ( Bleft( 0,0,0 right).) Точка ( C) – ( Cleft( 0,1,0 right).)
Так как ( AO) – медиана и высота треугольника ( ABC), то ( BO=OC=1.) ( AO) легко находится по теореме Пифагора в треугольнике ( BAO:) ( AO=sqrt{4-1}=sqrt{3}).
Тогда точка ( A) имеет координаты: ( Aleft( sqrt{3},1,0 right).)
Найдем аппликату точки ( {{A}_{1}}.) Для этого рассмотрим прямоугольный треугольник ( {{A}_{1}}AC.~)
( A{{A}_{1}}=sqrt{{{A}_{1}}{{C}^{2}}-A{{C}^{2}}}=1.)
Тогда получаем вот такие координаты: ( {{A}_{1}}left( sqrt{3},1,1 right).) Cоставляем уравнение плоскости ( BC{{A}_{1}}).
( left| {begin{array}{*{20}{c}}x&0&{sqrt 3 }\y&1&1\z&0&1end{array}} right| = 0.)
( x+sqrt{3}z-sqrt{3}z-sqrt{3}y=0)
( x-sqrt{3}z=0)
Тогда
( {{A}_{2}}=1, {{B}_{2}}=0, {{C}_{2}}=-sqrt{3}, {{D}_{2}}=0.)
Вычисляем угол между плоскостями:
( cosvarphi =frac{left| -sqrt{3} right|}{sqrt{1+{{left( -sqrt{3} right)}^{2}}}}=frac{sqrt{3}}{2}.)
Отсюда
( varphi =30{}^circ .)
Ответ: ( 30{}^circ .)
2. В правильной четырехугольной пирамиде ( displaystyle SABCD), все ребра которой равны ( displaystyle 1), найдите синус угла между плоскостью ( displaystyle SAD) и плоскостью, проходящей через точку ( displaystyle A) перпендикулярно прямой ( displaystyle BD).
Делаем рисунок:
Самое сложное – это понять, что это такая за таинственная плоскость, проходящая через точку ( A) перпендикулярно ( DB).
Ну что же, главное, это что? Главное – это внимательность! В самом деле, прямая ( AC) перпендикулярна ( BD). Прямая ( OS) также перпендикулярна ( BD).
Тогда плоскость, проходящая через эти две прямые, будет перпендикулярна прямой ( BD), и, кстати, проходить через точку ( A). Эта плоскость также проходит через вершину пирамиды.
Тогда искомая плоскость – ( SAC.) А плоскость ( SAD) нам уже дана. Ищем координаты точек ( displaystyle S,A,C,D).
- ( displaystyle Aleft( 0,1,0 right))
- ( displaystyle Cleft( 1,0,0 right))
- ( displaystyle Dleft( 0,0,0 right))
Координату точки ( S) найдем через точку ( O). Из маленького рисунка легко вывести, что координаты у точки ( O) будут такие: ( Oleft( frac{1}{2},frac{1}{2},0 right).~)
Что теперь осталось найти, чтобы найти координаты вершины пирамиды?
Еще нужно вычислить ее высоту.
Это делается при помощи все той же теоремы Пифагора: вначале докажи, что ( OB=frac{sqrt{2}}{2}) (тривиально из маленьких треугольничков, образующих квадрат в основании).
Так как по условию ( SB=1), то имеем:
( OS=sqrt{1-{{left( frac{sqrt{2}}{2} right)}^{2}}}=frac{1}{sqrt{2}}.)
Теперь все готово: координаты вершины:
( Sleft( frac{1}{2},frac{1}{2},frac{1}{sqrt{2}} right).~)
Составляем уравнение плоскости ( displaystyle DAS):
( left| {begin{array}{*{20}{c}}x&0&{frac{1}{2}}\y&1&{frac{1}{2}}\z&0&{frac{1}{{sqrt 2 }}}end{array}} right| = 0)
Ты уже спец в вычислении определителей. Без труда ты получишь:
( frac{1}{sqrt{2}}x-frac{1}{2}z=0)
Или иначе (если домножим обе части на корень из двух)
( x-frac{1}{sqrt{2}}z=0.)
Теперь найдем уравнение плоскости ( displaystyle SAC):
( left| {begin{array}{*{20}{c}}{x — 1}&{ — 1}&{ — frac{1}{2}}\y&1&{frac{1}{2}}\z&0&{frac{1}{{sqrt 2 }}}end{array}} right| = 0)
(ты ведь не забыл, как мы получаем уравнение плоскости, правда?
Если ты не понял, откуда взялась эта минус единица, то вернись к определению уравнения плоскости! Просто всегда до этого оказывалось так, что моей плоскости принадлежало начало координат!)
Вычисляем определитель:
( begin{array}{l}frac{x-1}{sqrt{2}}-frac{1}{2}z+frac{1}{2}z+frac{y}{sqrt{2}}=0\frac{x-1}{sqrt{2}}+frac{y}{sqrt{2}}=0\x+y-1=0end{array}).
(Ты можешь заметить, что уравнение плоскости совпало с уравнением прямой, проходящей через точки ( displaystyle A) и ( displaystyle C)! Подумай, почему!)
Теперь вычисляем угол:
( cosvarphi =frac{left| 1+1cdot 0-frac{1}{sqrt{2}}cdot 0 right|}{sqrt{1+{{left( -frac{1}{sqrt{2}} right)}^{2}}}cdot sqrt{{{1}^{2}}+{{1}^{2}}}~~}=frac{1}{sqrt{3}}.)
Нам же нужно найти синус:
( sinvarphi =sqrt{1-{{cos }^{2}}varphi }=sqrt{1-frac{1}{3}}=sqrt{frac{2}{3}}).
Ответ: ( sqrt{frac{2}{3}}.)
3. В правильной четырехугольной призме ( ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}) стороны основания равны ( displaystyle 1), а боковые ребра равны ( displaystyle 5). На ребре ( A{{A}_{1}}) отмечена точка ( displaystyle E) так, что ( AE:E{{A}_{1}}=2:3). Найдите угол между плоскостями ( ABC) и ( BE{{D}_{1}}.)
Каверзный вопрос: а что такое прямоугольная призма, как ты думаешь? Это же всего-то навсего хорошо известный тебе параллелепипед! Сразу же делаем чертеж! Можно даже отдельно не изображать основание, пользы от него здесь немного:
Плоскость ( ABC), как мы уже раньше заметили, записывается в виде уравнения:
( z=0.)
Теперь составляем плоскость ( BE{{D}_{1}}.)
( Bleft( 0,0,0 right),~Eleft( 1,0,2 right),~{{D}_{1}}left( 1,1,5 right).)
Cразу же составляем уравнение плоскости:
( left| {begin{array}{*{20}{c}}x&1&1\y&0&1\z&2&5end{array}} right| = 0)
( begin{array}{l}2y+z-2x-5y=0\-2x-3y+z=0\2x+3y-z=0end{array})
Ищем угол:
( cosvarphi =frac{1}{sqrt{4+9+1}}=frac{1}{sqrt{14}})
Ответ: ( arccos frac{1}{sqrt{14}}~~)
Теперь ответы к последним двум задачам:
4. ( arccosfrac{2}{3})
5. ( sqrt{frac{2}{3}})
Ну что же, теперь самое время немного передохнуть, ведь мы с тобой молодцы и проделали огромную работу!
Вычисление расстояния от точки до плоскости
Что нам потребуется для решения этой задачи?
- Координаты точки ( Mleft( {{x}_{0}},{{y}_{0}},{{z}_{0}} right).)
- Уравнение плоскости ( Ax+By+Cz+D=0.)
Итак, как только мы получим все необходимые данные, то применяем формулу:
( d=frac{left| A{{x}_{0}}+B{{y}_{0}}+C{{z}_{0}}+D right|}{sqrt{{{A}^{2}}+{{B}^{2}}+{{C}^{2}}}})
Как мы строим уравнение плоскости тебе уже должно быть известно из предыдущих задач, которые я разбирал в прошлой части. Давай сразу приступим к задачам.
Схема следующая: 1, 2 –я помогаю тебе решать, причем довольно подробно, 3, 4 – только ответ, решение ты проводишь сам и сравниваешь. Начали!
Решения:
1. Рисуем кубик с единичными ребрами, строим отрезок и плоскость, середину отрезка ( B{{C}_{1}}) обозначим буквой ( M)
Вначале давай начнем с легкого: найдем координаты точки ( displaystyle M). Так как ( displaystyle Bleft( 0,1,0 right),~{{C}_{1}}left( 1,1,1 right),~) то ( displaystyle Mleft( frac{1}{2},1,frac{1}{2} right).) (вспомни координаты середины отрезка!)
Теперь составляем уравнение плоскости по трем точкам ( displaystyle Aleft( 0,0,0 right),~{{B}_{1}}left( 0,1,1 right),~{{D}_{1}}left( 1,0,1 right).)
(left| {begin{array}{*{20}{c}}x&0&1\y&1&0\z&1&1end{array}} right| = 0)
( displaystyle x+y-z=0.)
( displaystyle A=1,B=1,C=-1,~D=0.)
Теперь я могу приступать к поиску расстояния:
( displaystyle d=frac{left| frac{1}{2}+1-frac{1}{2} right|}{sqrt{1+1+1}}=frac{1}{sqrt{3}})
Ответ: ( displaystyle frac{1}{sqrt{3}})
2. Вновь начинаем с чертежа, на котором отмечаем все данные!
Для пирамиды было бы полезно отдельно рисовать ее основание.
Даже тот факт, что я рисую как курица лапой, не помешает нам с легкостью решить эту задачу!
1. ( AO=OC=frac{1}{2}AC=frac{sqrt{{{2}^{2}}+{{2}^{2}}}}{2}=sqrt{2}).
Тогда ( OS=sqrt{S{{C}^{2}}-O{{C}^{2}}}=sqrt{3}.)
Теперь легко найти координаты точки ( S.)
Так как координаты точки ( O:Oleft( 1,1,0 right),~), то ( Sleft( 1,1,sqrt{3} right).)
2. Так как координаты точки ( C:) ( Cleft( 2,2,0 right),) а ( M) – середина отрезка ( SC), то
( Mleft( frac{3}{2},frac{3}{2},frac{sqrt{3}}{2} right).)
Без проблем найдем и координаты еще двух точек на плоскости ( ADM.) ( Dleft( 1,0,0 right),~Aleft( 0,0,0 right).) Составляем уравнение плоскости и упростим его:
(left| {left| {begin{array}{*{20}{c}}x&1&{frac{3}{2}}\y&0&{frac{3}{2}}\z&0&{frac{{sqrt 3 }}{2}}end{array}} right|} right| = 0)
( frac{3}{2}z-frac{sqrt{3}}{2}y=0)
( sqrt{3}y-3z=0)
( y-sqrt{3}z=0.)
Так как точка ( B) имеет координаты: ( Bleft( 0,2,0 right)), то вычисляем расстояние:
( d=frac{2}{sqrt{1+3}}=1.)
Ответ (очень редкий!): ( 1)
Ну что, разобрался?
Мне кажется, что здесь все так же технично, как и в тех примерах, что мы рассматривали с тобой в предыдущей части. Так что я уверен, что если ты овладел тем материалом, то тебе не составит труда решить оставшиеся две задачи.
Я лишь приведу ответы:
- ( frac{3sqrt{39}}{4})
- ( frac{sqrt{3}}{2})
Вычисление расстояния от прямой до плоскости
На самом деле, здесь нет ничего нового. Как могут располагаться прямая и плоскость друг относительно друга?
У них есть всего ( 2) возможности: пересечься, или прямая параллельна плоскости. Как ты думаешь, чем равно расстояние от прямой до плоскости, с которой данная прямая пересекается?
Мне кажется, что тут ясно, что такое расстояние равно нулю. Неинтересный случай.
Второй случай хитрее: тут уже расстояние ненулевое. Однако, так как прямая параллельна плоскости, то каждая точка прямой равноудалена от этой плоскости:
Таким образом:
Расстояние от плоскости до параллельной ей прямой равно расстоянию от любой точки прямой до плоскости.
А это значит, что моя задача свелась к предыдущей: ищем координаты любой точки на прямой, ищем уравнение плоскости, вычисляем расстояние от точки до плоскости.
На самом деле, такие задачи в ЕГЭ встречаются крайне редко. Мне удалось найти лишь одну задачу, и то данные в ней были такими, что метод координат к ней был не очень-то и применим!
Теперь перейдем к другому, гораздо более важному классу задач:
Вычисление расстояния точки до прямой
Что нам потребуется?
- Координаты точки, от которой мы ищем расстояние: ( {{M}_{0}}left( {{x}_{0}},{{y}_{0}},{{z}_{0}} right).)
- Координаты любой точки, лежащей на прямой ( {{M}_{1}}left( {{x}_{1}},{{y}_{1}},{{z}_{1}} right))
- Координаты направляющего вектора прямой ( vec{s}left( m,n,p right))
Какую применяем формулу?
Ответ: ( d=frac{left| overrightarrow{{{M}_{0}}{{M}_{1}}}times vec{s} right|}{sqrt{{{m}^{2}}+{{n}^{2}}+{{p}^{2}}}})
Что означает знаменатель данной дроби тебе и так должно быть ясно: это длина направляющего вектора прямой. Здесь очень хитрый числитель!
Выражение ( left| overrightarrow{{{M}_{0}}{{M}_{1}}}times vec{s} right|) означает модуль (длина) векторного произведения векторов ( overrightarrow{{{M}_{0}}{{M}_{1}}}) и ( vec{s}.)
Как вычислять векторное произведение, мы с тобой изучали в предыдущей части работы. Освежи свои знания, нам они сейчас очень пригодятся!
Таким образом, алгоритм решения задач будет следующий:
- Ищем координаты точки, от которой мы ищем расстояние: ( {{M}_{0}}left( {{x}_{0}},{{y}_{0}},{{z}_{0}} right).)
- Ищем координаты любой точки на прямой, до которой мы ищем расстояние: ( {{M}_{1}}left( {{x}_{1}},{{y}_{1}},{{z}_{1}} right))
- Строим вектор ( overrightarrow{{{M}_{0}}{{M}_{1}}}:) ( overrightarrow{{{M}_{0}}{{M}_{1}}}left( {{x}_{1}}-{{x}_{0}},{{y}_{1}}-{{y}_{0}},{{z}_{1}}-{{z}_{0}} right).)
- Строим направляющий вектор прямой ( vec{s}left( m,n,p right))
- Вычисляем векторное произведение ( overrightarrow{{{M}_{0}}{{M}_{1}}}times vec{s})
- Ищем длину полученного вектора: ( left| overrightarrow{{{M}_{0}}{{M}_{1}}}times vec{s} right|)
- Вычисляем расстояние: ( d=frac{left| overrightarrow{{{M}_{0}}{{M}_{1}}}times vec{s} right|}{sqrt{{{m}^{2}}+{{n}^{2}}+{{p}^{2}}}})
Работы у нас много, а примеры будут достаточно сложными! Так что теперь сосредоточь все внимание!
1. Дана правильная треугольная пирамида ( DABC) с вершиной ( D). Сторона основания пирамиды равна ( sqrt{6}), высота равна ( sqrt{30}).
Найдите расстояние от середины бокового ребра ( BD) до прямой ( MT), где точки ( M) и ( T) — середины ребер ( AC) и ( AB) соответственно.
2. Длины ребер ( AB,A{{A}_{1}}) и ( AD) прямоугольного параллелепипеда ( ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}) равны соответственно ( 12,text{ }16~) и ( 15.)
Найдите расстояние от вершины ( {{A}_{1}}) до прямой ( B{{D}_{1}}.)
3. В правильной шестиугольной призме ( ABCDEF{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}{{E}_{1}}{{F}_{1}}) все ребра которой равны ( 1) найдите расстояние от точки ( B) до прямой ( {{E}_{1}}{{F}_{1}}.)
Решения:
1. Делаем аккуратный чертеж, на котором отмечаем все данные:
Ну что же, работы нам предстоит немало! Принимаемся за нее, засучив рукава!
1. Чтобы найти координаты высоты пирамиды, нам нужно знать координаты точки ( displaystyle O.) Её аппликата равна нулю, а ордината равна ( displaystyle frac{sqrt{6}}{2}.)
Абсцисса ее равна длине отрезка ( displaystyle OS.) ( displaystyle AS=sqrt{A{{B}^{2}}-S{{B}^{2}}}=sqrt{6-frac{6}{4}}=frac{3}{sqrt{2}}.~)
Так как ( displaystyle AS) – высота равностороннего треугольника ( displaystyle ABC), то она делится в отношении ( displaystyle 2:1), считая от вершины, отсюда ( displaystyle OS=frac{3}{3sqrt{2}}=frac{1}{sqrt{2}}).
Окончательно, получили координаты:
( displaystyle Oleft( frac{1}{sqrt{2}},frac{sqrt{6}}{2},0 right).)
Тогда ( displaystyle D(left( frac{1}{sqrt{2}},frac{sqrt{6}}{2},sqrt{30} right)).
Координаты точки ( displaystyle A:Aleft( frac{3}{sqrt{2}},frac{sqrt{6}}{2},0 right).)
2. ( displaystyle K) – середина отрезка ( displaystyle BD:)
( displaystyle Kleft( frac{1}{2sqrt{2}},frac{sqrt{6}}{4},frac{sqrt{30}}{2} right).~)
3. ( displaystyle M) – середина отрезка ( displaystyle AC:)
( displaystyle Mleft( frac{3}{2sqrt{2}},~frac{frac{sqrt{6}}{2}+sqrt{6}}{2},0 right)=Mleft( frac{3}{2sqrt{2}},~frac{3sqrt{6}}{4},0 right).)
( displaystyle T) – середина отрезка ( displaystyle AB)
( displaystyle Tleft( frac{3}{2sqrt{2}},~frac{sqrt{6}}{4},0 right).~)
4. Координаты( displaystyle overrightarrow{KT}:overrightarrow{KT}left( frac{3}{2sqrt{2}}-frac{1}{2sqrt{2}},frac{sqrt{6}}{4}-frac{sqrt{6}}{4},~0-frac{sqrt{30}}{2} right)=overrightarrow{KT}left( frac{1}{sqrt{2}},~0,~-frac{sqrt{30}}{2} right).)
Координаты вектора ( displaystyle overrightarrow{TM}:)
( displaystyle overrightarrow{TM}left( 0,frac{3sqrt{6}}{4}-frac{sqrt{6}}{4},0 right)=overrightarrow{TM}left( 0,~frac{sqrt{6}}{2},0 right).)
5. Вычисляем векторное произведение:
( displaystyle overrightarrow{KT}times overrightarrow{TM}=frac{1}{sqrt{2}}cdot frac{sqrt{6}}{2}cdot overrightarrow{k}-frac{sqrt{30}}{2}cdot frac{sqrt{6}}{2}cdot vec{i}=frac{3sqrt{5}}{2}vec{i}+frac{sqrt{3}}{2}overrightarrow{k}=left( frac{3sqrt{5}}{2},0,~frac{sqrt{3}}{2} right).)
6. Длина вектора ( displaystyle TM): проще всего заменить, что отрезок ( displaystyle TM) – средняя линия треугольника ( displaystyle ABC), а значит, он равен половине основания ( displaystyle BC). Так что ( displaystyle left| text{ }!!~!!text{ }overrightarrow{TM} right|=frac{sqrt{6}}{2}).
7. Считаем длину векторного произведения:
( displaystyle left| overrightarrow{KT}times overrightarrow{TM} right|=sqrt{{{left( frac{3sqrt{5}}{2} right)}^{2}}+{{left( frac{sqrt{3}}{2} right)}^{2}}}=2sqrt{3}.)
8. Наконец, находим расстояние:
( displaystyle d=frac{left| overrightarrow{KT}times overrightarrow{TM} right|}{text{ }!!~!!text{ }left| text{ }!!~!!text{ }overrightarrow{TM} right|}=frac{2sqrt{3}}{frac{sqrt{6}}{2}}=2sqrt{2})
Уф, ну все!
Честно тебе скажу: решение этой задачи традиционными методами (через построения), было бы намного быстрее.
Зато здесь я все свел к готовому алгоритму!
Я так думаю, что алгоритм решения тебе ясен? Поэтому попрошу тебя решить оставшиеся две задачи самостоятельно. Сравним ответы?
2. ( displaystyle 12)
3. ( displaystyle 2)
Опять-таки повторюсь: эти задачи проще (быстрее) решать через построения, а не прибегая к координатному методу.
Я продемонстрировал такой способ решения лишь затем, чтобы показать тебе универсальный метод, который позволяет «ничего не достраивать».
Наконец, рассмотрим последний класс задач: Вычисление расстояния между скрещивающимися прямыми.
Вычисление расстояния между скрещивающимися прямыми
Здесь алгоритм решения задач будет схож с предыдущим. Что у нас есть:
- Направляющий вектор первой прямой: ( overrightarrow{{{a}_{1}}(}{{x}_{1}},{{y}_{1}},{{z}_{1}}).)
- Направляющий вектор второй прямой: ( overrightarrow{{{a}_{2}}(}{{x}_{2}},{{y}_{2}},{{z}_{2}}).)
- Любой вектор, соединяющий точки первой и второй прямой: ( overrightarrow{{{a}_{3}}}left( {{x}_{0}},{{y}_{0}},{{z}_{0}} right))
Как мы ищем расстояние между прямыми?
Формула следующая:
( d=frac{left| left( overrightarrow{{{a}_{3}}},~overrightarrow{{{a}_{1}}},overrightarrow{{{a}_{2}}} right) right|}{left| overrightarrow{{{a}_{1}}}times overrightarrow{{{a}_{2}}} right|})
Числитель – это модуль смешанного произведения (мы его вводили в предыдущей части), а знаменатель – как и в предыдущей формуле (модуль векторного произведения направляющих векторов прямых, расстояние между которыми мы с тобой ищем).
Я напомню тебе, что
тогда формулу для расстояния можно переписать в виде:
[d = frac{{left| begin{array}{l}begin{array}{*{20}{c}}{{x_0}}&{{y_0}}&{{z_0}}end{array}\begin{array}{*{20}{c}}{{x_1}}&{{y_1}}&{{z_1}}end{array}\begin{array}{*{20}{c}}{{x_2}}&{{y_2}}&{{z_2}}end{array}end{array} right|}}{{left| begin{array}{l}begin{array}{*{20}{c}}{overrightarrow i }&{overrightarrow j }&{overrightarrow k }end{array}\begin{array}{*{20}{c}}{{x_1}}&{{y_1}}&{{z_1}}end{array}\begin{array}{*{20}{c}}{{x_2}}&{{y_2}}&{{z_2}}end{array}end{array} right|}}]
Этакий определитель делить на определитель! Хотя, если честно, мне здесь совсем не до шуток!
Данная формула, на самом деле, очень громоздка и приводит к достаточно сложным вычислениям. На твоем месте я бы прибегал к ней только в самом крайнем случае!
Давай попробуем решить несколько задач, используя изложенный выше метод:
- В правильной треугольной призме ( ABC{{A}_{1}}{{B}_{1}}{{C}_{1}}), все рёбра которой равны ( 1), найдите расстояние между прямыми ( A{{A}_{1}}) и ( B{{C}_{1}}).
- Дана правильная треугольная призма ( ABC{{A}_{1}}{{B}_{1}}{{C}_{1}}) все рёбра основания которой равны ( 2sqrt{7}) Сечение, проходящее через боковое ребро ( A{{A}_{1}}) и середину ( M) ребра ( {{B}_{1}}{{C}_{1}}) является квадратом. Найдите расстояние между прямыми ( {{A}_{1}}B) и ( AM.)
Первую решаю я, а опираясь на нее, вторую решаешь ты!
1. Рисую призму и отмечаю прямые ( A{{A}_{1}}) и ( B{{C}_{1}}.)
Координаты точки С: ( C:Cleft( frac{sqrt{3}}{2},frac{1}{2},0 right),) тогда ( {{C}_{1}}left( frac{sqrt{3}}{2},frac{1}{2},1 right).~)
Координаты точки ( B:Bleft( 0,1,0 right).~)
Координаты вектора ( overrightarrow{B{{C}_{1}}}:~overrightarrow{B{{C}_{1}}}left( frac{sqrt{3}}{2},-frac{1}{2},1 right).)
Координаты точки ( {{A}_{1}}:{{A}_{1}}left( 0,0,1 right).)
Координаты вектора ( overrightarrow{A{{A}_{1}}}:~overrightarrow{A{{A}_{1}}}left( 0,0,1 right).)
Координаты вектора ( overrightarrow{AB}left( 0,1,0 right).)
[left( {B,overrightarrow {A{A_1}} overrightarrow {B{C_1}} } right) = left| {begin{array}{*{20}{l}}{begin{array}{*{20}{c}}0&1&0end{array}}\{begin{array}{*{20}{c}}0&0&1end{array}}\{begin{array}{*{20}{c}}{frac{{sqrt 3 }}{2}}&{ — frac{1}{2}}&1end{array}}end{array}} right| = frac{{sqrt 3 }}{2}]
Считаем векторное произведение между векторами ( AA) и ( overrightarrow{B{{C}_{1}}}:)
[overrightarrow {A{A_1}} cdot overrightarrow {B{C_1}} = left| begin{array}{l}begin{array}{*{20}{c}}{overrightarrow i }&{overrightarrow j }&{overrightarrow k }end{array}\begin{array}{*{20}{c}}0&0&1end{array}\begin{array}{*{20}{c}}{frac{{sqrt 3 }}{2}}&{ — frac{1}{2}}&1end{array}end{array} right| — frac{{sqrt 3 }}{2}overrightarrow k + frac{1}{2}overrightarrow i ]
Теперь считаем его длину:
( left| overrightarrow{A{{A}_{1}}}times overrightarrow{B{{C}_{1}}} right|=sqrt{{{left( -frac{sqrt{3}}{2} right)}^{2}}+{{left( frac{1}{2} right)}^{2}}}=1)
Тогда
( d=frac{frac{sqrt{3}}{2}}{1}=frac{sqrt{3}}{2}.)
Ответ: ( frac{sqrt{3}}{2}.)
Теперь постарайся аккуратно выполнить вторую задачу. Ответом на нее будет: ( frac{sqrt{6}}{2}).
Марина Николаевна Ковальчук
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Прямоугольная система координат
Чтобы определить понятие координат точек, нам необходимо ввести систему координат, в которой мы и будем определять ее координаты. Одна и та же точка в разных системах координат может иметь различные координаты. Здесь мы будем рассматривать прямоугольную систему координат в пространстве.
Возьмем в пространстве точку $O$ и введем для нее координаты $(0,0,0)$. Назовем ее началом системы координат. Проведем через нее три взаимно перпендикулярные оси $Ox$, $Oy$ и $Oz$, как на рисунке 1. Эти оси будут называться осями абсцисс, ординат и аппликат, соответственно. Осталось только ввести масштаб на осях (единичный отрезок) – прямоугольная система координат в пространстве готова (рис. 1)
Рисунок 1. Прямоугольная система координат в пространстве. Автор24 — интернет-биржа студенческих работ
Координаты точки
Теперь разберем, как определяют в такой системе координаты любой точки. Возьмем произвольную точку $M$ (рис. 2).
Рисунок 2. Произвольная точка. Автор24 — интернет-биржа студенческих работ
Построим на координатных осях прямоугольный параллелепипед, так, что точки $O$ и $M$ противоположные его вершины (рис. 3).
Рисунок 3. Построение прямоугольного параллелепипеда. Автор24 — интернет-биржа студенческих работ
«Координаты точки и координаты вектора. Как найти координаты вектора» 👇
Тогда точка $M$ будет иметь координаты $(X,Y,Z)$, где $X$ – значение на числовой оси $Ox$, $Y$ – значение на числовой оси $Oy$, а $Z$ – значение на числовой оси $Oz$.
Пример 1
Необходимо найти решение следующей задачи: написать координаты вершин параллелепипеда, изображенного на рисунке 4.
Рисунок 4. Параллелепипед. Автор24 — интернет-биржа студенческих работ
Решение.
Точка $O$ начало координат, следовательно, $O=(0,0,0)$.
Точки $Q$, $N$ и $R$ лежат на осях $Ox$, $Oz$ и $Oy$, соответственно, значит
$Q=(2,0,0)$, $N=(0,0,1.5)$, $R=(0,2.5,0)$
Точки $S$, $L$ и $M$ лежат в плоскостях $Oxz$, $Oxy$ и $Oyz$, соответственно, значит
$S=(2,0,1.5)$, $L=(2,2.5,0)$, $R=(0,2.5,1.5)$
Точка $P$ имеет координаты $P=(2,2.5,1.5)$
Координаты вектора по двум точкам и формула нахождения
Чтобы узнать, как найти вектор по координатам двух точек, необходимо рассмотреть введенную нами ранее систему координат. В ней от точки $O$ по направлению оси $Ox$ отложим единичный вектор $overline{i}$, по направлению оси $Oy$ — единичный вектор $overline{j}$, а единичный вектор $overline{k}$ нужно направлять по оси $Oz$.
Для того чтобы ввести понятие координат вектора, введем следующую теорему (здесь ее доказательство мы рассматривать не будем).
Теорема 1
Произвольный вектор в пространстве может быть разложен по трем любым векторам, которые не лежат в одной плоскости, причем коэффициенты в таком разложении будут единственным образом определены.
Математически это выглядит следующим образом:
$overline{δ}=moverline{α}+noverline{β}+loverline{γ}$
Так как векторы $overline{i}$, $overline{j}$ и $overline{k}$ построены на координатных осях прямоугольной системы координат, то они, очевидно, не будут принадлежать одной плоскости. Значит любой вектор $overline{δ}$ в этой системе координат, по теореме 1, может принимать следующий вид
$overline{δ}=moverline{i}+noverline{j}+loverline{k}$ (1)
где $n,m,l∈R$.
Определение 1
Три вектора $overline{i}$, $overline{j}$ и $overline{k}$ будут называться координатными векторами.
Определение 2
Коэффициенты перед векторами $overline{i}$, $overline{j}$ и $overline{k}$ в разложении (1) будут называться координатами этого вектора в заданной нами системе координат, то есть
$overline{δ}=(m,n,l)$
Линейные операции над векторами
Теорема 2
Теорема о сумме: Координаты суммы любого числа векторов определяются суммой их соответствующих координат.
Доказательство.
Будем доказывать эту теорему для 2-х векторов. Для 3-х и более векторов доказательство строится аналогичным образом. Пусть $overline{α}=(α_1,α_2,α_3)$, $overline{β}=(β_1,β_2 ,β_3)$.
Эти вектора можно записать следующим образом
$overline{α}=α_1overline{i}+ α_2overline{j}+α_3overline{k}$, $overline{β}=β_1overline{i}+ β_2overline{j}+β_3overline{k}$
$overline{α}+overline{β}=α_1overline{i}+α_2overline{j}+α_3overline{k}+β_1overline{i}+ β_2overline{j}+β_3overline{k}=(α_1+β_1 )overline{i}+(α_2+β_2 )overline{j}+(α_3+β_3)overline{k}$
Следовательно
$overline{α}+overline{β}=(α_1+β_1,α_2+β_2,α_3+β_3)$
Теорема доказана.
Замечание 1
Замечание: Аналогично, находится решение разности нескольких векторов.
Теорема 3
Теорема о произведении на число: Координаты произведения произвольного вектора на действительное число определяется произведением координат на это число.
Доказательство.
Возьмем $overline{α}=(α_1,α_2,α_3)$, тогда $overline{α}=α_1overline{i}+α_2overline{j}+α_3overline{k}$, а
$loverline{α}=l(α_1overline{i}+ α_2overline{j}+α_3overline{k})=lα_1overline{i}+ lα_2overline{j}+lα_3overline{k}$
Значит
$koverline{α}=(lα_1,lα_2,lα_3)$
Теорема доказана.
Пример 2
Пусть $overline{α}=(3,0,4)$, $overline{β}=(2,-1,1)$. Найти $overline{α}+overline{β}$, $overline{α}-overline{β}$ и $3overline{α}$.
Решение.
$overline{α}+overline{β}=(3+2,0+(-1),4+1)=(5,-1,5)$
$overline{α}-overline{β}=(3-2,0-(-1),4-1)=(1,1,3)$
$3overline{α}=(3cdot 3,3cdot 0,3cdot 4)=(9,0,12)$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
В данной публикации мы рассмотрим формулы, с помощью которых можно найти координаты вектора, заданного координатами его начальной и конечной точек, а также разберем примеры решения задач по этой теме.
- Нахождение координат вектора
- Примеры задач
Нахождение координат вектора
Для того, чтобы найти координаты вектора AB, нужно из координат его конечной точки (B) вычесть соответствующие координаты начальной точки (A).
Формулы для определения координат вектора
| Для плоских задач | AB = {Bx — Ax; By — Ay} |
| Для трехмерных задач | AB = {Bx — Ax; By — Ay; Bz — Az} |
| Для n-мерных векторов | AB = {B1 — A1; B2 — A2; … Bn — An} |
Примеры задач
Задание 1
Найдем координаты вектора AB, если у его точек следующие координаты: A = (2; 8), B = (5; 12).
Решение:
AB = {5 – 2; 12 – 8} = {3; 4}.
Задание 2
Определим координаты точки B вектора AB = {6; 14}, если координаты точки A = (2; 5).
Решение:
Координаты точки B можно вывести из формулы для расчета координат вектора:
Bx = ABx + Ax = 6 + 2 = 8.
By = ABy + Ay = 14 + 5 = 19.
Таким образом, B = (8; 19).