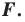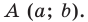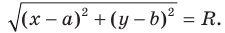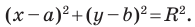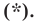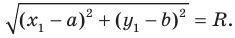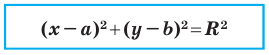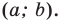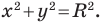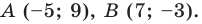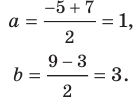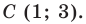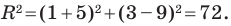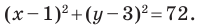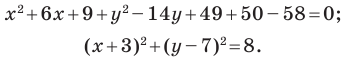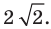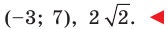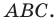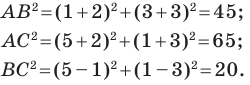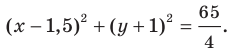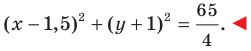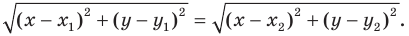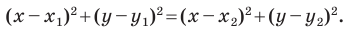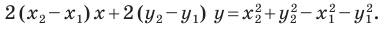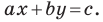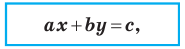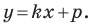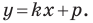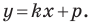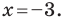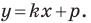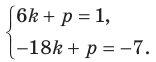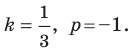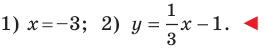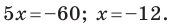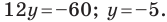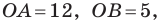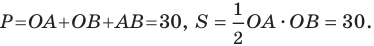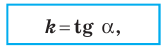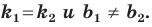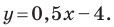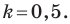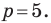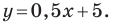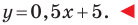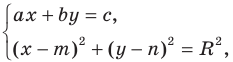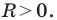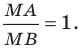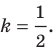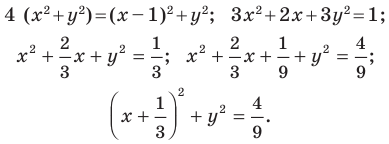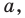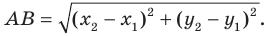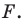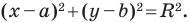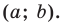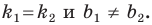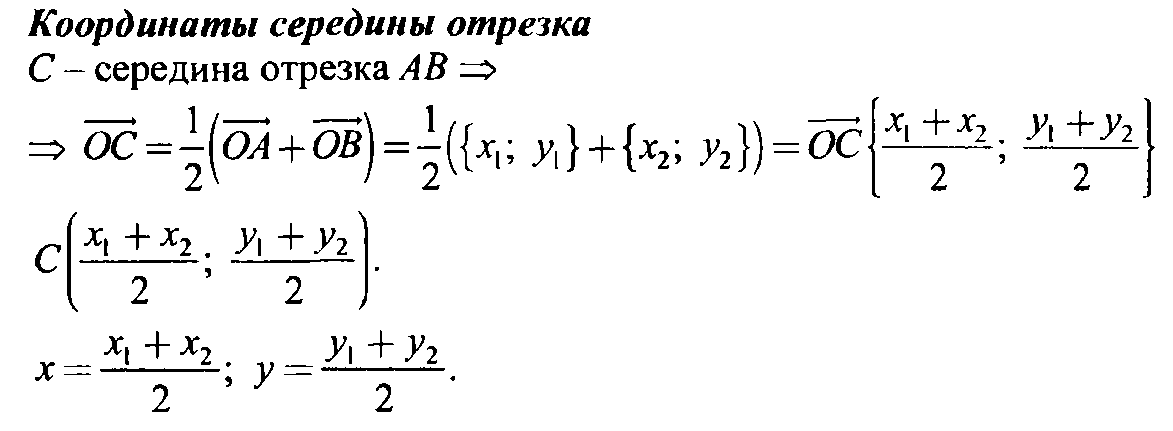Определение.
Середина отрезка — это точка, которая лежит на отрезке и находится на равном расстоянии от конечных точек.
В геометрических задачах часто можно столкнуться с необходимостью найти середину отрезка заданного координатами точек его концов, например в задачах поиска медианы, средней линии, …
Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка.
Формулы вычисления расстояния между двумя точками:
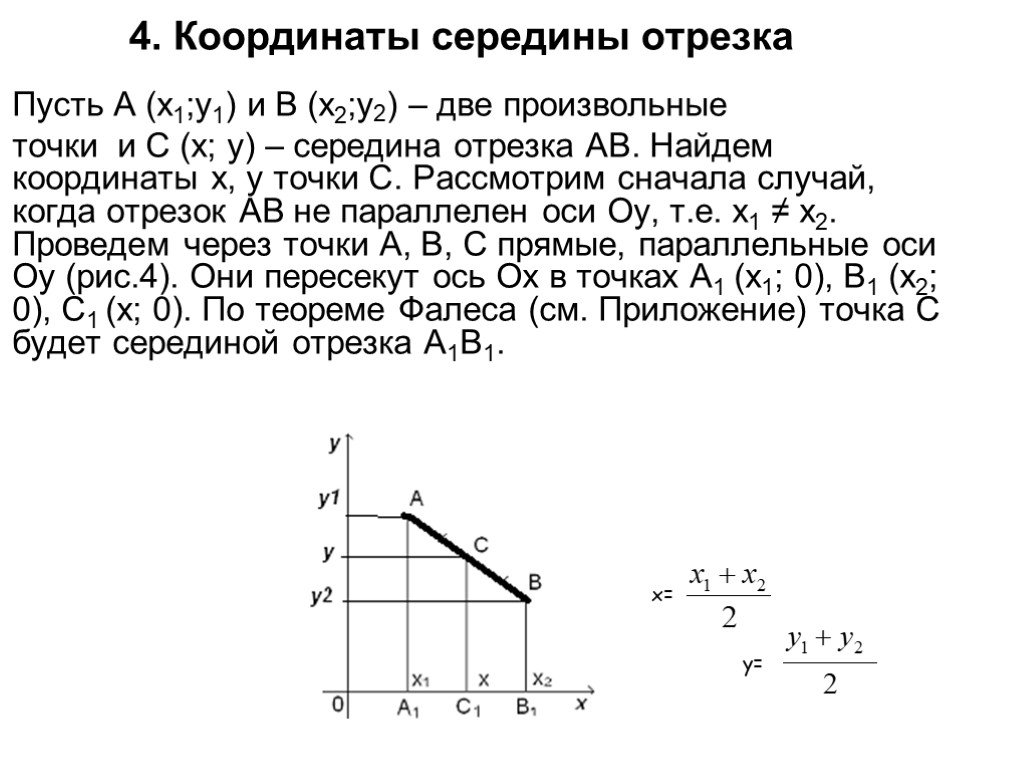
- Формула вычисления координат середины отрезка с концами A(xa, ya) и B(xb, yb) на плоскости:
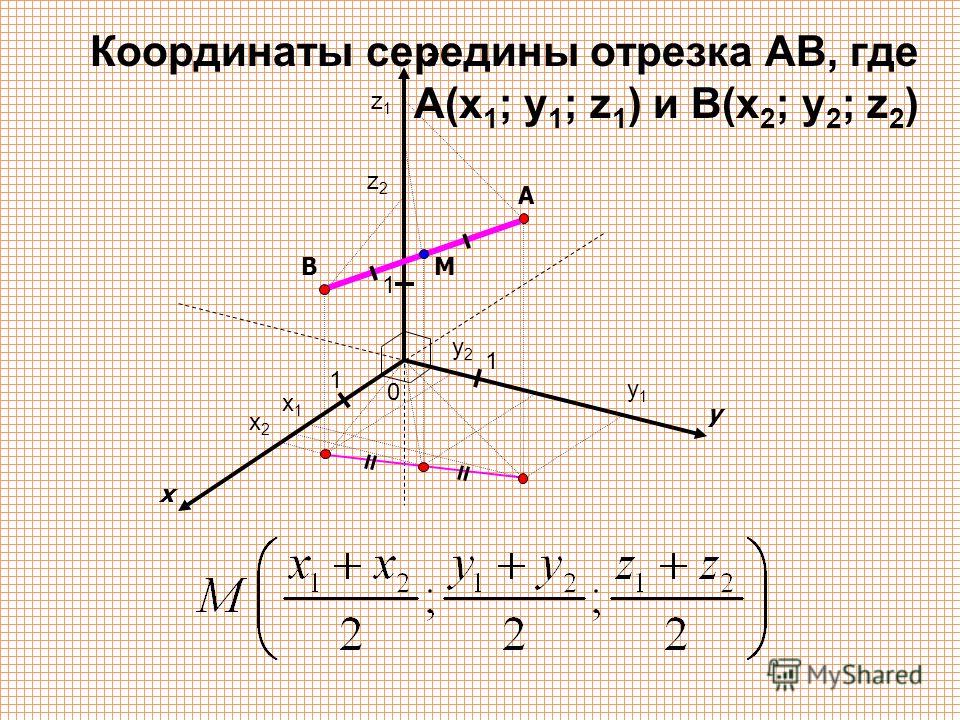
xc = xa + xb yc = ya + yb 2 2 - Формула вычисления координат середины отрезка с концами A(xa, ya, za) и B(xb, yb, zb) в пространстве:
xc = xa + xb yc = ya + yb zc = za + zb 2 2 2
Примеры задач на вычисление середины отрезка
Примеры вычисления координат середины отрезка на плоскости
Пример 1.
Найти координаты точки С, середины отрезка AB заданного точками A(-1, 3) и B(6, 5).
Решение.
| xc = | xa + xb | = | -1 + 6 | = | 5 | = 2.5 |
| 2 | 2 | 2 |
| yc = | ya + yb | = | 3 + 5 | = | 8 | = 4 |
| 2 | 2 | 2 |
Ответ: С(2.5, 4).
Пример 2.
Найти координаты точки В, если известны координаты точки C(1; 5), середины отрезка AB и точки A(-1, 3).
Решение.
xc =
xa + xb2
=> xb = 2xc — xa = 2·1-(-1)=2+1=3
yc =
ya + yb2
=> yb = 2yc — ya = 2·5-3=10-3=7
Ответ: B(3, 7).
Примеры вычисления координат середины отрезка в пространстве
Пример 3.
Найти координаты точки С середины отрезка AB заданного точками A(-1, 3, 1) и B(6, 5, -3).
Решение.
| xc = | xa + xb | = | -1 + 6 | = | 5 | = 2.5 |
| 2 | 2 | 2 |
| yc = | ya + yb | = | 3 + 5 | = | 8 | = 4 |
| 2 | 2 | 2 |
| zc = | za + zb | = | 1 + (-3) | = | -2 | = -1 |
| 2 | 2 | 2 |
Ответ: С(2.5, 4, -1).
Пример 4.
Найти координаты точки В если известны координаты точки C(1, 5, 2), середины отрезка AB и точки A(-1, 3, 10).
Решение.
xc =
xa + xb2
=> xb = 2xc — xa = 2·1-(-1)=2+1=3
yc =
ya + yb2
=> yb = 2yc — ya = 2·5-3=10-3=7
zc =
za + zb2
=> zb = 2zc — za = 2·2-10=4-10=-6
Ответ: B(3, 7, -6).
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Даны точки
Требуется найти координаты точкиK(x,y),

отрезокMN
в отношении
Рассмотрим векторы
Эти векторы коллинеарны
Из векторной алгебры известно, что если
векторы коллинеарны, то соответствующие
координаты пропорциональны. Имеем:
(по условию).
Из этих уравнений
легко найти x
и y
(2.1.1)
Если
то точкаK
является серединой отрезка MN.
Формулы (2.1) примут вид:
(2.1.2)
Это формулы
координат середины отрезка.
Пример 1.
Найти
координаты
точки K,
делящей отрезок MN,
где M(-1,4)
и N(2,1),
в отношении 2 : 1.
Решение.
По условию
Подставим координаты точкиM
и N
в формулы (2.1.1). Имеем:
Точка K
имеет координаты: x=1,
y=2.
Ответ: K(1,2).
Пример 2.
Отрезок АВ разделен на три равные части.
Определить координаты точек деления,
если А(3,-2), В(6,4).
Решение.
Обозначим точки деления С и D.
Точка D
делит отрезок АВ в отно-
шении АD:DB
= 2. Координаты точки D
найдем по формулам (2.1.1).
Итак, D(5,2).
Координаты точки
С можно найти аналогично, взяв
Существует другой
способ нахождения координат точки С.
Точка С является серединой отрезка АD.
По формулам (2.1.2) имеем
Ответ:
D(5,2)
; C(4,0).
Пример 3.
Найти точку пересечения медиан
треугольника АВС, где А(-1,3) ;
B(3,-2);
C(5,3).
Р
Пусть точка О – точка пересечения медиан
AM
и BN
треугольника ABC.
Точка М является серединой отрезка ВС.
По формулам (2.1.2) получим координаты
точки М:
Из школьного курса
планиметрии известно, что точка О делит
медиану АМ в отношении АО:ОМ = 2:1.
По формулам (2.1.1) получим
Ответ:
Точка пересечения медиан
Замечание: Точка
пересечения медиан треугольника является
его центром тяжести.
3. Прямая на плоскости.
3.1. Простейшей из
линий является прямая. Всякую прямую,
не параллельную оси ординат, можно
представить уравнением вида
,
(3.1.1)
где к есть тангенс
угла
образованного прямой с положительным
направлением оси абсцисс (ox).
Величину к называют
угловым
коэффициентом.
Величину b
– начальной
ординатой.
Если прямая
параллельна оси ox,
то
Уравнение прямой примет вид:y
= b
(3.1.2)
Если прямая
параллельна оси oy,
то
не существует. В этом случае уравнение
прямой будет иметь вид:x
= a
(3.1.3),
где а – абсцисса точки, через которую
проходит данная прямая ( точки пересечения
прямой с осью ox).
Пример 1.
Какую прямую представляет уравнение
Р
уравнение задает прямую, у которой
Так как
Поэтому данное уравнение представляет
прямую, проходящую через начало координат
(b
= 0) и образующую с осью ox
угол
Пример 2.
Написать
уравнение прямой, параллельной оси ox
и имеющей на-

ординату b
=
.
Решение: По
формуле (3.1.2) имеем y
=где
Итак, искомая
прямая задается уравнением
Ответ:
Пример 3.
Написать уравнение прямой, параллельной
оси oy
и проходящей
через точку
M(3,1).

По формуле (3.1.3) уравнение прямой имеет
вид x
= a
, где а – абсцисса точки М. а = 3. Уравнение
прямой x
= 3.
Ответ:
x
= 3.
3.2. Уравнение
прямой по точке и угловому коэффициенту.
Пусть прямая
проходит через точку
и имеет угловой коэффициент к. Уравнение
такой прямой можно записать в виде
(3.1.1)гдеb
— неизв
величина. Так как прямая проходит через
точку,
то координаты точки удовлетворяют
уравнению (3.1.1). ИмеемОтсюда
Подставим значение
“b”
в уравнение (3.1.1), получим
—
или
(3.2.1)
Полученное уравнение
называется уравнением прямой по точке
и угловому коэффициенту.
Пример 1.
Составить уравнение прямой, проходящей
через точку
и образующей с
положительным направлением оси ox
угол
Решение:
Так как
то
Применив формулу (3.2.1), получимy-(-2)=-1(x-1)
y+2
= -x+1
y=-x-1.
Ответ:
y=-x-1.
Пример 2.
Составить
уравнение прямой, проходящей через
точку А(-3,4) и имеющей угловой коэффициент
к = 2.
Решение:
Применяем
формулу (3.2.1) y
– 4 = 2 (x+3)
y
— 4 = 2x
+ 6
y
= 2x
+
10.
Ответ:
y
= 2x
+ 10.
Пример 3.
Составить
уравнение прямой, проходящей через
точку М(-1, 2) параллельно оси ox.
Решение:
Если прямая параллельна оси ox,
то угол между прямой и положительным
направлением оси ox
равен нулю. Следовательно,
По формуле (3.2.1) получимy
– 2 = 0 (x
+ 1)
y
– 2 = 0
Ответ:
y
= 2.
3
прямой по точке и нормальному вектору.
Пусть прямая
проходит через точку
Поднормальным
вектором
понимают вектор, который перпендикулярен
данной прямой. Обозначим его
Возьмем на прямой произвольную точкуM(x,y)
и рассмотрим вектор
Используя векторную алгебру, найдем
координаты вектораВектор
перпендикулярен вектору
.Из векторной
алгебры известно, что скалярное
произведение этих векторов равно нулю.
Следовательно,
(3.3.1)
Полученное уравнение
называется уравнением
прямой по точке и нормальному вектору.
Преобразуем полученное уравнение:
Ax + By —
A— B
=
0.Пусть
C = -A-B
,тогда
получим:
Ax
+ By + C = 0 (3.3.2)
Уравнение (3.3.2)
называется общим
уравнением прямой.
Напомним, что коэффициенты А и В в
уравнении определяют координаты
нормального вектора
Рассмотрим общее
уравнение прямой подробнее.
1). Если А = 0, то
уравнение примет вид
By
+ C
= 0 ; y
= —Прямая параллельна осиox.
(3.1.2)
2). Если В = 0, то
уравнение примет вид:
Ax
+ C
= 0, x
= —
Прямая параллельна оси oy.
(3.1.3.)
3). Если С = 0, то
уравнение примет вид: Ax
+ By
= 0. y
= —
Прямая проходит через начало координат
и имеет угловой коэффициент k
= —
См. пример 1 пункт 3.1.
Из общего
уравнения прямой, если
можно найти угловой коэффициент к. Для
этого выразимy
из этого уравнения : Ax
+ By
+ C
= 0.
By = — Ax –
C ; y = ——
Отсюда,
k
= —
(3.3.3)
Пример 1.
Прямая задана уравнением 3x
– 4y
+5 = 0. Найти координаты нормального
вектора.
Решение:
Координатами
нормального вектора
являются коэффициенты приx
и y
данного уравнения прямой. Имеем А = 3;
В = — 4.
Ответ:
Пример 2.
Составить уравнение прямой, проходящей
через точку М(2,-1) и имеющей нормальный
вектор
Решение:
Применяем
формулу (3.3.1). Имеем 0(x
– 2) + 2(y
+ 1) = 0
2y
+ 2 = 0
y
+ 1 = 0.
Ответ:
y
+ 1 = 0.
Пример 3.
Составить уравнение прямой, проходящей
через точку М(0; 1) перпендикулярно вектору
где А(-1; 2), В(1; -1).
Решение:
Найдем координаты вектора
—
(-1); -1-2);
(2;
-3).
Вектор является нормальным
векторомискомой
прямой. По формуле (3.3.1) имеем 2(x
– 0) -3(y
-1) = 0
2x
– 3y
+ 3 = 0.
Ответ:
2x
– 3y
+ 3 = 0.
3.4. Уравнение
прямой по точке и направляющему вектору.
Пусть прямая
проходит через точку
Направляющим вектором
данной прямой называется вектор,
параллельный этой прямой. Пусть дан
векторВозьмем на прямой произвольную точкуM(x,y)
и рассмотрим вектор
Векторы
и
коллинеарны,следовательно, их
соответствующие координаты пропорциональны.
(3.4.1)
Полученное уравнение
является уравнением прямой по
точке и направляющему вектору.
Пример 1.
Прямая задана
уравнением:
Написать координаты
направляющего вектора; найти координаты
точки, лежащей на прямой; составить
общее уравнение прямой.
Решение:
Направляющий
вектор
= (−1; 2). Точку
мы получим, приравняв нулю числители
данного уравнения:x
+ 2 = 0
x
=−2; y
– 3 = 0
y
= 3.
Итак,
(−2; 3).
Общее уравнение
прямой получим по свойству пропорций:
(x+2)∙2
= (y−3)∙(−
1)
2x
+ 4 = −y
+ 3
2x
+ y
+ 1 = 0.
Ответ:
(−1;
2),
(−2;
3), 2x
+ y
+ 1 = 0.
Пример 2.
Составить
уравнение прямой по точке М(2,-5) и
направляющему вектору
(-2,4).
Решение:
Применяем
формулу
(3.4.1). Имеем:
4(x-2)
= -2(y+5)
4x
— 8 = — 2y
– 10
4x
+ 2y
+ 2 = 0
2x
+ y
+ 1 =0.
Ответ: 2x
+ y
+ 1 = 0.
Пример 3.
Через точку
С(- 2, 1) провести прямую, параллельную
вектору
где А(2,-1), В(3,4).
Решение:
Вектор можно взять за
направляющий вектор данной прямой. (3-2; 4-(-1)) = (1;
5). Применяем
формулу (3.4.1). Имеем:
5(x
+ 2) = y
– 1
5x
+ 10 = y
– 1
5x
– y
+ 11 = 0.
Ответ:
5x
– y
+11 = 0.
3.5. Уравнение
прямой, проходящей через две заданные
точки.
Известно, что
через две данные точки можно провести
единственную прямую. П
прямая проходит через точкиЗа направляющий вектор
данной прямой можно взять вектор
.
Составим уравнение
прямой по точке и направляющему
вектору
По формуле (3.4.1)
имеем:
(3.5.1)
Если
то прямая параллельна осиoy.
Ее уравнение имеет вид:
(3.5.2)
Если
то прямая параллельна осиox.
Ее уравнение :
y
=
(3.5.3)
Пример 1.
Составить уравнение прямой АВ, если
А(2,-1); В(1,3).
Решение:
Применяем
формулу (3.5.1):
4(x
— 2) = -(y
+ 1)
4x
+ y
– 7 = 0.
Ответ:
4x
+ y
– 7 = 0.
Пример 2.
Составить уравнение прямой, проходящей
через точки М(4,-2) и N(4,5).
Решение:
Так как
то по формуле (3.5.2) уравнение прямой
имеет вид:
x = 4.
Прямая
параллельна оси oy.
Пример 3. Дан
треугольник АВС, у которого А(1,2), В(4,3),
С(1,3). Составить уравнения его сторон.
Решение: 1)
Найдем уравнение стороны АВ. ПО формуле
(3.5.1) имеем:
x
– 1 = 3(y
– 2)
x
– 3y
+ 5 = 0.
2) Сторона ВС
находится по формуле (3.5.3), так как
y
= 3.
3) Уравнение стороны
АС выпишем по формуле (3.5.2), так как
x
= 1.
Ответ:
AB:
x
– 3y
+ 5 = 0; BC:
y
= 3; AC:
x
= 1.
Пример 4.
Даны вершины треугольника АВС А(- 1, 3),
В(3,-2), С(5,3). Составить уравнение медианы,
проведенной из вершины В.

ВМ – медиана, тогда точка М является
серединой отрезка АС. По формулам (2.1.2)
имеем:
M(2,3).
Уравнение медианы
ВМ получим по формуле (3.5.1):
5(x-
3) = -(y
+2)
5x
+ y
– 13 = 0.
Ответ:
BM:
5x
+ y
– 13 = 0.
3.6. Уравнение
прямой в отрезках.
Если прямая отсекает
на осях отрезки а и b,
не равные нулю, то ее уравнение можно
записать в виде:
.
(3.6.1)
Такое уравнение
называется уравнением
в отрезках.
Рассмотрим это уравнение. Пусть x
= 0, тогда
Пусть y
= 0, тогда
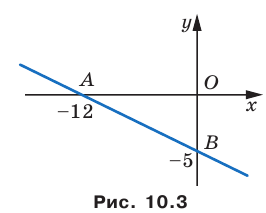
Прямая проходит
через точки А(а,0) и B(0,b).

Записать
уравнение прямой в отрезках. Построить
эту прямую.
3x
– 2y + 12 = 0.
Решение:
3x
– 2y
= — 12. Разделим обе части этого уравнения
на — 12. П
a = — 4, b = 6.
Построим полученную
прямую. Для этого отложим на оси ox
a
= — 4, на оси oy
b
= 6 и соединим полученные точки.
3.7. Расстояние
от точки до прямой.
Пусть прямая
задана уравнением Ax
+ By
+ C
= 0. Найдем расстояние от точки
до этой прямой. Подрасстоянием
от точки до прямой понимают длину о
где М – основание перпендикуляра,
опущенного из точкина данную прямую. Расстояние
находим по формуле:
(3.7.1)
Пример. Найти
расстояние от точки
до прямой 3x
+ 4y
– 22 =0.
Решение: По
формуле (3.7.1) получим:
Ответ:
d
= 4.
Соседние файлы в предмете Математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.20154.96 Кб8Содержание OneNote.onetoc2
- #
Вычисление координат некоторой точки С, которая делит заданный отрезок АВ в определенном отношении, может быть выполнено по формулам:
хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ),
где (хА; уА) и (хВ; уВ) – координаты концов заданного отрезка АВ; число λ = АС/СВ – отношение, в котором отрезок АВ делится точкой С, имеющей координаты (хС; уС).
Если отрезок АВ делится точкой С пополам, то число λ = 1 и формулы для хС и уС примут вид:
хС = (хА + хВ)/2, уС = (уА + уВ)/2.
Нужно иметь ввиду, что в задачах λ – это отношение длин отрезков, а поэтому числа, входящие в данное отношение не есть длины самих отрезков в заданной единице измерения. Например, АС = 12 см, СВ = 16 см: λ = АС/СВ = 12 см / 16 см = 3/4.
1. Поиск координат середины некоторого отрезка, по заданным координатам его концов
Пример 1.
Точки А(-2; 3) и В(6; -9) – концы отрезка АВ. Найти точку С, являющиеся серединой отрезка АВ.
Решение.
В условии задачи задано, что хА = -2; хВ = 6; уА = 3 и уВ = -9. Требуется найти С(хС ; уС).
Применяя формулы хС = (хА + хВ)/2, уС = (уА + уВ)/2, получим:
хС = (-2 + 6)/2 = 2, уС = (3 + (-9))/2 = -3.
Таким образом, точка С, являющаяся серединой отрезка АВ, имеет координаты (-2; 3) (рис. 1).
2. Вычисление координат конца некоторого отрезка, зная координаты его середины и другого конца
Пример 2.
Одним концом отрезка АВ является точка А, с координатами (-3; -5), а его серединой точка С(3; -2). Вычислите координаты второго конца отрезка – точки В.
Решение.
По условию задачи становится ясно, что хА = -3; уА = -5; хС = 3 и уС = -2.
Подставив эти значения в формулы хС = (хА + хВ)/2, уС = (уА + уВ)/2, получим:
3 = (-3 + хВ)/2 и
-2 = (-5 + уВ)/2.
Решив первое уравнение относительно хВ и второе относительно уВ, найдем: хВ = 9 и уВ = 1, получается, что нужная точка В будет задаваться координатами (9; 1) (рис. 2).
3. Вычисление координат вершин некоторого треугольника по заданным координатам середин его сторон
Пример 3.
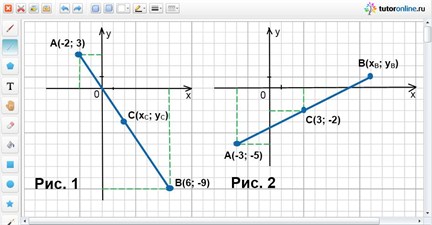
Серединами сторон треугольника АВС являются точки D(1; 3), E(-1; -2) и F(4; -1). Найти координаты вершин А, В и С данного треугольника.
Решение.
Пусть точка D и есть середина стороны АВ, точка Е – середина ВС и точка F – середина сторона АС (рис. 3). Необходимо найти точки А, В и С.
Обозначаем вершины треугольника через А(хА; уА), В(хВ; уВ) и С(хС; уС) и зная координаты точек D, Е и F, по формулам хС = (хА + хВ)/2, уС = (уА + уВ)/2 получим:
{1 = (хА + хВ)/2,
{-1 = (хВ + хС)/2,
{4 = (хА + хС)/2,
и
{3 = (уА + уВ)/2,
{-2 = (уВ + уС)/2,
{-1 = (уА + уС)/2.
Приведем уравнения к целому виду:
{хА + хВ = 2,
{хВ + хС = -2,
{хА + хС = 8,
и
{уА + уВ = 6,
{уВ + уС = -4,
{уА + уС = -2.
Решив системы, получим:
хА = 6; хВ = -4; хС = 2.
уА = 4; уВ = 2; уС = -6.
Точки А(6; 4), В(-4; 2) и С(2; -6) и есть необходимые вершины треугольника.
4. Вычисление координат точек, которые делят отрезок в определенном отношении, по заданным координатам концов этого отрезка
Пример 4.
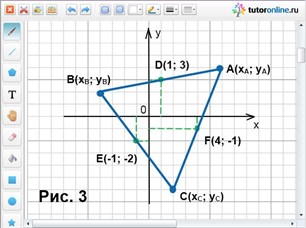
Отрезок АВ поделен точкой С в отношении 3 : 5 (считая от точки А к точке В). Концы отрезка АВ – точки А(2; 3) и В(10; 11). Найти точку С.
Решение.
В условии задачи сказано, что хА = 2; хВ = 10; уА = 3; уВ = 11; λ = АС/СВ = 3/5. Найти С(хС; уС) (рис. 4).
по формулам хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ) получим:
хС = (2 + 3/5 · 10) / (1 + 3/5) = 5 и уС = (3 + 3/5 · 11) / (1 + 3/5) = 6. Таким образом, имеем С(5; 6).
Выполним проверку: АС = 3√2, СВ = 5√2, λ = АС/СВ = 3√2/5√2 = 3/5.
Замечание. В условии задачи указано, что деление отрезка производится в заданном отношении от точки А к точке В. Если бы это не уточнялось, то задача имела бы два решения. Второе решение: деление отрезка от точки В к точке А.
Пример 5.
Некоторый отрезок АВ разделен в отношении 2 : 3 : 5 (считая от точки А к точке В), его концы – есть точки с координатами А(-11; 1) и В(9; 11). Найти точки деления данного отрезка.
Решение.
Обозначим точки деления отрезка от А к В через С и D. В условии задачи дано, что
хА = -11; хВ = 9; уА = 1; уВ = 11. Найти С(хС; уС) и D(хD; уD), если АС : СD : DB = 2 : 3 : 5.
Точка С делит отрезок АВ в отношении λ = АС/СВ = 2/(3 + 5) = 2/8 = 1/4.
По формулам хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ) получим:
хС = (-11 + ¼ · 9) / (1 + 1/4) = -7 и уС = (1 + ¼ · 11) / (1 + 1/4) = 3.
Таким образом, С(-7; 3).
Точка D – есть середина отрезка АВ. Применив формулы хD = (хА + хВ)/2, уD = (уА + уВ)/2, найдем:
хD = (-11 + 9)/2 = -1, уD = (1 + 11)/2 = 6. Значит, D имеет координаты (-1; 6).
5. Вычисление координат точек, которые делят отрезок, если заданы координаты концов этого отрезка и число частей, на которые этот отрезок разделен
Пример 6.
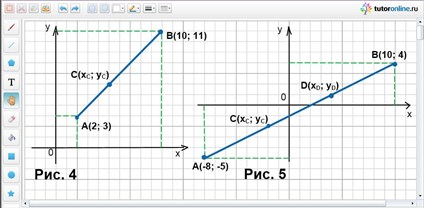
Концы отрезка – точки А(-8; -5) и В(10; 4). Найти точки С и D, которые делят этот отрезок на три равные части.
Решение.
Из условия задачи известно, что хА = -8; хВ = 10; уА = -5; уВ = 4 и n = 3. Найдем С(хС; уС) и D(хD; уD) (рис. 5).
Найдем точку С. Она делит отрезок АВ в отношении λ = 1/2. Деление производим от точки А к точке В. По формулам хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ) имеем:
хС = (-8 + ½ · 10) / (1 + 1/2) = -2 и уС = (-5 + ½ · 4) / (1 + 1/2) = -2. Таким образом, С(-2; -2).
Деление отрезка СВ выполняется в отношении 1 : 1, поэтому используем формулы
хD = (хА + хВ)/2, уD = (уА + уВ)/2:
хD = (-2 + 10)/2 = 4, уD = (-2 + 4)/2 = 1. Таким образом, D(4; 1).
Точки деления С(-2; -2) и D(4; 1).
Замечание: Точку D можно найти, производя деление отрезок АВ в отношении 2 : 1. В таком случае надо будет снова применить формулы хD = (хА + λхВ) / (1 + λ), уD = (уА + λуВ) / (1 + λ).
Пример 7.
Точки А(5; -6) и В(-5; 9) – концами отрезка. Найти точки, которые поделят данный отрезок на пять равных частей.
Решение.
Пусть последовательные точки деления от А к В будут С(хС; уС), D(хD; уD), Е(хE; уE) и F(хF; уF). В условия задачи сказано, что хА = 5; хВ = -5; уА = -6; уВ = 9 и n = 5.
Найдем по формулам хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ) точку С. Она делит отрезок АВ в отношении λ = 1/4:
хС = (5 + 1/4 · (-5)) / (1 + 1/4) = 3 и уС = (-6 + 1/4 · 9) / (1 + 1/4) = -3, получаем, что точка С имеет координаты (3; -3).
Деление отрезка АВ точкой D производится в отношении 2 : 3 (т.е. λ = 2/3), поэтому:
xD = (5 + 2/3 · (-5)) / (1 + 2/3) = 1 и уD = (-6 + 2/3 · 9) / (1 + 2/3) = 0, значит D(1; 0).
Найдем точку Е. Она делит отрезок АВ в отношении λ = 2/3:
XЕ = (5 + 3/2 · (-5)) / (1 + 3/2) = -1 и уЕ = (-6 + 3/2 · 9) / (1 + 3/2) = 3. Таким образом, Е(-1; 3).
Точка F делит отрезок АВ в отношении λ = 4/1, поэтому:
XF = (5 + 4 · (-5)) / (1 + 4) = -3 и уF = (-6 + 4 · 9) / (1 + 4) = 6, F(-3; 6).
Точки деления С(-2; -2); D(4; 1); Е(-1; 3) и F(-3; 6).
Остались вопросы? Не знаете, как решить задачу на деление отрезка?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Содержание:
Декартовы координаты на плоскости:
Изучая материал этой лекции, вы расширите свои знания о координатной плоскости.
Вы научитесь находить длину отрезка и координаты его середины, зная координаты его концов.
Сформируете представление об уравнении фигуры, выведете уравнения прямой и окружности.
Ознакомитесь с методом координат, позволяющим решать геометрические задачи средствами алгебры.
Расстояние между двумя точками с заданными координатами. Координаты середины отрезка
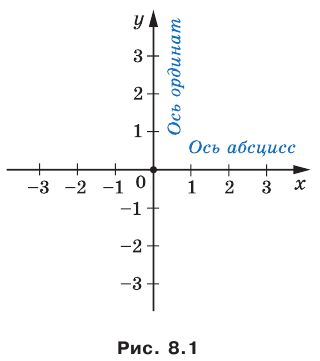
В 6 классе вы ознакомились с координатной плоскостью, то есть с плоскостью, на которой изображены две перпендикулярные координатные прямые (ось абсцисс и ось ординат) с общим началом отсчета (рис. 8.1). Вы умеете отмечать на ней точки по их координатам и наоборот, находить координаты точки, отмеченной на координатной плоскости.
Договорились координатную плоскость с осью
Координаты точки на плоскости 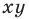
Вы знаете, как находить расстояние в между двумя точками, заданными своими координатами на координатной прямой. Для точек 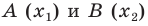
Научимся находить расстояние между точками 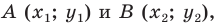
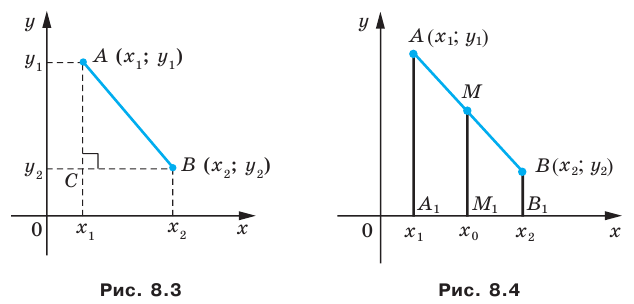
Рассмотрим случай, когда отрезок 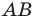
Через точки 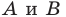
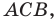
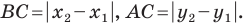
Тогда формулу расстояния между точками 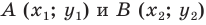
Докажите самостоятельно, что эта формула остается верной и для случая, когда отрезок 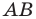
Пусть 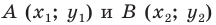
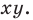
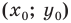
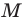
Рассмотрим случай, когда отрезок 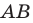
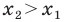
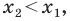
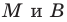
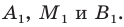
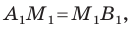
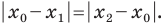
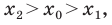
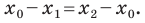

Формулы для нахождения координат середины отрезка остаются верными и для случая, когда отрезок 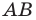
Пример №1
Докажите, что треугольник с вершинами в точках 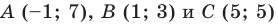
Решение:
Используя формулу расстояния между двумя точками, найдем стороны данного треугольника:
Следовательно, 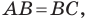
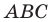
Поскольку 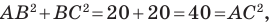
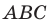
Пример №2
Точка 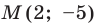
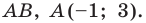
Решение:
Обозначим 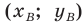
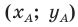
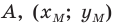
Поскольку 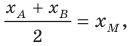
Аналогично
Ответ:
Пример №3
Докажите, что четырехугольник 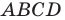
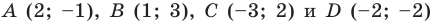
Решение:
Пусть точка 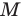
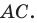
Следовательно,
Пусть точка 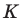
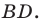
Следовательно,
Таким образом, точки 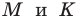
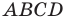
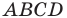
Найдем диагонали параллелограмма:
Следовательно, диагонали параллелограмма 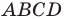
Уравнение фигуры. Уравнение окружности
Из курса алгебры 7 класса вы знаете, какую фигуру называют графиком уравнения. В этом пункте вы ознакомитесь с понятием уравнения фигуры.
Координаты 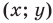
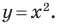
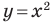
Определение. Уравнением фигуры 
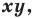
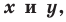
- если точка принадлежит фигуре
то ее координаты являются решением данного уравнения;
- любое решение
данного уравнения является координатами точки, принадлежащей фигуре
Например, уравнение прямой, изображенной на рисунке 9.2, имеет вид 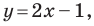
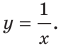
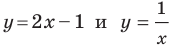
Если данное уравнение является уравнением фигуры 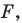
Пользуясь этими соображениями, выведем уравнение окружности радиуса 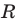
Пусть 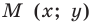
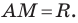
Отсюда
Мы показали, что координаты 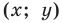
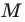
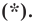
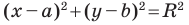
Пусть пара чисел 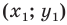
Тогда 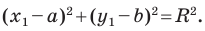
Это равенство показывает, что точка 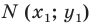
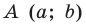
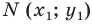
Итак, мы доказали следующую теорему.
Теорема 9.1. Уравнение окружности радиуса 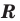
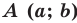
Верно и такое утверждение: любое уравнение вида 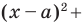
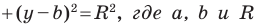
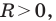
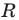
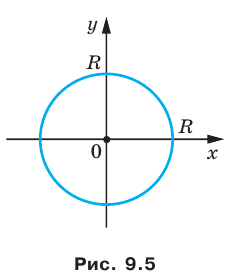
Если центром окружности является начало координат (рис. 9.5), то 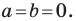
Пример №4
Составьте уравнение окружности, диаметром которой является отрезок 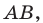
Решение:
Поскольку центр окружности является серединой диаметра, то можем найти координаты 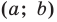
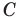
Следовательно,
Радиус окружности 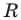
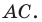
Следовательно, искомое уравнение имеет вид
Ответ:
Пример №5
Докажите, что уравнение 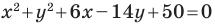
Решение:
Представим данное уравнение в виде
Следовательно, данное уравнение является уравнением окружности с центром в точке 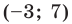
Ответ:
Пример №6
Докажите, что треугольник с вершинами в точках 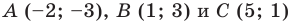
Решение:
Найдем квадраты сторон данного треугольника:
Поскольку 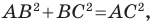
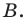
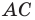
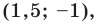
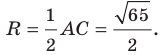
Ответ:
Уравнение прямой
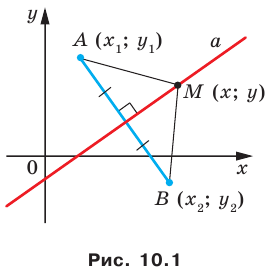
В предыдущем пункте, рассматривая окружность как ГМТ, равноудаленных от данной точки, мы вывели ее уравнение. Для того чтобы вывести уравнение прямой, рассмотрим ее как ГМТ, равноудаленных от двух данных точек.
Пусть 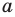
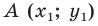
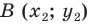
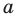
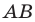
Пусть 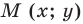
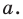
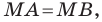
Мы показали, что координаты 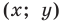
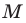
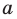
Теперь покажем, что любое решение уравнения 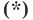
Пусть 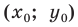
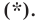
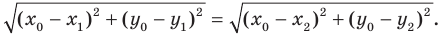
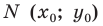
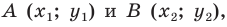
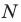
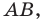
Итак, мы доказали, что уравнение 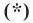
Однако из курса алгебры 7 класса вы знаете, что уравнение прямой выглядит гораздо проще, а именно: 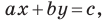
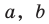
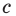
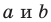
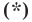
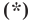
Раскроем скобки и приведем подобные слагаемые. Получим:
Обозначив 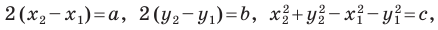
Поскольку точки 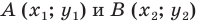
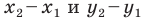
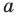
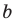
Итак, мы доказали следующую теорему.
Теорема 10.1. Уравнение прямой имеет вид?
где 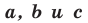
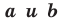
Верно и такое утверждение: любое уравнение вида 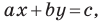
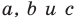
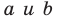
Если 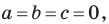
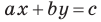
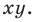
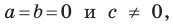
Из курса алгебры 7 класса вы знаете, что уравнение вида 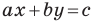
на уроках алгебры в 7 классе мы приняли без доказательства тот факт, что графиком линейной функции 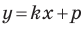
Перепишем уравнение 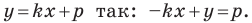
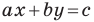
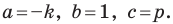
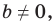
А любую ли прямую на плоскости можно задать уравнением вида 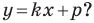
Дело в том, что прямая, перпендикулярная оси абсцисс, не может являться графиком функции, а следовательно, не может быть задана уравнением вида
Вместе с тем, если в уравнении прямой 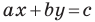
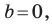
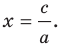
Если 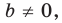
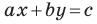
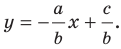
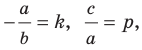
Следовательно, если 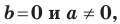
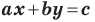
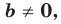
Уравнение невертикальной прямой удобно записывать в виде
Данная таблица подытоживает материал, рассмотренный в этом пункте.
Пример №7
Составьте уравнение прямой, проходящей через точки:
Решение:
1) Поскольку данные точки имеют равные абсциссы, то прямая 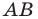
2) Поскольку данные точки имеют разные абсциссы, то прямая 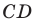
Подставив координаты точек 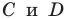
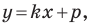
Решив эту систему уравнений, находим, что
Ответ:
Пример №8
Найдите периметр и площадь треугольника, ограниченного прямой 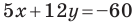
Решение:
Найдем точки пересечения данной прямой с осями координат.
С осью абсцисс: при 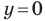
С осью ординат: при 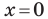
Следовательно, данная прямая и оси координат ограничивают прямоугольный треугольник 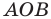
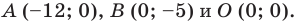
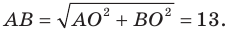
Ответ:
Угловой коэффициент прямой
Рассмотрим уравнение 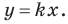
Покажем, что прямые 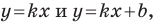
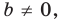
Точки 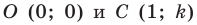
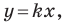
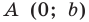
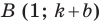
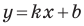
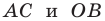
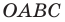
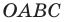
Теперь мы можем сделать такой вывод: если 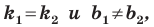
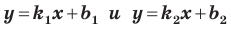
Пусть прямая 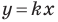
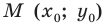
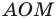
Если прямая 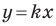
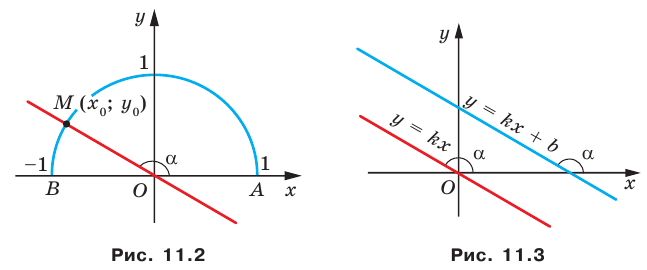
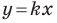
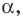
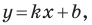
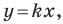
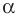
Рассмотрим прямую 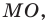
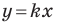
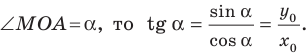
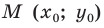
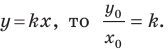
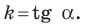
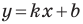
где 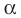
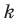
Если невертикальные прямые параллельны, то они образуют равные углы с положительным направлением оси абсцисс. Тогда тангенсы этих углов равны, следовательно, равны и их угловые коэффициенты. Таким образом,
если прямые 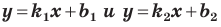
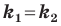
Выводы (1) и (2) объединим в одну теорему.
Теорема 11.1. Прямые 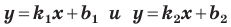
Пример №9
Составьте уравнение прямой, которая проходит через точку 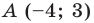
Решение:
Пусть уравнение искомой прямой 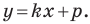
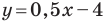
Следовательно, искомое уравнение имеет вид 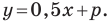
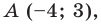
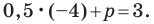
Искомое уравнение имеет вид
Ответ:
Метод координат
Мы часто говорим: прямая 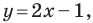
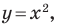
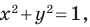
Проиллюстрируем сказанное на таком примере.
Из наглядных соображений очевидно, что прямая и окружность имеют не более двух общих точек. Однако это утверждение не является аксиомой, поэтому его надо доказывать.
Эта задача сводится к исследованию количества решений системы уравнений
где числа 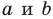
Решая эту систему методом подстановки, мы получим квадратное уравнение, которое может иметь два решения, одно решение или вообще не иметь решений. Следовательно, для данной системы существует три возможных случая:
- система имеет два решения — прямая и окружность пересекаются в двух точках;
- система имеет одно решение — прямая касается окружности;
- система не имеет решений — прямая и окружность не имеют общих точек.
С каждым из этих случаев вы встречались, решая задачи 10.17-10.19.
Метод координат особенно эффективен в тех случаях, когда требуется найти фигуру, все точки которой обладают некоторым свойством, то есть найти геометрическое место точек.
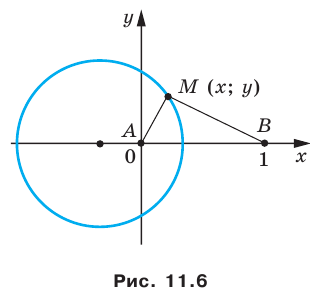
Отметим на плоскости две точки 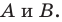
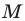
Это серединный перпендикуляр отрезка 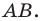
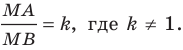
Плоскость, на которой отмечены точки 
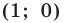
Пусть 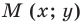
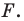
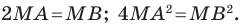
Следовательно, если точка 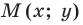
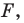
Пусть 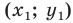
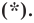
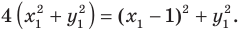
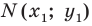
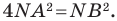
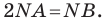
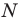
Таким образом, уравнением фигуры 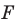
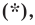
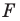
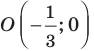
Мы решили задачу для частного случая, когда 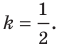
Как строили мост между геометрией и алгеброй
Идея координат зародилась очень давно. Ведь еще в старину люди изучали Землю, наблюдали звезды, а по результатам своих исследований составляли карты, схемы.
Во II в. до н. э. древнегреческий ученый Гиппарх впервые использовал идею координат для определения места расположения объектов на поверхности Земли.
Только в XIV в. французский ученый Николя Орем (ок. 1323-1382) впервые применил в математике идею Гиппарха: он разбил плоскость на клетки (как разбита страница вашей тетради) и стал задавать положение точек широтой и долготой.
Однако огромные возможности применения этой идеи были раскрыты лишь в XVII в. в работах выдающихся французских математиков Пьера Ферма и Рене Декарта. В своих трудах эти ученые показали, как благодаря системе координат можно переходить от точек к числам, от линий к уравнениям, от геометрии к алгебре.
Несмотря на то что П. Ферма опубликовал свою роботу на год раньше Р. Декарта, систему координат, которой мы сегодня пользуемся, называют декартовой. Р. Декарт в своей работе «Рассуждение о методе» предложил новую удобную буквенную символику, которой с незначительными изменениями мы пользуемся и сегодня. Вслед за Декартом мы обозначаем переменные последними буквами латинского алфавита 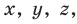
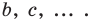
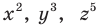
Справочный материал
Расстояние между двумя точками
Расстояние между точками 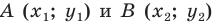
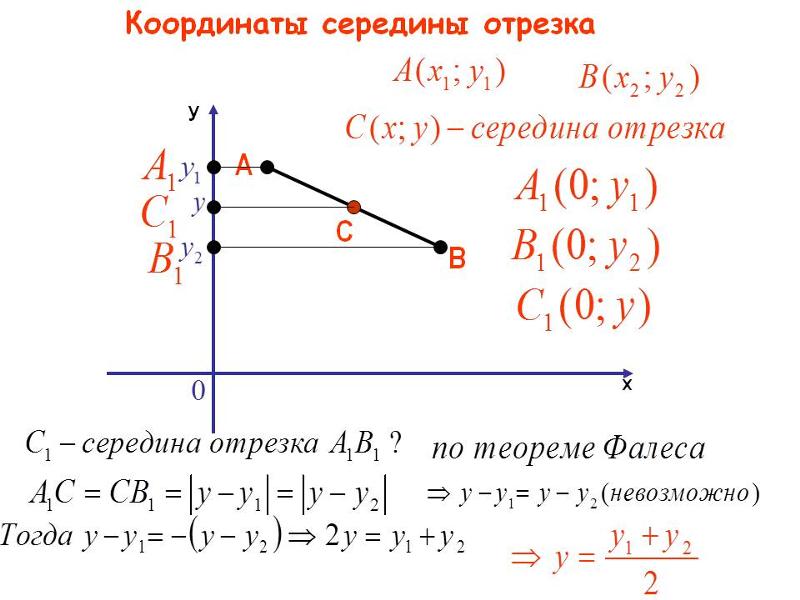
Координаты середины отрезка
Координаты 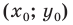
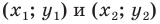
Уравнение фигуры
Уравнением фигуры 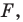
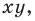
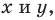
1) если точка принадлежит фигуре 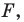
2) любое решение 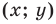
Уравнение окружности
Уравнение окружности радиуса 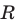
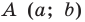
Любое уравнение вида 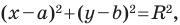
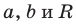
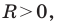
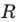
Уравнение прямой
Уравнение прямой имеет вид 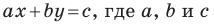
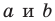
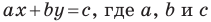
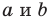
Если 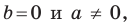
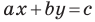
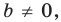
Угловой коэффициент прямой
Коэффициент 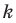
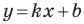
Необходимое и достаточное условие параллельности невертикальных прямых
Прямые 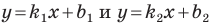
- Декартовы координаты в пространстве
- Геометрические преобразования в геометрии
- Планиметрия — формулы, определение и вычисление
- Стереометрия — формулы, определение и вычисление
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование
Определение длины отрезка по координатам. Нахождение координат середины отрезка: примеры, решения
Если вы хорошо заточенным карандашом прикоснетесь к тетрадному листу, то останется след, который дает представление о точке. (рис. 3
).
Отметим на листе бумаги две точки A
и B.
Эти точки можно соединить различными линиями (рис. 4
). А как соединить точки A
и B
самой короткой линией? Это можно сделать с помощь линейки (рис. 5
). Полученную линию называют отрезком
.
Точка и отрезок − примеры геометрических фигур
.
Точки A
и B
называют концами отрезка
.
Существует единственный отрезок, концами которого являются точки A
и B.
Поэтому отрезок обозначают, записывая точки, которые являются его концами. Например, отрезок на рисунке 5
обозначают одним из двух способов: AB
или BA.
Читают: «отрезок AB»
или «отрезок BA».
На рисунке 6
изображены три отрезка. Длина отрезка AB
равна 1
см. Он помещается в отрезке MN
ровно три раза, а в отрезке EF −
ровно 4
раза. Будем говорить, что длина отрезка
MN
равна 3
см, а длина отрезка EF −
4
см.
Также принято говорить: «отрезок MN
равен 3
см», «отрезок EF
равен 4
см». Пишут: MN =
3
см, EF =
4
см.
Длины отрезков MN
и EF
мы измерили единичным отрезком
, длина которого равна 1
см. Для измерения отрезков можно выбрать и другие единицы длины
, например: 1
мм, 1
дм, 1
км. На рисунке 7
длина отрезка равна 17
мм. Он измерен единичным отрезком, длина которого равна 1
мм, с помощью линейки с делениями. Также с помощью линейки можно построить (начертить) отрезок заданной длины (см. рис. 7
).
Вообще, измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается
.
Длина отрезка обладает следующим свойством.
Если на отрезке AB
отметить точку C,
то длина отрезка AB
равна сумме длин отрезков AC
и CB
(рис. 8
).
Пишут: AB = AC + CB.
На рисунке 9
изображены два отрезка AB
и CD.
Эти отрезки при наложении совпадут.
Два отрезка называют равными, если они совпадут при наложении.
Следовательно отрезки AB
и CD
равны. Пишут: AB = CD.
Равные отрезки имеют равные длины.
Из двух неравных отрезков бОльшим будем считать тот, у уоторого длина больше. Например, на рисунке 6
отрезок EF
больше отрезка MN.
Длину отрезка AB
называют расстоянием
между точками A
и B.
Если несколько отрезков расположить так, как показано на рисунке 10,
то получится геометрическая фигура, которую называют ломаная
. Заметим, что все отрезки на рисунке 11
ломаную не образуют. Считают, что отрезки, образуют ломаную, если конец первого отрезка совпадает с концом второго, а другой конец второго отрезка − с концом третьего и т. д.
Точки A, B, C, D, E −
вершины ломаной
ABCDE,
точки A
и E −
концы ломаной
, а отрезки AB, BC, CD, DE −
ее звенья
(см. рис. 10
).
Длиной ломаной
называют сумму длин всех ее звеньев.
На рисунке 12
изображены две ломаные, концы которых совпадают.
.
Пример 1
. Отрезок BC
на 3
см меньше отрезка AB,
длина которого равна 8
см (рис. 13
). Найдите длину отрезка AC.
Решение. Имеем: BC =
8
− 3
= 5
(см).
Воспользовавшись свойством длины отрезка, можно записать AC = AB + BC.
Отсюда AC =
8
+ 5
= 13
(см).
Ответ: 13
см.
Пример 2
. Известно, что MK =
24
см, NP =
32
см, MP =
50
см (рис. 14
). Найдите длину отрезка NK.
Решение. Имеем: MN = MP − NP.
Отсюда MN =
50
− 32
= 18
(см).
Имеем: NK = MK − MN.
Отсюда NK =
24
− 18
= 6
(см).
Ответ: 6
см.
Определить длину отрезка возможно разными способами. Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.
Длина отрезка с помощью линейки
Для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки.
Метод координат на плоскости
Если известны координаты отрезка (х1;у1) и (х2;у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Рассмотрим пример, как найти длину отрезка по координатам. Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50.
Метод координат в пространстве
Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях
. Как найти длину вектора?
- Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
- После этого нужно возвести каждую координату вектора в квадрат.
- Затем складываем квадраты координат.
- Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.
Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1;6;3) и В (3;-1;7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1; -1 — 6;7 — 3) = (2;-7;4).
Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.
Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим .
Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле
Если даны две точки пространства и , то длину отрезка можно вычислить по формуле
Примечание:
Формулы останутся корректными, если переставить местами соответствующие координаты:
и
, но более стандартен первый вариант
Пример 3
Решение:
по соответствующей формуле:
Ответ:
Для наглядности выполню чертёж
Отрезок – это не вектор
, и перемещать его куда-либо, конечно, нельзя.
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Обратите внимание на важный технический приём
– вынесение множителя из-под корня
. В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.
Вот другие распространенные случаи:
Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Готово.
Вывод:
если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки и . Найти длину отрезка .
Решение и ответ в конце урока.
Существуют три основных системы координат, используемых в геометрии, теоретической механике, других разделах физики: декартова, полярная и сферическая. В этих системах координат вся точка имеет три координаты. Зная координаты 2-х точек, дозволено определить расстояние между этими двумя точками.
Вам понадобится
- Декартовы, полярные и сферические координаты концов отрезка
Инструкция
1.
Разглядите для начала прямоугольную декартову систему координат. Расположение точки в пространстве в этой системе координат определяется координатами
x,y и z. Из начала координат к точке проводится радиус-вектор. Проекции этого радиус-вектора на координатные оси и будут координатами
этой точки.Пускай у вас сейчас есть две точки с координатами
x1,y1,z1 и x2,y2 и z2 соответственно.
Видео по теме
Существует целая группа заданий (входящих в экзаменационные типы задач), связанная с координатной плоскостью. Это задачи начиная с самых элементарных, которые решаются устно (определение ординаты или абсциссы заданной точки, либо точки симметричной заданной и другие), заканчивая задачами в которых требуется качественное знание, понимание и хорошие навыки (задачи связанные с угловым коэффициентом прямой).
Постепенно мы с вами рассмотрим все их. В этой статье начнём с элементарных. Это простые задачи на определение: абсциссы и ординаты точки, длинны отрезка, середины отрезка, синуса или косинуса угла наклона прямой.
Большинству эти задания будут не интересны. Но изложить их считаю необходимым.
Дело в том, что не все учатся в школе. Очень многие сдают ЕГЭ спустя 3-4 и более лет после её окончания и что такое абсцисса и ордината помнят смутно. Будем разбирать и другие задачи, связанные с координатной плоскостью, не пропустите, подпишитесь, на обновление блога.
емного теории.
Построим на координатной плоскости точку А с координатами х= 6, y=3.
Говорят, что абсцисса точки А равна шести, ордината точки А равна трём.
Если выразиться просто, то ось ох это ось абсцисс, ось оу это ость ординат.
То есть, абсцисса это точка на оси ох в которую проецируется точка заданная на координатной плоскости; ордината это точка на оси оу в которую проецируется оговоренная точка.
Длина отрезка на координатной плоскости
Формула для определения длины отрезка, если известны координаты его концов:
Как вы видите, длина отрезка — это длина гипотенузы в прямоугольными треугольнике с катетами равными
Х В – Х А и У В – У А
* * *
Середина отрезка. Её Координаты.
Формула для нахождения координат середины отрезка:
Уравнение прямой проходящей через две данные точки
Формула уравнения прямой походящей через две данные точки имеет вид:
где (х 1
;у 1
) и (х 2
;у 2
) координаты заданных точек.
Подставив значения координат в формулу, она приводится к виду:
y = kx + b
, где k — это угловой коэффициент прямой
Эта информация нам понадобиться при решении другой группы задач связанных с координатной плоскостью. Статья об этом будет, не пропустите!
Что ещё можно добавить?
Угол наклона прямой (или отрезка) это угол между осью оХ и этой прямой, лежит в пределах от 0 до 180 градусов.
Рассмотрим задачи.
Из точки (6;8) опущен перпендикуляр на ось ординат. Найдите ординату основания перпендикуляра.
Основание перпендикуляра опущенного на ось ординат будет иметь координаты (0;8). Ордината равна восьми.
Ответ: 8
Найдите расстояние от точки A
с координатами (6;8) до оси ординат.
Расстояние от точки А до оси ординат равно абсциссе точки А.
Ответ: 6.
A
(6;8) относительно оси Ox
.
Точка симметричная точке А относительно оси оХ имеет координаты (6;– 8).
Ордината равна минус восьми.
Ответ: – 8
Найдите ординату точки, симметричной точке A
(6;8) относительно начала координат.
Точка симметричная точке А относительно начала координат имеет координаты (– 6;– 8).
Её ордината равна – 8.
Ответ: –8
Найдите абсциссу середины отрезка, соединяющего точки
O
(0;0) и
A
(6;8).
Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (0;0) и (6;8).
Вычисляем по формуле:
Получили (3;4). Абсцисса равна трём.
Ответ: 3
*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку. Середину отрезка несложно будет определить по клеткам.
Найдите абсциссу середины отрезка, соединяющего точки A
(6;8) и B
(–2;2).
Для того, решить поставленную задачу необходимо найти координаты середины отрезка.
Вычисляем по формуле:
Получили (2;5). Абсцисса равна двум.
Ответ: 2
*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку.
Найдите длину отрезка, соединяющего точки (0;0) и (6;8).
Длина отрезка при данных координатах его концов вычисляется по формуле:
в нашем случае имеем О(0;0) и А(6;8). Значит,
*Порядок координат при вычитании не имеет значения. Можно из абсциссы и ординаты точки О вычесть абсциссу и ординату точки А:
Ответ:10
Найдите косинус угла наклона отрезка, соединяющего точки O
(0;0) и A
(6;8), с осью абсцисс.
Угол наклона отрезка – это угол между этим отрезком и осью оХ.
Из точки А опустим перпендикуляр на ось оХ:
То есть, угол наклона отрезка это угол
ВОА
в прямоугольном треугольнике АВО.
Косинусом острого угла в прямоугольном треугольнике является
отношение прилежащего катета к гипотенузе
Необходимо найти гипотенузу
ОА.
По теореме Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Таким образом, косинус угла наклона равен 0,6
Ответ: 0,6
Из точки (6;8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра.
Через точку (6;8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью оУ
.
Найдите расстояние от точки A
с координатами (6;8) до оси абсцисс.
Найдите расстояние от точки A
с координатами (6;8) до начала координат.
Как найти середину отрезка на координатной плоскости?
Как найти середину отрезка на координатной плоскости?
Расстояние между точками определяется модулем разницы их координат, т.
Как найти точку в векторе?
Основное соотношение. Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.
Как определить широту и долготу на карте?
Важно: Географическая долгота измеряется от 0 до 180° . Чтобы определить географическую широту, нужно от заданной точки провести воображаемую прямую вдоль ближайшей параллели. Это и будет географическая широта. Она будет указана сбоку на карте.
Как найти широту и долготу география?
Важно: Географическая долгота измеряется от 0 до 180° .
Как правильно писать географические координаты?
Как правильно вводить координаты
- Вместо d используйте символ градуса.
- Используйте в качестве десятичного разделителя точку, а не запятую. Неправильно: 2,17403 . …
- Указывайте сначала широту, а затем долготу.
- Для широты используйте значения в диапазоне от -90 до 90.
- Долготу указывайте в диапазоне от -180 до 180.
Как определить квадрат на топографической карте?
Квадрат, в котором находится цель (объект), указывают подписями (номерами) образующих его километровых линий, вначале нижней горизонтальной линии (абсциссы X), а затем левой вертикальной линии (ординаты У).
Что такое квадрат на карте?
Квадрат всегда указывается цифрами километровых линий, пересечением которых образован юго-западный (нижний левый) угол.
Что значит по улитке 8?
Во многих советских и российских военных фильмах, где по сюжету солдаты вынуждены прибегать к помощи артиллерии в ходя тяжёлого боя, вы могли слышать примерно следующую фразу: Требуется заградительный огонь по квадрату шестьдесят пять-двенадцать по улитке 8.
Как на топографических картах изображаются судоходные реки или судоходные участки рек?
Реки в зависимости от ширины русла изображаются масштабным или внемасштабным (в одну и две линии) условным знаком. … Судоходные реки (участки рек) и каналы выделяются на картах начертанием подписей их названий, которые в отличие от названий несудоходных рек пишутся без выделения заглавной буквы (приложение VII-4).
Каким цветом на топографических картах показаны горизонтали?
Горизонтали — это линии, соединяющие точки с одинаковой абсолютной высотой.
Что такое Ситуация на топографических картах и планах?
Ситуация — совокупность контуров и предметов местности. Рельеф — совокупность неровностей земной поверхности. Ситуация и рельеф местности изображаются на топографической карте условными знаками.
Что можно определить по топографической карте?
Топографическая карта содержит сведения об опорных геодезических пунктах, рельефе, гидрографии, растительности, грунтах, хозяйственных и культурных объектах, дорогах, коммуникациях, границах и других объектах местности. Полнота содержания и точность топографических карт позволяют решать технические задачи.
Чем географическая карта отличается от топографического плана?
Главное отличие топографической карты от географической — масштаб: на географической используют мелкий масштаб, на топографической — крупный.
Для чего создаются топографические карты?
Назначение топографических карт — представить участок конкретной местности в объемном трехмерном изображении. При помощи, так называемых горизонталей изображается рельеф местности. Это линии, соединяющие одинаковые высоты над уровнем моря.
Где используются топографические карты?
Топографические карты необходимы во всех областях хозяйственной деятельности, когда требуется точное и подробное изображение местности: при строительстве, на транспорте, в сельском хозяйстве, промышленности, военном деле и т.
Что обозначают пунктиром на карте?
Пунктиром изображаются четко определяемые на местности контуры участков растительного покрова, грунтов и пашен. Контуры пашен особым условным знаком не заполняются.
Что называется топографической картой?
«Топографическими картами называются такие карты, на которых неровности земной поверхности и все местные предметы изображены настолько подробно, что по ним можно представить действительную местность со всеми ее подробностями.
Что такое план местности кратко?
Теория: Всю Землю и большие её участки наносят на глобус, географические карты, а при изображении небольших территорий используют план местности. План местности — это чертёж, на котором условными знаками подробно показана небольшая территория в уменьшенном виде. План местности необходим людям многих профессий.
Калькулятор конечной точки
Создано Maciej Kowalski, кандидатом наук
Отредактировано Bogna Szyk и Jack Bowater
Последнее обновление: 26 сентября 2022 г.
Содержание:
- Определение конечной точки в геометрии
- Как найти конечную точку?
- Формула конечной точки
- Пример: использование калькулятора отсутствующей конечной точки
- Часто задаваемые вопросы
Добро пожаловать в Omni калькулятор конечной точки , где мы узнаем как найти конечную точку сегмента линии , если мы знаем его другой конец и его середину.
Итак, расслабьтесь, заварите себе чашку чая в дорогу, и приступим к делу !
Определение конечной точки в геометрии
В просторечии конечная точка — это точка, которая лежит на конце . Мы уверены, что это заявление было для вас таким же шоком, как и для нас, когда мы услышали его впервые. Но, с другой стороны, баклажан на вкус совсем не похож на яйцо, так что никогда нельзя быть слишком уверенным в угадывании значения слова , не так ли?
Однако бывают случаи, например, когда вы делите пиццу на несколько человек, когда вам нужно быть чуть точнее , а к кому еще обратиться за этим , как не к математикам ?
В своей простейшей форме определение конечной точки в геометрии фокусируется на отрезках , то есть прямых линиях, соединяющих две точки.
Для простоты расчетов назовем одну из них начальной точкой (как это сделано в калькуляторе конечных точек). Имейте в виду, однако, что начало может быть концом, если вы посмотрите на это с другой стороны .
Вот это прозвучало жутко философски , тебе не кажется? Но давайте оставим « Кто мы и куда мы идем?» вопросов на тот случай, когда мы не можем заснуть. Мы должны сосредоточиться на сегментах, которые мы упомянули, и на том, как найти конечные точки.0003
Как найти конечную точку?
Для того, чтобы получить конечную точку, нам нужно иметь некоторую точку отсчета для начала.
Простейшая и наиболее распространенная ситуация, когда нам не хватает конечной точки, хотя мы знаем начальную точку и середину . Последний — это просто, как следует из названия, точка, обозначающая середину сегмента. Это все, что нам нужно, чтобы найти конечную точку; в конце концов, он должен лежать на другом конце средней точки от начальной точки и находиться на таком же расстоянии.
Следовательно, интуитивно мы можем уже геометрически описать, как найти конечную точку .
- Имея начальную точку AAA и среднюю точку BBB, нарисуйте отрезок , соединяющий их.
- Нарисуйте линию , идущую дальше от BBB от AAA до бог знает куда.
- Измерьте расстояние от AAA до BBB и отметьте то же расстояние от BBB в обратном направлении.
- Приступайте к победному танцу .
Однако есть люди (и мы не утверждаем, что мы из тех людей), которым не очень нравится рисовать линии . Ведь для этого нужна линейка, а Лорд трудно найти… (Да, это была ужасная шутка, и мы склоняем головы от стыда. Но, тем не менее, с легким хихиканьем.)
🔎 Вместо рисования линий , вы можете использовать наш калькулятор расстояния для двух заданных точек.
Во всяком случае, для людей, предпочитающих числа и расчеты (и мы могли бы на самом деле предположить, что мы являемся этими людьми), мы сосредоточимся на том, как найти конечную точку алгебраически в следующем разделе. Пожалуйста, не бойтесь слова «алгебраически» — через секунду вы увидите, как оно переводится как « легко и без усилий » — девиз нашего недостающего калькулятора конечной точки .
Формула конечной точки
В координатной геометрии мы работаем с объектами, которые встроены в то, что мы называем евклидовым пространством .
Числа x1x_1x1 и x2x_2x2 обозначают положение точек относительно горизонтальной оси (обычно обозначаются xxx), а y1y_1y1 и y2y_2y2 используются для вертикальной оси (чаще всего обозначаются yyy). Вместе такая пара чисел (x1,y1)(x_1, y_1)(x1,y1) определяет точку в пространстве . Более того, координаты помогают нам анализировать более сложные объекты в нашем евклидовом пространстве . Например, они появляются в формуле конечной точки .
Скажем, у вас есть отрезок, идущий от A=(x1,y1)A = (x_1, y_1)A=(x1,y1) к… ну, мы пока не знаем. Теперь мы объясним как найти конечную точку B=(x2,y2)B = (x_2, y_2)B=(x2,y2) если мы знаем середину M=(x,y)M = (х, у)М=(х,у).
Из определения средней точки мы знаем, что расстояние от AAA до MMM должно быть таким же, как расстояние от MMM до BBB. Просто B находится с другой стороны. Это означает, что для нахождения ВВВ достаточно « сдвинуть » МММ по прямой, проходящей через ААА и МММ, на ту же длину, что и отрезок АМАМАМ. Или, если хотите пофантазировать, вектором АМАМАМ.
Другими словами, имеем:
x2=x+(x−x1)=2x−x1x_2 = x + (x — x_1) = 2x — x_1x2=x+(x−x1)=2x−x1, и
y2=y+(y−y1)=2y−y1y_2 = y + (y — y_1) = 2y — y_1y2=y+(y−y1)=2y−y1.
Подводя итог, если вам нравится иметь всю необходимую информацию в одном абзаце , то вот она.
💡 Конечная точка отрезка, идущего от A=(x1,y1)A = (x_1, y_1)A=(x1,y1) к средней точке M=(x,y)M = (x, y)M=(x,y) — это точка B=(2x−x1,2y−y1)B = (2x — x_1, 2y — y_1)B=(2x−x1,2y−y1).
Обратите внимание, что выше мы упомянули линию, проходящую через A и М .
AB . Если для вашего упражнения или задачи требуется дополнительная информация о них, ознакомьтесь с калькуляторами координатной геометрии Omni и найдите тот, который соответствует вашим потребностям !
Уф, сколько времени было потрачено на теорию! Как насчет того, чтобы оставить эту техническую чепуху и посмотреть числовой пример ? В конце концов, время – это деньги, по крайней мере, так говорит нам формула временной стоимости денег!
Пример: использование отсутствующего калькулятора конечной точки
Допустим, четыре месяца назад вы начали размещать видео на YouTube. Ничего особенного, просто несколько рецептов приготовления, которые являются традиционными для вашего региона. Это началось как хобби, но человек, похоже, наслаждаются шоу , и вы видите число зрителей, линейно увеличивающееся со временем .
Прежде всего, обратите внимание, что, хотя проблема вовсе не кажется геометрической, мы действительно можем найти ответ, используя определение конечной точки из геометрии . В конце концов, отправной точкой, то есть нулевым месяцем, было время, когда вы начали публиковать видео, так что на тот момент у нас было 90 157 0 90 158 зрителей. Сейчас мы находимся на четвертом месяце, который будет нашей средней точкой (поскольку мы хотим найти количество зрителей еще через четыре месяца). Другими словами, конечной точкой будет наш ответ .
Скажем, что на данный момент, у вас 54000 подписчиков , и давайте попробуем перевести все эти данные таким образом, чтобы калькулятор конечной точки понял, что мы от него хотим.
Согласно приведенному выше разделу, чтобы найти ответ, нам нужна начальная точка и средняя точка .
A = (x₁, y₁) и M = (x, y) соответственно. Для нас x будут обозначать количество месяцев в нас , а y будет количество зрителей . Поскольку нашей отправной точкой был нулевой месяц, а сейчас прошло 4 месяца, у нас есть (и мы можем ввести в калькулятор конечной точки)
x₁ = 0 ,
x = 4 .
Теперь пришло время для абонентов . Опять же, отправная точка была, когда у нас никого не было, а сейчас, спустя четыре месяца, мы на 54 000 . Следовательно, имеем
y₁ = 0 ,
г = 54 000 .
Как только мы введем все эти данные в калькулятор конечной точки, он выдаст ответ . Но давайте пока не будем раскрывать это! Как насчет того, чтобы увидеть , как найти конечную точку самостоятельно, используя формулу конечной точки ?
Давайте возьмем лист бумаги и вспомним информацию, которую мы уже упоминали выше.
A = (0, 0) . Сейчас , мы находимся на четвертом месяце с 54 000 подписчиков , что наполовину меньше того, что мы хотели бы рассчитать. Это означает, что наша средняя точка равна (4, 54,000) .
Все, что нам нужно сделать сейчас, это использовать формулу конечной точки из предыдущего раздела. Если обозначить координаты конечной точки как B = (x₂, y₂) , то
x₂ = 2*4 - 0 = 8 ,
y₂ = 2*54 000 - 0 = 108 0080 .
Это означает, что если тренд продолжится, мы должны получить 108,000 подписчиков за четыре месяца . Теперь, это довольно много, если вы спросите нас! К счастью, все это делается онлайн, поэтому проблем с социальным дистанцированием быть не должно.
Часто задаваемые вопросы
Как найти отсутствующую конечную точку?
Предположим, что у вас есть конечная точка A = (x₁, y₁) и средняя точка M = (x, y) :
-
Двойной координаты средних точек: 2x , 2 года .
-
Вычтите координату x известной конечной точки из первого значения , чтобы получить координату x отсутствующей конечной точки: x₂ = 2x - x₁ .
-
Вычтите координату y известной конечной точки из второго значения , чтобы получить координату y отсутствующей конечной точки: y₂ = 2y - y₁ .
-
Отлично, вы нашли недостающую конечную точку: B = (x₂, y₂) .
Могут ли одна из конечных точек и средняя точка иметь одинаковые координаты?
№ .
Какова другая конечная точка отрезка с одной конечной точкой в (1,3) и средней точкой в (3,5)?
Чтобы найти вторую конечную точку:
-
Двойные координаты средних точек:
2x = 6,2y = 10. -
Вычтите первое значение и известную координату x конечной точки:
6 - 1 = 5. -
Вычтите второе значение и известную координату y конечной точки:
10 - 3 = 7. -
Результирующие разности представляют собой x- и y-координаты отсутствующей конечной точки соответственно:
Б = (5,7).
Какое расстояние между двумя конечными точками (3,5) и (6,6)?
Для оценки недостающего расстояния:
-
Найти разность между соответствующими координатами :
Δx = 6 - 3 = 3,Δy = 6 - 5 = 1. -
Возведение обеих разностей в квадрат :
(Δx)² = 3² = 9,(Δy)² = 1² = 1. -
Добавьте эти два значения:
(Δx)² + (Δy)² = 9 + 1 = 10. -
Извлеките квадратный корень из суммы :
√((Δx)² + (Δy)²) = √10. -
Хорошая работа! Искомое расстояние равно
√10, что примерно равно3,16.
Мацей Ковальский, кандидат наук
Координаты начальной точки
Координаты средней точки
Координаты конечной точки
Ознакомьтесь с 38 похожими калькуляторами координатной геометрии 📈
Средняя скорость измененияБилинейная интерполяцияКатенарная кривая… Еще 35
Середина | Superprof
Как следует из названия, формула средней точки находит середину отрезка. Неважно, какой длины линия или в каком направлении она идет, вы можете использовать эту формулу на любой прямой линии, которую хотите.
В координатной геометрии существует множество формул, но есть что-то уникальное в формуле средней точки. Это единственная формула в координатной геометрии, которая может найти две координаты в одном решении. Ниже приведена формула для вычисления середины отрезка:
Представьте прямую, которая начинается в точке A и заканчивается в точке B. Чтобы вычислить середину этой линии, вам нужно знать координаты обеих точек.
Середина этой линии представлена как M на картинке выше. Поскольку у вас есть координаты обеих точек, теперь вы можете использовать формулу средней точки, чтобы найти координаты M. Либо вы можете использовать приведенную выше формулу напрямую, чтобы найти среднюю точку, либо разбить ее на два шага.
Второй шаг - разделить их оба на и вот как вы найдете середину, используя второй метод:
Примеры
Вычислить координаты середины отрезка AB.
Вычислите координаты точки C на отрезке AC, зная, что середина равна , а конечная точка .
Если и являются серединами сторон, составляющих треугольник, то каковы координаты вершин?
Если отрезок AB с концами и разделен на четыре равные части, каковы координаты точек деления?
Q is the midpoint of AB
P is the midpoint of AQ
R is the midpoint of QB
The best Maths tutors available
Поехали
Симметричная точка
Предположим, есть точка A и другая точка A'.
Вычислить симметричную точку с серединой .
Вычислите симметричную точку средней точки.
Три коллинеарные точки
Слово «коллинеарность» означает, что два или более объекта или вещи лежат на одной линии. В мире координатной геометрии коллинеарные точки означают, что две или более точек, лежащих на одной линии, независимо от того, как далеко они находятся, будут коллинеарными точками.
Определить, являются ли и совмещенными точками.
Рассчитайте значение a в следующих выровненных точках.
Координаты центра тяжести
Каждый объект в этой вселенной имеет центральную точку. В области физики это очень важная вещь. На самом деле, у них есть отдельный поддомен для этого. Найти центр непросто, существуют разные методы нахождения центра для разных объектов. В случае треугольников мы используем понятие центроида. В координатной геометрии координаты центроида определяют центр треугольника. Его находят тремя линейными линиями, пересекающими центр каждой стороны треугольника. Точка, в которой пересекаются все три линии, является точкой центра, рассмотрим приведенную выше диаграмму в качестве примера. У каждой стороны есть линия, проходящая через центр каждой стороны соответственно. Точка G — это точка, где пересекаются все три линии, и это центр треугольника. Ниже приведена формула для нахождения координат центра треугольника.
Обратите внимание, что эта формула действительна только для треугольника, если вы попытаетесь использовать эту формулу для других форм или объектов, она не будет работать.
Учитывая вершины треугольника и , вычислить координаты центроида.
Если две вершины треугольника равны и , а центр тяжести равен , вычислите третью вершину.
Если вы можете найти середину отрезка, вы можете разделить его на две равные части. Нахождение середины каждой из двух равных частей позволяет найти точки, необходимые для разделения всего отрезка на четыре равные части. Нахождение середины каждого из этих сегментов дает вам восемь равных частей и так далее.
Разделение отрезка
Вы можете разделить отрезок на множество равных частей. Это зависит от того, сколько частей вы хотите, но одно можно сказать наверняка, что все эти части будут равными. Разделите отрезок на две части, найдя его середину. Теперь у вас есть две части: начало линии до середины и от середины до конечной точки.
No related posts.

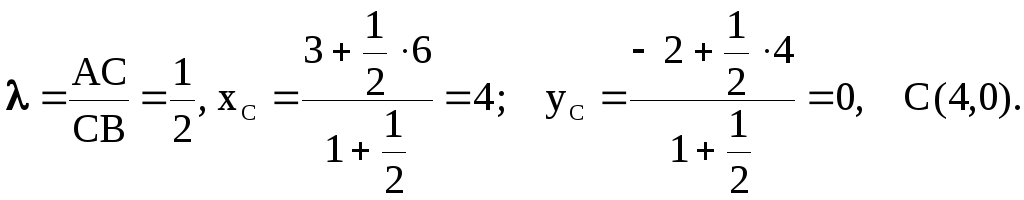
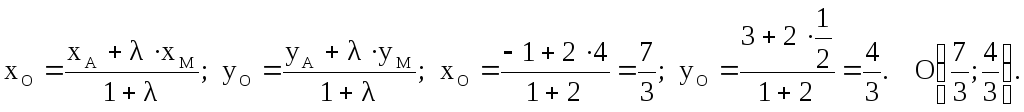



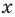
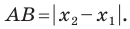
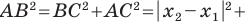

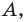
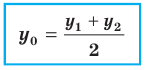
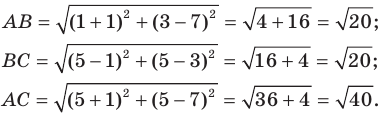

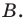
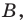
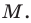
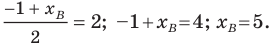
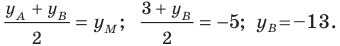
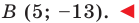
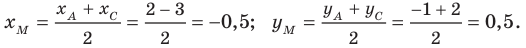
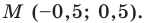
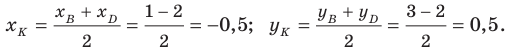
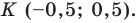
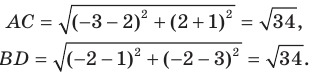

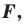 то ее координаты являются решением данного уравнения;
то ее координаты являются решением данного уравнения;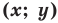 данного уравнения является координатами точки, принадлежащей фигуре
данного уравнения является координатами точки, принадлежащей фигуре