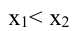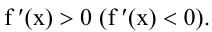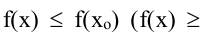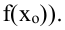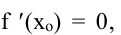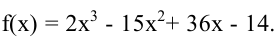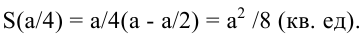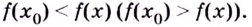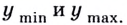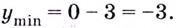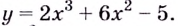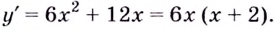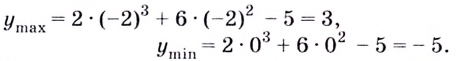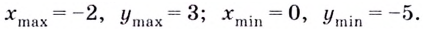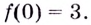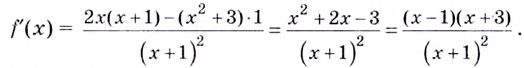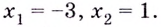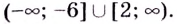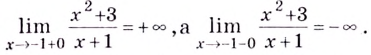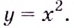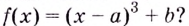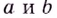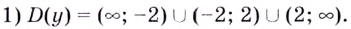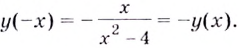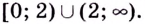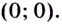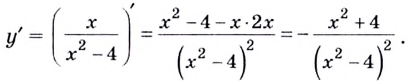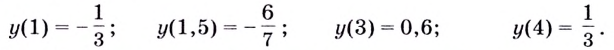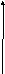Как найти точку экстремума функции принадлежащих отрезку - Исправление недочетов и поиск решений вместе с Examum.ru

Алгебра и начала математического анализа, 11 класс

Урок № 16. Экстремумы функции.

Перечень вопросов, рассматриваемых в теме

1) Определение точек максимума и минимума функции

2) Определение точки экстремума функции

3) Условия достаточные для нахождения точек экстремума функции

Глоссарий по теме

Возрастание функции. Функция y=f(x) возрастает на интервале X, если для любых х₁ и х₂, из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Максимум функции. Значение функции в точке максимума называют максимумом функции

Минимум функции. Значение функции в точке минимума называют минимумом функции

Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке).

Точка максимума функции. Точку х₀ называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство .

Точка минимума функции. Точку х₀ называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство .

Точки экстремума функции. Точки минимума и максимума называют точками экстремума.

Убывание функции. Функция y = f(x) убывает на интервале X, если для любых х₁ и х₂, из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Алгоритм исследования функции на монотонность и экстремумы:

1) Найти область определения функции D(f)

2) Найти f’ (x).

3) Найти стационарные (f'(x) = 0) и критические (f'(x) не

существует) точки функции y = f(x).

4) Отметить стационарные и критические точки на числовой

прямой и определить знаки производной на получившихся

промежутках.

5) Сделать выводы о монотонности функции и точках ее

экстремума.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.

Теоретический материал для самостоятельного изучения

Точки, в которых происходит изменение характера монотонности функции – это ТОЧКИ ЭКСТРЕМУМА.

Точку х = х₀ называют точкой минимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≥ f(x₀).
Точку х = х₀ называют точкой максимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≤ f(x₀).

Точки максимума и минимума – точки экстремума.

Функция может иметь неограниченное количество экстремумов.

Критическая точка – это точка, производная в которой равна 0 или не существует.

Важно помнить, что любая точка экстремума является критической точкой, но не всякая критическая является экстремальной.

Алгоритм нахождения максимума/минимума функции на отрезке:

найти экстремальные точки функции, принадлежащие отрезку,
найти значение функции в экстремальных точках из пункта 1 и в концах отрезка,
выбрать из полученных значений максимальное и минимальное.

Примеры и разбор решения заданий тренировочного модуля

№1. Определите промежуток монотонности функции у=х²-8х +5

Решение: Найдем производную заданной функции: у’=2x-8

2x-8=0

х=4

Определяем знак производной функции и изобразим на рисунке, следовательно, функция возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)

Ответ: возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)

№2. Найдите точку минимума функции у= 2х-ln(х+3)+9

Решение: Найдем производную заданной функции:

Найдем нули производной:

х=-2,5

Определим знаки производной функции и изобразим на рисунке поведение функции:

Ответ: -2,5 точка min

№3. Материальная точка движется прямолинейно по закону x(t) = 10t² − 48t + 15, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3с.

Решение: Если нас интересует движение автомобиля, то, принимая в качестве функции зависимость пройденного расстояния от времени, с помощью производной мы получим зависимость скорости от времени.

V=х'(t)= 20t – 48. Подставляем вместо t 3c и получаем ответ. V=12 мc

Ответ: V=12 мc

№4. На рисунке изображен график функции. На оси абсцисс отмечены семь точек: x1, x2, x3, x4, x5, x6, x7. Определите количество целых точек, в которых производная функции отрицательна.

Решение: Производная функции отрицательна на тех интервалах, на которых функция убывает. В данном случае это точки х3,х5,х7. Следовательно, таких точек 3

Ответ: 3

Источник

Содержание:

Экстремум функции

Функция y=f(x) называется возрастающей (убывающей) в некотором интервале, если при

Если дифференцируемая функция у = f(x) на отрезке 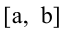возрастает (убывает), то ее производная на этом отрезке

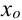
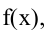
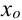
Точка называется точкой локального максимума (минимума) функции если существует окрестность точки для всех точек которой верно неравенство

Точки максимума и минимума называются точками экстремума, а значения функции в этих точках — ее экстремумами.

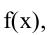
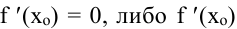
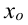
Необходимые условия экстремума. Если точка хо является точкой экстремума функции то либо не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек. Первое достаточное условие. Пусть — критическая точка. Если f'(х) при переходе через точку меняет знак плюс на минус, то в точке функция имеет максимум, в противном случае — минимум. Если при переходе через критическую точку производная не меняет знак, то в точке хо экстремума нет.

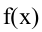
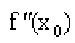
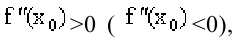
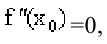
Второе достаточное условие. Пусть функция имеет производную f'(х) в окрестности точки и вторую производную в самой точке . Если то точка является точкой локального минимума (максимума) функции f(x). Если же то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

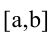
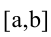
На отрезке функция у = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка .

Пример:

Найти экстремумы функции

Решение:

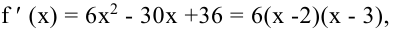
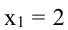
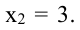
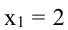
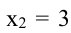
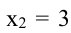
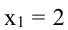
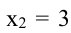
Так как то критические точки функции и Экстремумы могут быть только в этих точках. Так как при переходе через точку производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку производная меняет знак минус на плюс, поэтому в точке у функции минимум. Вычислив значения функции в точках и найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) =13.

Пример:

Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, а четвертой стороной примыкала к стене. Для этого имеется а погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?

Решение:

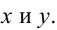
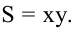
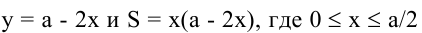
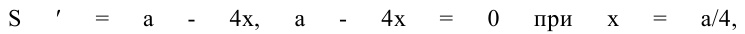
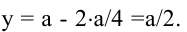
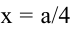
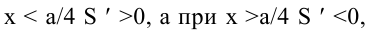
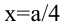
Обозначим стороны площадки через Площадь площадки равна Пусть у — это длина стороны, примыкающей к стене. Тогда по условию должно выполняться равенство 2х + у = а. Поэтому (длина и ширина площадки не могут быть отрицательными). откуда Поскольку — единственная критическая точка, проверим, меняется ли знак производной при переходе через эту точку. При значит, в точке функция S имеет максимум. Значение функции

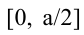
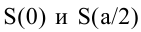
Поскольку S непрерывна на и ее значения на концах равны нулю, то найденное значение будет наибольшим значением функции.

Таким образом, наиболее выгодным соотношением сторон площадки при данных условиях задачи является у = 2х.

Пример:

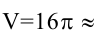
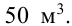
Требуется изготовить закрытый цилиндрический бак вместимостью Каковы должны быть размеры бака (радиус R и высота Н), чтобы на его изготовление пошло наименьшее количество материала?

Решение:

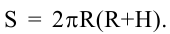
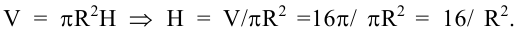
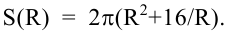
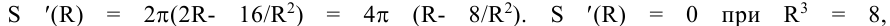
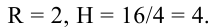
Площадь полной поверхности цилиндра равна Мы знаем объем цилиндра Значит, Находим производную этой функции:следовательно,

Экстремумы функции

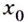
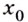
Введём несколько новых понятий. Окрестностью точки называется любой промежуток, для которого является внутренней точкой.

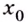
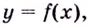
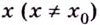
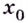
Точка называется точкой минимума (максимума) функции если для всех из некоторой окрестности точки выполняется неравенство

Точки минимума и максимума обозначают 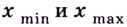соответственно.

Значение функции в точке минимума называется минимумом функции, а в точке максимума — максимумом функции. Обозначают их:

Точки минимума и максимума функции называют точками экстремума (лат. extremum — край, конец). Значения функции в точках её экстремума — её экстремальные значения, или экстремумы.

Например, для функции 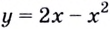точка является точкой максимума (рис. 77). Её максимум:

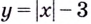
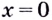
Для функции точка является точкой минимума (рис. 78). Её минимум:

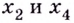
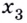
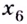
Функция, график которой изображён на рисунке 75, имеет четыре экстремальные точки: — точки максимума; и — точки минимума.

Точка экстремума функции не может принадлежать промежутку, на котором эта функция возрастает или убывает (почему?). Следовательно, те точки, в которых производная функции положительная или отрицательная, не могут быть точками её экстремума. Все остальные точки области определения функции являются её критическими точками. Поэтому точками экстремума функции могут быть только её критические точки. Это — необходимое условие существования экстремума.

Выбрать из критических точек функции точки экстремума позволяет достаточное условие существования экстремума.

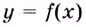
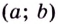
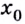
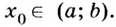
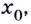
Пусть функция непрерывна на промежутке и — её критическая точка, Тогда: точка при переходе через которую в направлении роста аргумента производная меняет знак с «плюса» на «минус», является точкой максимума, а точка, при переходе через которую производная меняет знак с «минуса» на «плюс» — точкой минимума.

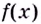
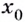
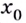
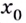
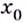
Действительно, если производная функции отрицательная, то при переходе через точку возрастание функции изменяется на убывание (рис. 79). В этом случае — точка максимума. Если же при переходе через точку убывание функции изменяется на возрастание, то — точка минимума (рис. 80).

Если же производная функции в точке 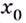равна нулю, а слева и справа от производная функции положительная (рис.81) или слева и справа отрицательная, то не является точкой экстремума.

Заказать решение задач по высшей математике

Пример №552

Найдите точки экстремума и экстремальные значения функции

Решение:

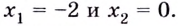
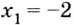
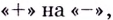
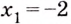
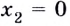
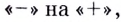
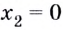
Критические точки функции: При переходе через точку производная меняет знаке поэтому —точка максимума. При переходе через точку производная меняет знак с поэтому — точка минимума (рис. 82).

Ответ.

Нахождение экстремумов функции можно оформлять в виде таблицы, как на с. 176. Особенно это удобно при общем исследовании функции, когда находят не только её экстремумы, но и другие свойства, строят её график.

Чтобы исследовать функцию, можно пользоваться следующей схемой:

найти область определения функции;
исследовать функцию на чётность, нечётность, периодичность;
найти точки пересечения графика функции с осями координат;
исследовать функцию на монотонность, то есть найти промежутки возрастания и убывания функции;
найти точки экстремума и экстремальные значения функции;
найти асимптоты графика функции;
построить график функции.

Пример №553

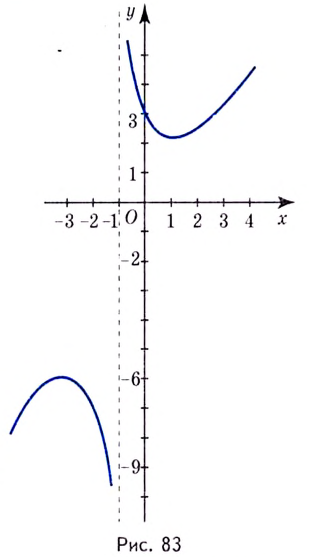
Исследуйте функцию 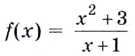и постройте её график.

Решение:

Область определения функции — все действительные числа, кроме 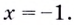Поскольку она не симметрична относительно нуля, то функция не может быть чётной или нечётной. Функция непериодическая.

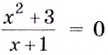
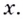
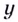
Уравнение не имеет решений, поэтому график функции не пересекает ось Ось он пересекает в точке с ординатой

Критические точки:

Составим и заполним таблицу.

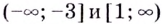
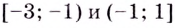
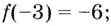
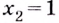
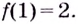
На промежутках функция возрастает, на промежутках функция убывает. — точка максимума, —точка минимума,

Область значений функции:

График функции имеет вертикальную асимптоту так как

График этой функции изображён на рисунке 83.

Пример №554

Может ли нечётная функция иметь экстремум в точке 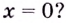А чётная функция?

Решение:

Нечётная функция не может. Если в окрестности точки 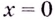функция имеет экстремум, то с одной стороны от нуля она возрастает, а с другой — убывает, или наоборот. А нечётная функция — или только возрастает, или только убывает в окрестности точки Чётная функция может. Например, функция

Пример №555

Существуют ли такие числа 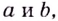при которых имеет экстремум функция

Решение:

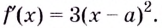
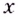
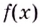
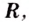
При любых действительных значениях В каждой точке производная данной функции неотрицательная. Функция возрастает на поэтому не может иметь экстремумов.

Ответ. Не существуют.

Пример №556

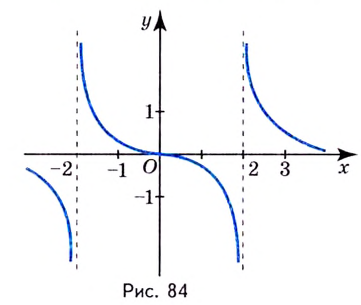
Исследуйте функцию 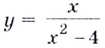и постройте её график.

Решение.

2) Функция — нечётная, поскольку

Следовательно, её график симметричен относительно начала координат и достаточно исследовать функцию на промежутке

3) если 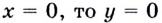— график пересекает оси координат только в точке

4) Найдём производную функции:

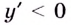
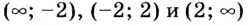
Очевидно, что для всех х из области определения. Следовательно, функция убывает на каждом из промежутков и не имеет максимумов и минимумов.

Для более точного построения вычислим значение функции в нескольких точках:

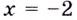
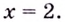
График функции имеет вертикальные асимптоты и (Убедитесь самостоятельно.)

График функции изображён на рисунке 84.

Методы решения систем линейных алгебраических уравнений (СЛАУ)
Скалярное произведение и его свойства
Векторное и смешанное произведения векторов
Преобразования декартовой системы координат
Определитель матрицы
Критерий совместности Кронекера-Капелли
Формулы Крамера
Матричный метод

Источник

Определение 1. Точканазываетсяточкоймаксимума
(минимума) функции,
если существует окрестность,
такая, чтодля всех.
Точки максимума и минимума функции
называются ееточками экстремума,
а значения функции в этих точках –экстремумами функции.

Заметим, что точкой экстремума функции
может быть только внутренняя точка
промежутка, в котором функция определена,
поскольку указанные в определении
неравенства должны выполняться в
некоторой окрестности точки
.

–точки
максимума,
– точки минимума функции.

О

х

Теорема
1 (необходимое
условие экстремума). Для того чтобы
дифференцируемая функция
имела в точкеэкстремум, необходимо
выполнение условия
.

Доказательство.
Пусть
–
точка экстремума дифференцируемой
функции.
Тогда найдется окрестностьточки,
в которойбудет наибольшим или наименьшим значением
функции.
Поэтому по теореме Ферма.
Теорема доказана.

Определение
2. Точки, в
которых производная равна нулю, называются
стационарными
точками
функции.

Из
доказанной теоремы следует, что точками
экстремума функции могут быть только
стационарные точки и точки, в которых
производная не существует. Такие точки
называют подозрительными на экстремум
или критическими
точками
функции.

Заметим,
что не всякая критическая точка является
точкой экстремума. Например, для функции
критической является стационарная
точка,
так каксуществует для всехх,
.
Но точкане является точкой экстремума этой
функции, так как функция всюду возрастает.

Таким образом, нам
надо найти условия, при которых критическая
точка является точкой экстремума –
достаточные условия экстремума. Есть
два типа таких условий. Одни используют
производную 1-го порядка, другие –
производную 2-го порядка.

Рассмотрим
достаточное условие экстремума,
опирающиеся на 1-ю производную функции.

Предположим,
что функция
непрерывна в окрестностикритической точкии в проколотой окрестностисуществует конечная
производная
,
сохраняющая определенный знак как
слева, так и справа от точки.
Тогда возможны следующие три случая:

1)
приипри,
то естьпри переходе через точкуменяет знак с плюса на минус. В этом
случае, в силу теоремы 3 § 8, функциявозрастает в промежуткеи убывает в промежутке,
поэтому значениеявляется наибольшим в окрестности,
то есть– точка максимума функции.

2)
приипри,
то естьпри переходе через точкуменяет знак с минуса на плюс. Рассуждая
как в 1-ом случае, приходим к выводу, что– точка минимума функции.

3)
При переходе через точку
не меняет знака. Тогда функция либо все
время возрастает, либо все время убывает,
так что в точкеэкстремума нет.

Таким
образом, достаточное условие экстремума
состоит в следующем:

если
производная функции при переходе через
критическую точку
меняет знак, то в этой точке функция
имеет экстремум. При перемене знака с
плюса на минус в точкефункция имеет максимум, с минуса на плюс
– минимум. Если же при переходе через
точкупроизводная знака не меняет, то в этой
точке экстремума нет.

Сформулируем
правило исследования функции на
экстремум. Нужно:

найти область
определения функции;
найти производную;
найти критические
точки функции из области определения,
то есть точки, в которых производная
равна нулю или не существует;
определить знак
производной слева и справа от каждой
из критических точек;
на
основании достаточного условия
экстремума сделать выводы относительно
каждой из критических точек.

Пример
1. Найдем
экстремумы функции
.

Решение.
Область определения
,существует во всех точках области
определения,,,,
– +

т.е.
при переходе через критическую точку
производная меняет знак с минуса на
плюс, поэтому–
точка минимума функции,– минимум функции.

Достаточное условие
экстремума функции, опирающееся на 2-ю
производную, формулируется следующим
образом.

Теорема
2. Пусть
и в точкесуществует 2-я производная. Тогда, если,
то–
точка минимума функции, а если,
то–
точка максимума функции.

Доказательство.
Пусть
.
Так какесть производная функции,
то по теореме 4 § 8 функцияв точкевозрастает, т.е. вблизи точкислева,
а справа,
т.е. при переходе через точкупроизводнаяменяет знак с минуса на плюс. Поэтому
по первому достаточному условию
экстремума функции точка−
точка минимума функции.

Если
,
то функцияв точкеубывает, меняя знак с плюса на минус,
поэтому точка−
точка максимума функции. Теорема
доказана.

Замечание.
Доказанная
теорема позволяет исследовать функции
на экстремум только в стационарных
точках, т.е. в точках, в которых первая
производная равна нулю. Вопрос остается
открытым и в том случае, когда вторая
производная равна нулю. В этом случае
нужно либо изучать поведение высших
производных, либо пользоваться правилом,
опирающимся на первую производную.

Пример
2. Найдем
экстремумы функции
.

Решение.
Область определения функции
,существует всюду в,– точка максимума,;– точки минимума,.

Остановимся
теперь на задаче о нахождении наибольшего
и наименьшего значений функции на
отрезке. Пусть функция
непрерывна на отрезке.
Тогда по 2-ой теореме Вейерштрасса она
принимает наи свое наибольшее, и свое наименьшее
значения. Однако в теореме Вейерштрасса
ничего не говорится о том, как искать
эти значения. Ясно, что эти значения
могут достигаться как во внутренних
точка отрезка, так и на его концах. Если
наименьшее (наибольшее) значение функции
достигается во внутренней точке отрезка,
то эта точка обязательно будет точкой
минимума (максимума) функции. А точки
экстремума функции обязательно находятся
в критических точках. Поэтому достаточно
сравнить значения функции на концах
отрезка и в критических точках, не
исследуя эти точки на экстремум.

Таким образом,
правило нахождения наибольшего и
наименьшего значений функции на отрезке
состоит в следующем. Нужно:

найти производную
данной функции;
найти критические
точки, принадлежащие данному отрезку;
вычислить значения
функции в найденных точках и на концах
отрезка;
из всех найденных
значений функции выбрать наибольшее
и наименьшее.

Пример
3. Найдем
наибольшее и наименьшее значения функции
на отрезке.

Решение.
Имеем
.
Из найденных стационарных точек функции
только.
Других критических точек нет, так как
производная определена всюду. Находим,,.
Видим, что,.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Готовимся к ЕГЭ

Пособие для учащихся

Исследование функций по графику
производной

В данной статье рассматриваются задачи входящие в ЕГЭ по
математике, в которых дан график производной функции (задание 7). В этих
задачах ставятся следующие вопросы:

1. В какой точке заданного отрезка функция принимает наибольшее
(или наименьшее) значение.

2. Найти количество точек максимума (или минимума) функции,
принадлежащих заданному отрезку.

3. Найти количество точек экстремума функции, принадлежащих
заданному отрезку.

4. Найти точку экстремума функции, принадлежащую заданному
отрезку.

5. Найти промежутки возрастания (или убывания) функции и в ответе
указать сумму целых точек, входящих в эти промежутки.

6. Найти промежутки возрастания (или убывания) функции. В ответе
указать длину наибольшего из этих промежутков.

7. Найти количество точек, в которых касательная к графику функции
параллельна прямой вида у = kx + b или совпадает с ней.

8. Найти абсциссу точки, в которой касательная к графику функции
параллельна оси абсцисс или совпадает с ней.

Краткая теория

1. Производная на интервалах возрастания имеет положительный знак.

Если производная в определённой точке из некоторого интервала
имеет положительное значение, то график функции на этом интервале
возрастает.

2. На интервалах убывания производная имеет отрицательный знак.

Если производная в определённой точке из некоторого интервала
имеет отрицательное значение, то график функции на этом интервале
убывает.

3. Производная в точке х равна угловому коэффициенту касательной,
проведённой к графику функции в этой же точке.

4. В точках экстремума (максимума-минимума) функции производная
равна нулю. Касательная к графику функции в этой точке параллельна оси
ох.

Многие путают график производной и график функции. Поэтому в таких
зданиях, где дан график, сразу же нужно обратить своё внимание в условии на
том, что дано: график функции или график производной функции?

Если это график производной функции, то рассматривать его нужно
как бы «отражение» самой функции, которое просто даёт нам информацию об этой
функции.

Рассмотрим алгоритм решения задания.

Задача

На рисунке изображен график у = f′(х) — производной
функции f(х), определенной на интервале (–2;21).

Ответим на следующие вопросы:

1. В какой точке отрезка [7;15] функция f(х) принимает
наибольшее значение.

На заданном отрезке производная функции отрицательна, значит,
функция на этом отрезке убывает (она убывает от левой границы интервала к
правой). Таким образом, наибольшее значение функции достигается на левой
границе отрезка, т. е. в точке 7.

Ответ: 7.

2. В какой точке отрезка [3;6] функция f(х) принимает
наименьшее значение.

По данному графику производной можем сказать следующее. На
заданном отрезке производная функции положительна, значит, функция на
этом отрезке возрастает (она возрастает от левой границы интервала к правой).
Таким образом, наименьшее значение функции достигается на левой границе
отрезка, то есть в точке х = 3.

Ответ: 3.

3. Найдите количество точек максимума функции f(х),
принадлежащих отрезку [0;20].

Точки максимума соответствуют точкам смены знака производной с
положительного на отрицательный. Рассмотрим, где таким образом меняется знак.

На отрезке (3;6) производная положительна, на отрезке (6;16)
отрицательна.

На отрезке (16;18) производная положительна, на отрезке (18;20)
отрицательна.

Таким образом, на заданном отрезке [0;20] функция имеет две точки
максимума х = 6 и х = 18.

Ответ: 2.

4. Найдите количество точек минимума функции f(х),
принадлежащих отрезку [0;4].

Точки минимума соответствуют точкам смены знака производной с
отрицательного на положительный. У нас на интервале (0;3)
производная отрицательна, на интервале (3;4) положительна.

Таким образом, на отрезке [0;4] функция имеет только одну точку
минимума х = 3.

!!! Будьте внимательны при записи ответа – записывается количество
точек, а не значение х, такую ошибку можно допустить из-за
невнимательности.

Ответ: 1.

5. Найдите количество точек экстремума функции f(х),
принадлежащих отрезку [0;20].

Обратите внимание, что необходимо найти количество точек
экстремума (это и точки максимума и точки минимума).

Точки экстремума соответствуют точкам смены знака производной (с
положительного на отрицательный или наоборот). На данном в условии графике это
нули функции. Производная обращается в нуль

в точках 3, 6, 16, 18.

Таким образом, на отрезке [0;20] функция имеет 4 точки экстремума.

Ответ: 4.

6. Найдите промежутки возрастания функции f(х). В
ответе укажите сумму целых точек, входящих в эти промежутки.

Промежутки возрастания данной функции f(х) соответствуют
промежуткам, на которых ее производная положительна, то есть интервалам (3;6) и
(16;18). Обратите внимание, что границы интервала не входят в него (круглые
скобки – границы не включены в интервал, квадратные – включены). Данные
интервалы содержат целые точки 4, 5, 17. Их сумма равна: 4 + 5 + 17 = 26

Ответ: 26.

7. Найдите промежутки убывания функции f(х) на
заданном интервале. В ответе укажите сумму целых точек, входящих
в эти промежутки.

Промежутки убывания функции f(х) соответствуют
промежуткам, на которых производная функции отрицательна. В данной задаче это
интервалы (–2;3), (6;16), (18;21).

Данные интервалы содержат следующие целые точки: –1, 0, 1, 2, 7,
8, 9, 10, 11, 12, 13, 14, 15, 19, 20. Их сумма равна:

( –1) + 0 + 1 + 2 + 7 + 8 + 9 + 10 +

+ 11 + 12 + 13 + 14 + 15 + 19 + 20 = 140

Ответ: 140.

!!! Необходимо обратить внимание в условии: включены ли границы в
интервал или нет. Если границы будут включены, то и в рассматриваемых в
процессе решения интервалах эти границы также необходимо учитывать.

8. Найдите промежутки возрастания функции f(х). В
ответе укажите длину наибольшего из них.

Промежутки возрастания функции f(х) соответствуют
промежуткам, на которых производная функции положительна. Мы уже указывали их:
(3;6) и (16;18). Наибольшим из них является интервал (3;6), его длина
равна 3.

Ответ: 3

9. Найдите промежутки убывания функции f(х). В ответе
укажите длину наибольшего из них.

Промежутки убывания функции f(х) соответствуют
промежуткам, на которых производная функции отрицательна. Мы уже указывали их,
это интервалы

(–2;3), (6;16), (18;21), их длины соответственно равны 5, 10, 3.

Длина наибольшего интервала равна 10.

Ответ: 10

10. Найдите количество точек, в которых касательная
к графику функции f(х) параллельна прямой у = 2х + 3 или
совпадает с ней.

Значение производной в точке касания равно угловому коэффициенту
касательной. Так как касательная параллельна прямой у = 2х + 3 или совпадает с
ней, то их угловые коэффициенты равны 2. Значит, необходимо найти количество
точек, в которых у′(х₀) = 2. Геометрически это соответствует
количеству точек пересечения графика производной с прямой у = 2. На
данном интервале таких точек 4.

Ответ: 4

11. Найдите точку экстремума функции f(х),
принадлежащую отрезку [0;5].

Точка экстремума функции это такая точка, в которой её производная
равна нулю, при чём в окрестности этой точки производная меняет знак (с
положительного на отрицательный или наоборот). На отрезке [0;5] график
производной пересекает ось абсцисс, производная меняет знак с отрицательного на
положительный. Следовательно, точка х = 3 является точкой экстремума.

Ответ: 3

12. Найдите абсциссы точек, в которых касательные к
графику у = f (x) параллельны оси абсцисс или совпадают с ней. В ответе укажите
наибольшую из них.

Касательная к графику у = f (x) может быть параллельна оси абсцисс
или совпадать с ней, только в точках, где производная равна нулю (это могут
быть точки экстремума или стационарные точки, в окрестностях которых
производная свой знак не меняет). По данному графику видно, что производная
равна нулю в точках 3, 6, 16,18. Наибольшая равна 18.

Можно построить рассуждение таким образом:

Значение производной в точке касания равно угловому коэффициенту
касательной. Поскольку касательная параллельна оси абсцисс или совпадает с ней,
её угловой коэффициент равен 0 (действительно тангенс угла в ноль
градусов равен нулю). Следовательно, мы ищем точку, в которой угловой
коэффициент, равен нулю, а значит, и производная равна нулю. Производная равна
нулю в той точке, в которой её график пересекает ось абсцисс, а это точки
3, 6, 16,18.

Ответ: 18

Решите самостоятельно

Задача № 1.

На рисунке изображен график у= f′(х) — производной
функции f(х), определенной на интервале (–8;4). В какой точке
отрезка [–7;–3] функция f(х) принимает наименьшее значение.

Задача № 2.

На рисунке изображен график у = f′(х) —
производной функции f(х), определенной на интервале (–7;14).
Найдите количество точек максимума функции f(х),
принадлежащих отрезку [–6;9].

Задача № 3.

На рисунке изображен график у = f′(х) —
производной функции f(х), определенной на интервале (–18;6).
Найдите количество точек минимума функции f(х), принадлежащих
отрезку [–13;1].

Задача № 4.

На рисунке изображен график у = f′(х) —
производной функции f(х), определенной на интервале (–11; –11). Найдите количество
точек экстремума функции f(х), принадлежащих отрезку [–10;
–10].

Задача № 5.

На рисунке изображен график у = f′(х) —
производной функции f(х), определенной на интервале (–7;4). Найдите
промежутки возрастания функции f(х). В ответе укажите сумму целых
точек, входящих в эти промежутки.

Задача № 6.

На рисунке изображен график у = f′(х) — производной
функции f(х), определенной на интервале (–5;7). Найдите промежутки
убывания функции f(х). В ответе укажите сумму целых точек, входящих
в эти промежутки.

Задача № 7.

На рисунке изображен график у = f′(х) —
производной функцииf(х), определенной на интервале (–11;3). Найдите
промежутки возрастания функции f(х). В ответе укажите длину
наибольшего из них.

Задача № 8.

На рисунке изображен график у = f′(х) — производной
функции f(х), определенной на интервале (–2;12). Найдите промежутки
убывания функции f(х). В ответе укажите длину наибольшего из них.

Задача № 9.

На рисунке изображен график у = f′(х) — производной
функции f(х), определенной на интервале (–10;2). Найдите количество
точек, в которых касательная к графику функции f(х) параллельна
прямой у = –2х – 11 или совпадает с ней.

Задача № 10.

На рисунке изображен график у = f′(х) — производной
функции f(х), определенной на интервале (–4;8). Найдите точку
экстремума функции f(х), принадлежащую отрезку [–2;6].

Задача № 11.

На рисунке изображен график у = f′(х) —
производной функции f(х). Найдите абсциссу точки, в которой
касательная к графику у=f(х) параллельна прямой

у = 2х – 2 или совпадает с ней.

Задача № 12.

На рисунке изображен график у = f′(х) —
производной функции f(х). Найдите абсциссу точки, в которой касательная
к графику

у = f(х) параллельна оси абсцисс или
совпадает с ней.

Ответы:

1	2	3	4	5	6	7	8	9	10	11	12
-7	1	1	5	-3	18	6	6	5	4	5	-3

Источник

Наталья Игоревна Восковская

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Экстремумы функции

Для того чтобы ввести понятие наибольшего и наименьшего значения функций, вначале познакомимся с таким понятием, как экстремумы функций. Это понятие нам будет необходимо не для самого определения значений таких функций, а для построения схемы нахождения таких промежутков для конкретно заданных функций.

Определение 1

Точка $x’$ входящая в область определения функции называется точкой экстремума, если она либо будет точкой максимума, либо будет точкой минимума для функции $f(x)$.

Определение 2

Точка $x’$ будет называться точкой максимума для введенной функции $f(x)$, если у она имеет такую окрестность, что для всех точек $x$, которые входят в эту окрестность, будет верно $f(x)le f(x'{rm })$.

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Определение 3

Точка $x_0$ будет называться точкой минимума для введенной функции $f(x)$, если она имеет такую окрестность, что для всех точек $x$, которые входят в эту окрестность, будет верно $f(x)ge f(x'{rm })$.

Чтобы полностью разобраться в данном понятии, далее введем понятие критической точки функции.

Определение 4

Точка $x’$ будет называться критической точкой для данной функции $f(x)$, если выполняются два следующих условия:

Точка $x’$ является внутренней точкой для области определения данной функции;
$f’left(x'{rm }right)=0$ или не существует.

Сформулируем без доказательства теоремы о необходимом (теорема 1) и достаточном (теорема 2) условии для существования точки экстремума.

Если $y=f(x)$ имеет экстремум в точке $x_0$, то либо её производная в ней равняется нулю, либо производная в ней не существует.

«Точки экстремума, наибольшее и наименьшее значение на промежутке» 👇

Теорема 2

Пусть точка $x’$ будет критической для $y=f(x)$ и принадлежит интервалу $(a,b)$, причем на каждом интервале $left(a,x'{rm }right) и (x'{rm },b)$ производная $f'(x)$ существует и сохраняет один и тот же знак. В этом случае:

Если в $(a,x'{rm })$ $f’left(xright) >0$, а в $(x'{rm },b)$ $f’left(xright)
Если в $(a,x'{rm })$ $f’left(xright)0$, то $x’$ —будет точкой минимума для этой функции.
Если и в $(a,x'{rm })$, и в $(x'{rm },b)$ производная $имеет один и тот же постоянный знак$, то $x’$ не будет точкой экстремума для этой функции.

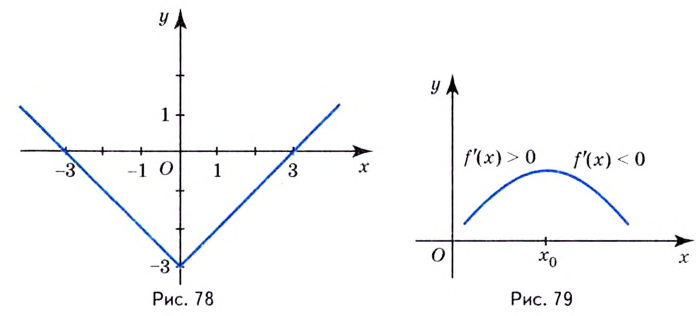
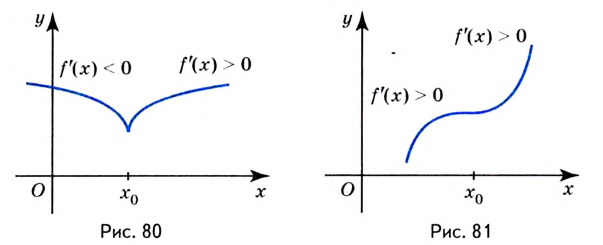
На рисунке 1 мы можем наглядно увидеть смысл теоремы 2.

Рисунок 1.

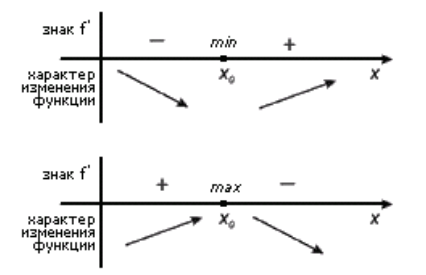
Примеры точек экстремумов вы можете видеть на рисунке 2.

Рисунок 2.

Правило исследования на экстремум

Найти $D(f)$;
Найти $f'(x)$;
Найти точки, где $f’left(xright)=0$;
Найти точки, где $f'(x)$ не будет существовать;
Отметить на координатной прямой $D(f)$ и все найденные в 3 и 4 пункте точки;
Определить знак $f'(x)$ на полученных промежутках;
Используя теорему 2, сделать заключение по поводу всех найденных точек.

Понятие наибольшего и наименьшего значений

Определение 5

Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наибольшее значение в точке $x’in X$, если выполняется

[fleft(xright)le f(x’)]

Определение 6

Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наименьшее значение в точке $x’in X$, если выполняется

[fleft(xright)ge f(x’)]

Чтобы найти наименьшее и наибольшее значение заданной функции на каком либо отрезке необходимо произвести следующие действия:

Найти $f'(x)$;
Найти точки, в которых $f’left(xright)=0$;
Найти точки, в которых $f'(x)$ не будет существовать;
Выкинуть из точек, найденных в пунктах 2 и 3 те, которые не лежат в отрезке $[a,b]$;
Вычислить значения в оставшихся точках и на концах $[a,b]$;
Выбрать из этих значений наибольшее и наименьшее.

Примеры задач

Пример 1

Найти наибольшее и наименьшее значения на [0,6]: $fleft(xright)=x^3-3x^2-45x+225$

Решение.

$f’left(xright)=3x^2-6x-45$;
$f’left(xright)=0$;
[3x^2-6x-45=0]
[x^2-2x-15=0]
[x=5, x=-3]
$f'(x)$ существует на всей $D(f)$;
$5in left[0,6right]$;
Значения:

[fleft(0right)=225] [fleft(5right)=50] [fleft(6right)=63]
Наибольшее значение равняется $225$, наименьшее равняется $50.$

Ответ: $max=225, min=50$.

Пример 2

Найти наибольшее и наименьшее значения на [-1,1]:$fleft(xright)=frac{x^2-4x+4}{x-2}$

Решение.

[fleft(xright)=frac{x^2-4x+4}{x-2}=frac{{(x-2)}^2}{x-2}=x-2, xne 2]

$f’left(xright)=(x-2)’=1$;

Точек экстремума нет.
Значения:

[fleft(-1right)=-3] [fleft(1right)=-1]

Ответ: $max=-1, min=-3$.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник