
В геометрии, точка Ферма в треугольнике, также называемая точка Торричелли или точка Ферма – Торричелли — это точка, в которой общее расстояние от трех вершин треугольника до точки является минимально возможным. Он назван так потому, что эта проблема была впервые поднята Ферма в частном письме Евангелисте Торричелли, который решил ее.
Точка Ферма дает решение геометрической медианы и задач дерева Штейнера для трех точек.
Содержание
- 1 Построение
- 2 Расположение X (13)
- 3 Расположение точки Ферма
- 3.1 Традиционная геометрия
- 3.2 Векторный анализ
- 3.3 Множители Лагранжа
- 4 Свойства
- 5 Псевдонимы
- 6 История
- 7 См. Также
- 8 Ссылки
- 9 Внешние ссылки
Построение
Точка Ферма треугольника с наибольшим углом не более 120 ° — это просто его первый изогонический центр или X (13), который строится следующим образом:
- Постройте равносторонний треугольник на каждом из двух произвольно выбранных стороны данного треугольника.
- Проведите линию от каждой новой вершины до противоположной вершины исходного треугольника.
- Две линии пересекаются в точке Ферма.
Альтернативный метод заключается в следующем:
- На каждой из двух произвольно выбранных сторон постройте равнобедренный треугольник с основанием рассматриваемой стороны, 30-градусными углами в основании и третьей вершиной. каждого равнобедренного треугольника, лежащего вне исходного треугольника.
- F или каждый равнобедренный треугольник начертит круг, в каждом случае с центром в новой вершине равнобедренного треугольника и с радиусом, равным каждой из двух новых сторон этого равнобедренного треугольника.
- Пересечение внутри исходного треугольника между две окружности — это точка Ферма.
Когда треугольник имеет угол больше 120 °, точка Ферма располагается в тупоугольной вершине.
Далее «случай 1» означает, что треугольник имеет угол, превышающий 120 °. «Случай 2» означает, что угол треугольника не превышает 120 °.
Расположение X (13)
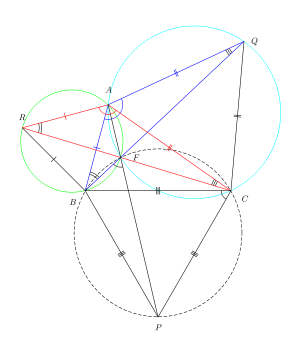
Рис. 2 показаны равносторонние треугольники ARB, AQC и CPB, прикрепленные к сторонам произвольного треугольника ABC. Вот доказательство, использующее свойства совпадающих точек, чтобы показать, что три прямые RC, BQ и AP на рис. 2 все пересекаются в точке F и пересекаются друг с другом под углами 60 °.
Треугольники RAC и BAQ конгруэнтны, потому что второй — это угол поворота первого на 60 ° относительно A. Следовательно, ARF = ∠ABF и ∠AQF = ACF. Согласно обратной теореме о вписанном угле, примененной к отрезку AF, точки ARBF являются параллельными (они лежат на окружности). Точно так же точки AFCQ совпадают.
ARB = 60 °, поэтому ∠AFB = 120 °, используя теорему о вписанном угле. Аналогично ∠AFC = 120 °.
Итак, ∠BFC = 120 °. Таким образом, ∠BFC и ∠BPC в сумме составляют 180 °. Используя теорему о вписанном угле, это означает, что точки BPCF совпадают. Итак, используя теорему о вписанном угле, примененную к отрезку BP, BFP = ∠BCP = 60 °. Поскольку ∠BFP + ∠BFA = 180 °, точка F лежит на отрезке AP. Итак, линии RC, BQ и AP являются параллельными (они пересекаются в одной точке). QED
Это доказательство применимо только в случае 2, поскольку, если BAC>120 °, точка A лежит внутри описанной окружности BPC, которая меняет относительные положения A и F. Однако его легко изменить, чтобы охватить случай 1. Тогда ∠AFB = ∠AFC = 60 °, следовательно, ∠BFC = ∠AFB = ∠AFC = 120 °, что означает, что BPCF является концикличным, поэтому ∠BFP = ∠BCP = 60 ° = ∠BFA. Следовательно, A лежит на FP.
Линии, соединяющие центры окружностей на рис. 2, перпендикулярны отрезкам AP, BQ и CR. Например, линия, соединяющая центр круга, содержащего ARB, и центр круга, содержащего AQC, перпендикулярна сегменту AP. Итак, линии, соединяющие центры окружностей, также пересекаются под углом 60 °. Следовательно, центры окружностей образуют равносторонний треугольник. Это известно как Теорема Наполеона.
Расположение точки Ферма
Традиционная геометрия

Для любого евклидова треугольника ABC и произвольной точки P пусть d (P) = PA + PB + PC, где PA обозначает расстояние между P и A. Целью этого раздела является определение точки P 0 такой, что d (P 0) < d(P) for all P ≠ P0. Если такая точка существует, то это будет точка Ферма. В дальнейшем Δ будет обозначать точки внутри треугольника и включать его границу Ω.
Ключевым результатом, который будет использоваться, является правило изгиба, которое утверждает, что если треугольник и многоугольник имеют одну общую сторону, а остальная часть треугольника лежит внутри многоугольника, тогда треугольник имеет более короткий периметр, чем многоугольник.. [Если AB является общей стороной, продлите AC, чтобы разрезать многоугольник в X. Тогда по неравенству треугольника периметр многоугольника>AB + AX + XB = AB + AC + CX + XB ≥ AB + AC + BC.]
Пусть P — любая точка вне Δ. Свяжите каждую вершину с этими удаленная зона; то есть полуплоскость за (расширенной) противоположной стороной. Эти 3 зоны покрывают всю плоскость, за исключением самого Δ, и P явно лежит в одной или двух из них. Если P находится в двух точках (скажем, пересечение зон B и C), то установка P ‘= A влечет d (P’) = d (A) < d(P) by the dogleg rule. Alternatively if P is in only one zone, say the A-zone, then d(P’) < d(P) where P’ is the intersection of AP and BC. So для каждой точки P вне Δ существует точка P ‘в Ω такая, что d (P ‘) < d(P).
Случай 1. Треугольник имеет угол ≥ 120 °.
Без ограничения общности предположим, что угол при A равен ≥ 120 °. Постройте равносторонний треугольник AFB и для любой точки P в Δ (кроме самой A) постройте Q так, чтобы треугольник AQP был равносторонним и имел указанную ориентацию. Тогда треугольник ABP представляет собой поворот на 60 ° треугольника AFQ вокруг A, так что эти два треугольника конгруэнтны, и отсюда следует, что d (P) = CP + PQ + QF, что является просто длиной пути CPQF. Поскольку P ограничено лежать в пределах ABC, по правилу изгиба длина этого пути превышает AC + AF = d (A). Следовательно, d (A) < d(P) for all P є Δ, P ≠ A. Now allow P to range outside Δ. From above a point P’ є Ω exists such that d(P’) < d(P) and as d(A) ≤ d (P’) it follows that d(A) < d(P) for all P outside Δ. Thus d(A) < d(P) for all P ≠ A which means that A is the Fermat point of Δ. In other words, точка Ферма лежит в тупоугольной вершине .
Случай 2. Треугольник не имеет угла ≥ 120 °.
Постройте равносторонний треугольник BCD и пусть P — любая точка внутри Δ и построим равносторонний треугольник CPQ. Тогда CQD — это поворот CPB на 60 ° относительно C, поэтому d (P) = PA + PB + PC = AP + PQ + QD, что является просто длиной пути APQD. Пусть P 0 — точка пересечения AD и CF. Эту точку принято называть первым изогоническим центром. Выполните то же упражнение с P 0, как и с P, и найдите точку Q 0. Из-за углового ограничения P 0 лежит внутри Δ, кроме того, BCF представляет собой поворот BDA на 60 ° вокруг B, поэтому Q 0 должен лежать где-то на AD. Поскольку CDB = 60 °, следует, что Q 0 лежит между P 0 и D, что означает, что AP 0Q0D является прямой линией, поэтому d (P 0) = AD. Более того, если P ≠ P 0, то либо P, либо Q не будут лежать на AD, что означает d (P 0) = AD < d(P). Now allow P to range outside Δ. From above a point P’ є Ω exists such that d(P’) < d(P) and as d(P0) ≤ d (P ‘) it следует, что d (P 0) < d(P) for all P outside Δ. That means P0- точка Ферма Δ. Другими словами, точка Ферма совпадает с первым изогоническим центром .
Векторный анализ
Пусть O, A, B, C, X — любые пять точек на плоскости. Обозначим векторы OA →, OB →, OC →, OX → { displaystyle { overrightarrow { mathrm {OA}}}, { overrightarrow { mathrm { OB}}}, { overrightarrow { mathrm {OC}}}, { overrightarrow { mathrm {OX}}}}
Множители Лагранжа
Другой подход к поиску точки внутри треугольника, от которой сумма расстояний до вершин треугольника минимальна, заключается в использовании одного из оптимизация (математика) методы. В частности, методом множителей Лагранжа и закона косинусов.
мы проводим линии от точки внутри треугольника к его вершинам и называем их X, Yи Z . Кроме того, пусть длины этих линий равны x, y и z соответственно. Пусть угол между X и Y равен α, Y и Z равен β. Тогда угол между X и Z равен (2π — α — β). Используя метод множителей Лагранжа, мы должны найти минимум лагранжиана L, который выражается как:
- L = x + y + z + λ 1 (x + y — 2xy cos (α) — a) + λ 2 (y + z — 2yz cos (β) — b) + λ 3 (z + x — 2zx cos (α + β) — c)
где a, b и c — длины сторон треугольника.
Приравнивание каждой из пяти частных производных δL / δx, δL / δy, δL / δz, δL / δα, δL / δβ к нулю и исключение λ 1, λ 2, λ 3 в конечном итоге дает sin (α) = sin (β) и sin (α + β) = — sin (β), поэтому α = β = 120 °. Однако устранение — долгое и утомительное дело, и конечный результат охватывает только случай 2.
Свойства

- Когда наибольший угол треугольника не превышает 120 °, X (13) является точкой Ферма.
- Углы, образуемые сторонами треугольника в X (13) все равны 120 ° (случай 2) или 60 °, 60 °, 120 ° (случай 1).
- описанные окружности трех построенных равносторонних треугольников совпадают в точке X (13).
- Трилинейные координаты для первого изогонического центра, X (13):
- csc (A + π / 3): csc (B + π / 3): csc (C + π / 3), или, что то же самое,
- сек (A — π / 6): sec (B — π / 6): sec (C — π / 6).
- Трилинейные координаты для второй изогонический центр, X (14):
- csc (A — π / 3): csc (B — π / 3): csc (C — π / 3), или, что то же самое,
- sec (A + π / 6): sec (B + π / 6): sec (C + π / 6).
- Трилинейные координаты для точки Ферма:
- 1 — u + uvw sec (A — π / 6): 1 — v + uvw sec (B — π / 6): 1 — w + uvw sec (C — π / 6)
- где u, v, w соответственно обозначают булевы переменные (A<120°), (B<120°), (C<120°).
- Изогональное сопряжение X (13) является первой изодинамической точкой, X (15):
- sin (A + π / 3): sin (B + π / 3): sin (C + π / 3).
- Изогональное сопряжение X (14) является второй изодинамической точкой, X (16):
- sin (A — π / 3): sin (B — π / 3): sin (C — π / 3).
- Следующие треугольники равносторонние:
- антипедальный треугольник of X (13)
- антипедальный треугольник X (14)
- педальный треугольник из X (15)
- педальный треугольник X (16)
- описанный треугольник X (15)
- описанный треугольником X (16)
- Прямые X (13) X (15) и X (14) X (16) параллельны прямой Эйлера. Три прямые пересекаются в точке бесконечности Эйлера, X (30).
- Точки X (13), X (14), центр описанной окружности и девятиточка центр лежит на окружности Лестера.
- Прямая X (13) X (14) пересекает линию Эйлера в средней точке X (2) и X (4).
- Ферма точка лежит в открытом ортоцентроидном диске, проколотом в его собственном центре, и может быть любой точкой в нем.
Псевдонимы
изогонические центры X (13) и X (14) также известны как первая точка Ферма и вторая точка Ферма соответственно. Альтернативными вариантами являются положительная точка Ферма и отрицательная точка Ферма . Однако эти разные имена могут сбивать с толку, и, возможно, их лучше избегать. Проблема в том, что большая часть литературы стирает различие между точкой Ферма и первой точкой Ферма, тогда как только в случае 2, приведенном выше, они фактически одинаковы.
История
Этот вопрос был предложен Ферма в качестве вызова Евангелисте Торричелли. Он решил проблему так же, как и Ферма, но вместо этого использовал пересечение описанных окружностей трех правильных треугольников. Его ученица, Вивиани, опубликовала решение в 1659 году.
См. Также
- Геометрическая медиана или точка Ферма – Вебера, точка, минимизирующая сумму расстояний до более чем трех заданных точек.
- Теорема Лестера
- Центр треугольника
- Точки Наполеона
- Задача Вебера
Ссылки
Внешние ссылки
- , Энциклопедия математики, EMS Press, 2001 [ 1994]
- Точка Ферма Криса Баучера, Демонстрационный проект Вольфрама.
- Обобщение Ферма-Торричелли в Эскизы динамической геометрии Интерактивный эскиз обобщает точку Ферма-Торричелли.
- Практический пример точки Ферма
- Интерактивный эскиз iOS
From Wikipedia, the free encyclopedia
Fig 1. Construction of the first isogonic center, X(13). When no angle of the triangle exceeds 120°, this point is the Fermat point.
In Euclidean geometry, the Fermat point of a triangle, also called the Torricelli point or Fermat–Torricelli point, is a point such that the sum of the three distances from each of the three vertices of the triangle to the point is the smallest possible[1] or, equivalently, the geometric median of the three vertices. It is so named because this problem was first raised by Fermat in a private letter to Evangelista Torricelli, who solved it.
The Fermat point gives a solution to the geometric median and Steiner tree problems for three points.
Construction[edit]
The Fermat point of a triangle with largest angle at most 120° is simply its first isogonic center or X(13), which is constructed as follows:
- Construct an equilateral triangle on each of two arbitrarily chosen sides of the given triangle.
- Draw a line from each new vertex to the opposite vertex of the original triangle.
- The two lines intersect at the Fermat point.
An alternative method is the following:
- On each of two arbitrarily chosen sides, construct an isosceles triangle, with base the side in question, 30-degree angles at the base, and the third vertex of each isosceles triangle lying outside the original triangle.
- For each isosceles triangle draw a circle, in each case with center on the new vertex of the isosceles triangle and with radius equal to each of the two new sides of that isosceles triangle.
- The intersection inside the original triangle between the two circles is the Fermat point.
When a triangle has an angle greater than 120°, the Fermat point is sited at the obtuse-angled vertex.
In what follows «Case 1» means the triangle has an angle exceeding 120°. «Case 2» means no angle of the triangle exceeds 120°.
Location of X(13)[edit]
Fig 2. Geometry of the first isogonic center.
Fig. 2 shows the equilateral triangles △ARB, △AQC, △CPB attached to the sides of the arbitrary triangle △ABC.
Here is a proof using properties of concyclic points to show that the three lines RC, BQ, AP in Fig 2 all intersect at the point F and cut one another at angles of 60°.
The triangles △RAC, △BAQ are congruent because the second is a 60° rotation of the first about A. Hence ∠ARF = ∠ABF and ∠AQF = ∠ACF. By the converse of the inscribed angle theorem applied to the segment AF, the points ARBF are concyclic (they lie on a circle). Similarly, the points AFCQ are concyclic.
∠ARB = 60°, so ∠AFB = 120°, using the inscribed angle theorem. Similarly, ∠AFC = 120°.
So ∠BFC = 120°. Therefore, ∠BFC + ∠BPC = 180°. Using the inscribed angle theorem, this implies that the points BPCF are concyclic. So, using the inscribed angle theorem applied to the segment BP, ∠BFP = ∠BCP = 60°. Because ∠BFP + ∠BFA = 180°, the point F lies on the line segment AP. So, the lines RC, BQ, AP are concurrent (they intersect at a single point). Q.E.D.
This proof applies only in Case 2, since if ∠BAC > 120°, point A lies inside the circumcircle of △BPC which switches the relative positions of A and F. However it is easily modified to cover Case 1. Then ∠AFB = ∠AFC = 60° hence ∠BFC = ∠AFB + ∠AFC = 120° which means BPCF is concyclic so ∠BFP = ∠BCP = 60° = ∠BFA. Therefore, A lies on FP.
The lines joining the centers of the circles in Fig. 2 are perpendicular to the line segments AP, BQ, CR. For example, the line joining the center of the circle containing △ARB and the center of the circle containing △AQC, is perpendicular to the segment AP. So, the lines joining the centers of the circles also intersect at 60° angles. Therefore, the centers of the circles form an equilateral triangle. This is known as Napoleon’s Theorem.
Location of the Fermat point[edit]
Traditional geometry[edit]
Fig 3. Geometry of the Fermat point
Given any Euclidean triangle △ABC and an arbitrary point P let 


A key result that will be used is the dogleg rule, which asserts that if a triangle and a polygon have one side in common and the rest of the triangle lies inside the polygon then the triangle has a shorter perimeter than the polygon:
- If AB is the common side, extend AC to cut the polygon at the point X. Then the polygon’s perimeter is, by the triangle inequality:
Let P be any point outside Δ. Associate each vertex with its remote zone; that is, the half-plane beyond the (extended) opposite side. These 3 zones cover the entire plane except for Δ itself and P clearly lies in either one or two of them. If P is in two (say the B and C zones’ intersection) then setting 



Case 1. The triangle has an angle ≥ 120°.
Without loss of generality, suppose that the angle at A is ≥ 120°. Construct the equilateral triangle △AFB and for any point P in Δ (except A itself) construct Q so that the triangle △AQP is equilateral and has the orientation shown. Then the triangle △ABP is a 60° rotation of the triangle △AFQ about A so these two triangles are congruent and it follows that 









Case 2. The triangle has no angle ≥ 120°.
Construct the equilateral triangle △BCD, let P be any point inside Δ, and construct the equilateral triangle △CPQ. Then △CQD is a 60° rotation of △CPB about C so
which is simply the length of the path APQD. Let P0 be the point where AD and CF intersect. This point is commonly called the first isogonic center. Carry out the same exercise with P0 as you did with P, and find the point Q0. By the angular restriction P0 lies inside △ABC. Moreover, △BCF is a 60° rotation of △BDA about B, so Q0 must lie somewhere on AD. Since ∠CDB = 60° it follows that Q0 lies between P0 and D which means AP0Q0D is a straight line so 






Vector analysis[edit]
Let O, A, B, C, X be any five points in a plane. Denote the vectors 
Adding a, b, c gives
If a, b, c meet at O at angles of 120° then i + j + k = 0, so
for all x. In other words,
and hence O is the Fermat point of △ABC.
This argument fails when the triangle has an angle ∠C > 120° because there is no point O where a, b, c meet at angles of 120°. Nevertheless, it is easily fixed by redefining k = − (i + j) and placing O at C so that c = 0. Note that |k| ≤ 1 because the angle between the unit vectors i, j is ∠C which exceeds 120°. Since
the third inequality still holds, the other two inequalities are unchanged. The proof now continues as above (adding the three inequalities and using i + j + k = 0) to reach the same conclusion that O (or in this case C) must be the Fermat point of △ABC.
Lagrange multipliers[edit]
Another approach to finding the point within a triangle, from which the sum of the distances to the vertices of the triangle is minimal, is to use one of the mathematical optimization methods; specifically, the method of Lagrange multipliers and the law of cosines.
We draw lines from the point within the triangle to its vertices and call them X, Y, Z. Also, let the lengths of these lines be x, y, z respectively. Let the angle between X and Y be α, Y and Z be β. Then the angle between X and Z is 2π − α − β. Using the method of Lagrange multipliers we have to find the minimum of the Lagrangian L, which is expressed as:
where a, b, c are the lengths of the sides of the triangle.
Equating each of the five partial derivatives 
Properties[edit]
The two isogonic centers are the intersections of three vesicae piscis whose paired vertices are the vertices of the triangle
- When the largest angle of the triangle is not larger than 120°, X(13) is the Fermat point.
- The angles subtended by the sides of the triangle at X(13) are all equal to 120° (Case 2), or 60°, 60°, 120° (Case 1).
- The circumcircles of the three constructed equilateral triangles are concurrent at X(13).
- Trilinear coordinates for the first isogonic center, X(13):[2]
- Trilinear coordinates for the second isogonic center, X(14):[3]
- Trilinear coordinates for the Fermat point:
-
- where u, v, w respectively denote the Boolean variables (A < 120°), (B < 120°), (C < 120°).
- The isogonal conjugate of X(13) is the first isodynamic point, X(15):[4]
- The isogonal conjugate of X(14) is the second isodynamic point, X(16):[5]
- The following triangles are equilateral:
- antipedal triangle of X(13)
- Antipedal triangle of X(14)
- Pedal triangle of X(15)
- Pedal triangle of X(16)
- Circumcevian triangle of X(15)
- Circumcevian triangle of X(16)
- The lines X(13)X(15) and X(14)X(16) are parallel to the Euler line. The three lines meet at the Euler infinity point, X(30).
- The points X(13), X(14), the circumcenter, and the nine-point center lie on a Lester circle.
- The line X(13)X(14) meets the Euler line at midpoint of X(2) and X(4).[6]
- The Fermat point lies in the open orthocentroidal disk punctured at its own center, and could be any point therein.[7]
Aliases[edit]
The isogonic centers X(13) and X(14) are also known as the first Fermat point and the second Fermat point respectively. Alternatives are the positive Fermat point and the negative Fermat point. However these different names can be confusing and are perhaps best avoided. The problem is that much of the literature blurs the distinction between the Fermat point and the first Fermat point whereas it is only in Case 2 above that they are actually the same.
History[edit]
This question was proposed by Fermat, as a challenge to Evangelista Torricelli. He solved the problem in a similar way to Fermat’s, albeit using the intersection of the circumcircles of the three regular triangles instead. His pupil, Viviani, published the solution in 1659.[8]
See also[edit]
- Geometric median or Fermat–Weber point, the point minimizing the sum of distances to more than three given points.
- Lester’s theorem
- Triangle center
- Napoleon points
- Weber problem
References[edit]
- ^ Cut The Knot — The Fermat Point and Generalizations
- ^ Entry X(13) in the Encyclopedia of Triangle Centers Archived April 19, 2012, at the Wayback Machine
- ^ Entry X(14) in the Encyclopedia of Triangle Centers Archived April 19, 2012, at the Wayback Machine
- ^ Entry X(15) in the Encyclopedia of Triangle Centers Archived April 19, 2012, at the Wayback Machine
- ^ Entry X(16) in the Encyclopedia of Triangle Centers Archived April 19, 2012, at the Wayback Machine
- ^ Kimberling, Clark. «Encyclopedia of Triangle Centers».
- ^ Christopher J. Bradley and Geoff C. Smith, «The locations of triangle centers», Forum Geometricorum 6 (2006), 57—70. http://forumgeom.fau.edu/FG2006volume6/FG200607index.html
- ^ Weisstein, Eric W. «Fermat Points». MathWorld.
External links[edit]
- «Fermat-Torricelli problem», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Fermat Point by Chris Boucher, The Wolfram Demonstrations Project.
- Fermat-Torricelli generalization at Dynamic Geometry Sketches Interactive sketch generalizes the Fermat-Torricelli point.
- A practical example of the Fermat point
- iOS Interactive sketch
Проектная работа
Введение
План:
1. Алгоритм построения точки Ферма-Торричелли;
2. Интересные свойства точки Ферма-Торричелли;
3. Физическая модель нахождения точки Ферма-Торричелли;
4. Настольная модель нахождения точки Ферма-Торричелли;
5. Определение точки Ферма-Торричелли на карте воронежской области;
1. Определение точки Ферма
Если все углы треугольника меньше 120 градусов, то
точкой Ферма называется такая точка треугольника, сумма расстояний от которой
до вершин треугольника является минимальной.
Иногда эту точку называют точкой Торричелли, поэтому в
дальнейшем эту замечательную точку треугольника будем называть точкой
Ферма-Торричелли, но в некоторых параграфах для удобства записи мы
воспользуемся только одним названием – точкой Ферма.
2. Алгоритм построения точки Ферма:
·
построить на сторонах
треугольника вне него равносторонние треугольники;
·
соединить отрезком каждую
вершину треугольника с вершиной равностороннего треугольника, построенного на
противоположной стороне;
·
построить точку
пересечения этих отрезков.
3. Интересные свойства точки Ферма
·
Каждая сторона треугольника
из точки Ферма видна под углом 120 градусов;
·
Если один из углов
треугольника равен 120 градусов, то точка Ферма совпадет с вершиной
треугольника;
·
Окружности описанные около
правильных треугольников пересекаются в точке Ферма.
4) Если внутри треугольника построить треугольник, стороны которого
являются средними линиями исходного треугольника, потом аналогично построить
третий, четвертый треугольник и т.д.; в каждом треугольнике построить свою
точку Ферма, то все точки Ферма будут лежать на одной прямой. Это свойство
будем называть коллинеарностью точек Ферма.
а) Построим произвольный треугольник и точку Ферма данного треугольника.
б) В заданном треугольнике построим треугольник, стороны которого
являются средними линиями исходного (красный треугольник).
в) Построим точку Ферма в красном треугольнике.
г) Построим треугольник, стороны которого являются средними линиями
красного (зеленый треугольник) и найдем для него точку Ферма.
д) Все точки Ферма лежат на одной прямой, т.е. коллинеарны.
4. Физическая модель точки Ферма
Самое интересное в работе было то, что мы сумели связать этот
интересный математический факт с физикой. А факт заключается в следующем: если
на тело действуют три одинаковые силы и они уравновешивают друг друга, то углы
между ними составляют 120 градусов. Этот факт мы использовали для построения
модели, которая позволяла практическим путем найти точку Ферма для любого
треугольника.
 |
Суть модели в следующем: на доске в виде решетки закреплены штыри с
подшипниками так что, их можно свободно переставить в любое отверстие
решетки. Эти штыри являются вершинами треугольника. Стороны треугольника
сделаны из резинки. Это для того, чтобы легко изменить вид треугольника.
Через каждый подшипник перекинута нить с одинаковым грузом на конце. Масса
каждого груза равна 100 грамм. Нити взяты специальные, нерастяжимые. Свободные
концы нитей связаны в один узел. Когда грузы будут отпущены, они натянут нити.
На этот узел со стороны нитей с грузом действуют силы натяжения этих нитей.
После того, как эти силы станут равными по величине и будут уравновешивать друг
друга, узел установится в искомой точке. Если измерить углы между нитями, то
будет видно, что они составляют между собой углы 120 градусов. Каждая сторона
треугольника из этой точки будет видна под углом 120 градусов, а этим свойством
обладает точка Ферма. В этом мы можем убедиться, если приставим к нашей модели
диск из оргстекла, где начерчены лучи, исходящие из одной точки и образующие
между собой угол 120 градусов. После того, как лучи и нити полностью
совместятся наложением, фломастером можно отметить местоположение точки Ферма
для данного треугольника.
Эта модель создана аналогично физической модели, но с
одной гирей. Она работает так же, как физическая модель, если взять достаточно
скользкие лески, «абсолютно» гладкую поверхность, шарниры и гири. Конечно,
здесь большую роль играют трение в шарнирах, масса гири, масса подвижного
шарнира, трение этого шарнира об стол. Но в зависимости от соотношения этих
параметров мы имеем прибор для физического обнаружения точки Торричелли и Ферма
одновременно. Следовательно, в случае пренебрежения трением во
всех осях и их толщиной, мы имеем схему механического доказательства
эквивалентности точек Ферма и Торричелли.
Можно утверждать, что из
соображения сил – это точка Торричелли, а из энергетических соображений – точка
Ферма.
Построение
Точки Ферма-Торричелли в Воронеже.
Построение точки Ферма для треугольников с углами, не превосходящими 120°.
Точка Ферма — точка плоскости, сумма расстояний от которой до вершин треугольника является минимальной. Точку Ферма также иногда называют точкой Торричелли или точкой Ферма-Торричелли. Точка Ферма даёт решение проблемы Штейнера для вершин треугольника. В английской литературе точку Ферма также называют изогональным центром (isogonic center) X(13).
История
Точка Ферма впервые предложена Ферма:
«Datis tribus punctis, quartum reperire, a quo si ducantur tres rectæ ad data puncta, summa trium harum rectarum sit minima quantitas». P. de Fermat, «Œuvres de Fermat», 1679, Livre I, Paris.(лат. «Для трех заданных точек найти четвертую, такую что если от неё провести прямые линии до данных точек, сумма расстояний будет наименьшей». П. Ферма).
Свойства
Теорема Лестера. В любом разностороннем треугольнике две точки Ферма, центр девяти точек и центр описанной окружности лежат на одной окружности (окружности Лестера).
Построение
Теорема (Э. Торричелли, Б. Кавальери, Т. Симпсон, Ф. Хейнен, Ж. Бертран). Построим на сторонах произвольного треугольника [math]displaystyle{ ABC }[/math] во внешнюю сторону равносторонние треугольники [math]displaystyle{ ABC’ }[/math], [math]displaystyle{ BCA’ }[/math], [math]displaystyle{ CAB’ }[/math]. Тогда шесть кривых — три окружности, описанные вокруг этих правильных треугольников, и прямые [math]displaystyle{ AA’ }[/math], [math]displaystyle{ BB’ }[/math], [math]displaystyle{ CC’ }[/math] пересекаются в одной точке [math]displaystyle{ X }[/math]. Если все углы треугольника [math]displaystyle{ ABC }[/math] не превосходят [math]displaystyle{ 120^circ }[/math], то [math]displaystyle{ X }[/math] лежит в треугольнике [math]displaystyle{ ABC }[/math] и является точкой Ферма [math]displaystyle{ S }[/math]. В этом случае углы между отрезками [math]displaystyle{ AS }[/math], [math]displaystyle{ BS }[/math] и [math]displaystyle{ CS }[/math] равны между собой и, значит, равны [math]displaystyle{ 120^circ }[/math]. Более того, длины отрезков [math]displaystyle{ AA’ }[/math], [math]displaystyle{ BB’ }[/math] и [math]displaystyle{ CC’ }[/math], называемых линиями Симпсона, тоже равны между собой и равны [math]displaystyle{ AS+BS+CS }[/math]. Если один из углов треугольника [math]displaystyle{ ABC }[/math] больше [math]displaystyle{ 120^circ }[/math], то [math]displaystyle{ X }[/math] лежит вне треугольника [math]displaystyle{ ABC }[/math], а точка Ферма [math]displaystyle{ S }[/math] совпадает с вершиной тупого угла.
Теорема дает алгоритм построения точки Ферма с помощью циркуля и линейки. В нетривиальном случае, когда все углы треугольника меньше [math]displaystyle{ 120^circ }[/math], точку Ферма находят как пересечение любых двух из шести кривых, описанных в теореме.
Экспериментальное построение точки Ферма.
Физически эту точку можно построить так: отметим на плоской гладкой горизонтальной поверхности точки [math]displaystyle{ A }[/math], [math]displaystyle{ B }[/math] и [math]displaystyle{ C }[/math] и просверлим в отмеченных местах сквозные отверстия; свяжем три нити и пропустим сверху их свободные концы через отверстия; привяжем к свободным концам грузы одинаковой массы; когда система придет в равновесие, узел окажется в точке Ферма для треугольника [math]displaystyle{ ABC }[/math].
Замечание
Кстати, на первом рисунке справа центры трёх равносторонних треугольников сами являются вершинами нового равностороннего треугольника (Теорема Наполеона). Кроме того, [math]displaystyle{ AA’=BB’=CC’ }[/math].
Нахождение точки Ферма. Множители Лагранжа
Есть подход к нахождению точки внутри треугольника, для которой сумма расстояний до вершин треугольника минимальна, заключается в использовании одного из методов оптимизации в математике. В частности, метод множителей Лагранжа и теоремы косинусов.
Мы рисуем линии от точки внутри треугольника до его вершин и называем их X, Y и Z. Кроме того, пусть длины этих линий равны x, y и z соответственно. Пусть угол между X и Y равен α, Y и Z — β. Тогда угол между X и Z равен (2π — α — β). Используя метод множителей Лагранжа, мы должны найти минимум лагранжиана L, который выражается как:
- L = x + y + z + λ1 (x2 + y2 − 2xy cos(α) − a2) + λ2 (y2 + z2 − 2yz cos(β) − b2) + λ3 (z2 + x2 − 2zx cos(α + β) − c2)
где a, b и c — длины сторон треугольника.
Приравнивая каждую из пяти частных производных δL/δx, δL/δy, δL/δz, δL/δα, δL/δβ нулю и исключая λ1, λ2, λ3, в конечном итоге получаем sin (α) = sin (β) и sin (α + β) = — sin (β), поэтому α = β = 120 °. Однако выкладки являются долгим и утомительным делом, и конечный результат охватывает только Случай 2, когда ни один из углов ≥ 120°.
Точка Торричелли
Точка Торричелли — точка треугольника, из которой все стороны видны под углом в [math]displaystyle{ 120^circ }[/math]. Существует только в треугольниках с углами, меньшими [math]displaystyle{ 120^circ }[/math], при этом она единственна и, значит, совпадает с точкой Ферма.
См. также
- Замечательные точки треугольника
- Проблема Штейнера
- Окружность Лестера
- Точки Торричелли
Примечания
Литература
- Энциклопедия для детей / Глав. ред. М. Д. Аксёнова. — М.: Аванта+, 2001. — Т. 11. Математика. — 688 с.
- А. О. Иванов, А. А. Тужилин. Теория экстремальных сетей. — Москва–Ижевск: Институт компьютерных исследований, 2003. — ISBN 5-93972-292-X.
Ссылки
- Точка Ферма
- Точка Торричелли
- Практический пример построения точки Ферма (англ.)
Содержание
☞
English version
§
Вспомогательная страница к разделу
ВЫЧИСЛЕНИЕ РАССТОЯНИЙ МЕЖДУ ГЕОМЕТРИЧЕСКИМИ ОБЪЕКТАМИ.
Благодарю Б.З.Тайбина за обнаружение 03.06.10 ошибки на настоящей странице и информирование о ней.
Задача Ферма-Торричелли и ее развитие
Обобщенная задача Ферма-Торричелли
Задача. Пусть заданы координаты $ K_{} $ точек пространства $ mathbb R^{n}_{} $ : $ {P_j=(x_{j1},dots,x_{jn})}_{j=1}^K $. Определить координаты точки
$ P_{ast}=(x_{ast 1},dots,x_{ast n}) $, решающей задачу оптимизации:
$$
min_{Pin mathbb R^n} F(P) qquad npu qquad F(P)= sum_{j=1}^Km_j |PP_j| .
$$
Здесь $ | cdot | $ означает евклидово расстояние: $ |P_1P_2|=sqrt{(x_{11}-x_{21})^2+dots+(x_{1n}-x_{2n})^2} $, а величины $ { m_j }_{j=1}^K $ обычно (и практически везде в настоящем разделе) считаются положительными и называются весами.
Задача известна под различными названиями: обобщенная задача Ферма-Торричелли, задача Ферма-Торричелли-Штейнера,
задача Вебера, задача о взвешенной геометрической медиане.
Будем говорить о наборе
$$
left{
begin{array}{l|c|l} P_1 & dots & P_K \
m_1 & dots & m_K
end{array}
right}
$$
как о конфигурации весов.
Плоский случай
Рассмотрим сначала плоский вариант задачи: пусть $ n=2_{} $, $ {P_j=(x_{j},y_j)}_{j=1}^K $,
$$
F(x,y)= sum_{j=1}^{K} m_j sqrt{(x-x_j)^2+(y-y_j)^2} .
$$
В этом случае поставленная задача называется задачей об оптимальном расположении (узловой) станции1), или — в случае $ K=3 $ — задачей о трёх заводах.
П
Пример. В городах $ P_{1},P_2,P_3 $ расположены источники полезных ископаемых: железной руды, угля и воды соответственно. Известно, что для производства одной тонны стали необходимо иметь $ m_{1} $ тонн руды, $ m_2 $ тонн угля и $ m_3 $ тонн воды. В предположении, что стоимость перевозки одной тонны груза не зависит от его природы, где следует расположить сталелитейное производство так, чтобы минимизировать транспортные издержки?

С конца XIX века подобные задачи стали предметом изучения в экономической географии. Систематические исследования были начаты Вильгельмом Лаунхардтом2)[6] и позднее развиты Альфредом Вебером3)[1] . Последний ввел понятие штандорта4) — оптимального места размещения производства, «склада».
Каков должен быть первый общий подход к отысканию таких пунктов? С угловыми вершинами штандортной фигуры штандорт связан линиями — их Вебер называет «компонентами»,— по которым и происходит передвижение соответствующих тяжестей. Положим, что мы имеем перед собой производство, работающее с двумя локализованными материалами, причем на выработку $ 1_{} $ тонны продукта требуется $ 3/4 $ тонны одного материала и $ 1/2 $ тонны другого. В таком случае мы получаем штандортную фигуру, на «материальных компонентах» которой передвигаются веса в $ 3/4 $ и $ 1/2 $, в то время как «потребительская компонента» отягощена $ 1_{} $.

В XX веке эти задачи выделились в подраздел теории исследования операций, известный в настоящее время как facility location problem или location theory (location analysis).
Частный случай задачи при $ n=2 , K=3 $ и $ m_1=m_2=m_3=1 $ известен как (классическая) задача Ферма-Торричелли: для трех неколлинеарных точек плоскости
$ P_1=(x_1,y_1), P_2= (x_2,y_2) $ и $ P_3= (x_3,y_3) $ требуется определить
$$
min_{(x,y)} F(x,y) quad npu quad F(x,y)= sum_{j=1}^3 sqrt{(x-x_j)^2+(y-y_j)^2} .
$$
Datis tribus punctis, quartum reperire, a quo si ducantur tres rectæ ad data puncta, summa trium harum rectarum sit minima quantitas
(лат.) Для трех заданных точек найти четвертую, такую что если от нее провести прямые линии до данных точек, сумма расстояний будет наименьшей) P. de Fermat, «Œuvres de Fermat», 1679, Livre I, Paris.
Рассмотрим теперь различные подходы к решению общей задачи. Для определения координат стационарной точки $ P_{ast}=(x_{ast},y_{ast}) $ составим градиентную систему уравнений:
$$
left{ begin{array}{lll}
displaystyle frac{partial F}{partial x} &= displaystyle frac{m_1(x-x_1)}{sqrt{(x-x_1)^{2}+(y-y_1)^2}}+dots+ frac{m_K(x-x_K)}{sqrt{(x-x_K)^2+(y-y_K)^2}} & = 0 \
displaystyle frac{partial F}{partial y} &= displaystyle frac{m_1(y-y_1)}{sqrt{(x-x_1)^2+(y-y_1)^2}}+dots+ frac{m_K(y-y_K)}{sqrt{(x-x_K)^2+(y-y_K)^2}} & = 0
end{array}
right.
$$
Система эта нелинейная и даже неалгебраическая относительно $ x_{} $ и $ y_{} $, поэтому уже проблема установления существования (и количества) ее вещественных решений решается специально разработанными под нее методами.
Механическое решение
Если обозначить
$$
frac{x-x_j}{sqrt{(x-x_j)^{2}+(y-y_j)^2}} = cos gamma_j, frac{y-y_j}{sqrt{(x-x_j)^{2}+(y-y_1)^2}} = sin gamma_j ,
$$
где $ gamma_j $ означает угол, образованный вектором $ overrightarrow{PP_{j}} $ с осью абсцисс, то уравнения градиентной системы можно переписать в виде:
$$
left{ begin{array}{ll}
m_1cos gamma_1 + m_2 cos gamma_2 + dots + m_Kcos gamma_K &=0,\
m_1sin gamma_1 + m_2 sin gamma_2 + dots + m_K sin gamma_K &=0 .
end{array} right.
$$
Если под $ m_{j} $ понимать величину силы, приложенной в точке $ P_{} $, и направленной к $ P_{j} $,
то приведенные уравнения означают, что суммы проекций этих сил на координатные оси равны нулю, т.е. в точке $ P_{ast} $ силы должны уравновешиваться. Это обстоятельство используют для экспериментального определения точки $ P_{ast} $. На плоской доске, располагаемой горизонтально к поверхности Земли, рисуют многоугольник, подобный многоугольнику $ P_1 P_2 ldots P_K $ и просверливают в его вершинах отверстия, через которые опускают нити, связанные одним узлом. Если к свободным концам этих нитей подвесить грузы массами, пропорциональными $ m_{j} $, то при равновесии этой системы общий узел нитей будет находиться в искомой точке $ P_{ast} $.

Интуитивно понятно также, что если вес $ m_{i} $, приложенный сквозь отверстие $ P_{i} $, окажется много большим оставшихся весов, то узел затянется именно в это отверстие. Оказывается при возрастании $ m_{i} $ такое затягивание произойдет раньше выполнения условия $ m_i = displaystyle sum_{jne i} m_j $. См.
☟
НИЖЕ.
Геометрическое решение

Известно для случая $ K=3 $ точек на плоскости для произвольных значений весов $ { m_j } $ и для случая $ K=4 $ точек в случае одинаковых весов.
Исторически самое первое из известных решений задачи было предложено Торричелли в период до 1640 г.5). для случая $ K=3 $ точек и одинаковых весов $ m_1=m_2=m_3=1 $ (классическая задача Ферма-Торричелли). Алгоритм предлагал нахождение точки $ P_{ast} $ в идеологии классической геометрии: circinus et regula6). На сторонах треугольника $ P_1P_2P_{3} $, как на основаниях, строятся новые треугольники — равносторонние; эти треугольники должны располагаться с внешней стороны треугольника $ P_1P_2P_{3} $. Для каждого треугольника строится описывающая его окружность. Пересечение этих трех окружностей и дает точку $ P_{ast} $. На рисунке показано нахождение точки $ P_{ast} $ для случая $ P_1=(1,1),P_2=(3,5),P_3=(7,2) $.
С той поры было придумано много вариантов построения точки $ P_{ast} $. Так, к примеру, в этой же точке $ P_{ast} $ пересекаются прямые $ T_1 P_2 $ и $ T_2 P_1 $, и, вдобавок,
$$ |T_1P_2|=|T_2P_1|=|P_{ast} P_1|+|P_{ast} P_2|+|P_{ast} P_3| = min_{Pin mathbb R^2} sum_{j=1}^3 |PP_j| . $$
Это решение обобщается в [2,6] на случай различных весов. Рассмотрим систему уравнений из предыдущего пункта:
$$
left{ begin{array}{ll}
m_1cos gamma_1 + m_2 cos gamma_2 + m_3cos gamma_3 &=0,\
m_1sin gamma_1 + m_2 sin gamma_2 + m_3 sin gamma_3&=0 .
end{array} right.
$$
Из этих уравнений выразим $ cos gamma_1 $ и $ sin gamma_1 $ и подставим в равенство
$$
1=cos^2 gamma_1+ sin^2 gamma_1 =
$$
$$
=left(frac{m_2}{m_1} cos gamma_2 + frac{m_3}{m_1} cos gamma_3 right)^2+left(frac{m_2}{m_1} sin gamma_2 + frac{m_3}{m_1} sin gamma_3 right)^2 =
$$
$$
= frac{m_2^2}{m_1^2}+ frac{m_3^2}{m_1^2} + 2, frac{m_2m_3}{m_1^2} cos (gamma_2-gamma_3) .
$$
Обратим внимание, что естественным ограничением на условие задачи оказывается $ |cos (gamma_2 -gamma_3)| le 1 $, что равносильно $ m_1le m_2+m_{3} $ (сумма двух весов должна быть не меньше третьего; на самом деле условие того, что искомая точка $ P_{ast} $ будет отличаться от вершин $ P_1,P_2,P_3 $ более жесткое — см.
☟
НИЖЕ). Далее, из последнего равенства следует:
$$
Rightarrow sin^2 (gamma_2 -gamma_3) =frac{-m_1^4-m_2^4-m_3^4+2, m_1^2m_2^2+2, m_1^2m_3^2+2,m_2^2m_3^2}{4,m_2^2m_3^2} .
$$
Аналогичные равенства справедливы и для синусов оставшихся пар углов.
Отсюда получаем условие, которое должно выполняться в искомой точке $ P_{ast} $:
$$
frac{|sin (gamma_2 -gamma_3)|}{m_1} =frac{|sin (gamma_1 -gamma_3)|}{m_2} = frac{|sin (gamma_1 -gamma_2)|}{m_3} .
$$
Геометрический смысл разности $ gamma_1 -gamma_2 $ понятен из рисунка: это величина угла $ widehat{P_1 P_{ast}P_2} $. Можно образно сказать, что точки $ P_{1} $ и $ P_{2} $ «видно» из точки $ P_{ast} $ под углом $ gamma_2 -gamma_1 $.
В случае $ m_1=m_2=m_3=1 $ последнее равенство характеризует точку треугольника, которая известна под названием точки Ферма-Торричелли: это такая точка, из которой все его вершины «видны» под углом $ 2, pi/3 $. Точка Ферма-Торричелли не всегда существует — она имеется только у треугольников, углы которых не превосходят той же величины $ 2, pi/3 $.
Т
Теорема [3,4]. Точка Ферма-Торричелли существует только для треугольника $ P_{1}P_2P_3 $, у которого величина каждого угла меньше $ 2pi/3 $. В этом случае она единственна и в ней достигается
$$ min_{Pin mathbb R^2} (|PP_1|+|PP_2|+|PP_3|) , . $$
Если величина одного из углов треугольника $ ge 2pi/3 $, то минимум достигается при помещении точки $ P_{} $ в эту вершину.
П
Пример. Для точек $ P_1=(1,1), P_2=(3,5), P_3= (7,2) $ точка Ферма-Торричелли изображена на рисунке

Ее точные координаты приведены
☟
НИЖЕ .
♦
Вернемся к рассмотрению общего случая неравных весов.
На стороне $ P_{2}P_3 $ треугольника $ P_{1}P_2P_3 $ строится треугольник $ P_2P_3Q $, в котором
$$ |P_3Q|=frac{m_2}{m_1}|P_2P_3|, |P_2Q|=frac{m_3}{m_1}|P_2P_3| , $$
и который расположен по другую сторону от прямой $ P_2P_3 $ по отношению к треугольнику $ P_{1}P_2P_3 $.
Построенный треугольник очевидно оказывается подобным так называемому весовому треугольнику, т.е.
треугольнику с длинами сторон формально совпадающими с $ m_1,m_2,m_3 $.
Утверждается, что прямая $ QP_1 $ пересекает окружность, описанную вокруг треугольника $ P_2P_3Q $ в искомой точке $ P_{ast} $. В самом деле (см. рисунок ниже), по теореме синусов для треугольника $ P_2P_3Q $ будет выполнено:
$$
frac{sin nu_1 }{|P_2P_3|} =frac{sin nu_2 }{|P_3Q|} =frac{sin nu_3 }{|P_2Q|} quad iff quad frac{sin nu_1 }{m_1}=frac{sin nu_2 }{m_2}=frac{sin nu_3 }{m_3} .
$$
По построению точки $ P_{ast} $ будут иметь место соотношения:
$$ mu_1+nu_1=mu_2+nu_2= mu_3+nu_3= pi , $$
и, следовательно, ограничения на углы $ mu_1, mu_2, mu_3 $ оказываются такими же, как и на $ |gamma_3-gamma_2 |, |gamma_3-gamma_1 |, |gamma_2-gamma_1 | $.
Длина отрезка $ |P_1Q| $ позволяет определить величину минимального значения функции:
$$ m_1 |P_1Q| = m_1 |P_{ast} P_1|+m_2 |P_{ast} P_2|+ m_3 |P_{ast} P_3| = min_{Pin mathbb R^2} sum_{j=1}^3 m_j|PP_j| . $$
В предыдущих рассуждениях предполагается, что точка $ P_{ast} $ лежит внутри треугольника $ P_{1}P_2P_3 $. В противном случае, решением задачи будет одна из вершин треугольника.
П
Пример. Найти точку $ P_{ast} $ для конфигурации
$$
left{
begin{array}{c|c|c}
P_{1}=(2,6) & P_{2}=(1,1) & P_{3}=(5,1) \
m_{1}=2 & m_{2}=3 & m_{3}=4
end{array} right} .
$$
Решение. Здесь $ |P_2P_3|=4 $, следовательно $ |P_2Q|=4 cdot 2 = 8, |P_3Q|=4 cdot 3/2 = 6 $. Этими условиями определяем точку $ Q_{} $ — как одну из двух точек пересечения окружностей (радиуса $ 8_{} $ с центром в точке $ P_{2} $ и радиуса $ 6_{} $ с центром в $ P_3 $).

Её координаты: $ approx (6.5,-4.8) $. Проводим окружность через точки $ P_2,P_3,Q $. Прямая $ QP_1 $ пересекает ее в искомой точке $ P_{ast} approx (3.9, 1.4) $ при
минимальном значении для минимизируемой функции: $ F(x_{ast},y_{ast}) approx 23.4 $.
Точные значения приведены
☟
НИЖЕ.
♦
Для $ K=4 $ точек на плоскости геометрическое решение известно только для случая одинаковых весов.
Т
Теорема [Фаньяно]. Если точки $ P_{1},P_2,P_3, P_{4} $ образуют выпуклый четырехугольник, то
$$ min_{Pin mathbb R^2} left(|PP_1|+|PP_2|+|PP_3|+|PP_{4}| right)$$
достигается в точке $ P_{ast} $, лежащей на пересечении диагоналей четырехугольника:
$$ x_{ast}=frac{(x_1-x_3)(x_2y_4-y_2x_4)-(x_2-x_4)(y_3x_1-y_1x_3)}{(x_3-x_1)(y_2-y_4)-(x_2-x_4)(y_3-y_1)}, $$
$$ y_{ast}=frac{(y_1-y_3)(x_2y_4-y_2x_4)-(y_2-y_4)(y_3x_1-y_1x_3)}{(x_3-x_1)(y_2-y_4)-(x_2-x_4)(y_3-y_1)} , . $$
Если же точки $ P_{1},P_2,P_3, P_{4} $ не образуют выпуклый четырехугольник, и точка $ P_{i} $ лежит внутри треугольника, образованного тремя оставшимися точками, то минимум суммы расстояний достигается в точке $ P_{i} $.
Аналитическое решение: координаты точки Ферма-Торричелли
Пусть $ {P_j= (x_{j},y_j)}_{j=1}^3 $. Обозначим
$$
r_{jell}=sqrt{(x_j-x_{ell})^2+(y_j-y_{ell})^2}=|P_jP_{ell}| quad npu {j,ell} subset {1,2,3} .
$$
Т
Теорема.[11] Пусть все углы треугольника $ P_{1}P_2P_3 $ меньше $ 2pi /3 $, или, что то же, выполнены условия:
$$ r_{12}^2+r_{13}^2+r_{12}r_{13}-r_{23}^2>0, r_{23}^2+r_{12}^2+r_{12}r_{23}-r_{13}^2>0, r_{13}^2+r_{23}^2+r_{13}r_{23}-r_{12}^2>0 . $$
Точка $ P_{ast} $ Ферма-Торричелли имеет координаты
$$
x_{ast}=frac{kappa_1kappa_2kappa_3}{2 sqrt{3} |S| d} left(frac{x_1}{kappa_1}+frac{x_2}{kappa_2}+frac{x_3}{kappa_3} right),
y_{ast}=frac{kappa_1kappa_2kappa_3}{2 sqrt{3} |S| d} left(frac{y_1}{kappa_1}+frac{y_2}{kappa_2}+frac{y_3}{kappa_3} right)
$$
при
$$ |P_1P_{ast}|+|P_2P_{ast}|+|P_3P_{ast}|= sqrt{d} . $$
Здесь
$$
d=frac{1}{sqrt{3}}(kappa_1+kappa_2+kappa_3)=frac{r_{12}^2+r_{13}^2+r_{23}^2}{2}+ sqrt{3}, |S| ,
$$
$$
left{
begin{array}{lcl}
kappa_1=frac{sqrt{3}}{2}(r_{12}^2+r_{13}^2-r_{23}^2)+|S| , \
kappa_2=frac{sqrt{3}}{2}(r_{23}^2+r_{12}^2-r_{13}^2)+|S| , \
kappa_3=frac{sqrt{3}}{2}(r_{13}^2+r_{23}^2-r_{12}^2)+|S| ;
end{array} right.
$$
и
$$
S=x_1y_2+x_2y_3+x_3y_1-x_1y_3-x_3y_2-x_2y_1=
$$
$$
=left|begin{array}{cc}
x_2-x_1 & x_3-x_1 \
y_2-y_1 & y_3-y_1
end{array}
right|=
left| begin{array}{ccc}
1 & 1 & 1 \
x_1 & x_2 & x_3 \
y_1 & y_2 & y_3
end{array}
right| .
$$
Если выписать символьные представления для $ x_{ast} $ и $ y_{ast} $ в виде функций от параметров $ {x_j,y_j}_{j=1}^3 $, то можно осуществить сокращение на общий множитель $ |S| $ числителей и знаменателей получившихся в теореме дробей
☟
Т
Теорема.[5,11] Пусть все углы треугольника $ P_{1}P_2P_3 $ меньше $ 2pi /3 $.
Точка $ P_{ast} $ Ферма-Торричелли имеет координаты
$$
x_{ast}=frac{X}{2sqrt{3}d}, y_{ast}= frac{Y}{2sqrt{3}d}
$$
при
$$ |P_1P_{ast}|+|P_2P_{ast}|+|P_3P_{ast}|= sqrt{d} . $$
Здесь
$$ d=frac{r_{12}^2+r_{13}^2+r_{23}^2}{2}+sqrt{3} cdot | S | ; $$
$$
X=sqrt{3} [x_1r_{23}^2+x_2r_{13}^2+x_3r_{12}^2] +(x_1+x_2+x_3) cdot |S|+
$$
$$
+3 operatorname{sign} (S) [(y_2-y_1)(x_1x_2+y_1y_2)+(y_1-y_3)(x_1x_3+y_1y_3)+(y_3-y_2)(x_2x_3+y_2y_3)];
$$
$$
Y=sqrt{3} [y_1r_{23}^2+y_2r_{13}^2+y_3r_{12}^2]+ (y_1+y_2+y_3) cdot |S| —
$$
$$
-3 operatorname{sign} (S)[(x_2-x_1)(x_1x_2+y_1y_2)+(x_1-x_3)(x_1x_3+y_1y_3)+(x_3-x_2)(x_2x_3+y_2y_3)] ;
$$
$$
S=x_1y_2+x_2y_3+x_3y_1-x_1y_3-x_3y_2-x_2y_1=
$$
$$
=left|begin{array}{cc}
x_2-x_1 & x_3-x_1 \
y_2-y_1 & y_3-y_1
end{array}
right|=
left| begin{array}{ccc}
1 & 1 & 1 \
x_1 & x_2 & x_3 \
y_1 & y_2 & y_3
end{array}
right| .
$$
П
Пример. При $ P_1=(1,1),P_2=(3,5),P_3=(7,2) $ будет:
$$ x_{ast}=frac{2}{687} left( 1029 + 79 sqrt{3}right) approx 3.3939,qquad y_{ast}=frac{1}{687} left( 1053 + 647 sqrt{3} right) approx 3.1639 , $$
$$ |P_{ast}P_1|+|P_{ast}P_2|+|P_{ast}P_3| = sqrt{41+22sqrt{3}}approx 8.8941 . $$
При $ P_1=(1,2),P_2=(3,3),P_3=(4,1) $ :
$$ x_{ast}=frac{1}{6}(15+sqrt{3}) approx 2.7886,qquad y_{ast}=frac{1}{2}(3+sqrt{3}) approx 2.3660 ; $$
$$ |P_{ast}P_1|+|P_{ast}P_2|+|P_{ast}P_3| = sqrt{5,(2+sqrt{3})}approx 4.3197 , . $$
Проверка равенства
$$
frac{(x_{ast}-x_1)(x_{ast}-x_2)+(y_{ast}-y_1)(y_{ast}-y_2)}{sqrt{((x_{ast}-x_1)^2+(y_{ast}-y_1)^2)((x_{ast}-x_2)^2+(y_{ast}-y_2)^2)}}=-frac{1}{2}
$$
произведена.
Аналитическое решение обобщенной задачи Ферма-Торричелли
Получено только для случая $ K=3 $.
Т
Теорема.[11] Обозначим величину угла треугольника $ P_{1}P_2P_3 $ при вершине $ P_{j} $ через $ alpha_j $. Если нарушено $ j $-е из трех условий
begin{align*}
m_2^2+m_3^2+2, m_2m_3 cos alpha_1 & > m_1^2 , \
m_1^2+m_3^2+2, m_1m_3 cos alpha_2 & > m_2^2,\
m_1^2+m_2^2+2, m_1m_2 cos alpha_3 & > m_3^2,
end{align*}
то минимум функции
$$ F(x,y)=sum_{j=1}^3 m_j sqrt{(x-x_j)^2+(y-y_j)^2} $$
достигается в точке $ P_{j}=(x_j,y_j) $. Если все неравенства выполняются, то $ min F(x,y) $ достигается в точке $ P_{ast} $ с координатами:
$$
x_{ast}=frac{K_1K_2K_3}{4 |S| sigma d} left(frac{x_1}{K_1}+frac{x_2}{K_2}+frac{x_3}{K_3} right),
y_{ast}=frac{K_1K_2K_3}{4 |S| sigma d} left(frac{y_1}{K_1}+frac{y_2}{K_2}+frac{y_3}{K_3} right) .
$$
при
$$
F(x_{ast},y_{ast})=min_{(x,y)} F(x,y)=sqrt{d} .
$$
Здесь
$$
d= 2, |S| sigma +
$$
$$
+frac{1}{2}left[m_1^2(r_{12}^2+r_{13}^2-r_{23}^2)+
m_2^2(r_{23}^2+r_{12}^2-r_{13}^2)+m_3^2(r_{13}^2+r_{23}^2-r_{12}^2) right] ;
$$
$$
r_{jell}=sqrt{(x_j-x_{ell})^2+(y_j-y_{ell})^2}=|P_jP_{ell}| quad npu {j,ell} subset {1,2,3} ;
$$
$$
S=x_1y_2+x_2y_3+x_3y_1-x_1y_3-x_3y_2-x_2y_1=
$$
$$
=left|begin{array}{cc}
x_2-x_1 & x_3-x_1 \
y_2-y_1 & y_3-y_1
end{array}
right|=left|
begin{array}{ccc}
1 & 1 & 1 \
x_1 & x_2 & x_3 \
y_1 & y_2 & y_3
end{array}
right| ;
$$
$$
sigma= frac{1}{2} sqrt{-m_1^4-m_2^4-m_3^4+2,m_1^2m_2^2+2,m_1^2m_3^2+2,m_2^2m_3^2} ;
$$
$$
left{
begin{array}{ccc}
K_1&=&(r_{12}^2+r_{13}^2-r_{23}^2)sigma+(m_2^2+m_3^2-m_1^2) |S| , \
K_2&=&(r_{23}^2+r_{12}^2-r_{13}^2)sigma+(m_1^2+m_3^2-m_2^2) |S| , \
K_3&=&(r_{13}^2+r_{23}^2-r_{12}^2)sigma+(m_1^2+m_2^2-m_3^2) |S| .
end{array}
right.
$$
П
Пример. Для конфигурации
$$
left{begin{array}{c|c|c}
P_{1}=(2,6) & P_{2}=(1,1) & P_{3}=(5,1) \
m_{1}=2 & m_{2}=3 & m_{3}=4
end{array}
right}
$$
точка $ P_{ast} $ имеет координаты
$$
x_{ast}=frac{4103+1833 sqrt{15}}{2866}approx 3.9086 , y_{ast} =frac{29523-4481 sqrt{15}}{8598}approx 1.4152 , .
$$
Минимальное значение для функции:
$$ min F(x,y)= m_1|P_{ast}P_1|+m_2|P_{ast}P_2|+m_3|P_{ast}P_3|= 2sqrt{79+15sqrt{15}} approx 23.4174 , . $$
♦
Если выписать символьные представления для $ x_{ast} $ и $ y_{ast} $ в виде функций от параметров $ {x_j,y_j,m_j}_{j=1}^3 $, то можно осуществить сокращение на общий множитель $ |S| $ в числителе и в знаменателе получившихся в теореме дробей.
Правда, результат такого сокращения выглядит довольно громоздко: см.
☞
ЗДЕСЬ.
Аналитическое решение: исключение переменных
В случае $ K>3 $ точек аналитическое решение для обобщенной задачи Ферма-Торричелли вряд ли может быть получено. Тем не менее, можно попытаться продвинуться аналитикой возможно дальше, именно:
свести поиск координаты точки $ P_{ast} $ к решению системы полиномиальных (алгебраических) уравнений и попытаться применить к этой системе методы исключения переменных.
П
Пример. Выяснить динамику поведения точки $ P_{ast} $ для конфигурации
$$
left{
begin{array}{c|c|c|c}
P_{1}=(1,1) & P_{2}=(3,5) & P_{3}=(7,2) & P_{4}=(6,6) \
m_{1}=1 & m_{2}=1 & m_{3}=1 & m_{4}=m
end{array}
right}
$$
в зависимости от изменения параметра $ m_{} $.
Решение. При каждом конкретном значении параметра $ m_{} $ координаты стационарной точки $ P_{ast} $ можно найти применением численных методов, но нас интересует хоть какое-то функциональное представление для $ P_{ast} (m) $.
Градиентную систему уравнений
$$
left{ begin{array}{lll}
frac{ partial F}{partial x} &= frac{(x-1)}{sqrt{(x-1)^{2}+(y-1)^2}}+frac{(x-3)}{sqrt{(x-3)^{2}+(y-5)^2}}+frac{(x-7)}{sqrt{(x-7)^{2}+(y-2)^2}}+ frac{m(x-6)}{sqrt{(x-6)^2+(y-6)^2}} & = 0 \
frac{partial F}{partial y} &= frac{(y-1)}{sqrt{(x-1)^{2}+(y-1)^2}}+frac{(y-5)}{sqrt{(x-3)^{2}+(y-5)^2}}+frac{(y-2)}{sqrt{(x-7)^{2}+(y-2)^2}}+ frac{m(y-6)}{sqrt{(x-6)^2+(y-6)^2}} & = 0
end{array}
right.
$$
преобразуем к алгебраической. Это можно сделать различными методами и результат существенно зависит от организации процесса (т.е. алгебраическая система, включающая в себя множество решений исходной, определяется не единственным образом). Мы укажем пока только конечный результат (один из возможных):
$$ F_1(x,y,m)=0, F_2(x,y,m)=0 ; $$
здесь $ F_{1} $ и $ F_{2} $ полиномы степени $ 6_{} $ по каждой переменной $ x_{} $ или $ y_{} $ и степени $ 12_{} $ по обеим переменным. Из этой системы, посредством вычисления результанта, можно исключить переменные $ x_{} $ или $ y_{} $ и получить алгебраические уравнения вида
$$ mathcal X(x,m)=0, mathcal Y(y,m)=0, $$
которым удовлетворяют координаты стационарных точек при каждом фиксированном значении $ m_{} $. Оказывается, эти уравнения можно упростить (отбросить посторонние сомножители), сведя к уравнениям степени $ 12 $ по каждой из переменных $ x_{} $ или $ y_{} $.
Их выражения
☞
ЗДЕСЬ.
Дальнейшее упрощение вряд ли возможно: уравнения неприводимы над $ mathbb Q_{} $, и, скорее всего, неразрешимы в радикалах.
Можно пойти другим путем: исключать параметр $ m_{} $ с целью нахождения неявного представления кривой, на которой расположены стационарные точки при всех возможных значениях $ m_{} $. Результант $ mathcal R_m(F_1,F_2) $ оказывается полиномом степени $ 96 $ по $ x_{} $ и $ y_{} $, и этот полином факторизуется в виде
$$ 65536 (2x-y-1)^8(x^2-14x+53-4y+y^2)^8(x^2-12,x+72-12y+y^2)^8 Phi_0^2(x,y) Phi^2(x,y) . $$
Собственно кривая стационарных точек задается одним множителем:
$$ Phi(x,y) = 0 $$
при
$$
Phi(x,y)
=3,y(-7,y+10,x)(8,x-y)(2,x-9,y)(x^2+y^2)^4+
$$
$$
+8,(160,x^5-2594,x^4y+10117,x^3y^2+3152,x^2y^3-6209,xy^4+183,y^5)(x^2+y^2)^3-
$$
$$
-4,(10144,x^6-106368,x^5y+344359,x^4y^2+303368,x^3y^3+32554,x^2y^4-193808,xy^5-16853,y^6)(x^2+y^2)^2
$$
$$
+dots -1152, (2823793,x^2-22813720,xy-56866,y^2)+4409856 (1491,x+1234,y)-2110116096 .
$$
Полное выражение для функции $ Phi $ и картина всей кривой $ Phi=0 $ целиком достаточно сложны: см.
☞
ЗДЕСЬ. На рисунке выделена только ветвь, которая соответствует реальной динамике стационарной точки.

«Контрольные» точки на этой ветви:
x
$ left(frac{2}{687}(1029 + 79sqrt{3}),frac{1}{687}(1053 + 647sqrt{3}) right) $ — точка Ферма-Торричелли треугольника $ P_1P_2P_{3} $, соответствует значению $ m=0 $;
x
$ left(frac{29}{7},frac{29}{7}right) $ — точка пересечения диагоналей четырехугольника $ P_1P_2P_3P_4 $, соответствует значению $ m_{}=1 $ (см.
☞
теорему Фаньяно);
♦
$ (6,6) $ — вершина $ P_{4} $, соответствует значению $ m approx 2.4436 $ (точное значение
☞
ЗДЕСЬ);
♦
$ (1,1) $ — вершина $ P_{1} $, соответствует значению $ m approx -2.4184 $ (вообще говоря, в постановке задачи говорится только о положительных значениях весов, но почему бы не осуществить аналитическое продолжение? );
x
$ (frac{11}{3},frac{11}{3}) $, соответствует $ m=1-sqrt{2/5} approx 0.3675 $.
Общий случай
Обращаемся к задаче в $ mathbb R^{n}_{} $. Стационарные точки функции
$$ F(P)=sum_{j=1}^Km_j |PP_j| $$
являются решениями градиентной системы уравнений
$$
frac{partial F}{partial x_1}=0,dots, frac{partial F}{partial x_n}=0 ,
$$
которую можно записать в векторном виде
$$
sum_{j=1}^K m_jfrac{PP_j}{|PP_j|} = mathbb O_{ntimes 1} .
$$
При этом следует иметь в виду, что, во-первых, при некоторых конфигурациях система может оказаться несовместной и, во-вторых, искомый минимум функции может достигаться в одной из точек $ {P_j} $ (которые последней системой не «отлавливаются»).
Существование и единственность решения
Т
Теорема. Пусть точки $ {P_j}_{j=1}^K subset mathbb R^n $ все различны. Минимум функции
$$ F(P)=sum_{j=1}^K m_j |PP_j| $$
существует и единствен. При этом
1.
если существует точка $ P_{i} $ такая, что выполняется условие
$$
left|sum_{j=1 atop j ne i}^K m_j frac{P_jP_i}{|P_jP_i|} right| le m_i , $$
то $ min F(P) $ достигается в точке $ P_{i} $;
2.
если для любого значения $ i in {1,dots,K} $ выполняется условие
$$
left|sum_{j=1 atop j ne i}^K m_j frac{P_jP_i}{|P_jP_i|} right| > m_i , $$
то $ min F(P) $ достигается в точке $ P_{ast} $, удовлетворяющей градиентной системе уравнений
$$ sum_{j=1}^K m_j frac{PP_j}{|PP_j|}=mathbb O_{ntimes 1}, ; $$
и, в этом случае, $ P_{ast} notin {P_j}_{j=1}^K $.
Доказательство
☞
ЗДЕСЬ
П
Пример. При каких значениях параметра $ m_{} $ в конфигурации
$$
left{
begin{array}{c|c|c|c}
P_{1}=(1,1) & P_{2}=(3,5) & P_{3}=(7,2) & P_{4}=(6,6) \
m_{1}=1 & m_{2}=1 & m_{3}=1 & m_{4}=m
end{array}
right}
$$
$ min sum_{j=1}^4 m_j|PP_j| $ достигается в точке $ P_4 $?
Решение. Формируем условие
$$
left| m_1 frac{(1,1)- (6,6)}{sqrt{50}}+m_2frac{(3,5)- (6,6)}{sqrt{10}}+m_3 frac{(7,2)- (6,6)}{sqrt{17}} right| le m_4 .
$$
Ответ. При $ m ge sqrt{3+4/sqrt{5}+3sqrt{2/17}+sqrt{2/85}} approx 2.4436 $.
Заметим, что попадание точки $ P_{ast} $ в вершину $ P_{i} $ происходит при значениях $ m_{i} $ меньших, чем сумма оставшихся весов.
=>
В случае $ n=2, K=3 $ условия теоремы переформулируются в терминах углов $ alpha_1,alpha_2, alpha_3 $ треугольника $ P_1P_2P_{3} $. Так, например, условие
2
эквивалентно
$$
m_2^2+m_3^2+2, m_2m_3 cos alpha_1 > m_1^2 , m_1^2+m_3^2+2, m_1m_3 cos alpha_2 > m_2^2, m_1^2+m_2^2+2, m_1m_2 cos alpha_3 > m_3^2, .
$$
Если $ m_1=m_2=m_3 $, то эти условия означают, что все углы треугольника меньше $ 2pi/3 $.
В общем же случае (не обязательно равных весов) этим условиям можно придать следующую геометрическую интерпретацию. Их выполнение означает, что рассматривая величины весов $ m_1,m_2,m_3 $ в качестве длин отрезков, мы можем построить из этих отрезков треугольник — он так и называется: «весовой треугольник» [1].

Обозначим углы этого треугольника $ beta_1, beta_2, beta_3 $ в соответствии с рисунком.
Тогда, по теореме косинусов, получаем:
$$ cos alpha_j+ cos beta_j > 0 quad npu quad jin {1,2,3} , . $$
Численное решение
Рассмотрим задачу в $ mathbb R^{n}_{} $ сначала для случая одинаковых весов $ m_1=dots=m_K=1 $. Перепишем градиентную систему уравнений
$$
frac{P-P_1}{|PP_1|}+dots+frac{P-P_K}{|PP_K|}= mathbb O_{ntimes 1},
$$
задающую стационарные точки функции $ F(P) $, в эквивалентном виде
$$
P=underbrace{left(frac{P_1}{|PP_1|}+dots+frac{P_K}{|PP_K|} right) bigg/ left(frac{1}{|PP_1|}+dots+frac{1}{|PP_K|} right)}_{=Phi(P)} , .
$$
Решать последнюю систему будем методом простой итерации. Возьмем в качестве начального приближения произвольную точку $ P^{(0)} notin {P_j}_{j=1}^K $ и строим последовательность по рекурсивной формуле
$$
P^{(k)}=Phi(P^{(k-1)}) quad npu quad k in mathbb N .
$$
Утверждается, что эта последовательность сходится к точке $ P_{ast} $, являющейся точкой минимума функции $ F(P)=sum_{j=1}^K |PP_j| $.
Метод известен как алгоритм Вайсфельда [14].
П
Пример. Для $ P_1=(1,1), P_2=(3,5), P_3=(7,2) $ возьмем $ P^{(0)}=(2,2) $. Итерационная последовательность
$$
left(begin{array}{c} 2 \ 2 end{array} right) to left(begin{array}{c} 2.4979 \ 2.1974 end{array} right)
to left(begin{array}{c} 2.8581 \ 2.4862 end{array} right) to left(begin{array}{c} 3.1122 \ 2.7295 end{array} right)
to dots to P^{(7)} =left(begin{array}{c} 3.3_{displaystyle 879} \ 3.1_{displaystyle 089} end{array} right) to dots
$$
сходится к точке Ферма-Торричелли $ P_{ast}approx (3.3939, 3.1639 ) $.
♦
П
Пример. Для $ P_1=(1,1,0), P_2=(5,1,0), P_3=(2,6,0), P_4=(3,3,5) $ возьмем $ P^{(0)}=(1,1,1) $. Итерационная последовательность
$$
left(begin{array}{c} 1 \ 1 \ 1 end{array} right)
to left(begin{array}{c} 1.9583 \ 1.8361 \ 0.6226 end{array} right)
to left(begin{array}{c} 2.3007 \ 2.1007 \ 0.7319 end{array} right)
to left(begin{array}{c} 2.5077 \ 2.2665 \ 0.8386 end{array} right)
to dots
to P^{(7)}= left(begin{array}{c} 2.6_{displaystyle 781} \ 2.42_{displaystyle 28} \ 0.9_{displaystyle 552} end{array} right) to dots
$$
сходится к точке $ P_{ast} approx (2.6823, 2.4298, 0.9607) $.
♦
Проблемы сходимости возникают в случае, когда искомая точка $ P_{ast} $ близка к одной из $ {P_j}_{j=1}^K $.
П
Пример. Для
$$ P_1=(0,0), P_2=(1,0), P_3=(-4,7) $$
координаты точки Ферма-Торричелли: $ P_{ast}approx (0.0023,0.0039) $. Итерационная последовательность, стартующая из $ P^{(0)}=(0,1) $, не дает этой точности при $ 200 $ итерациях.
♦
Метод очевидным образом обобщается и на случай, когда веса в конфигурации не обязательно одинаковы: в рекурсивной формуле следует взять
$$
Phi(P)=left(frac{m_1P_1}{|PP_1|}+dots+frac{m_KP_K}{|PP_K|} right) bigg/ left(frac{m_1}{|PP_1|}+dots+frac{m_K}{|PP_K|} right) .
$$
Обратная задача
Задача. Подобрать величины весов $ {m_j}_{j=1}^K $ так, чтобы минимум функции $ displaystyle F(P)=sum_{j=1}^K m_j |PP_j| $ находился в наперед заданной точке $ P_{ast} notin {P_j}_{j=1}^K $.
В отличие от «прямой» задачи, обратная имеет довольно простое решение. Начнем рассмотрение со случая плоскости: $ n=2, K=3 $.
Т
Теорема [11]. Пусть вершины треугольника $ P_{1}P_2P_3 $ пронумерованы против часовой стрелки. Тогда для значений
$$
m_1^{ast} = |P_{ast}P_1| cdot left|
begin{array}{ccc}
1 & 1 & 1 \
x_{ast} & x_2 & x_3 \
y_{ast} & y_2 & y_3
end{array}
right|,
m_2^{ast} = |P_{ast}P_2| cdot left|
begin{array}{ccc}
1 & 1 & 1 \
x_1 & x_{ast} & x_3 \
y_1 & y_{ast} & y_3
end{array}
right|,
m_3^{ast} = |P_{ast}P_3| cdot left|
begin{array}{ccc}
1 & 1 & 1 \
x_1 & x_2 & x_{ast} \
y_1 & y_2 & y_{ast}
end{array}
right|
$$
функция
$$ F(x,y) = sum_{j=1}^3 m_{j}^{ast} sqrt{(x-x_j)^2+(y-y_j)^2} $$
имеет стационарную точкой точку $ P_{ast}=(x_{ast},y_{ast}) $. Если последняя выбирается внутри треугольника
$ P_{1}P_2P_3 $, то величины $ m_1^{ast},m_2^{ast},m_3^{ast} $ все положительны и
$$
F(x_{ast},y_{ast})=min_{(x,y)in mathbb R^2} F(x,y)=
left|
begin{array}{cccc}
1 & 1 & 1 & 1\
x_{ast} & x_1 & x_2 & x_3 \
y_{ast} & y_1 & y_2 & y_3 \
x_{ast}^2+y_{ast}^2 & x_1^2+y_1^2 & x_2^2+y_2^2 & x_3^2+y_3^2
end{array}
right| .
$$
Доказательство теоремы, а также геометрический смысл величин из ее формулировки
☞
ЗДЕСЬ.
Решение обратной задачи определяется с точностью до сомножителя, т.е. тройка решений $ (m_1,m_2,m_3) $ определяется отношением $ m_1:m_2:m_3 $. С учетом этого обстоятельства, решение обратной задачи единственно.
П
Пример. Поместить в точках $ P_{1}=(2,6),P_{2}=(1,1), P_{3}=(5,1) $ соответствующие веса $ {m_j^{ast}} $ так, чтобы точка минимума
функции $ F(x,y) $ находилась бы в точке
$$ P_{ast} = left(frac{ 4103+1833 sqrt{15}}{2866} , frac{29523-4481 sqrt{15}}{8598} right) . $$
Решение. Формулы из теоремы дают:
$$
left{begin{array}{ccl}
m_1^{ast}&=& displaystyle frac{2(20925-4481sqrt{15})}{18481401}sqrt{316380606+35999826sqrt{15}} ,\
m_2^{ast}&=& displaystyle frac{2(15105-2342sqrt{15})}{6160467}sqrt{75400161-9169767sqrt{15}} , \
m_3^{ast}&=& displaystyle frac{8(-1185+15988sqrt{15})}{18481401}sqrt{8335761-2050623sqrt{15}} ,
end{array}
right.
$$
при
$$
F(x_{ast},y_{ast})=frac{1}{4299}(-333980+193436sqrt{15}) .
$$
Сравним этот результат с полученным
☝
ВЫШЕ. В соответствии с замечанием, должно выполняться:
$ m_1^{ast} : m_2^{ast} : m_3^{ast} = 2 : 3 : 4 $.
А проверьте!
♦
§
Обобщение результата в многомерный случай $ n>2 $ для числа точек $ K=n+1 $
☞
ЗДЕСЬ.
Смежные задачи
Дерево Штейнера
Задача. Пусть заданы точки $ P_1,dots,P_K $ на плоскости. Требуется построить связную систему $ mathbf L_{} $ прямолинейных отрезков на той же плоскости, чтобы
1.
любые две точки $ P_{j} $ и $ P_{ell} $ могли быть связаны ломаной линией, звенья которой входили бы в состав системы $ mathbf L_{} $;
2.
общая длина всей системы $ mathbf L_{} $ была наименьшей.
Такая система $ mathbf L_{} $ называется минимальным деревом Штейнера, ее построение и применения см. в [3,4].
На первый взгляд кажется, что эта задача эквивалентна задаче Ферма-Торричелли в случае одинаковых весов и речь идет о поиске единственной точки $ P_{ast} $ на плоскости. На самом деле, решение этой задачи для случая $ K ge 4 $ предполагает построение нескольких вспомогательных точек.
П
Пример. Построить минимальное дерево Штейнера для точек
$$ P_1=(0,3), P_2=(0,0), P_3=(4,0), P_4=(4,3) , . $$

Решение. Будем пробовать варианты решения задачи, последовательно добавляя вспомогательные точки. Если не добавлять дополнительных точек вообще, то эта задача относится к классу задач построения минимального покрывающего дерева7). В такой постановке решением рассматриваемого примера будет ломаная $ P_1P_2P_3P_4 $ длиной $ 3+4+3=10 $.

Если разрешено добавить одну дополнительную точку, то решением задачи, в соответствии с
☝
теорему Фаньяно, будет система из двух диагоналей прямоугольника:

Тем не менее, выигрыша в длине дерева не получим: $ 5+5=10 $. Но если разрешено добавлять две дополнительных точки, то расположив их в
$ P_{ast}=left(frac{sqrt{3}}{2},frac{3}{2} right) $ и $ P_{ast ast}=left(4-frac{sqrt{3}}{2},frac{3}{2} right) $

получим суммарную длину равной $ 4+ 3sqrt{3} approx 9.196152 $.
Можно ли улучшить этот результат добавлением еще большего количества дополнительных точек? Ответ отрицателен: оказывается, что для произвольной конфигурации системы $ {P_j}_{j=1}^4 $ количество дополнительных точек, необходимых для решения задачи о минимальном дереве, никогда не превысит двух.
♦
В рассмотренном примере точка $ P_{ast} $ является точкой Ферма-Торричелли для треугольника $ P_1 P_2 P_{ast ast} $, а точка $ P_{ast ast} $ —
точкой Ферма-Торричелли для треугольника $ P_3 P_4 P_{ast } $. Это свойство оказывается принципиальным для решения общей задачи: для любой конфигурации точек $ { P_j }_{j=1}^K subset mathbb R^2 $ минимальное дерево Штейнера является графом, соединяющим эти точки с дополнительными узлами графа, составляющими некоторое множество $ { S_{ell} }_{ell=1}^M $. Мощность этого дополнительного множества находится в пределах
$$ 0 le M le K-2 , ,$$
и, при условии, что оно не пусто, любой его элемент является точкой Ферма-Торричелли для некоторой тройки точек из объединения $ { P_j }_{j=1}^K bigcup { S_{ell} }_{ell=1}^M $. Степень каждой вершины $ { P_j }_{j=1}^K $ графа равна либо $ 1_{} $ либо $ 2_{} $.
§
Задача о минимальном дереве Штейнера обсуждается
☞
ЗДЕСЬ.
Мультифокусные эллипсы
Для случая $ n=2_{} $ рассмотрим задачу о линиях уровня функции
$$
F(x,y)= sum_{j=1}^{K} sqrt{(x-x_j)^2+(y-y_j)^2} ,
$$
т.е. о кривых $ F(x,y)=c $ при различных значениях $ c_{} $. В случае $ K=2 $ решение задачи хорошо известно — это либо эллипс с фокусами в точках $ P_1=(x_1,y_1),P_2=(x_2,y_2) $,
либо отрезок, соединяющий эти точки, либо пустое множество (мнимый эллипс). Что за кривые соответствуют случаям $ K ge 3 $? Например, каково геометрическое место точек, сумма расстояний от которых до фиксированных точек $ P_1,P_2,P_3 $ является постоянной величиной? Этот вопрос был задан Декартом Ферма в 1638 г. (и именно отсюда возникла у Ферма постановка задачи о поиске минимума функции $ F_{} $).
Эти кривые называются мультифокусными (мультифокальными) эллипсами,полиэллипсами или обобщенными эллипсами. В немецком языке известны также под названием Tschirnhaus’sche Eikurve — яйцеобразные кривые Чирнгауза 
Они могут считаться алгебраическими кривыми — последовательным возведением их уравнений в квадрат можно избавиться от радикалов.
П
Пример. Для $ P_1=(1,1),P_2=(3,5),P_3=(7,2) $ семейство трехфокусных эллипсов (алгебраических кривых порядка $ 8_{} $) выглядит так (числа на кривых — значения константы $ c_{} $):

Каким значениям $ c_{} $ соответствуют кривые, проходящие через точки $ P_1, P_2, P_3 $ ?
♦
В случае когда веса $ { m_j } $ могут быть различными, линии уровня функции
$$
F(x,y)= sum_{j=1}^{K} m_jsqrt{(x-x_j)^2+(y-y_j)^2} ,
$$
не имеют установившегося названия. В случае $ K=2 $ в литературе встречаются под названием овалы Декарта; сам Декарт называл их эллипсами второго рода. Если $ Kge 3 $ и величины весов $ { m_j } $ рационально соизмеримы, то этот случай может быть быть рассмотрен как предельный случай мультифокусного эллипса — когда некоторые из фокусов сливаются в один. Этими кривыми в середине XIX века интересовался (из любознательности) один шотландский ученый [7]. В случае $ K=3 $ кривые
известны в экономической географии под названием изодапан9); каждая такая кривая состоит из точек одинаковой суммарной стоимости транспортных перевозок до них из $ {P_j} $.
A
Анимация трехмерного аналога мультифокусного эллипса
☞
ЗДЕСЬ (470 Kb).
Треугольно-оптимизационные задачи
Задача 1. Построить максимальный равносторонний треугольник $ Q_1Q_2Q_3 $, описанный вокруг заданного треугольника $ P_{1}P_{2}P_3 $ (на каждой стороне треугольника $ Q_{1}Q_{2}Q_3 $ должна лежать одна вершина треугольника $ P_1P_2P_3 $).
Т
Теорема. Пусть все углы треугольника $ P_{1}P_{2}P_3 $ меньше $ 2pi/3 $. Высота искомого треугольника $ Q_1Q_2Q_3 $ равна $ |P_{ast}P_1|+|P_{ast}P_2|+|P_{ast}P_3| $, где $ P_{ast} $ — точка Ферма-Торричелли треугольника $ P_{1}P_{2}P_3 $. Стороны треугольника $ Q_1Q_2Q_3 $ перпендикулярны прямым $ P_{ast}P_1, P_{ast}P_2 $ и $ P_{ast}P_3 $.
Задача 2. Построить минимальный равносторонний треугольник $ R_1R_2R_3 $, вписанный в заданный треугольник $ P_{1}P_{2}P_3 $ (на каждой стороне треугольника $ P_{1}P_{2}P_3 $ должна лежать одна вершина треугольника $ R_1R_2R_3 $).
На удивление, ссылок в интернете на решение задачи 2 я не нашел, за исключением
☞
ЭТОЙ. Задача похожа на задачу Фаньяно о построении произвольного треугольника минимального периметра, вписанного в данный остроугольный [4]; однако требование равносторонности треугольника в условии задачи существенно меняет ее решение.
Т
Теорема. Пусть все углы треугольника $ P_{1}P_{2}P_3 $ меньше $ 2pi/3 $. Стороны искомого треугольника $ R_1R_2R_3 $ параллельны сторонам треугольника $ Q_1Q_2Q_3 $,
решающего предыдущую задачу. Имеет место соотношение между площадями трех треугольников — исходного, максимального описанного и минимального вписанного:
$$
frac{ S_{triangle Q_1Q_2Q_3}}{ S_{triangle P_1P_2P_3}}=frac{ S_{triangle P_1P_2P_3}}{S_{triangle R_1R_2R_3}} .
$$
Стационарные точки семейства потенциалов
Задача. Найти стационарные точки функции
$$
F(P)= sum_{j=1}^K m_j left|PP_j right|^L .
$$
Здесь $ {P,P_1,dots,P_K} subset mathbb R^n $, $ L_{} $ предполагается вещественным ненулевым числом, а величины $ { m_{j} }_{j=1}^K $ — произвольными вещественными числами (не обязательно положительными).
В случае $ L=1 $ мы получаем обобщенную задачу Ферма-Торричелли, рассмотренную выше. В случае $ L=2 $ решением задачи является единственная точка
$$ P_{ast}= frac{sum_{j=1}^K m_jP_j}{ sum_{j=1}^K m_j} $$
— точка глобального минимума функции $ F(P) $. В случае всех положительных $ {m_j}_{j=1}^K $ и $ nin {2,3} $ точка $ P_{ast} $ является центром масс (барицентром) системы материальных точек, расположенных в точках $ {P_j}_{j=1}^K $.
Нас интересует решение задачи для других показателей $ L_{} $. Поставленной задаче можно придать физический смысл. Пусть в пространстве имеется конфигурация
$$
left{begin{array}{c|c|c} P_1 & dots & P_K \
m_1 & dots & m_K
end{array}
right}
$$
из $ K_{} $ фиксированных (неподвижных) точечных заряженных частиц, которые воздействуют на пробный точечный единичный заряд величины, помещенный в точку $ P_{} $; при этом сила воздействия $ j_{} $-го заряда прямо пропорциональна величине заряда $ m_{j} $ и пропорциональна некоторой степени $ L_{} $ расстояния от этого заряда до пробного. Требуется найти точку $ P_{ast} in mathbb R^{n}_{} $, при помещении в которую пробного заряда, последний будет неподвижен (находиться в положении равновесия).

Особый интерес представляет частный случай поставленной задачи: $ L=-1 $. Этому случаю соответствует два физических потенциала — кулоновский (электростатический) и ньютоновский (гравитационный)10).
Стационарные точки этого семейства потенциалов задаются градиентной системой уравнений
$$
left{frac{partial F}{partial x_{ell}}= L sum_{j=1}^{K} m_j |PP_j|^{L-1} frac{(x_{ell}-x_{jell})}{|PP_j|} = 0 right}_{ell=1}^n ,
quad npu quad begin{array}{c} {P_j=(x_{j1},dots,x_{jn})}_{j=1}^K, \ P=(x_1,dots,x_n) end{array} ,
$$
которая при четных значениях $ L_{} $ является алгебраической (или может быть немедленно приведена к алгебраической в случае отрицательных $ L_{} $); в остальных же случаях она будет содержать радикалы, от которых можно избавиться только последовательным возведением уравнений в квадрат. Уже для случая кулоновского потенциала $ L=-1, n=2, K=3 $ это приводит к алгебраическим уравнениям высокой степени с громоздкими коэффициентами.
П
Пример. Пусть $ P_1=(1,1), P_2=(5,1) , P_3=(2,6) $.
Проанализировать поведение множества стационарных точек функции
$$
F(x,y)=frac{1}{sqrt{(x-1)^2+(y-1)^2}}+ frac{m_2}{sqrt{(x-5)^2+(y-1)^2}}+frac{m_3}{sqrt{(x-2)^2+(y-6)^2}}
$$
в зависимости от значений $ m_2, m_3 $, рассматриваемых в качестве параметров.
Решение. Градиентная система уравнений
$$
begin{array}{rrr}
displaystyle frac{x-1}{sqrt{(x-1)^2+(y-1)^2}^3}& displaystyle +frac{m_2(x-5)}{sqrt{(x-5)^2+(y-1)^2}^3}& displaystyle +frac{m_3(x-2)}{sqrt{(x-2)^2+(y-6)^2}^3}=0, , \
displaystyle frac{y-1}{sqrt{(x-1)^2+(y-1)^2}^3}& displaystyle +frac{m_2(y-1)}{sqrt{(x-5)^2+(y-1)^2}^3}& displaystyle +frac{m_3(y-6)}{sqrt{(x-2)^2+(y-6)^2}^3}=0 ,
end{array}
$$
может быть преобразована в алгебраическую в ходе следующей процедуры. Обозначим $ A_1, A_2 $ и $ A_3 $ слагаемые в любом из этих уравнений.
Последовательное возведение в степень по схеме
$$ A_1+A_2+A_3=0 quad Rightarrow quad (A_1+A_2)^2=A_3^2 quad Rightarrow quad (2, A_1A_2)^2 = (A_3^2-A_1^2 — A_2^2)^2 $$
приводит систему к алгебраической
$$
F_1(x,y,m_2,m_3)=0, F_2(x,y,m_2,m_3)=0 .
$$
Здесь $ F_{1} $ и $ F_{2} $ — полиномы степени $ 28 $ по переменным $ x_{} $ и $ y_{} $ с коэффициентами порядков до $ 10^{19} $. Нахождение всех решений
этой системы — даже для конкретных (фиксированных) значений параметров $ m_2 $ и $ m_3 $ — становится вычислительно сложной задачей. А ведь требуется решить еще более
сложную задачу: проследить динамику этого множества при изменении параметров!
Сложность поставленной задачи — по сравнению с обобщенной задачей Ферма-Торичелли — заключается еще и в том, что что число вещественных решений системы больше единицы;
в зависимости от значений параметров, число стационарных точек — от $ 2_{} $ до $ 4_{} $.
♦
Гипотеза [Максвелл] [8,15]. Число стационарных точек кулоновского поля любой конфигурации $ K_{} $ стационарных зарядов в $ mathbb R^3 $ не превосходит $ (K-1)^2 $. Не доказана11).
Что общего у поставленной в начале пункта задачи с обобщенной задачей Ферма-Торричелли? — То, что похожим образом решается обратная задача.
Рассмотрим сначала плоский случай.
Т
Теорема [12, 13]. Пусть точки $ P_{1}=(x_1,y_1),P_2=(x_2,y_2),P_3=(x_3,y_3) $ неколлинеарны. Тогда для значений
$$
m_1^{ast} = |P_{ast}P_1|^{2-L} left|
begin{array}{ccc}
1 & 1 & 1 \
x_{ast} & x_2 & x_3 \
y_{ast} & y_2 & y_3
end{array}
right|,
m_2^{ast} = |P_{ast}P_2|^{2-L} left|
begin{array}{ccc}
1 & 1 & 1 \
x_1 & x_{ast} & x_3 \
y_1 & y_{ast} & y_3
end{array}
right|,
m_3^{ast} = |P_{ast}P_3|^{2-L} left|
begin{array}{ccc}
1 & 1 & 1 \
x_1 & x_2 & x_{ast} \
y_1 & y_2 & y_{ast}
end{array}
right|
$$
функция
$$ F(x,y) = sum_{j=1}^3 m_{j}^{ast} |PP_j|^L $$
имеет стационарную точку $ P_{ast}=(x_{ast},y_{ast}) $. При этом
$$
F(x_{ast},y_{ast})=
left|
begin{array}{cccc}
1 & 1 & 1 & 1\
x_{ast} & x_1 & x_2 & x_3 \
y_{ast} & y_1 & y_2 & y_3 \
x_{ast}^2+y_{ast}^2 & x_1^2+y_1^2 & x_2^2+y_2^2 & x_3^2+y_3^2
end{array}
right| .
$$
Доказательство фактически повторяет приведенное
☞
ЗДЕСЬ.
Подчеркнем, что, фактически, этот результат решает задачу теории управления: подбором параметров системы удается обеспечить наперед заданное положение равновесия в кулоновском (ньютоновском) поле. Тут же возникает (традиционный для теории управления) вопрос об устойчивости полученного равновесия, т.е., иными словами, о том является ли полученная стационарная точка точкой минимума для потенциала. Пока отложим ответ на этот вопрос, заметив — исключительно из соображений исторического сюрприза, что теория управления возникла из задачи, которую сформулировал в 1868 г. один ученый, фамилию которого наблюдательный читатель настоящего раздела легко угадает! Намек: Эдвард Раус (Edward John Routh) — один из авторов критерия Рауса-Гурвица — был однокурсником этого ученого.
Для случая $ L=1 $ стационарная точка потенциала (Ферма-Торричелли) единственна для каждого фиксированного набора значений весов. Решение обратной задачи тоже было единственным — с точностью до домножения вектора весов $ (m_1^{ast},m_2^{ast},m_3^{ast} ) $ на сомножитель. Для других показателей $ L_{} $ стационарных точек у соответствующих потенциалов может быть несколько. Примером может являться случай кулоновского потенциала $ L=-1 $. Наряду с точкой $ P_{ast} $, гарантированной условием теоремы, будет существовать еще, по крайней мере, одна «посторонняя» стационарная точка $ tilde P_{ast} $. Следовательно, решение обратной задачи определяется не единственным образом: существует набор весов $ (widetilde{m}_1^{ast},widetilde{m}_2^{ast},widetilde{m}_3^{ast}) $, обеспечивающий стационарность точки $ tilde P_{ast} $ и непропорциональный набору $ (m_1^{ast},m_2^{ast},m_3^{ast}) $.
Результат предыдущей теоремы позволяет существенно упростить решение «прямой» задачи.
Т
Теорема [12, 13].Обозначим
$$
S_1(x,y)=
left|
begin{array}{ccc}
1 & 1 & 1 \
x & x_2 & x_3 \
y & y_2 & y_3
end{array}
right|,
S_2(x,y)=
left|
begin{array}{ccc}
1 & 1 & 1 \
x_1 & x & x_3 \
y_1 & y & y_3
end{array}
right|,
S_3(x,y)=
left|
begin{array}{ccc}
1 & 1 & 1 \
x_1 & x_2 & x \
y_1 & y_2 & y
end{array}
right| , .
$$
Любое решение системы
$$ partial F / partial x = 0, partial F / partial y = 0 , $$
отличное от $ { P_j } $, удовлетворяет соотношению
$$
m_1:m_2:m_3=|PP_1|^{2-L} S_1(x,y):|PP_2|^{2-L} S_2(x,y):|PP_3|^{2-L} S_3(x,y) .
$$
В случае, когда $ L_{} $ четно, вторая система ни чем не лучше первой: степени получающихся алгебраических уравнений одинаковы. Но вот в случае, когда $ L_{} $ — нечетно (как в случае кулоновского потенциала), преимущество второй системы становится очевидным: избавиться от радикалов можно однократным возведением в квадрат.
=>
Для нечетных значений $ Lin mathbb Z $ стационарные точки функции $ F_{} $ удовлетворяют системе алгебраических уравнений
$$
left{ begin{array}{ll}
m_2^2S_1^2(x,y) |PP_1|^{2(2-L)} — m_1^2S_2^2(x,y) |PP_2|^{2(2-L)} & =0, \
m_2^2S_3^2(x,y) |PP_3|^{2(2-L)} — m_3^2S_2^2(x,y) |PP_2|^{2(2-L)} & =0.
end{array}
right.
$$
П
Пример. В рассмотренном выше примере функции
$$
F(x,y)=frac{1}{sqrt{(x-1)^2+(y-1)^2}}+ frac{m_2}{sqrt{(x-5)^2+(y-1)^2}}+frac{m_3}{sqrt{(x-2)^2+(y-6)^2}}
$$
предложенный алгоритм приводит к системе
$$
widetilde F_1(x,y,m_2,m_3)=0, widetilde F_2(x,y,m_2,m_3)=0 ,
$$
при
$$
begin{array}{c}
widetilde F_1(x,y,m_2,m_3)= \
=m_2^2,(5,x+3,y-28)^2(x^2+y^2-2,x-2,y+2)^3 -(5,x-y-4)^2(x^2+y^2-10,x-2,y+26)^3 , \
widetilde F_2(x,y,m_2,m_3)= \
=m_2^2,(4,y-4)^2(x^2+y^2-4,x-12,y+40)^3 -m_3^2,(5,x-y-4)^2(x^2+y^2-10,x-2,y+26)^3.
end{array}
$$
Здесь $ deg widetilde F_1 = deg widetilde F_2 =8 $ относительно переменных $ x_{} $ и $ y_{} $; это можно считать существенным успехом в сравнении с $ 28 $-й степенью уравнений, полученных в ходе первоначального решения.
Допустим, мы хотим исследовать динамику множества вещественных решений этой системы при различных фиксированных значениях $ m_2 $ и для произвольных значений $ m_3 $. Для получения неявного задания кривой
$$ H(x,y,m_2) = 0 , $$
которая будет состоять из решений системы при всевозможных значениях $ m_3 $, мы должны исключить этот параметр из системы. Но он, фактически, уже исключен: первое уравнение от него не зависит! Иными словами, утверждается, что уравнение
$$ m_2^2,(5,x+3,y-28)^2(x^2+y^2-2,x-2,y+2)^3 -(5,x-y-4)^2(x^2+y^2-10,x-2,y+26)^3=0 $$
при каждом фиксированном значении $ m_{2}=m_{2ast} $ определяет на плоскости $ (x,y) $ кривую, целиком состоящую из стационарных точек семейства кулоновских потенциалов
$$ left{ frac{1}{sqrt{(x-1)^2+(y-1)^2}}+ frac{m_{2ast}}{sqrt{(x-5)^2+(y-1)^2}}+frac{m_3}{sqrt{(x-2)^2+(y-6)^2}} right}_{m_3 in mathbb R} . $$
Изобразим несколько таких кривых на рисунке (числа на кривых обозначают величины $ m_2 $; ветви одинакового цвета соответствуют одинаковым значениям этого заряда).

♦
§
Более подробное исследование этой задачи
☞
ЗДЕСЬ.
Задачи
Источники
При составлении настоящего раздела существенно использовалось содержание обзорной статьи
[*]
. Martini H. Fermat-Torricelli problem. Encyclopedia of Mathematics. Supplement III. Kluwer Academic Publishers. 2001, C.149-151
[1]. Weber A. Über den Standort der Industrien. Teil I: Reine Theorie des Standorts. J.C.B.Mohr, 1909. Tübingen.
Вебер А. Теория размещения промышленности. М.-Л. «Книга». 1926. (На самом деле, последняя книга — не перевод оригинальной книги Вебера, а изложение ее содержания переводчиком Н.Морозовым12)).
[2]. Дингельдэй Фр. Сборникъ задачъ по приложенiю дифференцiальнаго и интегральнаго исчисленiй. С.-Петербург. 1912
[3]. Курант Р., Роббинс Г. Что такое математика? М.МЦНМО. 2004
[4]. Протасов В.Ю. Максимумы и минимумы в геометрии. М.МЦНМО. 2005
[5]. Уланов Е.А., Утешев А.Ю. Аналитическое решение обобщенной задачи Ферма-Торричелли-Штейнера./ / Процессы управления и устойчивость: Труды 42-й международной научной конференции аспирантов и студентов / Под ред. А. С. Ерёмина, Н. В. Смирнова. СПб.: Издат. Дом С.-Петерб. гос. ун-та, 2011. С. 201–206.
[6]. Launhardt W. Kommercielle Tracirung der Verkehrswege. Zeitschrift f. Architekten u.Ingenieur-Vereinis im Königreich Hannover. V. 18, pp. 516-534, 1872. Текст
☞
ЗДЕСЬ.
[7]. Maxwell J.C. Paper on the Description of Oval Curves. Observations on Circumscribed Figures Having a Plurality of Foci, and Radii of Various Proportions. 1846.
«The Scientific Letters and Papers of James Clerk Maxwell: 1846-1862» Vol. 1, Cambridge University Press. 1990
[8]. Maxwell J.C. A Treatise on Electricity and Magnetism. Vol. 1. Dower, New York. 1954
[9]. Maxwell J.C. On Governors. Proc. Royal Soc. London. 1868, V.16: pp. 270–283.
[10]. Sturm R. Über die Punkte kleinster Entfernungssumme von gegebenen Punkten. J. Reine Angew. Math., V. 97, pp.49-61, 1884.
[11]. Uteshev A.Yu. Analytical Solution for the Generalized Fermat-Torricelli Problem. Amer.Math.Monthly. V. 121, N 4, pp.318-331, 2014. Текст
☞
ЗДЕСЬ (pdf).
[12]. Uteshev A.Yu., Yashina M.V. Stationary Points for the Family of Fermat-Torricelli-Coulomb-like potential functions. Proc. 15th Workshop CASC (Computer Algebra in Scientific Computing), Berlin 2013. Springer. Lecture Notes in Computer Science. V.8136 pp. 412-426,
2013.
[13]. Uteshev A.Yu., Yashina M.V. On Maxwell’s Conjecture for Coulomb Potential Generated by Point Charges. Springer. Transactions on Computational Sciences XXVII. Lecture Notes in Computer Science. V. 9570, pp. 68-80, 2016. Текст
☞
ЗДЕСЬ (pdf)
[14]. Weiszfeld E. Sur le point pour lequel la somme des distances de $ n_{} $ points donnés est minimum. Tohoku Math. Journal. V. 43, pp. 355–386, 1937.
[15]. Gabrielov A., Novikov D., Shapiro B. Mystery of Point Charges. Proc. London Math. Soc. Ser. 3. V. 95, pp. 443-472, 2007.






























