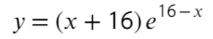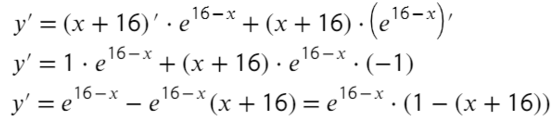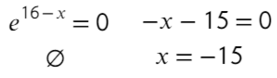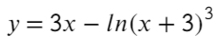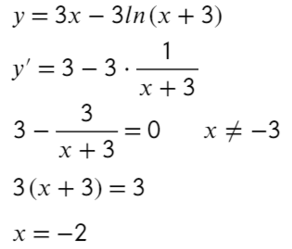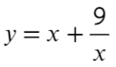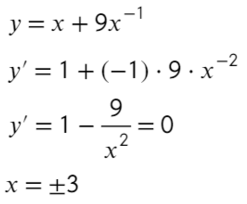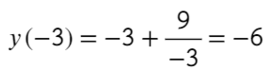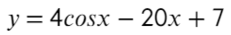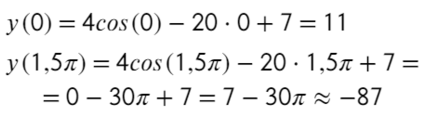Как найти точку функции наименьшего значения функции - Исправление недочетов и поиск решений вместе с Examum.ru

Наталья Игоревна Восковская

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Экстремумы функции

Для того чтобы ввести понятие наибольшего и наименьшего значения функций, вначале познакомимся с таким понятием, как экстремумы функций. Это понятие нам будет необходимо не для самого определения значений таких функций, а для построения схемы нахождения таких промежутков для конкретно заданных функций.

Определение 1

Точка $x’$ входящая в область определения функции называется точкой экстремума, если она либо будет точкой максимума, либо будет точкой минимума для функции $f(x)$.

Определение 2

Точка $x’$ будет называться точкой максимума для введенной функции $f(x)$, если у она имеет такую окрестность, что для всех точек $x$, которые входят в эту окрестность, будет верно $f(x)le f(x'{rm })$.

Определение 3

Точка $x_0$ будет называться точкой минимума для введенной функции $f(x)$, если она имеет такую окрестность, что для всех точек $x$, которые входят в эту окрестность, будет верно $f(x)ge f(x'{rm })$.

Чтобы полностью разобраться в данном понятии, далее введем понятие критической точки функции.

Определение 4

Точка $x’$ будет называться критической точкой для данной функции $f(x)$, если выполняются два следующих условия:

Точка $x’$ является внутренней точкой для области определения данной функции;
$f’left(x'{rm }right)=0$ или не существует.

Сформулируем без доказательства теоремы о необходимом (теорема 1) и достаточном (теорема 2) условии для существования точки экстремума.

Если $y=f(x)$ имеет экстремум в точке $x_0$, то либо её производная в ней равняется нулю, либо производная в ней не существует.

«Точки экстремума, наибольшее и наименьшее значение на промежутке» 👇

Теорема 2

Пусть точка $x’$ будет критической для $y=f(x)$ и принадлежит интервалу $(a,b)$, причем на каждом интервале $left(a,x'{rm }right) и (x'{rm },b)$ производная $f'(x)$ существует и сохраняет один и тот же знак. В этом случае:

Если в $(a,x'{rm })$ $f’left(xright) >0$, а в $(x'{rm },b)$ $f’left(xright)
Если в $(a,x'{rm })$ $f’left(xright)0$, то $x’$ —будет точкой минимума для этой функции.
Если и в $(a,x'{rm })$, и в $(x'{rm },b)$ производная $имеет один и тот же постоянный знак$, то $x’$ не будет точкой экстремума для этой функции.

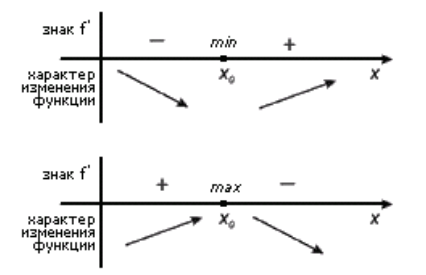
На рисунке 1 мы можем наглядно увидеть смысл теоремы 2.

Рисунок 1.

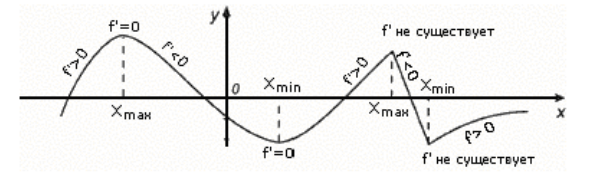
Примеры точек экстремумов вы можете видеть на рисунке 2.

Рисунок 2.

Правило исследования на экстремум

Найти $D(f)$;
Найти $f'(x)$;
Найти точки, где $f’left(xright)=0$;
Найти точки, где $f'(x)$ не будет существовать;
Отметить на координатной прямой $D(f)$ и все найденные в 3 и 4 пункте точки;
Определить знак $f'(x)$ на полученных промежутках;
Используя теорему 2, сделать заключение по поводу всех найденных точек.

Понятие наибольшего и наименьшего значений

Определение 5

Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наибольшее значение в точке $x’in X$, если выполняется

[fleft(xright)le f(x’)]

Определение 6

Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наименьшее значение в точке $x’in X$, если выполняется

[fleft(xright)ge f(x’)]

Чтобы найти наименьшее и наибольшее значение заданной функции на каком либо отрезке необходимо произвести следующие действия:

Найти $f'(x)$;
Найти точки, в которых $f’left(xright)=0$;
Найти точки, в которых $f'(x)$ не будет существовать;
Выкинуть из точек, найденных в пунктах 2 и 3 те, которые не лежат в отрезке $[a,b]$;
Вычислить значения в оставшихся точках и на концах $[a,b]$;
Выбрать из этих значений наибольшее и наименьшее.

Примеры задач

Пример 1

Найти наибольшее и наименьшее значения на [0,6]: $fleft(xright)=x^3-3x^2-45x+225$

Решение.

$f’left(xright)=3x^2-6x-45$;
$f’left(xright)=0$;
[3x^2-6x-45=0]
[x^2-2x-15=0]
[x=5, x=-3]
$f'(x)$ существует на всей $D(f)$;
$5in left[0,6right]$;
Значения:

[fleft(0right)=225] [fleft(5right)=50] [fleft(6right)=63]
Наибольшее значение равняется $225$, наименьшее равняется $50.$

Ответ: $max=225, min=50$.

Пример 2

Найти наибольшее и наименьшее значения на [-1,1]:$fleft(xright)=frac{x^2-4x+4}{x-2}$

Решение.

[fleft(xright)=frac{x^2-4x+4}{x-2}=frac{{(x-2)}^2}{x-2}=x-2, xne 2]

$f’left(xright)=(x-2)’=1$;

Точек экстремума нет.
Значения:

[fleft(-1right)=-3] [fleft(1right)=-1]

Ответ: $max=-1, min=-3$.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.

Вот какие типы задач могут встретиться в этом задании:

Нахождение точек максимума и минимума функций

Исследование сложных функций

Нахождение наибольших и наименьших значений функций на отрезке

Нахождение точек максимума и минимума функций

1. Найдите точку максимума функции $displaystyle y=-{{x^2+289}over{x}}.$

Найдем производную функции.

Приравняем производную к нулю. Получим:

$x^2=289Leftrightarrow left[ begin{array}{c} x=17, hfill \ x=-17. end{array} right.$

Исследуем знаки производной.

В точке x = 17 производная меняет знак с «плюса» на «минус». Значит, x= 17 — точка максимума функции y(x).

Ответ: 17.

2. Найдите точку минимума функции

Найдем производную функции.

Приравняем производную к нулю.

$4x-5+{{1}over{x}}=0Leftrightarrow 4x^2-5x+1=0Leftrightarrow left[ begin{array}{c} x=1, \ x={{1}over{4}}. end{array} right.$

Определим знаки производной.

В точке x = 1 производная меняет знак с «минуса» на «плюс». Значит, x= 1 — точка минимума функции y(x).

Ответ: 1.

Исследование сложных функций

3. Найдите точку максимума функции $y=2^{5-8x-x^2}.$

Перед нами сложная функция $y=2^{5-8x-x^2}.$ Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.

Так как функция y=2^t монотонно возрастает, точка максимума функции $y=2^{5-8x-x^2}$ будет при том же x_0 , что и точка максимума функции А ее найти легко.

$t^{$

$t^{$ при x=-4 . В точке x = -4 производная ${{ t}}^{{$ меняет знак с «плюса» на «минус». Значит, x= - 4 — точка максимума функции .

Заметим, что точку максимума функции можно найти и без производной.

Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при $x=-frac{8}{2}=-4.$

Ответ: — 4.

4. Найдите абсциссу точки максимума функции $y=sqrt{4-4x-x^2}.$

Напомним, что абсцисса — это координата по

Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.

Так как функция монотонно возрастает, точка максимума функции $y=sqrt{4-4x-x^2}$ является и точкой максимума функции

Это вершина квадратичной параболы $tleft(xright)=4-4x-x^2;x_0=frac{-4}{2}=-2.$

Нахождение наибольших и наименьших значений функций на отрезке

5. Найдите наибольшее значение функции на отрезке

Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.

Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.

${3x}^2+4x-4=0;$

$D=64;x=frac{-4pm 8}{6};x_1=frac{2}{3},x_2=-2.$

Найдем знаки производной.

В точке x = - 2 производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции y(x) . Поскольку при функция y(x) убывает, $y_{max}left(xright)=yleft(-2right)=12.$ В этой задаче значение функции на концах отрезка искать не нужно.

Ответ: 12.

6. Найдите наименьшее значение функции $y={4x}^2-10x+2lnx-5$ на отрезке

Найдем производную функции $y={4x}^2-10x+2lnx-5$ и приравняем ее к нулю.

при $x_1=1,x_2=frac{1}{4}.$

Найдем знаки производной.

Точка x_1=1 — точка минимума функции . Точка $x_2=frac{1}{4}$ не лежит на отрезке Поэтому

и Значит, наименьшее значение функции на отрезке достигается при x=1. Найдем это значение.

$y_{min}left(xright)=yleft(1right)=4-10-5=-11.$

Ответ: -11.

7. Найдите наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

Иногда перед тем, как взять производную, формулу функции полезно упростить.

Мы применили формулу для логарифма произведения. при $x=frac{1}{9}.$

Если то Если , то

Значит, $x=frac{1}{9}$ — точка минимума функции y(x) . В этой точке и достигается наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

$y_{min}left(xright)=yleft(frac{1}{2}right)=1+3=4.$

Ответ: 4.

8. Найдите наибольшее значение функции на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

Найдем производную функции

Приравняем производную к нулю: $14-frac{7}{{cos}^2x}=0.$

${cos}^2x=frac{1}{2}.$

${cos}^2x=pm frac{1}{sqrt{2}}=pm frac{sqrt{2}}{2}$ . Поскольку $xin left[-frac{pi }{3};frac{pi }{3}right], y$ если $x=pm frac{pi }{4}.$

Найдем знаки производной на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

При $x=frac{pi }{4}$ знак производной меняется с «плюса» на «минус». Значит, $x=frac{pi }{4}$ — точка максимума функции y(x).

Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при $x=-frac{pi }{3}$ и $x =frac{pi }{4}.$

$yleft(frac{pi }{4}right)=-7+11=4;$

Мы нашли, что $y_{max}left(xright)=yleft(frac{pi }{4}right)=-7+11=4.$

Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при $-frac{pi }{3}$ не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.

Ответ: 4.

9. Найдите наименьшее значение функции $y=e^{2x}-{8e}^x+9$ на отрезке [0;2].

Снова сложная функция. Запишем полезные формулы:

${{(e}^{-x})}^{$

${left(e^{cx}right)}^{$

${(e}^{x+a})$

Найдем производную функции $y=e^{2x}-{8e}^x+9.$

если e^x=4. Тогда x=ln4.

При x=ln4 знак производной меняется с «минуса» на «плюс». Значит, x=ln4 — точка минимума функции y(x).

Ответ: -7.

10. Найдите наибольшее значение функции на отрезке $left[0;frac{pi }{2}.right]$

Как всегда, возьмем производную функции и приравняем ее к нулю.

$sinx=frac{sqrt{3}}{2}.$

По условию, $xin left[0;frac{pi }{2}right]$ . На этом отрезке условие $sinx=frac{sqrt{3}}{2}$ выполняется только для $x=frac{pi }{3}.$ Найдем знаки производной слева и справа от точки $x=frac{pi }{3}.$

В точке $x_0=frac{pi }{3}$ производная функции меняет знак с «плюса» на «минус». Значит, точка $x_0=frac{pi }{3}$ — точка максимума функции y(x) . Других точек экстремума на отрезке $left[0;frac{pi }{2}right]$ функция не имеет, и наибольшее значение функции на отрезке $left[{ 0};frac{pi }{{ 2}}right]$ достигается при ${ x=}frac{pi }{{ 3}}.$

$y_{max}left(xright)=yleft(frac{pi }{3}right)=12.$

Ответ: 12.

11.Найдите наименьшее значение функции на отрезке $left[0;frac{pi }{2}right].$

Найдем производную функции и приравняем ее к нулю. — нет решений.

Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.

Поскольку , получим, что для всех , и функция монотонно возрастает при $xin left[0;frac{pi }{2}right].$

Значит, наименьшее свое значение функция принимает в левом конце отрезка $left[{ 0};frac{pi }{{ 2}}right]$ , то есть при x=0.

$y_{min}left(xright)=yleft(0right)=6.$

Ответ: 6

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 11 Профильного ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

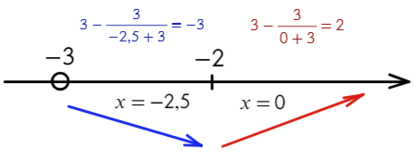
Рассмотрим примеры, в которых дан график производной и требуется определить, в какой точке данного отрезка функция принимает наименьшее значение.

№1

На рисунке изображён график производной функции f(x), определённой на интервале (-10;8). В какой точке отрезка [-8;-1] функция f(x) принимает наименьшее значение?

Решение:

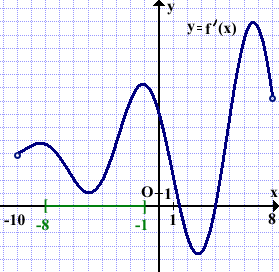
Выделяем отрезок [-8;-1].

На этом отрезке производная f'(x) принимает положительные значения.

Значит, на [-8;-1] функция f(x) возрастает, то есть бо́льшему значению аргумента соответствует бо́льшее значение функции:

x₁,x₂ ∈[-8;-1], x₂>x₁, ⇒ f(x₂)>f(x₁).

Следовательно, наименьшее значение f(x) принимает при наименьшем значении аргумента, то есть на левом конце отрезка, при x=-8.

Ответ: -8.

№2

На рисунке изображён график производной функции f(x), определённой на интервале (-6;8). В какой точке отрезка [-3;6] функция f(x) принимает наименьшее значение?

Решение:

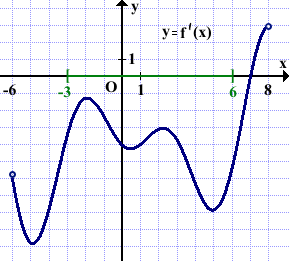
Выделяем отрезок [-3;6].

На этом отрезке f'(x)<0, поэтому f(x) убывает, то есть бо́льшему значению аргумента соответствует меньшее значение функции:

x₁,x₂ ∈[-3;6], x₂>x₁, ⇒ f(x₂)<f(x₁).

Поэтому наименьшее значение функция f(x) в этом случае принимает при наибольшем значении аргумента, то есть на правом конце отрезка, при x=6.

Ответ: 6.

№3

Функция y=f(x) определена на промежутке (-9;6). На рисунке изображён график её производной. Найти абсциссу точки, в которой функция y=f(x) принимает наименьшее значение.

Решение:

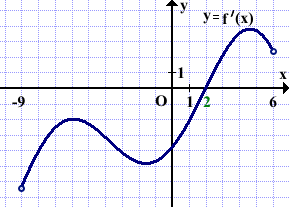
В точке с абсциссой x=2 производная меняет знак с минуса на плюс.

Значит, x=2 — точка минимума.

Производная f'(x) существует на всём интервале (-9;6), следовательно, функция f(x) на (-9;6) непрерывна.

Если непрерывная функция f(x) имеет на заданном интервале (a;b) только одну точку экстремума x_o и это точка минимума, то на (a;b) функция принимает своё наименьшее значение в точке x_o.

Таким образом, наименьшее значение функция f(x) принимает в точке с абсциссой x=2.

Ответ: 2.

№4

Функция y=f(x) определена и непрерывна на отрезке [-4;9]. На рисунке изображён график её производной. Найти точку x_o, в которой функция принимает наименьшее значение, если f(9)≤f(-4).

Решение:

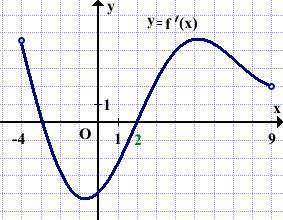
На промежутках (-4;-3) и (2;9) производная f'(x) принимает положительные значения, поэтому функция f(x) на этих промежутках возрастает.

На промежутке (-3;2) производная f'(x)<0, поэтому функция f(x) убывает.

Так как функция определена и непрерывна на отрезке [-4;9], то точки -4, -3, 2 и 9 можно включить в промежутки монотонности.

Следовательно, функция f(x) возрастает на промежутках [-4;-3] и [2;9] и убывает на [-3;2].

На промежутках возрастания своё наименьшее значение функция принимает на левом конце отрезка. На отрезке [2;9] наименьшее значение f(x) принимает в точке x=2 (точке минимума), на [-4;-3] — в точке x=-4.

Так как на [2;9] функция f(x) возрастает, то f(2)<f(9).

По условию, f(9)≤f(-4). Значит, f(2)<f(-4).

Таким образом, наименьшее значение функция f(x) принимает в точке x=2.

Ответ: 2.

Источник

Определение

Наибольшим или наименьшим значением функции в определенной области называют наибольшее или наименьшее значение, которое достигает эта функция на указанной области.

Чтобы найти наибольшее или наименьшее значение функции в данной области, нужно решить задачу на экстремум, то есть найти производную заданной функции, приравнять её к нулю и найти точки, в которых производная функции обращается в нуль. Потом из этих точек нужно выбрать только те, которые входят в нашу заданную область. Затем нужно вычислить значение функций в этих точках. Кроме этого, нужно найти значение функции в граничных точках заданной области (если это отрезок) и сравнить их со значениями в точках экстремума. Потом можно сделать вывод о наименьшем или наибольшем значении функции в данной области.

Пример 1

Определить наименьшее и наибольшее значения функции y=x3−6×2+9y=x^3-6x^2+9 на отрезке [−1;2][-1;2].

Решение

Сначала вычисляем производную исходной функции:

y′=3×2−12xy’=3x^2-12x

Затем приравниваем ее к нулевому значению и решаем уравнение:

3×2−12x=03x^2-12x=0

x(3x−12)=0x(3x-12)=0

x1=0x_1=0

x2=4x_2=4

Затем — непосредственный поиск максимального и минимального значений функции на заданном отрезке. Важно отметить, что точка x=4x=4 не входит в заданный отрезок, поэтому значение функции в этой точке вычислять не требуется.

Находим значение функции в точке x1x_1:

f(0)=9f(0)=9

Кроме этого, нужно найти значение функции в граничных точках нашего отрезка, то есть в точках x=−1x=-1 и x=2x=2:

f(−1)=−1−6+9=2f(-1)=-1-6+9=2

f(2)=8−24+9=−7f(2)=8-24+9=-7

Получаем, что на заданном отрезке, наименьшее значение функции, которое равно −7-7, достигается в точке x=2x=2 , а наибольшее значение, равное 99, достигается в точке x=0x=0.

Пример 2

Найти наибольшее и наименьшее значение функции-параболы y=3x2y=3x^2 на всей области её определения.

Решение

Функция y=3x2y=3x^2 определена на всем интервале от минус бесконечности к плюс бесконечности. Найдем производную этой функции:

y′=6xy’=6x

Приравниваем производную к нулю:

6x=06x=0

x=0x=0

Точка x=0x=0 — единственный экстремум этой функции. В этой точке функция равна f(0)=0f(0)=0. Остается решить максимум это или минимум.

Так как график нашей функции это парабола, ветви которой направлены вверх (поскольку 3>03>0), то точка x=0x=0 — точка минимума этой функции. Следовательно, функция y=3x2y=3x^2 достигает своего минимального значения в точке x=0x=0 равного 00. Максимального значения эта функция не имеет. Оно только приближается к сколь угодно большому числу когда значение аргумента стремится к плюс или минус бесконечности.

Тест по теме “Наибольшие и наименьшие значения функции”

Не можешь разобраться в этой теме?

Обратись за помощью к экспертам

Гарантированные бесплатные доработки

Быстрое выполнение от 2 часов

Проверка работы на плагиат

Источник

Значения функции и точки максимума и минимума

Наибольшее значение функции

Наменьшее значение функции

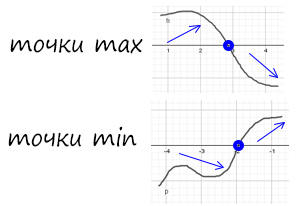
Точки max

Точки min

Как говорил крестный отец: «Ничего личного». Только производные!

Статью Как посчитать производные? надеюсь, ты изучил, без этого дальше будет проблематично.

12 задание по статистике считается достаточно трудным, а все потому, что ребята не прочитали эту статью (joke). В большинстве случаев виной всему невнимательность.

12 задание бывает двух видов:

Найти точку максимума / минимума (просят найти значения «x»).
Найти наибольшее / наименьшее значение функции (просят найти значения «y»).

Как же действовать в этих случаях?

Найти точку максимума / минимума

Взять производную от предложенной функции.
Приравнять ее к нулю.
Найденный или найденные «х» и будут являться точками минимума или максимума.
Определить с помощью метода интервалов знаки и выбрать, какая точка нужна в задании.

Задания с ЕГЭ:

Найдите точку максимума функции

Берем производную:

Приравняем ее к нулю:
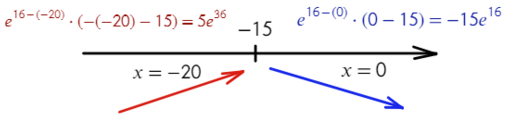
Получили одно значение икса, для нахождения знаков подставим −20 слева от корня и 0 справа от корня в преобразованную производную (последняя строчка с преобразованием):

Все верно, сначала функция возрастает, затем убывает — это точка максимума!
Ответ: −15

Найдите точку минимума функции

Преобразуем и возьмем производную:

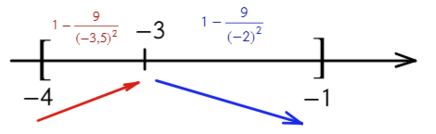
Получается один корень «−2», однако не стоит забывать о «−3», она тоже будет влиять на изменение знака.

Отлично! Сначала функция убывает, затем возрасает — это точка минимума!

Ответ: −2

Найти наибольшее / наименьшее значение функции

Взять производную от предложенной функции.
Приравнять ее к нулю.
Найденный «х» и будет являться точкой минимума или максимума.
Определить с помощью метода интервала знаки и выбрать, какая точка нужна в задании.
В таких заданиях всегда задается промежуток: иксы, найденные в пункте 3, должны входить в данный промежуток.
Подставить в первоначальное уравнение полученную точку максимума или минимума, получаем наибольшее или наименьшее значение функции.

Задания с ЕГЭ:

Найдите наибольшее значение функции на отрезке [−4; −1]

Преобразуем и возьмем производную:
«3» не вдходит в промежуток [−4; −1]. Значит, остается проверить «−3» — это точка максимума?

Подходит, сначала функция возрастает, затем убывает — это точка максимума, и в ней будет наибольшее значение функции. Остается только подставить в первоначальную функцию:

Ответ: −6

Найдите наибольшее значение функции на отрезке [0; 1,5π]

Наибольшее значение функции равно «11» при точке максимума (на этом отрезке) «0».

Ответ: 11

Выводы:

70% ошибок заключается в том, что ребята не запоминают, что в ответ на наибольшее/наименьшее значение функции нужно написать «y», а на точку максимума/минимума написать «х».
Нет решения у производной при нахождении значений функции? Не беда, подставляй крайние точки промежутка!
Ответ всегда может быть записан в виде числа или десятичной дроби. Нет? Тогда перерешивай пример.
В большинстве заданий будет получаться одна точка и наша лень проверять максимум или минимум будет оправдана. Получили одну точку — можно смело писать в ответ.
А вот с поиском значения функции так поступать не стоит! Проверяйте, что это нужная точка, иначе крайние значения промежутка могут оказаться больше или меньше.

Будь в курсе новых статеек, видео и легкого математического юмора.

Источник