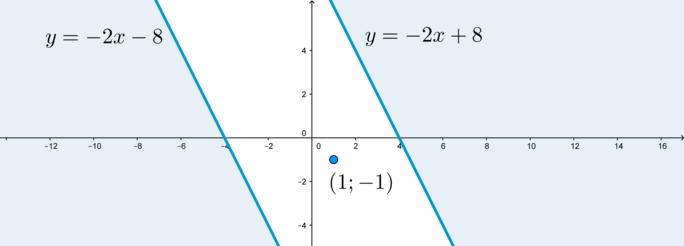Как найти точку касания двух окружностей параметр - Исправление недочетов и поиск решений вместе с Examum.ru

Две окружности на плоскости.
Общие касательные к двум окружностям

Взаимное расположение двух окружностей

Взаимное расположение на плоскости двух окружностей радиусов r₁ и r₂ с центрами O₁ и O₂ определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов

r₁ – r₂ лежит внутри другой

Расстояние между центрами окружностей меньше разности их радиусов

d r₁ и r₂ с центрами O₁ и O₂ определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов

r₁ – r₂ лежит внутри другой

Расстояние между центрами окружностей меньше разности их радиусов

d r₁ и r₂ с центрами O₁ и O₂ определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей меньше разности их радиусов

d внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также
две общих внешних касательных. Других общих касательных нет.

Каждая из окружностей лежит вне другой

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

Фигура	Рисунок	Свойства
Две окружности на плоскости
Каждая из окружностей лежит вне другой
Внешнее касание двух окружностей
Внутреннее касание двух окружностей
Окружности пересекаются в двух точках
Каждая из окружностей лежит вне другой

Внешнее касание двух окружностей

Внутреннее касание двух окружностей

Окружности пересекаются в двух точках


Каждая из окружностей лежит вне другой
Расстояние между центрами окружностей больше суммы их радиусов
Внешнее касание двух окружностей
Расстояние между центрами окружностей равно сумме их радиусов
Внутреннее касание двух окружностей
Окружности пересекаются в двух точках
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r₁ – r₂ лежит внутри другой
Внутренняя касательная к двум окружностям
Внутреннее касание двух окружностей
Окружности пересекаются в двух точках
Внешнее касание двух окружностей

Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.

Внешняя касательная к двум окружностям

Внутренняя касательная к двум окружностям

Внутреннее касание двух окружностей

Окружности пересекаются в двух точках

Внешнее касание двух окружностей

Каждая из окружностей лежит вне другой

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.

Формулы для длин общих касательных и общей хорды двух окружностей

Внешняя касательная к двум окружностям

Внутренняя касательная к двум окружностям

Внутреннее касание двух окружностей

Окружности пересекаются в двух точках

Внешнее касание двух окружностей

Каждая из окружностей лежит вне другой

Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле

Фигура	Рисунок	Формула
Внешняя касательная к двум окружностям
Внутренняя касательная к двум окружностям
Общая хорда двух пересекающихся окружностей

Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле

Внешняя касательная к двум окружностям

Внутренняя касательная к двум окружностям

Общая хорда двух пересекающихся окружностей

Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Внешняя касательная к двум окружностям

Внутренняя касательная к двум окружностям

Общая хорда двух пересекающихся окружностей

Длина общей хорды двух окружностей вычисляется по формуле

Доказательства формул для длин общих касательных и общей хорды двух окружностей

Утверждение 1 . Если расстояние между центрами двух окружностей радиусов r₁ и r₂ равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле

что и требовалось доказать.

Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r₁ и r₂ равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле

что и требовалось доказать.

Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r₁ и r₂ равно d , то длина общей хорды AB этих окружностей вычисляется по формуле

Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3,

Касание окружностей

Говорят, что две окружности касаются, если они имеют единственную общую точку. Эта точка называется точкой касания окружностей. Касание окружностей бывает внутренним и внешним.

Внутреннее касание

Касание называется внутренним, если центры окружностей лежат по одну сторону от точки касания окружностей. Построим две окружности, первая с центром A и радиусом AC, отметим на радиусе AC точку B, это будет центр второй окружности с радиусом BC:

Построенные окружности имеют только одну общую точку C. Говорят, что они касаются внутренним образом.

При внутреннем касании двух окружностей, расстояние между их центрами равно разности их радиусов.

Внешнее касание

Касание называется внешним, если центры окружностей лежат по разные стороны от точки касания. Построим две окружности, первая с центром A и радиусом AC, вторая с центром B и радиусом BC:

Построенные окружности имеют только одну общую точку C. Говорят, что они касаются внешним образом.

При внешнем касании двух окружностей, расстояние между их центрами равно сумме их радиусов.

Касание двух окружностей

Две окружности, имеющие общую точку, касаются в этой точке, если они имеют в ней общую касательную.

Общая точка двух окружностей называется точкой касания окружностей.

Касание окружностей может быть внешним и внутренним.

Внешнее касание окружностей — это касание, при котором центры окружностей лежат по разные стороны от общей касательной.

Внутреннее касание окружностей — касание, при котором центры окружностей лежат по одну сторону от общей касательной.

Касающиеся окружности имеют только одну общую точку — точку касания.

Центры касающихся окружностей и их общая точка касания лежат на одной прямой.

При любом виде касания по свойству касательной касательная перпендикулярна радиусам, проведённым в точку касания:

По теореме о существовании и единственности прямой, перпендикулярной данной,через точку A можно провести только одну прямую, перпендикулярную данной прямой k.

Следовательно, все три точки: центры окружностей O1, O2 и A лежат на одной прямой.

Что и требовалось доказать .

При внешнем касании расстояние между центрами окружностей равно сумме их радиусов:

При внутреннем касании расстояние между центрами окружностей равно разности радиусов:

источники:

http://izamorfix.ru/matematika/planimetriya/kasanie_okruj.html

Касание двух окружностей

Источник

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Решение задач с окружностями

Задание
1

#3079

Уровень задания: Равен ЕГЭ

Найдите все значения (a), при каждом из которых система уравнений [begin{cases}
x(x^2+y^2-2y-8)=|x|cdot (2y-8)\
y=x+a end{cases}]

имеет ровно три решения.

(Задача от подписчиков)

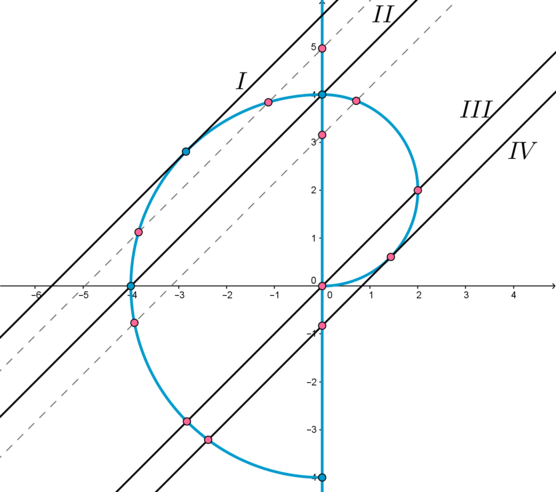
1) Изобразим график первого уравнения.

а) При (x>0) уравнение принимает вид: [x(x^2+y^2-2y-8)=x(2y-8) quadRightarrowquad x^2+(y-2)^2=4] Мы получили уравнение окружности (назовем ее (s)) с центром в точке ((0;2)) и радиусом (2).

б) При (x=0) уравнение принимает вид: [0cdot (0+y^2-2y-8)=0cdot (2y-8) quadRightarrowquad 0=0] Таким образом, мы получили верное равенство. Следовательно, мы получили множество точек, абсцисса (x) которых равна нулю.

в) При (x<0) уравнение принимает вид: [x(x^2+y^2-2y-8)=-x(2y-8) quadRightarrowquad x^2+y^2=16] Мы получили уравнение окружности (назовем ее (S)) с центром в точке ((0;0)) и радиусом (4).

2) Уравнение (y=x+a) задает множество прямых, параллельных прямой (y=x) (это прямые, угол наклона которых к положительному направлению оси (Ox) равен (45^circ)).
Таким образом, получаем такую картинку (голубым цветом изображен график первого уравнения):

3) Для того, чтобы система имела 3 решения, нужно, чтобы при некотором фиксированном (a) прямая (y=x+a) пересекала “голубой график” ровно в трех точках.
Таким образом, нам подходят следующие случаи:
— когда прямая (y) находится между (I) и (II) (не включая эти случаи). Случай (I) – касание прямой (y) и окружности (S). Случай (II) – прохождение прямой (y) через точку пересечения окружности (S) и прямой (x=0).
— когда прямая (y) находится между (II) и (III) (не включая (II) и включая (III)). Случай (III) – прохождение прямой (y) через точку пересечения окружности (s) и прямой (x=0).
— когда прямая (y) находится в положении (IV) – касается окружности (s).

Рассмотрим каждый из этих случаев по отдельности.

Между (I) и (II).
– Найдем значение (a), при котором прямая (y) находится в положении (I). В этом случае (a>0).

Пусть (A(0;a), B(-a;0)) – точки пересечения (y) с осями координат, (K) – точка касания. Тогда (OKperp AB) (как радиус, проведенный в точку касания). Длина (OA=a), (OB=a), (OK=4), (triangle AOB) прямоугольный. Тогда (AB=asqrt2). Тогда [S_{triangle AOB}=dfrac12 OKcdot AB=dfrac12 OBcdot OA
quadRightarrowquad a=4sqrt2.] – Найдем значение (a), при котором прямая (y) находится в положении (II). В этом случае (y) проходит через точку ((0;4)), следовательно, [4=0+a quadRightarrowquad a=4]

Таким образом, нам подходят значения (ain (4;4sqrt2)).

Между (II) и (III).
– Найдем (a), при котором прямая (y) находится в положении (III). В этом случае она проходит через точку ((0;0)), то есть (a=0).

Таким образом, нам подходят (ain [0;4)).

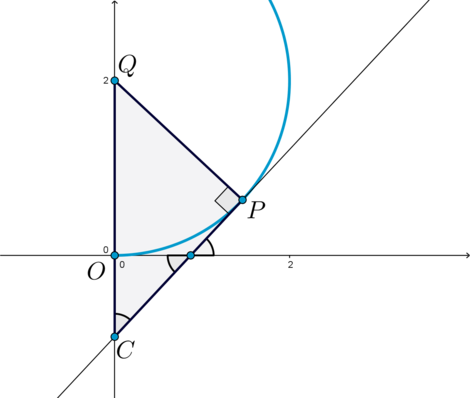
Положение (IV).

В этом случае (a<0). Пусть (Q) – центр окружности (s), (P) – точка касания, (C) – точка пересечения (y) с осью ординат. Тогда (triangle QPC) – прямоугольный. Ранее мы говорили, что прямая (y) наклонена к положительному направлению оси (Ox) под углом (45^circ), откуда будет следовать, что и (angle QCP=45^circ). Радиус (QP=2), отрезок (OC=-a) (так как (a<0)), (QO=2). Следовательно, [sinangle QCP=sin 45^circ=dfrac{sqrt2}2=dfrac{QP}{QC}=
dfrac{2}{2-a}
quadRightarrowquad a=-2sqrt2+2.]

Таким образом, обобщая все решение, находим ответ: [ain {-2sqrt2+2}cup[0;4)cup(4;4sqrt2).]

Ответ:

({-2sqrt2+2}cup[0;4)cup(4;4sqrt2))

Задание
2

#3202

Уровень задания: Равен ЕГЭ

Найдите все значения параметра (a), при каждом из которых система [begin{cases}
(x-2a+3)^2+(y-a)^2=2,25\
(x+3)^2+(y-a)^2=a^2+2a+1 end{cases}]

имеет единственное решение.

(Задача от подписчиков)

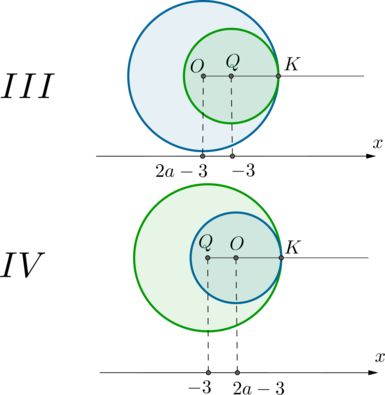
Оба уравнения системы при (ane -1) задают окружности: первое уравнение – окружность с центром в точке (O(2a-3; a)) и радиуса (R_1=1,5); второе – окружность с центром в точке (Q(-3;a)) и радиуса (R_1=|a+1|).
При (a=-1) второе уравнение задает точку (A(-3;-1)), которая не является решением первого уравнения. Следовательно, при (a=-1) система не имеет решений, значит, (a=-1) – не подходит.

Рассмотрим случай, когда (ane-1).
Система будет иметь единственное решение, когда окружности будут касаться друг друга (внутренним или внешним образом). Заметим, что центры обеих окружностей находятся на прямой (y=a). То есть линия центров окружностей параллельна оси абсцисс.

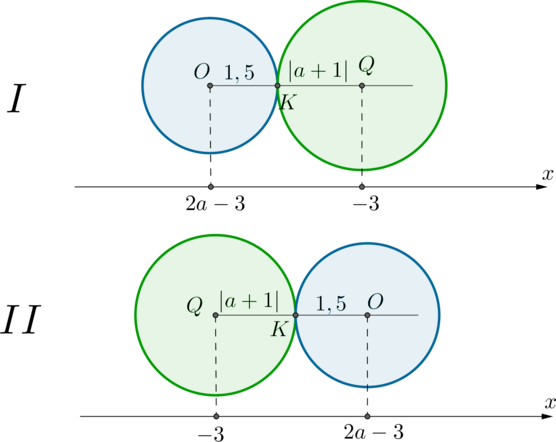
1) Пусть окружности касаются внешним образом в точке (K). Это одна из двух картинок:

Заметим, что, с одной стороны, расстояние между центрами окружностей равно сумме радиусов: (OQ=|a+1|+1,5), а с другой стороны, равно (|-3-(2a-3)|=2|a|). Получаем уравнение: [|a+1|+1,5=2|a|quadLeftrightarrowquad
left[begin{gathered}begin{aligned} &begin{cases} a< -1\
-2a=-a-1+1,5end{cases}\
&begin{cases} -1<a<0\
-2a=a+1+1,5 end{cases}\
&begin{cases} ageqslant 0\
2a=a+1+1,5 end{cases} end{aligned}end{gathered}right. quad
Leftrightarrowquad a=-dfrac56; dfrac52]

2) Пусть окружности касаются внутренним образом в точке (K). Это также одна из двух картинок (а также симметричные картинки, то есть когда точка касания находится слева):

В этих случаях длина отрезка (OQ), с одной стороны, равна (|-3-(2a-3)|=2|a|), а с другой стороны, она равна разности радиусов: (big|1,5-|a+1|big|) (ставим модуль, потому что неизвестно, какой радиус больше, то есть как окружность с центром (O) может быть вписана в окружность с центром (Q), так и наоборот). Получаем уравнение: [2|a|=big|1,5-|a+1|big| quadLeftrightarrowquad
left[begin{gathered}begin{aligned} & 2a=|a+1|-1,5\
&2a=1,5-|a+1| end{aligned}end{gathered}right.
quadLeftrightarrowquad a=-dfrac12; dfrac16]

Таким образом, окончательный ответ: [ain left{-dfrac56;
-dfrac12; dfrac16; dfrac52right}]

Ответ:

(left{-dfrac56; -dfrac12; dfrac16; dfrac52right})

Задание
3

#3977

Уровень задания: Равен ЕГЭ

Найдите все значения параметра (a), при которых система [begin{cases} (2x^2-4x+3y^2+6y+5)(8-|2x+y|)leqslant 0\
x^2-4x+y^2=a end{cases}]

имеет единственное решение.

(Задача от подписчиков)

1) Преобразуем неравенство системы:

((2x^2-4x+2+3y^2+6y+3-2-3+5)(8-|2x+y|)leqslant 0
quadLeftrightarrow)

(Leftrightarrowquad (2(x-1)^2+3(y+1)^2)(8-|2x+y|)leqslant
0quadLeftrightarrow)

(Leftrightarrowquad left[begin{gathered}begin{aligned}
&begin{cases} 2(x-1)^2+3(y+1)^2leqslant 0\
8-|2x+y|geqslant 0end{cases}\[2ex]
&begin{cases} 2(x-1)^2+3(y+1)^2geqslant 0\
8-|2x+y|leqslant 0end{cases} end{aligned}end{gathered}right.)

Т.к. сумма квадратов всегда неотрицательна, то данная совокупность равносильна:

[left[begin{gathered}begin{aligned}
&begin{cases}
2(x-1)^2+3(y+1)^2=0\
|2x+y|leqslant 8
end{cases}\[2ex]
&begin{cases}
2(x-1)^2+3(y+1)^2geqslant 0\
|2x+y|geqslant 8
end{cases}
end{aligned}end{gathered}right.
quadLeftrightarrowquad
left[begin{gathered}begin{aligned} &begin{cases}
x=1\
y=-1\
|2cdot 1+1|leqslant 8
end{cases}\[2ex]
&begin{cases}
x,yinmathbb{R}\
|2x+y|geqslant 8
end{cases}
end{aligned}end{gathered}right.
quadLeftrightarrowquad
left[begin{gathered}begin{aligned}
&begin{cases}
x=1\
y=-1
end{cases}\[2ex]
&|2x+y|geqslant 8
end{aligned}end{gathered}right.]

Т.к. (|2x+y|geqslant равносильно (2x+ygeqslant или (2x+yleqslant -8), то данная совокупность задает область, состоящую из части плоскости, находящейся не ниже прямой (y=-2x+8), из части плоскости, находящейся не выше прямой (y=-2x-8), а также из точки ((1;-1)):

2) Преобразуем уравнение системы: [x^2-4x+y^2=aquadLeftrightarrowquad x^2-4x+4+y^2=a+4quadLeftrightarrowquad
(x-2)^2+y^2=a+4]

Данное уравнение при (a+4>0) задает окружность с центром в точке (O(2;0)) и радиусом (R=sqrt{a+4}); при (a+4=0) задает точку ((2;0)); при (a+4<0) – пустое множество.

Т.к. точка ((2;0)) не попадает в область, заданную неравенством, то при (a+4leqslant 0) система точно не будет иметь решений.

3) Рассмотрим случай (a+4>0).

Система будет иметь единственное решение тогда и только тогда, когда окружность будет иметь ровно одну общую точку с областью. Это возможно в одном из двух случаев:

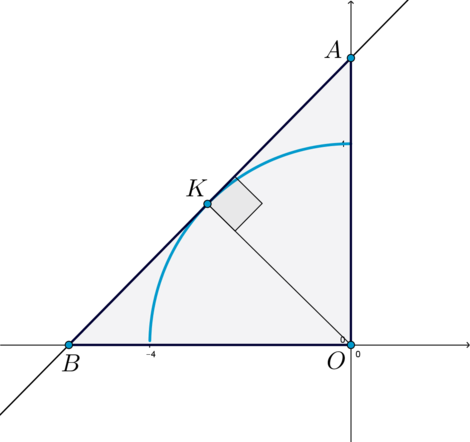
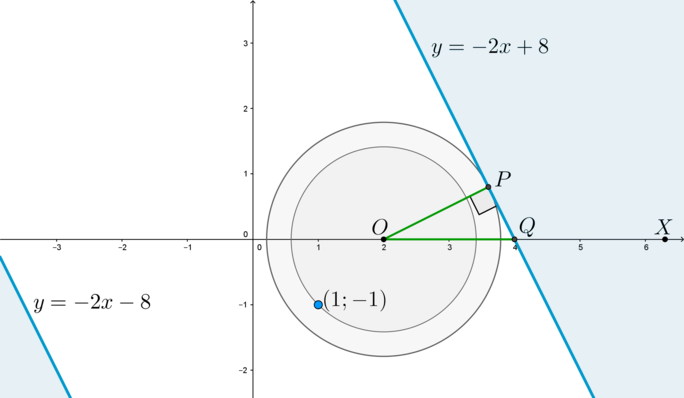
(1) Если окружность коснется границы области (y=-2x+8).
Пусть (P) – точка касания (то есть (OPperp y=-2x+8)). Рассмотрим прямоугольный (triangle OPQ), где (Q=(4;0)) – точка пересечения прямой (y=-2x+8) с осью абсцисс.

Т.к. угловой коэффициент прямой (y=-2x+8) равен (-2), то (mathrm{tg},angle PQX=-2), следовательно, (mathrm{tg},angle
PQO=2). Тогда [sin angle PQO=dfrac{2}{sqrt5}
quadRightarrowquad dfrac{OP}{OQ}=dfrac2{sqrt5} quad
Rightarrowquad OP=OQcdot dfrac2{sqrt5}=dfrac4{sqrt5}.]

Т.к. (OP) и есть радиус окружности, то [dfrac4{sqrt5}=sqrt{a+4} quad Rightarrowquad a=-dfrac45.]

(2) Если окружность проходит через точку ((1;-1)).
Это значит, что расстояние между точками (O) и ((1;-1)) равно радиусу окружности, следовательно, [sqrt{a+4}=sqrt{(2-1)^2+(0+1)^2}quad Leftrightarrowquad a=-2.]

Ответ:

(big{-2;-frac45big})

Задание
4

#3980

Уровень задания: Равен ЕГЭ

Найдите все значения параметра (a), при которых система [begin{cases}
left(|x|-3right)^2+left(|y|-2right)^2=1\
y=ax+1\xy<0end{cases}] имеет ровно два решения.

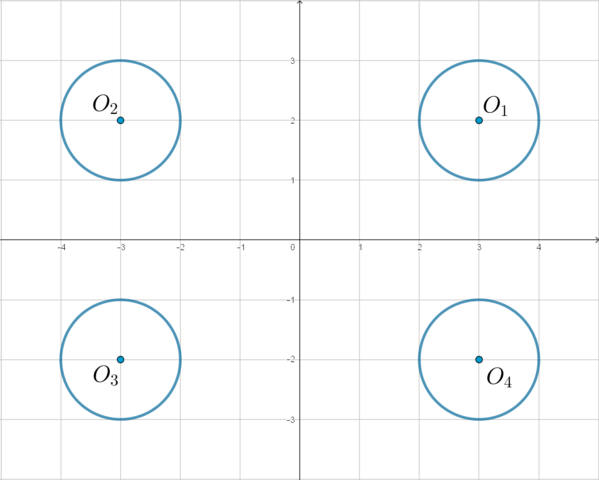
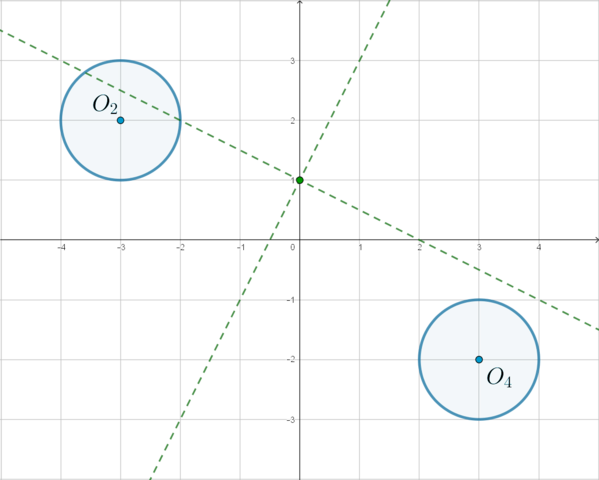
Рассмотрим первое уравнение системы. Оно задает 4 окружности. Действительно, пусть (x>0, y>0). Тогда уравнение примет вид ((x-3)^2+(y-2)^2=1) – это окружность с центром в точке (O_1(3;2)) и (r=1).
Если (x<0, y>0), то уравнение примет вид ((x+3)^2+(y-2)^2=1) – и это уравнение окружности с центром (O_2(-3;2)) и (r=1). И т.д.
Таким образом, получаем:

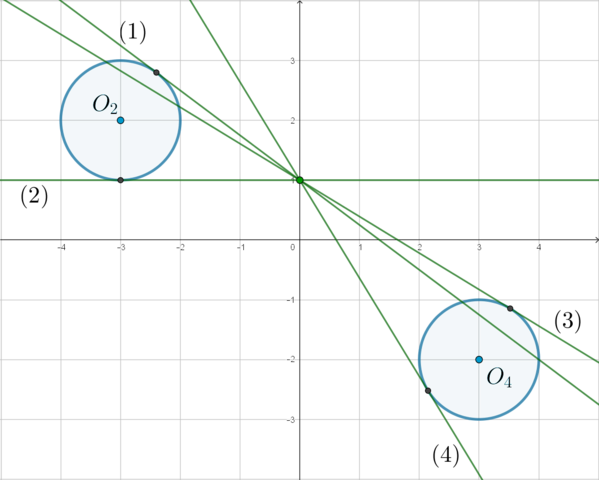
Рассмотрим третье неравенство системы (xy<0). Следовательно, либо (x>0, y<0), либо (x<0, y>0). Таким образом, учитывая это неравенство, остаются только две окружности: в (IV) и (II) четвертях. Уравнение (y=ax+1) задает прямую, у которой неизвестен угловой коэффициент, и которая проходит через точку ((0;1)):

Какие у нас могут быть случаи пересечения прямой с этими окружностями так, чтобы в итоге было ровно две точки пересечения?
а) прямая пересекает одну окружность, а вторую – нет;
б) прямая касается обеих окружностей.
Заметим, что так как окружности расположены симметрично относительно начала координат, то для того, чтобы прямая могла одновременно касаться обеих окружностей, она должна проходить через начало координат (то есть она тоже должна быть симметрична относительно начала координат). Наша прямая через начало координат не проходит. Следовательно, она не может касаться обеих окружностей сразу. Значит, случай б) невозможен. Остается только случай а).
Таким образом, нам нужно для начала рассмотреть все ситуации, когда прямая будет касаться какой-то из окружностей.

((1)) и ((2)) – случаи, когда прямая касается второй окружности (будем ее так называть, потому что у нее центр в (O_2)); ((3)) и ((4)) – случаи, когда прямая касается четвертой окружности.
Заметим, что эти случаи по возрастанию параметра (a) можно упорядочить так: ((4)rightarrow(1)rightarrow(3)rightarrow(2)).
Таким образом, нам нужны будут значения параметра, принадлежащие ((a_{4}; a_{1})) и ((a_{3}; a_{2})) (здесь (a_{i}) – значения параметра (a), которое соответствует расположению прямой в случае ((i))).
Значит, найдем (a_{1}, a_{2}, a_{3}, a_{4}).
Найдем значения (a), когда прямая (y=ax+1) касается второй окружности: [begin{cases} (x+3)^2+(y-2)^2=1\
y=ax+1end{cases}quadRightarrowquad (a^2+1)x^2+2(3-a)x+9=0] Так как прямая и окружность касаются, то есть имеют одну точку пересечения, то полученное уравнение должно иметь один корень, следовательно, его дискриминант должен быть равен нулю: [D=0quadRightarrowquad a=-dfrac34; 0] Значит, (a_2=0; a_1=-frac34).
Аналогично найдем, что (a_3=frac{-9+sqrt{17}}8), (a_4=frac{-9-sqrt{17}}8).
Следовательно, ответ: [ain left(dfrac{-9-sqrt{17}}8; -dfrac34right)cupleft(dfrac{-9+sqrt{17}}8;
0right)]

Ответ:

(ain left(frac{-9-sqrt{17}}8;
-frac34right)cupleft(frac{-9+sqrt{17}}8; 0right))

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды

Источник

Задачи с параметрами. Условия касания.

Темы для повторения:

Геометрический смысл производной

Графический метод решения задач с параметрами

Друзья, мы продолжаем тему «Задачи с параметрами». Это №18 Профильного ЕГЭ по математике. В этой статье рассказано, как в решении задач с параметрами применяется производная.

Рассмотрим следующую задачу:

При каких значениях параметра a уравнение $left|x-2right|=a{log}_2left|x-2right|$ имеет ровно 2 решения?

Поскольку логарифмы определены для положительных чисел, Это значит, что xne 2.

Сделаем замену При каждому значению соответствует два значения

Получим уравнение $t=a{log}_2t.$

В левой части уравнения — линейная функция, в правой — логарифмическая. Это функции разных типов. Пытаться справиться с таким уравнение аналитически — бесполезно. Попробуем графический способ.

Если a=0 , то t=0 и условие не выполняется. Рассмотрим по отдельности случаи и

Пусть . Нарисуем графики функций $y_1=frac{t}{a}$ и $y_2={log}_2t.$ Функция $y_2={log}_2t$ монотонно возрастает при . Обозначим Функция y_1=bt монотонно убывает при .

Докажем, что графики функций y_1=bt и $y_2={log}_2t$ имеют единственную точку пересечения при и любом

Рассмотрим функцию $z(t)={y_2-y}_1={log}_2t-bt.$ Функция z(t) является монотонно возрастающей при (как сумма монотонно возрастающих функций ${log}_2t$ и -bt ), следовательно, каждое свое значение, в том числе и значение z=0 , она принимает ровно один раз.

Уравнение ${log}_2t-bt=0$ имеет единственное решение при положительных и Значит, при всех исходное уравнение имеет ровно 2 решения. Теперь случай

$y_{}={log}_2t$

Уравнение ${log}_2t=bt$ имеет единственное решение, если прямая y=bt касается графика функции $y_{}={log}_2t.$ Мы помним, как записываются условия касания:

$left{begin{matrix}f(x)=kx+b \f$

В нашем случае

Учитывая, что $b=frac{1}{a}$ , получим:

$left{ begin{array}{c}frac{t}{a}={log}_2t \frac{1}{a}=frac{1}{tln2} end{array}Leftrightarrow left{ begin{array}{c}a=tln2 \frac{1}{ln2}={log}_2t end{array}right.right.$

${log}_2e={log}_2t,, , t=e,, , a=eln2$

Мы получили, что, t=e — точка касания. При этом a=eln2 .

Ответ:

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задачи с параметрами. Условия касания.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Автор

Сообщение

Заголовок сообщения: Определение координат первой точки касания двух окружностей

Добавлено: 15 июл 2010, 23:34

Одарённый

Зарегистрирован:
03 июл 2010, 17:38
Сообщений: 120
Cпасибо сказано: 40
Спасибо получено:
3 раз в 3 сообщениях
Очков репутации: 2

Помогите решить задачку.
Дано: радиус большой окружности R = 200; радиус малой окружности r = 50. Расстояние между осями окружностей равно 150мм.
Известно:, что большая окружность приближается к малой окружности вертикально вниз по оси Y до неизвестной точки касания А, расположенной на малой окружности.
Определить: координаты точки касания А малой окружности радиусом r с большой окружностью радиусом R.

Вложения:

1.JPG [ 24.33 Кб | Просмотров: 193 ]

Вернуться к началу

Ingener	Заголовок сообщения: Re: Определение координат первой точки касания двух окружностей Добавлено: 16 июл 2010, 10:00
	llorin писал(а): Координаты точки [math]A(x;y)[/math] находятся из подобия треугольников и т. Пифагора: [math]x=frac{r}{r+R}cdot150,~~~~y=frac{r}{r+R}cdotsqrt{(r+R)^2-150^2}[/math]. Так, что [math]A(30;40)[/math]. Здравствуйте. Опять вы очень оригинально решили эту задачку. Но всё же, для того, что бы её решить, необходимо сначала доказать, что при прямая с длиной (R+r), проведенная из центра малой окружности до центра большой окружности будет проходить через точку касания А. Вы можете аналитически по формулам привести доказательство?
Вернуться к началу

Ingener	Заголовок сообщения: Re: Определение координат первой точки касания двух окружностей Добавлено: 20 июл 2010, 12:51
	llorin писал(а): 1-ый способ: Точка касания А — центр гомотетии данных окружностей с коэффициентом [math]-frac{r}{R}[/math]. Посмотрел свойства гомотетии из раздела планиметрии. Поясните пожалуйста, что означает коэффициент гомотетии? И как вы определили, что здесь имеет место быть гомотетия.
Вернуться к началу