Как найти точку максимума функции 8ln - Исправление недочетов и поиск решений вместе с Examum.ru

Задания

Версия для печати и копирования в MS Word

Тип 11 № 131037

Найдите точку максимума функции

Решение.

Это задание ещё не решено, приводим решение прототипа.

Найдите точку максимума функции

Заметим, что Область определения функции  — открытый луч Найдем производную заданной функции:

Найдем нули производной:

Найденная точка лежит на луче Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка максимума

Ответ: −6.

Аналоги к заданию № 77489: 131075 131027 131029 … Все

Кодификатор ФИПИ/Решу ЕГЭ:

3.2.1 Монотонность функции. Промежутки возрастания и убывания;

3.2.5 Точки экстремума функции;

3.2.6 Наибольшее и наименьшее значения функции;

4.2.1 Применение производной к исследованию функций и построению графиков;

4.2.1.3* Наименьшее (наибольшее) значение функции на бесконечном промежутке.

Прототип задания

Видеокурс

Источник

Тема 11.

Исследование функций с помощью производной

Поиск точек экстремума у смешанных функций

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

исследование функций с помощью производной

Решаем задачи

Найдите точку максимума функции

Показать ответ и решение

Функция определена при всех Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем
ее производную:

1
y′ = x+-5-− 2

Найдем нули производной:

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на
каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких
промежутков:

PICT

При производная положительна, то есть функция возрастает; при производная
отрицательна, то есть функция убывает. Следовательно, является точкой максимума.

Найдите точку максимума функции

2
y =2x − 5x+lnx− 3

Показать ответ и решение

Функция определена при всех x >0 . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее
производную:

′ 1 4x2 − 5x+ 1
y = 4x − 5+ x =----x-----

Найдем нули производной:

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из
которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

PICT

При производная положительна, то есть функция возрастает; при производная отрицательна, то
есть функция убывает; при производная положительна, то есть функция возрастает. Следовательно, x =0,25 является
точкой максимума.

Найдите точку минимума функции 2
y = 2x − 5x+ lnx − 3.

Показать ответ и решение

Функция определена при всех x >0. Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее
производную:

1 4x2− 5x+ 1
y′ = 4x− 5+ x =----x-----

Найдем нули производной:

PICT

При производная положительна, то есть функция возрастает; при производная
отрицательна, то есть функция убывает; при производная положительна, то есть функция возрастает.
Следовательно, x = 1 является точкой минимума.

Найдите точку минимума функции

Показать ответ и решение

4
y′ = 4− x+-7

Найдем нули производной:

PICT

При производная отрицательна, то есть функция y =y(x) убывает; при производная
положительна, то есть функция возрастает. Следовательно, x= −6 является точкой минимума.

Найдите точку минимума функции

Показать ответ и решение

Функция определена при всех . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем
ее производную:

1
y′ = 2− x+-3

Найдем нули производной:

y′ = 0 ⇒ x + 3= 1 ⇔ x = −2,5
2

PICT

При производная отрицательна, то есть функция убывает; при производная
положительна, то есть функция возрастает. Следовательно, является точкой минимума.

Найдите точку минимума функции

Найдите точку минимума функции .

Показать ответ и решение

Обозначим .

Найдем производную функции:

′ ′ ′ ′ ′ 1 1 2x + 21
f (x) = (2x− ln(x+ 11)+ 8) = (2x) − (ln(x + 11) + (8) = 2− x-+-11-+ 0 = 2 − x+-11-=-x+-11

Легко видеть, что полученная дробь зануляется при − 21
x = 2 и не определена при .

Применим метод интервалов для определения знаков производной. Обе критические точки встречаются в нечетном
числе множителей, следовательно, знак в них будет меняться.

В точке минимума функции её производная обнуляется и меняет знак с «» на «», так как до точки
минимума функция убывала, а после — начала возрастать. Значит, — точка минимума функции

Найдите точку максимума функции 2
y = 2x − 25x +39lnx− 54.

Показать ответ и решение

Функция определена при всех x >0. Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее
производную:

39 4x2− 25x+ 39
y′ = 4x− 25+-x = -----x------

Найдем нули производной:

PICT

При производная положительна, то есть функция y =y(x) возрастает; при x∈ (3; 13)
4 производная
отрицательна, то есть функция убывает; при x ∈ (13;+∞ )
4 производная положительна, то есть функция возрастает.
Следовательно, x = 3 является точкой максимума.

Найдите точку максимума функции

2
y = 0,5x − 7x +12 lnx +8

Показать ответ и решение

12 x2− 7x+ 12
y′ = x− 7+-x = ----x-----

Найдем нули производной:

PICT

При производная положительна, то есть функция возрастает; при производная отрицательна,
то есть функция убывает; при производная положительна, то есть функция возрастает. Следовательно, x = 3
является точкой максимума.

Найдите точку максимума функции

3
y =2ln(x +4) − 8x− 19

Показать ответ и решение

Функция определена при всех x> −4 . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее
производную:

′ 6(x +4)2 6
y = (x+-4)3-− 8= x+-4 − 8

Найдем нули производной:

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из
которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

PICT

Найдите точку максимума функции

2
y = ln(x+ 4) +2x+ 7

Показать ответ и решение

′ 2(x+ 4) 2
y= (x+-4)2 +2 = x+4-+2

Найдем нули производной:

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из
которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

PICT

При производная положительна, то есть функция возрастает; при производная отрицательна, то
есть функция убывает. Следовательно, x= −5 является точкой максимума.

Найдите точку максимума функции

2
y =2x − 13x +9lnx+ 8

Показать ответ и решение

′ 9 4x2 − 13x+ 9
y = 4x− 13+ x =----x-----

Найдем нули производной:

9
y′ = 0 ⇒ 4x2− 13x +9 =0 ⇔ x= 1;4

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из
которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

PICT

При производная положительна, то есть функция y =y(x) возрастает; при x ∈(1;9)
4 производная отрицательна, то есть
функция убывает; при x∈(9;+∞ )
4 производная положительна, то есть функция возрастает. Следовательно, x =1 является точкой
максимума.

Найдите точку максимума функции

Показать ответ и решение

Функция определена при всех x> −7 . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее
производную:

′ 8
y = x+-7 − 8

Найдем нули производной:

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из
которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

PICT

При производная положительна, то есть функция возрастает; при производная отрицательна, то
есть функция убывает. Следовательно, x= −6 является точкой максимума.

Найдите точку максимума функции

5
y = ln(x+5) − 5x

Показать ответ и решение

Функция определена при всех x> −5 . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее
производную:

′ 5(x +5)4 5
y = (x+-5)5-− 5= x+-5 − 5

Найдем нули производной:

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из
которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

PICT

При производная положительна, то есть функция возрастает; при производная отрицательна, то
есть функция убывает. Следовательно, x= −4 является точкой максимума.

Найдите точку минимума функции

3
y = 3x − ln(x +3)

Показать ответ и решение

Функция определена при всех x> −3 . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее
производную:

′ 3(x +3)2 3
y = 3− (x+-3)3-= 3− x+-3

Найдем нули производной:

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из
которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

PICT

При производная отрицательна, то есть функция y =y(x) убывает; при производная положительна, то есть
функция возрастает. Следовательно, является точкой минимума.

Найдите точку минимума функции

2 6−x
y = (x − 8x+ 8)⋅e

Показать ответ и решение

′ 6− x 2 6−x 6−x 2
y =(2x− 8)e − (x − 8x+8)e =− e (x − 10x+ 16)

Найдем нули производной:

′ 2
y = 0 ⇒ x − 10x+ 16= 0 ⇔ x= 2;8

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из
которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

PICT

При производная отрицательна, то есть функция убывает; при производная положительна, то есть
функция возрастает; при производная отрицательна, то есть функция убывает. Следовательно, x =2 является точкой
минимума.

Найдите точку минимума функции

2 2−x
y = (x +3) ⋅e

Показать ответ и решение

′ 2−x 2 2−x 2−x 2
y = 2(x +3)e − (x+ 3) e =− e (x +4x +3)

Найдем нули производной:

′ 2
y = 0 ⇒ x + 4x+3 =0 ⇔ x= −3;−1

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из
которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

PICT

Найдите точку максимума функции

2 4−x
y = (x +6) ⋅e

Показать ответ и решение

′ 4−x 2 4− x 4−x 2
y= 2(x+6)e − (x+ 6)e = −e (x + 10x +24)

Найдем нули производной:

′ 2
y = 0 ⇒ x + 10x+24 =0 ⇔ x= −6;−4

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из
которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

PICT

Найдите точку минимума функции

2 x−5
y = (x − 2) ⋅e

Показать ответ и решение

′ x−5 2 x− 5 x−5 2
y = 2(x − 2)e + (x− 2) e =e (x − 2x)

Найдем нули производной:

′ 2
y= 0 ⇒ x − 2x =0 ⇔ x= 0;2

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из
которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

PICT

При производная положительна, то есть функция возрастает; при производная отрицательна, то есть
функция убывает; при производная положительна, то есть функция возрастает. Следовательно, x= 2 является точкой
минимума.

Найдите точку максимума функции

2 x−6
y = (x − 2) ⋅e

Показать ответ и решение

′ x−6 2 x− 6 x−6 2
y = 2(x − 2)e + (x− 2) e =e (x − 2x)

Найдем нули производной:

′ 2
y= 0 ⇒ x − 2x =0 ⇔ x= 0;2

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из
которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

PICT

При производная положительна, то есть функция возрастает; при производная отрицательна, то есть
функция убывает; при производная положительна, то есть функция возрастает. Следовательно, x= 0 является точкой
максимума.

Источник

12. Исследование функций с помощью производной

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Поиск точек экстремума у сложных функций

(blacktriangleright) Сложная функция (композиция двух функций) — это функция (f=f(x)), представимая в виде (f=f(t(x))), где (t=t(x)) – функция, являющаяся “новой переменной” для функции (f).

То есть в такой функции можно ввести новую переменную (t) так, что функция полностью будет зависеть от этой новой переменной.

(blacktriangleright) Производная такой функции ищется по правилу: [{Large{f'(x)=f'(t)cdot t'(x)}}]

Примеры:

(1)) Функция (f(x)=cos {(x^2+1)}). Если сделать замену (t(x)=x^2+1), то функция примет вид (f(t)=cos t).
Найдем (f'(t)=(cos t)’=-sin t=(text{переход к переменной
}x)=-sin
{(x^2+1)})
Найдем (t'(x)=(x^2+1)’=2x)
Значит, (f'(x)=-2xcdot sin{(x^2+1)})

(2)) Функция (f(x)=x^3 +x^2). Для этой функции не существует никакой замены, кроме тождественной ((t(x)=x)). Значит она – не сложная.
Ее производную можно найти обычным способом, т.к. она элементарная:
(f'(x)=3x^2+2x)

(3)) Функция (f(x)=sin x^2 + x). Для этой функции не существует никакой замены, кроме тождественной ((t(x)=x)).
Но обычными способами вычислить ее производную не удастся. Заметим, что эта функция представлена в виде суммы двух, причем одна из них сложная ((g(x)=sin x^2)), а другая – элементарная ((h(x)=x)).
Т.к. мы знаем, что (f’=g’+h’), то найдем в отдельности производные функций (g) и (h).

Тогда (f'(x)=2xcdot cos x^2 + 1)

(blacktriangleright) Для того, чтобы найти точки экстремума, необходимо схематично изобразить график функции.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания ((f’>0)) и убывания ((f'<0)) функции, критические точки (где (f’=0) или (f’) не существует).
[begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{1} & c & 0\&&\
textbf{2} & x^a & acdot x^{a-1}\&&\
textbf{3} & ln x & dfrac1x\&&\
textbf{4} & log_ax & dfrac1{xcdot ln a}\&&\
textbf{5} & e^x & e^x\&&\
textbf{6} & a^x & a^xcdot ln a\&&\
textbf{7} & sin x & cos x\&&\
textbf{8} & cos x & -sin x\[1ex]
hline
end{array} quad quad quad quad
begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{9} & mathrm{tg}, x & dfrac1{cos^2 x}\&&\
textbf{10} & mathrm{ctg}, x & -,dfrac1{sin^2 x}\&&\
textbf{11} & arcsin x & dfrac1{sqrt{1-x^2}}\&&\
textbf{12} & arccos x & -,dfrac1{sqrt{1-x^2}}\&&\
textbf{13} & mathrm{arctg}, x & dfrac1{1+x^2}\&&\
textbf{14} & mathrm{arcctg}, x & -,dfrac1{1+x^2}\[0.5ex]
hline
end{array}]

Задание
1

#2363

Уровень задания: Равен ЕГЭ

Найдите точку минимума функции (y = e^{x^2 + 1}).

ОДЗ: (x) – произвольный.

1) [y’ = e^{x^2 + 1}cdot 2x = 2xe^{x^2 + 1}]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [2xe^{x^2 + 1} = 0qquadLeftrightarrowqquad x = 0,.] Производная существует при любом (x).

2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика:

Таким образом, (x = 0) – точка минимума функции (y).

Ответ: 0

Задание
2

#2364

Уровень задания: Равен ЕГЭ

Найдите точку максимума функции (y = e^{-x^2 + 2x}).

ОДЗ: (x) – произвольный.

1) [y’ = e^{-x^2 + 2x}cdot (-2x + 2) = -2(x — 1)e^{-x^2 + 2x}]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [-2(x — 1)e^{-x^2 + 2x} = 0qquadLeftrightarrowqquad x = 1,.] Производная существует при любом (x).

2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика:

Таким образом, (x = 1) – точка максимума функции (y).

Ответ: 1

Задание
3

#887

Уровень задания: Равен ЕГЭ

Найдите точку минимума функции

(y = e^{x^2 — 2016x + 2017}).

1) [y’ = e^{x^2 — 2016x + 2017}cdot(2x — 2016).]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [e^{x^2 — 2016x + 2017}cdot(2x — 2016) = 0qquadLeftrightarrowqquad x — 2016 = 0] (так как (e^t > 0) при любом (t)), откуда находим (x = 1008). Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.

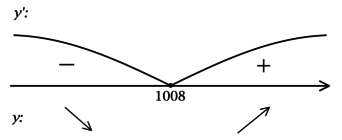
2) Найдём промежутки знакопостоянства (y’):

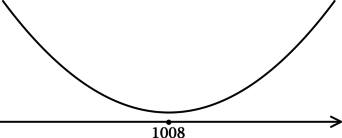
3) Эскиз графика (y):

Таким образом, (x = 1008) – точка минимума функции (y).

Ответ: 1008

Задание
4

#885

Уровень задания: Равен ЕГЭ

Найдите точку минимума функции

(y = log_{7}(x^2 + 16x + 100)).

ОДЗ: (x^2 + 16x + 100 > 0). Решим на ОДЗ:

1) [y’ = dfrac{1}{ln 7}cdotdfrac{2x + 16}{x^2 + 16x + 100}.]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{1}{ln 7}cdotdfrac{2x + 16}{x^2 + 16x + 100} = 0qquadLeftrightarrowqquad 2x + 16 = 0] – на ОДЗ, откуда находим (x = -8). Так как (x^2 + 16x + 100 = x^2 + 16x + 64 + 36 = (x+8)^2 + 36 > 0), то производная определена для любого (x). Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.

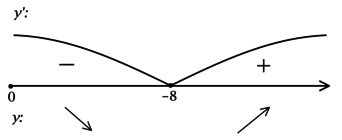
2) Найдём промежутки знакопостоянства (y’):

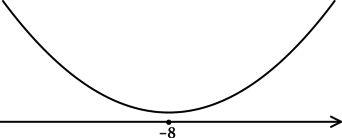
3) Эскиз графика (y):

Таким образом, (x = -8) – точка минимума функции (y).

Ответ: -8

Задание
5

#886

Уровень задания: Равен ЕГЭ

Найдите точку минимума функции

(y = log_{2016}(x^2 — 10x + 201)).

ОДЗ: (x^2 — 10x + 201 > 0). Решим на ОДЗ:

1) [y’ = dfrac{1}{ln 2016}cdotdfrac{2x — 10}{x^2 — 10x + 201}.]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{1}{ln 2016}cdotdfrac{2x — 10}{x^2 — 10x + 201} = 0qquadLeftrightarrowqquad 2x — 10 = 0] – на ОДЗ, откуда находим (x = 5). Так как (x^2 — 10x + 201 = x^2 — 10x + 25 + 176 = (x-5)^2 + 176 > 0), то производная определена для любого (x). Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.

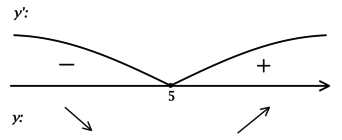
2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика (y):

Таким образом, (x = 5) – точка минимума функции (y).

Ответ: 5

Задание
6

#888

Уровень задания: Равен ЕГЭ

Найдите точку минимума функции

(y = sqrt{x^2 — 12x + 40}).

ОДЗ: (x^2 — 12x + 40 geq 0). Решим на ОДЗ:

1) [y’ = dfrac{2x — 12}{2sqrt{x^2 — 12x + 40}} = dfrac{x — 6}{sqrt{x^2 — 12x + 40}}.]

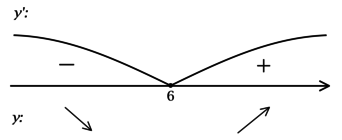
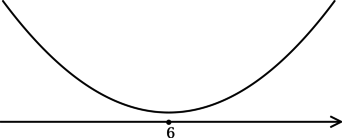
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{x — 6}{sqrt{x^2 — 12x + 40}} = 0qquadLeftrightarrowqquad x — 6 = 0] – на ОДЗ, откуда находим (x = 6). Так как (x^2 — 12x + 40 = x^2 — 12x + 36 + 4 = (x-6)^2 + 4 > 0), то производная функции (y) определена при любом (x). Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика (y):

Таким образом, (x = 6) – точка минимума функции (y).

Ответ: 6

Задание
7

#889

Уровень задания: Равен ЕГЭ

Найдите точку максимума функции

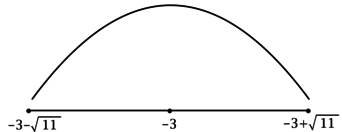
(y = sqrt{-x^2 + 2 — 6x}).

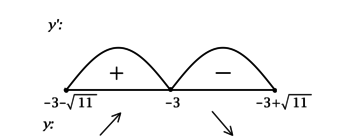
ОДЗ: (-x^2 + 2 — 6x geq 0), что равносильно (x^2 + 6x — 2leq 0), откуда находим (-3-sqrt{11} leq x leq -3 + sqrt{11}). Решим на ОДЗ:

1) [y’ = dfrac{-2x — 6}{2sqrt{-x^2 + 2 — 6x}} = -dfrac{x + 3}{sqrt{-x^2 + 2 — 6x}}.]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad -dfrac{x + 3}{sqrt{-x^2 + 2 — 6x}} = 0qquadLeftrightarrowqquad x + 3 = 0] – на ОДЗ, откуда находим (x = -3). Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’) на ОДЗ:

3) Эскиз графика (y):

Таким образом, (x = -3) – точка максимума функции (y).

Ответ: -3

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды

Источник

Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.

Вот какие типы задач могут встретиться в этом задании:

Нахождение точек максимума и минимума функций

Исследование сложных функций

Нахождение наибольших и наименьших значений функций на отрезке

Нахождение точек максимума и минимума функций

1. Найдите точку максимума функции $displaystyle y=-{{x^2+289}over{x}}.$

Найдем производную функции.

Приравняем производную к нулю. Получим:

$x^2=289Leftrightarrow left[ begin{array}{c} x=17, hfill \ x=-17. end{array} right.$

Исследуем знаки производной.

В точке x = 17 производная меняет знак с «плюса» на «минус». Значит, x= 17 — точка максимума функции y(x).

Ответ: 17.

2. Найдите точку минимума функции

Найдем производную функции.

Приравняем производную к нулю.

$4x-5+{{1}over{x}}=0Leftrightarrow 4x^2-5x+1=0Leftrightarrow left[ begin{array}{c} x=1, \ x={{1}over{4}}. end{array} right.$

Определим знаки производной.

В точке x = 1 производная меняет знак с «минуса» на «плюс». Значит, x= 1 — точка минимума функции y(x).

Ответ: 1.

Исследование сложных функций

3. Найдите точку максимума функции $y=2^{5-8x-x^2}.$

Перед нами сложная функция $y=2^{5-8x-x^2}.$ Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.

Так как функция y=2^t монотонно возрастает, точка максимума функции $y=2^{5-8x-x^2}$ будет при том же x_0 , что и точка максимума функции А ее найти легко.

$t^{$

$t^{$ при x=-4 . В точке x = -4 производная ${{ t}}^{{$ меняет знак с «плюса» на «минус». Значит, x= - 4 — точка максимума функции .

Заметим, что точку максимума функции можно найти и без производной.

Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при $x=-frac{8}{2}=-4.$

Ответ: — 4.

4. Найдите абсциссу точки максимума функции $y=sqrt{4-4x-x^2}.$

Напомним, что абсцисса — это координата по

Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.

Так как функция монотонно возрастает, точка максимума функции $y=sqrt{4-4x-x^2}$ является и точкой максимума функции

Это вершина квадратичной параболы $tleft(xright)=4-4x-x^2;x_0=frac{-4}{2}=-2.$

Нахождение наибольших и наименьших значений функций на отрезке

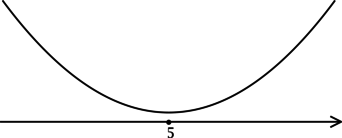
5. Найдите наибольшее значение функции на отрезке

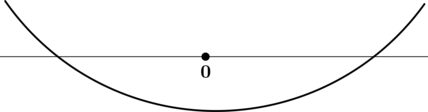
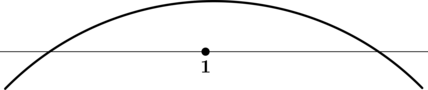
Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.

Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.

${3x}^2+4x-4=0;$

$D=64;x=frac{-4pm 8}{6};x_1=frac{2}{3},x_2=-2.$

Найдем знаки производной.

В точке x = - 2 производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции y(x) . Поскольку при функция y(x) убывает, $y_{max}left(xright)=yleft(-2right)=12.$ В этой задаче значение функции на концах отрезка искать не нужно.

Ответ: 12.

6. Найдите наименьшее значение функции $y={4x}^2-10x+2lnx-5$ на отрезке

Найдем производную функции $y={4x}^2-10x+2lnx-5$ и приравняем ее к нулю.

при $x_1=1,x_2=frac{1}{4}.$

Найдем знаки производной.

Точка x_1=1 — точка минимума функции . Точка $x_2=frac{1}{4}$ не лежит на отрезке Поэтому

и Значит, наименьшее значение функции на отрезке достигается при x=1. Найдем это значение.

$y_{min}left(xright)=yleft(1right)=4-10-5=-11.$

Ответ: -11.

7. Найдите наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

Иногда перед тем, как взять производную, формулу функции полезно упростить.

Мы применили формулу для логарифма произведения. при $x=frac{1}{9}.$

Если то Если , то

Значит, $x=frac{1}{9}$ — точка минимума функции y(x) . В этой точке и достигается наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

$y_{min}left(xright)=yleft(frac{1}{2}right)=1+3=4.$

Ответ: 4.

8. Найдите наибольшее значение функции на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

Найдем производную функции

Приравняем производную к нулю: $14-frac{7}{{cos}^2x}=0.$

${cos}^2x=frac{1}{2}.$

${cos}^2x=pm frac{1}{sqrt{2}}=pm frac{sqrt{2}}{2}$ . Поскольку $xin left[-frac{pi }{3};frac{pi }{3}right], y$ если $x=pm frac{pi }{4}.$

Найдем знаки производной на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

При $x=frac{pi }{4}$ знак производной меняется с «плюса» на «минус». Значит, $x=frac{pi }{4}$ — точка максимума функции y(x).

Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при $x=-frac{pi }{3}$ и $x =frac{pi }{4}.$

$yleft(frac{pi }{4}right)=-7+11=4;$

Мы нашли, что $y_{max}left(xright)=yleft(frac{pi }{4}right)=-7+11=4.$

Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при $-frac{pi }{3}$ не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.

Ответ: 4.

9. Найдите наименьшее значение функции $y=e^{2x}-{8e}^x+9$ на отрезке [0;2].

Снова сложная функция. Запишем полезные формулы:

${{(e}^{-x})}^{$

${left(e^{cx}right)}^{$

${(e}^{x+a})$

Найдем производную функции $y=e^{2x}-{8e}^x+9.$

если e^x=4. Тогда x=ln4.

При x=ln4 знак производной меняется с «минуса» на «плюс». Значит, x=ln4 — точка минимума функции y(x).

Ответ: -7.

10. Найдите наибольшее значение функции на отрезке $left[0;frac{pi }{2}.right]$

Как всегда, возьмем производную функции и приравняем ее к нулю.

$sinx=frac{sqrt{3}}{2}.$

По условию, $xin left[0;frac{pi }{2}right]$ . На этом отрезке условие $sinx=frac{sqrt{3}}{2}$ выполняется только для $x=frac{pi }{3}.$ Найдем знаки производной слева и справа от точки $x=frac{pi }{3}.$

В точке $x_0=frac{pi }{3}$ производная функции меняет знак с «плюса» на «минус». Значит, точка $x_0=frac{pi }{3}$ — точка максимума функции y(x) . Других точек экстремума на отрезке $left[0;frac{pi }{2}right]$ функция не имеет, и наибольшее значение функции на отрезке $left[{ 0};frac{pi }{{ 2}}right]$ достигается при ${ x=}frac{pi }{{ 3}}.$

$y_{max}left(xright)=yleft(frac{pi }{3}right)=12.$

Ответ: 12.

11.Найдите наименьшее значение функции на отрезке $left[0;frac{pi }{2}right].$

Найдем производную функции и приравняем ее к нулю. — нет решений.

Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.

Поскольку , получим, что для всех , и функция монотонно возрастает при $xin left[0;frac{pi }{2}right].$

Значит, наименьшее свое значение функция принимает в левом конце отрезка $left[{ 0};frac{pi }{{ 2}}right]$ , то есть при x=0.

$y_{min}left(xright)=yleft(0right)=6.$

Ответ: 6

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 11 Профильного ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Здравствуйте, Дорогие друзья! Продолжаем рассматривать задания связанные с исследованием функций. Рекомендую повторить теорию, необходимую для решения задач на нахождение максимального (минимального) значения функции и на нахождение точек максимума (минимума) функции.

Задачи с логарифмами на нахождение наибольшего (наименьшего) значения функции мы уже рассмотрели. В этой статье рассмотрим три задачи, в которых стоит вопрос нахождения точек максимума (минимума) функций, при чём в заданной функции присутствует натуральный логарифм.

Теоретический момент:

По определению логарифма – выражение стоящее под знаком логарифма должно быть больше нуля. *Это обязательно нужно учитывать не только в данных задачах, но и при решении уравнений и неравенств содержащих логарифм.

Алгоритм нахождения точек максимума (минимума) функции:

1. Вычисляем производную функции.

2. Приравниваем её к нулю, решаем уравнение.

3. Полученные корни отмечаем на числовой прямой. *Также на ней отмечаем точки, в которых производная не существует. Получим интервалы, на которых функция возрастает или убывает.

4. Определяем знаки производной на этих интервалах (подставляя произвольные значения из них в производную).

5. Делаем вывод.

Найдите точку максимума функции у = ln (х–11)–5х+2

Сразу запишем, что х–11>0 (по определению логарифма), то есть х > 11.

Рассматривать функцию будем на интервале (11;∞).

Найдём производную заданной функции:

Найдем нули производной:

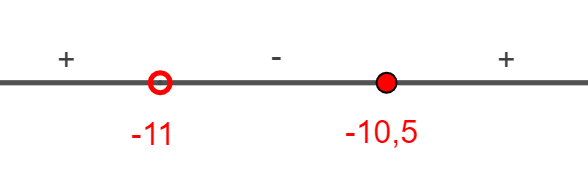
Точка х = 11 не входит в область определения функции и в ней производная не существует. Отмечаем на числовой оси две точки 11 и 11,2. Определим знаки производной функции, подставляя произвольные значения из интервалов (11;11,2) и (11,2;+∞) в найденную производную, и изобразим на рисунке поведение функции:

Таким образом, в точке х=11,2 производная функции меняет знак с положительного на отрицательный, значит это искомая точка максимума.

Ответ: 11,2

Решите самостоятельно:

Найдите точку максимума функции у=ln (х+5)–2х+9.

Посмотреть решение

Найдите точку минимума функции у=4х– ln (х+5)+8

Сразу запишем, что х+5>0 (по свойству логарифма), то есть х>–5.

Рассматривать функцию будем на интервале (– 5;+∞).

Найдём производную заданной функции:

Найдем нули производной:

Точка х = –5 не входит в область определения функции и в ней производная не существует. Отмечаем на числовой оси две точки –5 и –4,75. Определим знаки производной функции, подставляя произвольные значения из интервалов (–5;–4,75) и (–4,75;+∞) в найденную производную, и изобразим на рисунке поведение функции:

Таким образом, в точке х= –4,75 производная функции меняет знак с отрицательного на положительный, значит это искомая точка минимума.

Ответ: – 4,75

Решите самостоятельно:

Найдите точку минимума функции у=2х–ln (х+3)+7.

Посмотреть решение

Найдите точку максимума функции у = х²–34х+140lnх–10

По свойству логарифма выражение, стоящее под его знаком больше нуля, то есть х > 0.

Функцию будем рассматривать на интервале (0; +∞).

Найдём производную заданной функции:

Найдем нули производной:

Решая квадратное уравнение, получим: D = 9 х₁ = 10 х₂ = 7.

Точка х = 0 не входит в область определения функции и в ней производная не существует. Отмечаем на числовой оси три точки 0, 7 и 10.

Ось ох разбивается на интервалы: (0;7), (7;10), (10; +∞).

Определим знаки производной функции, подставляя произвольные значения из полученных интервалов в найденную производную, и изобразим на рисунке поведение функции:

Таким образом, в точке х = 7 производная функции меняет знак с положительного на отрицательный, значит это искомая точка максимума.

Ответ: 7

Решите самостоятельно:

Найдите точку максимума функции у = 2х² –13х+9lnх+8

Посмотреть решение

В данной рубрике продолжим рассматривать задачи, не пропустите!

На этом всё. Успехов вам!

С уважением, Александр Крутицких

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник