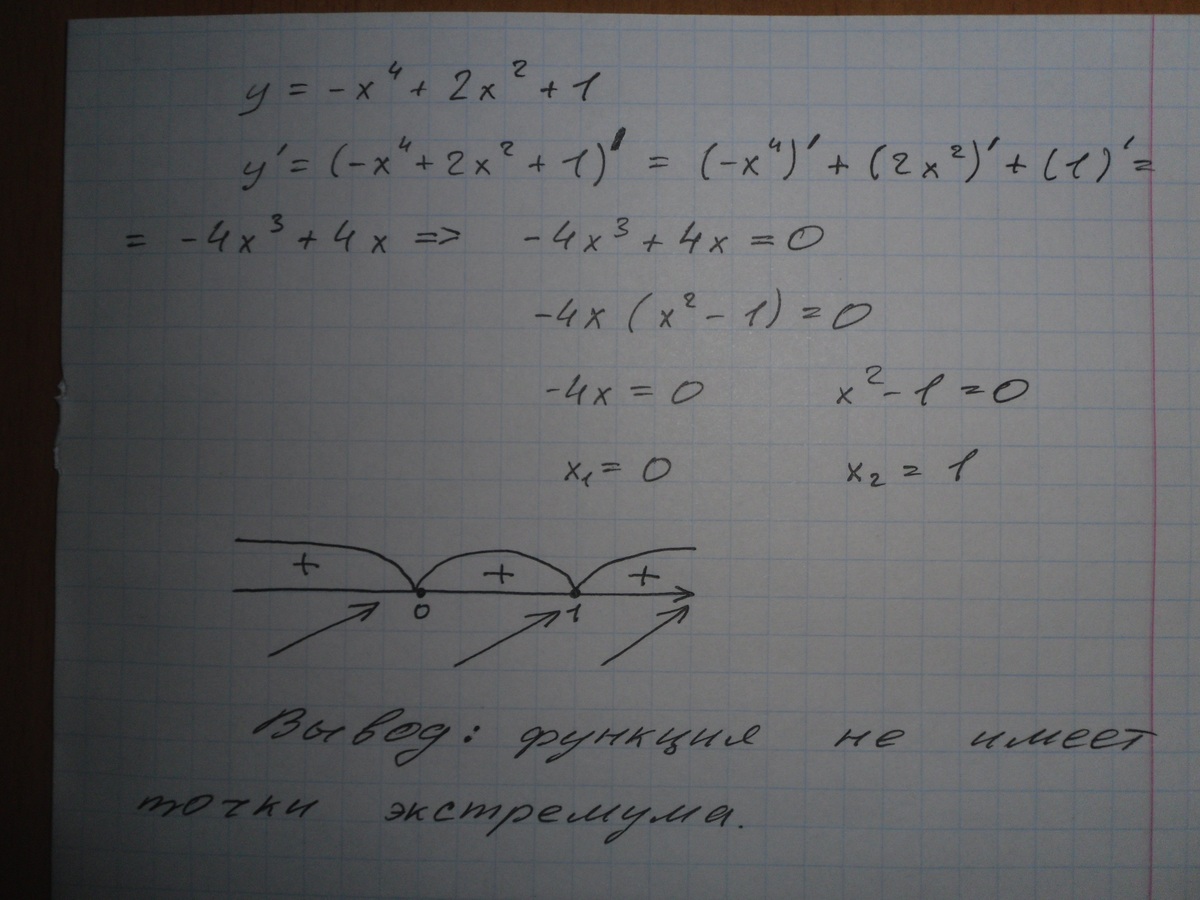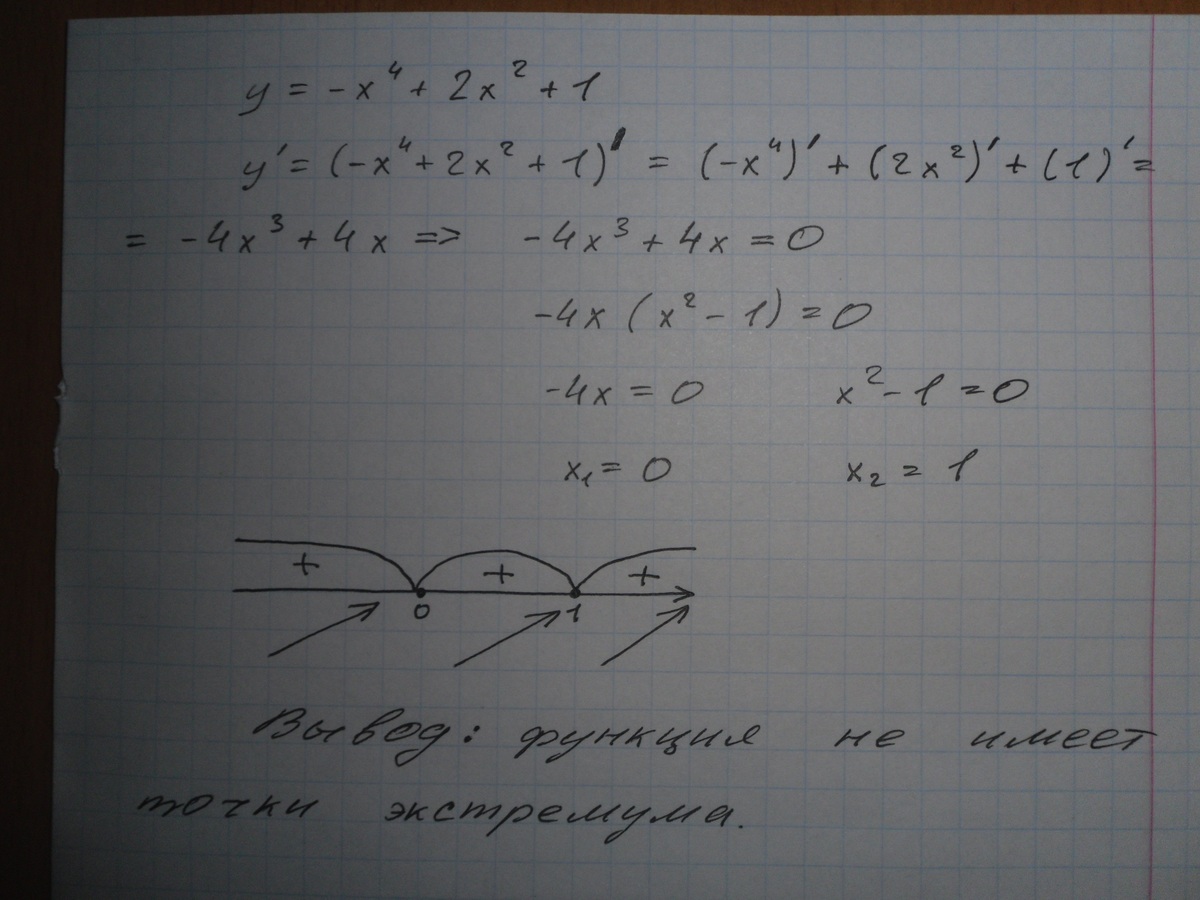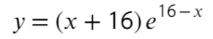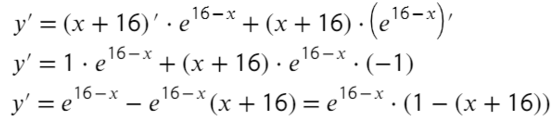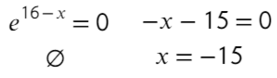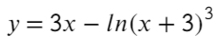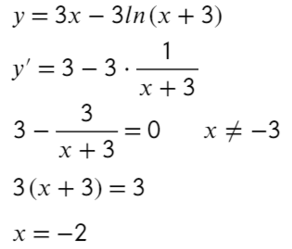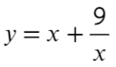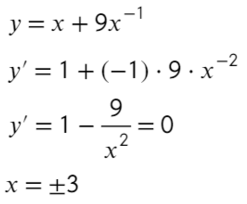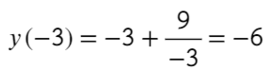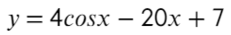Как найти точки минимума и максимума функции
Содержание:
-
Минимум и максимум функции
- Точка минимума, минимум функции
- Точка максимума, максимум функции
- Исследование функций на экстремумы
- Примеры задач
Минимум и максимум функции
Минимумом и максимумом функции, другими словами экстремумами, называют точки, в которых функция меняет характер монотонности (с возрастания на убывание и наоборот). Важно понимать, что экстремумы это не максимальные и минимальные значения функции. Обозначаются следующим образом:
- (y_{min}, y_{max}) — минимум, максимум функции или экстремумы;
- (x_{min}, x_{max}) — точки минимума, максимума функции;
- (y_{наиб}, y_{наим}) — наибольшее (максимальное), наименьшее (минимальное) значение функции.
Точка минимума, минимум функции
Точка минимума — такая точка (x_0), если у неё существует окрестность, для всех точек которой выполняется неравенство (f(x)geq f(x_0))
Минимум функции — значение функции в точке минимума (x_0)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Простыми словами, точка минимума — это та, где убывание функции меняется на возрастание.
Точка максимума, максимум функции
Точка максимума — такая точка (x_0), если у неё существует окрестность, для всех точек которой выполняется неравенство (f(x)leq f(x_0))
Максимум функции — значение функции в точке максимума (x_0)
Простыми словами, точка максимума — это та, где возрастание функции меняется на убывание.
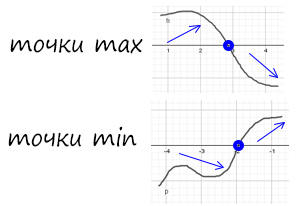
Точки максимума и минимума на графике:
Исследование функций на экстремумы
Теорема. Если функция f(x) имеет экстремум в точке (x=x_0,) то в ней производная либо равна 0, либо не существует.
Алгоритм нахождения экстремумов с помощью производной:
-
Найти область определения функции — D(y).
-
Определить производную — f ‘(x).
-
Определить стационарные точки y = f(x), т.е. те, которые принадлежат D(y), f ‘(x) в них обращается в ноль, отыскать критические точки, в которых производной не существует (пример: (f^,(x)=frac1{2sqrt x}), производной не существует при x = 0).
-
Исследовать характер изменения функции f (x) и знак f ‘(x) в промежутках, на которые найденные критические точки делят область определения (при отрицательном знаке производной функция убывает, при положительном — возрастает).
-
Относительно каждой критической точки определить, является ли она точкой максимума, минимума (возрастание меняется на убывание — точка максимума, убывание на возрастание — минимума) или не является точкой экстремума (то есть, меняется ли знак производной при переходе через исследуемую точку).
-
Вычислить значения функции в точках экстремума.
Примеры задач
Задача 1
Исследовать на экстремумы функцию (f(x)=x^3-3x^2.)
Решение задачи по алгоритму:
1) (D(y): xin(-infty;+infty)), т.е. x — любое число.
2) Производная: (f'(x)=3x^2-6x) .
3) Из пункта 1 следует, что критических точек нет. Найдем стационарные:
Приравниваем f ‘(x) к 0, решаем квадратное уравнение (3x^2-6x=0), получаем (x_1=0),(;x_2=2.)
4) Отметим на горизонтальной оси координат точки 0 и 2. Подставим любое x из интервала ((-infty;0)) в f'(x), например, пусть x = -1, тогда (f'(x)=3{(-1)}^2-6(-1)=3+6=9). Получаем f ‘(x)>0, значит на исследуемом интервале f(x) возрастает. Аналогично рассмотрим оставшиеся интервалы. Итого, на отрезке (0;2) производная отрицательна, функция убывает, а на интервале ((2;+infty)) производная положительна, возрастает. Из этого следует, что x=0 — точка максимума, а x=2 — минимума.
5) Найдем значение экстремумов функции.
(f(0)=0-3times0=0)
(f(2)=2^3-3times2^2=8-12=-4)
Ответ: (x_{min}=2,;y_{min}=-4;;x_{max}=0,;y_{max}=0) или (0;0) — минимум функции, (2;-4) — максимум.
Задача 2
Найти промежутки монотонности функции (f(x)=frac x{x^2-4}).
1) (D(y): xinmathbb{R},;)кроме(;pm2)
2) (f'(x)=frac{1(x^2-4)-xtimes2x}{{(x^2-4)}^2}=-frac{x^2+4}{{(x^2-4)}^2})
3) Итак, как выяснилось в пункте 1, критические точки 2 и -2. Если мы приравняем f ‘(x) к 0, чтобы найти стационарные точки, то увидим, что уравнение не будет иметь корней. Значит, стационарных точек нет. Из этого следует, что функция монотонна на всей области определения. Проверим, возрастает она или убывает. Для этого решаем неравенство (-frac{x^2+4}{{(x^2-4)}^2}leq0) и получим, что неравенство верно при любом x, значит функция убывает.
Не забываем, что в ответе, указывая промежуток, обязательно нужно исключить критические точки -2 и 2 т.к. в них функция не определена.
Ответ: f(x) убывает на промежутке ((-infty;-2)cup(-2;2)cup(2;+infty)).
Задача 3
Докажите, что функция (f(x)=x^5+2x^3-4) возрастает на всех числовой прямой.
1) (D(y): xinmathbb{R}), значит критических точек нет.
2) (f'(x)=5x^4+6x)
3) Приравняем f'(x) к 0 и найдем корень: x = 0. Отметим 0 на числовой прямой и определим знак производной на промежутках ((-infty;0)) и ((0;+infty)). Получим, что производная положительна на обоих промежутках, следовательно функция возрастает на всей числовой прямой.
Утверждение доказано
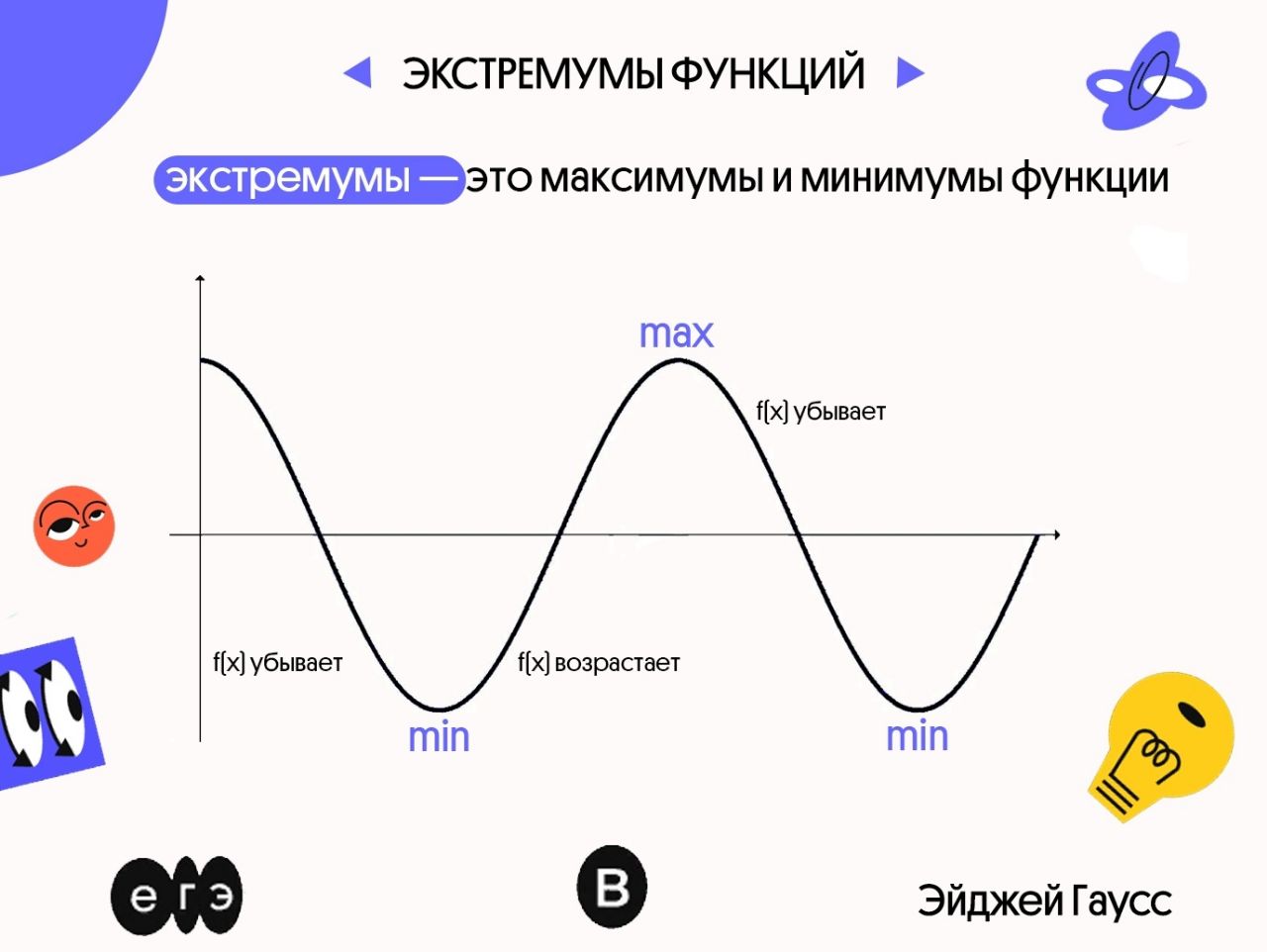
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).


Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.
(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.
(- 9): функция возрастает, а потом убывает – максимум.
(-7): минимум.
(3): максимум.
Все вышесказанное можно обобщить следующими выводами:
— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции (f'(x)).
- Найдите корни уравнения (f'(x)=0).
- Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
— если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
— если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
— если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:
(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является (-2).
Ответ. (-2).
Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов
Скачать статью
Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.
Вот какие типы задач могут встретиться в этом задании:
Нахождение точек максимума и минимума функций
Исследование сложных функций
Нахождение наибольших и наименьших значений функций на отрезке
Нахождение точек максимума и минимума функций
1. Найдите точку максимума функции
Найдем производную функции.
Приравняем производную к нулю. Получим:
Исследуем знаки производной.
В точке производная
меняет знак с «плюса» на «минус». Значит,
— точка максимума функции
Ответ: 17.
2. Найдите точку минимума функции
Найдем производную функции.
Приравняем производную к нулю.
Определим знаки производной.
В точке производная
меняет знак с «минуса» на «плюс». Значит,
— точка минимума функции
Ответ: 1.
Исследование сложных функций
3. Найдите точку максимума функции
Перед нами сложная функция Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.
Так как функция монотонно возрастает, точка максимума функции
будет при том же
, что и точка максимума функции
А ее найти легко.
при
. В точке
производная
меняет знак с «плюса» на «минус». Значит,
— точка максимума функции
.
Заметим, что точку максимума функции можно найти и без производной.
Графиком функции является парабола ветвями вниз, и наибольшее значение
достигается в вершине параболы, то есть при
Ответ: — 4.
4. Найдите абсциссу точки максимума функции
Напомним, что абсцисса — это координата по
Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.
Так как функция монотонно возрастает, точка максимума функции
является и точкой максимума функции
Это вершина квадратичной параболы
Нахождение наибольших и наименьших значений функций на отрезке
5. Найдите наибольшее значение функции на отрезке
Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.
Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.
Найдем знаки производной.
В точке производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции
. Поскольку при
функция
убывает,
В этой задаче значение функции на концах отрезка искать не нужно.
Ответ: 12.
6. Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю.
при
Найдем знаки производной.
Точка — точка минимума функции
. Точка
не лежит на отрезке
Поэтому
и
Значит, наименьшее значение функции на отрезке
достигается при
Найдем это значение.
Ответ: -11.
7. Найдите наименьшее значение функции на отрезке
Иногда перед тем, как взять производную, формулу функции полезно упростить.
Мы применили формулу для логарифма произведения. при
Если то
Если
, то
Значит, — точка минимума функции
. В этой точке и достигается наименьшее значение функции на отрезке
Ответ: 4.
8. Найдите наибольшее значение функции на отрезке
Найдем производную функции
Приравняем производную к нулю:
. Поскольку
если
Найдем знаки производной на отрезке
При знак производной меняется с «плюса» на «минус». Значит,
— точка максимума функции
Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при и
Мы нашли, что
Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.
Ответ: 4.
9. Найдите наименьшее значение функции на отрезке [0;2].
Снова сложная функция. Запишем полезные формулы:
Найдем производную функции
если
Тогда
При
знак производной меняется с «минуса» на «плюс». Значит,
— точка минимума функции
Ответ: -7.
10. Найдите наибольшее значение функции на отрезке
Как всегда, возьмем производную функции и приравняем ее к нулю.
По условию, . На этом отрезке условие
выполняется только для
Найдем знаки производной слева и справа от точки
В точке производная функции меняет знак с «плюса» на «минус». Значит, точка
— точка максимума функции
. Других точек экстремума на отрезке
функция не имеет, и наибольшее значение функции
на отрезке
достигается при
Ответ: 12.
11.Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю. — нет решений.
Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.
Поскольку , получим, что
для всех
, и функция
монотонно возрастает при
Значит, наименьшее свое значение функция принимает в левом конце отрезка , то есть при
Ответ: 6
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 11 Профильного ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Что будем изучать:
1. Введение.
2. Точки минимума и максимума.
3. Экстремум функции.
4. Как вычислять экстремумы?
5. Примеры.
Введение в экстремумы функций
Ребята, давайте посмотрим на график некоторой функции:
Заметит, что поведение нашей функции y=f (x) во многом определяется двумя точками x1 и x2. Давайте внимательно посмотрим на график функции в этих точках и около них.
До точки x2 функция возрастает, в точке x2 происходит перегиб, и сразу после этой точки функция убывает до точки x1. В точке x1
функция опять перегибается, и после этого — опять возрастает.
Точки x1 и x2 пока так и будем называть точками перегиба. Давайте проведем касательные в этих точках:
Касательные в наших точках параллельны оси абсцисс, а значит, угловой коэффициент касательной равен нулю. Это значит, что и производная нашей функции в этих точках равна нулю.
Посмотрим на график вот такой функции:
Касательные в точках x2 и x1 провести невозможно. Значит, производной в этих точках не существует. Теперь посмотрим опять на наши точки на двух графиках. Точка x2 — это точка, в которой функция достигает наибольшего значения в некоторой области (рядом с точкой x2). Точка x1 — это точка, в
которой функция достигает своего наименьшего значения в некоторой области (рядом с точкой x1).
Точки минимума и максимума
- Определение: Точку x= x0 называют точкой минимума функции y=f(x), если существует окрестность точки x0, в которой выполняется неравенство: f(x) ≥ f(x0).
- Определение: Точку x=x0 называют точкой максимума функции y=f(x), если существует окрестность точки x0, в которой выполняется неравенство: f(x) ≤ f(x0).
- Ребята, а что такое окрестность?
- Определение: Окрестность точки — множество точек, содержащее нашу точку, и близкие к ней.
Окрестность мы можем задавать сами. Например, для точки x=2, мы можем определить окрестность в виде точек 1 и 3.
Вернемся к нашим графикам, посмотрим на точку x2, она больше всех других точек из некоторой окрестности, тогда по определению — это точка максимума. Теперь посмотрим на точку x1, она меньше всех других точек из некоторой окрестности, тогда по определению — это точка минимума.
Ребята, давайте введем обозначения:
ymin — точка минимума,
ymax — точка максимума.
Важно! Ребята, не путайте точки максимума и минимума с наименьшим и наибольшим значение функции. Наименьшее и наибольшее значения ищутся на всей области определения заданной функции, а точки минимума и максимума в некоторой окрестности.
Экстремумы функции
Для точек минимума и максимума есть общей термин – точки экстремума.
Экстремум (лат. extremum – крайний) – максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума.
Соответственно, если достигается минимум – точка экстремума называется точкой минимума, а если максимум – точкой максимума.
Как же искать экстремумы функции?
Давайте вернемся к нашим графикам. В наших точках производная либо обращается в нуль (на первом графике), либо не существует (на втором графике).
- Тогда можно сделать важное утверждение: Если функция y= f(x) имеет экстремум в точке x=x0, то в этой точке производная функции либо равна нулю, либо не существует.
- Точки, в которых производная равна нулю называются стационарными.
- Точки, в которых производной функции не существует, называются критическими.
Как вычислять экстремумы?
Ребята, давайте опять вернемся к первому графику функции:
Анализируя этот график, мы говорили: до точки x2 функция возрастает, в точке x2 происходит перегиб, и после этой точки функция убывает до точки x1. В точке x1 у функции опять перегибается, и после этого
функция опять возрастает.
На основании таких рассуждений, можно сделать вывод, что функция в точках экстремума меняет характер монотонности, а значит и производная функция меняет знак. Вспомним: если функция убывает, то производная меньше либо равно нулю, а если функция возрастает, то производная больше либо равна нулю.
Обобщим полученные знания утверждением:
Теорема: Достаточное условие экстремума: пусть функция y=f(x) непрерывна на некотором промежутке Х и имеет внутри промежутка стационарную или критическую точку x= x0. Тогда:
- Если у этой точки существует такая окрестность, в которой при x < x0 выполняется f’(x) < 0, а при x > x0 выполняется f’(x)>0, то точка x0 – точка минимума функции y= f(x).
- Если у этой точки существует такая окрестность, в которой при x < x0 выполняется f ’(x)>0, а при x> x0 выполняется f’(x)Если у этой точки существует такая окрестность, в которой и слева и справа от точки x0 знаки производной одинаковы, то в точке x0 экстремума нет.
Для решении задач запомните такие правила: Если знаки производных определены то:
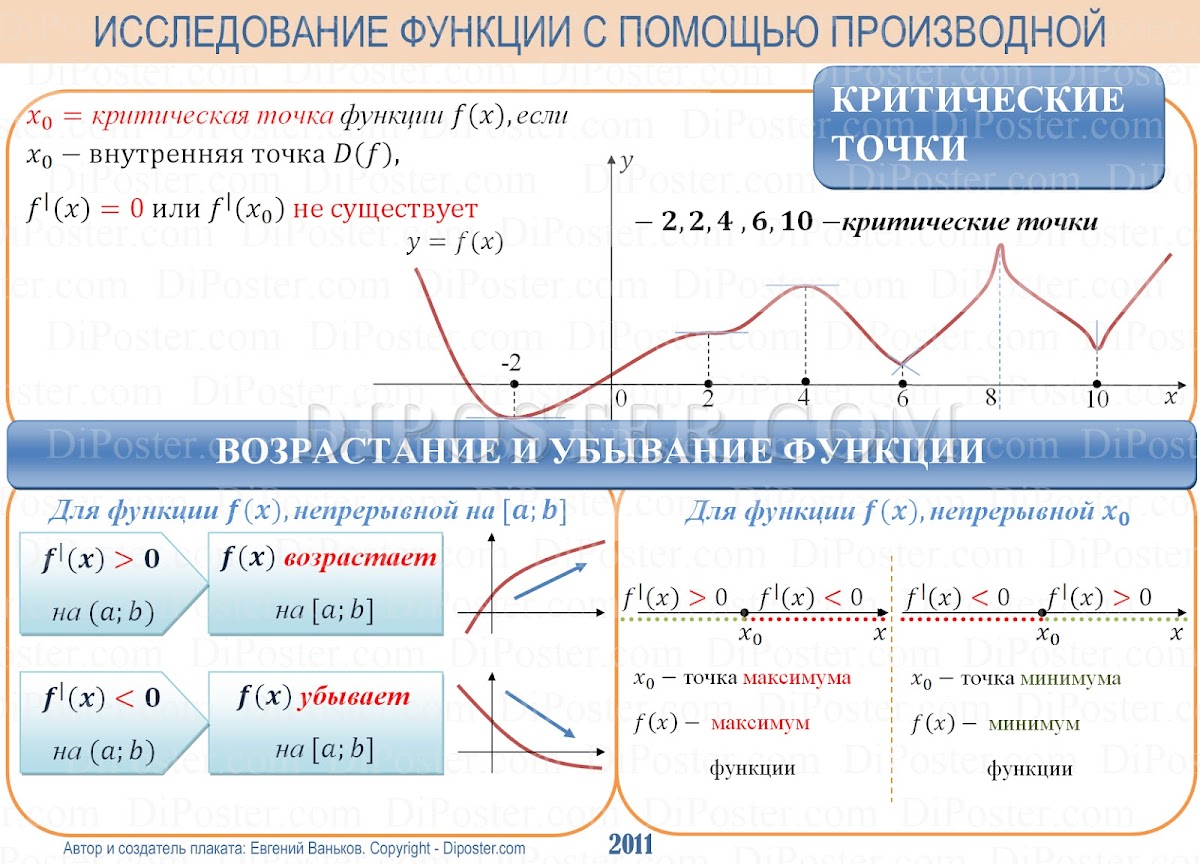
Алгоритм исследования непрерывной функции y= f(x) на монотонность и экстремумы:
- Найти производную y’.
- Найти стационарные(производная равна нулю) и критические точки (производная не существует).
- Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
- По указанным выше утверждениям сделать вывод о характере точек экстремума.
Примеры нахождения точки экстремумов
1) Найти точки экстремума функции и определить их характер: y= 7+ 12*x — x3
Решение: Наша функция непрерывна, тогда воспользуемся нашим алгоритмом:
а) y’= 12 — 3×2,
б) y’= 0, при x= ±2,
г) посмотрим на наш рисунок, где изображены правила определения экстремумов. Точка x= -2 — точка минимума функции, точка x= 2 — точка максимума функции.
Ответ: x= -2 — точка минимума функции, x= 2 — точка максимума функции.
2) Найти точки экстремума функции и определить их характер.
Решение: Наша функция непрерывна. Воспользуемся нашим алгоритмом:
а)
б) в точке x= 2 производная не существует, т.к. на нуль делить нельзя,
Область определения функции: [2; +∞], в этой точки экстремума нет, т.к. окрестность точки не определена. Найдем значения, в которой производная равна нулю:
в) Отметим стационарные точки на числовой прямой и определим знаки производной:
г) посмотрим на наш рисунок, где изображены правила определения экстремумов. Точка x= 3 — точка минимума функции.
Ответ: x= 3 — точка минимума функции.
- 3) Найти точки экстремума функции y= x — 2cos(x) и определить их характер, при -π ≤ x ≤ π.
-
в) отметим стационарные точки на числовой прямой и определим знаки производной:
г) посмотрим на наш рисунок, где изображены правила определения экстремумов.
- 4) Найти точки экстремума функции и определить их характер:
Решение: Наша функция непрерывна, воспользуемся нашим алгоритмом:
а) y’= 1 + 2sin(x),
б) найдем значения в которой производная равна нулю: 1 + 2sin(x)= 0, sin(x)= -1/2, т.к. -π ≤ x ≤ π, то: x= -π/6, -5π/6,
Точка x= -5π/6 — точка максимума функции.
Точка x= -π/6 — точка минимума функции.
Ответ: x= -5π/6 — точка максимума функции, x= -π/6 — точка минимума функции.
Решение: Наша функция имеет разрыв только в одной точке x= 0. Воспользуемся алгоритмом:
а)
б) найдем значения в которой производная равна нулю: y’= 0 при x= ±2,
в) отметим стационарные точки на числовой прямой и определим знаки производной:
г) посмотрим на наш рисунок, где изображены правила определения экстремумов.
Точка x= -2 точка минимума функции.
Точка x= 2 — точка минимума функции. В точке x= 0 функция не существует.
Ответ: x= ±2 — точки минимума функции.
Задачи для самостоятельного решения
а) Найти точки экстремума функции и определить их характер: y= 5×3 — 15x — 5.
б) Найти точки экстремума функции и определить их характер:
в) Найти точки экстремума функции и определить их характер: y= 2sin(x) — x при π ≤ x ≤ 3π.
г) Найти точки экстремума функции и определить их характер:
Источник: https://mathematics-tests.com/algebra-10-klass-urok-ekstremumy-funktsii
Значения функции и точки максимума и минимума
Неопубликованная запись
- Наменьшее значение функции
- Точки max
- Точки min
Как говорил крестный отец: «Ничего личного». Только производные!
Статью Как посчитать производные? надеюсь, ты изучил, без этого дальше будет проблематично.
12 задание по статистике считается достаточно трудным, а все потому, что ребята не прочитали эту статью (joke). В большинстве случаев виной всему невнимательность.
12 задание бывает двух видов:
- Найти точку максимума / минимума (просят найти значения «x»).
- Найти наибольшее / наименьшее значение функции (просят найти значения «y»).
Как же действовать в этих случаях?
Найти точку максимума / минимума
- Взять производную от предложенной функции.
- Приравнять ее к нулю.
- Найденный или найденные «х» и будут являться точками минимума или максимума.
- Определить с помощью метода интервалов знаки и выбрать, какая точка нужна в задании.
Задания с ЕГЭ:
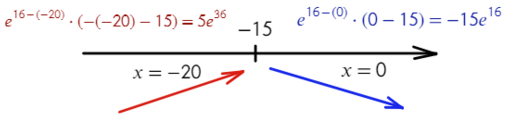
Найдите точку максимума функции
- Приравняем ее к нулю:
- Получили одно значение икса, для нахождения знаков подставим −20 слева от корня и 0 справа от корня в преобразованную производную (последняя строчка с преобразованием):

Ответ: −15
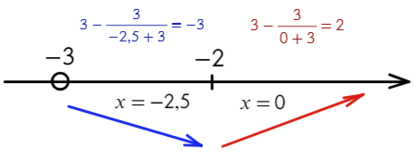
Найдите точку минимума функции
- Преобразуем и возьмем производную:
- Получается один корень «−2», однако не стоит забывать о «−3», она тоже будет влиять на изменение знака.
- Отлично! Сначала функция убывает, затем возрасает — это точка минимума!
Ответ: −2
Найти наибольшее / наименьшее значение функции
- Взять производную от предложенной функции.
- Приравнять ее к нулю.
- Найденный «х» и будет являться точкой минимума или максимума.
- Определить с помощью метода интервала знаки и выбрать, какая точка нужна в задании.
- В таких заданиях всегда задается промежуток: иксы, найденные в пункте 3, должны входить в данный промежуток.
- Подставить в первоначальное уравнение полученную точку максимума или минимума, получаем наибольшее или наименьшее значение функции.
- Задания с ЕГЭ:
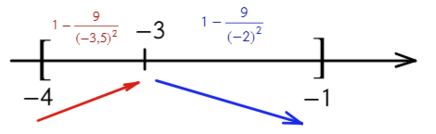
- Найдите наибольшее значение функции на отрезке [−4; −1]
- Преобразуем и возьмем производную:
- «3» не вдходит в промежуток [−4; −1]. Значит, остается проверить «−3» — это точка максимума?
- Подходит, сначала функция возрастает, затем убывает — это точка максимума, и в ней будет наибольшее значение функции. Остается только подставить в первоначальную функцию:
- Ответ: −6
- Найдите наибольшее значение функции на отрезке [0; 1,5π]
- Берем производную:
- Находим, чему равняется sin(x):
- Но такое невозможно! Sin(x)…
- Получается, что уравнение не имеет решения, и в таких ситуациях нужно подставлять крайние значения промежутка в первоначальное уравнение:
- Наибольшее значение функции равно «11» при точке максимума (на этом отрезке) «0».
Ответ: 11
Выводы:
- 70% ошибок заключается в том, что ребята не запоминают, что в ответ на наибольшее/наименьшее значение функции нужно написать «y», а на точку максимума/минимума написать «х».
- Нет решения у производной при нахождении значений функции? Не беда, подставляй крайние точки промежутка!
- Ответ всегда может быть записан в виде числа или десятичной дроби. Нет? Тогда перерешивай пример.
- В большинстве заданий будет получаться одна точка и наша лень проверять максимум или минимум будет оправдана. Получили одну точку — можно смело писать в ответ.
- А вот с поиском значения функции так поступать не стоит! Проверяйте, что это нужная точка, иначе крайние значения промежутка могут оказаться больше или меньше.
Будь в курсе новых статеек, видео и легкого математического юмора.
Источник: https://ik-study.ru/ege_math/znachieniia_funktsii_i_tochki_max_i_min0
Максимумы, минимумы и экстремумы функций
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
— Производная положительна там, где функция возрастает. — Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.
(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.
- (- 9): функция возрастает, а потом убывает – максимум.
- (-7): минимум.
- (3): максимум.
- Все вышесказанное можно обобщить следующими выводами:
— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус. — Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции (f'(x)).
- Найдите корни уравнения (f'(x)=0).
- Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2: — если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума; — если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
— если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.
Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54). Решение: 1. Найдем производную функции: (y’=15x^4-60x^2).
- 2. Приравняем её к нулю и решим уравнение:
- (15x^4-60x^2=0) (|:15) (x^4-4x^2=0) (x^2 (x^2-4)=0) (x=0) (x^2-4=0)
- (x=±2)
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является (-2).
Ответ. (-2).
Источник: http://cos-cos.ru/math/327/
Урок алгебры в 11 классе Максимум и минимум функции
Урок №33. Алгебра и НМА в 11 классе. Дата 06.11.18 г.
Учитель математики Абкелямова З.Н.
Тема урока: Анализ контрольной работы.Максимум и минимум функции.
- Цели: изучить понятие максимума и минимума функции;
- Составить алгоритм нахождения максимального и минимального значения функции.
- Мотивация: на успешность подготовки к ЕГЭ по математике.
- Ход урока.
- Русский математик XIX века Чебышев говорил , что « особенную важность имеют методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как располагать своими средствами для достижения наибольшей выгоды.»
-
Подготовка к изучению новой темы.
-
При исследовании поведения функции вблизи точки удобно пользоваться понятием окрестности.
Окрестностью точки а называется любой интервал , содержащий эту точку.
Определение. Точка х0 называется точкой максимума функции f(х), если существует такая окрестность точки х, что для всех х≠х0 из этой окрестности выполняется неравенство f(x) f(x0).
Пусть график некоторой функции имеет вот такой вид.
а) Если рассмотреть значение функции в точкехна этом графике то оно будет наибольшим (максимальным), чем в любой другой точке из близлежащей окрестности. В этом случае говорят, чтох0 — точка максимума (max).
Точках из области определения функции называется точкой максимума, если длялюбого из окрестноститочки хвыполняется неравенство f(x).
Максимум и минимум функции объединяют словом экстремум( с латинского — крайний), а точки максимума и минимума называют точками экстремума (экстремальными точками)Изучая график можно прийти к выводу, что наиболее «заметными» точками области определения являются какие точки Х, в которых возрастание функции сменяется убыванием (х=-6; х=2; х=7), или, наоборот убывание сменяется возрастанием (х=-7,5; х=-1,5; х=4). Эти точки называются соответственно точками максимума хmax=-6 хmax=2 хmax=7 и минимума хmin=-7,5; хmin=2; хmin=7.
- Точку отрезка [а;в], в которой функция достигает наибольшего значения на отрезке называют точкой максимума на отрезке.
- Значение функции в этой точке и есть максимум функции на отрезке.
- Точку отрезка [а;в], в которой функция достигает наименьшего значения на отрезке называют точкой минимума на отрезке.
- Значение функции в этой точке и есть минимум функции на отрезке.
- Названия и обозначения максимума и минимума происходит от латинских слов maximum ( наибольшее) minimum ( наименьшее).
-
На рисунке изображён график непрерывной функции на отрезке [а;в]
2,5 – точка максимума на отрезке [-3;5] .
0– точка минимума на отрезке [-3;5] .
Для точек максимума и минимума принято общее название . Их называют точками экстремума: хmax и хmin.
Значения функции в этих точках называют соответственно максимума и минимума функции уmax, ymin.
-
Пусть надо найти наибольшее и наименьшее значение функции на отрезке [а;в] и имеющей производную на интервале (а,в). Важную роль при нахождении наибольшего и наименьшего значения функции , при построении графика играют критические точки.
Определение. Внутренние точки области определения , в которых производная равна нулю или не существуют называются критическими точками.
-
Найти критические точки функции
№5.6 а), в), №5.7 а),в).
№5.6 а) у= 2х3-3х2 [-3;3] .
- у ʹ=6х2-6х у ʹ=0 х= 0, х=1- критические точки
- в) у=3х4+х3+7 [-3;2]
- у ʹ=12х3+3х2 у ʹ=0 х=0, х=-1 –критические точки
- №5.7 а) у= [-1;1]
- у ʹ= у ʹ=0 х=0 производная не существует, следовательно
- х=0 критическая точка
- 6) В ЕГЭ В11 нахождение наибольшего и наименьшего значения функции.
- Алгоритм нахождения точек экстремума
-
Найти производную функции.
-
Решить уравнение f ´(х)=0, и найти тем самым стационарные точки или критические точки
-
Найти критические точки функции на интервале (а,в);
-
Вычислить значения функции в найденных точках, принадлежащих интервалу (а,в);
-
Вычислить значения функции на концах отрезка, т.е. в точках х=а, х=в;
-
Среди всех вычисленных значений функции выбрать наибольшее и наименьшее.
Замечания.
- Если функция у=f(x) на [а;в], имеет точку максимума (минимума), то в этой точке функция принимает наибольшее или наименьшее значение.
- Если функция у=f(x) на [а;в] не имеет критических точек, то это означает, что на нем функция монотонно возрастает или убывает. Следовательно, свое наибольшее значение функция принимает на одном конце отрезка, а наименьшее на другом.
-
Найти наибольшее и наименьшее значение функции f(x)=3х2+4х3+1 на отрезке [-2;1] . (Решает учитель)
- fʹʹ(x)=(3х2+4х3+1) ʹ=6х+12х2. Для любого хЄR найдем производную f(x)
- fʹʹ(x)=0
- 6х+12х2=0
- Х( 6+12х)=0
- Х=0 или 6+12х=0
- Х= —
- Х=0 и х= — критические точки, принадлежат заданному отрезку.
- 0Є[-2;1], — Є[-2;1],
- Найдем значения функции в заданных точках.
- f(0)=1
- f(- =1,25
- f(-2)=-11
- f(1)=8 сравнив значения функций, выбираем наибольшее и наименьшее значение функции на отрезке.
- max f(x)= f(1) =8
- min f(x)= f(-2)=-11
- Ответ : 8,11.
- Г) № 5.10 а) в) ( для тех кто работает быстро, за каждый верно выполненный пример ученик получает +, три + «5» в журнал)
- №5.11 а)в)
Домашнее задание №5.10 (в,г) 5.14 стр 120.
дополнительное задание.Найти наибольшее значение функции у= 12 cosх+6х-2+6 на отрезке [0;].
- Тема урока: Максимум и минимум функции.
- Цели: закрепить навык нахождения наибольшего и наименьшего значения функции на отрезке путем решения разнообразных задач.
- Ход урока.
-
Проверка домашнего задания.
-
№5.6 б) f(х) =5х3-15х на отрезке [-2;2]
- f’ (х) =15х2 -15 f(х) =0 х=1 х=-1 критические точки
- г) у=х4-4х2 на отрезке [-4;4]
- у’=4х3 -8х у’=0 х1=0 х2= х=- критические точки
- № 5.7 б) у= на отрезке
- У’= у’=0 х=0 производная не существует, следовательно, х=0 критическая точка
- г) у= 2 -х на промежутке (0; 2]
- У’= у’=0 х=0 производная не существует, следовательно
- Х=0 критическая точка.
- № 5.8 б) у=ех-хе на отрезке [-2;2]
- У’= ех-х у’=0 ех-е=0
- Х=1
- г) у= cos2х +х на отрезке [- π; π]
- у’= -2sin 2х+1 у’=0 -2sin 2х+1=0
- х= (-1)к +к, кЄZ
- х= ; π ; Є [- π; π]
- № 5.10 б) у= х3+ 3х на отрезке [-1;2]
- У’= 3х2+3 у=0 3х2+3=0
- Критических точек нет , значит функция достигает свое наибольшее и наименьшее значение на концах отрезка.
- У(-1)=-4
- У(2)=14 Г) у= х3- 3х на отрезке [-1;2]
- У’=3х2-3 у=0 3х2-3=0
- Х=-1 х=1 -1;1 Є [-1;2]
- У(-1)=0 у(3)=18 у(1)=-2 у(-2)=-2
- Наибольшее значение 18, наименьшее значение -2.
№ 5.11 б) наибольшее значение 3, наименьшее значение -3.
-
(Два ученика на обратной стороне доски)
- Взять производные функций
- Cos3х, ех, (х-14)ех-13, ln(2х+3), tg2х
- Класс делает в тетрадях и потом проверяем.
- Верно ли , что если функция у= f(x) непрерывна на отрезке[а;в] , то существуют точки этого отрезка, в которых функция принимает свое наибольшее и наименьшее значение. (да)
- Какую точку отрезка [а;в] называют точкой максимума и минимума функции у= f(x); точкой минимума функции у= f(x).
- Как называются значения функции в этих точках?
- Какие точки отрезка [а;в] называются критическими точками функции? Как найти эти точки?
- Как найти максимум и минимум функции на отрезке?
- Работа по графику .
- Указать точки максимума и минимума функции.
- Назвать максимум и минимум функции на отрезке.

Работа с классом.
-
Найдите наибольшее значение функции у=-х2 +10х на отрезке [0;7].
( У(0)=0, у(7)=21, у(15)=25)
-
Найдите наименьшее значение функции у=(х-21)ех-20 на отрезке
[19;21].
У(19)= у(20)=-1 у(21)=0
-
Найдите наибольшее значение функции у= 7 cosх+7х-на отрезке [0;].
-
У() =16 у(0)= 7- +9 у(=
-
Аналогично определяется максимум и минимум функции на интервале и полуинтервале.
-14-

Хmax=-5,5 ymin=4
Хmin- нет, т.к. х=3 не входит в (-5,5;3)
- Работа с классом. ( у доски работает ученик)
- Найти наибольшее значение функции у= -2х2 на промежутке (-2;2).
- Решение.
- У`= х3-4х у=0 х=0 х=2 х=-2 критические точки , но х=2 и х=-2 не входят в данный промежуток.
Найдем значение функции у(0)=0, а у= (х2-8) 0 при каждом х, таком , что 0х|, то на интервале (-2;2) функция имеет максимум в точке х=0.
На интервале (-2;2) функция не имеет минимума, так как у= -2х2 -4при каждом х, таком, что |х|2 и -2 не принадлежат (-2;2), следовательно у=0 максимум функции.
Обучающая самостоятельная работа.
-
найдите наибольшее значение функции у=(х-8)ех-7 на отрезке [6;8].
-
найдите наибольшее значение функции у=7х-6sinх+8 на отрезке [].
3) найти наименьшее значение функции у=х2-3х+lnх+3 на отрезке [;]
На задания даётся 15 минут. С помощью проектора ученики проверяют решение.
Решение.
-
у=(х-8)ех-7 на отрезке[6;8].
- у’=ех-7(х-7) у’=0 х=7 критическая точка
- у(6)= у(7)=-1 у(8)=0
- наибольшее значение функции равно 0
-
у=7х-6sinх+8 на отрезке [].
- у’=7- 6cosх у’=0 6cosх=7 х= критических точек нет
- у(-=14 у(0)=8
- наибольшее значение функции равно 8
- 3) у=х2-3х+lnх+3 на отрезке [;] ОДЗ: х
- у’=2х-3+ у’=0 2х2-3х+1=0
- х=1 х= не принадлежит [;]
- у(1)=1 у()= ln+3 у()= ln +3
- наименьшее значение функции равно1.
- Домашнее задание: рассмотреть из открытого банка заданий — 5 функций.
Источник: https://infourok.ru/urok-algebri-v-klasse-maksimum-i-minimum-funkcii-3350394.html
Урок 16. экстремумы функции — Алгебра и начала математического анализа — 11 класс — Российская электронная школа
Алгебра и начала математического анализа, 11 класс
Урок № 16. Экстремумы функции.
- Перечень вопросов, рассматриваемых в теме
- 1) Определение точек максимума и минимума функции
- 2) Определение точки экстремума функции
- 3) Условия достаточные для нахождения точек экстремума функции
- Глоссарий по теме
Возрастание функции. Функция y=f(x) возрастает на интервале X, если для любых х1 и х2, из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.
- Максимум функции. Значение функции в точке максимума называют максимумом функции
- Минимум функции. Значение функции в точке минимума называют минимумом функции
- Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке).
Точка максимума функции. Точку х0 называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство .
Точка минимума функции. Точку х0 называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство .
Точки экстремума функции. Точки минимума и максимума называют точками экстремума.
Убывание функции. Функция y = f(x) убывает на интервале X, если для любых х1 и х2, из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.
- Алгоритм исследования функции на монотонность и экстремумы:
- 1) Найти область определения функции D(f)
- 2) Найти f’ (x).
- 3) Найти стационарные (f'(x) = 0) и критические (f'(x) не
- существует) точки функции y = f(x).
- 4) Отметить стационарные и критические точки на числовой
- прямой и определить знаки производной на получившихся
- промежутках.
- 5) Сделать выводы о монотонности функции и точках ее
- экстремума.
- Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Точки, в которых происходит изменение характера монотонности функции – это ТОЧКИ ЭКСТРЕМУМА.
- Точку х = х0 называют точкой минимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≥ f(x0).
- Точку х = х0 называют точкой максимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≤ f(x0).
- Точки максимума и минимума – точки экстремума.
- Функция может иметь неограниченное количество экстремумов.
- Критическая точка – это точка, производная в которой равна или не существует.
- Важно помнить, что любая точка экстремума является критической точкой, но не всякая критическая является экстремальной.
- Алгоритм нахождения максимума/минимума функции на отрезке:
- найти экстремальные точки функции, принадлежащие отрезку,
- найти значение функции в экстремальных точках из пункта 1 и в концах отрезка,
- выбрать из полученных значений максимальное и минимальное.
- Примеры и разбор решения заданий тренировочного модуля
- №1. Определите промежуток монотонности функции у=х2 -8х +5
- Решение: Найдем производную заданной функции: у’=2x-8
- 2x-8=0
- х=4
- Определяем знак производной функции и изобразим на рисунке, следовательно, функция возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)
- Ответ: возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)
- №2. Найдите точку минимума функции у= 2х-ln(х+3)+9
х=-2,5
Определим знаки производной функции и изобразим на рисунке поведение функции:
Ответ: -2,5 точка min
№3. Материальная точка движется прямолинейно по закону x(t) = 10t2 − 48t + 15, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3с.
Решение: Если нас интересует движение автомобиля, то, принимая в качестве функции зависимость пройденного расстояния от времени, с помощью производной мы получим зависимость скорости от времени.
V=х'(t)= 20t – 48. Подставляем вместо t 3c и получаем ответ. V=12 мc
Ответ: V=12 мc
№4. На рисунке изображен график функции. На оси абсцисс отмечены семь точек: x1, x2, x3, x4, x5, x6, x7. Определите количество целых точек, в которых производная функции отрицательна.
Решение: Производная функции отрицательна на тех интервалах, на которых функция убывает. В данном случае это точки х3,х5,х7. Следовательно, таких точек 3
Ответ: 3
Источник: https://resh.edu.ru/subject/lesson/3987/conspect/
Конспект по «Машинному обучению». Математический анализ. Градиентный спуск

Вспомним математический анализ
Непрерывность функции и производная
Пусть , — предельная точка множества (т.е. ), .
- Определение 1 (предел функции по Коши):
- Функция стремится к при , стремящемся к , если
Обозначение: . Определение 2:
- Интервалом называется множество ;
- Интервал, содержащий точку , называется окрестностью этой точки.
- Проколотой окрестностью точки называется окрестность точки, из которой исключена сама эта точка.
Обозначение:
- или — окрестность точки ;
- — проколотая окрестность точки ;
Определение 3 (предел функции через окрестности): Определения 1 и 3 равносильны.
Определение 4 (непрерывность функции в точке):
- непрерывна в
- непрерывна в
Из определений 3 и 4 видно, что
( непрерывна в , где — предельная точка )
- Определение 5:
- Функция называется непрерывной на множестве , если она непрерывна в каждой точке множества .
- Определение 6:
- Функция , определённая на множестве , называется дифференцируемой в точке , предельной для множества , если существует такая линейная относительно приращения аргумента функция [дифференциал функции в точке ], что приращение функции представляется в виде
- Величина называется производной функции в точке .
Также
Определение 7:
- Точка называется точкой локального максимума (минимума), а значение функции в ней — локальным максимумом (минимумом) функции , если :
- Точки локального максимума и минимума называются точками локального экстремума, а значения функции в них — локальными экстремумами функции.
- Точка экстремума функции называется точкой внутреннего экстремума, если является предельной точкой как для множества , так и для множества .
Лемма 1 (Ферма):
Если функция дифференцируема в точке внутреннего экстремума , то её производная в этой точке равна нулю: .
Утверждение 1 (теорема Ролля):
Если функция непрерывна на отрезке , дифференцируема в интервале и , то найдётся точка такая, что .
- Теорема 1 (теорема Лагранжа о конечном приращении):
- Если функция непрерывна на отрезке и дифференцируема в интервале , то найдётся точка такая, что
Следствие 1 (признак монотонности функции): Если в любой точке некоторого интервала производная функции неотрицательная (положительная), то функция не убывает (возрастает) на этом интервале.
Следствие 2 (критерий постоянства функции):
Непрерывная на отрезке функция постоянна не нём тогда и только тогда, когда её производная равна нулю в любой точке отрезка (или хотя бы интервала ).
Частная производная функции многих переменных
Через обозначают множество:
- Определение 8:
- Функция , определённая на множестве , называется дифференцируемой в точке , предельной для множества , если
где — линейная относительно функция [дифференциал функции в точке (обозн.
или )], а при .
- Соотношение (1) можно переписать в следующем виде:
или Если перейти к координатной записи точки , вектора и линейной функции , то равенство (1) выглядит так где — связанные с точкой вещественные числа. Необходимо найти эти числа.
Обозначим
где — базис в .
- При из (2) получаем
- Из (3) получаем
Определение 9: Предел (4) называется частной производной функции в точке по переменной . Обозначается:
- Пример 1:
Градиентный спуск
Пусть , где .
- Определение 10:
- Градиентом функции называется вектор, -й элемент которого равен :
Градиент — это то направление, в котором функция быстрее всего возрастает. А значит, направление, в котором она быстрее всего убывает, — это и есть направление, обратное градиенту, то есть .
- Целью метода градиентного спуска является поиск точки экстремума (минимума) функции.
- Обозначим через вектор параметров функции на шаге . Вектор обновления параметров на шаге :
В формуле выше параметр — это скорость обучения, которая регулирует размер шага, который мы делаем в направлении склона-градиента.
В частности, могут возникать две противоположные друг другу проблемы:
- если шаги будут слишком маленькими, то обучение будет слишком долгим, и повышается вероятность застрять в небольшом неудачном локальном минимуме по дороге (первое изображение на картинке ниже);
- если слишком большие, можно бесконечно прыгать через искомый минимум взад-вперёд, но так и не прийти в самую нижнюю точку (третье изображение на картинке ниже).
Пример: Рассмотрим пример работы метода градиентного спуска в простейшем случае (). То есть . Пусть . Тогда: В случае, когда , получается ситуация, как на третьем изображении картинки выше. Мы постоянно перепрыгиваем точку экстремума. Пусть . Тогда: Видно, что итеративно мы приближаемся к точке экстремума. Пусть . Тогда: Точка экстремума найдена за 1 шаг.
Список используемой литературы:
- «Математический анализ. Часть 1», В.А. Зорич, Москва, 1997;
- «Глубокое обучение. Погружение в мир нейронных сетей», С. Никуленко, А. Кадурин, Е. Архангельская, ПИТЕР, 2018.
Источник: https://habr.com/post/474338/
Необходимые и достаточные условия существования экстремумов. Примеры
Экстремумом функции называется максимальное (минимальное) значение функции на заданном множестве. Точка, в которой достигается экстремум называется точкой экстремума.
Точка называется точкой локального максимума функции , если выполняется условие:
Аналогично точка называется точкой локального минимума функции , если выполняется условие:
Точки, в которых производная равна нулю, называются стационарными точками.Точки, в которых функция непрерывна, а её производная либо равна нулю, либо не существует, называются критическими точками.
Теорема (необходимое условие экстремума)
Если точка — точка экстремума функции , то она критическая.
Доказательство
По условию точка — точка экстремума функции по теореме Ферма производная точка является критической.
Пример:
Найти экстремум функции .
Найдем производную этой функции: критические точки задаются уравнением . Корни этого уравнения и .
Как видно по рисунку функция имеет максимум в точке 1, а минимум в точке 3. Подставим эти значения чтобы убедиться в исходную функцию: и в точке функция имеет минимум, равный -4, а в точке функция имеет максимум, равный 0.
Замечания:
Не всякая критическая точка является точкой экстремума.
Пример:
- Рассмотрим функцию . Построим график этой функции:
- Производная данной функции в точке по определению является критической точкой, однако в этой точке функция не имеет экстремума.
Теорема (первое достаточное условие экстремума в терминах первой производной)
Пусть функция определена и дифференцируема в некоторой окрестности точки , кроме, быть может, самой точки и непрерывна в этой точке. Тогда:
- Если производная меняет знак с «-» на «+» при переходе через точку : и , то — точка строго минимума функции
- Если производная меняет знак с «+» на «-» при переходе через точку : и , то — точка строго максимума функции
Доказательство
Пусть, например, меняет знак с «-» на «+». Рассмотрим точку на сегменте Воспользуемся теоремой о конечных приращениях Лагранжа: , . Поскольку при переходе через точку функция меняет знак с «-» на «+», то и , то
Аналогично рассмотрим сегмент , получим
— точка строгого минимума функции.
Замечания:
Если — точка строго экстремума, то из этого не следует, что производная меняет знак при переходе через точку
Теорема (второе достаточное условие строгого экстремума в терминах второй производной)
Пусть дана функция , она определена в некоторой окрестности точки , ее первая производная и пусть , тогда:
- Если , то точка — точка строгого минимума;
- Если , то точка — точка строгого максимума.
Доказательство
Докажем теорему для первого случая, когда . По скольку непрерывна, то на достаточно малом интервале , т.к , то возрастает в этом интервале. , значит на интервале и на интервале .
Таким образом функция убывает на интервале и возрастает на интервале по первому достаточному условию экстремума функция в точке имеет минимум.
Аналогично доказывается второй случай теоремы.
Замечания:
Если и , то функция может и не иметь экстремум в точке
Теорема (третье достаточное условие строгого экстремума в терминах производных порядка больше двух)
Пусть функция определена в некоторой окрестности точки , и в этой точке существуют производные до n-го порядка пусть , и , Тогда:
- Если (т.е — четное), то — точка экстремума:
- если , то — точка локального максимума;
- если , то — точка локального минимума;
- Если (т.е — нечетное), то — не является точкой экстремума.
Доказательство
Воспользуемся формулой Тейлора в окрестности точки с остатком в форме Пеано: .
По скольку все производные до порядка включительно равны нулю получим: Запишем полученное выражение в виде: . Выражение . Пусть , . Отсюда следует, что сохранение или изменение знака приращения функции во время перехода через точку зависит от четности . Последний факт и доказывает теорему.
Список литературы:
максимум из 4 баллов
| Таблица загружается |
| Нет данных |
Место Имя Записано Баллы Результат
Источник: https://ib.mazurok.com/2013/05/17/extremum-of-the-function/
Значения функции и точки максимума и минимума

Наменьшее значение функции
Точки max
Точки min
Как говорил крестный отец: «Ничего личного». Только производные!
Статью Как посчитать производные? надеюсь, ты изучил, без этого дальше будет проблематично.
12 задание по статистике считается достаточно трудным, а все потому, что ребята не прочитали эту статью (joke). В большинстве случаев виной всему невнимательность.
12 задание бывает двух видов:
- Найти точку максимума / минимума (просят найти значения «x»).
- Найти наибольшее / наименьшее значение функции (просят найти значения «y»).
Как же действовать в этих случаях?
Найти точку максимума / минимума
- Взять производную от предложенной функции.
- Приравнять ее к нулю.
- Найденный или найденные «х» и будут являться точками минимума или максимума.
- Определить с помощью метода интервалов знаки и выбрать, какая точка нужна в задании.
Задания с ЕГЭ:
Найдите точку максимума функции
- Берем производную:
- Приравняем ее к нулю:
- Получили одно значение икса, для нахождения знаков подставим −20 слева от корня и 0 справа от корня в преобразованную производную (последняя строчка с преобразованием):
Все верно, сначала функция возрастает, затем убывает — это точка максимума!
Ответ: −15
Найдите точку минимума функции
- Преобразуем и возьмем производную:
- Получается один корень «−2», однако не стоит забывать о «−3», она тоже будет влиять на изменение знака.
- Отлично! Сначала функция убывает, затем возрасает — это точка минимума!
Ответ: −2
Найти наибольшее / наименьшее значение функции
- Взять производную от предложенной функции.
- Приравнять ее к нулю.
- Найденный «х» и будет являться точкой минимума или максимума.
- Определить с помощью метода интервала знаки и выбрать, какая точка нужна в задании.
- В таких заданиях всегда задается промежуток: иксы, найденные в пункте 3, должны входить в данный промежуток.
- Подставить в первоначальное уравнение полученную точку максимума или минимума, получаем наибольшее или наименьшее значение функции.
Задания с ЕГЭ:
Найдите наибольшее значение функции на отрезке [−4; −1]
- Преобразуем и возьмем производную:
- «3» не вдходит в промежуток [−4; −1]. Значит, остается проверить «−3» — это точка максимума?
- Подходит, сначала функция возрастает, затем убывает — это точка максимума, и в ней будет наибольшее значение функции. Остается только подставить в первоначальную функцию:
Ответ: −6
Найдите наибольшее значение функции на отрезке [0; 1,5π]
- Наибольшее значение функции равно «11» при точке максимума (на этом отрезке) «0».
Ответ: 11
Выводы:
- 70% ошибок заключается в том, что ребята не запоминают, что в ответ на наибольшее/наименьшее значение функции нужно написать «y», а на точку максимума/минимума написать «х».
- Нет решения у производной при нахождении значений функции? Не беда, подставляй крайние точки промежутка!
- Ответ всегда может быть записан в виде числа или десятичной дроби. Нет? Тогда перерешивай пример.
- В большинстве заданий будет получаться одна точка и наша лень проверять максимум или минимум будет оправдана. Получили одну точку — можно смело писать в ответ.
- А вот с поиском значения функции так поступать не стоит! Проверяйте, что это нужная точка, иначе крайние значения промежутка могут оказаться больше или меньше.
Будь в курсе новых статеек, видео и легкого математического юмора.