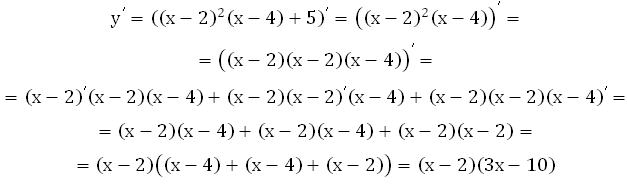Степенная функция. В данной статье мы рассмотрим вычисление максимума (минимума) указанной функции. В предыдущей статье мы с вами рассмотрели задачи на нахождение максимума (минимума) функции с числом «е». Здесь представлены примеры без числа «е». Некоторые примеры, в которых требуется найти наибольшее или наименьшее значение функции, вообще можно решить без нахождения производной.
В любом случае, советую вам ознакомится с этой статьёй, если вы ещё этого не сделали. Рассмотрим задачи:
Найдите точку максимума функции у = (х – 2)2(х – 4)+5
Для этого найдём производную, приравняем её к нулю, найдём корни полученного уравнения:
Обратите внимание, что мы сразу представили результат в виде произведения, рекомендую делать именно так. Зачем вам упрощать его до многочлена, а затем снова раскладывать его на множители? Для дальнейших действий проще сразу представить в виде произведения.
Находим нули производной:
Полученные точки разбивают числовую ость на интервалы.
Посмотрим, как ведёт себя график функции на этих интервалах. Возьмём значения из них, подставим их в производную и определим знак:
На интервале (–∞;2) функция возрастает, на интервале (2;10/3) функция убывает. Значит х = 2 это точка максимума.
Второй способ:
Перебираем значения х от – 5 до 5 подставляем в функцию и вычисляем. Затем по полученным значениям функции определяем точку максимума.
Почему берём интервал от – 5 до 5? Потому, что большинство ответов на ЕГЭ в подобных задачах лежат в этих пределах. Если будет необходимо, то берите интервал шире. Для наглядности можете построить график.
Решите предложенным способом самостоятельно, а затем посмотрите решение.
*Данный способ использовать осторожно, в будущем возможно изменение типов заданий входящих в ЕГЭ и такой подход может не сработать.
Ответ: 2
Найдите точку максимума функции у = (х – 3)2(х – 10) – 9
Это аналогичная задача.
Для этого найдём производную, приравняем её к нулю, найдём корни полученного уравнения:
Находим нули производной:
Полученные точки разбивают числовую ость на интервалы.
Посмотрим, как ведёт себя график функции на этих интервалах. Возьмём значения из интервалов, подставим их в производную и определим знак:
На интервале (–∞;3) функция возрастает, на интервале (3;23/3) функция убывает. Значит, х = 3 это точка максимума.
Вторым способом попробуйте решить сами.
Ответ: 3
Найдите наименьшее значение функции у = (х–3)2(х–6)–1 на отрезке [4;6].
Так как интервал дан (при чём он небольшой), то здесь рекомендую подставить целые значения из него (4, 5 и 6) в функцию:
Наименьшее значение функции на заданном отрезке равно – 5.
Ответ: – 5
Решите самостоятельно:
Посмотреть решение
Найдите наибольшее значение функции у=(х+6)2(х–1)–6 на отрезке [– 9;–2].
Данную задачу можно решать любым из двух способов. Интервал здесь маленьким не назовёшь, но и в то же время он невелик.
Решим её подстановкой всех значений из интервала.
Подставим – 9, – 8, – 7, – 6, – 5, – 4, – 3, –2.
Наибольшее значение функции равно – 6.
Ответ: – 6
Решите самостоятельно:
Посмотреть решение
Подведём итог. Как видите, задачи решаются по простому алгоритму. Важно для успешного решения знать таблицу производных, правила дифференцирования и производную сложной функции, свойства производной для исследования графиков функций.
Конечно, когда используем метод подстановки значений из интервала, то знать всё это, казалось бы, не обязательно, но такой подход помогает не всегда. Советую использовать его лишь как дополнительный инструмент.
Мы продолжим рассматривать задачи в этой рубрике, не пропустите!
Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Задания
Версия для печати и копирования в MS Word
Тип 11 № 287311
i
Найдите точку максимума функции
Решение.
Это задание ещё не решено, приводим решение прототипа.
Найдите точку максимума функции
Поскольку функция возрастающая, заданная функция достигает максимума в той же точке, в которой достигает максимума выражение
Квадратный трехчлен
с отрицательным старшим коэффициентом достигает максимума в точке
в нашем случае — в точке 3.
Ответ: 3.
Аналоги к заданию № 245181: 287305 287403 560729 … Все
Кодификатор ФИПИ/Решу ЕГЭ:
3.2.1 Монотонность функции. Промежутки возрастания и убывания;
3.2.5 Точки экстремума функции;
3.2.6 Наибольшее и наименьшее значения функции;
3.3.3 Квадратичная функция, её график;
3.3.6 Показательная функция, её график.
Прототип задания
Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.
Вот какие типы задач могут встретиться в этом задании:
Нахождение точек максимума и минимума функций
Исследование сложных функций
Нахождение наибольших и наименьших значений функций на отрезке
Нахождение точек максимума и минимума функций
1. Найдите точку максимума функции
Найдем производную функции.
Приравняем производную к нулю. Получим:
Исследуем знаки производной.
В точке производная
меняет знак с «плюса» на «минус». Значит,
— точка максимума функции
Ответ: 17.
2. Найдите точку минимума функции
Найдем производную функции.
Приравняем производную к нулю.
Определим знаки производной.
В точке производная
меняет знак с «минуса» на «плюс». Значит,
— точка минимума функции
Ответ: 1.
Исследование сложных функций
3. Найдите точку максимума функции
Перед нами сложная функция Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.
Так как функция монотонно возрастает, точка максимума функции
будет при том же
, что и точка максимума функции
А ее найти легко.
при
. В точке
производная
меняет знак с «плюса» на «минус». Значит,
— точка максимума функции
.
Заметим, что точку максимума функции можно найти и без производной.
Графиком функции является парабола ветвями вниз, и наибольшее значение
достигается в вершине параболы, то есть при
Ответ: — 4.
4. Найдите абсциссу точки максимума функции
Напомним, что абсцисса — это координата по
Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.
Так как функция монотонно возрастает, точка максимума функции
является и точкой максимума функции
Это вершина квадратичной параболы
Нахождение наибольших и наименьших значений функций на отрезке
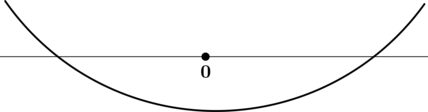
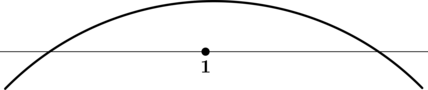
5. Найдите наибольшее значение функции на отрезке
Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.
Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.
Найдем знаки производной.
В точке производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции
. Поскольку при
функция
убывает,
В этой задаче значение функции на концах отрезка искать не нужно.
Ответ: 12.
6. Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю.
при
Найдем знаки производной.
Точка — точка минимума функции
. Точка
не лежит на отрезке
Поэтому
и
Значит, наименьшее значение функции на отрезке
достигается при
Найдем это значение.
Ответ: -11.
7. Найдите наименьшее значение функции на отрезке
Иногда перед тем, как взять производную, формулу функции полезно упростить.
Мы применили формулу для логарифма произведения. при
Если то
Если
, то
Значит, — точка минимума функции
. В этой точке и достигается наименьшее значение функции на отрезке
Ответ: 4.
8. Найдите наибольшее значение функции на отрезке
Найдем производную функции
Приравняем производную к нулю:
. Поскольку
если
Найдем знаки производной на отрезке
При знак производной меняется с «плюса» на «минус». Значит,
— точка максимума функции
Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при и
Мы нашли, что
Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.
Ответ: 4.
9. Найдите наименьшее значение функции на отрезке [0;2].
Снова сложная функция. Запишем полезные формулы:
Найдем производную функции
если
Тогда
При
знак производной меняется с «минуса» на «плюс». Значит,
— точка минимума функции
Ответ: -7.
10. Найдите наибольшее значение функции на отрезке
Как всегда, возьмем производную функции и приравняем ее к нулю.
По условию, . На этом отрезке условие
выполняется только для
Найдем знаки производной слева и справа от точки
В точке производная функции меняет знак с «плюса» на «минус». Значит, точка
— точка максимума функции
. Других точек экстремума на отрезке
функция не имеет, и наибольшее значение функции
на отрезке
достигается при
Ответ: 12.
11.Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю. — нет решений.
Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.
Поскольку , получим, что
для всех
, и функция
монотонно возрастает при
Значит, наименьшее свое значение функция принимает в левом конце отрезка , то есть при
Ответ: 6
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 11 Профильного ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
28 апреля 2012
По определению, показательная функция — это выражение вида y = ax, где a > 0. Но в задаче B15 встречаются только функции вида y = ex. В крайнем случае, y = ekx + b. Причина в том, что производные этих функций считаются очень легко:
(ex)’ = ex;
(ekx + b)’ = k · ekx + b.
Как видите, если в показателе стоит просто переменная x, ничего не меняется. А если там будет линейное выражение вида kx + b, то спереди добавляется множитель k. Эта формула — частный случай производной сложной функции.
Задачи на вычисление наибольшего/наименьшего значения
Все задачи B15 с показательной функцией решаются по стандартной схеме — см. «Общая схема решения задач B15». Но если требуется найти наименьше/наибольшее значение функции, есть одна фишка:
Показатель должен быть равен нулю. Потому что e0 = 1 — нормальное число, его можно записать в ответ. В отличие от чисел e1, e2, которые вообще не представимы в виде десятичной дроби.
Данное замечание реально сокращает объем вычислений. Аналогичное правило есть у логарифмов — см. «Как считать логарифмы еще быстрее». И это вполне логично, поскольку логарифмы и показательные функции — родственные объекты.
А теперь разберем конкретные задачи.
Задача. Найдите наименьшее значение функции на отрезке [−1; 5]:
y = (x2 − 5x + 5)ex − 3
Сначала находим производную и раскладываем ее на множители:
y’ = ((x2 − 5x + 5)ex − 3)’ = … = (x2 − 3x)ex − 3 = x(x − 3)ex − 3
Затем приравниваем полученное выражение к нулю и находим корни:
x(x − 3)ex − 3 = 0;
x1 = 0; x2 = 3.
Оба корня принадлежат отрезку [−1; 5]. Итого получаем четыре точки: два корня и два конца отрезка. Осталось вычислить значение функции в этих точках:
y(−1) = ((−1)2 − 5 · (−1) + 5)e−1 − 3 = … = 11e−4;
y(0) = (02 − 5 · 0 + 5)e0 − 3 = … = 5e−3;
y(3) = (32 − 5 · 3 + 5)e3 − 3 = … = −1;
y(5) = (52 − 5 · 5 + 5)e5 − 3 = … = 5e2.
Заметим, что из этих четырех чисел в бланк можно записать только y = −1. Кроме того, это единственное отрицательное число. Следовательно, это число и будет наименьшим.
Задача. Найдите наибольшее значение функции на отрезке [0; 6]:
y = (2x − 7)e8 − 2 · x
Как и в прошлый раз, вычисляем производную функции и раскладываем ее на множители:
y’ = (y = (2x − 7)e8 − 2 · x)’ = … = (16 − 4x)e8 − 2 · x = 4(4 − x)e8 − 2 · x
Приравниваем производную к нулю и находим корни:
y’ = 0;
4(4 − x)e8 − 2 · x = 0;
x = 4.
Корень x = 4 принадлежит отрезку [0; 6]. Мы ищем наибольшее значение, поэтому подставляем этот корень, а также концы отрезка в исходную функцию. Имеем:
y(0) = (2 · 0 − 7)e8 − 2 · 0 = … = −7e8;
y(4) = (2 · 4 − 7)e8 − 2 · 4 = … = 1;
y(6) = (2 · 6 − 7)e8 − 2 · 6 = … = 5e−4.
Итак, ответом может быть только число y = 1.
Задачи на вычисление точек максимума/минимума
В задачах на точки максимума/минимума нельзя применять приведенное выше правило, поэтому считаем все по стандартной схеме.
Задача. Найдите точку минимума функции:
y = (x − 12)ex − 11
В первую очередь считаем производную:
y’ = (y = (x − 12)ex − 11)’ =
= (x − 12)’ · ex − 11 + (x − 12) · (ex − 11)’ =
= 1 · ex − 11 + (x − 12)ex − 11 =
= (1 + x − 12)ex − 11 =
= (x − 11)ex − 11
Приравниваем производную к нулю:
y’ = 0;
(x − 11)ex − 11 = 0;
x − 11 = 0;
x = 11.
Множитель ex − 11 никогда не равен нулю, поэтому мы избавились от него. Осталось начертить координатную ось и расставить знаки производной:
Итак, в точке x = 11 знак производной меняется с минуса на плюс. Считаем всегда в направлении оси — слева направо. Значит, x = 11 — это точка минимума.
Задача. Найдите точку максимума функции:
y = (2x2 − 34x + 34)e6 − x
Снова считаем производную:
y’ = ((2x2 − 34x + 34)e6 − x)’ =
= (2x2 − 34x + 34)’ · e6 − x + (2x2 − 34x + 34) · (e6 − x)’ =
= (4x − 34)e6 − x + (2x2 − 34x + 34) · (−1) · e6 − x
Напомню, что производная сложной показательной функции считается по формуле:
(ekx + b)’ = k · ekx + b;
(e6 − x)’ = (−1) · e6 − x.
Производная получилась довольно навороченная. Разложим ее на множители, для этого вынесем e6 − x за скобку. Имеем:
(4x − 34)e6 − x + (2x2 − 34x + 34) · (−1) · e6 − x =
= e6 − x · (4x − 34 − 2x2 + 34x − 34) =
= e6 − x · (−2x2 + 38x − 68)
Приравниваем полученное выражение к нулю:
e6 − x · (−2x2 + 38x − 68) = 0;
−2x2 + 38x − 68 = 0;
x2 − 19x + 34 = 0;
…
x1 = 17; x2 = 2.
Множитель e6 − x снова можно безболезненно убрать, поскольку он никогда не равен нулю. Осталось отметить полученные точки и знаки производной на координатной прямой:
Обратите внимание: на рисунке отмечены знаки производной функции: y = e6 − x · (−2x2 + 38x − 68) — а вовсе не многочлена x2 − 19x + 34, как думают некоторые ученики. В скобках стоит квадратичная функция, ее график — парабола ветвями вниз, поскольку a = −2 < 0.
В точке x = 17 знак производной меняется с плюса на минус. Значит, это точка максимума, что и требовалось найти.
Смотрите также:
- Задача B15: частный случай при работе с квадратичной функцией
- Специфика работы с логарифмами в задаче B15
- Тест к уроку «Что такое числовая дробь» (легкий)
- Типичные задачи B12 с функциями
- Однородные тригонометрические уравнения: общая схема решения
- ЕГЭ 2022, задание 6. Касательная и уравнение с параметром
12. Исследование функций с помощью производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Поиск точек экстремума у сложных функций
(blacktriangleright) Сложная функция (композиция двух функций) — это функция (f=f(x)), представимая в виде (f=f(t(x))), где (t=t(x)) – функция, являющаяся “новой переменной” для функции (f).
То есть в такой функции можно ввести новую переменную (t) так, что функция полностью будет зависеть от этой новой переменной.
(blacktriangleright) Производная такой функции ищется по правилу: [{Large{f'(x)=f'(t)cdot t'(x)}}]
Примеры:
(1)) Функция (f(x)=cos {(x^2+1)}). Если сделать замену (t(x)=x^2+1), то функция примет вид (f(t)=cos t).
Найдем (f'(t)=(cos t)’=-sin t=(text{переход к переменной
}x)=-sin
{(x^2+1)})
Найдем (t'(x)=(x^2+1)’=2x)
Значит, (f'(x)=-2xcdot sin{(x^2+1)})
(2)) Функция (f(x)=x^3 +x^2). Для этой функции не существует никакой замены, кроме тождественной ((t(x)=x)). Значит она – не сложная.
Ее производную можно найти обычным способом, т.к. она элементарная:
(f'(x)=3x^2+2x)
(3)) Функция (f(x)=sin x^2 + x). Для этой функции не существует никакой замены, кроме тождественной ((t(x)=x)).
Но обычными способами вычислить ее производную не удастся. Заметим, что эта функция представлена в виде суммы двух, причем одна из них сложная ((g(x)=sin x^2)), а другая – элементарная ((h(x)=x)).
Т.к. мы знаем, что (f’=g’+h’), то найдем в отдельности производные функций (g) и (h).
Тогда (f'(x)=2xcdot cos x^2 + 1)
(blacktriangleright) Для того, чтобы найти точки экстремума, необходимо схематично изобразить график функции.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания ((f’>0)) и убывания ((f'<0)) функции, критические точки (где (f’=0) или (f’) не существует).
[begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{1} & c & 0\&&\
textbf{2} & x^a & acdot x^{a-1}\&&\
textbf{3} & ln x & dfrac1x\&&\
textbf{4} & log_ax & dfrac1{xcdot ln a}\&&\
textbf{5} & e^x & e^x\&&\
textbf{6} & a^x & a^xcdot ln a\&&\
textbf{7} & sin x & cos x\&&\
textbf{8} & cos x & -sin x\[1ex]
hline
end{array} quad quad quad quad
begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{9} & mathrm{tg}, x & dfrac1{cos^2 x}\&&\
textbf{10} & mathrm{ctg}, x & -,dfrac1{sin^2 x}\&&\
textbf{11} & arcsin x & dfrac1{sqrt{1-x^2}}\&&\
textbf{12} & arccos x & -,dfrac1{sqrt{1-x^2}}\&&\
textbf{13} & mathrm{arctg}, x & dfrac1{1+x^2}\&&\
textbf{14} & mathrm{arcctg}, x & -,dfrac1{1+x^2}\[0.5ex]
hline
end{array}]
Задание
1
#2363
Уровень задания: Равен ЕГЭ
Найдите точку минимума функции (y = e^{x^2 + 1}).
ОДЗ: (x) – произвольный.
1) [y’ = e^{x^2 + 1}cdot 2x = 2xe^{x^2 + 1}]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [2xe^{x^2 + 1} = 0qquadLeftrightarrowqquad x = 0,.] Производная существует при любом (x).
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика:
Таким образом, (x = 0) – точка минимума функции (y).
Ответ: 0
Задание
2
#2364
Уровень задания: Равен ЕГЭ
Найдите точку максимума функции (y = e^{-x^2 + 2x}).
ОДЗ: (x) – произвольный.
1) [y’ = e^{-x^2 + 2x}cdot (-2x + 2) = -2(x — 1)e^{-x^2 + 2x}]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [-2(x — 1)e^{-x^2 + 2x} = 0qquadLeftrightarrowqquad x = 1,.] Производная существует при любом (x).
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика:
Таким образом, (x = 1) – точка максимума функции (y).
Ответ: 1
Задание
3
#887
Уровень задания: Равен ЕГЭ
Найдите точку минимума функции
(y = e^{x^2 — 2016x + 2017}).
1) [y’ = e^{x^2 — 2016x + 2017}cdot(2x — 2016).]
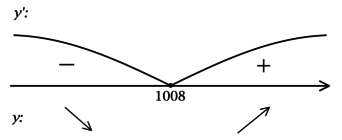
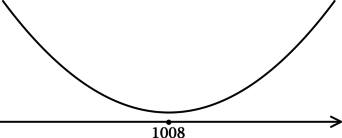
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [e^{x^2 — 2016x + 2017}cdot(2x — 2016) = 0qquadLeftrightarrowqquad x — 2016 = 0] (так как (e^t > 0) при любом (t)), откуда находим (x = 1008). Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика (y):
Таким образом, (x = 1008) – точка минимума функции (y).
Ответ: 1008
Задание
4
#885
Уровень задания: Равен ЕГЭ
Найдите точку минимума функции
(y = log_{7}(x^2 + 16x + 100)).
ОДЗ: (x^2 + 16x + 100 > 0). Решим на ОДЗ:
1) [y’ = dfrac{1}{ln 7}cdotdfrac{2x + 16}{x^2 + 16x + 100}.]
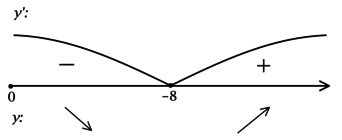
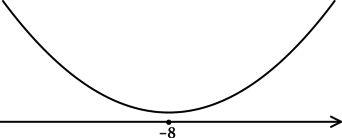
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{1}{ln 7}cdotdfrac{2x + 16}{x^2 + 16x + 100} = 0qquadLeftrightarrowqquad 2x + 16 = 0] – на ОДЗ, откуда находим (x = -8). Так как (x^2 + 16x + 100 = x^2 + 16x + 64 + 36 = (x+8)^2 + 36 > 0), то производная определена для любого (x). Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика (y):
Таким образом, (x = -8) – точка минимума функции (y).
Ответ: -8
Задание
5
#886
Уровень задания: Равен ЕГЭ
Найдите точку минимума функции
(y = log_{2016}(x^2 — 10x + 201)).
ОДЗ: (x^2 — 10x + 201 > 0). Решим на ОДЗ:
1) [y’ = dfrac{1}{ln 2016}cdotdfrac{2x — 10}{x^2 — 10x + 201}.]
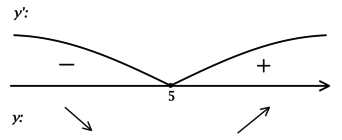
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{1}{ln 2016}cdotdfrac{2x — 10}{x^2 — 10x + 201} = 0qquadLeftrightarrowqquad 2x — 10 = 0] – на ОДЗ, откуда находим (x = 5). Так как (x^2 — 10x + 201 = x^2 — 10x + 25 + 176 = (x-5)^2 + 176 > 0), то производная определена для любого (x). Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика (y):
Таким образом, (x = 5) – точка минимума функции (y).
Ответ: 5
Задание
6
#888
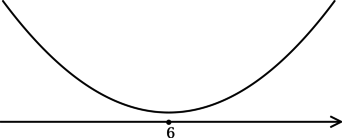
Уровень задания: Равен ЕГЭ
Найдите точку минимума функции
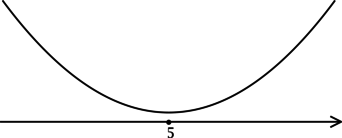
(y = sqrt{x^2 — 12x + 40}).
ОДЗ: (x^2 — 12x + 40 geq 0). Решим на ОДЗ:
1) [y’ = dfrac{2x — 12}{2sqrt{x^2 — 12x + 40}} = dfrac{x — 6}{sqrt{x^2 — 12x + 40}}.]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{x — 6}{sqrt{x^2 — 12x + 40}} = 0qquadLeftrightarrowqquad x — 6 = 0] – на ОДЗ, откуда находим (x = 6). Так как (x^2 — 12x + 40 = x^2 — 12x + 36 + 4 = (x-6)^2 + 4 > 0), то производная функции (y) определена при любом (x). Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика (y):
Таким образом, (x = 6) – точка минимума функции (y).
Ответ: 6
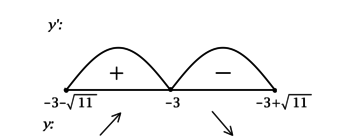
Задание
7
#889
Уровень задания: Равен ЕГЭ
Найдите точку максимума функции
(y = sqrt{-x^2 + 2 — 6x}).
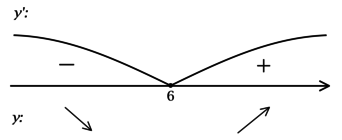
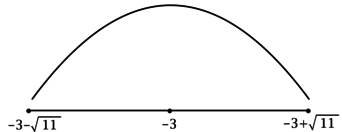
ОДЗ: (-x^2 + 2 — 6x geq 0), что равносильно (x^2 + 6x — 2leq 0), откуда находим (-3-sqrt{11} leq x leq -3 + sqrt{11}). Решим на ОДЗ:
1) [y’ = dfrac{-2x — 6}{2sqrt{-x^2 + 2 — 6x}} = -dfrac{x + 3}{sqrt{-x^2 + 2 — 6x}}.]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad -dfrac{x + 3}{sqrt{-x^2 + 2 — 6x}} = 0qquadLeftrightarrowqquad x + 3 = 0] – на ОДЗ, откуда находим (x = -3). Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’) на ОДЗ:
3) Эскиз графика (y):
Таким образом, (x = -3) – точка максимума функции (y).
Ответ: -3

УСТАЛ? Просто отдохни