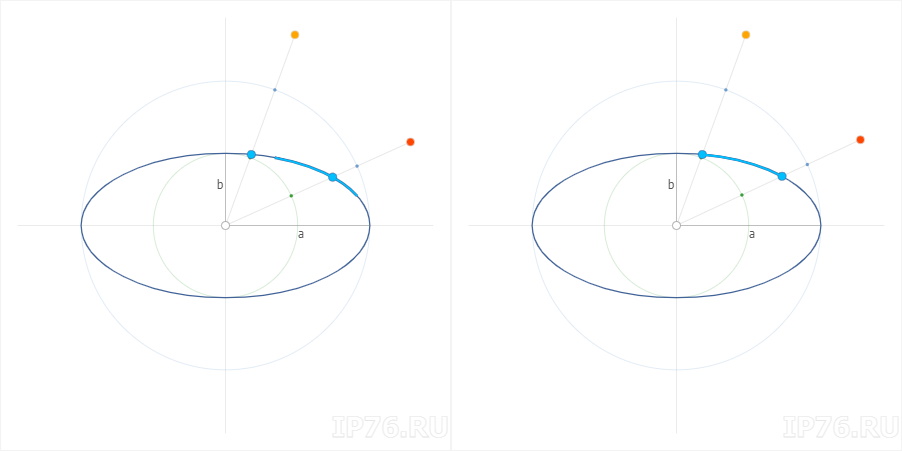
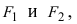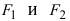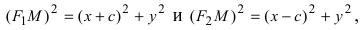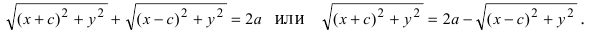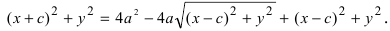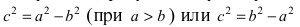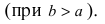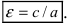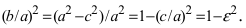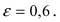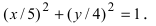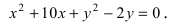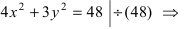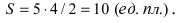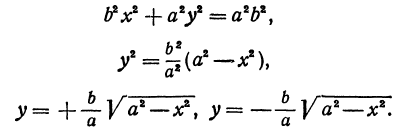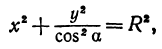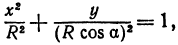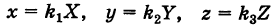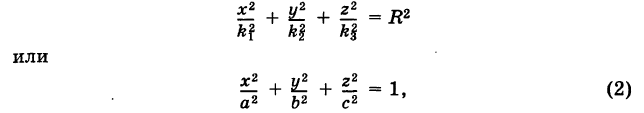Для нахождения координат точки эллипса по углу существует простое и элегантное решение. Понимаю, что для маститого математика это решение является очевидным. Однако, для меня в то далекое время, когда инет был диким, связь модемной, а я сильно молодым, это таковым не являлось.
ВНИМАНИЕ! Если Вы искали как найти координаты точки по углу от произвольной прямой и совсем не подразумевали эллипс, то Вам сюда.
Калькулятор точки на эллипсе
Давайте посмотрим, как это выглядит на практике. Потом теория. Оранжевый маркер отвечает за угол, на основании которого считаем координаты. Красный — параметрический угол, о котором ниже.
Маркеры кликабельны и таскабельны.
Если есть вопросы, предложения по калькулятору или заметили ошибку, буду очень рад обратной связиx
Эллипс:
a:
b:
Углы (град.):
Get a better browser, bro…
Параметрическое уравнение эллипса
Обратимся, как обычно, к Википедии. Находим там следующее:
Каноническое уравнение эллипса может быть параметризовано:
Очевидно, что t — это угол, и это не «наш» угол. Это какой-то другой угол, который функционально связан с «нашим». «Нашим» называю угол, от которого требуется посчитать координаты.
Таким образом, задача нахождения координат точки эллипса по углу сводится к задаче нахождения угла t, зависящим от требуемого. Нахождением этой зависимости и займемся.
Подготовка
У нас есть эллипс, описанный двумя полуосями a и b. Представим две окружности, имеющих общий центр. Меньшая окружность (зеленая) имеет радиус b. Большая окружность (синяя) имеет радиус a.
Проведем прямую из общего центра [X0;Y0] в произвольную точку плоскости [X;Y]. В результате пересечения с этими окружностями получаются две точки [X1;Y1] и [X2;Y2].
α – угол между прямой и осью X.
| Малая окружность | X1 = b × cos α | Y1 = b × sin α |
| Большая окружность | X2 = a × cos α | Y2 = a × sin α |
Нахождение зависимости
Используя уравнение (1) посчитаем координаты точки на эллипсе [X’;Y’] для угла α. Проведем прямую из центра [X0;Y0] в точку [X’;Y’]. Угол β – угол между этой прямой и осью X.
Задача сводится к тому, чтобы найти такой α, при котором β был бы равен интересующему нас углу. Таким образом, угол α будет являться параметром в уравнении (1) для требуемого угла β.
Найдем зависимость между получившимся углом β и углом α. На рисунке видно, что прилегающий к углу катет (синий) равен ранее рассчитанному X2, а противолежащий (зеленый) равен Y1:
X’ = X2 = a × cos α
Y’ = Y1 = b × sin α
Опыт показывает, что тут зачастую возникает легкий ступор. Возможно, рисунок вводит в некое заблуждение. Видим треугольник, и если с синим катетом вопросов нет, то с зеленым — масса. Почему синус от α? Угол «вона где», тут синус вообще не от того угла и т.д.
Смотрим на пересечение прямой и малой (зеленой) окружности. Зеленый катет прилетает именно оттуда. Именно так координату Y’ и рассчитывали, согласно уравнению(1). Рисунок — это иллюстрация, не метод решения.
Тангенс угла β в этом случае равен:
(3) Тангенс угла β
Используя формулу тангенса произведем дальнейшие преобразования:
(4) Зависимость тангенса α от тангенса β
Таким образом, видим прямую зависимость угла α, который нужен нам в качестве параметра в уравнении(1), от угла β, координаты точки от которого хотим получить.
Нахождение координат
Угол α находим через арктангенс. В Delphi (и не только) для этих целей используется функция ArcTan2 из модуля math. Она корректно возвращает знак ± угла в зависимости от квадранта, а также предусмотрительно нечувствительна к возможным коллизиям, типа деления на 0.
Находим синус и косинус от требуемого угла β и подставляем в параметры функции ArcTan2, согласно последней формуле (4):
|
//— находим параметр (некий угол) для уравнения — SinCos(Angle,sn,cs); t := ArcTan2(a*sn, b*cs); |
Получившийся в результате вызова ArcTan2 угол есть ничто иное, как параметр t в параметрическом уравнении (1). Подставив его в уравнение, находим координаты точки на эллипсе, отстоящей на заданный угол от оси X.
О параметре
Практический смысл параметра t состоит в том, что это угол окружности до «сплющивания». Этот тот угол окружности, который будет соответствовать точке эллипса при заданном угле. Попытаюсь на практике показать.
В JavaScript’е нет понятия эллипс. Тем более нет понятия дуги эллипса. Но можно нарисовать окружность (через дугу) и «сплющить». Может быть такой номер пройдет и с дугой?
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
// рисует дугу эллипса function drawArcEllipse(ctx, center, a, b, start, finish, colorLine=‘none’, widthLine=0.0, angle=0.0) { if (a==0.0) return; var t1 = start; var t2 = finish; ctx.beginPath(); // сохраняем контекст ctx.save(); // перемещение координат в центр эллипса ctx.translate(center.x, center.y); // поворот плоскости на угол, если требуется if (angle!=0.0) ctx.rotate(angle); // сжимаем по вертикали ctx.scale(1, b/a); // рисуем дугу ctx.arc(0, 0, a, t1, t2); // восстанавливает контекст ctx.restore(); if (colorLine!=‘none’) ctx.strokeStyle = colorLine; if (widthLine>0.0) ctx.lineWidth = widthLine; ctx.stroke(); ctx.closePath(); } |
На рисунке слева видим, что дуга расположена совершенно неправильно. Очевидно, что надо использовать какие-то другие углы. Вот тут на помощь приходит параметр эллипса. Это как раз тот самый угол, который обеспечивает «попадание» в нужный нам угол при «сплющивании» окружности.
Перепишем функцию с учетом нахождения параметра:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
// рисует дугу эллипса function drawArcEllipse(ctx, center, a, b, start, finish, colorLine=‘none’, widthLine=0.0, angle=0.0) { if (a==0.0) return; var sn = Math.sin(start); var cs = Math.cos(start); var t1 = Math.atan2(a*sn, b*cs); sn = Math.sin(finish); cs = Math.cos(finish); var t2 = Math.atan2(a*sn, b*cs); ctx.beginPath(); // сохраняем контекст ctx.save(); // перемещение координат в центр эллипса ctx.translate(center.x, center.y); // поворот плоскости на угол, если требуется if (angle!=0.0) ctx.rotate(angle); // сжимаем по вертикали ctx.scale(1, b/a); // рисуем дугу ctx.arc(0, 0, a, t1, t2); // восстанавливает контекст ctx.restore(); if (colorLine!=‘none’) ctx.strokeStyle = colorLine; if (widthLine>0.0) ctx.lineWidth = widthLine; ctx.stroke(); ctx.closePath(); } |
На рисунке справа видим, что все встало на свои места. Идеальная дуга )
Координаты точки наклонного эллипса
Перенесено в отдельную статью.
Практика
Две функции. Первая находит параметр t по углу. Вторая производит расчет координат. Из второй не вызываю первую, т.к. получится двойное вычисление полуосей. Код не настолько велик, чтобы его нельзя было продублировать.
|
//****************************************************************** // Найти угол, который будет использован в расчете точки на элипсе // Т.е. тот самый параметр t в параметрическом уравнении эллипса: // x = a * cos t // y = b * sin t //****************************************************************** function GetEllipseAngleParam(ARect : TRectF; Angle : Extended) : Extended; var sn,cs : Extended; // синус/косинус a,b : Extended; // полуоси по X/Y begin a := ARect.Width/2; b := ARect.Height/2; SinCos(Angle,sn,cs); result := ArcTan2(a * sn, b * cs); end; |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
//******************************************************************** // Найти координату точки на эллипсе по углу отклонения //******************************************************************** function CalcEllipsePointCoord(ARect : TRectF; Angle : extended) : TPointF; var sn,cs : Extended; // синус/косинус a,b : Extended; // полуоси по X/Y cnt : TPointF; // центр t : Extended; // параметр для уравнения эллипса begin // инициализация полуосей a := ARect.Width/2; b := ARect.Height/2; // центр эллипса cnt := ARect.CenterPoint; // находим параметр (некий угол) для уравнения SinCos(Angle,sn,cs); t := ArcTan2(a * sn, b * cs); // считаем результат по параметрическому уравнению SinCos (t, sn, cs); result.X := cnt.x + a * cs; result.Y := cnt.Y + b * sn; end; |
Скачать исходник + исполнямый файл
Друзья, спасибо за внимание!
Надеюсь, материал после правок стал понятней.
Подписывайтесь на телегу.
Если есть вопросы, с удовольствием отвечу )
Координаты точки эллипса по углу
IP76 > Координаты точки эллипса по углу
Для нахождения координат точки эллипса по углу существует простое и элегантное решение. Понимаю, что для маститого математика это решение является очевидным. Однако, для меня в то далекое время, когда инет был диким, связь модемной, а я сильно молодым, это таковым не являлось.
Калькулятор точки на эллипсе
Давайте посмотрим, как это выглядит на практике. Потом теория. Оранжевый маркер отвечает за угол, на основании которого считаем координаты. Красный — параметрический угол, о котором ниже.
Get a better browser, bro…
Параметрическое уравнение эллипса
Обратимся, как обычно, к Википедии. Находим там следующее:
Каноническое уравнение эллипса может быть параметризовано:
Очевидно, что t — это угол, и это не «наш» угол. Это какой-то другой угол, который функционально связан с «нашим». «Нашим» называю угол, от которого требуется посчитать координаты.
Таким образом, задача нахождения координат точки эллипса по углу сводится к задаче нахождения угла t, зависящим от требуемого. Нахождением этой зависимости и займемся.
Подготовка
У нас есть эллипс, описанный двумя полуосями a и b. Представим две окружности, имеющих общий центр. Меньшая окружность (зеленая) имеет радиус b. Большая окружность (синяя) имеет радиус a.
Проведем прямую из общего центра [X0;Y0] в произвольную точку плоскости [X;Y]. В результате пересечения с этими окружностями получаются две точки [X1;Y1] и [X2;Y2].
α – угол между прямой и осью X.
| Малая окружность | X1 = b × cos α | Y1 = b × sin α |
| Большая окружность | X2 = a × cos α | Y2 = a × sin α |
Таблица 1. Координаты точек пересечения прямой с окружностями
Нахождение зависимости
Используя уравнение (1) посчитаем координаты точки на эллипсе [X’;Y’] для угла α. Проведем прямую из центра [X0;Y0] в точку [X’;Y’]. Угол β – угол между этой прямой и осью X.
Задача сводится к тому, чтобы найти такой α, при котором β был бы равен интересующему нас углу. Таким образом, угол α будет являться параметром в уравнении (1) для требуемого угла β.
Найдем зависимость между получившимся углом β и углом α. На рисунке видно, что прилегающий к углу катет (синий) равен ранее рассчитанному X2, а противолежащий (зеленый) равен Y1:
X’ = X2 = a × cos α
Y’ = Y1 = b × sin α
Опыт показывает, что тут зачастую возникает легкий ступор. Возможно, рисунок вводит в некое заблуждение. Видим треугольник, и если с синим катетом вопросов нет, то с зеленым — масса. Почему синус от α? Угол «вона где», тут синус вообще не от того угла и т.д.
Смотрим на пересечение прямой и малой (зеленой) окружности. Зеленый катет прилетает именно оттуда. Именно так координату Y’ и рассчитывали, согласно уравнению(1). Рисунок — это иллюстрация, не метод решения.
Тангенс угла β в этом случае равен:
(3) Тангенс угла β
Используя формулу тангенса произведем дальнейшие преобразования:
(4) Зависимость тангенса α от тангенса β
Таким образом, видим прямую зависимость угла α, который нужен нам в качестве параметра в уравнении(1), от угла β, координаты точки от которого хотим получить.
Нахождение координат
Угол α находим через арктангенс. В Delphi (и не только) для этих целей используется функция ArcTan2 из модуля math. Она корректно возвращает знак ± угла в зависимости от квадранта, а также предусмотрительно нечувствительна к возможным коллизиям, типа деления на 0.
Находим синус и косинус от требуемого угла β и подставляем в параметры функции ArcTan2, согласно последней формуле (4):
Кривые второго порядка. Эллипс: формулы и задачи
Понятие о кривых второго порядка
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:

где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Эллипс, заданный каноническим уравнением
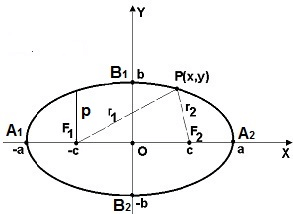
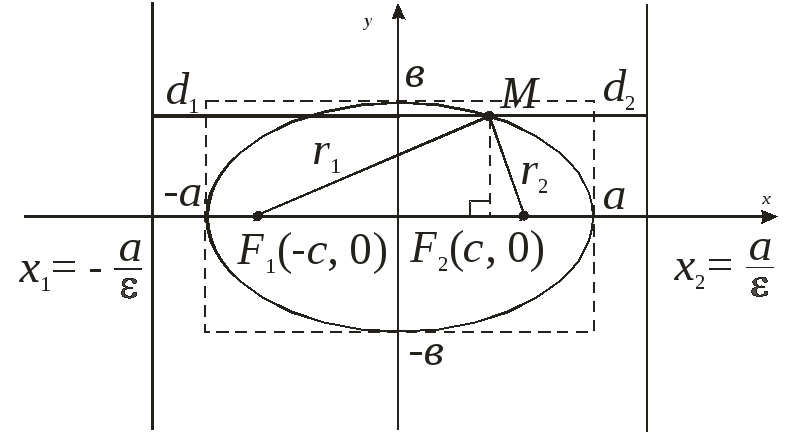
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как 

Каноническое уравнение эллипса имеет вид:

где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка 

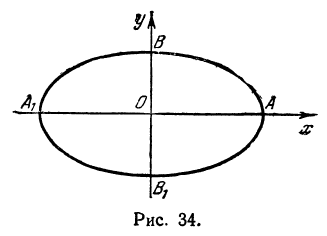
Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат — в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат — малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b , то уравнение эллипса принимает вид 
Пример 1. Проверить, является ли линия, заданная общим уравнением 
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5 , меньшая полуось — это b = 4 . Получаем каноническое уравнение эллипса:

Точки 


называются фокусами.
называется эксцентриситетом эллипса.
Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,
— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат — каноническое уравнение эллипса:

Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет 
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:

Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением 
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:

Получаем фокусы эллипса:
Решить задачи на эллипс самостоятельно, а затем посмотреть решение
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) расстояние между фокусами 30, а большая ось 34
2) малая ось 24, а один из фокусов находится в точке (-5; 0)
3) эксцентриситет 
Продолжаем решать задачи на эллипс вместе
Если 



Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями

называются директрисами эллипса (на чертеже — красные линии по краям).
Из двух вышеприведённых уравнений следует, что для любой точки эллипса

где 



Пример 7. Дан эллипс 
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. 

Получаем уравнение директрис эллипса:
Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки 

Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:

Теперь можем получить и квадрат длины меньшей полуоси:
Уравнение эллипса готово:
Пример 9. Проверить, находится ли точка 

Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:

Получили единицу, следовательно, точка находится на эллипсе.
Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:
Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.

так как из исходного уравнения эллипса 
Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
Эллипс — определение и вычисление с примерами решения
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 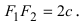
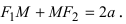
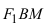
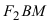
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 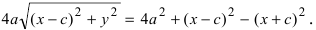
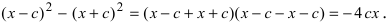
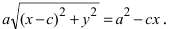
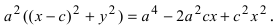
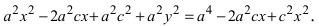
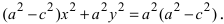
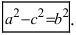
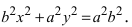
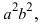
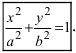
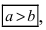
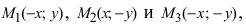
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 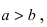
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 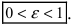
Если 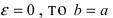
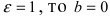
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 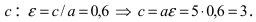
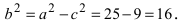
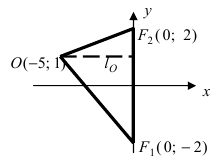
Пример:
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 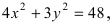
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
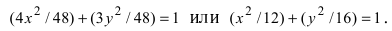
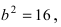
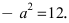
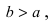
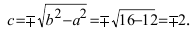
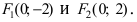
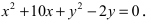
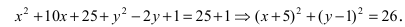
Построим в декартовой системе координат треугольник 
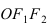
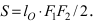
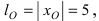
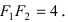
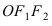
Эллипс в высшей математике
где 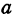
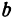
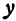
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 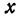
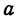
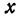
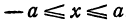
При 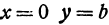
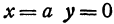
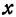

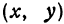
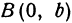
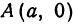
Полученная линия называется эллипсом. Число 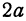
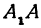
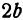
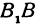
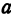
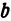
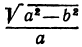
Пример:
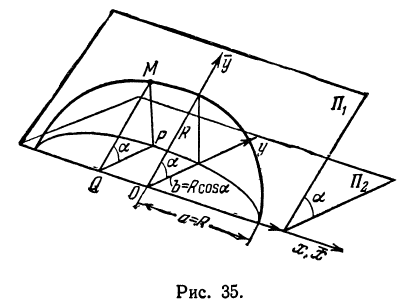
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом 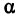
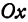
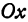
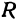
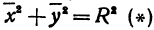
Пусть точка 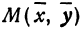
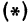
Обозначим проекцию точки 
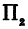
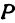
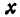
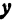
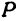

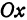
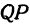
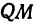
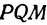
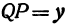
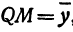
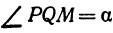
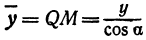

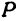
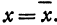
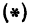
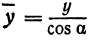
а это есть уравнение эллипса с полуосями 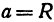
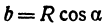
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 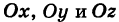
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 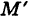
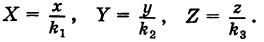
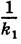
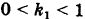
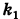
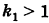
Подставляя эти формулы в уравнение (1), будем иметь
где 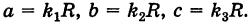
Величины 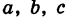
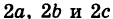
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
источники:
http://function-x.ru/curves_ellipse.html
http://www.evkova.org/ellips
I’ve been working on this one for a while now because I was trying to test a coordinate for overlap with an ellipse, and I came up with something much easier to find the point on an ellipse given an angle from the center. If you use a general first degree equation for the line and substitute into the equation for an ellipse then you can solve for x and y (the points where the line intercepts the ellipse).
To find the general first degree equation of a line, you can use this formula :
$$(y_1 — y_2)*x + (x_2 — x_1)*y + (x_1*y_2 — x_2*y_1) = 0$$
Since the ellipse is centered on the origin and the line passes through it as well, you can simplify the equation for the line by substituting $x_1 = 0$ and $y_1 = 0$ and you come up with :
$$-y_2*x + x_2*y = 0$$
Solve for x and y and you get $$x = frac{x_2*y}{y_2} , y = frac{y_2*x}{x_2}$$
Next use the equation for an ellipse $$frac{x^2}{a^2} + frac{y^2}{b^2} = 1$$
and substitute in x and y and solve for $y^2$ and $x^2$ respectively. You come up with these two equations :
$$y^2 = frac{a^2*b^2*y_2^2}{(b^2*x_2^2 + a^2*y_2^2)} , x^2 = frac{a^2*b^2*x_2^2}{b^2*x_2^2 + a^2*y_2^2}$$
If you know the point on the line you can substitute in $x_2$ and $y_2$, but since all we have is an angle, we’ll have to re-derive our line equation. It’s not hard though. To find the x and y coordinates of a point using a radius (which we won’t need) and an angle, you just use a little trigonometry. The x value of the triangle is $r*cos{theta}$ and the y value is $r*sin{theta}$. Substitute these in for $x_2$ and $y_2$ above and you get $-rsin{theta}*x + rcos{theta}*y = 0$. Notice you can divide by the radius now to remove it from the equation, leaving us with $-sin{theta}*x + cos{theta}*y = 0$. Re-substitute into the earlier equation and you get $y = sin{theta}$ and $x = cos{theta}$. Substitute these into the equations for $y^2$ and $x^2$ and you come up with the following equations.
$$y = pmfrac{absin{theta}}{sqrt{(bcos{theta})^2 + (asin{theta})^2}} , x = pmfrac{abcos{theta}}{sqrt{(bcos{theta})^2 + (asin{theta})^2}}$$
You now know another formula to find the coordinates of a point on an ellipse given only an angle from the center, or to determine whether a point is inside an ellipse or not by comparing radii. 
(схема 21)
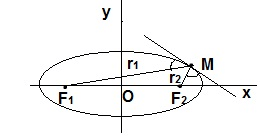
Эллипсом называется
геометрическое место точек плоскости, сумма расстояний от каждой из которых до
двух данных точек этой плоскости, называемых
фокусами, есть величина постоянная, равная 2a.
Обозначим фокусы через F1 и F2,
расстояние между ними через 2c, а сумму расстояний от произвольной точки эллипса до
фокусов – через 2a. По определению 2a>2c, то есть a>c .
Выберем систему координат
так, чтобы
фокусы F1 и F2
лежали на оси 0x, а начало координат совпадало с серединой отрезка F1F2. Тогда фокусы имют координаты: F1(–c;0) и F2(c;0). Пусть M(x;y) –
произвольная точка эллипса (текущая точка). Тогда по определению эллипса можно записать
По сути, мы получили уравнение эллипса. Упростим его с помощью ряда несложных математических преобразований:
Так как, a>c, то a2–c2>0, то можно обозначить a2–c2=b2. Тогда
последнее уравнение имеет вид:

Это
уравнение равносильно первоначальному. Оно называется каноническим уравнением
эллипса – кривой
второго порядка.
Установим форму эллипса, пользуясь его каноническим
уравнением.
1. Уравнение (2.17) содержит x и y
только в четных степенях, поэтому
если точка (x;y)
принадлежит эллипсу, то
ему также принадлежат
точки (–x;y), (x;–y), (–x;–y). Отсюда: эллипс симметричен относительно осей 0x и 0y, а также
относительно точки O(0;0), которую называют центром эллипса.
2. Найдем точки пересечения эллипса с осями координат.
Положив y=0, найдем точки A1(a;0) и A2(–a;0), в которых ось 0x пересекает эллипс. Положив в уравнении
(2.17) x=0, находим точки пересечения эллипса с осью 0y: B1(0;b) и B2(0;–b). Точки A1, A2, B1, B2 называются вершинами эллипса. Отрезки А1А2,
В1В2, а также
их длины 2a и 2b – соответственно большая и малая оси эллипса (рис. 2.4).
3. Из уравнения (2.17) следует, что каждое слагаемое в
левой части не превосходит единицы,
т.е.:

Следовательно, все точки эллипса лежат внутри
прямоугольника, ограниченного прямыми x= ± a
и y= ± b.
4. В уравнении (2.17) левая часть – сумма
неотрицательных слагаемых, т.е. при возрастании одного слагаемого другое будет
уменьшаться, если |x| возрастает, |y|
уменьшается и наоборот.
Из сказанного следует, что эллипс имеет форму
овальной замкнутой кривой. Форма эллипса зависит от отношения
(2.17) принимает вид: x2+y2=a2. Отношение 

0<ε<1, так как 0<c<a.
Отсюда видно, что чем меньше эксцентриситет эллипса,
тем будет менее эллипс сплющенным; при ε=0 эллипс
превращается в окружность.
Пусть M(x;y) – произвольная точка эллипса с фокусами F1 и F2. Длины
отрезков |MF1|=r1 и |MF2|=r2 – фокальные
радиусы точки M, r1+r2=2a. Имеют место формулы: r1=a+εx и r2=a – εx.
Прямые 
эллипса.
Если r – расстояние от произвольной точки до какого–нибудь фокуса,
d –
расстояние от этой же точки до соответствующей этому фокусу директрисы (рис. 2.5), то отношение
постоянная, равная эксцентриситету эллипса: 
Из равенства a2–c2=b2
следует, что a>b. Если же
наоборот, то уравнение (2.17) определяет эллипс, большая ось которого 2b лежит на
оси 0y, а малая ось 2a – на оси 0x. Фокусы такого
эллипса находятся в точках F1(0;c) и F2(0;–c), где 
Пример 2.5. Составить уравнение линии, для каждой точки
которой отношение расстояний от нее до
точки A(3;0) и до прямой x=12, равно числу ε=0,5. Полученное
уравнение привести к простейшему виду.
Решение. Пусть M(x;y) – текущая (произвольная) точка искомого
геометрического множества точек. Опустим перпендикуляр MB на прямую
. Тогда точка B(12;y). По условию задачи

По формуле расстояния
двумя точками получаем:
Отсюда
Полученное уравнение представляет собой эллипс вида 
Определим фокусы эллипса F1(–c;0) и F2(c;0). Для эллипса справедливо равенство b2=a2–c2,
откуда c2=a2–b2 =9 и c=3. То есть,
F1(–3;0) и F1(3;0)–
фокусы эллипса (точки F2 и A совпадают).
Эксцентриситет эллипса
Примечание. Если эллипс (окружность) вращать вокруг одной из его
осей, то описываемая им поверхность будет эллипсоидом вращения (сферой)
Пример 2.6. В геодезии используется система географических координат,
основанная на понятии геоида. Геоид – поверхность Земли,
ограниченная уровенной поверхностью, продолженной под континенты. Поверхность
геоида отличается от физической поверхности Земли, на которой резко выражены
горы и океанические впадины.
Тело, поверхность которого более всего соответствует
поверхности геоида, имеет определенные размеры и ориентирована соответственно в
теле Земли, называется референц–эллипсоидом. В нашей стране с 1946 года для всех
геодезических работ принят референц–эллипсоид Красовского с
параметрами a=6 378 245 м, b=6 356 863 м, α=1: 298,3.
Линия, проходящая вертикально через центр эллипсоида
является полярной осью. Линия, проходящая через центр эллипсоида,
перпендикулярно к полярной оси, – экваториальной осью. При пересечении
поверхности эллипсоида плоскостью, проходящей через его центр, перпендикулярно
к полярной оси, образуется окружность, называемая экватором. Окружность,
полученная от пересечения поверхности эллипсоида плоскостью, параллельной
плоскости экватора, называется параллелью. Линия пересечения
поверхности эллипсоида с плоскостью, проходящей через заданную точку и полярную
ось, называется меридианом данной точки. Положение точки на земной поверхности
определяется пересечением параллели и меридиана, проходящих через нее. Угол φ между плоскостью экватора и отвесной
линией называется географической широтой. Для определения долгот
точек один из меридианов (Гринвичский) принимают за начальный или нулевой. Угол
λ, составленный плоскостью меридиана,
проходящего через данную точку, и плоскостью начального меридиана, называется
географической долготой
Гипербола – геометрическое место точек плоскости, модуль разности расстояний от
каждой из которых до двух данных точек этой плоскости – фокусов, есть величина
постоянная, равная 2a.
Обозначим фокусы через
F1 и F2, расстояние между ними через 2c, а модуль
разности расстояний от каждой точки
гиперболы до фокусов через 2a. По определению 2a<2c, то есть a<c.
Выберем систему координат x0y так, чтобы фокусы F1 и F2 лежали на оси 0x, а начало координат совпало с серединой отрезка F1F2. Тогда фокусы будут иметь координаты F1(c;0) и F2(–c;0). На этой основе выведем уравнение гиперболы. Пусть M(x;y) – ее произвольная точка. Тогда по определению |MF1–MF2|=2a, то есть

где
b2=a2–c2.
Гипербола – линия 2–го порядка.
Установим форму гиперболы, исходя из ее канонического
уравнения.
1. Уравнение (2.18) содержит x и y только в
четных степенях. Следовательно, гипербола симметрична относительно осей координат
0x и 0y, и относительно точки O(0;0) – центра гиперболы.
2. Найдем точки пересечения гиперболы с осями координат. Положив в
уравнении (2.18) y=0, находим две точки пересечения гиперболы с осью 0x: A1(a;0) и A2(–a;0).
Положив в (2.18) x=0, получаем y2= – b2,
чего быть не может. Т.е. гипербола ось 0y не пересекает.
Точки A1(a;0) и A2(–a;0) – вершины гиперболы, а отрезок |A1A2|=2a – действительная ось. Отрезок |B1B2|=2b,
соединяющий точки B1(0;b) и B2(0;–b) – мнимая ось (рис. 2.6). Прямоугольник
со сторонами 2a и 2b – основной
прямоугольник гиперболы.
3. Из уравнения (2.18) следует, что уменьшаемое 
от прямой x=a (правая
ветвь гиперболы) и слева от прямой x=–a (левая
ветвь) (рис. 2.6).
4. Из уравнения (2.18) гиперболы видно, что
когда |x| возрастает, то |y| также
возрастает. Это
следует из того, что разность 
сохраняет значение, равноe единице. Следовательно, гипербола имеет форму,
состоящую из двух неограниченных ветвей.
Прямая L называется асимптотой некоторой неограниченной кривой, если расстояние d от точки M этой кривой до прямой L стремится к нулю при неограниченном
удалении точки M вдоль кривой
от начала координат.
Покажем, что гипербола 

данные прямые и гипербола (2.18) симметричны относительно координатных
осей, то достаточно рассмотреть только точки, расположенные в первой четверти.
Возьмем на прямой 
ту же абсциссу, что и точка M(x;y) на гиперболе 
Очевидно: так как числитель есть величина постоянная, а знаменатель дроби увеличивается с возравстанием переменной х, то длина отрезка |MN| стремится
к нулю. Так как |MN| больше
расстояния d от точки M до прямой L, то d стремится к нулю тем более (и подавно). Следовательно, прямые

асимптоты гиперболы (рис. 2.7).
Построение гиперболы начинают с нанесения ее основного прямоугольника на координатную плоскость. Далее проводят диагонали этого прямоугольника, которые являются асимптотами гиперболы, затем отмечают ее вершины, фокусы и строят ветви гиперболы.
Эксцентриситет гиперболы –
отношение расстояния между фокусами к величине её действительной оси,
обозначается ε: 
как у гиперболы c>a, то
эксцентриситет ее больше единицы. Эксцентриситет характеризует форму гиперболы. Так как 
эксцентриситет гиперболы, тем меньше отношение 
значит, тем более вытянут ее основной прямоугольник.
Эксцентриситет
равносторонней гиперболы равен 

,
для точек
правой ветви гиперболы имеют вид: r1=εx+a, r2=εx–a; для точек
левой ветви: r1=–(εx+a), r2=–(εx–a).
Прямые
гиперболы. Тот факт, что для гиперболы ε>1, то 
левая – между центром и левой вершиной. Директрисы
гиперболы имеют тоже свойство 
Уравнение 
на рисунке 2.7 пунктиром).
Значит, гиперболы

имеют общие
асимптоты. Такие гиперболы называются сопряженными.
Примечание. Если у кривой 2–го порядка смещен центр в некоторую
точку O’(x0;y0), то она
называется нецентральной кривой. Уравнение такой кривой имеет вид:
Примечание. При вращении гиперболы вокруг ее действительной оси
образуется двуполостный гиперболоид, вокруг ее мнимой оси – однополостный гиперболоид
Подробно данные уравнения рассмотрены в теме:
«Исследование общего уравнения 2–ой степени» (смотри схему 10), частными
случаями которого являются данные формулы.
Вопросы
для самопроверки
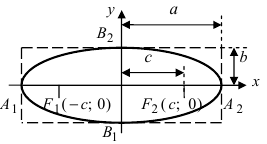
Эллипсом называют плоскую кривую, состоящую из точек, сумма расстояний которых от двух определённых точек плоскости является неизменной, строго заданной величиной, равной суммарной длине двух больших его полуосей (2a). Эти две точки называются фокусами эллипса.
F1 и F2 – фокусы эллипса;
а – большая полуось;
b – малая полуось
с – фокусное расстояние
Теорема
Фокусное расстояние эллипса и его полуоси связаны между собой соотношением [boldsymbol{a^{2}=b^{2}+c^{2}}]
Доказательство:
Когда точка M на линии эллипса находится на его пересечении с вертикальной осью, из теоремы Пифагора выходит, что
r1 + r2 = 2*√(b2 + c2)
Когда точка M пересекает горизонтальную ось
r1 + r2 = а – c + а + c
По определению эллипса r1 + r 2 = const
Это позволяет после приравнивания получить
a² = b² + c²
r1 + r2 = 2а
Что и требовалось доказать.
Уравнение эллипса
Каноническим уравнением эллипса называют уравнение [boldsymbol{1=left(x^{2} / a^{2}right)+left(y^{2} / b^{2}right)}]
Доказательство уравнения:
Введём прямоугольную декартову систему координат.
Сначала докажем, что координаты любой из точек на эллипсе удовлетворяют приведённому каноническому уравнению. Затем покажем, что любое из решений уравнения является координатами точки, лежащей на линии эллипса. Из этого будет следовать удовлетворение каноническому уравнению только тех точек, которые лежат на поверхности эллипса. Опираясь на этот факт и на определение эллипса можно будет однозначно сделать вывод, что написанное нами уравнением является каноническим уравнением или, как ещё говорят, основной формулой эллипса.
- Пусть М(х, у) будет точкой эллипса, т.е. сумму её фокальных радиусов примем равной 2а, т. е. r1 + r2 = 2a.
С помощью формулы расстояния, разделяющего две точки на координатной плоскости, можно легко найти фокальные радиусы точки M.r1 = √[(x + c)2 + y2]
r2 = √[(x — c)2 + y2]Из этих уравнений получаем √[(x + c)2 + y2] + √[(x — c)2 + y2] = 2a
Если один из корней перенести в правую часть и возвести всё в квадрат, то придём к выражению
(x + c)2 + y2 = 4a2 – 4a√[(x — c)2 + y2] + (x – c)2 + y2После сокращения приходим к 2xc = 4a2 – 4a√[(x-c)2 + y2] – 2xc
После приведения подобных членов, сокращения на 4 и уединения радикала будем иметь
a√[(x-c)2 + y2] = a2 – xcВозведём это выражение в квадрат
a2(x-c)2 + a2 y2 = a4 – 2a2xc + x2c2Если раскрыть скобки и сократить на -2a2 xc, то a2x2 + a2c2 + a2y2 = a4 + x2c2
Отсюда легко получить (a2 – c2)x2 + a2y2 = a2(a2 – c2)
Из этого следует, что b2x2 +a2y2 = a2b2 - Пусть некоторые числа (x, y) полностью удовлетворяют каноническому уравнению
1 = (x2/a2) + (y2/b2)
Пусть нам дана точка M(x,y) на координатной плоскости 0xy
Из канонического уравнения следует, что Y2 = b2(1- x2/a2)
Если это равенство подставить в выражение для фокальных радиусов, которые имеет точка M, то можно получить
r1 = √[(x + c)2 +y2] = √[x2 +2xc + c2 +b2 – b2x2/a2] = √[x2(1 – b2/a2) + 2xc +c2 +b2] =
= √[x2(a2 – b2)/a2 + 2xc + (c2 + b2)] = √[x2 (c2/a2) + 2xc +a2] = √[x(c/a) +a]2 = |a +xε|
т. е. r1 = |a +xε|
Отношение 2с/2a = c/a = ε называется эксцентриситетом эллипса. Оно у него всегда меньше 1.
То же самое просчитываем для r2.
Т. к. x2/a2 больше или равно 1 или x больше или равно большой полуоси (a), то можно сделать вывод о справедливости неравенства a≥|x|> |x|* ε = |xε|
Отсюда явно следует, что a+-|xε|>0 или a+-xε > 0 и r1 = a + xε, r2 = a — xε
Из полученных равенств выходит, что r1 + r2 = 2a, это значит, что точка M однозначно является точкой эллипса. Это нам и нужно было доказать.
Свойства эллипса
- У эллипса имеются две взаимно перпендикулярные оси симметрии.
Доказательство:
Переменные x и y в уравнение эллипса входят лишь во второй степени. Это означает, что если точка M с координатами (x,y) ему принадлежит, то и точки М1 (-x, y) и M2 (x, -y) тоже принадлежат ему. Легко проверить, что указанные координаты удовлетворяют каноническому уравнению эллипса. M1 симметрична по отношению к оси X, а M2 по отношению к оси Y. Получается, что у эллипса есть две взаимно перпендикулярные точки симметрии. - У эллипса есть центр симметрии.
Доказательство:
Если координаты точки М(x,y) будут удовлетворять уравнению эллипса, то и точка
N (–x; –y) ему тоже будет удовлетворять. M и N симметричны по отношению к началу координат. Это как раз и означает, что у эллипса имеется центр симметрии. - Эллипс пересекает каждую из осей в двух точках.
Доказательство:
Возьмём произвольную точку эллипса M(x,y). Расстояние этой точки до фокусов будетr1 = √[(x + c)2 + y2]
r2 = √[(x — c)2 + y2]Теперь давайте рассмотрим выражение
(x+-c)2 + y2 = x2 +- 2xc + c2+ y2 =
= x2 +- 2xc + a2 – b2 +y2 = x2 +- 2xc+ a2 — b2 + b2(1-x2/a2) =
= (a2 – b2)*x2/a2 +-2xc +a2 = c2*x2/a2+-2xa(c/a) + a2 = (a +c*x/a)2Эксцентриситет эллипса, как сказано ранее, меньше 1. Т. к. |x|≤ a, то a – εx > 0. Поэтому
F1M = a + εx и F2M = a – εx. Напомним, что ε – это эксцентриситет эллипса.
А теперь несколько свойств эллипса без доказательств.
- Эллипс можно получить, сжав окружность.
- Если через эллипс проходят две прямые, то отрезок, концами которого являются середины отрезков созданных при пересечении прямых, обязательно пересекает середину, центр эллипса.
- Угол, созданный касательной к эллипсу и его радиусом, проходящем через фокусы указанной геометрической фигуры, в любых случаях пересекает середину эллипса.
- Уравнение касательной к эллипсу в точке М, имеющей координаты xM и yM
1 = (x*xM)/a2 + (y*yM)/b2 - Эволюта эллипса представляет собой астероиду, растянутую вдоль его малой оси.
- Угол между касательной к эллипсу и одним его фокальным радиусом (r1) имеет ту же величину, что и угол, разделяющий касательную и другой фокальный радиус (r2) фигуры.
Как построить эллипс
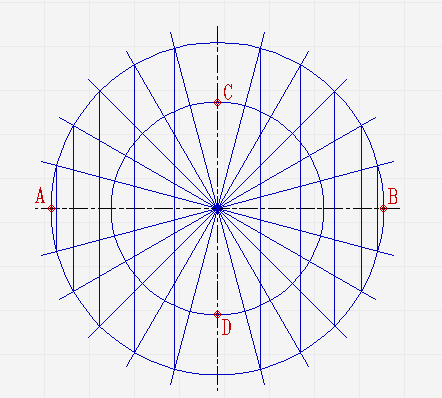
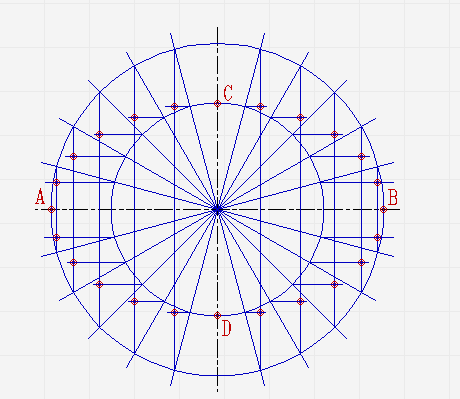
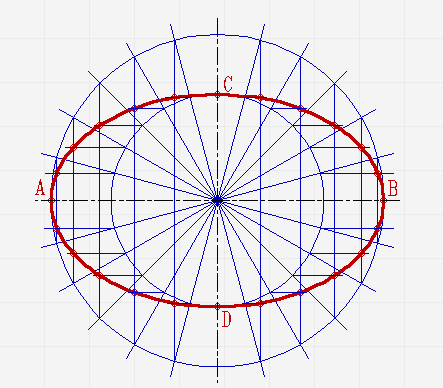
Расскажем, как построить эллипс по его большой и малой полуосям и с помощью циркуля.
Построение эллипса по его большой и малой осям
Считается самым простым, не требующим серьёзных навыков.
Проведите две перпендикулярные оси;
От места пересечения осей на вертикальной отложите верх и вниз отрезки. Они будут составлять малую ось эллипса. На горизонтальной отложите отрезки вправо и влево. Из них будет состоять большая ось;
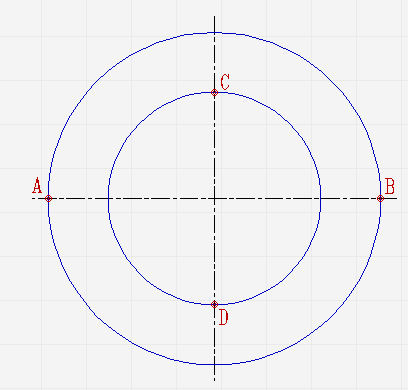
Проведите две концентрические окружности. Одну диаметром AB, диаметром CD;
Проведите ещё диаметры в различных направлениях;
В местах, где лучи соприкасаются с окружностями, проведите линии параллельные малой и большой осям эллипса, пока они не пересекутся в точках, которые принадлежат эллипсу;
Соедините полученные точки плавной линией.
Нет времени решать самому?
Наши эксперты помогут!
Как построить эллипс с помощью циркуля
Во многом здесь всё аналогично предыдущему способу, поэтому перегружать текст иллюстрациями не будем.
Порядок действий следующий:
- Проведите две перпендикулярные линии. Они будут осями эллипса, а точка их пересечения центром геометрической фигуры;
- Определитесь с величиной большой и малой полуосей, если их значения не заданы в условии задачи;
- Установите раствор циркуля на длину большой полуоси (a). Поместите циркуль в точку O и отметьте на одной из линий две точки, P1 и P2. Установите раствор циркуля на длину малой полуоси. Опять поместите его в точку O и отметьте на другой из линий ещё две точки, обозначьте их как Q1 и Q2. Отрезки P1P2 и Q1Q2 будут большой и малой полуосями будущего эллипса;
- Установите раствор циркуля на величину a. Поместите циркуль в точке Q1 или Q2. После этого обозначьте циркулем на отрезке P1P2 точки F1 и F2. Это будут фокусы фигуры.
- Отметьте на P1P2 любую точку и обозначьте её T. Поставьте в этой точке циркуль и измерьте этим инструментом расстояние до P1. Затем начертите окружность данного радиуса из фокуса F1. После этого нужно сделать ещё одну окружность с радиусом величиной с расстояние от T до P2, но уже с центром из F2;
- Отметьте точки, в которых пересекаются обе окружности. Повторяйте процедуру, описанную в предыдущем пункте с новыми точками, отмечаемыми на отрезке P1P2;
- Соедините точки пересечения окружностей сплошной линией, когда построите их достаточное количество. Так у вас получится построить фигуру эллипс с помощью циркуля.
Примеры решения задач
Задача 1
Эллипс задан уравнением 16x2 + 25y2 = 400. Требуется найти большую и малую полуоси эллипса, координаты его фокусов и эксцентриситет.
Решение:
Разделим полученное уравнение на 400. Этим мы приведём его к виду
(x2/25) + (y2/16) =1. Большая полуось равна 5, корню квадратному из 25, а малая 4, корню квадратному из 16.
Из соотношения a² = b² + c² находим фокусное расстояние. Оно равно
c=+-√(a2 – b2) = +-√(25-16) = +-3, а значит координаты фокусов будут
F1(-3,0) и F2 (3,0). Эксцентриситет ε = с/a = 3/5.
Ответ: a = 5, b = 4, ε = 3/5.
Задача 2
Выяснить, является ли эллипсом линия, заданная как
9x2 + 25y2 – 225 = 0
Преобразуем данное нам уравнение к каноническому виду. Для этого:
Перенесём 225 в правую сторону
9x2 + 25y2 = 225
Поделим обе части этого уравнения на 225
(9x2/225) + (25y2/225) = 1
Сократим дроби и получим
(x2/25) + (y2/9) = 1
Как видим, нам удалось получить каноническое уравнение эллипса в чистом виде, т. е. исходное уравнение представляет собой эллипс, что и требовалось выяснить.
Ответ: 9x2 + 25y2 – 225 = 0 является уравнением эллипса.
Задача 3
Составить каноническое уравнение эллипса если расстояние между фокусами равно 8, а большая ось 10.
Решение:
Если большая ось равняется 10, значит полуось будет 5.
Если фокусное расстояние равно 8, то число c из координат фокусов будет 4.
Далее нужно подставить и вычислить
4 = √(25-b2)
Возведём это уравнение в квадрат
16 = 25 – b2
Перенесём b2 влево, а 16 вправо
b2 = 25 – 16 =9
В результате этих не сложных преобразований и вычислений получим каноническое уравнение
(x2/25) + (y2/9) = 1
Ответ: (x2/25) + (y2/9) = 1.
Задача 4
Получить каноническое уравнение эллипса, если его эксцентриситет равен 12/13, а большая полуось равна 26.
Решение:
Из уравнения эксцентриситета ε = с/a находим, что a = 13, а величина с = 12. Далее нужно вычислить квадрат длины меньшей полуоси
c = √(169 – b2)
Возведём обе части уравнения в квадрат
c2 = 169 – b2
Отсюда
b2 = 169 – 144 = 25
Далее остаётся лишь составить каноническое уравнение
(x2/169) + (y2/25) = 1
Ответ: (x2/169) + (y2/25) = 1
Задача 5
Найти фокусы у эллипса, который задан уравнением (x2/25) + (y2/16) = 1
Решение:
Нам нужно найти число с, которое определяет первые координаты фокусов
c = √(25-16) =3
Фокусы заданного эллипса будут равны
F1(-3,0) и F2(3,0).
Ответ: F1(-3,0) и F2(3,0).