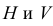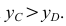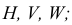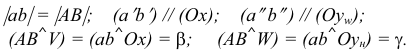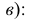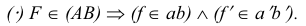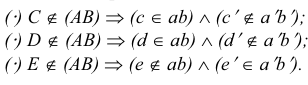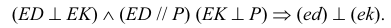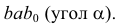Проекции точек на поверхностях геометрических тел
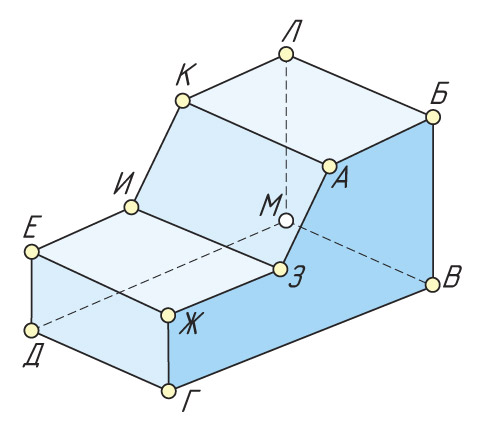
Вы уже знаете, как построить проекции предмета или объекта. Часто при изготовлении изделий необходимо по заданным проекциям определить геометрическую форму предметов и их частей. Предмет можно рассматривать как комбинацию различных геометрических элементов: вершин, ребер, граней и т. д.
Укажите количество вершин, ребер и граней изображенного предмета.
|
Для точного построения изображений ряда деталей необходимо уметь находить проекции отдельных точек. Чтобы построить проекции точки, принадлежащей поверхности геометрического тела, необходимо понять, на какой поверхности или на каком элементе поверхности (ребре, вершине, грани) находится эта точка. Представив любую деталь как совокупность геометрических тел, можно легко найти проекцию точки. |
 |
|
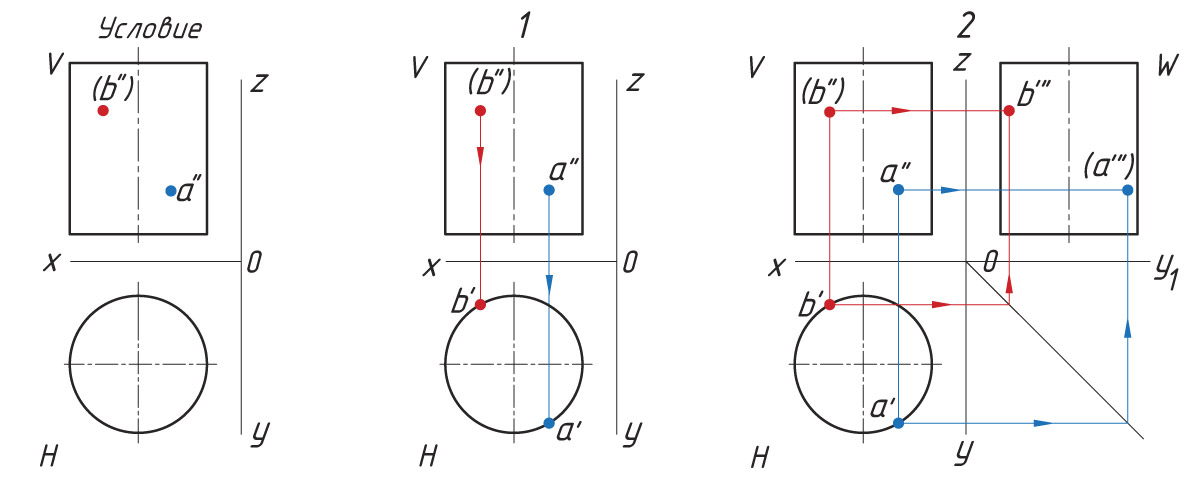
Рассмотрим проекции точки на геометрических телах. Проецирование точек на поверхности цилиндра Последовательность проецирования точек 1. Находят горизонтальные проекции точек а′ и b′. Так как горизонтальная проекция боковой проекции цилиндра отображается в виде круга, то проекции точек а′ и b′ будут находиться на нем. Для их нахождения проводят вертикальные линии связи из проекций точек а″ и b″ до пересечения с окружностью. 2. Проекции точек а′″ и b′″ находят на пересечении линий проекционной связи. |
 |
Направление взгляда на плоскости проекций H, W помогает определить видимость проекций точек на горизонтальной и профильной плоскости проекций. Например, проекции а′ и b′ на плоскости H видны. Проекция а′″ на плоскости W не видна (показана в скобках), проекция b′″ видна (показана без скобок).
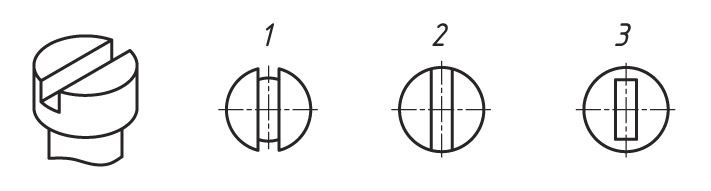
Определите, какая из горизонтальных проекций на рисунке является проекцией наглядного изображения головки винта.
|
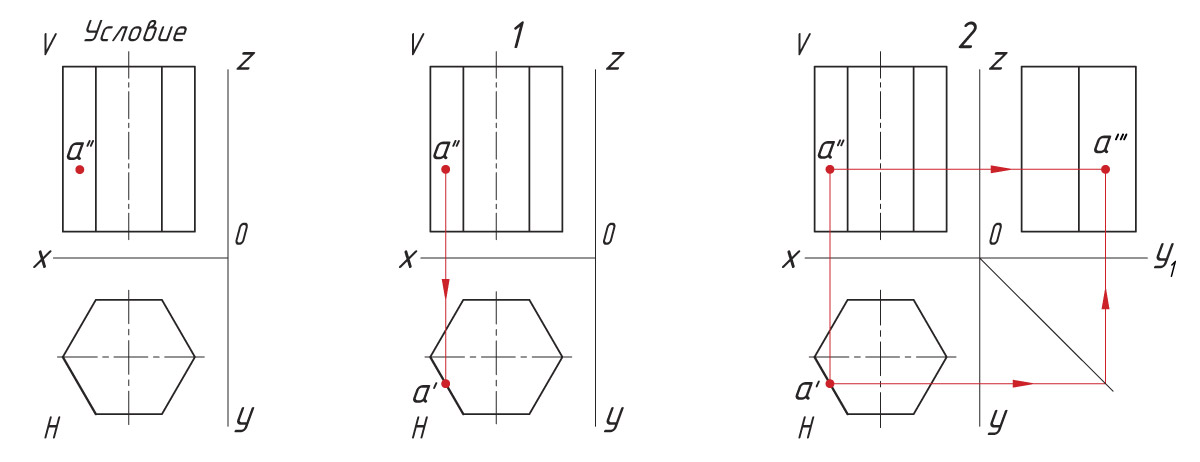
Проецирование точек на поверхности призмы Последовательность проецирования точек 1. Находят горизонтальную проекцию точки а′. Для ее нахождения проводят вертикальную линию связи из проекции точки а″ до пересечения с шестиугольником (горизонтальная проекция призмы). 2. Проекцию точки а′″ находят на пересечении линий проекционной связи. |
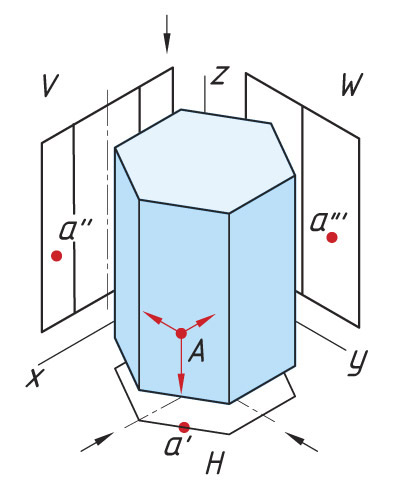 |
Опишите последовательность проецирования точки, находящейся на ребре призмы. Выполните это построение.
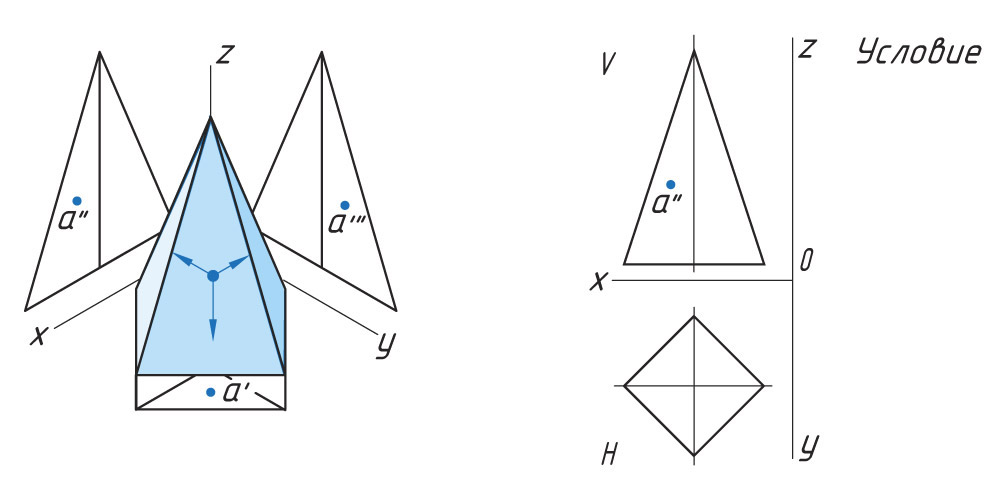
Проецирование точек на поверхности пирамиды
Построение проекции точки, лежащей на ребре
Если точка находится на ребре предмета, то сначала необходимо выполнить проекцию ребра, а затем при помощи линий проекционной связи найти проекции точки, лежащей на ребре.
Как вы считаете, можно ли таким способом спроецировать точку, находящуюся не на ребре, а на грани четырехгранной пирамиды? Свои предположения проверьте на практике.
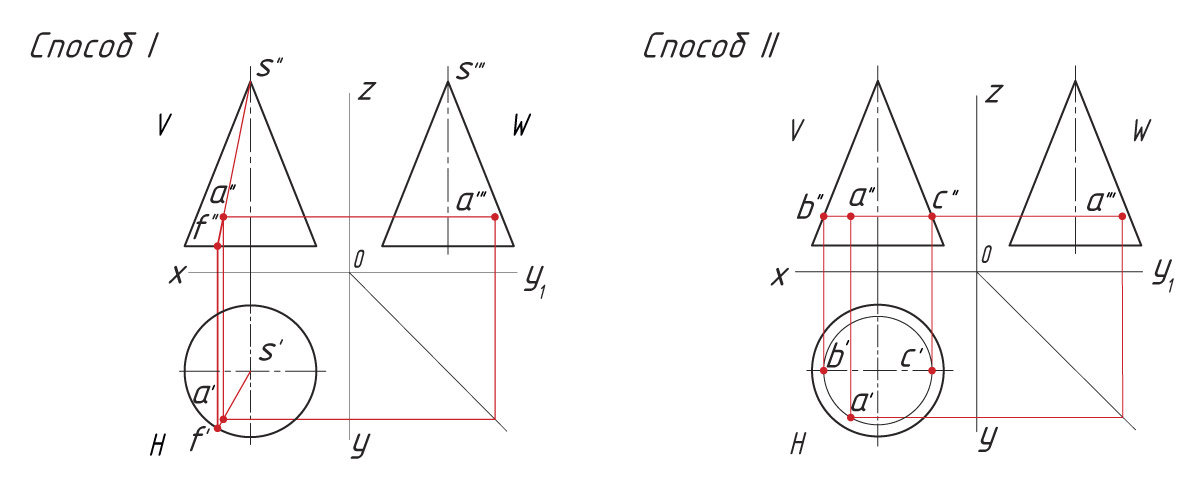
Общий метод определения точки, лежащей на поверхности геометрического тела, заключается в следующем: через точку на поверхности проводят вспомогательную прямую, проекции которой легко определяются на данной поверхности.
Построение проекции точки, лежащей на грани
Задана фронтальная проекция а″ точки А, лежащая на боковой поверхности четырехгранной пирамиды.
Проекции точек можно определить несколькими способами. Рассмотрим каждый из них.
|
Способ I. 1. Находят горизонтальную проекцию точки а′: вспомогательной прямой соединяют заданную проекцию точки а″ с проекцией вершины пирамиды s″ и продлевают ее до пересечения с основанием в точке f″. |
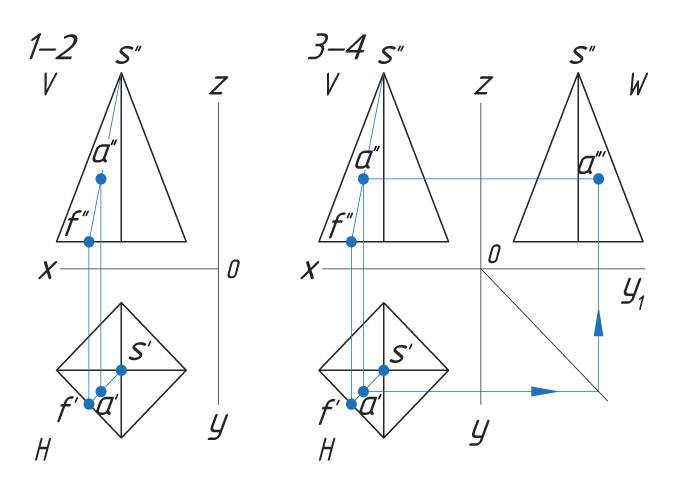 |
|
Способ II. 1. Через проекцию а″ точки А проводят вспомогательную прямую и получают точки пересечения с ребрами пирамиды 1″ и 2″. |
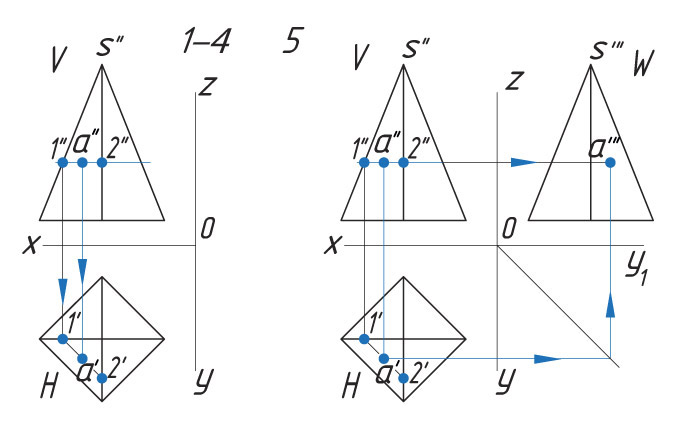 |
На ваш взгляд, изменится ли положение проекции точки, если вспомогательную прямую провести не параллельно, а наклонно к горизонтальной плоскости?
|
Проецирование точек на поверхности конуса. На поверхности конуса проекции точек можно также определить двумя способами. Способ I заключается в определении проекций точки с помощью вспомогательной линии — образующей, расположенной на поверхности конуса и проведенной через точку А. |
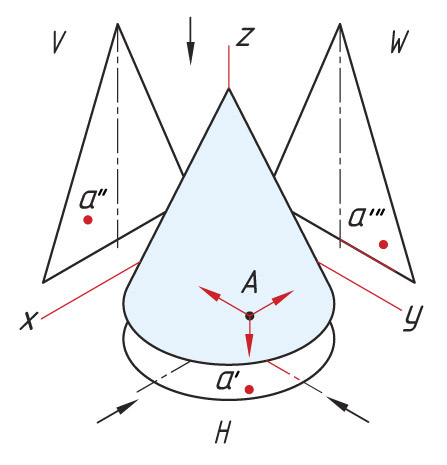 |
Лекция № 2. Точка
1. Проекции точки на две плоскости проекций
Рассмотрим проекции точек на две плоскости, для чего возьмем две перпендикулярные плоскости (рис. 4), которые будем называть горизонтальной фронтальной и плоскостями. Линию пересечения данных плоскостей называют осью проекций. На рассмотренные плоскости спроецируем одну точку А с помощью плоской проекции. Для этого необходимо опустить из данной точки перпендикуляры Аа и A на рассмотренные плоскости.
Проекцию на горизонтальную плоскость называют горизонтальной проекцией точки А, а проекцию а́ на фронтальную плоскость называют фронтальной проекцией.
Точки, которые подлежат проецированию, в начертательной геометрии принято обозначать с помощью больших латинских букв А, В, С. Для обозначения горизонтальных проекций точек применяют малые буквы а, b, с… Фронтальные проекции обозначают малыми буквами со штрихом вверху а́, b́, с́…
Применяется также и обозначение точек римскими цифрами I, II,… а для их проекций — арабскими цифрами 1, 2… и 1́, 2́…
При повороте горизонтальной плоскости на 90° можно получить чертеж, в котором обе плоскости находятся в одной плоскости (рис. 5). Данная картина называется эпюром точки.
Через перпендикулярные прямые Аа и Аа́ проведем плоскость (рис. 4). Полученная плоскость является перпендикулярной фронтальной и горизонтальной плоскостям, потому что содержит перпендикуляры к этим плоскостям. Следовательно, данная плоскость перпендикулярна линии пересечения плоскостей. Полученная прямая пересекает горизонтальную плоскость по прямой аах, а фронтальную плоскость — по прямой а́ах. Прямые аах и а́ах являются перпендикулярными оси пересечения плоскостей. То есть Аааха́ является прямоугольником.
При совмещении горизонтальной и фронтальной плоскостей проекции а и а́ будут лежать на одном перпендикуляре к оси пересечения плоскостей, так как при вращении горизонтальной плоскости перпендикулярность отрезков аах и а́ах не нарушится.
Получаем, что на эпюре проекции а и а́ некоторой точки А всегда лежат на одном перпендикуляре к оси пересечения плоскостей.
Две проекции а и а́ некоторой точки А могут однозначно определить ее положение в пространстве (рис. 4). Это подтверждается тем, что при построении перпендикуляра из проекции а к горизонтальной плоскости он пройдет через точку А. Точно так же перпендикуляр из проекции а́ к фронтальной плоскости пройдет через точку А, т. е. точка А находится одновременно на двух определенных прямых. Точка А является их точкой пересечения, т. е. является определенной.
Рассмотрим прямоугольник Aaaха́ (рис. 5), для которого справедливы следующие утверждения:
1) Расстояние точки А от фронтальной плоскости равно расстоянию ее горизонтальной проекции а от оси пересечения плоскостей, т. е.
Аа́ = аах;
2) расстояние точки А от горизонтальной плоскости проекций равно расстоянию ее фронтальной проекции а́ от оси пересечения плоскостей, т. е.
Аа = а́ах.
Иначе говоря, даже без самой точки на эпюре, используя только две ее проекции, можно узнать, на каком расстоянии от каждой из плоскостей проекций находится данная точка.
Пересечение двух плоскостей проекций разделяет пространство на четыре части, которые называют четвертями (рис. 6).
Ось пересечения плоскостей делит горизонтальную плоскость на две четверти — переднюю и заднюю, а фронтальную плоскость — на верхнюю и нижнюю четверти. Верхнюю часть фронтальной плоскости и переднюю часть горизонтальной плоскости рассматривают как границы первой четверти.
При получении эпюра вращается горизонтальная плоскость и совмещается с фронтальной плоскостью (рис. 7). В этом случае передняя часть горизонтальной плоскости совпадет с нижней частью фронтальной плоскости, а задняя часть горизонтальной плоскости — с верхней частью фронтальной плоскости.
На рисунках 8-11 показаны точки А, В, С, D, располагающиеся в различных четвертях пространства. Точка А расположена в первой четверти, точка В — во второй, точка С — в третьей и точка D — в четвертой.
При расположении точек в первой или четвертой четвертях их горизонтальные проекции находятся на передней части горизонтальной плоскости, а на эпюре они лягут ниже оси пересечения плоскостей. Когда точка расположена во второй или третьей четверти, ее горизонтальная проекция будет лежать на задней части горизонтальной плоскости, а на эпюре будет находиться выше оси пересечения плоскостей.
Фронтальные проекции точек, которые расположены в первой или второй четвертях, будут лежать на верхней части фронтальной плоскости, а на эпюре будут находиться выше оси пересечения плоскостей. Когда точка расположена в третьей или четвертой четверти, ее фронтальная проекция — ниже оси пересечения плоскостей.
Чаще всего при реальных построениях фигуру располагают в первой четверти пространства.
В некоторых частных случаях точка (Е) может лежать на горизонтальной плоскости (рис. 12). В этом случае ее горизонтальная проекция е и сама точка будут совпадать. Фронтальная проекция такой точки будет находиться на оси пересечения плоскостей.
В случае, когда точка К лежит на фронтальной плоскости (рис. 13), ее горизонтальная проекция k лежит на оси пересечения плоскостей, а фронтальная ḱ показывает фактическое местонахождение этой точки.
Для подобных точек признаком того, что она лежит на одной из плоскостей проекций, служит то, что одна ее проекция находится на оси пересечения плоскостей.
Если точка лежит на оси пересечения плоскостей проекций, она и обе ее проекции совпадают.
Когда точка не лежит на плоскостях проекций, она называется точкой общего положения. В дальнейшем, если нет особых отметок, рассматриваемая точка является точкой общего положения.
2. Отсутствие оси проекций
Для пояснения получения на модели проекций точки на перпендикулярные плоскости проекций (рис. 4) необходимо взять кусок плотной бумаги в форме удлиненного прямоугольника. Его нужно согнуть между проекциями. Линия сгиба будет изображать ось пересечения плоскостей. Если после этого согнутый кусок бумаги вновь расправить, получим эпюр, похожий на тот, что изображен на рисунке.
Совмещая две плоскости проекций с плоскостью чертежа, можно не показывать линию сгиба, т. е. не проводить на эпюре ось пересечения плоскостей.
При построениях на эпюре всегда следует располагать проекции а и а́ точки А на одной вертикальной прямой (рис. 14), которая перпендикулярна оси пересечения плоскостей. Поэтому, даже если положение оси пересечения плоскостей остается неопределенным, но ее направление определено, ось пересечения плоскостей может находиться на эпюре только перпендикулярно прямой аа́.
Если на эпюре точки нет оси проекций, как на первом рисунке 14 а, можно представить положение этой точки в пространстве. Для этого проведем в любом месте перпендикулярно прямой аа́ ось проекции, как на втором рисунке (рис. 14) и согнем чертеж по этой оси. Если восстановить перпендикуляры в точках а и а́ до их пересечения, можно получить точку А. При изменении положения оси проекций получаются различные положения точки относительно плоскостей проекций, но неопределенность положения оси проекций не влияет на взаимное расположение нескольких точек или фигур в пространстве.
3. Проекции точки на три плоскости проекций
Рассмотрим профильную плоскость проекций. Проекции на две перпендикулярные плоскости обычно определяют положение фигуры и дают возможность узнать ее настоящие размеры и форму. Но бывают случаи, когда двух проекций оказывается недостаточно. Тогда применяют построение третьей проекции.
Третью плоскость проекции проводят так, чтобы она была перпендикулярна одновременно обеим плоскостям проекций (рис. 15). Третью плоскость принято называть профильной.
В таких построениях общую прямую горизонтальной и фронтальной плоскостей называют осью х, общую прямую горизонтальной и профильной плоскостей — осью у, а общую прямую фронтальной и профильной плоскостей — осью z. Точка О, которая принадлежит всем трем плоскостям, называется точкой начала координат.
На рисунке 15а показана точка А
Конец ознакомительного фрагмента.
Содержание:
Для полного выявления наружных и внутренних форм деталей и их соединений вводят три и более плоскости проекций.
Введем в систему плоскостей
Три взаимно-перпендикулярные плоскости делят пространство на восемь частей, восемь октантов (рис. 3.2) (от лат. octo — восемь).
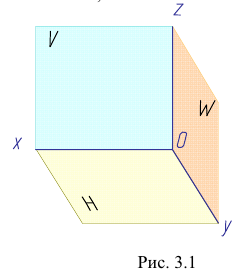
В нашей стране принята европейская система расположения проекций. Ось х направлена от начала координат влево, у — вперед (к нам), z — вверх. Обратные направления координатных осей считаются отрицательными.
Чертеж точки
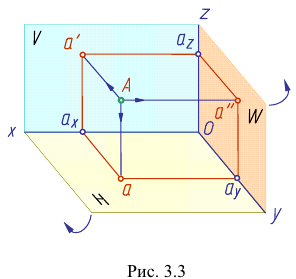
Опустим из точки А проецирующие лучи (перпендикуляры) до пересечения с плоскостями проекций Н, V и W. Точки пересечения перпендикуляров с плоскостями проекций — это проекции точки на каждую из плоскостей проекций:
- а — горизонтальная;
- а‘ — фронтальная;
- а » — профильная.
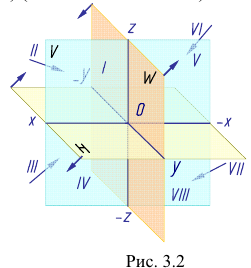
Данное наглядное изображение тонки в системе плоскостей Н, V и W (рис. 3.3) неудобно для черчения из-за сложности. Преобразуем его так, чтобы горизонтальная и профильная плоскости проекций совпали с фронтальной плоскостью проекций, образуя одну плоскость чертежа (рис. 3.4).
Это преобразование осуществляют путем поворота вокруг оси х плоскости Н на угол 90° вниз и плоскости W на угол 90° вправо вокруг оси z. В результате указанного совмещения плоскостей получаем чертеж, называемый эпюр Монжа (от франц, 
На эпюре мы не можем показать пространственную картину расположения плоскостей проекций и точки. Но эпюр обеспечивает точность изображений при значительной простоте построений.
В дальнейшем эпюр Монжа, а также проекционные чертежи будем называть одним словом — чертеж (или комплексный чертеж).
Горизонтальная и фронтальная проекции точки 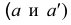
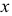
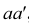
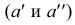
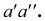
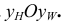
Таким образом, на комплексном чертеже трех ортогональных проекций точки
- две проекции находятся на одной линии связи;
- линии связи перпендикулярны осям проекций;
- две проекции точки определяют положение се третьей проекции;
- две проекции точки определяют ее положение в пространстве.
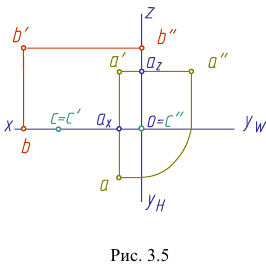
Положение точки в пространстве задается при помощи трех се координат (абсциссы 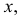
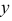
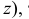
По отношению к плоскостям проекций точка может занимать как общее (точка А), так и частные (точки В и С) положения (рис. 3.5). Если точка лежит в плоскости проекций, то две ее проекции лежат на осях проекций (точка В). У такой точки одна ее координата равна нулю. Если точка принадлежит одновременно двум плоскостям проекций (точка С), то она лежит на оси проекций. Две ее проекции совпадают, а третья совпадает с точкой О — началом координат. В атом случае две ее координаты равны нулю. Если точка принадлежит трем плоскостям проекций, то она расположена в начале координат.
Таким образом, величины отрезков линий связи на чертеже определяют численное расстояние проецируемой точки до плоскости проекций. Отрезок 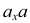
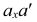
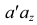
Взаимное положение двух точек. Условия видимости на чертеже
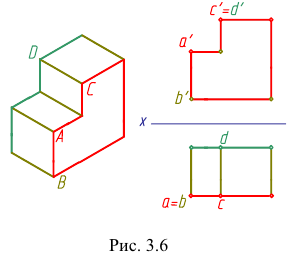
Рассмотрим чертеж модели, изображенной на рис. 3.6. Проекции некоторых точек совпадают, так как они расположены на одной проецирующей прямой. Например, на горизонтальной плоскости совпали проекции а и b вершин А и В — они лежат на одной горизонтально — проецирующей прямой. На фронтальной плоскости совпали проекции с ‘ и d ‘ вершин С и D — они лежат на одной фронтально-проецирующей прямой.
Точки, лежащие на одной проецирующей прямой, называют конкурирующими. А и В — горизонтально-конкурирующие точки, а С и D — фронтально-конкурирующие точки и т.д.
Ясно, что если две точки лежат на одной проецирующей прямой, то одна из них закрывает другую. Как определить, какая из них будет видимая и какая невидимая?
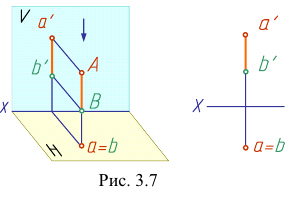
Из двух горизонтально- конкурирующих точек на горизонтальной плоскости видима та, которая расположена в пространстве выше. Анализируя положение фронтальных проекций точек (рис. 3.7), определяем, что точка А имеет большую координату z, чем точка В.
Следовательно, точка А расположена выше точки В и при проецировании на горизонтальную плоскость проекций закроет точку В. Точка А на горизонтальной плоскости видима, точка В — невидима. На фронтальной плоскости они обе видимы.
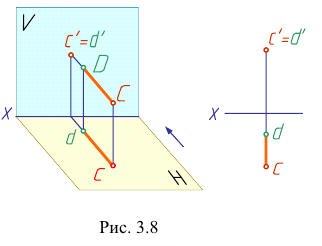
Из двух фронтально- конкурирующих точек на фронтальной плоскости проекций будет видима та, которая расположена ближе к наблюдателю, стоящему лицом к фронтальной плоскости проекций (рис. 3.8).
Какая из точек ближе к наблюдателю, можно определить по горизонтальным проекциям. Например, сравнивая горизонтальные проекции точек D и С , заключаем, что на фронтальной плоскости проекций видима точка С, а точка D — невидима, так как
Из двух профильно-конкурирующих точек на профильной плоскости проекций будет видима та точка, которая расположена левее.
Итак, если на чертеже одноименные проекции точек не совпадают или совпадает только одна пара проекций, то такие точки в пространстве не совпадают, а удалены друг от друга на определенное расстояние (рис. 3.7, 3.8).
Чертёж отрезка прямой. Прямые частного положения
Наглядное изображение отрезка АВ прямой и его ортогональное проецирование на плоскость Р показано на рис. 3.9. Рассмотрим ортогональное проецирование отрезка АВ с учетом свойств параллельного проецирования. Проецирующие прямые 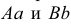
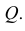
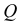
Наглядное изображение проецирования отрезка АВ прямой на две плоскости проекций в системе Н,V показано на рис. 3.10, чертеж — на рис. 3.1 I.
Если какая-либо точка принадлежит прямой, то ее проекция принадлежит проекции прямой. Например, точка D (рис. 3.9) принадлежит прямой АВ, ее проекции — проекциям прямой.
Относительно плоскостей проекции прямая может занимать различные положения:
- — не параллельное ни одной из плоскостей проекций
- — параллельное одной из плоскостей проекций (прямая может и принадлежать этой плоскости);
- — параллельное двум плоскостям проекций, то есть перпендикулярное третьей.
Прямую, не параллельную ни одной из плоскостей проекций, называют прямой общего положения (рис. 3.9 — 3.11).
Прямую, параллельную одной из плоскостей проекций или двум плоскостям проекций (то есть перпендикулярную третьей), называют прямой частного положения.
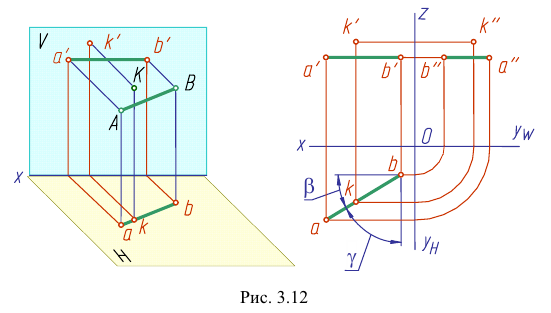
На рис. 3.12 — 3.14 приведены наглядные изображения и чертежи прямых частного положения — прямых, параллельных плоскостям проекций. Такие прямые называют прямыми уровня.
Различают три вида таких прямых.
Прямая АВ параллельна плоскости Н
Такую прямую называют «горизонтальной прямой» (рис. 3.12). Фронтальная проекция прямой 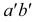
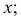
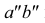
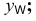
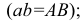
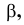
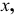
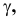
Прямая CD параллельна плоскости V
Такую прямую называют «фронтальной прямой» (рис. 3.13).
Горизонтальная проекция прямой cd параллельна оси х; профильная проекция 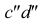
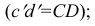
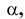
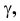
Прямая EF параллельна плоскости IF
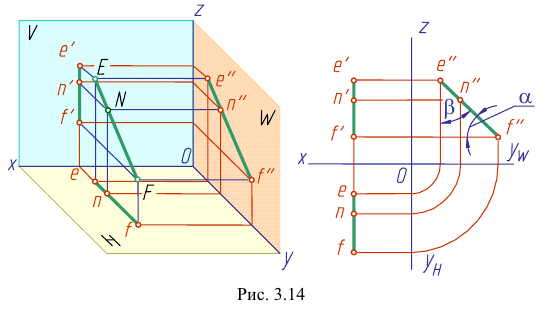
Такая прямая носит название «профильная прямая» (рис. 3.14).
Горизонтальная проекция прямой 
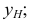
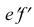
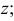
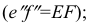
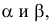
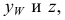
Следовательно, каждая линия уровня проецируется в истинную величину на ту плоскость проекции, которой она параллельна. На ту же плоскость проекций проецируются без искажения и углы, которые эта прямая образует с остальными двумя плоскостями проекций.
На рис. 3.15 приведены чертежи прямых, перпендикулярных плоскостям проекций. Такие прямые называются проецирующими прямыми. Различают три вида таких прямых.
Прямая АВ перпендикулярна плоскости Н
АВ — горизонтально-проецирующая прямая. Ее проекция 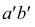
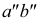
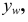
Прямая CD перпендикулярна плоскости V
CD — фронтально-проецирующая прямая. Ее проекция cd перпендикулярна оси х, проекция c»d“ перпендикулярна оси z, проекции с’ и d’ совпадают (рис. 3.15, б):
Прямая EF перпендикулярна плоскости W
EF — профильно-проецирующая прямая. Ее проекция 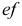
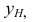
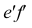
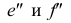
Из чертежа видно, что проецирующая прямая является вместе с тем и прямой двойного уровня, так как она параллельна одновременно двум другим плоскостям проекций
Следовательно, на две плоскости проекций проецирующие прямые проецируются без искажения, то есть в натуральную величину, а на третью — в точку.
Взаимное положение точки и прямой
Точка и прямая в пространстве могут быть различно расположены относительно друг друга и плоскости проекций.
Если точка в пространстве принадлежит прямой, то ее проекции принадлежат соответствующим проекциям этой прямой.
Если это положение нарушается, то точка данной прямой не принадлежит. На рис. 3.12 — 3.14 это положение показано на наглядных изображениях и чертежах прямых линий и точек.
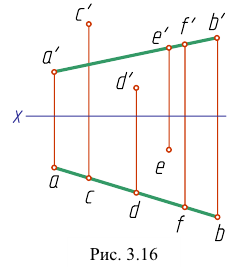
Рассмотрим еще раз это положение на плоскостном чертеже (рис. 3.16). Точка F принадлежит прямой АВ, так как горизонтальная проекция 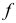
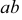
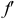
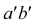
Точка С лежит над прямой АВ, точка D лежит под прямой АВ. точка Е лежит за прямой АВ.
Следы прямой
Точки пересечения прямой линии с плоскостями проекций называются следами прямой. На рис. 3.17. а точка М — горизонтальный след прямой, точка 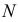
Горизонтальная проекция 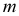
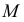
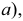
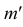
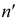
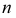
Чтобы построить на плоскостном чертеже горизонтальный след прямой (точки 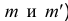
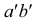
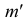
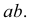
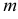
Для построения проекций фронтального следа (точек 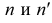
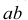
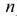
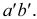
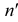
Прямая может пересекать и профильную плоскость проекций, то есть иметь профильный след. Этот след на профильной плоскости проекций совпадает со своей проекцией. Фронтальная и горизонтальная проекции его лежат соответственно на осях
- Чертежи на заказ
Взаимное положение двух прямых
Прямые в пространстве могут занимать различные взаимные положения:
- — пересекаться, то есть иметь одну общую точку;
- — быть параллельными, если точка пересечения прямых удалена в бесконечность;
- — скрещиваться, то есть не иметь обшей точки.
Пересекающиеся прямые
Если прямые пересекаются, то их одноименные проекции пересекаются между собой и точки пересечения проекций лежат на одной линии связи.
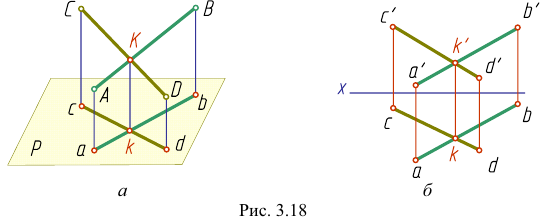
Наглядное изображение двух прямых АВ и CD, пересекающихся в точке К, приведено на рис. 3.18, 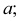
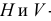
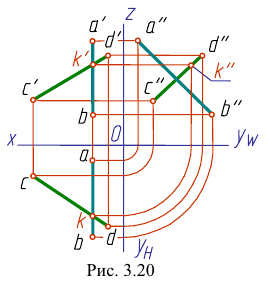
Если одна из прямых профильная, то чтобы ответить на вопрос, пересекаются ли прямые, следует построить их профильные проекции.
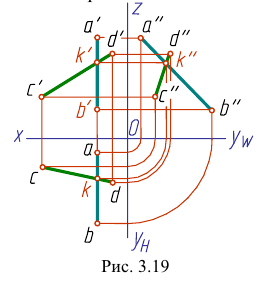
На рис. 3.19 все проекции точки 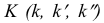
На рис. 3.20 профильная проекция 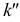
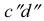
Это значит, что прямые АВ и CD не пересекаются, они скрещиваются.
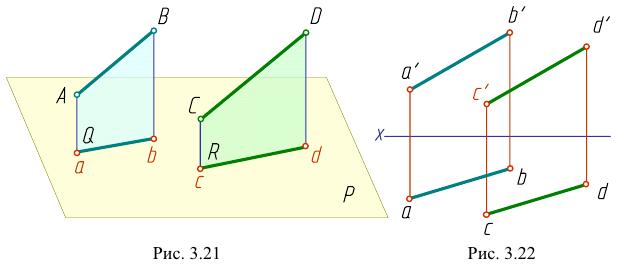
Параллельные прямые
Если прямые в пространстве параллельны, то их одноименные проекции параллельны между собой. Действительно, на рис. 3.21 проецирующие плоскости 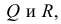
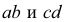
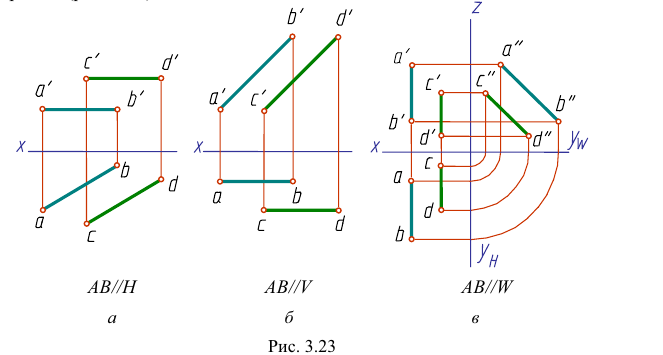
- горизонтальных прямых (рис. 3.23, а);
- фронтальных прямых (рис. 3.23, б);
- профильных прямых (рис. 3.23,
О параллельности прямых в пространстве можно судить по параллельности их одноименных проекций на двух плоскостях проекций.
При этом нужно учитывать некоторые условия.
Для прямых общего положения:
Если одноименные проекции прямых общего положения параллельны в системе двух любых плоскостей проекций, то прямые парал лельны (рис. 3.22).
Для прямых частного положения:
Если одноименные проекции прямых параллельны одной из осей проекций, то прямые параллельны при условии параллельности одноименных проекций на той плоскости проекций, которой параллельны прямые (рис. 3.23).
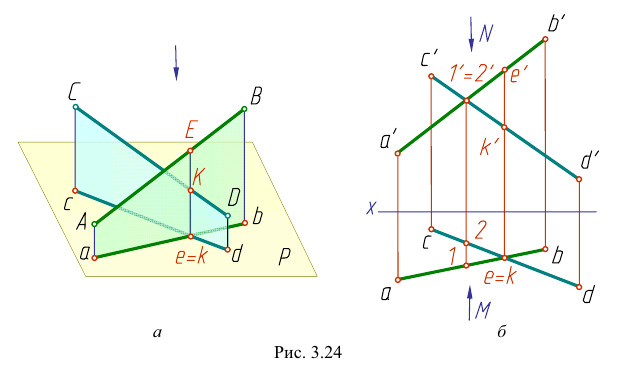
Скрещивающиеся прямые
Если прямые в пространстве нс пересекаются, а скрещиваются (рис. 3.24), то хотя на чертеже их одноименные проекции и пересекаются, но точки пересечения проекций не лежат на одной линии связи. Эти точки не являются общими для прямых.
Сравнивая положение таких точек, определяют, какая из изображенных на чертеже прямых выше другой или ближе другой к наблюдателю. На рис. 3.24, а видно, что точка Е (принадлежащая прямой АВ) расположена выше точки К (принадлежащей прямой CD). При взгляде сверху по указанной стрелке точка Е закрывает точку К. Соответственно и на чертеже (рис. 3.24, б) фронтальная проекция е’ расположена выше фронтальной проекции 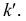
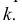
На плоскости V совпадают фронтальные проекции 1′ и 2′ точек прямых АВ и CD. При взгляде спереди по стрелке М видно, что точка 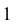
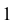
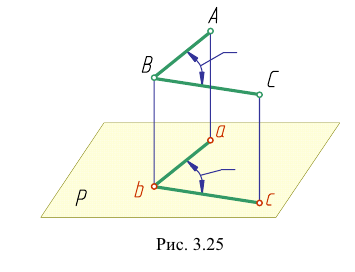
Проецирование плоских углов
Любой линейный угол образуется двумя пересекающимися прямыми. На плоскости проекций он проецируется в общем случае с искажением. Однако, если обе стороны угла параллельны какой-либо плоскости проекций, то на эту плоскость угол проецируется без искажения. Например, стороны угла АВС (рис. 3.25) параллельны горизонтальной плоскости Р. поэтому угол 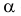
Исключение составляет прямой угол. Он проецируется в истинную величину даже тогда, когда лишь одна из его сторон параллельна плоскости проекций. Рассмотрим теорему о проецировании прямого угла.
Теорема. Прямой угол проецируется в виде прямого угла, если одна из его сторон параллельна плоскости проекций, а вторая ей не пер пендикулярна. Пусть сторона DE прямого угла DEK параллельна плоскости Р, а сторона ЕК ей нс перпендикулярна (рис. 3.26). Требуется доказать, что его проекция — угол 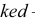
Доказательство. Пусть угол 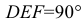
Через прямые EF и Ее проведем дополнительную плоскость 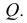
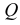
Возьмем на перпендикуляре 
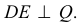
Но, как видно непосредственно из чертежа, только одна сторона DE угла DEK параллельна плоскости Р.
Вторая сторона его ЕК наклонна к плоскости Р.
Итак, для того чтобы прямой угол проецировался в натуральную величину, достаточно, чтобы одна его сторона была параллельна плоскости проекций (рис. 3.26, б, в).
Определение истинной величины отрезка прямой
Отрезки прямых общего положения не проецируются в истинную величину ни на одну из плоскостей проекций. Однако в ряде задач необходимо определить по чертежу длину отрезка прямой общего положения и углы наклона прямой к плоскостям проекций.
В этом случае используют способ построения прямоугольного треугольника.
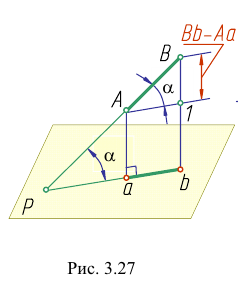
Теорема. Истинная величина отрезка прямой общего положения равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка на одну из плоскостей проекций, а другим — разность расстояний концов отрезка до этой же плоскости.
Доказательство. Из рис. 3.27 следует, что истинная величина отрезка АВ будет являться гипотенузой прямоугольного треугольника 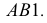
Определим истинную величину отрезка АВ и угол наклона его к плоскости Н (угол 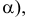
Построим прямоугольный треугольник, у которого одним катетом будет горизонтальная проекция отрезка, а вторым — разность расстояний концов отрезка до плоскости Н (разность z координат точек А и В). Истинная величина отрезка АВ равна гипотенузе abOt а угол наклона его к плоскости Н — угол
На рис. 3.28, 6 показано определение истинной величины отрезка АВ и угла наклона его к плоскости V- угла
- Прямая линия
- Плоскость
- Поверхности
- Изображения и обозначения на чертежах
- Моделирование трехмерных объектов в KOMПAC-3D
- Метод проекций
- Методы проецирования
- Образование проекций
Способы задания геометрических мест точек в пространстве
В стереометрии любую пространственную фигуру можно рассматривать как геометрическое место точек (г.м.т.), т.е. как множество точек, каждая из которых удовлетворяет заданному характеристическому свойству (точка, не принадлежащая этому множеству, не удовлетворяет этому свойству). Например, в элементарной геометрии сфера определяется как г.м.т., равноудаленных от заданной точки (центра сферы), круговая цилиндрическая поверхность как г.м.т., равноудаленных от заданной прямой (оси цилиндрической поверхности) и т.п.
В аналитической геометрии пространственные геометрические фигуры задаются как множества решений соответствующих уравнений. Рассмотрим, например, уравнение с тремя неизвестными
. Его решением называется тройка чисел, при подстановке которых вместо неизвестных уравнение превращается в верное числовое равенство. Каждое решение
уравнения
можно рассматривать как точку
в координатном пространстве с абсциссой
, ординатой
и аппликатой
. Таким образом, множество
точек
, координаты которых удовлетворяют уравнению
, образуют в координатном пространстве некоторую фигуру
.Например, уравнение
(или
) в прямоугольной системе координат
задает сферу единичного радиуса с центром
(рис.4.2,в).
Переход к этому способу описания геометрических фигур базируется на введении системы координат в пространстве, которая позволяет вместо точек (элементарных геометрических объектов) оперировать с числами (элементарными алгебраическими объектами). В разд.2 подчеркивалось, что введение системы координат устанавливает взаимно однозначное соответствие между точками пространства и их координатами (упорядоченными наборами из трех чисел), т.е. соответствие, удовлетворяющее двум условиям:
1) разным точкам пространства соответствуют разные наборы координат, отличающиеся хотя бы одной координатой;
2) любому набору координат соответствует некоторая точка.
Введение системы координат позволяет задать любую геометрическую фигуру уравнением, связывающим координаты таким образом, что координаты любой точки, принадлежащей заданной фигуре, удовлетворяют этому уравнению, а координаты точки, не принадлежащей фигуре, не удовлетворяют уравнению. Такой способ описания геометрических фигур применяется в аналитической геометрии.
Общие уравнения геометрических мест точек в пространстве
Уравнением множества точек (уравнением г.м.т.) в координатном пространстве называется равенство, связывающее координаты точек, верное для координат точек, принадлежащих множеству
, и неверное для координат точек, не принадлежащих
. Например, уравнение множества в аффинной системе координат
имеет вид:
(4.1)
в частности, в прямоугольной системе координат в цилиндрической системе координат
(4.2)
в сферической системе координат
(4.3)
где и
— некоторые функции трех аргументов.
Уравнения (4.1)-(4.3) представляют собой аналитическую запись функциональной зависимости между координатами точек в пространстве, образующих геометрическое место точек. В частных случаях одна из координат может быть выражена через другую, т.е. одна координата задается как явная функция другой координаты. Тогда получается уравнение, разрешенное относительно этой координаты, например:
Заметим, что уравнениями вида в прямоугольной системе координат
задаются графики функций двух переменных.
Пример 4.1. Изобразить в координатном пространстве (в прямоугольной системе координат) множества точек, координаты которых удовлетворяют следующим уравнениям:
а) ;
б) ;
в) ;
г) ;
д) .
Решение. а) Уравнению удовлетворяют только те точки пространства, у которых абсцисса равна единице
, а ординаты и аппликаты могут принимать любые значения. Эти точки принадлежат плоскости, параллельной координатной плоскости
и пересекающей ось абсцисс в точке
(рис.4.1,а).
б) На плоскости заданное уравнение определяет две пересекающиеся прямые
, при этом аппликата
не входит в уравнение и поэтому может принимать любые значения. Следовательно, заданное уравнение определяет две пересекающиеся по оси
плоскости, проходящие через прямые
и
на плоскости
(рис.4.1,6).
в) Уравнение равносильно системе уравнений
которая определяет прямую, совпадающую с осью аппликат (рис.4.1,в).
г) Выражение есть квадрат расстояния от точки
до ее ортогональной проекции
на ось
. Поэтому уравнению
(или
) удовлетворяют только те точки, которые удалены от оси аппликат на расстояние, равное 1. Это множество точек является круговой цилиндрической поверхностью радиуса 1 (рис.4.1,г).
д) Учитывая неравенства: , делаем вывод, что левая часть заданного уравнения неотрицательна и равна нулю только при одновременном выполнении условий
. Следовательно, заданное уравнение определяет множество точек первого октанта системы координат
(рис.4.1,д).
Пример 4.2. Применяя цилиндрические или сферические координаты, изобразить множества точек, заданных в прямоугольной системе координат уравнениями:
a) ;
б) ;
в) .
Решение. а) Запишем уравнение в цилиндрической системе координат , где
. Это уравнение не зависит от полярного угла
. При любом фиксированном значении
уравнение
определяет параболу. Например, при
получаем параболу
в плоскости
. Следовательно, описываемое множество точек можно получить, вращая параболу
вокруг ее оси симметрии
(рис.4.2,а). Получаемая при этом поверхность называется параболоидом вращения.
б) Запишем уравнение в цилиндрической системе координат (напомним, что полярный радиус
по определению). Это уравнение не зависит от полярного угла
. При любом фиксированном значении
уравнение
определяет угол, составленный из двух лучей
. Например, при
получаем два луча
в плоскости
. Следовательно, описываемое множество точек можно получить, вращая угол вокруг оси
, проходящей через вершину угла. При этом получаем коническую поверхность (рис.4.2,б).
в) Запишем уравнение в сферической системе координат
(напомним, что радиус
по определению). Это уравнение не зависит от широты
и долготы
. Следовательно, это множество точек, равноудаленных от начала координат, т.е. сфера (рис.4.2,в).
Пример 4.3. В координатном пространстве (в прямоугольной системе координат) отмечены точки
и
. Вывести уравнение геометрического места точек
, отношение расстояний от каждой из которых до двух заданных точек равно
:
а) для , то есть
;
б) для , то есть
.
Решение. а) Точка равноудалена от заданных точек. Запишем уравнение
в координатной форме:
Отсюда получаем , т.е.
. Следовательно, искомое г.м.т. — это плоскость, перпендикулярная отрезку
и проходящая через его середину (рис.4.3,а).
б) Запишем уравнение в координатной форме:
Возводя обе части уравнения в квадрат и приводя подобные члены, получаем , т.е. уравнение сферы с центром в начале координат и радиусом
.
Заметим, что при любом положительном искомое геометрическое место точек является сферой (сферой Аполлония).
Уравнения пересечений и объединений геометрических мест точек в пространстве
Рассмотрим основные операции с множествами точек, заданными своими уравнениями в координатном пространстве.
Пусть множества и
в аффинной системе координат
заданы общими уравнениями
и
соответственно.
Пересечение множеств
и
состоит из точек, координаты которых удовлетворяют системе уравнений
Не трудно составить одно уравнение, равносильное этой системе, например:
Объединение множеств
и
состоит из точек, координаты которых удовлетворяют совокупности уравнений
равносильной одному уравнению, например:
Включение с алгебраической точки зрения означает, что уравнение
является следствием уравнения
, т.е.
Равенство означает, что уравнения
и
равносильны (эквивалентны), т.е.
В частности, равносильные уравнения, описывающие одно и то же геометрическое место точек, получаются при тождественных алгебраических преобразованиях, например при умножении обеих частей уравнения на отличное от нуля число, при приведении подобных членов, при переносе членов из одной части уравнения в другую с изменением знака на противоположный и т.п.
Полученные соотношения, сводящие операции с множествами в пространстве к алгебраическим операциям с уравнениями этих геометрических мест точек, не зависят от выбора системы координат. Например, в прямоугольной системе координат аналогичные соотношения получаем, полагая
и
, в цилиндрической системе координат
при
и
, в сферической
при
и
Плоские сечения
Пусть в прямоугольной системе координат фигура
определяется уравнением
(4.4)
Подставляя в уравнение некоторое фиксированное значение , получаем уравнение с двумя неизвестными
. Это уравнение описывает некоторое множество на координатной плоскости
. Запишем уравнение в виде равносильной ему системы уравнений
(4.5)
Второе уравнение системы определяет плоскость, параллельную координатной плоскости . Следовательно, система (4.5) описывает множество точек фигуры
, принадлежащих плоскости
(см. рис.4.4,а), т.е. плоское сечение фигуры
. Каждую фигуру
, заданную уравнением
, можно представить как совокупность ее плоских сечений (4.5) при всех значениях постоянной
. Тем самым исследование и построение пространственной фигуры сводится к исследованию и построению ее плоских сечений. В этом состоит идея метода сечений. Разумеется, можно рассматривать сечения фигуры
плоскостями
(рис.4.4,б) или
, параллельными координатным плоскостям
или
соответственно.
Цилиндрические фигуры
Фигура, состоящая из параллельных прямых, называется цилиндрической. Прямые называются образующими цилиндрической фигуры.
Пусть в прямоугольной системе координат фигура
определяется уравнением
(4.6)
в котором неизвестная отсутствует. Обозначим через
множество решений этого уравнения как уравнения с двумя неизвестными
и
, а также соответствующее множество точек на координатной плоскости
(при
). Тогда вместе с любой точкой
уравнению (4.6) удовлетворяют также и все точки прямой, параллельной оси аппликат
и проходящей через точку
. Таким образом, фигура
является цилиндрической, ее образующие параллельны оси
и пересекают плоскость
в точках множества
(рис.4.5,а). Уравнения
или
также описывают цилиндрические фигуры, образующие которых параллельны оси ординат или абсцисс соответственно.
Конические фигуры
Фигура, состоящая из лучей, имеющих общее начало, называется конической. Лучи называются образующими, а их общее начало — вершиной конической фигуры.
Пусть в сферической системе координат фигура
определяется уравнением вида (4.3):
(4.7)
в котором неизвестная отсутствует. Обозначим через
множество решений этого уравнения как уравнения с двумя неизвестными
и
, а также соответствующее множество точек на сфере
. Тогда вместе с любой точкой
уравнению (4.7) удовлетворяют также и все точки луча
, исходящего из начала
системы координат. Таким образом, фигура
является конической, ее вершина совпадает с началом координат, а образующие пересекают множество
(рис.4.5,б).
Фигуры вращения
Пусть в цилиндрической системе координат фигура
определяется уравнением вида (4.2):
(4.8)
в котором неизвестная отсутствует. Обозначим через
множество решений этого уравнения как уравнения с двумя неизвестными
и
, а также соответствующее множество точек на плоскости
(т.е. на плоскости
, соответствующей прямоугольной системе координат). Тогда вместе с любой точкой
уравнению (4.8) удовлетворяют также и все точки
окружности радиуса
с центром в точке
на оси аппликат
, плоскость, содержащая окружность, перпендикулярна этой оси (рис.4.6). Таким образом, фигуру
можно представить как фигуру вращения, полученную путем вращения множества
вокруг оси аппликат (оси вращения).
Параметрические уравнения геометрических мест точек в пространстве
Функциональная зависимость между координатами точек пространства, например в прямоугольной системе координат , может быть задана в параметрической форме, в которой координаты выражаются в виде Функций вспомогательной переменной, называемой параметром:
(4.9)
где — параметр, принимающий действительные значения. В общем случае при задании множества не обязательно использовать один параметр, т.е. вспомогательных переменных может быть несколько, например, двухпараметрическое множество точек описывается системой:
(4.10)
где — параметры, принимающие действительные значения. Каждую из систем (4.9), (4.10) называют параметрическим уравнением геометрического места точек.
Пример 4.4. Изобразить в координатном пространстве (в прямоугольной системе координат) множества точек, координаты которых удовлетворяют следующим параметрическим уравнениям:
Решение. 1) Из первого уравнения следует, что все точки заданного множества принадлежат координатной плоскости . Из двух последних уравнений следует, что
. Таким образом, заданное множество — это прямая
в плоскости
(рис.4.7,а).
2) Исключим из первых двух уравнений параметр . Возведя обе части каждого уравнения в квадрат и сложив почленно результаты, получим уравнение окружности
. Параметром
служит величина угла поворота радиус-вектора изображающей точки, измеряемого от положительного направления оси абсцисс (см. рис.3.4,а). При равномерном увеличении угла поворота
равномерно увеличивается аппликата изображающей точки, так как
. Следовательно, заданная система описывает винтовую линию (рис.4.7,б) при
.
3) Запишем заданное параметрическое уравнение в матричном виде
а затем в векторной форме , где
— радиус- вектор произвольной точки
. Полученное уравнение является аффинным уравнением плоскости, проходящей через концы базисных векторов
(рис.4.7,в).
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

13
ребер, осей вращения, центровых линий) с проведением между ними линий проекционной связи. Также необходимо указывать оси симметрии каждого из изображений.
На рис. 23 представлены чертежи следующих поверхностей: цилиндра, призмы, четверти тора и шара.
Рис. 23
Условие принадлежности точки поверхности геометрической фигуры можно сформулировать так:
точка принадлежит поверхности геометрической фигуры, если она находится на линии, принадлежащей этой поверхности.
Применительно к простейшей поверхности — плоскости условие принадлежности примет вид:
точка принадлежит плоскости, если она лежит на прямой, принадлежащей этой плоскости.
Проиллюстрируем это условие на примере.
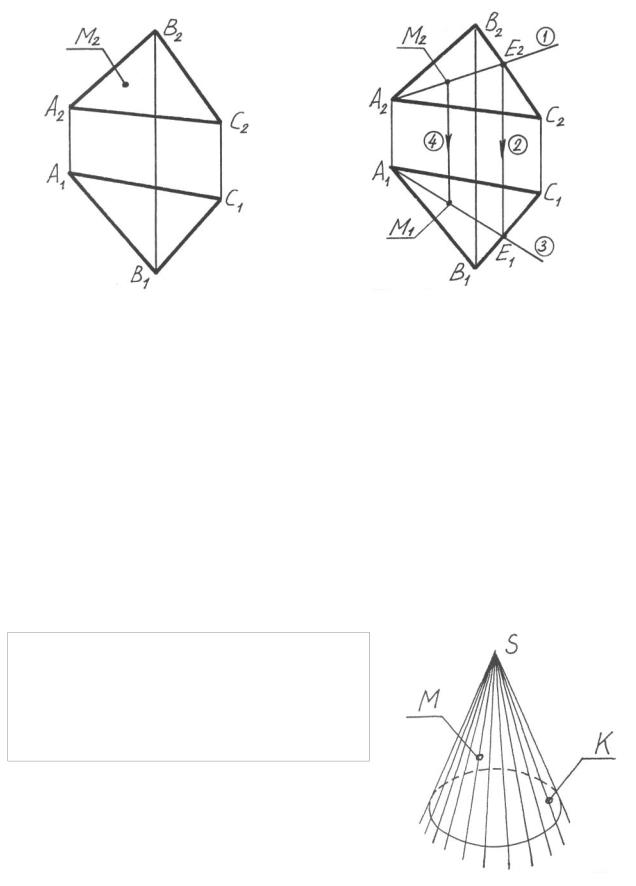
Пример. Определить недостающую проекцию точки М, если известно, что она принадлежит плоскости Σ ( АВС) (рис. 24).
Для определения недостающей проекции точки М – М1 сначала проводится фронтальная проекция вспомогательной прямой АЕ — А2Е2 (рис. 25). Затем строится горизонтальная ее проекция A1E1 и с помощью линии проекционной связи устанавливается на ней положение горизонтальной проекции М1. Последовательность действий при решении примера показана на рис. 25 стрелками и цифрами 1 — 4 .
14
Некоторые замечания по представленному выше решению.
1. При решении примера использовано условие принадлежности точки линии:
если точка принадлежит линии, то ее горизонтальная проекция принадлежит горизонтальной проекции линии, а фронтальная проекция точки — фронтальной проекции линии.
2.В качестве вспомогательной прямой может быть не только прямая АЕ, но
илюбая другая, лежащая в плоскости треугольника ABC.
3.Между проекциями заданной плоскости не проведена ось проекций X. Ее наличие не обязательно, так как ось X определяет лишь линию пересечения плоскостей проекций и не оказывает влияния на проекции фигуры, а, следовательно, и на решение задачи.
При решении задач по определению принадлежности точек поверхностям геометрических фигур на них проводят вспомогательные линии. Эти линии должны быть простейшими, т.е. прямыми или окружностями.
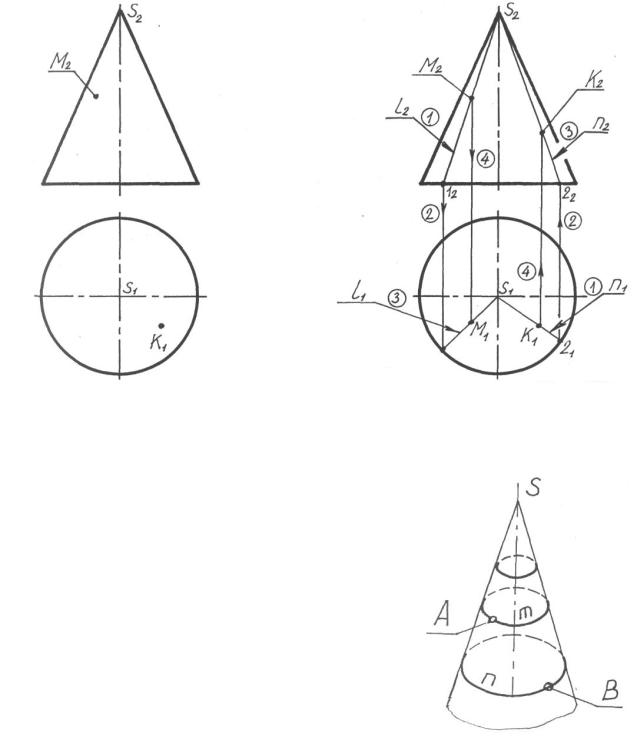
Например, принадлежность точки поверхности конуса можно установить с помощью прямой, проходящей через заданную точку и вершину конуса S (рис. 26).
Рис. 26
15
Рассмотрим пример построения недостающих проекций точек М и К, принадлежащих поверхности конуса (рис. 27).
Недостающие проекции точек — М1 и К2 определяются в данном случае с помощью прямых l и n, проведенных на поверхности конуса через вершину S. Последовательность построений показана на рис. 28 стрелками и цифрами 1 — 4.
|
Рис. 27 |
Рис.28 |
|
Принадлежность точек |
поверхности |
конуса можно установить также с помощью окружностей, проведенных на ее поверхности (рис. 29).
На рис. 30 изображен конус с осью, перпендикулярной горизонтальной плоскости проекций, поэтому окружности т и п, проведенные на поверхности этого конуса через точки А и В, проецируются на П2 в отрезки прямых т2 и п2, а на П1 – в окружности т1 и п1 (рис. 31).
Рис. 29
16
Рис. 30 Рис. 31
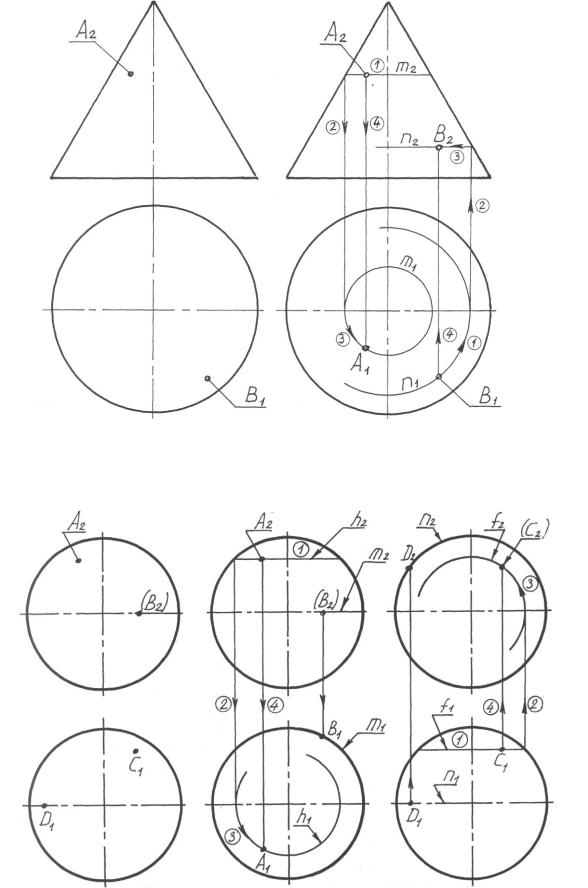
Принадлежность точек А, В, С и D поверхности шара (рис. 32, а) может быть установлена с помощью окружностей m, n, h и f, проведенных на поверхности этого шара через данные точки (см. рис. 32, б, в).

17
Рис. 32 Так как поверхности геометрических фигур не прозрачны, то некоторые точ-
ки и их соответствующие проекции могут оказаться невидимыми. Условимся невидимые проекции точек указывать на чертеже в скобках. Примерами невидимых проекций точек являются фронтальные проекции точек В – (В2) (см. рис. 32, б) и С – (С2) (см. рис. 32, в).
Задачи для закрепления изученного материала
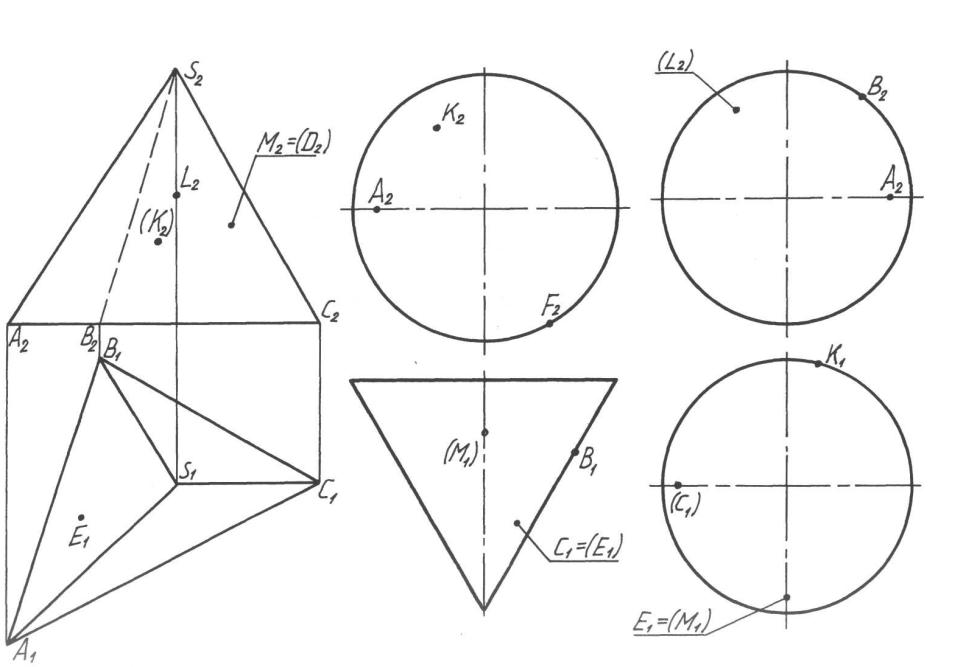
1. Построить чертеж конуса, если известно, что его ось перпендикулярна П2 , удалена от П1 на расстояние 45 мм, а от П3 — на 40 мм. Высота конуса 75 мм, основание имеет диаметр 70 мм и находится на П2.
По двум данным координатам точек А, В и С определить положение их трех проекций, при условии, что точки находятся на поверхности конуса. А(60, 15, z),
В(25, у, 60), С(х, 40, 35). Проекции невидимых точек указать в скобках.
Определить по чертежу недостающие координаты точек и записать их на сво-
бодном месте чертежа. Найденные по чертежу координаты точек подчеркнуть. z
2. Построить недостающие проекции точек, принадлежащих поверхностям заданных фигур
18
у