Нахождение проекций точек на поверхности конуса
Для нахождения недостающих проекций точек на поверхности конуса могут применяться следующие линии, принадлежащие поверхности конуса: окружность — параллель конуса (рис. 2.7, а), прямая — образующая конуса (рис. 2.7, б). Рассмотрим оба способа.
Пример 2.1. На поверхности конуса заданы проекции А2 и В, (см. рис. 2.7). Найдите недостающие проекции точек Ли В на поверхности конуса.
Рис. 2.7. Нахождение проекций точек на поверхности конуса
Способ 1. На рис. 2.7, а точка А задана проекцией А. Для нахождения недостающих проекций точки А воспользуемся вышеизложенным алгоритмом.
- 1. Через заданную проекцию точки Аг проводим линию, принадлежащую поверхности конуса — параллель.
- 2. Строим проекции параллели на других изображениях конуса. Па виде сверху она представляет собой окружность радиусом Rvна виде слева — отрезок.
- 3. На проекциях линии находим соответствующие проекции точек.
- 4. На пересечении окружности радиусом Л., с вертикальной линией связи, опущенной из А2, отмечаем проекцию Л,.
- 5. На виде сверху измеряем координату от проекции А, до горизонтальной оси и откладываем ее на проведенной линии связи на виде слева — получаем проекцию Л3.
- 6. Отмечаем проекцию А.л как невидимую. Проекция А., задана как видимая, следовательно, точка лежит в той части конической поверхности, которая обращена к наблюдателю (на виде сверху это часть, расположенная ниже горизонтальной оси). Таким образом, на виде слева ее проекция не видна.
Способ 2. Па рис. 2.7, 6 точка В задана проекцией В,. Построение недостающих проекций аналогично построению проекций точки А, за исключением того, что вместо окружности используется образующая конуса, пересекающая его основание в точке 1.
Коническая поверхность вращения
Коническая поверхность вращения — это линейчатая поверхность, образованная вращением прямолинейной образующей, которая пересекает криво-линейную направляющую (окружность) и проходит через неподвижную точку оси вращения, называемую вершиной.
Конусом называют геометрическое тело, ограниченное конической поверхностью и плоскостью основания, пересекающего все его образующие.
Конус называют прямым, если ось вращения перпендикулярна его основанию. Конус называют круговым, так как направляющей является окружность Конус с двумя параллельными основаниями, т.е. конус со срезанной вершиной, называют усеченным.
Построение проекций прямого кругового конуса
На рис. 4.71 показан пример построения проекций прямою кругового конуса с горизонтально-проецирующей осью вращения 

Для построения проекций конуса требуется выполнить графо-аналитические действия в следующем порядке:
1-е действие. По заданному условию построить горизонтальную проекцию очерка прямого кругового конуса, которая представляет собой окружность заданного радиуса 
2-е действие. Выполнить графический анализ построенной горизонтальной проекции конуса:
- Круг радиуса
является невидимой проекцией основания конуса.
- Круг радиуса
с вершиной конуса
является видимой проекцией боковой поверхности конуса.
- Обозначить на горизонтальной проекции характерные образующие конуса
и
которые будут определять очерки фронтальной и профильной проекций конуса.
3-е действие. Построить фронтальную проекцию (очерк) конуса, которая представляет собой треугольник 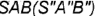
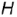
4-е действие. Построить профильную проекцию (очерк) конуса:
- ‘Задать на окружности горизонтальной проекции конуса положение базовой линии (б.о.), совпадающей с горизонтальной линией оси этой окружности.
- Выбрать положение базовой оси
(б.о.), которая будет совпадать с вертикальной осью
вращения на профильной проекции конуса.
- Профильная проекция конуса представляет собой треугольник
ограниченный:
слева и справа очерковыми образующими 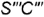
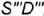
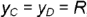
вершиной 
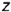
профильными проекциями характерных образующих 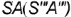
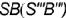
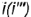
. Запомните характерные признаки очерков прямого круговою конуса на чертеже — окружность основания и два треугольника.
. Характерные признаки очерков прямого кругового усеченного конуса окружность основания и две равнобокие трапеции.
Построение проекции точек, лежащих на поверхности конуса
Принадлежность точки поверхности конуса определяется ее принадлежностью образующей поверхности и принадлежностью круговым параллелям (окружностям), по которой точка вращается вокруг оси конуса. Следовательно, проекции точки можно строить либо по принадлежности образующей, либо по принадлежности круговой параллели.
На рис. 4.71 показан пример построения горизонтальных и профильных проекций точек 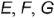
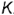
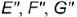
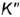
Посфоение горизонтальных проекций заданных точек:
горизонтальные проекции точек 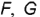
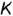
Рассмотрим графический алгоритм для построения горизонтальных проекции точек, лежащих на боковой поверхности конуса (на примере заданной точки , по их при надежности круговым параллелям:
Графический алгоритм I:
1-е действие. Провести фронтальную проекцию вспомогательной круговой параллели 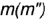
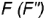
2-е действие. Провести окружность горизонтальной проекции параллели 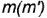
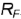
3-е действие. Построить по вертикальной линии связи горизонтальную проекцию точки 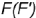
Повторить действия графического алгоритма 1 и построить аналогично горизонтальные проекции 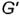
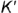
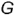
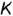
Построение профильных проекций заданных точек. Точки 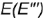
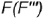
точка 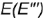
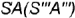
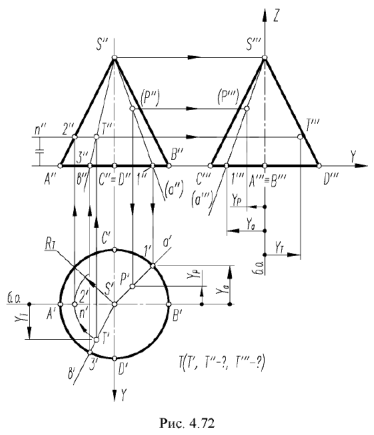
На рис. 4.72 показан пример построения горизонтальной и профильной проекции точки 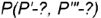
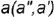
- Построение горизонтальной проекции точки по принадлежности образующей выполняется по графическому алгоритму II:
1-е действие. Провести через вершину конуса 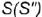
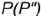
2-е действие. Построить горизонтальную проекцию образующей 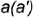
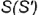
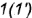
3-е действие. Построить по вертикальной линии связи горизонтальную проекцию точки 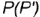
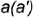
- Построение профильной проекции невидимой точки
выполняется по принадлежности образующей
, построенной но координате
.
На рис. 4.72 показано построение фронтальной и профильной проекции точки по ее заданной горизонтальной проекции. Построение выполнено по приведенным алгоритмам I и II, но в обратном порядке:
1-е действие. Провести на горизонтальной проекции конуса радиусом 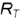
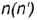
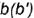
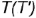
2-е действие. Построить фронтальные проекции вспомогательной параллели 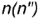
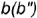
параллель 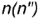
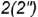
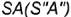
образующую 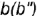
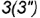
3-е действие. Построить по вертикальной линии связи фронтальную проекцию точки 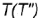
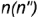
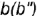
Конические сечения
Рассмотрим пять возможных случаев расположения секущей плоскости относительно оси конуса и его образующих, определяющих форму линии ее пересечения с поверхностью конуса (математические доказательства не приводятся):
1-й случаи. Гели секущая плоскость проходит через вершину конуса, то эта плоскость пересекает коническую поверхность по двум образующим 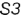

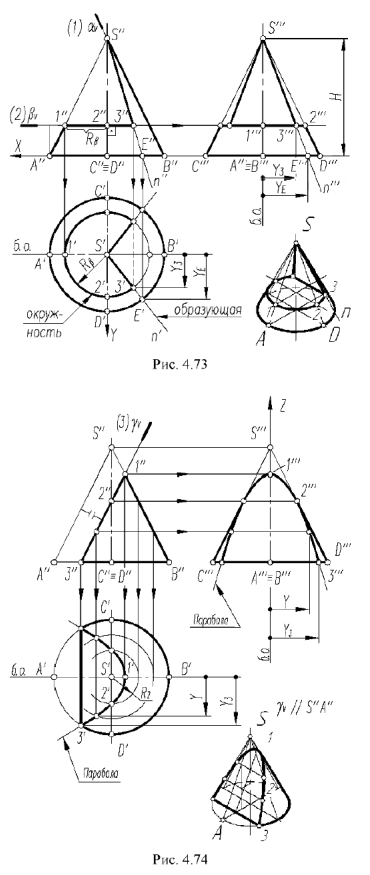
2-й случай. Если секущая плоскость расположена перпендикулярно оси конуса, то эта плоскость пересекает коническую поверхность но окружности (горизонтальная плоскость рис. 4.73).
3-й случай. Если секущая плоскость расположена параллельно одной образующей конуса, то эта плоскость пересекает коническую поверхность по параболе (фронтально-проецирующая плоскость 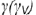

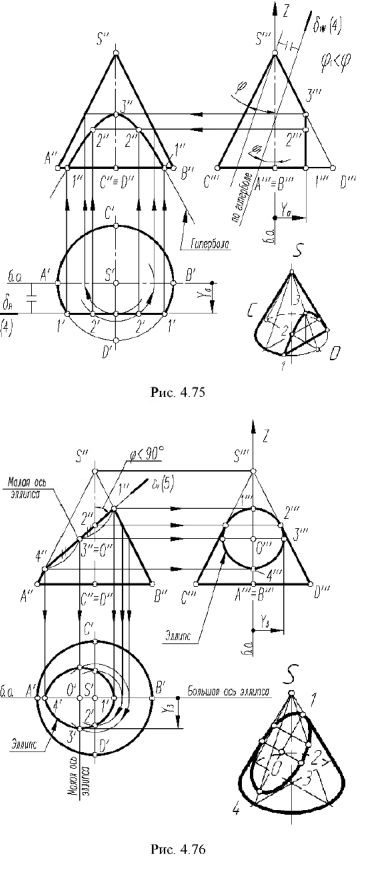
4-и случай. Если секущая плоскость расположена параллельно двум образующим конуса, то эта плоскость пересекает коническую поверхность по гиперболе (фронтальная плоскость 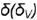

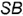
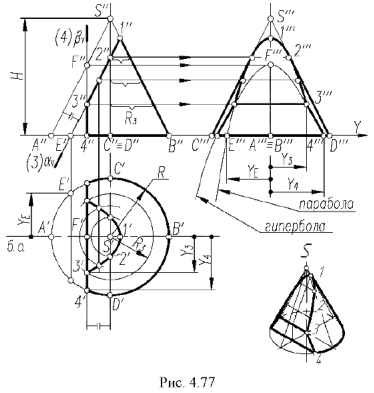
5-й случай. Если плоскость пересекает все образующие конуса под углом, отличным от прямого (или иначе, не параллельна ни одной образующей конуса), то эта плоскость пересекает коническую поверхность по эллипсу (фронтально-проецирующая плоскость ), рис 4.76).
Рассмотрим построение на проекциях конуса линии пересечения для всех пяти случаев сечений.
1-й и 2-й случаи. На рис. 4.73 показано построение проекций прямого кругового конуса с вырезом, образованным сечениями конической поверхности фронтально-проецирующей плоскостью 

Плоскость 

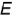
Плоскость пересекает поверхность конуса по окружности радиуса ограниченной линией 3-3 пересечения плоскостей выреза.
Построение горизонтальной и профильной проекций конуса с вырезом и оформление очерков этих проекций видно из чертежа.
3-й случай. На рис. 4.74 показано построение проекций конуса со срезом фронтально-проецирующей плоскостью 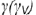

Плоскость пересекает поверхность конуса по параболе, горизонтальная и профильная проекции которой строятся по отмеченным характерным точкам 1, 2 и 3 и промежуточной точке (не обозначена)
Построение проекций этих точек выполнено по их принадлежности:
- проекции промежуточной точки построены по ее принадлежности соответствующей параллели (профильные проекции — по координате
).
Оформление очерков проекций видно из чертежа.
4-й случай. На рис. 4.75 показано построение проекций конуса со срезом фронтальной плоскостью 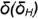


Плоскость 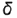
Оформление очерков проекций видно из чертежа.
На рис 4 75 на профильной проекции конуса показано положение секущей плоскости 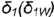
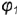
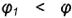
5-й ыучай. На рис. 4.76 показано построение проекции конуса со срезом фронтально-проецирующей плоскостью 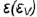
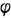
Плоскость 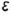
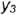
Оформление очерков проекций видно из чертежа.
. Количество взятых промежуточных точек должно быть минимальным, но достаточным, чтобы построить на проекциях конуса формы кривых второго порядка (параболы, гиперболы и эллипса), которые выполняют на чертеже по построенным характерным и промежуточным точкам с помощью лекала.
Построении проекции прямого конуса со срезами плоскостями частного положения
На рис. 4.77 показан пример построения проекций прямого круговою конуса со срезами фронтально-проецирующей плоскостью 

Для построения проекций конуса со срезами следует выполнить графический алгоритм, определяющий порядок действий при решении всех подобных задач.
1-е действие. Построить на чертеже тонкими линиями по заданному радиусу основания 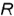
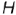


2-е действие. Обозначить на фронтальной проекции характерные точки пересечения плоскостей срезов с образующими и основанием конуса и выпол-иить графический анализ сечений:
1. Фронтально-проецирующая плоскость 
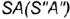
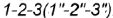
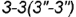


- Профильная плоскость
параллельна двум образующим конуса
и
и пересекает его поверхность по участку гиперболы
, которая проецируется в отрезок и ограничена вырожденными в точки фронтально-проецирующими линиями пересечения плоскостей срезов
и
и плоскости
с основанием конуса (4-4).
3-е действие. Достроить горизонтальную проекцию конуса со срезами, построив проекции плоскостей срезов по горизонтальным проекциям обозначенных точек и определить видимость плоскостей срезов:
1. Плоскость среза 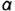
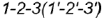
- Плоскость среза
определяет вертикальный видимый отрезок
вырожденной в линию проекции профильной плоскости, точки
которой лежат на очерковой окружности основания конуса.
. Поскольку горизонтальная проекция имеет вертикальную симметрию, точки обозначены на одной ее половине (нижней).
4-е действие. Выполнить графический анализ построенной горизонтальной проекции конуса для определения ее очерка и внутреннего контура:
- Горизонтальный очерк определяют участок окружности и отрезок
.
- Внутренний контур определяет видимый участок параболы
.
5-е действие. Достроить профильную проекцию конуса со срезами, пост-роив проекции плоскостей срезов по профильным проекциям обозначенных точек, и определить видимость плоскостей срезов:
1. Плоскость среза а определяет видимый участок параболы , построенный по профильным проекциям обозначенных точек:
- Плоскость среза
определяют видимые участки гиперболы
, ограниченные видимым отрезком
(построен) и видимым отрезком
. точки которого построены но координате
.
6-е действие. Выполнить графический анализ построенной профильной проекции конуса для определения ее очерка и внутреннего контура.
- Профильный очерк определяют:
- Внутренний контур определяют:
7-е действие. Оформить чертеж конуса, выполнив толстыми сплошными линиями очерки и видимый внутренний контур каждой его проекции (оставить сплошными тонкими линиями полные очерки проекций и линии построения).
Эта теория взята со страницы задач по начертательной геометрии:
Возможно эти страницы вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Сечение поверхности конуса плоскостью общего положения
При пересечении прямого кругового конуса с плоскостью могут образовываться следующие кривые второго порядка: окружность, эллипс, гипербола и парабола. Вид этих кривых зависит от угла наклона секущей плоскости к оси конической поверхности.
Ниже мы рассмотрим задачу, в которой требуется построить проекции и натуральную величину сечения конуса ω плоскостью α . Начальные данные представлены на рисунке ниже.
Определение высшей и низшей точки сечения. Границы видимости
Построение линии пересечения следует начинать с нахождения её характерных точек. Они определяют границы сечения и его видимость по отношению к наблюдателю.
Через ось конической поверхности проведем вспомогательную плоскость γ, параллельную П2. Она пересекает конус ω по двум образующим, а плоскость α по фронтали fγ. Точки 1 и 2 пересечения fγ с образующими являются граничными точками. Они делят сечение на видимую и невидимую части.
Определим высшую и низшую точки линии пересечения. Для этого через ось конуса перпендикулярно h0α введем дополнительную секущую плоскость β. Она пересекает коническую поверхность по образующим SL и SK, а плоскость α по прямой MN. Искомые точки 3 = SL ∩ MN и 4 = SK ∩ MN определяют большую ось эллипса. Его центр находится в точке O, которая делит отрезок 3–4 пополам.
Определение промежуточных точек и построение проекций эллипса
Чтобы построить проекции сечения наиболее точно, найдем ряд дополнительных точек. В случае с эллипсом целесообразно определить величину его малого диаметра. Для этого через центр O проводим вспомогательную горизонтальную плоскость δ. Она пересекает коническую поверхность по окружности диаметром AB, а плоскость α – по горизонтали hδ. Строим горизонтальные проекции окружности и прямой hδ. Их пересечение определяет точки 5′ и 6′ малого диаметра эллипса.
Для построения промежуточных точек 7 и 8 вводим вспомогательную горизонтальную плоскость ε. Проекции 7′ и 8′ определяются аналогично 5′ и 6′, как это показано на рисунке.
Соединив найденные точки плавной кривой, мы получили контур эллиптического сечения. На рисунке он обозначен красным цветом. Фронтальная проекция контура меняет свою видимость в точках 1 и 2, как это было отмечено выше.
Построение натуральной величины сечения методом совмещения
Чтобы найти натуральную величину сечения, повернем плоскость α до совмещения её с горизонтальной плоскостью. В качестве оси вращения будем использовать след h0α. Его положение в процессе преобразований останется неизменным.
Построение начинается с определения направления фронтального следа f1α. На прямой f0α возьмем произвольную точку E и определим её проекцию E’. Из E’ опустим перпендикуляр к h0α. Пересечение данного перпендикуляра с окружностью радиусом XαE» определяет положение точки E’1. Через Xα и E’1 проводим f1α.
Строим проекцию горизонтали h’1δ ∥ h0α, как это показано на рисунке. Точки O’1 и 5′1, 6′1 лежат на пересечении h’1δ с прямыми, проведенными перпендикулярно h0α из O’ и 5′, 6′. Аналогично на горизонтали h’1ε находим 7′1 и 8′1.
Строим проекции фронталей f’1γ ∥ f1α, f’3 ∥ f1α и f’4 ∥ f1α. Точки 1′1, 2′1, 3′1 и 4′1 лежат на пересечении этих фронталей с перпендикулярами, восстановленными к h0α из 1′, 2′, 3′ и 4′ соответственно.
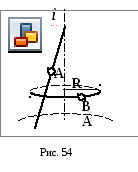
Точка принадлежит
поверхности конуса, если она принадлежит
линии этой поверхности.
В качестве
линии берется либо образующая конуса
(для точки А), либо параллель, проходящая
через данную точку (для точки В). Радиус
параллели R
замеряют от оси вращения до образующей
конуса (рис.54).
Дано:
— прямой круговой конус 1,2,3,4
Построить:
11
,21
, 31,
41 -?
.
1.
Постройте горизонтальную проекцию
точки 1.
Эта точка является
опорной точкой, так как принадлежит
очерку поверхности — главному фронтальному
меридиану.
Очерковая
образующая проецируется на горизонтальную
плоскость проекций в виде отрезка
прямой, проходящей через горизонтальную
осевую.
Спроецируйте
точку 1 на горизонтальную проекцию
очерковой образующей.
2.
Постройте горизонтальную проекцию
точки 2.
Точка 2 является
опорной точкой, так как принадлежит
очерку поверхности — экватору.
Экватор
проецируется на горизонтальную плоскость
проекций в виде окружности.
3.
Спроецируйте
точку 2 на горизонтальную проекцию
экватора.
Так как
вертикальная линия связи дважды
пересекает горизонтальную проекцию
экватора, получают две проекции 21
и 21I.
Точка 2 – видимая,
а 2I
– невидимая.
4.
Постройте горизонтальную проекцию
точки 3.
Для построения
недостающей проекции точки воспользуйтесь
вспомогательной линией – образующей
конуса.
5.
Постройте
горизонтальную проекцию образующей
конуса (задача имеет два решения).
6.
Спроецируйте
точку 3 на горизонтальные проекции
вспомогательных образующих. Для этого
проведите из фронтальной проекции
точки 32
вертикальную линию связи до пересечения
с горизонтальными проекциями
вспомогательных образующих. Получится
две проекции 31
и 31I.
7.
Постройте горизонтальную проекцию
точки 4.
Для построения
недостающей проекции точки воспользуйтесь
вспомогательной линией – параллелью.
8.
Через
фронтальную проекцию точки 42
проведите параллель (фронтальная
проекция параллели – отрезок прямой).
9. Замерьте радиус
параллели R.
10. Горизонтальную
проекцию параллели проведите радиусом
R
11. Спроецируйте
точку 4 на горизонтальную проекцию
параллели. Получится две проекции 41
и 41I.
7.4 Цилиндр
Цилиндр
– геометрическое тело, ограниченное
цилиндрической поверхностью и двумя
плоскостями.
Цилиндрическая
поверхность
образуется при вращении прямой линии
(образующей) вокруг неподвижной оси i,
параллельной образующей (рис.55).
1.Спроецируйте
нижнее основание цилиндра
на горизонтальную плоскость проекций.
Получится окружность, а на фронтальной
и профильной проекции — отрезок прямой,
равный диаметру окружности. Аналогично
спроецируйте верхнее основание.
2.Спроецируйте
контурные образующие на
фронтальную и профильную плоскости
проекций в виде прямых, перпендикулярных
к проекции основания и равных высоте
цилиндра. На П1
образующие проецируются в точки.
3.Постройте
комплексный чертеж цилиндра.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сечение поверхности конуса плоскостью общего положения
При пересечении прямого кругового конуса с плоскостью могут образовываться следующие кривые второго порядка: окружность, эллипс, гипербола и парабола. Вид этих кривых зависит от угла наклона секущей плоскости к оси конической поверхности.
Ниже мы рассмотрим задачу, в которой требуется построить проекции и натуральную величину сечения конуса ω плоскостью α . Начальные данные представлены на рисунке ниже.
Содержание
- Определение высшей и низшей точки сечения. Границы видимости
- Построение промежуточных точек и проекций эллипса
- Построение натуральной величины сечения методом совмещения
Определение высшей и низшей точки сечения. Границы видимости
Построение линии пересечения следует начинать с нахождения её характерных точек. Они определяют границы сечения и его видимость по отношению к наблюдателю.
Через ось конической поверхности проведем вспомогательную плоскость γ, параллельную П2. Она пересекает конус ω по двум образующим, а плоскость α по фронтали fγ. Точки 1 и 2 пересечения fγ с образующими являются граничными точками. Они делят сечение на видимую и невидимую части.
Определим высшую и низшую точки линии пересечения. Для этого через ось конуса перпендикулярно h0α введем дополнительную секущую плоскость β. Она пересекает коническую поверхность по образующим SL и SK, а плоскость α по прямой MN. Искомые точки 3 = SL ∩ MN и 4 = SK ∩ MN определяют большую ось эллипса. Его центр находится в точке O, которая делит отрезок 3–4 пополам.
Определение промежуточных точек и построение проекций эллипса
Чтобы построить проекции сечения наиболее точно, найдем ряд дополнительных точек. В случае с эллипсом целесообразно определить величину его малого диаметра. Для этого через центр O проводим вспомогательную горизонтальную плоскость δ. Она пересекает коническую поверхность по окружности диаметром AB, а плоскость α – по горизонтали hδ. Строим горизонтальные проекции окружности и прямой hδ. Их пересечение определяет точки 5′ и 6′ малого диаметра эллипса.
Для построения промежуточных точек 7 и 8 вводим вспомогательную горизонтальную плоскость ε. Проекции 7′ и 8′ определяются аналогично 5′ и 6′, как это показано на рисунке.
Соединив найденные точки плавной кривой, мы получили контур эллиптического сечения. На рисунке он обозначен красным цветом. Фронтальная проекция контура меняет свою видимость в точках 1 и 2, как это было отмечено выше.
Построение натуральной величины сечения методом совмещения
Чтобы найти натуральную величину сечения, повернем плоскость α до совмещения её с горизонтальной плоскостью. В качестве оси вращения будем использовать след h0α. Его положение в процессе преобразований останется неизменным.
Построение начинается с определения направления фронтального следа f1α. На прямой f0α возьмем произвольную точку E и определим её проекцию E’. Из E’ опустим перпендикуляр к h0α. Пересечение данного перпендикуляра с окружностью радиусом XαE» определяет положение точки E’1. Через Xα и E’1 проводим f1α.
Строим проекцию горизонтали h’1δ ∥ h0α, как это показано на рисунке. Точки O’1 и 5′1, 6′1 лежат на пересечении h’1δ с прямыми, проведенными перпендикулярно h0α из O’ и 5′, 6′. Аналогично на горизонтали h’1ε находим 7′1 и 8′1.
Строим проекции фронталей f’1γ ∥ f1α, f’3 ∥ f1α и f’4 ∥ f1α. Точки 1′1, 2′1, 3′1 и 4′1 лежат на пересечении этих фронталей с перпендикулярами, восстановленными к h0α из 1′, 2′, 3′ и 4′ соответственно.
Для построения кривой линии, получаемой при пересечении конической
поверхности плоскостью, следует в общем случае находить точки
пересечения образующих с секущей плоскостью.
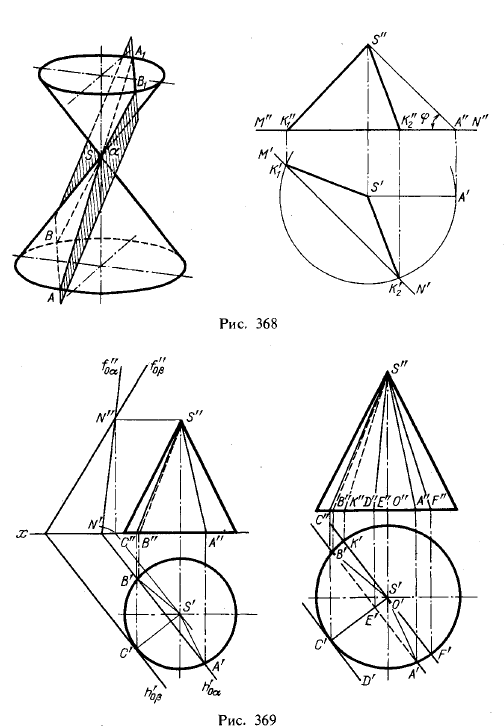
Если плоскость, пересекающая коническую поверхность, проходит через
вершину этой поверхности, то получаются две прямые — образующие (рис.
368, АА1 и ВВ1)
Рассмотрим пример построения, которым иллюстрируется такое пересечение конической поверхности.
Положим, что в плоскости, заданной точкой S и горизонтальной прямой
MN (рис. 368, справа), надо провести через точку S прямую, составляющую с
пл. π1 некоторый угол φ.
Геометрическим местом прямых, составляющих угол φ с пл. π1, является
коническая поверхность вращения, ось которой перпендикулярна к пл. π1
и вершиной, до условию, должна быть точка S. Следовательно, заданная
плоскость проходит через вершину конуса и рассекает его поверхность по
прямым — образующим. Эти прямые и будут искомыми: они проходят через
точку S в заданной плоскости под заданным углом φ к пл. π1
Теперь остается изобразить конус (он изображен частично), для чего
проведена прямая S» А» и дуга окружности из точки S’, как из центра,
радиусом S’A’, причем основание конуса взято в горизонтальной плоскости,
проходящей через заданную прямую MN.
Остальное ясно из чертежа. Данное построение сравните с выполненным на рис. 245 и 246 в § 38.
На рис. 369 слева изображен прямой круговой конус, поставленный на
пл: π1. Пл. β является касательной к данному конусу; касание происходит
по образующей SC, след h’0β касается окружности —
горизонтальной проекции основания конуса; то, что точка S лежит в пл. β,
устанавливается при помощи горизонтали SN. Пл. а проходит через вершину
данного конуса и пересекает его по образующим SA и SB.
На том же рисунке справа плоскости показаны не в следах. Плоскость,
касательная к конусу, задана образующей SC и прямой CD, касательной к
окружности основания конуса. Плоскость, проходящая через вершину и
рассекающая конус по образующим SA и SB, задана прямой АВ в плоскости
основания конуса и прямой SE, проходящей через вершину конуса и
пересекающей прямую АВ в точке Е.
Если плоскость проходит через ось конуса, то она его пересекает по
образующим с максимальным для данного конуса углом между ними. На рис.
369 справа это — образующие SF и SK; угол между ними равен углу с
вершиной между очерковыми прямыми в фронтальной проекции конуса.
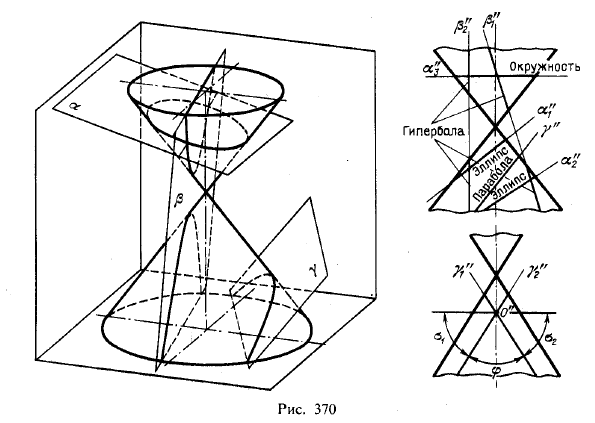
Если же конус вращения пересекается плоскостью, не проходящей, через
его вершину, то в пересечении получается одна из следующих четырех
кривых: 1) эллипс, если секущая плоскость пересекает все образующие
одной полости поверхности или, иначе, не параллельна ни одной из
образующих конуса (рис. 370, плоскости α,α1 и α2); в этом случае угол между секущей плоскостью и осью конуса больше угла между этой осью и образующей конуса; 2) окружность1), если секущая плоскость перпендикулярна к оси конуса (рис. 370, плоскость α3); 3) парабола, если секущая плоскость параллельна только одной из образующих (рис. 370, пл. γ); в этом
случае углы между секущей плоскостью и осью конуса и между этой осью и
образующей конуса равны между собой; 4) гипербола, если секущая
плоскость параллельна двум образующим (рис. 370, плоскости β, β1 и β2); при этом угол между секущей плоскостью и осью конуса меньше угла между этой осью и образующей конуса.
На рис. 370 справа внизу показаны углы φ, σ1 и σ2. Угол φ — между следами γ»1 и γ»2
плоскостей, пересекающих конус по параболам. Если проводить следы через
точку О» внутри угла φ, то этим определяются плоскости, пересекающие
конус по гиперболам, а если через точку О» внутри углов σ1 и σ2, то по эллипсам.
Рассмотрим доказательство того, что при пересечении конуса вращения
плоскостью, не параллельной ни одной из его образующих (и не проходящей
через его вершину), получается эллипс.
Как бы в данном случае ни были расположены в пространстве конус и
секущая плоскость, всегда можно преобразованием чертежа привести их в
положение, когда ось конуса окажется перпендикулярной к пл. π1, а
секущая плоскость — фронтально-проецирующей. Именно в таком положении
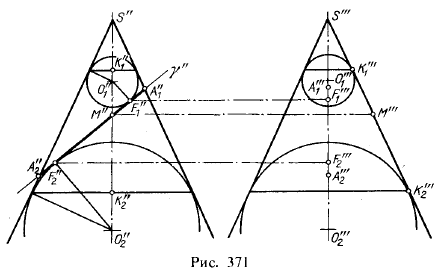
показаны конус и пересекающая его пл. γ на рис. 371, причем даны две
проекции конуса — фронтальная и профильная.
‘) Можно рассматривать как эллипс с равными в пределе осями.
В конус вписаны сферы, касательные к пл. γ в точках F1 и F2, а к конусу — по параллелям, проходящим соответственно через точки К1 и К2. Точки F1 и F2 получаются в плоскости главного меридиана и, следовательно, расположены на одной прямой с точками А1 и A2, принадлежащими фигуре сечения конуса пл. γ. Эта фигура сечения проецируется на пл. π2 в виде отрезка А»1А»2.
Рассмотрим образующую конуса, лежащую в профильной плоскости, и отметим на ней точки К1 и К2, в которых вписанные шары касаются этой образующей, и точку М, принадлежащую той же образующей и кривой сечения конуса пл. γ. Известно,
что отрезки касательных, проведенных из какой-либо точки к сфере,
определяемые этой точкой и точками касания, равны между собой. Отсюда MK1 = MFl и MK2 = MF2. Складывая почленно, получаем MK1 + МК2 = MF1 + MF2. Но МК1 + МК2 = K1K2, т. е. сумма расстояний некоторой точки, взятой на кривой сечения, до двух постоянных точек F1 и F2, принадлежащих плоскости этого сечения, является величиной постоянной, равной в данном случае отрезку К1К2.
Этот отрезок образующей конуса расположен между двумя его параллелями
и не зависит от выбора точки М на кривой сечения. Действительно, если
на кривой сечения конуса была бы взята не точка М, а другая точка, то
проходящая через нее образующая кйснулась бы обеих сфер в точках на тех
же параллелях. Отрезок этой образующей между точками касания был бы
равен тому же отрезку К1К2
Сделанный вывод показывает, что точка М принадлежит геометрическому
месту точек, сумма расстояний которых до двух данных точек имеет
некоторое постоянное значение. Это соответствует определению эллипса.
Подобным образом делаются выводы и для случаев пересечения конуса вращения по параболе и гиперболе.
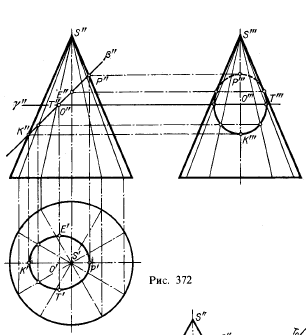
На рис. 372 изображен конус вращения с сечением его
фронтально-проецирующей плоскостью. Точки пересечения следа β» с
фронтальными проекциями образующих представляют собой проекции точек
искомой кривой пересечения, в данном случае эллипса. По этим проекциям
найдены проекции на плоскостях π1 и π3.
Одна из осей эллипса (большая) проецируется на пл. π2 отрезком К»Р». Другая (малая) ось эллипса, перпендикулярная к пл. π2, проецируется в одну точку — в середину отрезка К»Р».
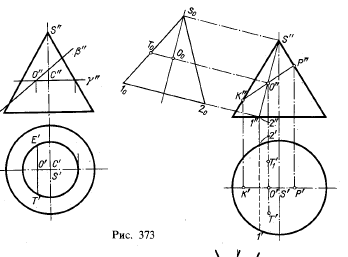
Если провести пл. γ через точку О перпендикулярно к оси конуса (в
данном случае параллельно пл. π1 то проекция малой оси получится (рис.
373) как хорда Т’Е’ окружности — горизонтальной проекции сечения конуса
пл. γ.
Проекцию малой оси можно получить также построением, показанным на
рис. 373 справа. Конус пересечен по треугольнику, повернутому и
наложенному на пл. π2. Отрезок О0Т0 равен малой полуоси. Откладывая этот отрезок от точки О’ перпендикулярно к К’Р’, получаем малую ось (Т’Т’1 = 2О0Т0).
Проекции фигуры сечения на пл. 7π1 и π3 — эллипсы. Проекция на π3 может оказаться и окружностью: в этой проекции при некотором наклоне секущей плоскости проекции осей эллипса могут оказаться равными.
Проекция же фигуры сечения
(эллипса) на плоскости, перпендикулярной к оси конуса (в данном случае на пл. π1), окружностью быть не может 1).
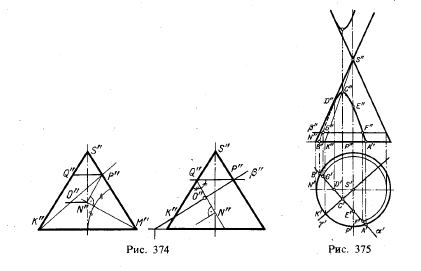
На рис. 374 слева показано, как для некоторого конуса найти
направление фронтального следа фронтально-проецирующих плоскостей,
пересекающих этот конус по эллипсам, проецирующимся на π3 в
виде окружности. Построение производится на фронтальной проекции конуса.
Биссектриса угла S»M»K» пересекает ось симметрии проекции в точке N».
Проведя в этой точке перпендикуляр к биссектрисе M»N», находим точку Р».
Прямая, проведенная через точки К» и Р», дает направление для
фронтальных следов искомых секущих плоскостей. Дело сводится к
построению диагонали равнобочной трапеции К»M»P»Q», в которую можно
вписать окружность с центром в точке N». Проводя через точку N» прямую
параллельно Q»P», получим точку О» — проекцию центра эллипса,
фронтальная проекция которого — отрезок К»Р».
Будет ли проецироваться на π3 в виде окружности эллипс,
получаемый при пересечении конуса пл. β (рис. 374, справа)? Построение
на рис. 374 дает один из приемов проверки: через точку Р» проводим
прямую, параллельную основанию, проводим биссектрису угла P»Q»K»,
получаем точку N». Так как перпендикуляр, проведенный в точке N» к этой
биссектрисе, не проходит через точку К», то проекция сечения на π3 окажется эллипсом, а не окружностью.
На рис. 375 показано построение фронтальной проекции гиперболы,
полученной при пересечении конуса вращения горизонтально-проецирующей
плоскостью.
Так как горизонтальная проекция гиперболы совпадает со следом α’, то в
пересечении α’ с горизонтальной проекцией основания определяются точки
А’ и В’, а по ним проекции А» и В»:
Для нахождения точки С» — наивысшей точки проекции гиперболы на пл.
π2 — проведена вспомогательная горизонтально-проецирующая пл. γ через
ось конуса перпендикулярно к следу α’. Горизонтальная проекция С’
искомой точки С получается в пересечении α’ и γ’; найдя фронтальную
проекцию образующей SK, отмечаем на ней точку С».
Далее, определена точка D», в которой фронтальная проекция гиперболы
разделяется на видимую и невидимую части. Эта точка находится при помощи
образующей SN.
Для нахождения других точек гиперболы можно провести несколько
образующих в пределах той части поверхности конуса, которая отмечена
буквами SAKB, или несколько вспомогательных секущих плоскостей. На рис.
375 указана одна из таких вспомогательных плоскостей — горизонтальная
пл. β, пересекающая поверхность конуса по окружности. При помощи этой
плоскости найдены точки F и G.
На второй полости конической поверхности получается вторая ветвь гиперболы.
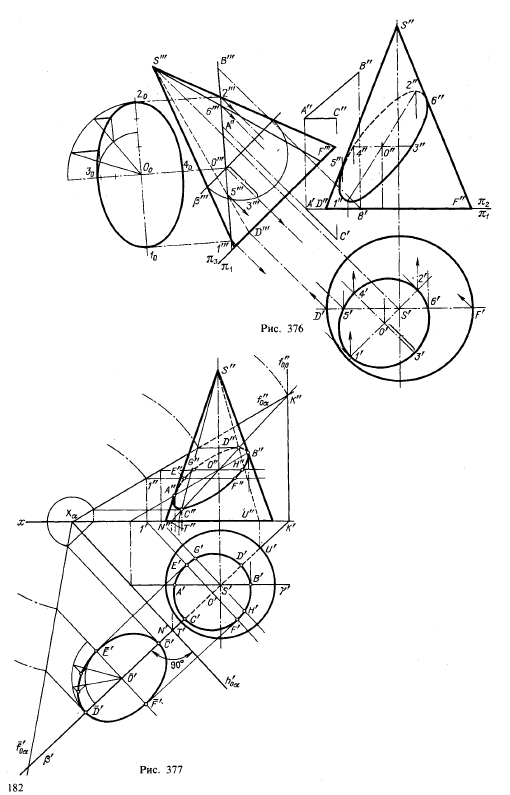
На рис. 376 показано построение проекций фигуры сечения прямого
кругового конуса плоскостью общего положения, заданной горизонталью АС и
фронталью АВ, и натурального вида фигуры сечения.
Построение выполнено при помощи способа перемены плоскостей проекций. Введена дополнительная плоскость проекций π3, выбранная так, чтобы она была перпендикулярна не только к пл. π1 но и к секущей плоскости: ось π3/π1 проведена перпендикулярно к проекции А’С. На пл. π3
секущая плоскость проецируется в виде прямой, на которой расположена
проекция фигуры сечения (отрезок 1″‘2″‘). Этим определена болыцая ось
эллипса, по которому конус пересекается данной плоскостью. В точке О'»,
делящей отрезок 1′»2′» пополам, находится проекция центра эллипса.
Плоскость β, проведенная перпендикулярно к оси конуса, позволяет найти
малую ось эллипса (на рис. 376 проведена полуокружность и в ней отрезок
0″‘3″‘ равный половине малой оси эллипса). По точкам 0″ Г», 2″‘ найдены
проекции О’, Г, 2′, а затем проекции О»‘, 1″‘, 2″‘, отстоящие от оси п2/п1 на то же расстояние, на каком находятся проекции О'», 1″‘, 2″‘ от оси π3/π1. Точка 2″ — наивысшая на фронтальной проекции, точка 1″ — наинизшая из точек эллипса — фронтальной проекции
1) Интересующихся доказательством отсылаем к предыдущим изданиям.
сечения. Для определения положения точек 5″ и 6″, в которых эллипс на
фронтальной проекции разделяется на «видимую» и «невидимую» части,
построены проекции S»‘D»‘ и S»‘F»‘ образующих SD и SF, найдены точки 5″‘
и 6″‘, по ним проекции 5′ и 6’ и затем 5″ и 6″. Но можно было найти
хотя бы только точку 5″ и провести через нее прямую, параллельную
проекции А»В», так как плоскость главного меридиана конуса пересекает
данную секущую плоскость по фронтали.
Малая ось эллипса проецируется на пл. π1 в свою натуральную величину
(отрезок 3’4′), располагаясь на горизонтальной секущей плоскости, и
является также малой осью для эллипса — горизонтальной проекции фигуры
сечения. Натуральный вид этой фигуры получен построением эллипса по его
большой оси (1020 = 1″‘2″‘) и малой оси (3040 = 3’4′).
На рис. 377 показано аналогичное построение при задании секущей плоскости ее следами.
Построение проекций сечения начато с нахождения точек, лежащих на
очерке фронтальной проекции конуса. Для этого проведена через ось конуса
вспомогательная секущая плоскость γ, параллельная пл. π2,
след этой плоскости — γ’. Пл.γ пересекает пл. α по фронтали, а конус —
по двум образующим. Точки А и В, получающиеся при пересечении фронтали с
образующими, принадлежат искомой линии пересечения конуса с плоскостью
α.
В точках А» и В» фронтальная проекция линии пересечения касается
очерка фронтальной проекции конуса и разделяется на две части: видимую и
невидимую. Далее, построены еще две характерные точки 1), а именно
высшая и низшая точки сечения, для чего проведена вспомогательная
секущая пл. β, горизонтально-проецирующая, перпендикулярная к следу h’0α и проходящая через ось конуса. Пл. β рассекает конус по образующим
ST(S»T», S’T) и SU (S»U», S’U’), а пл. α — по линии NK(N»K», N’K’).
Точки С и D, получающиеся в пересечении образующих ST и SU с прямой NK,
будут искомыми точками. Отрезок CD является большой осью эллипса,
получающегося при пересечении данного конуса пл. α. Проекция CD’
является большой осью эллипса — горизонтальной проекции фигуры сечения.
Разделив CD пополам, получим положение центра эллипса; точки О» и О’
являются центрами эллипсов — проекций фигуры сечения.
Для нахождения промежуточных точек линии пересечения удобно
пользоваться горизонтальными секущими плоскостями, так как они
пересекают поверхность конуса по окружностям, а пл. α — по горизонталям.
Пригодны для этого построения лишь те плоскости, у которых фронтальные
следы помещаются в пределах между С» и D», так как в данном случае выше
точки D» и ниже точки С» не может быть точек, принадлежащих линии
пересечения. На рис. 377 показано построение точек Е, F, G, Н при
помощи двух таких плоскостей; одна из них проведена через точку О,
благодаря чему определен отрезок E’F’, представляющий собой малую ось
эллипса, получающегося при пересечении конуса ил. α, и в то же время
малую ось горизонтальной проекции этого эллипса.
Отрезки C»D» и E»F» являются сопряженными диаметрами для эллипса —
фронтальной проекции фигуры сечения. По ним можно найти оси эллипса 2).
Натуральный вид сечения найден совмещением секущей плоскости с пл.
π1. Эллипс может быть построен по большой и малой осям, длины которых
найдены путем совмещения концевых точек осей C‘ и D‘ для большой оси, E‘
и F‘ — для малой.
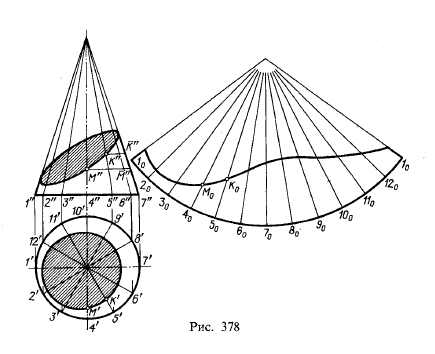
На рис. 378 показано построение развертки. Боковая поверхность развертывается в круговой сектор. Угол сектора подсчитывается по формуле 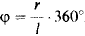
Для того чтобы нанести на развернутой боковой поверхности конуса
линию сечения, проводят ряд образующих конуса и определяют длины их
отрезков: затем наносят образующие на развернутую боковую поверхность
конуса и откладывают длины отрезков этих образующих.
На рис. 378 построена развертка боковой поверхности и па ней нанесена
линия сечения. Длина отрезков образующих определена поворотом
образующих до положения, параллельного пл. π2 (это построение показано для двух образующих).
1) Характерными точками называют такие точки кривой пересечения, как
наиболее удаленная и наиболее близкая к плоскости проекций, точки, делящие кривую на видимую и невидимую части, концы осей эллипсов.
2) О сопряженных диаметрах эллипса см. § 21.
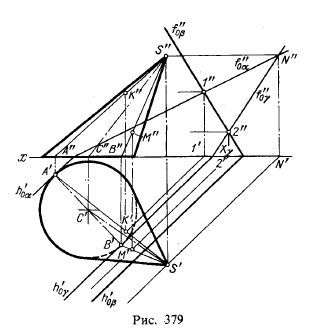
На рис. 379 показано нахождение наиболее и наименее удаленных от пл. π1
точек кривой пересечения некоторого конуса плоскостью общего положения
β. Для построения этих точек проведены касательные к конусу плоскостей α
и γ так, что их следы h’0α и h’0γпараллельны h’0β этим определяются те образующие конической поверхности, на которых должны находиться искомые точки К и М.
Сначала строятся горизонтальные проекции К’ и М’ в точках пересечения
горизонтальных проекций горизонталей, по которым плоскости α и γ
пересекают пл. β с горизонтальными проекциями образующих SA и SB, а
затем на фронтальных проекциях этих образующих отмечаются проекции К» и
М».
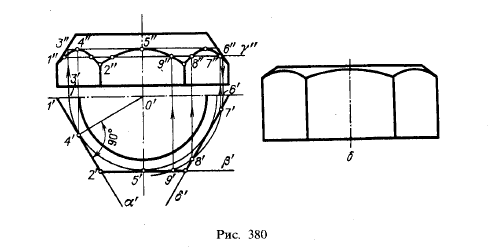
На рис. 380, а показано построение кривых, получающихся на
поверхности конуса вращения при пересечении его гранями правильной
шестиугольной призмы 1). Две из боковых граней расположены в
горизонтально-проецирующих плоскостях α и δ, а третья грань — во
фронтальной пл. β. Положение этих плоскостей относительно оси конуса
позволяет сразу определить, какие кривые получатся в пересечении.
Получаются гиперболы, причем одна из них проецируется на пл. π2 без искажения.
Для нахождения точек кривых взяты параллели на конусе. Прежде всего
найдены крайние точки 1′, 4′, 2′, 5′ на горизонтальной проекции, а по
ним определены точки 1″, 4″, 2″, 5″ на фронтальной проекции. Затем при
помощи вспомогательной горизонтальной пл. γ определена сначала точка 6″
на очерке фронтальной проекции конуса, затем получена точка 6′ и при
помощи окружности радиуса О’6′ построены точки 7′, 8′ и 9′, по которым
найдены точки 7″, 8″ и 9″.
На рис. 380,б изображена шестигранная гайка (дан только вид спереди);
кривые, отделяющие боковые грани гайки от ее конической части,
представляют собой гиперболы, построение проекций которых аналогично
показанному на рис. 380, а.
Вопросы к § 57
- В чем заключается общий прием построения кривой линии, получающейся при пересечении конической поверхности плоскостью?
- Как надо провести плоскость, чтобы пересечь коническую поверхность по прямым линиям?
- Какие кривые получаются при пересечении конуса вращения плоскостями?
- В любую ли коническую поверхность можно вписать сферы?
- Как строится малая ось эллипса, получаемого при пересечении конуса вращения плоскостью?
- В какую кривую проецируется эллипс, получаемый при пересечении конуса вращения, на плоскость, перпендикулярную к оси конуса?
- Как строится развертка боковой поверхности конуса вращения?
- Что представляют собой кривые на гайке с конической фаской на ней?
Конические поверхности
Объединение всех прямых, проходящих через каждую точку данной кривой и некоторую фиксированную точку пространства, не лежащую на этой кривой, называется конической поверхностью. Данная кривая называется направляющей, данная фиксированная точка — вершиной, а прямые — образующими конической поверхности (рис. 233).
Легко видеть, что конические поверхности состоят из двух полостей с общей вершиной.
Конические и цилиндрические поверхности обладают замечательным свойством: все они разворачиваются на плоскость без складок и разрывов, и, наоборот, из плоских листов материала, согнув их, можно получать поверхности конической и цилиндрической формы. Благодаря этому свойству они получили большое применение в технике.
Выведем уравнение конической поверхности. Если М — произвольная точка этой поверхности, отличная от вершины S, а N — точка пересечения образующей SM с направляющей L, то векторы (overrightarrow) и (overrightarrow) коллинеарны. Поэтому существует число λ такое, что
(overrightarrow) = λ (overrightarrow). (1)
Пусть для простоты кривая L лежит в плоскости хОу и имеет уравнение
а вершина S лежит на оси Oz и имеет координаты (0; 0; с), с =/= 0. Тогда’
(overrightarrow) = (х; у; z — с), (overrightarrow) = (ξ ; η; — с),
где (х; у; z ) — координаты точки М, а (ξ ; η ) — координаты точки N на плоскости хОу. Из векторного равенства (1) получаем следующие равенства для координат:
Так как координаты ξ , η удовлетворяют уравнению (2), то координаты (х; у; z) удовлетворяют уравнению
Это и есть уравнение конической поверхности с вершиной в точке S (0; 0; с), с =/= 0, и направляющей F(х; у) = 0. Таким образом, уравнение конической поверхности (3) получается из уравнения направляющей (2) заменой х на ( frac ) и у на (frac).
Задача. Составить уравнение конической поверхности с вершиной в точке
(0; 0; с), с > 0, и направляющей
Данная коническая поверхность имеет уравнение
После соответствующих преобразований получаем искомое уравнение:
Уравнение конической поверхности с вершиной и направляющей
Глава 46. Поверхности второго порядка
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
(1).
Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c — сжатым. В случае, когда a=b=c , эллипсоид представляет собой сферу.
Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями
, (2)
. (3)
Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), — двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b ) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.
Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями
, (4)
, (5)
где p и q — положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), — гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q , параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).
Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).
Выберем какую-нибудь плоскость; обозначим ее буквой . Зададим, кроме того, некоторое положительное число q . Пусть М — произвольная точка пространства, не лежащая на плоскости , — основание перпендикуляра, опущенного на плоскость из точки М. Переместим точку М по прямой в новое положение так, чтобы имело место равенство
и чтобы после перемещения точка осталась с той же стороны от плоскости , где она была первоначально (рис. 6). Точно так же мы поступим со всеми точками пространства, не лежащими на плоскости ; точки, которые расположены на плоскости , оставим на своих местах. Таким образом, все точки пространства, за исключением тех, что лежат на плоскости , переместятся; при этом расстояние от каждой точки до плоскости изменится в некоторое определенное число раз, общее для всех точек. Описываемое сейчас перемещение точек пространства называется его равномерным сжатием к плоскости ; число q носит название коэффициента сжатия.
Пусть дана некоторая поверхность F ; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F ’. Будем говорить, что поверхность F ’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).
ПРИМЕР. Доказать, что произвольный трехосный эллипсоид
может быть получен из сферы
в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия и к плоскости Oxz с коэффициентом сжатия .
ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом и пусть — точка, в которую переходит при этом точка . Выразим координаты x’, y’, z ’ точки М’ через координаты x, y, z точки М. Так как прямая MM ’ перпендикулярна к плоскости Oxy , то x’=x, y’=y . С другой стороны, так как расстояние от точки М’ до плоскости Oxy равно расстоянию от точки М до этой плоскости, умноженному на число , то .
Таким образом, мы получаем искомые выражения:
, , (6)
, , (7)
Предположим, что M(x; y; z ) — произвольная точка сферы
.
Заменим здесь x, y, z их выражениями (7); получим
,
.
Следовательно, точка M’(x’; y’; z ’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам
, , ;
тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.
Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.
имеет две системы прямолинейных образующих, которые определяются уравнениями:
, ;
, ,
где и — некоторые числа, не равные одновременно нулю. Гиперболический параболоид
также имеет две системы прямолинейных образующих, которые определяются уравнениями
, ;
, .
Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L . Точка S называется вершиной конуса; линия L — направляющей.
Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).
Тема: Линейные операции над векторами. Скалярное произведение векторов (стр. 7 )
 |
Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 |
В этом случае уравнение конической поверхности имеет вид

Если направляющая является эллипсом с центром на оси Oz,
то получаем поверхность, называемую конусом второго порядка, уравнение этой поверхности имеет вид:

Ось Oz в этом случае является осью конуса второго порядка.
Сечения конуса второго порядка:
Пусть плоскость p не проходит через вершину конуса второго порядка, тогда плоскость p пересекает конус:
а) по эллипсу, если p пересекает все образующие конуса;
б) по гиперболе, если p параллельна двум образующим конуса;
в) по параболе, если p параллельна одной образующей конуса.
2. Получите уравнение конической поверхности (1).
3. Получите уравнение конической поверхности второго порядка (2).
III. Основные типовые задачи.
Составление уравнения конической поверхности по координатам вершины и уравнению направляющей.
IV. Примеры решения задач.
Задача 1. Написать уравнение конической поверхности, вершина которой находится в начале координат, а направляющая задана уравнениями
Пусть точка M(x, y, z) – произвольная точка конической поверхности. Проведем через эту точку образующую l, она пересечет направляющую в точке 


Выразим из последней системы 




Подставим найденные выражения во второе уравнение системы (3)






Подставляем (4) и (5) в первое уравнение системы (3)



Полученное уравнение является искомым уравнением конической поверхности.
V. Задачи для самостоятельного решения.
1) Написать уравнение конической поверхности, если:
а) направляющая в плоскости xOy задана уравнением 
б) направляющая в плоскости xOy задана уравнением 
в) направляющая в плоскости xOy задана уравнением 
г) направляющая в плоскости xOy задана уравнением 
2) Составить уравнение конической поверхности с вершиной в точке S(1; 2; 4), образующие которой составляют с плоскостью 
3) Написать уравнение конической поверхности, направляющая которой задана уравнениями 

4) Найти уравнение конической поверхности с вершиной в начале координат, которая проходит через линию пересечения:
а) гиперболоида 

б) эллипсоида 

5) Напишите уравнение круговой конической поверхности, если известны уравнения ее оси l: 
6) Доказать, что уравнение 
I. Теоретические сведения.
Определение. Эллипсоидом называется множество точек пространства, координаты которых в некоторой системе координат удовлетворяют следующему уравнению

Уравнение (1) называется каноническим уравнением эллипсоида. Числа a,b,c>0 – полуоси эллипсоида.
Из уравнения эллипсоида можно получить ряд свойств:
1) Все точки эллипсоида расположены внутри прямоугольного параллелепипеда, ограниченного плоскостями 


2) Плоскости симметрии эллипсоида: xOy, yOz, xOz;
оси симметрии эллипсоида: Ox, Oy, Oz;
центр симметрии эллипсоида: начало координат.
3) Вершинами поверхности называются точки пересечения с осями симметрии. Вершины эллипсоида: 




Исследование эллипсоида методом сечений.
Рассмотрим сечения эллипсоида плоскостями, параллельными плоскостям симметрии.
1) Сечение плоскостью a, параллельной плоскости 


а) Если 



б) если 
в) если 
2) Сечение плоскостью b, параллельной плоскости 


а) Если 



б) если 
в) если 
3) Сечение плоскостью g, параллельной плоскости 


а) Если 



б) если 
в) если 
На рис.1 показаны сечения эллипсоида координатными плоскостями.
4. Покажите, что координатные плоскости являются плоскостями симметрии эллипсоида.
5. Покажите, что координатные оси являются осями симметрии эллипсоида.
6. Покажите, что начало координат является центром симметрии эллипсоида.
7. Найдите уравнение линии, образующейся при пересечении эллипсоида 
8. Пересекаются ли эллипсоид 

III. Основные типовые задачи.
9. Составление канонического уравнения эллипсоида.
10. Исследование сечений эллипсоида.
IV. Примеры решения задач.
Задача 1. Написать каноническое уравнение эллипсоида, который проходит через точку 

Каноническое уравнение эллипсоида имеет вид 





По условию точка 



Следовательно, искомое уравнение эллипсоида имеет вид

Ответ: 
Задача 2. Установить, что плоскость 

Координаты общих точек эллипсоида и плоскости удовлетворяют системе уравнений:
Выразив из первого уравнения z и подставив его во второе, получим


Последнее уравнение определяет в плоскости 






V. Задачи для самостоятельного решения.
11. Написать каноническое уравнение эллипсоида, который:
а) проходит через точку 

б) проходит через точку 

в) проходит через точку 

г) пересекает плоскость yOz по эллипсу 

д) пересекает плоскость xOz по эллипсу 

12. Написать каноническое уравнение эллипсоида, проходящего через точки (2, 2, 4), (0, 0, 6), (2, 4, 2).
13. Исследовать методом сечений эллипсоид 
14. Установить, что плоскость 

15. Доказать, что эллипсоид 

16. Даны вершины эллипсоида 


I. Теоретические сведения.
1. Однополостный гиперболоид.
Определение. Однополостным гиперболоидом называется множество точек пространства, координаты которых в некоторой системе координат удовлетворяют следующему уравнению

Уравнение (1) называется каноническим уравнением однополостного гиперболоида.
Из уравнения гиперболоида можно получить ряд свойств:
1) Однополостный гиперболоид фигура неограниченная.
2) Плоскости симметрии однополостного гиперболоида: xOy, yOz, xOz;
оси симметрии однополостного гиперболоида: Ox, Oy, Oz;
центр симметрии однополостного гиперболоида: начало координат.
3) Вершинами поверхности называются точки пересечения с осями симметрии. Вершины однополостного гиперболоида: 


Исследование однополостного гиперболоида методом сечений.
1) Сечение плоскостью a, параллельной плоскости 


Из уравнении (3) следует, что при всех значениях h сечением однополостного гиперболоида является эллипс.
2) Сечение плоскостью b, параллельной плоскости 


а) Если 



б) если 
в) если 
3) Сечение плоскостью g, параллельной плоскости 







б) если 
в) если 
2. Двуполостный гиперболоид.
Определение. Двуполостным гиперболоидом называется множество точек пространства, координаты которых в некоторой системе координат удовлетворяют следующему уравнению

Уравнение (8) – каноническое уравнение двуполостного гиперболоида.
Из уравнения гиперболоида можно получить ряд свойств:
1) Внутри полосы, ограниченной плоскостями 
3) Плоскости симметрии двуполостного гиперболоида: xOy, yOz, xOz;
оси симметрии двуполостного гиперболоида: Ox, Oy, Oz;
центр симметрии двуполостного гиперболоида: начало координат.
3) Вершины двуполостного гиперболоида: 
Исследование двуполостного гиперболоида методом сечений.
1) Сечение плоскостью a, параллельной плоскости 


а) Если 
б) если 
в) если 
2) Сечение плоскостью b, параллельной плоскости 


При любом значении h получаем гиперболу с действительной осью параллельной оси Oz. В частности, если 


3) Сечение плоскостью g, параллельной плоскости 


При любом значении h получаем гиперболу с действительной осью параллельной оси Oz. В частности, если 


1. Покажите, что координатные плоскости являются плоскостями симметрии однополостного (двуполостного) гиперболоида.
2. Покажите, что координатные оси являются осями симметрии однополостного (двуполостного) гиперболоида.
3. Покажите, что начало координат является центром симметрии однополостного (двуполостного) гиперболоида.
4. Найдите уравнение линии, образующейся при пересечении гиперболоида 
5. Найдите уравнение линии, образующейся при пересечении гиперболоида 
III. Основные типовые задачи.
1. Составление канонического уравнения гиперболоида.
2. Исследование сечений гиперболоида.
IV. Примеры решения задач.
Задача 1. Написать каноническое уравнение однополостного гиперболоида, если он пересекает плоскость xOy по эллипсу 

Каноническое уравнение однополостного гиперболоида имеет вид 
Получаем уравнение эллипса, лежащего в плоскости xOy

По условию задачи этот эллипс задан уравнением 

Проводя аналогичные рассуждения, можно получить уравнение гиперболу, получающейся в сечении гиперболоида с плоскостью yOz

По условию, это гипербола 

Таким образом, искомое уравнение гиперболоида имеет вид

Ответ: 
Задача 2. Напишите уравнение плоскости, параллельной плоскости yOz и пересекающей однополостный гиперболоид 
Уравнение плоскости параллельной плоскости yOz имеет вид x=h. Линия пересечения этой плоскости с гиперболоидом задается системой
Откуда получаем уравнение


Последнее уравнение – это каноническое уравнение гиперболы, действительная полуось которой равна 




Следовательно, искомая плоскость имеет уравнение 
Ответ: 
V. Задачи для самостоятельного решения.
1. Написать каноническое уравнение однополостного гиперболоида, если поверхность:
а) проходит через точку 

б) пересекает плоскость xOy по окружности 

2. Написать уравнение двуполостного гиперболоида в канонической системе координат, если точки 


3. Найти множество точек, для каждой из которых мод, 3), (0, 0, –3) есть величина постоянная, равная 4.
4. Определите вид линии пересечения однополостного гиперболоида 

5. Доказать, что двуполостный гиперболоид 

6. Найти точки пересечения поверхности 

Тема: Параболоиды.
Прямолинейные образующие поверхностей второго порядка
I. Теоретические сведения.
1. Эллиптический параболоид.
Определение. Эллиптическим параболоидом называется множество точек пространства, координаты которых в некоторой системе координат удовлетворяют следующему уравнению

Уравнение (1) – каноническое уравнение эллиптического параболоида.
Из уравнения параболоида следует:
1) Все точки эллиптического параболоида лежат выше плоскости xOy;
2) Плоскости симметрии эллиптического параболоида: yOz, xOz;
ось симметрии эллиптического параболоида: Oz;
центра симметрии у эллиптического параболоида нет.
3) Вершина эллиптического параболоида: О(0; 0; 0) – начало координат.
Исследование эллиптического параболоида методом сечений.
1) Сечение плоскостью a, параллельной плоскости 


а) Если 
б) если 
в) если 
2) Сечение плоскостью b, параллельной плоскости 


При любом значении h получаем параболу, ось которой параллельна оси Oz, В частности, если 


3) Сечение плоскостью g, параллельной плоскости 



При любом значении h получаем параболу, ось которой параллельна оси Oz, ветви направлены вверх. В частности, если 


2. Гиперболический параболоид.
Определение. Гиперболическим параболоидом называется множество точек пространства, координаты которых в некоторой системе координат удовлетворяют следующему уравнению

Уравнение (8) – каноническое уравнение гиперболического параболоида.
Из уравнения параболоида следует:
1) Гиперболический параболоид поверхность неограниченная;
2) Плоскости симметрии гиперболического параболоида: yOz, xOz;
ось симметрии: Oz;
центра симметрии у гиперболического параболоида нет.
3) Вершина: О(0; 0; 0) – начало координат.
Исследование гиперболического параболоида методом сечений.
1) Сечение плоскостью a, параллельной плоскости 


а) Если 
б) если 
в) если 
2) Сечение плоскостью b, параллельной плоскости 


При любом значении h получаем параболу, ось которой параллельна оси Oz, В частности, если 


3) Сечение плоскостью g, параллельной плоскости 



При любом значении h получаем параболу, ось которой параллельна оси Oz, ветви направлены вниз. В частности, если 


3. Прямолинейные образующие поверхностей второго порядка.
Определение. Прямая l называется прямолинейной образующей поверхности второго порядка, если каждая точка этой прямой лежит на поверхности.
Очевидно, что образующие конических и цилиндрических поверхностей являются прямолинейными образующими. Кроме того, прямолинейные образующие имеют однополостный гиперболоид и гиперболический параболоид. У однополостного гиперболоида и гиперболического параболоида существует два семейства прямолинейных образующих, таких что:
1) через каждую точку поверхности проходят по одной прямолинейной образующей из каждого семейства;
2) любые две прямолинейные образующие одного семейства являются скрещивающимися.
Прямолинейные образующие однополостного гиперболоида задаются следующими системами уравнений:
I. 

где k и l – любые числа.
Прямолинейные образующие гиперболического параболоида задаются следующими системами уравнений:
I. 

1) Докажите, что линией пересечения эллиптического параболоида 

2) Покажите, что плоскость xOy не является плоскостью симметрии гиперболического параболоида.
3) Напишите каноническое уравнение гиперболического параболоида с вершиной в начале координат, ось которого совпадает с осью Oy.
4) Определите вид линии пересечения гиперболического параболоида 

5) Сколько прямолинейных образующих проходит через каждую точку гиперболического параболоида, конуса, цилиндра, однополостного гиперболоида?
III. Основные типовые задачи.
1) Составление канонического уравнения параболоида.
2) Исследование параболоида методом сечений.
3) Составление уравнений прямолинейных образующих поверхностей второго порядка.
IV. Примеры решения задач.
Задача 1. Найти фигуру, состоящую из всех точек, одинаково удаленных от данной плоскости a и данной точки А, не лежащей в этой плоскости.
Обозначим расстояние между точкой А и плоскостью a через р. Введем в пространстве систему координат так, чтобы начало координат находилось посередине между точкой А и плоскостью a, плоскость xOy была параллельна плоскости a. Тогда точка А имеет координаты 




По условию 





Таким образом, искомое множество точек есть эллиптический параболоид, заданный последним уравнением.
Ответ: 
Задача 2. Исследовать методом сечений поверхность 
Исследуем сечения гиперболического параболоида координатными плоскостями и плоскостями им параллельными.
1) Сечение плоскостью a, параллельной плоскости 

а) Если 
б) если 
в) если 
2) Сечение плоскостью b, параллельной плоскости 

При любом значении h получаем параболу, ось которой параллельна оси Oz, В частности, если 


3) Сечение плоскостью g, параллельной плоскости 

При любом значении h получаем параболу, ось которой параллельна оси Oz, ветви направлены вниз. В частности, если 


Задача 3. Написать уравнения двух систем прямолинейных образующих однополостного гиперболоида 

Приведем уравнение гиперболоида к каноническому виду:

Перенесем второе слагаемое в правую часть

Применим формулу разности квадратов

Равенство имеет место в том случае, если множители в левой и правой частях пропорциональны
I. 
Мы получили уравнения двух систем прямолинейных образующих однополостного гиперболоида. Теперь найдем те из них, которые проходят через данную точку 
I.

Подставляя это соотношение в систему I, получаем




I.

Подставляем в II:


Ответ: 
V. Задачи для самостоятельного решения.
1) Найти уравнение параболоида с центром в начале координат, ось которого совпадает с осью Oz и который проходит через точки
(1; –2; 1) и (–3; –3; 2).
2) Дана плоскость a и перпендикулярная к ней прямая l. Найти множество точек пространства, для каждой из которых квадрат расстояния до прямой l в три раза больше расстояния до плоскости a.
3) Напишите каноническое уравнение гиперболического параболоида с вершиной в начале координат, ось которого совпадает с осью Oy, если известно, что он проходит через точки 

4) Доказать, что эллиптический параболоид 

5) Найдите прямолинейные образующие параболоида 
6) Убедившись, что точка А(–2; 0; 1) лежит на гиперболическом параболоиде 
7) Найдите прямолинейные образующие гиперболоида 


9) На гиперболическом параболоиде 

10) Написать уравнение плоскости, параллельной плоскости 

http://a-geometry.narod.ru/problems/problems_46.htm
http://pandia.ru/text/78/609/25488-7.php


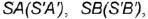
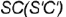 и
и 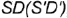 которые будут определять очерки фронтальной и профильной проекций конуса.
которые будут определять очерки фронтальной и профильной проекций конуса.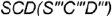 ограниченный:
ограниченный: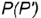
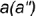
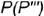 выполняется по принадлежности образующей
выполняется по принадлежности образующей 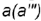 , построенной но координате
, построенной но координате  .
.
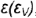
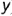 ).
).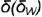
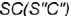 и
и 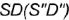 и пересекает его поверхность по участку гиперболы
и пересекает его поверхность по участку гиперболы 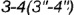 , которая проецируется в отрезок и ограничена вырожденными в точки фронтально-проецирующими линиями пересечения плоскостей срезов
, которая проецируется в отрезок и ограничена вырожденными в точки фронтально-проецирующими линиями пересечения плоскостей срезов 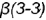 и плоскости
и плоскости 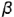 определяет вертикальный видимый отрезок
определяет вертикальный видимый отрезок 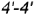 вырожденной в линию проекции профильной плоскости, точки
вырожденной в линию проекции профильной плоскости, точки 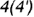 которой лежат на очерковой окружности основания конуса.
которой лежат на очерковой окружности основания конуса.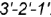 .
.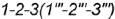
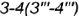 , ограниченные видимым отрезком
, ограниченные видимым отрезком 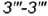 (построен) и видимым отрезком
(построен) и видимым отрезком 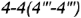 . точки которого построены но координате
. точки которого построены но координате 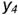 .
.