Как найти точку на плоскости призмы - Исправление недочетов и поиск решений вместе с Examum.ru

Проекции точек на поверхностях геометрических тел

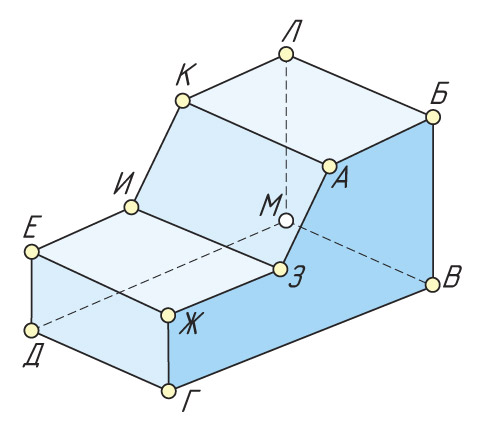
Вы уже знаете, как построить проекции предмета или объекта. Часто при изготовлении изделий необходимо по заданным проекциям определить геометрическую форму предметов и их частей. Предмет можно рассматривать как комбинацию различных геометрических элементов: вершин, ребер, граней и т. д.

Укажите количество вершин, ребер и граней изображенного предмета.

Для точного построения изображений ряда деталей необходимо уметь находить проекции отдельных точек. Чтобы построить проекции точки, принадлежащей поверхности геометрического тела, необходимо понять, на какой поверхности или на каком элементе поверхности (ребре, вершине, грани) находится эта точка. Представив любую деталь как совокупность геометрических тел, можно легко найти проекцию точки.

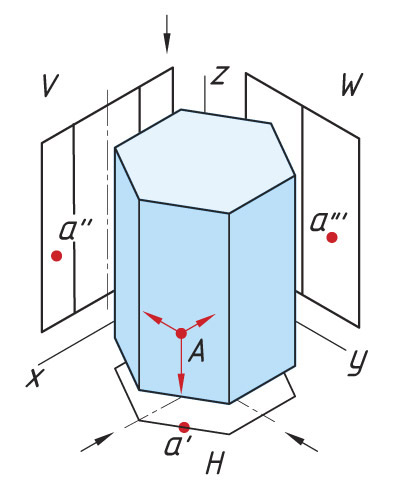
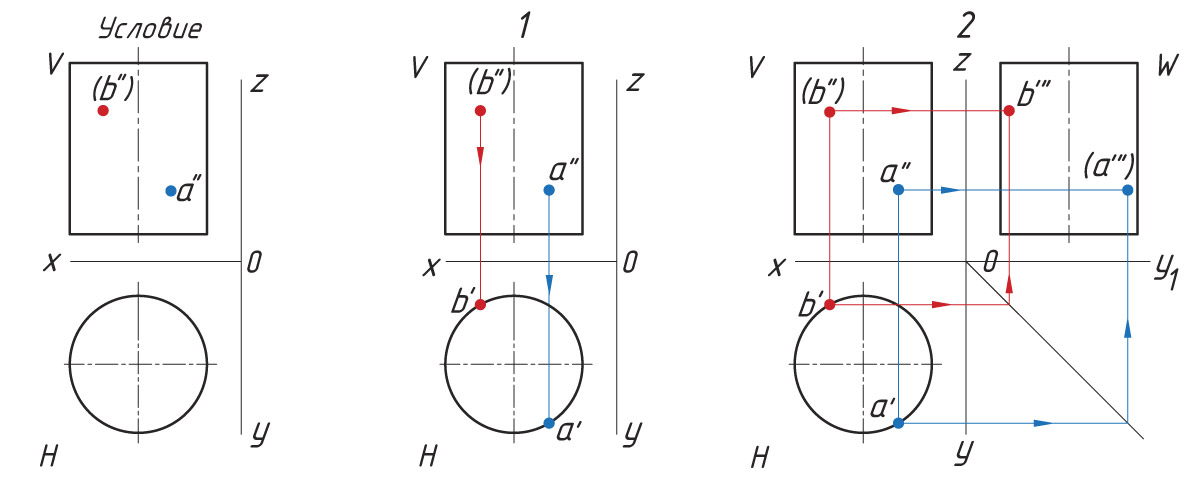
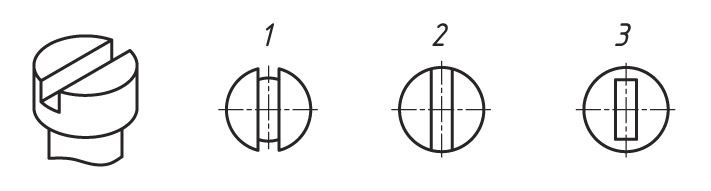
Рассмотрим проекции точки на геометрических телах.

Проецирование точек на поверхности цилиндра

Последовательность проецирования точек
Заданы фронтальные проекции а″ и b″ точек А и В, лежащие на боковой поверхности цилиндра. Проекция а″ находится на видимой части поверхности цилиндра (на плоскости V показана без скобок), b″ находится на невидимой части поверхности цилиндра (на плоскости V показана в скобках).

1. Находят горизонтальные проекции точек а′ и b′. Так как горизонтальная проекция боковой проекции цилиндра отображается в виде круга, то проекции точек а′ и b′ будут находиться на нем. Для их нахождения проводят вертикальные линии связи из проекций точек а″ и b″ до пересечения с окружностью.

2. Проекции точек а′″ и b′″ находят на пересечении линий проекционной связи.

Направление взгляда на плоскости проекций H, W помогает определить видимость проекций точек на горизонтальной и профильной плоскости проекций. Например, проекции а′ и b′ на плоскости H видны. Проекция а′″ на плоскости W не видна (показана в скобках), проекция b′″ видна (показана без скобок).

Определите, какая из горизонтальных проекций на рисунке является проекцией наглядного изображения головки винта.

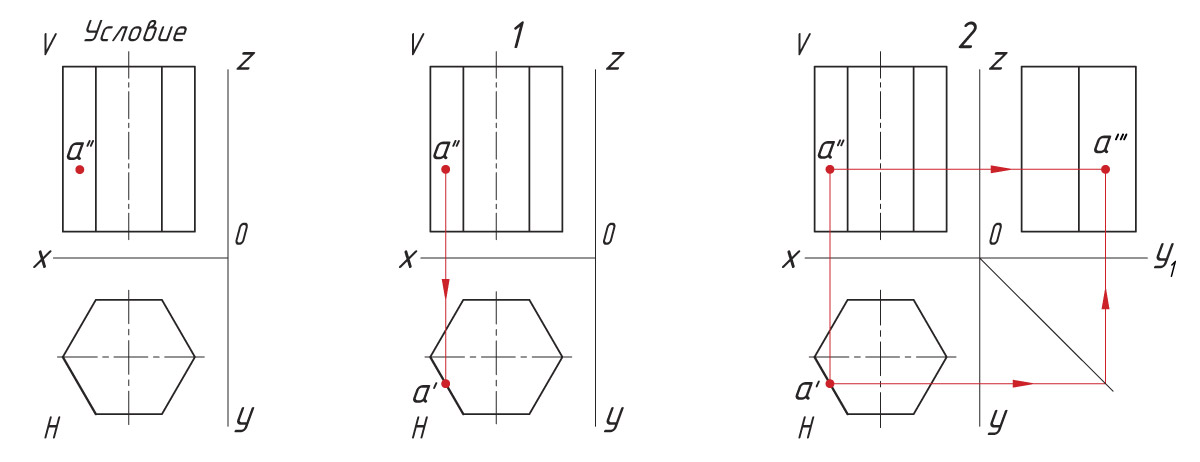
Проецирование точек на поверхности призмы

Последовательность проецирования точек
Задана фронтальная проекция а″ точки А, лежащая на боковой поверхности шестигранной призмы.

1. Находят горизонтальную проекцию точки а′. Для ее нахождения проводят вертикальную линию связи из проекции точки а″ до пересечения с шестиугольником (горизонтальная проекция призмы).

2. Проекцию точки а′″ находят на пересечении линий проекционной связи.

Опишите последовательность проецирования точки, находящейся на ребре призмы. Выполните это построение.

Проецирование точек на поверхности пирамиды

Построение проекции точки, лежащей на ребре
Если точка находится на ребре предмета, то сначала необходимо выполнить проекцию ребра, а затем при помощи линий проекционной связи найти проекции точки, лежащей на ребре.

Как вы считаете, можно ли таким способом спроецировать точку, находящуюся не на ребре, а на грани четырехгранной пирамиды? Свои предположения проверьте на практике.

Общий метод определения точки, лежащей на поверхности геометрического тела, заключается в следующем: через точку на поверхности проводят вспомогательную прямую, проекции которой легко определяются на данной поверхности.

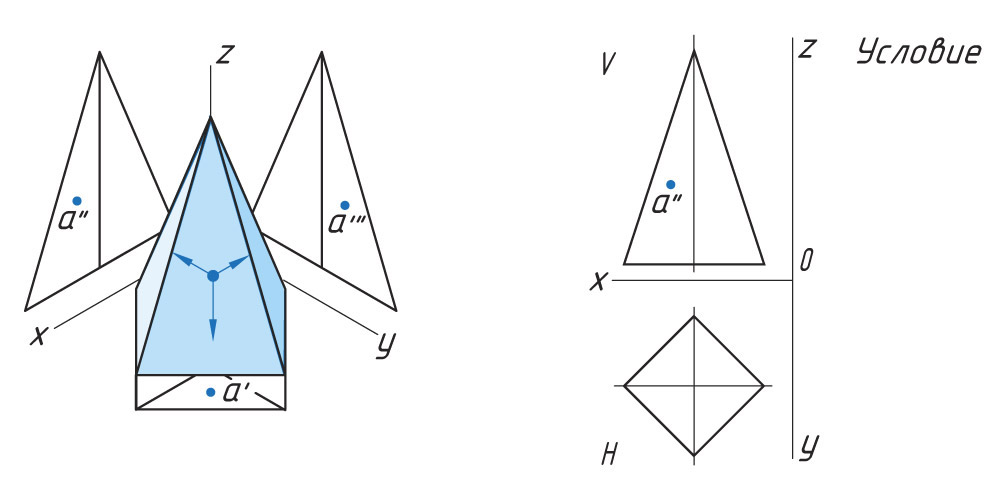
Построение проекции точки, лежащей на грани
Задана фронтальная проекция а″ точки А, лежащая на боковой поверхности четырехгранной пирамиды.

Проекции точек можно определить несколькими способами. Рассмотрим каждый из них.

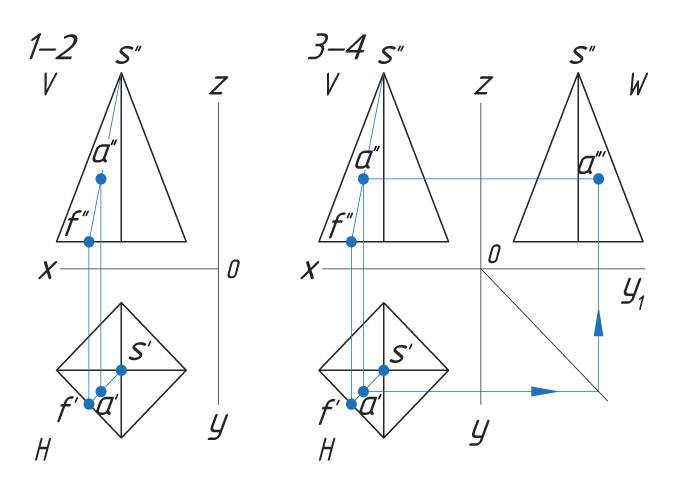
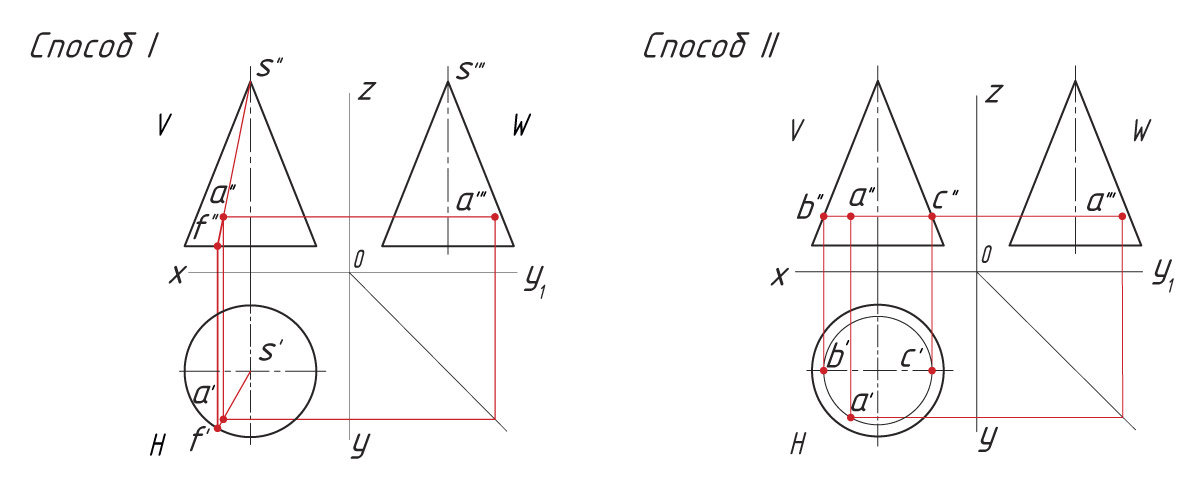
Способ I.

1. Находят горизонтальную проекцию точки а′: вспомогательной прямой соединяют заданную проекцию точки а″ с проекцией вершины пирамиды s″ и продлевают ее до пересечения с основанием в точке f″.
2. Проводят вертикальную линию связи из проекции f″ до пересечения с основанием на плоскости H в точке f′.
3. Точку f′ соединяют с вершиной пирамиды s′. На нее проводят вертикальную линию связи из проекции а″ до пересечения в точке а′.
4. Проекции точки а′″ находят на пересечении линий проекционной связи.

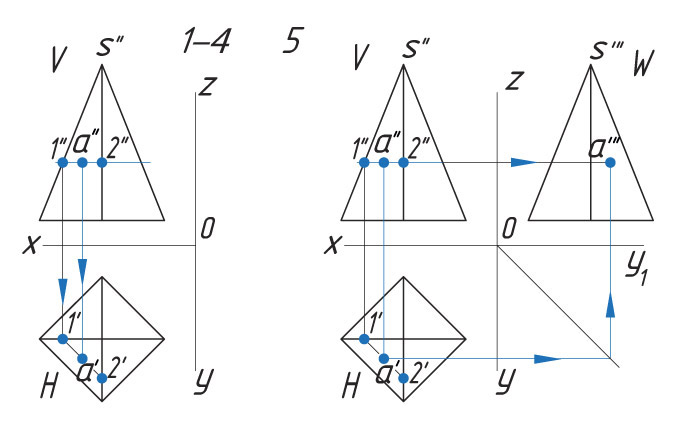
Способ II.

1. Через проекцию а″ точки А проводят вспомогательную прямую и получают точки пересечения с ребрами пирамиды 1″ и 2″.
2. Опустив из точки 1″ вертикальную линию связи до пересечения с соответствующим ребром на плоскости H, получают горизонтальную проекцию точки 1′.
3. Для нахождения проекции 2′ проводят из точки 1′ вспомогательную прямую, параллельную основанию до пересечения с ребром.
4. Горизонтальную проекцию а′ определяют, опустив вертикальную линию связи из точки а″ до пересечения со вспомогательной прямой 1′2′.
5. Проекцию точки а′″ находят на пересечении линий проекционной связи.

На ваш взгляд, изменится ли положение проекции точки, если вспомогательную прямую провести не параллельно, а наклонно к горизонтальной плоскости?

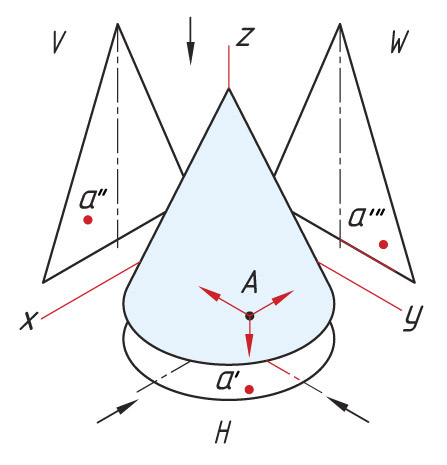
Проецирование точек на поверхности конуса. На поверхности конуса проекции точек можно также определить двумя способами.

Способ I заключается в определении проекций точки с помощью вспомогательной линии — образующей, расположенной на поверхности конуса и проведенной через точку А.
В способе II через точку А проводят вспомогательную плоскость, которая пересечет конус по окружности, расположенной в плоскости, параллельной основанию конуса.

Источник

9 декабря, 2013 Анна Веселова

Здравствуйте! Сегодня мы научимся создавать ассоциативный чертеж по готовой 3d модели призмы и пирамиды. Их мы построили на уроке по 3d моделированию

Урок 2. Создаем 3d модели призмы, пирамиды, цилиндра и конуса. Или как создать четыре 3d модели за 10 минут.

Также на этом уроке вы узнаете, как находить проекции точек на чертежах призмы и пирамиды.

Создаем ассоциативный чертеж по 3d модели

Для того, чтобы создать ассоциативный чертеж выполним следующее: создаем чертеж→на компактной панели выбираем кнопку

панель стандартные виды

«Вид»→ ниже выбираем «Стандартные виды»→в открывшемся окне выбираем файл с 3d моделью (расширение .m3d)

выбираем 3d модель призмы

→ на панели свойств, вкладка «схема» подбираем количество видов и расстояние между ними→жмем на поле чертежа и все, три проекции призмы или пирамиды готовы.

схема видов чертежа

Остается только вставить изометрию и оформить чертеж по ГОСТу.

Чтобы вставить изометрию открываем файл с 3d моделью призмы (пирамиды) и пересохраняем ее как рисунок в формате .png.

сохраняем модель в формате рисунка

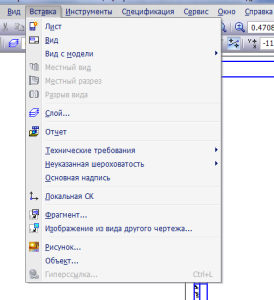
Возвращаемся к созданию ассоциативного чертежа. В строке главного меню жмем на вкладку «Вставка»→ «Рисунок»→ в открывшемся окне выбираем рисунок с призмой (пирамидой)→ вставляем рисунок в чертеж.

вставляем рисунок в чертеж

Как найти проекции точек на пирамиде и призме?

Как найти проекции точек на призме?

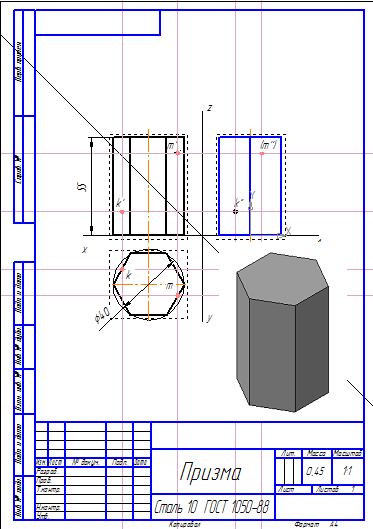
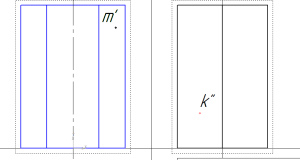
В задании на построение геометрических тел требуется найти недостающие проекции точек К и М (задачник Мироновой Р.С., стр. 65).

проекции точек на призме

Найдем проекции точек на призме.

Задана фронтальная проекция точки М – m’ и профильная проекция точки К – k’’.

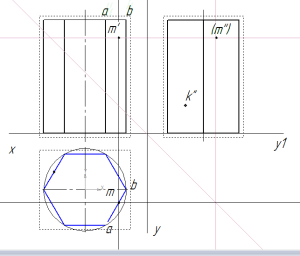
Найдем горизонтальную проекцию точки m. Для этого построим вспомогательную прямую через точку m’ до пересечения с горизонтальной проекцией призмы.

находим проекции точек на призме

Как видно из рисунка, точка m’ принадлежит грани ab. Поэтому горизонтальная проекция m будет находиться в месте пересечения вспомогательной прямой с гранью ab на горизонтальной проекции призмы.

Профильную проекцию находят с по линиям связи, построенным из m’ и m. Так как на профильной проекции призмы точку m’’ не видно, она взята в скобки.

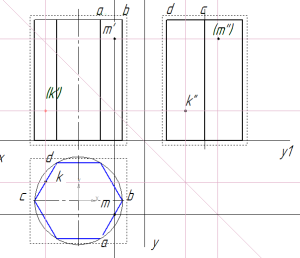
Для того, чтобы найти недостающие проекции точки К поступаем аналогично.

строим горизонтальную и фронтальную проекции точек

По линиям связи находим горизонтальную проекцию k, принадлежащую грани cd. Фронтальную проекцию (k’) также строим по линиям связи.

Как найти проекции точек на пирамиде?

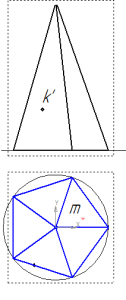
Точка М на пирамиде задана горизонтальной проекцией m, точка К – фронтальной проекцией k’.

точки на пирамиде

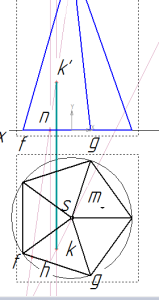
строим горизонтальную проекцию точки

Начнем с нахождения горизонтальной проекции k. Для этого через вершину пирамиды и k’ проводим вспомогательную прямую. Затем через полученную точку n проводим линию связи до пересечения с гранью fg. Через полученную точку h и вершину s проводим еще одну вспомогательную прямую.

И по линии связи опускаемся из точки k’ до пересечения с этой прямой hs. Горизонтальная проекция k найдена.

Профильную проекцию k’’ находим по линиям связи без дополнительных построений.

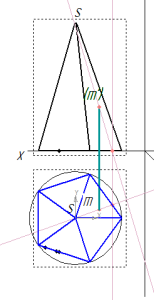
Фронтальную проекцию m’ находим аналогично построению горизонтальной проекции k. Описывать процесс не буду. Вот вам рисунок.

строим фронтальную проекцию точки М

Профильную проекцию m’’ найти особого труда не составит, все по тем же линиям связи.

Таким образом находят проекции точек на пирамиде и призме.

Чтобы лучше все уяснить посмотрите видеоурок.

Скачать чертежи бесплатно можно здесь

Теперь-то вы точно сможете быстро создать ассоциативный чертеж и найти по указанию преподавателя проекции точек на пирамиде или призме.

The following two tabs change content below.

Bio
Latest Posts

Рада приветствовать Вас в своем блоге! Я создала его с целью помочь всем желающим освоить программу Компас 3d. Мы пройдем весь путь от азов черчения до создания серьезных сборок. Присоединяйтесь!

Понравился материал? Подпишись на обновления!

Вы можете пропустить чтение записи и оставить комментарий. Размещение ссылок запрещено.

Источник

Точка принадлежит
поверхности, если она находится на линии
этой поверхности. План решения задачи
на принадлежность точки поверхности
включает:

определение
вида заданной поверхности;
выбор
графически простой для построения на
чертеже линии поверхности, проходящей
через заданную точку (прямая или
окружность);
построение
проекций этой линии на чертеже;
построение
искомых проекций точки.

Для лучшего
представления и понимания эпюр каждой
поверхности сопровождается наглядным
изображением, а стрелкой указывается
направление взгляда (фронтальная
проекция – вид спереди).

Точки и линии на поверхности призмы

Рассмотрим
построение точки и линии на поверхности
прямой призмы.

очки и линии на поверхности пирамиды

S₂

остроить профильную проекцию
пирамиды и недостающие проекции точки
и прямой.

m₂

В₂

E₂

C₂(G₂)

D₂(F₂)

А₁

В₁

С₁

D₁

E₁

G₁

F₁

S₁

m₁

очки и линии на поверхности цилиндра

Построить профильную
проекцию цилиндра и недостающие проекции
точки и прямой.

очки и линии на поверхности конуса

Построить профильную
проекцию конуса и недостающие проекции
точки и прямой.

Точки и линии
на поверхности сферы

остроение проекций точек на сфере
понятно из построения точкиF,
заданной на фронтальной проекции сферы.
Горизонтальная проекцияF₁точкиFнайдена с
помощью параллели, проходящей через
точку F
(F₂).
На горизонтальной проекции радиус
параллелиR_F,
проведенный из центра сферы, пересекается
с линией связи от фронтальной проекцииF₂точки
F. Для построения
профильной проекцииF₃точки F
необходимо замерить координатуyточкиF (у_F).

Построить
недостающие проекции точек и обозначить
их на наглядном изображении.

Точки и линии на поверхности тора

остроение проекций точек на торе
понятно из построения точкиА
(через параллель с
радиусом R_А),
заданной на фронтальной проекции тора

Построить недостающие
проекции точек и обозначить их на
наглядном изображении.

Лекция
№ 5

СЕЧЕНИЕ
ПОВЕРХНОСТЕЙ ПРОЕЦИРУЮЩИМИ

ПЛОСКОСТЯМИ

1. Сечение
многогранников проецирующими плоскостями
(призма, пирамида). 2. Сечение поверхностей
вращения проецирующими плоскостями
(цилиндр, конус, сфера).

1
СЕЧЕНИЕ МНОГОГРАННИКОВ ПРОЕЦИРУЮЩИМИ

ПЛОСКОСТЯМИ

лоскость пересекает многогранник
по плоским многоугольникам. Для построения
многоугольника необходимо найти его
вершины (точки пересечения плоскости
с ребрами и гранями).

Призма

Пирамида

2
СЕЧЕНИЕ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ
ПРОЕЦИРУЮЩИМИ ПЛОСКОСТЯМИ

При построении
точек сечения применяется способ
построения точек по принадлежности.

Сечение
цилиндра

Любая плоскость
может пересекать поверхность прямого
кругового цилиндра:

по
окружности,
если плоскость
сечения перпендикулярна его образующим
(рис. 63), такоесечение называется
нормальным;
по двум
образующим,
если секущая
плоскость
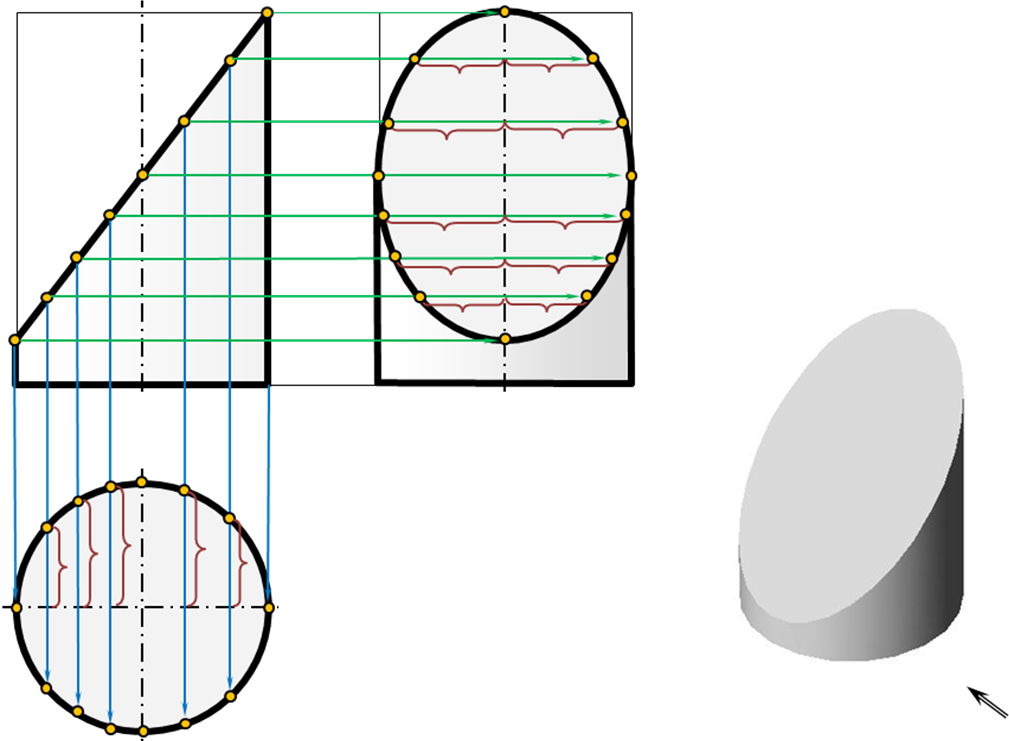
параллельна оси цилиндра (рис. 64);по эллипсу, если секущая
плоскостьнаклонена
к оси цилиндра и пересекает все
его образующие (построить три проекции
цилиндра).

Сечение конуса

Конус
является геометрическим
телом, которое может
иметь в сечении пять различных фигур:

треугольник,
если
секущая плоскость
пересекает конус через вершину по
двум образующим (рис. 65, а, б);

окружность,
если секущая
плоскость
параллельна основанию или перпендикулярна
оси, а конус прямой круговой
(рис. 66);

эллипс,
если
секущая плоскость пересекает
все образующие конуса под
некоторым углом к основанию конуса
(рис. 67);

параболу,
если
секущая плоскость параллельна
одной из образующих конуса
(рис. 68);

гиперболу,
если секущая
плоскость параллельна
оси конуса или параллельна
двум его образующим (рис. 69).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

←Метод координат

Задача 1

Задача 2

Задача 3

Задача1:

Основанием призмы АВСА₁В₁С₁ является правильный треугольник АВС со стороной 6. Боковое ребро АА₁ призмы равно 6 и образует со сторонами АВ и АС углы по 60⁰.
Определите:

а) угол между прямыми АА₁ и СВ₁;
б) расстояние от точки B₁ до плоскости А₁СВ;

Наша заданная призма не прямая, а наклонная, так как ребро АА₁ не перпендикулярно основанию. Это обстоятельство в значительной степени усложняет решение задачи Две боковые грани у нее не привычные прямоугольники, а ромбы со стороной, равной 6. Почему? Потому что боковые ребра у призмы параллельны, а в нашей задаче они еще и равны ребрам основания призмы. Третья боковая грань — прямоугольник, а в данной задаче — квадрат, так как все ребра призмы равны.

Конечно же ее, эту задачу, можно решить геометрически, что мы и сделаем, частично.

а) Угол между скрещивающимися прямыми АА₁и СВ₁определяется при помощи построения прямой, параллельной одной из скрещивающихся и пересекающих вторую из скрещивающихся прямых. В данной задаче это вообще несложно, так как прямая АА₁ параллельна плоскости СВ₁С₁ . Ну, и расстояние между прямыми находим построением дополнительной плоскости МАА₁.

Рассмотрим плоскость СВ₁С₁. Эта плоскость параллельна АА₁, так как прямые ${AA_1} parallel {CC_1} parallel {BB_1}$ . Это квадрат по условию, а следовательно, ${AA_1} parallel {M M_1}$ . Тогда угол между прямыми будет $widehat{( AA_1) (CB_1)}$ = ∠M₁OB₁ = 45°.

Кстати, представьте, что вам требуется найти угол между прямыми АС₁ и А₁В. В этом случае найти эти значения геометрически не так уж и просто. Как и определение расстояния от точки до плоскости.

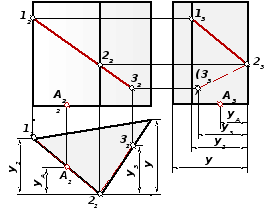
Мы же пойдем другим путем, присоединим к нашей призме систему координат, определим координаты узловых точек и найдем, все что нужно по координатам прямых и плоскостей. (Кликните, чтобы увеличить чертеж).

Чтобы сделать рисунок более понятным, я закрасила грани и основания разным цветом. Предлагаю посмотреть на призму в проекциях на координатные плоскости, как бы со всех сторон. Соответственно на рисунке 1 смотрим на плоскость х0у, на рисунке 2 — z0y, а на рисунках 3 и 4 — плоскость z0x слева и справа от призмы.

Переходим к расчету координат узловых точек. Вспомним, что наша призма состоит их двух треугольников (основания призмы), двух ромбов (боковые грани) и квадрата (третья боковая грань). Чтобы определиться, насколько отстоит верхнее основание от нижнего, нам необходимо выяснить положение точки А₁.

Боковая грань АА₁С₁С — ромб углом 60⁰, а следовательно, его диагональ равна стороне. А это значит, что точка А₁ равноудалена от точек А и С. Точно также можно рассмотреть грань АА₁В₁В.

Получается, что точка А₁ равноудалена от точек А, В и С. А это значит, что координаты х и у можно определить по чертежу. Фактически, на чертеже представлена проекция нашей призмы на плоскость хОу. Учитывая, что треугольник ΔАВС правильный, и сторона его равна 6, можно сказать, что проекция точки А₁ — центр описанной окружности, а АА₁ — ее радиус. Найду его по теореме синусов, а вы можете и по-другому, вариантов много.

$[frac{a}{sin A} = frac{b}{sin B} = frac{c}{sin C} = 2R]$

$[AA_1 = frac{6}{2sin 60^0} = frac{3cdot2}{sqrt3} = 2sqrt3]$

Координата z для нижнего основания призмы равна 0, а для верхнего определяем его из рисунка2, где АА₁ — гипотенуза треугольника, а высота (она же координата z) — катет. Координата $z = sqrt{6^2 - (2sqrt3)^2} = 2sqrt6$

Итак, точки и их координаты: Нижнее основание

В верхнем основании каждая точка сдвигается на вдоль оси Ох, и координата

Переходим к следующему вопросу

б) По координатам узловых точек будем искать расстояние от вершины призмы до плоскости. Расстояние от точки В₁ до плоскости А₁СВ определим по формуле

$[rho = frac{left|{Ax_b + By_b + Cz_ba +D}right|}{sqrt{A^2 + B^2 + C^2}}]$

Осталась «самая ерунда» — найти эти самые A, B, C и D. Ну что ж, ищем.

Для этого составляем и решаем систему уравнений, основываясь на точках плоскости: .

$[begin{Bmatrix}{Acdot 0 +Bcdot(2sqrt3) + Ccdot(2sqrt6) + 1 = 0}\{Acdot (-3) +Bcdot(3sqrt3) + Ccdot 0 + 1 = 0}\{Acdot 3 +Bcdot(3sqrt3) + Ccdot(0) + 1 = 0}]$

$[begin{Bmatrix}{0 +{2sqrt3}B + {2sqrt6}C + 1 = 0}\{-3 A +{3sqrt3}B + 0 + 1 = 0}\{ 3A +{3sqrt3}B + 0 + 1 = 0}]$

Складываем второе и третье уравнение, получаем: $B = - frac{2}{6sqrt3} = - frac{sqrt3}{9}$

Из второго уравнения: $3A = 3sqrt3 B + 1 = 3sqrt3 cdot(-frac{sqrt3}{9}) + 1 = 0$ ,

Из первого уравнения:

Подставляем В и находим С : $2sqrt6 C = -2sqrt3 (- frac{sqrt3}{9}) -1 = frac{2}{3} - 1 = -frac{1}{3}$

$[C = -frac{1}{3cdot2sqrt6 } = - frac{sqrt6}{36}]$

(Кстати, уравнение нашей плоскости будет $0cdot x - frac{sqrt3}{9} y - frac{sqrt6}{36} z + 1 = 0$ . )

Теперь ищем расстояние от точки до плоскости:

$[rho = frac{left|{0cdot(-3) + (- frac{sqrt3}{9})cdot{5sqrt3} + ( - frac{sqrt6}{36}){2sqrt6} +1}right|}{sqrt{0^2 + (- frac{sqrt3}{9})^2 + ( - frac{sqrt6}{36})^2}}]$

Ответ: 45º,

Задача2 (вариант Ларина №272):

Дан куб АВСDА₁В₁С₁D₁ c ребром 2.

а) Докажите, что плоскости A₁BD и B₁D₁C параллельны
б) Найдите расстояние между плоскостями A₁BD и B₁D₁C.

С первым пунктом все просто: Плоскости параллельны, потому что пересекающиеся прямые их попарно параллельны.

Переходим к пункту б). Координаты точек будут

Составляем систему уравнения плоскости с координатами точек, через которые она проходит, чтобы определить коэффициенты А B, C и D:

$[begin{Bmatrix}{Acdot 0 +Bcdot 0 + Ccdot2 + 1 = 0}\{Acdot 2 +Bcdot 2 + Ccdot2 + 1 = 0}\{Acdot 0 +Bcdot 2 + Ccdot0 + 1 = 0}]$

$[begin{Bmatrix}{ 0 +0 + 2C + 1 = 0}\{2A +2B + 2C+ 1 = 0}\{ 0 +2B + 0 + 1 = 0}]$

Получаем: $B = -frac{1}{2}$ , $C = -frac{1}{2}$ , $A = frac{1}{2}$

Уравнение плоскости B₁D₁C будет $frac{1}{2}x -frac{1}{2}y - frac{1}{2}z+ 1 = 0$

Домножим на 2, чтобы избавиться от дробей

Получается, что у первого уравнения . Но если плоскости параллельны, а они у нас параллельны, их уравнения имеют одинаковые коэффициенты А, В, и С, но разные D. Ищем Для этого подставляем в уравнение плоскости B₁D₁C вместо D=1 , будет

, а вместо x, y, z — координаты точки, например, A₁( 2; 0; 2 ), принадлежащей плоскости A₁BD. Получим

Получается, что

Подставляем в формулу для определения расстояния между параллельными плоскостями

$[rho = frac{left |{D_1 -D_2 }right |}{sqrt{A^2 + B^2 + C^2}}]$

$[rho = frac{left |{2-0 }right |}{sqrt{1^2 + (-1)^2 + (-1)^2}} = frac{2}{sqrt3} = frac{2sqrt3}{3}]$

Ответ: $frac{2sqrt3}{3}$

Задача 3→

Источник

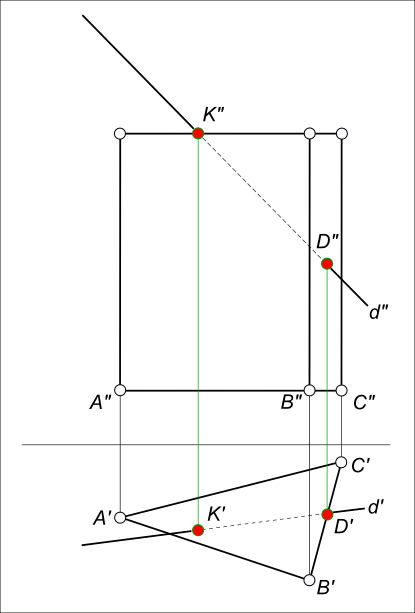
Пересечение прямой с призмой

Построить пересечение прямой с призмой: d ∩ ABC

Пересечение прямой с призмой

Из чертежа видно что:
— ребра призмы перпендикулярны горизонтальной плоскости проекций H, на этом основании боковые грани призмы ABC занимают проецирующее положение к H;
— основания призмы проецируются на фронтальную плоскость проекции V в прямые линии, на этом основании основания призмы ABC занимают проецирующее положение к V.

Используем это чтобы построить пересечение прямой с призмой:
— пересечение боковой грани призмы BC с прямой d = D` и затем по линии связи D»;
— пересечение верхнего основания призмы с прямой d = K» и затем по линии связи K`.

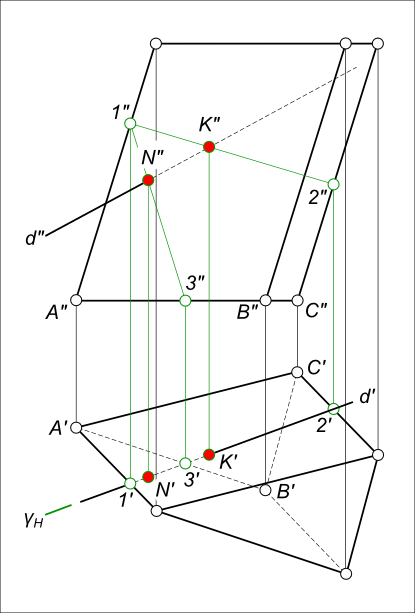
Пересечение прямой с призмой: d ∩ ABC

Пересечение прямой с призмой

Здесь прямая d и призма ABC занимают общее положение, поэтому искать точки пересечения будем, применяя алгоритм пересечения прямой с плоскостью:

— Заключаем прямую d в вспомогательную горизонтально-проецирующую плоскость γ;
— Находим точки пересечения этой плоскости с боковыми ребрами призмы A, C и с ребром основания призмы AB — точки 1, 2 и 3 соответственно:
— γ_H ∩ ребро A` = 1` ⇒ 1″;
— γ_H ∩ ребро C` = 2` ⇒ 2″;
— γ_H ∩ ребро A`B` = 3` ⇒ 3″;
— Соединив полученные точки прямыми линиями, находим их точки пересечения с прямой d и в то же время с гранями призмы:
— 1″-2″ ∩ d» = K» ⇒ K`;
— 1″-3″ ∩ d» = N» ⇒ N`.

Определение видимости для горизонтальной плоскости проекций производим с помощью конкурирующих точек:
— в точке 1` имеет место пересечение ребра A` и прямой d`, перемещаясь вверх по линии связи точки 1 находим, что соответствующая ей точка прямой d» находится ниже соответствующей ей точка ребра A», а это означает что на горизонтальной плоскости проекций видима точка принадлежащая ребру A`;
— в точке 2` имеет место пересечение ребра C` и прямой d`, перемещаясь вверх по линии связи точки 2 находим, что соответствующая ей точка прямой d» находится выше соответствующей ей точка ребра C», а это означает что на горизонтальной плоскости проекций видима точка принадлежащая прямой d`

Определение видимости для фронтальной плоскости проекций производим аналогично.

Источник